1 Introduction

In recent years, mobile application development is swiftly expanding because users prefer to continue their social, entertainment, and business activities while on the go. Mobile-to-mobile (M2M) communication is widely employed in inter-vehicular communications, intelligent highway applications and mobile ad-hoc applications [9]. Due to the increased bandwidth of wireless networks and improved processing power of mobile devices, transmission of video over M2M communication have received much attention [5]. However, reliable video communication over M2M communication is an important challenging task. Due to both the transmitter and receiver are in motion, packet loss and link breaks occur more frequently. The classical Rayleigh, Rician, and Nakagami fading channels are not applicable to M2M video communications. Experimental results and theoretical analysis demonstrate that cascaded fading channels provide an accurate statistical model for M2M communication [3, 7, 11–14].

To provide reliable M2M video communication, cooperative communication has emerged as a core component of M2M video transmission networks, since it provides high data rate communication over large geographical areas. A union bound on the bit error rate (BER) of M2M cooperative systems using amplify-and-forward (AF) relaying was derived in [6]. The end-to-end performance of a mobile-relay-based M2M system with variable-gain AF (VAF) relaying was investigated in [19]. The outage probability (OP) performance of a VAF relaying M2M system was investigated in [18]. An approximation for the average symbol error probability (SEP) was derived for fixed-gain AF relaying using moment generating function (MGF) method in [16]. Exact average bit error probability (BEP) expressions for mobile-relay-based M2M cooperative networks with incremental DF (IDF) relaying were derived in [20]. The moment generating function (MGF) approach was used to derive a lower bound on the exact average symbol error probability (SEP) for AF relaying M2M systems in [17]. Exact BEP expressions for threshold digital relaying M2M cooperative networks were derived in [15].

Another technique which can improve the error resiliency of video transmission networks is multiple-input-multiple-output (MIMO), which arises as a promising tool to enhance the reliability and capacity of wireless systems. However, MIMO brings a corresponding increase in hardware complexity since multiple radio frequency chains must be implemented. In this situation, transmit antenna selection (TAS) arises as a practical way of reducing the system complexity while achieving the full diversity order. In [2], the exact and asymptotic expressions for the symbol error rate (SER) of TAS in a two-hop AF relay network over Nakagami-m fading channels were derived. The expressions for exact, approximate, and asymptotic SER of TAS MIMO systems for several modulation schemes over η-μ fading channels were derived in [8]. In [1], a comprehensive analytical framework on the performance of MIMO multi-hop AF relay network employing TAS in the presence of randomly located interferers over Rayleigh fading channels was provided.

The M2M video transmission quality was measured by OP performance. When the OP performance is poor, the M2M video transmission will be interrupted. However, to the best knowledge of the author, the OP performance of the AF relaying M2M video transmission networks with TAS over N-Nakagami fading channels has not been investigated. In [15–20], only the three-node-based cooperation model is considered. In [1, 2, 8], the performance of TAS is investigated over Rayleigh, Nakagami-m, and η-μ fading channels. Motivated by the above discussion, in this paper, we aim to extend the three-node-based cooperation model to multiple-relay-based cooperation model for video transmission, which is more complex. Moreover, TAS is examined over N-Nakagami fading channels. The N-Nakagami fading channels are more complex than Rayleigh, Nakagami-m, and η-μ fading channels. This makes the analysis cumbersome. The main contributions are listed as follows:

  1. 1.

    We derive exact closed-form OP expressions for optimal and suboptimal TAS schemes. The derived OP expressions are in closed-form, which is very convenient to numerically and analytically handle.

  2. 2.

    Based on the derived OP expressions, the power allocation problem is formulated. The optimum transmit power distribution between the source and relay nodes can be determined by the power allocation parameter.

  3. 3.

    Through Monte Carlo simulations, the accuracy of the analytical results under different conditions is verified. Results are presented which show that the power allocation parameter has a significant effect on the OP performance.

The rest of the paper is organized as follows. The M2M video transmission networks model is presented in Section 2. Section 3 provides the exact closed-form OP expressions for optimal TAS scheme. The exact closed-form OP expressions for suboptimal TAS scheme are derived in Section 4. Section 5 conducts Monte Carlo simulations to verify the analytical results. Concluding remarks are given in Section 6.

2 The system model

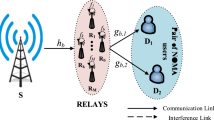
The cooperation model consists of a single mobile source (MS) node, L mobile relay (MR) nodes, and a single mobile destination (MD) node, as shown in Fig. 1. The MS is equipped with N t antennas, MD is equipped with N r antennas, whereas MR is equipped with a single antenna. The MS node can act as the transmitter. The MR nodes can act as the transmitter or receiver. The MD node can act as the receiver. Figures 2 and 3 respectively present the block diagram of the transmitter and receiver.

Fig. 1
figure 1

The system model

Full size image
Fig. 2
figure 2

The block diagram of the transmitter

Full size image
Fig. 3
figure 3

The block diagram of the receiver

Full size image

MS i denote the ith transmit antenna at MS, MD j denote the jth receive antenna at MD. h = h k , k∈{SDij, SRil, RDlj}, represent the complex channel coefficients of MS i  → MD j , MS i  → MR l , and MR l  → MD j links, respectively. In the M2M video transmission networks, h follows the N-Nakagami distribution. During the two time slots, the total energy used by the MS and MR l is E, and K is the power allocation parameter.

Assume that MS i is used to transmit the signal, during the first time slot, the received signal r SDij at MD j and MR l can be written as

$$ {r}_{\mathrm{SD}ij}=\sqrt{KE}{h}_{\mathrm{SD}ij}x+{n}_{\mathrm{SD}ij} $$
(1)
$$ {r}_{\mathrm{SR}il}=\sqrt{G_{\mathrm{SR}il}KE}{h}_{\mathrm{SR}il}x+{n}_{\mathrm{SR}il} $$
(2)

where x denotes the transmitted signal after channel coding and modulation, n SRil and n SDij are the complex Gaussian random variables with zero-mean and variance N 0/2 per dimension.

During the second time slot, the received signal at MD j is therefore given by

$$ {r}_{\mathrm{RD}lj}=\sqrt{c_{ilj}E}{h}_{\mathrm{SR}il}{h}_{\mathrm{RD}lj}x+{n}_{\mathrm{RD}lj} $$
(3)

where n RDlj is a conditionally complex Gaussian random variable.

For AF relaying, c ilj is given as [6]

$$ {c}_{ilj}=\frac{K\left(1-K\right){G}_{\mathrm{SR}il}{G}_{\mathrm{RD}lj}E/{N}_0}{1+K{G}_{\mathrm{SR}il}E/{N}_0+\left(1-K\right){G}_{\mathrm{RD}lj}{\left|{h}_{\mathrm{RD}lj}\right|}^2E/{N}_0} $$
(4)

Maximal ratio combining (MRC) and equal gain combining (EGC) have better performance compared with selection combining (SC) but they require higher receiver complexity. To simplify the receiver structure, we use the SC scheme. If SC method is used at the MD j , the output signal-to-noise ratio (SNR) can then be calculated as

$$ {\gamma}_{ij}= \max \left({\gamma}_{\mathrm{SD}ij},{\gamma}_{\mathrm{SRD}ij}\right) $$
(5)

where γ SRDij denotes the output SNR of end-to-end link via the best relay, and

$$ {\gamma}_{\mathrm{SD}ij}=\frac{K{\left|{h}_{\mathrm{SD}ij}\right|}^2E}{N_0}=K{\left|{h}_{\mathrm{SD}ij}\right|}^2\overline{\gamma} $$
(6)

It is assumed that the perfect channel state information (CSI) is available at the MS, MR, MD nodes. The MR nodes utilize their individual uplink CSI to select the best MR that yields the maximum received SNR. The best MR sends flag packets to the MD, announcing that it is ready to cooperate. The MD utilizes the downlink CSI to calculate the received SNR from the best MR. The MD orders the received SNR from N t source antennas, and then feedbacks the index of the selected source antenna that yields the maximum received SNR to MS. The best relay is selected based on the following criterion

$$ {\gamma}_{\mathrm{SR}\mathrm{D}ij}={\displaystyle \underset{1\le l\le L}{ \max }}\left(\frac{\gamma_{\mathrm{SR}il}{\gamma}_{\mathrm{RD}lj}}{1+\overline{\gamma_{\mathrm{SR}il}}+{\gamma}_{\mathrm{RD}lj}}\right) $$
(7)
$$ {\gamma}_{\mathrm{SR}il}=\frac{G_{\mathrm{SR}il}K{\left|{h}_{\mathrm{SR}il}\right|}^2E}{N_0}={G}_{\mathrm{SR}il}K{\left|{h}_{\mathrm{SR}il}\right|}^2\overline{\gamma} $$
(8)
$$ \overline{\gamma_{\mathrm{SR}il}}=\frac{G_{\mathrm{SR}il}KE}{N_0}={G}_{\mathrm{SR}il}K\overline{\gamma} $$
(9)
$$ {\gamma}_{\mathrm{RD}lj}=\frac{\left(1-K\right){G}_{\mathrm{RD}lj}{\left|{h}_{\mathrm{RD}lj}\right|}^2E}{N_0}=\left(1-K\right){G}_{\mathrm{RD}lj}{\left|{h}_{\mathrm{RD}lj}\right|}^2\overline{\gamma} $$
(10)

Here, we adopt the method in [4] to obtain an approximate γ SRDij . In this method, we replace γ RDlj in the denominator by its expectation, and approximate γ SRDij as

$$ {\gamma}_{\mathrm{SR}\mathrm{DA}ij}={\displaystyle \underset{1\le l\le L}{ \max }}\left(\frac{\gamma_{\mathrm{SR}il}{\gamma}_{\mathrm{RD}lj}}{1+\overline{\gamma_{\mathrm{SR}il}}+\overline{\gamma_{\mathrm{RD}lj}}}\right) $$
(11)
$$ \overline{\gamma_{\mathrm{RD}lj}}=\frac{\left(1-K\right){G}_{\mathrm{RD}lj}E}{N_0}=\left(1-K\right){G}_{\mathrm{RD}lj}\overline{\gamma} $$
(12)

The output SNR given in (5) can be given as

$$ {\gamma}_{ij}= \max \left({\gamma}_{\mathrm{SD}ij},{\gamma}_{\mathrm{SRDA}ij}\right) $$
(13)

Using SC method for N r antennas at the MD, the output SNR can then be calculated as

$$ {\gamma}_{{\mathrm{SC}}_i}={\displaystyle \underset{1\le j\le {N}_{\mathrm{r}}}{ \max }}\left({\gamma}_{ij}\right) $$
(14)

The optimal TAS scheme should select the transmit antenna w that maximizes the output SNR for N r antennas at the MD, namely

$$ w={\displaystyle \underset{1\le i\le {N}_{\mathrm{t}}}{ \max }}\left({\gamma}_{{\mathrm{SC}}_i}\right)={\displaystyle \underset{1\le i\le {N}_{\mathrm{t}},1\le j\le {N}_{\mathrm{r}}}{ \max }}\left({\gamma}_{ij}\right) $$
(15)

The suboptimal TAS scheme should select the transmit antenna that only maximizes the instantaneous SNR of the direct link MS i  → MD j , namely

$$ k={\displaystyle \underset{1\le i\le {N}_{\mathrm{t}},1\le j\le {N}_{\mathrm{r}}}{ \max }}\left({\gamma}_{\mathrm{SD}ij}\right) $$
(16)

3 The OP of optimal TAS scheme

The OP of optimal TAS scheme can be expressed as

$$ \begin{array}{l}{F}_{\mathrm{optimal}}= \Pr \left({\displaystyle \underset{1\le i\le {N}_{\mathrm{t}},1\le j\le {N}_{\mathrm{r}}}{ \max }}\left({\gamma}_{ij}\right)<{\gamma}_{\mathrm{t}\mathrm{h}}\right)\\ {}\begin{array}{cc}\hfill \hfill & \hfill =\hfill \end{array}{\left( \Pr \left({\gamma}_{\mathrm{SD}}<{\gamma}_{\mathrm{t}\mathrm{h}}\right) \Pr \left({\gamma}_{\mathrm{SRDA}}<{\gamma}_{\mathrm{t}\mathrm{h}}\right)\right)}^{N_{\mathrm{t}}\times {N}_{\mathrm{r}}}\\ {}\begin{array}{cc}\hfill \hfill & \hfill =\hfill \end{array}{\left({G}_1{G}_2\right)}^{N_{\mathrm{t}}\times {N}_{\mathrm{r}}}\end{array} $$
(17)

where γ th is a given threshold for correct detection at the MD.

Next, the G 1 is evaluated.

$$ \begin{array}{l}{G}_1= \Pr \left({\gamma}_{\mathrm{SD}}<{\gamma}_{\mathrm{th}}\right)\\ {}=\frac{1}{{\displaystyle \prod_{t=1}^N\varGamma \left({m}_t\right)}}{G}_{1,N+1}^{N,1}\left[\frac{\gamma_{\mathrm{th}}}{\overline{\gamma_{\mathrm{SD}}}}{\displaystyle \prod_{t=1}^N\frac{m_t}{\varOmega_t}}\left|{}_{m_1,....,{m}_N,0}^1\right.\right]\end{array} $$
(18)
$$ \overline{\gamma_{\mathrm{SD}}}=K\overline{\gamma} $$
(19)

where G[·] is Meijer’s G-function, N is the number of random variables, m is the fading coefficient and Ω is a scaling factor [7].

Next, the G 2 is evaluated.

$$ \begin{array}{l}{G}_2= \Pr \left({\gamma}_{\mathrm{SRDA}}<{\gamma}_{\mathrm{th}}\right)\\ {}={\left(\frac{1}{{\displaystyle \prod_{t=1}^N\varGamma \left({m}_t\right)}{\displaystyle \prod_{tt=1}^N\varGamma \left({m}_{tt}\right)}}{G}_{1,2N+1}^{2N,1}\left[\frac{\gamma_{\mathrm{th}}}{\overline{\chi}}{\displaystyle \prod_{t=1}^N\frac{m_t}{\varOmega_t}}{\displaystyle \prod_{tt=1}^N\frac{m_{tt}}{\varOmega_{tt}}}\left|{}_{m_1,....,{m}_{2N},0}^1\right.\right]\right)}^L\end{array} $$
(20)
$$ \overline{\chi}=\frac{\overline{\gamma_{\mathrm{SR}}}\overline{\gamma_{\mathrm{RD}}}}{1+\overline{\gamma_{\mathrm{SR}}}+\overline{\gamma_{\mathrm{RD}}}} $$
(21)
$$ \overline{\gamma_{\mathrm{SR}}}=K{G}_{\mathrm{SR}}\overline{\gamma} $$
(22)
$$ \overline{\gamma_{\mathrm{RD}}}=\left(1-K\right){G}_{\mathrm{RD}}\overline{\gamma} $$
(23)

4 The OP of suboptimal TAS scheme

For the suboptimal TAS scheme, the output SNR at MD can then be calculated as

$$ {\gamma}_{\mathrm{SC}}= \max \left({\gamma}_{\mathrm{SD}k},{\gamma}_{\mathrm{up}k}\right) $$
(24)

The CDF of γ SDk can be given as

$$ \begin{array}{l}{F}_{\gamma_{\mathrm{SD}k}}(r)= \Pr \left({\displaystyle \underset{1\le i\le {N}_{\mathrm{t}},1\le j\le {N}_{\mathrm{r}}}{ \max }}\left({\gamma}_{\mathrm{SD}ij}\right)<r\right)\\ {}={\left(\frac{1}{{\displaystyle \prod_{t=1}^N\varGamma \left({m}_t\right)}}{G}_{1,N+1}^{N,1}\left[\frac{r}{\overline{\gamma_{\mathrm{SD}}}}{\displaystyle \prod_{t=1}^N\frac{m_t}{\varOmega_t}}\left|{}_{m_1,....,{m}_N,0}^1\right.\right]\right)}^{N_{\mathrm{t}}\times {N}_{\mathrm{r}}}\end{array} $$
(25)

The CDF of γ upk can be given as

$$ {F}_{\gamma_{\mathrm{up}k}}(r)={\left(\frac{1}{{\displaystyle \prod_{t=1}^N\varGamma \left({m}_t\right)}{\displaystyle \prod_{tt=1}^N\varGamma \left({m}_{tt}\right)}}{G}_{1,2N+1}^{2N,1}\left[\frac{r}{\overline{\chi}}{\displaystyle \prod_{t=1}^N\frac{m_t}{\varOmega_t}}{\displaystyle \prod_{tt=1}^N\frac{m_{tt}}{\varOmega_{tt}}}\left|{}_{m_1,....,{m}_{2N},0}^1\right.\right]\right)}^L $$
(26)

The OP of suboptimal TAS scheme can be expressed as

$$ \begin{array}{l}{F}_{\mathrm{suboptimal}}={\left(\frac{1}{{\displaystyle \prod_{d=1}^N\varGamma \left({m}_d\right)}}{G}_{1,N+1}^{N,1}\left[\frac{\gamma_{\mathrm{t}\mathrm{h}}}{\overline{\gamma_{\mathrm{SD}}}}{\displaystyle \prod_{d=1}^N\frac{m_d}{\varOmega_d}}\left|{}_{m_1,....,{m}_N,0}^1\right.\right]\right)}^{N_{\mathrm{t}}\times {N}_{\mathrm{r}}}\times \\ {}{\left(\frac{1}{{\displaystyle \prod_{t=1}^N\varGamma \left({m}_t\right)}{\displaystyle \prod_{tt=1}^N\varGamma \left({m}_{tt}\right)}}{G}_{1,2N+1}^{2N,1}\left[\frac{\gamma_{\mathrm{t}\mathrm{h}}}{\overline{\chi}}{\displaystyle \prod_{t=1}^N\frac{m_t}{\varOmega_t}}{\displaystyle \prod_{tt=1}^N\frac{m_{tt}}{\varOmega_{tt}}}\left|{}_{m_1,....,{m}_{2N},0}^1\right.\right]\right)}^L\end{array} $$
(27)

5 Numerical results

In this section, we present Monte-Carlo simulations to confirm the derived analytical results. The total energy is E = 1. To indicate the location of MR with respect to the MS and MD, the relative geometrical gain μ (in decibels) is defined [10].

Figures 4 and 5 present the OP performance of optimal TAS scheme and suboptimal TAS scheme, respectively. The simulation parameters are N = 2, m = 1, K = 0.5, N t = 1, 2, 3, L = 2, N r = 2, μ = 0 dB. The given threshold is γ th = 5 dB. From Figs. 4 and 5, we can find that the analytical results match perfectly with the simulations. As expected, the OP is improved as the number of transmit antennas increased. For example, using optimal TAS scheme, SNR = 12 dB, when N t = 1, the OP is 2.8 × 10−2, N t = 2, the OP is 7.8 × 10−4, N t = 3, the OP is 2.2 × 10−5. With N t fixed, an increase in the SNR decreases the OP.

Fig. 4
figure 4

The OP performance of optimal TAS scheme

Full size image
Fig. 5
figure 5

The OP performance of suboptimal TAS scheme

Full size image

In Fig. 6, we compare the theoretical OP performance of optimal and suboptimal TAS schemes by varying the number of antennas N t. The simulation parameters are N = 2, m = 2,K = 0.5,μ = 0 dB, N t = 2, 3, L = 2, N r = 2. The given threshold is γ th = 5 dB. To avoid clutter, we have not plotted the simulation based results. In all cases, as expected, when N t is fixed, optimal TAS scheme has a better OP performance in all SNR regimes. As predicted by our analysis, the performance gap between two schemes decreases when N t is increased. The OP performance gap between optimal TAS scheme with N t = 2 and suboptimal TAS scheme with N t = 3 is negligible.

Fig. 6
figure 6

The OP performance comparison of two TAS schemes

Full size image

For optimization of the power allocation, we consider the OP as the objective function. The OP should be minimized with respect to the power-allocation parameter K. Figure 7 presents the effect of the power-allocation parameter K on the OP performance with optimal TAS scheme. The simulation parameters are N = 2, m = 2, μ = 0 dB, N t = 2, L = 2, N r = 2. The given threshold is γ th = 5 dB. Simulation results show that the OP performance is improved with the SNR increased. For example, when K = 0.7, the OP is 3.1 × 10−1 with SNR = 5 dB, 5.1 × 10−3 with SNR = 10 dB, 1.7 × 10−6 with SNR = 15 dB. When SNR = 5 dB, the optimum value of K is 0. 99; SNR = 10 dB, the optimum value of K is 0.79; SNR = 15 dB, the optimum value of K is 0. 70. This indicates that the equal power allocation (EPA) scheme is not the best scheme.

Fig. 7
figure 7

The effect of the power-allocation parameter K on the OP performance

Full size image

Unfortunately, an analytical solution for power allocation values in the general case is very difficult. We use Golden-Section search method to solve this optimization problem. The optimum power allocation (OPA) values can be obtained a priori for given values of operating SNR and propagation parameters. The OPA values can be stored for use as a lookup table in practical implementation.

In Table 1, we present optimum values of K with the relative geometrical gain μ. simulation parameters are N = 2,m = 2, μ = 5 dB, 0 dB,-5 dB, N t = 2, L = 2, and the given threshold is γ th = 5 dB. For example, when μ = 5 dB, the SNR is low, nearly all the power should be used by MS. As the SNR increased, the optimum values of K are reduced, and more than 50 % of the power should be used by MS.

Table 1 OPA parameters K
Full size table

6 Conclusions

The exact closed-form OP expressions for the AF relaying M2M video transmission networks with two TAS schemes are derived in this paper. The simulation results show that the power-allocation parameter K has an important influence on the OP performance. Expressions were derived which can be used to evaluate the OP performance of vehicular communication systems employed in inter-vehicular, intelligent highway and mobile ad-hoc video transmission applications.