Simulation of Boriding Kinetics of AISI D2 Steel using Two Different Approaches

Diffusion of boron in FeB and Fe₂B layers under solid boriding of steel AISI D2 (the Russian counterpart is Kh12MF) is simulated. Two approaches are used to assess the diffusion coefficients in solid-phase boriding, i.e., the concept of the mean value of diffusion coefficient in the FeB – Fe₂B system and consideration of the growth kinetics of each of the two boride layers with the use of a system of conventional differential equations describing the partial chemical reactions by a parabolic law (the Dybkov method). The activation energies of boron diffusion in the FeB and Fe₂B layers of steel AISI D2 are computed. The condition of extreme boriding is used to verify the two approaches experimentally. Comparative analysis of the computed and published data shows their good agreement.

INTRODUCTION

Boriding is a thermochemical treatment involving diffusion of atomic boron from a boron-containing environment [1]. As a rule, boriding is conducted at 800 – 1500°C for 0.5 – 10 h. In accordance with the binary Fe – B phase diagram, hard wear- and corrosion-resistant boride layers form on the surface of iron alloys [2,3,4,5]. Various methods of boriding such as gas [6, 7], liquid [8], paste [9], powder-pack [10], fluidized-bed [11], plasma-assisted [12], and plasma paste [13] ones are known today.

The most frequently used method is solid-phase boriding from powders due to its engineering and economic advantages over the other methods [14]. Two different approaches are used to simulate the growth kinetics of single-phase (Fe₂B) and double-phase (FeB and Fe₂B) boride layers on cast irons [15, 16], armco iron [6, 9, 17] and steels [10, 18,19,20,21,22,23,24,25] in order to choose the thickness of the boride layers optimum from the standpoint of applications.

The aim of the present work was to simulate boron diffusion in solid-phase boriding of steel AISI D2 with the help of the two approaches and to assess their reliability.

METHODS OF SIMULATION

To determine the diffusion coefficients of boron in FeB in Fe₂B layers forming on steel AISI D2 (the Russian counterpart is Kh12MF) in the temperature range of 1223 – 1273 K, we used two approaches and the experimental data base of [26]. The first approach was based on the concept of the mean diffusion coefficient (the kinetic approach) [27]. In the second approach knows as the Dybkov method [28] we analyzed the chemical reactions occurring in solid-phase boriding of AISI D2 from powder mixtures. The simulation by this method gave us computed values of the activation energy of boron diffusion in steel AISI D2, which were compared to the reported data and to the experimental results.

Kinetic Approach

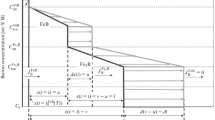
This approach based on the mean diffusion coefficient stipulates a linear concentration profile in each boride layer (FeB or Fe₂B) (Fig. 1). Variable u (t ) describes the position of the FeB/Fe2B interface or the thickness of the FeB layer and variable v (t ) describes the position of the Fe₂B/substrate interface or the total thickness of the boride layer. The solubility of boron in the substrate is very low (C₀ = 35 × 10 ^–4 wt.% B) [32]. The thickness u of the FeB layer is described by the equation

$$ u(t)={k}_1{\left[t-{t}_0^{\mathrm{FeB}}(T)\right]}^{0.5}, $$

(1)

Fig. 1.

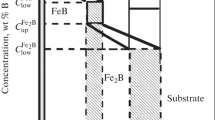
Profile of boron content in a FeB + Fe₂B double layer: ${C}_{\mathrm{up}}^{\mathrm{FeB}}=16.40\kern0.5em \mathrm{wt}.\%\mathrm{B}\ \mathrm{and}\ {C}_{\mathrm{low}}^{\mathrm{FeB}}=16.23\kern0.5em \mathrm{wt}.\%\mathrm{B}$are the maximum and minimum boron concentrations in the FeB layer, respectively; ${C}_{\mathrm{up}}^{{\mathrm{Fe}}_2\mathrm{B}}=9\kern0.5em \mathrm{wt}.\%{C}_{\mathrm{low}}^{{\mathrm{Fe}}_2\mathrm{B}}=8.83\kern0.5em \mathrm{wt}.\%\mathrm{B}$ are the maximum and minimum boron concentrations in the Fe₂B layer, respectively; C_ads is the concentration of the adsorbed boron [31].

where k₁is the constant of parabolic growth on the FeB/Fe₂B interface for the incubation period of nucleation of the boride ${t}_0^{\mathrm{FeB}}(T).$

The thickness v of the layer of FeB + Fe₂B is determined by the formula

$$ v(t)={k}_2{\left[t-{t}_0^{{\mathrm{Fe}}_2\mathrm{B}}(T)\right]}^{0.5}, $$

(2)

where k₂ is the constant of parabolic growth on the Fe₂B/substrate interface for the incubation period of nucleation of the boride ${t}_0^{{\mathrm{Fe}}_2\mathrm{B}}(T).$

The thickness l of the layer of Fe₂B is determined by the formula

$$ l(t)={k}_2{\left[t-{t}_0^{{\mathrm{Fe}}_2\mathrm{B}}(T)\right]}^{0.5}-{k}_1{\left[t-{t}_0^{\mathrm{Fe}\mathrm{B}}(T)\right]}^{0.5}. $$

(3)

Equations (1) and (3) can be transformed mathematically into

$$ u(t)={k}_1^{\prime}\sqrt{t}, $$

(4)

$$ l(t)={k}_2^{\prime}\sqrt{t}, $$

(5)

where u (t ) and v (t ) are the thicknesses of the FeB and Fe₂B layers (for the incubation period of nucleation of the borides $\left.{t}_0^{\mathrm{i}}=0\right)$and${k}_2^{\prime }$ and ${k}_2^{\prime }$ are new constants of their parabolic growth, respectively.

The mean value of the diffusion coefficient D of the dissolved component in the single-phase layer is determined from the equation for the single-phase system based on the second Fick’s law with non-constant coefficient [27]

$$ D=-\frac{1}{2t}\left(\frac{\mathrm{d}x}{\mathrm{d}C}\right)\underset{0}{\overset{C}{\int }}x\mathrm{d}C, $$

(6)

where D is the diffusion coefficient of the dissolved component, dx/dC is the inverse of the derivative of the concentration profile of the dissolved component C (x, t ) with respect to the diffusion path in this phase. Equation (6) may be generalized to a system of n phases. Then it is transformed into an expression relating the mean value of the diffusion coefficient D_ijof the dissolved substance in the ith phase (i = 1, 2,..., n ) with parameters γ_ij, i.e.,

$$ {D}_i=\frac{\varDelta {x}_i\left(\sum \limits_{j=1}^n{g}_{ij}\varDelta {x}_j\right)}{2 t\varDelta {c}_i}, $$

(7)

where ∆x_i is the thickness of the layer of the ith phase dependent on the constant of parabolic growth ${k}_i^{\prime }.$ The value of γ_ij is determined from the formula

$$ {\upgamma}_{ij}=\left[\begin{array}{c}{\overline{C}}_i\\ {}\frac{1}{4}\left(3{\overline{C}}_i+{C}_i^{(2)}\right)\\ {}{\overline{C}}_j\end{array}\right]{\displaystyle \begin{array}{l}j\prec i\\ {}j=i;\\ {}j\succ i\end{array}} $$

(8)

where ${\overline{C}}_i$is the mean value of the concentration of the dissolved component in the ith phase, i = (1, 2, ..., n ), and ${C}_i^{(1)}$ and ${C}_i^{(2)}$ are the maximum and minimum concentration of the dissolved component in the ith phase, respectively.

As an alternative, the author of [29] suggests the method of Boltzmann–Matano for obtaining a relation similar to (7) and suitable for a gas/solid system. The Matano method with the Matano plane enters the problem of interdiffusion and is inapplicable for describing nitriding. However, the final result of [29] is correct. The author of [29] assesses the diffusion coefficients on nitrogen in the iron nitrides ε and γ^′) in the process of gas nitriding of pure iron by comparing the results of his computations to the results of the diffusion model suggested in [30].

In the present work, we used the first approach (the method of the mean diffusion coefficient) for assessing the coefficients of boron diffusion in the FeB and Fe₂B layers formed on the surface of steel AISI D2. Consequently, Eq. (7) may be transformed for a diffusion zone with two phases (FeB and Fe₂B) in the following way:

$$ {D}_{\mathrm{B}}^{\mathrm{FeB}}=\frac{k_1^{\prime}\left({\upgamma}_{11}{k}_1^{\prime }+{\upgamma}_{12}{k}_2^{\prime}\right)}{2\left({C}_{\mathrm{up}}^{\mathrm{FeB}}-{C}_{\mathrm{low}}^{\mathrm{FeB}}\right)}, $$

(9)

$$ {D}_{\mathrm{B}}^{{\mathrm{Fe}}_2\mathrm{B}}=\frac{k_2^{\prime}\left({\upgamma}_{21}{k}_1^{\prime }+{\upgamma}_{22}{k}_2^{\prime}\right)}{2\left({C}_{\mathrm{up}}^{{\mathrm{Fe}}_2\mathrm{B}}-{C}_{\mathrm{low}}^{{\mathrm{Fe}}_2\mathrm{B}}\right)}, $$

(10)

where

$$ {\displaystyle \begin{array}{l}{\overline{c}}_{\mathrm{Fe}\mathrm{B}}=0.5\left({C}_{\mathrm{up}}^{\mathrm{Fe}\mathrm{B}}+{C}_{\mathrm{low}}^{\mathrm{Fe}\mathrm{B}}\right);\\ {}{\overline{c}}_{{\mathrm{Fe}}_2\mathrm{B}}=0.5\left({C}_{\mathrm{up}}^{{\mathrm{Fe}}_2\mathrm{B}}+{C}_{\mathrm{low}}^{{\mathrm{Fe}}_2\mathrm{B}}\right);\\ {}{\upgamma}_{11}=\frac{3{\overline{c}}_{\mathrm{Fe}\mathrm{B}}+{c}_{\mathrm{low}}^{\mathrm{Fe}\mathrm{B}}}{4}=16.2934;\\ {}{\upgamma}_{22}=\frac{3{\overline{c}}_{{\mathrm{Fe}}_2\mathrm{B}}+{c}_{\mathrm{low}}^{{\mathrm{Fe}}_2\mathrm{B}}}{4}=8.9150\\ {}{\upgamma}_{12}={\overline{c}}_{{\mathrm{Fe}}_2\mathrm{B}}=8.9150;\kern1em {\upgamma}_{21}={\overline{c}}_{{\mathrm{Fe}}_2\mathrm{B}}=8.9150.\end{array}} $$

The dependence of the thickness v of the total FeB + Fe₂B boride layer on the time is described by the equation

$$ v=\left[1+\upeta (T)\right]\sqrt{\frac{2{D}_{\mathrm{B}}^{\mathrm{FeB}}\left({C}_{\mathrm{up}}^{\mathrm{FeB}}-{C}_{\mathrm{low}}^{\mathrm{FeB}}\right)}{\upeta (T)\left[{\upgamma}_{11}\upeta (T)+{\upgamma}_{12}\right]}t.} $$

(11)

The ratio of the thicknesses of the FeB and Fe₂B layers η is determined by the formula

$\frac{-\left({\upgamma}_{12}-{\upgamma}_{21}\frac{\begin{array}{l}\eta =u(t)/l(t)=\\ {}{D}_{\mathrm{B}}^{\mathrm{Fe}\mathrm{B}}\left({C}_{\mathrm{up}}^{\mathrm{Fe}\mathrm{B}}-{C}_{\mathrm{low}}^{\mathrm{Fe}\mathrm{B}}\right)\end{array}}{D_{\mathrm{B}}^{{\mathrm{Fe}}_2\mathrm{B}}\left({C}_{\mathrm{up}}^{{\mathrm{Fe}}_2\mathrm{B}}-{C}_{\mathrm{low}}^{{\mathrm{Fe}}_2\mathrm{B}}\right)}\right)+\sqrt{\varDelta }}{2{\upgamma}_{11}}.$Z (11a)

It can be seen that parameter η depends on the temperature. The term ∆ is the discriminant of the quadratic equation

$$ {\displaystyle \begin{array}{l}\varDelta ={\left({\upgamma}_{12}-{\upgamma}_{21}\frac{D_{\mathrm{B}}^{\mathrm{Fe}\mathrm{B}}\left({C}_{\mathrm{up}}^{\mathrm{Fe}\mathrm{B}}-{C}_{\mathrm{low}}^{\mathrm{Fe}\mathrm{B}}\right)}{D_{\mathrm{B}}^{{\mathrm{Fe}}_2\mathrm{B}}\left({C}_{\mathrm{up}}^{{\mathrm{Fe}}_2\mathrm{B}}-{C}_{\mathrm{low}}^{{\mathrm{Fe}}_2\mathrm{B}}\right)}\right)}^2+\\ {}\kern2em 4{\upgamma}_{11}{\upgamma}_{22}\frac{D_{\mathrm{B}}^{\mathrm{Fe}\mathrm{B}}\left({C}_{\mathrm{up}}^{\mathrm{Fe}\mathrm{B}}-{C}_{\mathrm{low}}^{\mathrm{Fe}\mathrm{B}}\right)}{D_{\mathrm{B}}^{{\mathrm{Fe}}_2\mathrm{B}}\left({C}_{\mathrm{up}}^{{\mathrm{Fe}}_2\mathrm{B}}-{C}_{\mathrm{low}}^{{\mathrm{Fe}}_2\mathrm{B}}\right)}.\end{array}} $$

(11b)

with positive solution.

Approach Based on the Dybkov Method

An alternative diffusion model suggested by Dybkov [28] was used to study the growth kinetics of boride layers (FeB and Fe₂B) on steel AISI D2. This approach employs a parabolic law of growth of each boride layer. The approach is based on the partial chemical reactions occurring on the two forming interfaces. The thickness of the layer varies as a result of these chemical reactions. The growth kinetics of the FeB and Fe₂B boride layers may be described by a system of ordinary differential equations used to compute the variation of the thickness of each of the layers during the boriding process with time, i.e.,

$$ \frac{\mathrm{d}u(t)}{\mathrm{d}t}=\frac{k_{\mathrm{Fe}\mathrm{B}}}{u(t)}-\frac{rg}{p}-\frac{k_{{\mathrm{Fe}}_2\mathrm{B}}}{l(t)}; $$

(12)

$$ \frac{\mathrm{d}\mathrm{l}(t)}{\mathrm{d}t}=\frac{k_{{\mathrm{Fe}}_2\mathrm{B}}}{l(t)}-\frac{q}{sg}\frac{k_{\mathrm{Fe}\mathrm{B}}}{u(t)}, $$

(13)

where u (t ) and l (t ) are the thicknesses of the FeB and Fe₂B layers, respectively; k_FeB is the growth constant of phase FeB, k_Fe2B is the growth constant of phase Fe₂B; g = 0.60 is the ratio of the molar volumes of phases FeB and Fe₂B; p = q = r = 1, s = 2 (as obtained from the stoichiometric coefficients for phases FeB and Fe₂B) [28]. Equations (12) and (13) may be transformed into

$$ \frac{\mathrm{d}u(t)}{\mathrm{d}t}=\frac{k_{\mathrm{Fe}\mathrm{B}}}{u(t)}-0.6\frac{k_{{\mathrm{Fe}}_2\mathrm{B}}}{l(t)}; $$

(14)

$$ \frac{\mathrm{d}\mathrm{l}(t)}{\mathrm{d}t}=\frac{k_{{\mathrm{Fe}}_2\mathrm{B}}}{l(t)}-0.833\frac{k_{{\mathrm{Fe}}_2\mathrm{B}}}{u(t)}. $$

(15)

The two kinetic parameters k_FeB and ${k}_{{\mathrm{Fe}}_2\mathrm{B}}$ should be corrected in order to introduce the experimental data in the form of the thicknesses of the boride layers taken from [26]. This may give us the values for each growth rate constant. Substituting (4) and (5) into the respective systems of ordinary differential equations (14) and (15) and differentiating with respect to the time we obtain the following equations relating the two growth rate constants (k_FeB and${k}_{{\mathrm{Fe}}_2\mathrm{B}}$) to the constants of parabolic growth ${k}_1^{\prime }$ and ${k}_2^{\prime }$ , i.e.,

$$ {k}_{\mathrm{FeB}}={k}_1^{\prime}\left({k}_1^{\prime }+0.50{k}_2^{\prime}\right); $$

(16)

$$ {k}_{{\mathrm{Fe}}_2\mathrm{B}}={k}_2^{\prime}\left(0.833{k}_1^{\prime }+{k}_2^{\prime}\right). $$

(17)

RESULTS AND DISCUSSION

To determine the diffusion coefficients of boron in the FeB and Fe₂B layers for the two approaches, we used the experimental results of [26] obtained in the study of borided steel AISI D2 of the following chemical composition (in wt.%): 1.40 – 1.60 C, 0.30 – 0.60 Si, 0.30 – 0.60 Mn, 11.00 – 13.00 Cr, 0.70 – 1.20 Mo, 0.80 – 1.10 V, 0.030 P, 0.030 S. In [26], the solid-phase boriding of steel AISI D2 was conducted at 1223 – 1253 K for 3 – 10 h, which yielded double FeB – Fe₂B layers. The source of boron in these experiments was B₄C boron carbide. To provide reproducibility of the measurements of the thickness of boride layers in different cross sections of the specimens, the number of the measurements was 80. Computed values of diffusion coefficients of boron in FeB and Fe₂B layers are required for predicting the thickness of boride layers under the specified boriding conditions.We used the experimental results of [26] presented in Table 1 to determine the values of ${k}_1^{\prime }$ and ${k}_2^{\prime }.$Constants ${k}_1^{\prime }$ and ${k}_2^{\prime }$ were determined from the slopes of the straight lines describing the dependences u₂ (t ) and v₂ (t ) according to equations (1) and (2) [26]. The incubation time ${t}_{\mathrm{o}}^{\mathrm{i}}$ of formation of each of the borides was determined for zero thickness of the boride layer. It has been shown that the value of ${t}_{\mathrm{o}}^{\mathrm{i}}$ decreases with growth of the boriding temperature [19].

Table 1. Experimental Constants of Parabolic Growth of Interfaces and Incubation Time of Formation of Borides in Steel AISI D2 under Boriding

Figure 2 presents the variation of the thickness of the boride layers during boriding at different temperatures (experimental results). The slopes of the curves in Fig. 2 were used to determine the values of the equivalent constants of parabolic growth ${k}_1^{\prime }$ and ${k}_2^{\prime }$.

Fig. 2.

Dependence of the thickness u of FeB (u ) (a) and Fe₂B (l ) (b ) layers on steel AISI D2 on the duration of boriding t at 1223, 1253 and 1273 K.

Table 2 presents the equivalent experimental constants of parabolic growth obtained from the slopes of straight lines u (t ) and v (t ). The table also gives the values of the diffusion coefficient of boron for each boride layer and temperatures 1223 – 1273 K as computed by Eqs. (9) and (10).

Table 2. Experimental Constants of Parabolic Growth (k_i ) and Computed Mean Diffusion Coefficients of Boron (D_i ) in FeB and Fe₂B Layers

Figure 3 presents the temperature dependences of the mean diffusion coefficients of boron in the FeB and Fe₂B layers computed within the first approach for 1223 – 1273K. Using the Arrhenius relation, we obtained the following equations for the temperature dependence of the coefficients of boron diffusion in the FeB and Fe₂B layers:

$$ {D}_{\mathrm{B}}^{\mathrm{FeB}}=1.8\times {10}^{-3}\exp \left(\frac{-208.04\mathrm{kJ}/\mathrm{mole}}{RT}\right); $$

(18)

Fig. 3.

Temperature dependences of coefficients of boron diffusion in layers FeB (a) and Fe₂B (b ) on steel AISI D2 according to the Arrhenius relations.

and

$$ {D}_{\mathrm{B}}^{{\mathrm{Fe}}_2\mathrm{B}}=7.683\times {10}^{-4}\exp \left(\frac{-197.64\mathrm{kJ}/\mathrm{mole}}{RT}\right), $$

(19)

where R = 8.314 J/mole ∙ K and T is the Kelvin temperature.

In the method of mean diffusion coefficient, the activation energy of boron diffusion was determined from the slopes of the straight lines presented in Fig. 3.

The values of the activation energy of boron diffusion in the FeB and Fe₂B layers computed with the help of Eqs. (9) and (10) are equal to 208.04 and 197.46 kJ/mole respectively. For steel AISI D2 the value of the activation energy will depend on the chemical composition and on the surface morphology of the boride layer/substrate interface. The alloying elements present in the steel lower the flow of active boron due to the decrease in the rate of its diffusion. For this reason, the interface of the boride layer and the matrix becomes plane [33].

To determine the activation energy of boron diffusion in the FeB and Fe₂B layers formed on the surface of steel AISI D2 we used the second approach based on the diffusion model of Dybkov [28]. The model involves solution of the system or ordinary differential equations (14) and (15). At first, we computed the growth rate constants for layers FeB and Fe₂B using equations (16) and (17). The values of these constants are presented in Table 3.

Table 3. Growth Rate Constants for Layers FeB and Fe₂B Required for Computation by the Dybkov Model

Figure 4 presents the temperature dependences of the growth rate constants of layers FeB and Fe₂B expressed in m²/sec in accordance with the Arrhenius relation. We used the least squares method to obtain

$$ {k}_{\mathrm{FeB}}=3.849\times {10}^{-5}\exp \left(\frac{-207.84\mathrm{kJ}}{RT}\right); $$

(20)

$$ {k}_{{\mathrm{Fe}}_2\mathrm{B}}=2.635\times {10}^{-5}\exp \left(\frac{-197.04\mathrm{kJ}}{RT}\right). $$

(21)

Fig. 4.

Temperature dependences of growth rate constants for layers FeB (a) and Fe₂B (b ) according to the Arrhenius relations.

Using the straight lines given in Fig. 4 we may determine the values of the activation energy of boron diffusion in layers FeB and Fe₂B. According to the Dybkov model, these energies are 207.84 and 197.04 kJ/mole respectively. Comparative analysis has shown that the experimental values of the activation energy are comparable to the values computed by the method of the mean diffusion coefficient. Table 4 presents the activation energy of boron diffusion in borated steels determined in [13, 26, 34,35,36,37,38,39,40] and in the present study. It can be seen that the activation energy depends of different factors, i.e., the boriding method, the treatment temperature, the computation method, the chemical composition of the borided substrate, and the chemical reactions occurring in the boriding process. In the case of plasma paste boriding the activation energy spent for forming the borided layers is lower than in solid-phase boriding [10, 13, 15, 18]. We have established that the activation energy of boron diffusion in the FeB and Fe₂B layers on steel AISI D2 obtained by the two approaches are close. They may be interpreted as the amount of energy for the diffusion path of boron in preferred crystallographic direction [001] [17].

Table 4. Activation Energies of Boron Diffusion in Some Borated Steels

Both approaches have been checked experimentally for extreme boriding conditions, i.e., at 1243 K for 2, 4, and 6 h. Table 5 presents the thickness of the total boride layer determined experimentally and computed by equations (14) and (15) with the use of the Runge–Kutta method. Both approaches provide satisfactory coincidence with the experimental results.

Table 5. Experimental and Computed Values of the Thickness of Boride Layers FeB + Fe₂B Obtained at 1243 K

CONCLUSIONS

The diffusion coefficients of boron in the FeB and Fe₂B layers formed on steel AISI D2 under solid-phase boriding in the range of 1223 – 1273 K were assessed within two approaches, i.e., the method of the mean diffusion coefficient and the Dybkov model. The values of the coefficients computed by these methods for the FeB and Fe₂B layers are 208 and 197 kJ/mole, respectively. Comparison of the experimental values of the thickness of the boride layers obtained by boriding at 1243 K for 2, 4, and 6 h to the computed results has shown good coincidence.