Introduction

Among the various problems of the science of metals which interested M. M. Shteinberg during the whole of his life the nature of martensitic transformation had an important place. In the Chelyabinsk period he headed numerous researches of the influence of alloying elements, stresses, magnetic fields, aging effects, size of γ-grains and other factors on the martensitic point and on the kinetics of martensitic transformation in iron alloys.

In the early 1950s he studied the kinetics of martensitic transformation in almost carbonless iron alloys with 8, 15 and 19% Ni together with A. A. Popov at the Ural Polytechnic Institute [1]. It was one of the first works where isothermal formation of martensite in iron-nickel alloys was discovered. As the temperature was decreased, the rate of the isothermal reaction grew. However, the authors did not manage to plot the lower branch of the C-curve.

Later on, already in Chelyabinsk, Shteinberg participated in a study of the transformation of austenite in Fe – Ni alloys under the conditions of continuous cooling [2]. It was established for the first time that the γ → α transformation in such alloys could develop in two stages with different temperatures of implementation. For example, for an alloy with 15% Ni the temperatures of the upper stage were 390 – 340°C for cooling rates from 80 to 3 × 103 K/sec. Further increase of the cooling rate caused step lowering of the transition temperature to 270°C, and this temperature remained invariable upon increase in the cooling rate to the maximum tested value of 5 × 105 K/sec. The structure of the α-phase in both cases was represented by packets of lath crystals. Shteinberg termed the upper stage an isothermal martensitic transformation and the lower stage an athermal one. The succession of the structural changes upon transition from the structure of equiaxed grains of pure iron to a structure of packet martensite (or bainite) of the upper stage is described in detail in [3, 4]. The theory considered below refers to this very hightemperature stage of the γ → α transformation.

When it became known that the isothermal martensite of the Fe – Ni alloys containing 27% Ni had a structure of complexly arranged packets of lath crystals in contrast to the athermal lenticular martensite of the high-nickel alloys containing twins and forming truss-like structures of martensite crystals, Shteinberg put forward a suggestion that the nature of the autocatalytic formation of crystals of twinned and packet martensite should differ. Shteinberg’s works devoted to martensitic transformation have influenced directly the development of the theory presented below.

The aim of the present work was to analyze theoretically the kinetics of the isothermal formation of packet martensite in Fe – Ni alloys.

Results and Discussion

Isothermal Transformation in Iron-Nickel Alloys

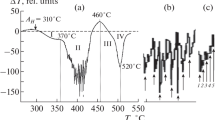
We have mentioned already that martensite in Fe – Ni alloys can form under isothermal conditions. Figure 1 presents the curves of isothermal formation of martensite in an iron alloy with 14.95% Ni (containing no more than 0.01% C) obtained in [1] and [5]. In both cases the development of the transformation was detected with the help of a Shteinberg magnetometer.

Fig. 1
figure 1

Curves of isothermal transformation ( f is the fraction of the transformation, t is the time) in a Fe – 14.95% Ni alloy at different temperatures (given at the curves): a) data of [1]; b ) data of [5].

Full size image

A typical feature of these curves is incompleteness of the reaction, which is common for martensitic transformations under isothermal conditions, though the limiting fraction of the transformation f m increases upon decrease in the temperature. It can be seen from Fig. 2 that this dependence is describable well by an equation

Fig. 2
figure 2

Dependence of – ln (1 – f m) on the temperature of transformation T for the curves presented in Fig. 1: ○) data of [1] (Fig. 1a ); ×) data of [5] (Fig. 1b ).

Full size image
$$ {f}_{\mathrm{m}}=1- \exp \left(-{a}_1\left({T}_s-T\right)\right), $$
(1)

where a 1 = 0.025, and the upper temperature boundary of the transformation T s = 405°C. This kind of dependence is known as the Koistinen–Marburger equation [6].

The incompleteness of the transformation does not allow us to describe it using the usual Avrami equation [7]

$$ f=1- \exp \left(-K{t}^n\right), $$
(2)

where f is the fraction of the transformation, t is the time, and K and n are constant factors, because at t→∞it gives f → 1. We may attempt to generalize equation (2) formally for the case of an incomplete phase transformation, i.e.,

$$ -{f}_{\mathrm{m}} \ln \left(1-\frac{f}{f_{\mathrm{m}}}\right)=K{t}^n. $$
(3)

A similar expression (at n = 1) has been used in [8], where it did not contain factor f m in front of the logarithm, though it plays a very important role because at a low f, when ln (1 – f/f m) ≈ f/f m, it provides transition to an expression

$$ f\approx K{t}^n, $$
(4)

which also follows from equation (2). Thus, it is supposed that at the initial moments the system “does not know” whether the transformation will be finished in future, since we assume that the incompleteness of the transformation is a result of the action of the formed α-phase on the kinetics of the transformation.

We take logarithms of (3)

$$ \ln \left(-{f}_{\mathrm{m}} \ln \left(1-\frac{f}{f_{\mathrm{m}}}\right)\right)= \ln K+n \ln t, $$
(5)

to obtain factors n and K by substituting experimental data for the axes \( y= \ln \left(-{f}_{\mathrm{m}} \ln \left(1-\frac{f}{f_{\mathrm{m}}}\right)\right) \) and x = ln t. Such plots are given in Fig. 3 for the experimental data of Fig. 1. It can be seen that in many cases the curves have an inflection at which the parameter n changes from 1.8 – 2.4 to 0.7 – 1.0.

Fig. 3
figure 3

Curves of isothermal transformation (see Fig. 1) plotted in double logarithmic coordinates.

Full size image

It is well known that in iron-nickel alloys containing up to 27 – 29% Ni martensite has a structure of lath crystals grouped into packets. Martensite of a similar morphology is observed in low- and medium-carbon steels. All laths within a packet have a habit close to one and the same plane (111)γ so that the packet contains crystals of six orientations of the 24 possible ones within the Kurdyumov–Sachs orientation relations [9]. Some authors report that growth in the nickel content in Fe – Ni alloys is accompanied by grouping of laths in a packet into intermediate formations. i.e., blocks, within which the laths have a single orientation [10, 11] or, according to more recent researches, two close orientations [12]. In carbon steels the tendency seems to be reverse, i.e., the blocks become smaller upon growth in the carbon content and virtually disappear at about 0.4% C [11, 13]. This may be the reason behind the fact that lath blocks have not been observed in electron microscope studies of packet martensite [9, 14–18] performed primarily for mediumcarbon steels. A similar study of carbonless alloys with 15 – 18% Ni has confirmed the presence of similarly oriented laths within a packet of blocks [19]. It seems that the special features of the substructure of a packet are connected with compensation of elastic stresses appearing upon formation of neighbor laths and their plastic relaxation during the transformation [13, 18]. Thus, packet martensite has a complex hierarchical structure. We may expect that it should influence the kinetics of the transformation.

Kinetics of Formation of Packet Martensite

The authors of [10, 11, 20], who studied the process of formation of packet martensite, report that it may develop in two ways, namely, (1) parallel laths may form directly one near another so that the packet gains thickness in a continuous front and (2) new laths may nucleate in parallel to the earlier formed ones but at some distance from them so that the packet preserves an austenite layer, which is later filled with laths too. Successive and independent nucleation of laths occurs simultaneously [10], but the stronger the block structure of the packet the more pronounced the second process [11]. Let us consider it in greater detail basing ourselves on work [21].

In the model of independent nucleation we should introduce three rates of nucleation, i.e., the rate of nucleation of independently oriented laths each of which can become a center of nucleation of a packet I p , the rate of autocatalytic nucleation of the initial laths of blocks stimulated by the formation of the first laths of a packet I b , and the rate of autocatalytic nucleation of laths inside a block under the action of the first lath of the block I l.

We will assume that a lath crystal grows to the final size virtually instantaneously and that the average volume of laths remains unchanged in the course of the transformation. Then, according to the Kolmogorov equation [7], the fraction of the transformation in an individual block is determined from the equation

$$ {f}_{\mathrm{b}}(t)=1- \exp \left(-{\displaystyle \underset{0}{\overset{t}{\int }}{I}_1{V}_1\mathrm{d}\uptau}\right)=1- \exp \left(-{I}_1{V}_1t\right), $$
(6)

where V l is the mean volume of a lath crystal.

Suppose that the initiation of a packet, i.e., the formation of its first lath has occurred at some moment of time, which will be treated as a reference mark. The appearance of the first lath stimulates the process of initiation of blocks, which is assumed to occur not instantaneously but at some nucleation rate I b . The transformed volume within a block nucleated at moment τ is equal to V b f b(t − τ). We use the Kolmogorov equation again and compute the volume fraction of the transformation inside a packet, i.e.,

$$ \begin{array}{c}\hfill {f}_{\mathrm{p}}(t)=1- \exp \left(-{\displaystyle \underset{0}{\overset{t}{\int }}{I}_{\mathrm{b}}{V}_{\mathrm{b}}{f}_{\mathrm{b}}\left(t-\uptau \right)\mathrm{d}\uptau}\right)=\hfill \\ {}\hfill 1- \exp \left(-{I}_{\mathrm{b}}{V}_{\mathrm{b}}\left(t-\frac{1}{I_1{V}_1}\left(1- \exp \left({I}_1{V}_1t\right)\right)\right)\right).\hfill \end{array} $$
(7)

Finally, the fraction of the transformation f(t) in all the initial austenite grains, and hence in the specimen, can be determined by integrating with respect to all the moments of packet initiation, i.e.,

$$ \begin{array}{c}\hfill f(t)=1- \exp \left(-{I}_{\mathrm{p}}{V}_{\mathrm{p}}\left(t-\frac{\upeta^{-\upeta} \exp \left(\upeta \right)}{I_1{V}_1}\times \right.\right.\hfill \\ {}\hfill \left.\left.{\displaystyle \underset{ \exp \left(-{I}_1{V}_1t\right)}{\overset{\upeta}{\int }} \exp \left(-x\right){x}^{\upeta -1}\mathrm{d}x}\right)\right),\hfill \end{array} $$
(8)

where η = I b V b /I l V l. Expressions (7) and (8) can be transformed into the following expressions, respectively,

$$ {f}_{\mathrm{p}}(t)\approx 1- \exp \left(-\frac{I_{\mathrm{b}}{V}_{\mathrm{b}}\times {I}_1{V}_1}{2}{t}^2\right); $$
(9a)
$$ {f}_{\mathrm{p}}(t)\approx 1- \exp \left(-\frac{I_{\mathrm{p}}{V}_{\mathrm{p}}\times {I}_{\mathrm{b}}{V}_{\mathrm{b}}\times {I}_1{V}_1}{6}{t}^3\right), $$
(9b)

at a high duration of the process

$$ {f}_{\mathrm{p}}(t)\approx 1- \exp \left(-{I}_{\mathrm{b}}{V}_{\mathrm{b}}t\right) $$
(10a)

And

$$ f(t)\approx 1- \exp \left(-{I}_{\mathrm{p}}{V}_{\mathrm{p}}t\right). $$
(10b)

If the packets do not contain blocks, expressions (7), (9a) and 10a) will describe the fraction of the transformation not in a packet but in all of the grains.

Thus, a two- or three-stage hierarchy in the structure of martensite (lath – packet or lath – block – packet) should result in an apparent transition of the kinetics of the transformation from the Avrami equation (2) with n = 2 or n = 3 to n = 1. Figure 4 presents functions (7) and (8) in double logarithmic axes. It can be seen that the inclined lines corresponding to n = 2 (n = 3) and n = 1 are their asymptotes indeed. Note that the transition from one value of n to another is rather smooth, and the value of n determined from the experimental points matching a bounded range of fractions of the transformation may be an intermediate one between the two extreme points.

Fig. 4
figure 4

Plots of functions (7) (a) and (8) (b ) (the computation was performed for η = 2/π = 0.6366 [21]).

Full size image

Allowance for Incompleteness of the Transformation

As for the second feature mentioned above, i.e., the incompleteness of the transformation at a constant temperature, it has been explained by different factors. The most known attempt to create a theory of isothermal development of martensitic reaction has been made by the authors of [22]. They based themselves on the concept of existence of prepared nuclei and presumed that two competing processes develop in the course of the transformation, namely, autocatalytic formation of new nuclei and absorption of nuclei by the formed martensite. The reaction stops when the rate of the absorption of nuclei becomes equal to the rate of their autocatalytic formation. In some works [23, 24] the theory was applied to isothermal transformation in the Fe – Ni – Mn alloys. In the domestic literature the understanding of the cause of the stop of martensitic transformation under isothermal conditions is somewhat different. It is associated with the change in the condition of the initial phase during the transformation [25–31]. Accumulation of defects in the austenite increases the force of resistance to the motion of the phase boundary, i.e., lowers the total thermodynamic stimulus of the transformation. When it becomes zero, the transformation stops, and its further development becomes possible only upon decrease in the temperature.

According to [27, 31] a complete change in the free energy ΔG tot at γ → α transformation per mole of the formed α-phase can be written as follows:

$$ \varDelta {G}_{\mathrm{tot}}=-\varDelta {G}_{\mathrm{ch}}+\varDelta {G}_s(f), $$
(11)

where ∆G ch is the difference in the chemical free energies of the γ- and α-phases. The transformation can develop if ∆G tot < 0, i.e., if ∆G ch ≥ ∆G s . Thus, the energy of the distortions ∆G s is the thermodynamic stimulus of the transformation. Let us consider the kinetics of the isothermal transformation from this standpoint [32].

The quantity ∆G s seems to involve the following terms:

  1. (1)

    the free energy spent for formation of dislocations and microtwins in the α-phase;

  2. (2)

    the energy of the field of elastic distortions in the γ-phase;

  3. (3)

    the energy of the phase boundaries;

  4. (4)

    the work spent for resisting the compressive stresses caused by the volume expansion under the conditions of simultaneous occurrence of the transformation;

  5. (5)

    the work of plastic deformation in the layers of the γ-phase enveloping the formed crystal under the action of shear stresses;

  6. (6)

    the work performed upon intersection of semi-coherent phase boundaries by dislocations of the γ-phase;

  7. (7)

    the growth in the thermodynamic stimulus caused by the decrease in the actual size of the γ-grains due to their breaking by martensite crystals (blocks, packets).

Some of these terms do not depend on the fraction of the transformation and some increase upon growth of f. Dependence ∆G s (f) can be expanded into a series with respect to f or, more exactly, with respect to \( {\displaystyle \underset{0}{\overset{f}{\int }}\frac{\mathrm{d}f}{1-f}=- \ln \left(1-f\right),} \) because the distortions are accumulated in the initial phase, the content of which is equal to (1 – f ) at every moment of time. We will limit ourselves to two terms of the expansion, i.e.,

$$ \varDelta {G}_s(f)\approx \varDelta {G}_s^0-\uplambda \mathrm{l}\mathrm{n}\left(1-f\right). $$
(12)

Then

$$ \varDelta {G}_{\mathrm{tot}}\approx \varDelta G+\varDelta {G}_s^0-\uplambda \mathrm{l}\mathrm{n}\left(1-f\right). $$
(13)

At the start of the transformation f = 0; therefore, the location of the martensitic point T s is determined by the condition

$$ \varDelta G\left({T}_s\right)=\varDelta {G}_s^0. $$
(14)

At any temperature below T s there forms a limiting content f m of α-phase so that

$$ \varDelta G(T)-\varDelta {G}_s^0=-\uplambda \mathrm{l}\mathrm{n}\left(1-{f}_{\mathrm{m}}\right). $$
(15)

Since

$$ \varDelta G-\varDelta {G}_s^0\approx \varDelta S\left({T}_s-T\right), $$
(16)

where ∆S is the difference in the entropies of the γ- and α-phases [34], we have

$$ {f}_{\mathrm{m}}=1- \exp \left(-\frac{\varDelta S}{\uplambda}\left({T}_s-T\right)\right). $$
(17)

This expression is similar to that of Koistinen–Marburger (1), which holds for many alloys in a wide temperature range. The latter circumstance is an evidence of the fact that equation (12) is valid for a wide range of f and not only for the low values.

With allowance for (13) and (15) the change in the free energy of the system in the transformation process is described by the expression

$$ \varDelta {G}_{\mathrm{tot}}=-\uplambda \mathrm{l}\mathrm{n}\frac{1-f}{1-{f}_{\mathrm{m}}}. $$
(18)

We differentiate the Avrami equation (2) with respect to time and find the rate of the transformation

$$ \frac{\mathrm{d}f}{\mathrm{d}t}=nK\left(1-f\right){t}^{n-1}. $$
(19)

This equation will be valid only in the initial stages, when the action of the accumulated martensite on the course of the reaction may be neglected.

The main feature of martensitic transformation, which also concerns the alloys with packet martensite, is the fact that a crystal grows to the final size during a time period much shorter than the time to nucleation of the next crystal [30]. In other words, the kinetics of martensitic transformation is governed by nucleation. The kinetic factor K(T) in the Avrami equation depends only on the nucleation rate I (see above), i.e.,

$$ K(T)={k}_0{I}^n. $$
(20)

Several theories are used to explain martensite nucleation [33–35], in which the dependence of the nucleation rate on ∆G has different forms. Like the authors of [36] we will use the approach where nucleation of martensite is treated as a conventional activated process with energy barrier Q described by the equation

$$ I={k}_1\frac{\varDelta {G}_{\mathrm{tot}}}{RT} \exp \left(-\frac{Q}{RT}\right), $$
(21)

where k 1 is a constant. Then, with allowance for (18), the kinetic equation (19) acquires the form

$$ -\frac{\mathrm{d}z}{z^n}={k}_0{\left({k}_1 \exp \left(-\frac{Q}{RT}\right)\times \frac{\uplambda}{RT}\right)}^nn{t}^{n-1}\mathrm{d}t, $$
(22)

where \( z= \ln \frac{1-f}{1-{f}_{\mathrm{m}}} \).After integration we find that for n ≠1

$$ \begin{array}{c}\hfill \frac{z_0}{n-1}\left({\left(\frac{z_0}{z}\right)}^{n-1}-1\right)=\frac{- \ln \left(1-{f}_{\mathrm{m}}\right)}{n-1}\times \hfill \\ {}\hfill \left({\left(1-\frac{ \ln \left(1-f\right)}{ \ln \left(1-{f}_{\mathrm{m}}\right)}\right)}^{n-1}-1\right)={k}_0{I}_0^n{t}^n,\hfill \end{array} $$
(23a)

where z 0 = − ln(1 − f m) and \( {I}_0={k}_1 \exp \left(-\frac{Q}{RT}\right)\times \frac{\varDelta G-\varDelta {G}_s^0}{RT} \) is the rate of nucleation at moment t = 0. If n = 1, the solution of (22) has another form, i.e.,

$$ {z}_0 \ln \left(\frac{z}{z_0}\right)= \ln \left(1-{f}_{\mathrm{m}}\right) \ln \left(1-\frac{ \ln \left(1-f\right)}{ \ln \left(1-{f}_{\mathrm{m}}\right)}\right)={k}_0{I}_0t. $$
(23b)

Figure 5 presents C-curves of isothermal transformation in alloy Fe – 14.95% Ni computed with the help of Eqs. (23a) and (23b) and the experimental data of [1] and [5] represented by symbols. It can be seen that the computed results agree well with the experimental data.

Fig. 5
figure 5

Experimental (the symbols) and computed [by equations (23)] (the lines) C-curves of isothermal transformation in alloy Fe – 14.95% Ni at Q = 7 kJ/mole [36]; k 0 n/1 k 1 = 3.6 × 10 – 4 sec – 1 : solid lines) at n = 2; dashed lines) for f = 0.50 and f = 0.75 at n = 1.

Full size image

Let us return to equation (17) and analyze it from the standpoint of a mechanical analogy [29, 37, 38], in accordance with which the difference in the free energies of unit volumes of the initial and forming martensite phases Δg ch = ΔG ch/V m, where V m is the gram-molecular volume, is understood as a generalized thermodynamic force acting on the interface of the phases [28]. Since stress τ performs work τγ upon a shift by γ, the “chemical” stress on the interface will be equal to

$$ \uptau =\frac{1}{\upgamma_0{V}_{\mathrm{m}}}\varDelta {G}_{\mathrm{ch}}, $$
(24)

where γ0 is the value of the shear strain due to martensitic transformation. On the other hand, the condition of delay of martensitic transformation within the mechanical analogy may be written similarly to the relation between the stress and the strain in the stage of strain hardening [39], i.e.,

$$ \uptau \hbox{-} {\uptau}_S=\varLambda {\upgamma}^{1/q}, $$
(25)

where γ is the total shear stain due to the transformation, which is determined from the equation

$$ \upgamma ={\displaystyle \underset{0}{\overset{f_{\mathrm{m}}}{\int }}\frac{\upgamma_0\mathrm{d}f}{1-f}={\upgamma}_0\left(- \ln \left(1-{f}_{\mathrm{m}}\right)\right).} $$
(26)

[Formation of a fraction df of martensite is accompanied by shear γ0 df accumulated in the initial phase; the content of the phase is (1 – f)]. Then Eq. (25) can be reduced to the form

$$ \varDelta {G}_{\mathrm{ch}}-\varDelta {G}_s^0={\uplambda}_q{\left(- \ln \left(1-{f}_{\mathrm{m}}\right)\right)}^{1/q}. $$
(27)

The limiting content of martensite, which can form at some temperature T, will be determined by the equation

$$ {f}_{\mathrm{m}}=1- \exp \left(-{\left(\frac{\varDelta {G}_{\mathrm{ch}}-\varDelta {G}_s^0}{\uplambda_{\mathrm{m}}}\right)}^q\right), $$
(28)

or, with allowance for (16), by

$$ {f}_{\mathrm{m}}=1- \exp \left(-{\left({a}_q\left({T}_s-T\right)\right)}^q\right), $$
(9)

where a q  = ΔS/λ q . This relation differs from (17) by the presence of exponent q. In fact, it has been obtained by the author of [27] for the case of (−ln(1 − f m)) ≈ f m.

We can determine the parameters of (29) by plotting an experimental dependence f m(T) in a double logarithmic scale, when it transforms into an equation of a straight line with slope ratio q, i.e.,

$$ \ln \left(- \ln \left(1-{f}_{\mathrm{m}}\right)\right)= \ln {a}_q^q+q \ln \left({T}_s-T\right). $$
(30)

We have done this for 25 steels, the experimental functions f m (T ) for which are presented in monograph [40]. The obtained values of q and a q equal to 2.2 ± 0.6 and (7.8 ± 2.3) × 10 – 3, respectively. On the other hand, it is known that the Koistinen–Marburger equation (1) corresponding to q = 1 is obeyed for many steels and alloys [41]. The authors of [42] suggest a formula similar to Eq. (29) and collate a concentration dependence for both parameters entering the formula; accordingly, parameter q for carbon steels ranges within 1.0 – 1.4, which is somewhat lower than the values obtained with the help of the data of [40].

At a low temperature deviations from (29) have been quite frequent, which is explainable by decrease in ∆S with closeness to 0 K in accordance with the third law of thermodynamics. However, we have observed a similar dependence for martensitic transformation in cobalt [43], where the change in the entropy at the transformation temperatures is insubstantial [44]. In the early stages of the transformation q is close to unity. We may assume that a possible cause of the change in q may be breakage of grains of the β-phase by martensite plates, which should result in elevation of the shear resistance in accordance with the Hall–Petch law or splitting of dislocations in the β-phase under the action of the elastic fields of martensite crystals [45]. The significance of parameter q and of the factors affecting it requires an additional study. Note that when we studied the transformation in cobalt, the temperatures of the start of the forward (β → α) and backward (α → β) martensitic transformation depended on the grain size d, as in the Hall–Petch equation [46]. This confirms the validity of the mechanical analogy: grain-boundary hardening should result in growth of \( {\uptau}_s=\frac{1}{\upgamma_0{V}_{\mathrm{m}}}\varDelta {G}_s^0 \) and a change in the temperature of the start of the transformation proportional to d –1/2.

About the Thermodynamic Stimulus of the Transformation

In the computations presented above we used the values of the thermodynamic stimulus of martensitic transformation, i.e., of the difference ∆G in the free energies of the γ- and α-phases of Fe – Ni alloys from classical work [34] obtained by generalizing all the thermodynamic data available at the moment, which have proved quite successful. However, the reported values of the total energy, energy of mixing, and free energy for each of the two phases exhibit quite high scattering largely explainable by the impossibility of making tests at low temperatures, when the establishment of an equilibrium condition requires much time, while in some concentration ranges one or the other phase may not exist at all. In the recent years it became possible to amend the values of the thermodynamic functions in the low-temperature range on the basis of computations of the total energy of the phases “from the first principles.” Such data for the Fe – Ni system based on the first-principle computations of Mirzoev and Yalalov are presented in [47]. They show that the energy of mixing of bcc solid solutions is positive and increases monotonically upon growth in the nickel concentration, whereas for disordered solid solutions it is positive at concentrations lower than about 50% Ni (Fig. 6) and negative at higher concentrations. The difference in the energies of fcc and bcc phases [47] also presented in Fig. 6 is close to the data of [34] extrapolated for 0 K. Thus, the recent methods confirm the data.

Fig. 6
figure 6

Energy of mixing of the α-phase (G α) and γ-phase (G γ) for Fe – Ni alloys, difference ∆G in the phase energies determined by computation “from the first principles” [47], and difference ∆G' in the phase energies computed using the data of [34] at 0 K.

Full size image

Let us finish the present paper by stating that the memory of M. M. Shteinberg and the gratitude to him is living in the hearts of his disciples.