Families of Stress-Strain, Relaxation, and Creep Curves Generated by a Nonlinear Model for Thixotropic Viscoelastic-Plastic Media Accounting for Structure Evolution Part 3. Creep Curves

A systematic analytical study of the mathematical properties of the previously constructed nonlinear model for shear flow of thixotropic viscoelastic-plastic media, which takes into account the mutual influence of the deformation process and structure evolution, is continued. A set of two nonlinear differential equations describing the processes of shear at a constant rate and stress relaxation is obtained. Equation set describing creep is derived; a general solution of the Cauchy problem for the set is constructed in an explicit form (the equations of the families of creep, and structuredness curves are derived). For arbitrary six material parameters and (increasing) material function that govern the model, basic properties of the families stress-strain curves at constant strain rates, stress relaxation curves and creep curves generated by the model, and the features of structuredness evolution under these types of loading are analytically studied. The dependences of these curves on time, shear rate, stress level, initial strain, and initial structuredness of the material, as well as on the material parameters and function of the model, are studied. Several indicators of the applicability of the model are found which are convenient to check with experimental data. It was examined what effects typical for viscoelastic-plastic media can be described by the model and what unusual effects (unusual properties) are generated by a change in structuredness in comparison with typical stress-strain curves, relaxation curves, and creep curves of structurally stable materials. In particular, it is proved that creep curves always increase in time and have oblique asymptote, and structuredness under constant stress is always monotonous (unlike other loading modes), but can decrease or increase depending on the relation between the stress level and initial structuredness. The same condition controls creep curves to be convex up or down: at a certain (calculated) critical load creep curves change from convexity up (under smaller loads) to convexity down, and the structuredness becomes ascending instead of descending. The analysis proved the ability of the model to describe behavior of not only liquid-like viscoelastoplastic media, but also solid-like (thickening, hardening, hardened) media: creep, relaxation, recovery, a number of typical properties of experimental relaxation curves, creep and stress-strain curves, strain rate and strain hardening, flow under constant stress and so on.

Introduction

This article is the third part of the entire large article ([1, 2] are the first and second parts) and a continuation of the study [3,4,5] devoted to the formulation of a uniaxial prototype of a nonlinear Constitutive Equation (CE) for the shear flow of thixotropic viscoelastic-plastic media, taking into account the mutual influence of deformation processes and structure evolution, and its reduction to Cauchy problem for a set of two nonlinear differential equations

$$\dot{s}={ae}^{\beta w}-{se}^{\left(\beta -\alpha \right)w},$$

(1)

$$\dot{w}=c\left[\left(1-w\left(1+bg\left(s\right)\right)\right)\right]$$

(2)

for dimensionless shear stress s(t) and structuredness degree w(t) (t > 0 is a dimensionless time). The purpose of the article is to study analytically basic properties of integral curves, phase portrait, flow curves, stress-strain curve families at constant strain rates, stress relaxation curves, and creep curves generated by the model with arbitrary Material Parameters (MPs) a, b, c, α > 0 , β ≥ 0 (see below) and Material Function (MF) g(s) , to study their dependence on loading parameters and the features of structuredness evolution under these types of loading, to elucidate the main effects that the model can or can’t describe (boundaries of its applicability area and its indicators) [6,7,8].

The description of isothermal shear deformation of materials (pastes, gels, suspensions, polymers in a highly elastic and viscous state, in the form of melts and concentrated solutions, resins, bitumens, ductile metals and alloys, etc.) is based on the nonlinear Maxwell model

$${\dot{\gamma }=\dot{\tau }/G+\tau /\eta ,}$$

(3)

where τ is a shear stress, $\dot{\gamma }=v$ is a simple shear rate (it was considered as a constant, given parameter, in [1,2,3,4]), and MPs depend on the change in the structure of the material in the process of deformation [2]; we will assume that shear modulus G and dynamic viscosity η depend on one dimensionless structural parameter w(t) : G = G(w) , η = η(w) , w(t) ∈[0;1] , w(0) = w₀ , w₀ ∈ [0;1] . As explained in more detail in [1], w(t) denotes the structuredness degree (characterizing the degree of crosslinking or the degree of crystallinity of the polymer, porosity, average grain size of polycrystalline materials, their shape and orientation, the state of grain boundaries, etc.), for example, the ratio of the concentration of supramolecular or intermolecular bonds (entanglements, hydrogen bonds, chemical crosslinks, etc.) at the current moment of time to some maximum possible value of the concentration of bonds for a given temperature. At this stage, we will characterize the current structure of the material with only one structural parameter w(t), without distinguishing between the mechanisms of influence of different elements of the supramolecular structure on viscosity (or neglecting them); for now, it will only matter that the material has a structure that is destroyed under the action of shear stress and can restore. Even such a simple approach allows us to describe a large number of observed effects [1,2,3,4,5] (provided there is a thoughtful formulation of evolution equation for w(t)).

The quantities η = (w) and G = G(w) have to be non-decreasing functions of structuredness, so we can assume these functions exponential following the traditions of kinetics:

$$\eta \left(w\right)={\eta }_{0}{e}^{\alpha w},G\left(w\right)={G}_{0}{e}^{\beta w},{\eta }_{0},{G}_{0}>\text{0,0}\le \beta <\alpha $$

(4)

Since viscosity is usually more dependent on structure (and temperature) than shear modulus, then β < α. Relaxation time of the Maxwell model (3) T = η / G is expressed by the formula T (w) = Te^{(α -β)w}, T₀ = η₀/ G₀, and therefore the limitation β < α is equivalent to postulating an increase of T (w) with increase in w . The change in structuredness occurs as a result of the competition of two main processes: the destruction of existing crosslinks (structural bonds) and the formation of new ones. As stress increases, rate of destruction (i.e., decrease of w(t)) increases (as a result, the viscosity drops), and the rate of formation of new crosslinks can be considered constant (in the first approximation, at a fixed temperature) and proportional to the density of vacancies 1 - w . Therefore, the kinetic equation for structuredness can be taken in the form

$$\dot{w}={k}_{1}\left(1-w\right)-{k}_{2}g\left(s\right)w,$$

(5)

where k₁, k₂ > 0 is a MPs (s^–1), determining the rates of formation and destruction of crosslinks (generally speaking, they depend on the temperature), g(s) , s ≥ 0 , is an increasing (non-strictly) piecewise-smooth function such that g(0) = 1 and g(+∞) = +∞ (the role of this restriction is indicated in [1,2,3,4,5]), which specifies the structuredness decay rate dependence on the dimensionless stress s = τ (t) / τ_c (τ_c is some characteristic shear stress: yield stress or simply τ_c = G₀ or τ_c = 0.01 G₀). For example, MFs of the following form were considered in [1, 2]

$$g\left(s\right)={e}^{hs},g\left(s\right)=1+{\left(hs\right)}^{2},g\left(s\right)=1+hs,g=1+1\text{n}\left(1+hs\right),h>0.$$

(6)

The case g(s) = 1 for s = [0; s₀] isn’t forbidden.

Thus, in the model (3)-(5) (governed by six MPs: k₁, k₂, η₀, G₀,α > 0 , β ≥ 0, and single MF g(s) the kinetics of two interconnected processes is taken into account: shear flow and structural changes in the material [3,4,5]. Introduction of dimensionless time $\overline{t }=t/{T}_{0}$ (after simplifying the notation and replacing t with t) [1, 5] gives model equations (3)-(5) in dimensionless form (1), (2), where

$$a=\nu {\eta }_{0}/{\tau }_{c}=\nu {T}_{0}{G}_{0}/{\tau }_{c}, b={k}_{2}/{k}_{1},c={k}_{1}{T}_{0}$$

are dimensionless MPs: a depends on the shear rate ν and initial viscosity, b and c characterize the struggle between processes of crosslink formation and destruction and the ratio of their rates to T₀ .

The equilibrium points of the set (1), (2) (at constant shear rate) are solutions of the equations set

$$s={ae}^{\alpha w},w=F\left(s\right),$$

(7)

$$F\left(s\right):=1/B\left(s\right), B\left(s\right):=1+bg\left(s\right),s\ge 0.$$

(8)

They depend only on three parameters α, a, b and MF g (and do not depend on parameters c, G₀, β from Eqs. (2) and (4)). Function B(s) depends on the ratio bg(s) of rate of crosslinks destruction to the rate of their formation in Eq. (5); B(s) is (non-strictly) increasing (as the MF a = 10 increasing) and always B(s) ≥ 1 + b > 1 (since g(s) ≥ 1). Function F (s) is a decreasing function with range of values (0; (1 + b)^-1], F (0) = (1 + b)^-1, F (s) → 0 as s → ∞, since g(+∞) = +∞. The function F (s) plays a key role in the analysis of integral curves, stress-strain and creep curves. In the first part of the article [1], it was proved that for any MPs a, b, α, c,η₀ , G₀ > 0 , β ≥ 0 and any non-decreasing MF g(s) solution (s_*, w_*) of the set (7) exists and is unique (in domain w ∈ (0;1) and s > 0).

First part of the article [1] was devoted to the formulation of the model, its analysis and preparation of the mathematical foundation for the second (main) part: proof of the uniqueness and stability of the equilibrium point of a nonlinear set of equations (1), (2), analytical study of the dependences of the equilibrium point and equilibrium apparent viscosity on all material parameters, possible types of phase portraits and properties of the integral and phase curves of the model. For arbitrary MPs and MF it is proved that the (unique) equilibrium point of the set (1), (2), is always stable and exactly three cases are possible: the equilibrium position is a node, or a degenerate node, or a focus, so saddle or center cases are not possible ([1], Theorem 2, Fig. 3_I). The equations of the flow curve s_*(a) and the apparent viscosity curve μ = τ_* / v = η₀s_*(a)/ a were studied, it was proved that the model leads to an increasing dependence s_*(a) and to the descending viscosity curve μ (a), the limits of viscosity were found at a shear rate tending to zero and to infinity ([1], Theorem 1, Fig. 2_I)). The analysis proved that the model (3)-(5) describes the most important qualitative properties of typical experimental flow and viscosity curves observed for various pseudoplastic fluids [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. The behavior of integral and phase curves of the model, the evolution of this behavior with an increase in the shear rate, and the influence of the nonmonotonicity of structuredness w(t) on it were illustrated in detail. The first part [1] also contained an overview of the state of the issue and an extensive bibliography, substantiation of the relevance of the model and its analysis, and the objectives of the article. Therefore, in the third part of the article, the review is omitted, the bibliography is shortened, and the introduction contains only the basic formulas (1)-(8), that will be required for further presentation.

In the second part of the article [2] we have investigated the properties of stress-strain curves (SSC) at a constant rate s(t; a, w₀) and relaxation curves (RC) s(t; s₀, w₀) generated by the model (1), (2), and features of the evolution of the structure under these types of loading depending on the MPs, MF, shear rate a , initial structuredness w₀ of the material and initial stress s₀ . Thereby, we began systematic analysis of the model ability to describe the behavior of not only liquid-like, but also solid-like (thickening, hardening, solidified) thixotropic media, to describe the effects inherent in solid viscoelastic-plastic materials: relaxation, creep, recovery, typical behavior of stress-strain diagrams, strain rate and strain hardening, flow under constant stress, high velocity sensitivity, etc. (similar to systematic analytical study of related physically nonlinear CE of Maxwell type in [8, 35,36,37,38,39]). We proved that SSC s(γ; a, w₀) can be both increasing functions of γ and can have decreasing sections resembling a “yield tooth” or damped oscillations, that all SSCs possess horizontal asymptotes (steady flow stress), monotonically dependent on shear rate, and flow stress increases with shear rate growth, that the instantaneous shear modulus, on the contrary, depends on the initial structuredness w₀ , but does not depend on shear rate. Under certain restrictions on the MPs, the model is also capable of providing a bilinear form of SSCs, which is typical for an ideal elastoplastic model, but with strain rate sensitivity. It has been established that the family of SSCs s(γ; a, w₀) does not have to be increasing function either of w₀ or a : in a certain range of shear rates, in which the equilibrium point is a “mature” focus and pronounced oscillations of SSCs are observed; SSCs with different a can intertwine [2]. We proved that for any material parameters and functions, all RC s(t; s₀, w₀ ) decrease in time and have a common asymptote s = 0 as t → ∞ (as RCs generated by the linear Maxwell model or by parallel connections of the Maxwell models [6], or by a nonlinear Maxwell-type viscoelasticity CE (16) [36]). The family of RCs γ₀ doesn’t always increase with respect to stress for t > 0 (in contrast to experimental RCs of structurally stable materials, and families of RCs generated by the linear viscoelasticity theory, or Rabotnov’s or Maxwell’s nonlinear CE (16) [6, 36]). It turned out that the model (3)-(5) is capable to describe either an increase of s(t; s₀ , w₀) with s₀ or the effect of non-monotonic dependence on s₀ [2].

The simple shear rate $\dot{\gamma }=\nu$ [1,2,3,4,5] was supposed constant and was included in the dimensionless parameter a = νη₀ / τ_c. Under such loading γ (t) = vt and one can examine not only the flow curve and the viscosity curve, but also the constant consider a different loading regime (constant stress s(t) at t > 0 rather than $\dot{\gamma }$ = const ), and rewrite (1), (2) as a set of rate stress-strain diagrams and the relaxation curves generated by the model [2]. To investigate creep, it is necessary to equations for shear angle γ (t ) and structuredness w(t). The main task of the third part of the article is to derive equation for creep curves (CC) under constant stress generated by the model (1), (2) and to study their basic properties and structure evolution influence on them. The SSC family s(γ; a, w₀) depends on the shear rate a and on the initial structuredness w₀ of the material, the RC family s(t; s₀, w₀) depends on w₀ and initial stress s₀ (or initial shear angle γ₀ = s₀ / G(w₀)), and the creep curves family γ (t; $\overline{s },$ w₀) depends on w₀ and given stress level $\overline{s }$. The general properties (intervals of monotonicity and convexity, extrema, asymptotes, etc.) of the dependences of SSC, RC, and CC are studied not only with respect to the main arguments (shear strain γ and time), but also with respect to loading parameters and initial structuredness: for example, we examine whether the SSC family s(γ; a, w₀) depends monotonously on a and w₀, and how they affect the modulus of elasticity (instantaneous modulus) and the SSC asymptote, i.e., the stress of a steady flow s_*. In addition, we examine how the structuredness w(t) changes at different loading parameters (a, s₀ or $\overline{s }$) depending on the MPs and MF of the model and what unusual effects (unusual properties of SSC, RC, and CC) the variability of w(t) in comparison to typical SSC, RC and CC of structurally stable materials.

1. Properties of the Creep Curves Family Generated by the Model

The set of differential equations for unknowns w(t) and γ(t ) as functions of dimensionless time t , describing creep at constant stress, can be obtained by setting s(t) = $\overline{s }$ = const in (1), (2) at γ (t; $\overline{s }$, w₀ ) . In the creep regime, the stress is known, another pair of unknown processes is sought, the value a = vη₀ / τ_c is not constant and dimensionless function a(t) is proportional to the (dimensional) shear rate v , i.e., creep rate v = $\dot{\gamma }$ (t) / T₀. The factor 1/T₀ appeared here due to the fact that in the notations introduced in the process of drawing the dimensionless form (1), (2) of the model [1], t is the dimensionless time, obtained by dividing by T₀, and the dot denotes derivative with respect to t, rather than with respect to physical time (as in the original definition of quantities v and a). Then, the set (1), (2) turns into the set of the following equations for w(t) and γ (t )

$$a=\overline{s}{e }^{-\alpha w},a=\dot{\gamma }\left(t\right)/\Upsilon ,$$

(9)

$$\dot{w}=cB\left(\overline{s }\right)w+c,t>0$$

(10)

with parameters $\overline{s }$ > 0 , w₀ ∈ [0;1] , Υ = T₀τ_c / η₀, b, c,α > 0. The function B(s) = 1 + bg(s) increases (since g(s) increases) and always B($\overline{s }$) ≥ B(0) = 1+ b > 1 (since g(s) ≥ 1 ). Obviously, the solutions w(t), γ (t) will depend on a stress level s and on initial values w(0) = w₀ and γ (0) = γ₀ (instantaneous elastic deformation).

Equation (10) does not contain the unknown (t); it is linear and has general solution of the form w = Ae^-cBt + B^-1. The Cauchy problem solution with initial condition w(0) = w₀ has the form

$$w\left(t,\overline{s },{w}_{0}\right)=\left[{w}_{0}-F\left(\overline{s }\right)\right]{e}^{-cB\left(\overline{s }\right)t}+F\left(\overline{s }.\right)$$

(11)

Function F (s) = 1 / B(s) is defined in Eq. (8). It decreases, F (0) = (1 + b)^-1 and F (s) → 0 as s → ∞ (since g(+∞) = +∞). Structuredness (11) doesn’t depend on parameter α.

Structuredness (11) decreases with time if F ($\overline{s }$) < w₀ (for sufficiently high stress and initial structuredness) and increases if F ($\overline{s }$) > w₀ (i.e., at sufficiently low $\overline{s }$ and w₀). Structuredness (11) has the limit w_∞ = F ($\overline{s }$) as t → ∞ (horizontal asymptote), which depends on the MP b, MF g(s) and stress s , but does not depend on w₀. The steady value w_∞ = F ($\overline{s }$) decreases with $\overline{s }$ and tends to zero as $\overline{s }$ → ∞. Curves w(t) move downwards as s grows and change from increasing to decreasing at $\overline{s }$ obeying the equation F ($\overline{s }$) = w₀ (at this value $\overline{s }$ structuredness w(t) is constant). Equation (11) implies that constant load erase gradually any difference in initial value w₀ (Fig. 2b): the difference w(t; $\overline{s }$, w₀₂ ) - w(t; $\overline{s }$, w₀₁) tends to zero exponentially as t → ∞ for any w₀₂ ≠ w₀₁.

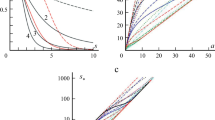
Figure 1a shows F (s) graphs for b = 0.1 and various MF (6) with h = 1: logarithmic (curve 0), four power functions g = 1 + (hs)ⁿ, n = 1...4 (curves 1-4) and exponential MF (red curve). They present steady structuredness w_∞ = F ($\overline{s }$). Every graph (except for 0,1) has inflection point (for any n > 1 ). As n → ∞, curve family F (s; n) tends to a step function F_∞ = w₀[h(s) - h(s -1)] ( F_∞ (s) ≡ 0 for s > 1 ). For comparison, F (s) graph for b = 0.001 and g = e^hs (red dash curve) is given.

Fig. 1.

The steady structuredness w_∞ = F (s ) (a) and steady creep rate r($\overline{s }$) = a(∞) (see Eq.(13)) (b) for seven models with b = 0.1 and various MF (6).

Substituting Eq. (11) into Eq. (9) makes it possible to find the dependence of the logarithm of the dimensionless creep rate on time and stress ($\overline{s }$ > 0):

$$1\text{n} a=1\text{n} \overline{s }+\alpha \left[F\left(\overline{s }\right)-{w}_{0}\right]{e}^{-cB\left(\overline{s }\right)t}-\alpha F\left(\overline{s }\right).$$

(12)

Function (12) is also monotonic in time for t > 0 (decreases or increases depending on the sign of the factor F ($\overline{s }$) - w₀ in Eq. (12)) and has a limit ln $\overline{s }$ -α F ($\overline{s }$) as t → ∞. Therefore, the dimensionless creep rate a(t) is monotonic in time, and has finite limits as t → 0 + or t → ∞:

$$a\left(0\right)=\overline{s}{e }^{-\alpha {w}_{0}},a\left(\infty \right)=\text{exp}\left(1\text{n} \overline{s }-\alpha F\left(\overline{s }\right)\right)=\overline{s}{e }^{-\alpha F\left(\overline{s }\right)}.$$

(13)

The limit a(0) is proportional to $\overline{s },$ depends on w₀ (decreases with w₀) but does not depend on the MF. The steady creep rate r = a(∞), as well as w_∞, does not depend on the parameter w₀, but depends (nonlinearly) on MF and stress level.

Since α > 0 and the function F ($\overline{s }$) decreases, then both factors in a(∞) always increase with $\overline{s }$ (the second one as a composition of two decreasing functions). However, the estimate $\overline{s }$ e^-α < r($\overline{s }$) < $\overline{s }$ is always true since F ($\overline{s }$) < 1 and e^{-αF (}$\overline{s }$⁾ > e^-α;r($\overline{s }$) / $\overline{s }$ → 1 as $\overline{s }$ → ∞ since F (∞) = 0. Inequality r($\overline{s }$) > 0 for any $\overline{s }$ > 0 implies that the model cannot describe materials with bounded creep at any (even small) stress levels as t → ∞. In the linear viscoelasticity limits a(0) and a(∞) can be infinite, and for the linear Maxwell model creep rate is constant in time and the Creep Curves (CC) has the form γ (t; $\overline{s }$) = $\overline{s }$ (C + rt). For the nonlinear Maxwell-type CE (16) studied in the papers [8, 35,36,37,38,39], creep curves are linear too, but the creep rate depends nonlinearly on stress [35]).

Figure 1b shows steady creep rate r($\overline{s }$) graphs (see Eq. (13)) for models with b = 0.1 and same MFs (6) with h = 1 as in Fig. 1a: logarithmic (curve 0), four power functions g(s) = 1 + (hs)ⁿ for n = 1...4 (curves 1-4) and exponential MF (red curve). For comparison there is also r($\overline{s }$) graph for b = 0.001 for g = e^hs (red dash curve). All graphs tend to asymptote r = $\overline{s }$ as $\overline{s }$ → ∞.

Figure 2a shows structuredness graphs w(t) at w₀ = 0.5 and stresses s = 0, 5, 6, 7, 8, 9, 10 for two models with b = 0.001 , c = 0.25 , α = 2 , β = 1, G₀ = 100 and two different MFs: 1) MF g = e^hs , h = 1 (red curves 0-6); 2) MF g = 1+ hs, h = 100 at $\overline{s }$ = 1, 5, 10, 50, 100 (curves 1’-5’). Specifying h = 100 makes it possible to lower the stress levels (and the rate of structure breaking) by a factor of 100 in order to make them at least comparable with those chosen for exponential MF. Red dashed curve 0 presents w(t) graph for $\overline{s }$ = 0 (it is invariant to the choice of MF). When stress grows, the graphs w(t) shift downwards and change from increasing to decreasing at stress level that satisfies equation F ($\overline{s }$) = w₀ (at this stress w(t) is constant, see curve 3’ for linear MF at $\overline{s }$ = 10).

Fig. 2.

Structuredness graphs (see Eq.(11)) generated by two models with exponential or linear MF (6): at various stresses for w₀ = 0.5 (a) and at fixed $\overline{s }$ = 8 and different w₀ = 0, 0.1, 0.3, 0.6, 0.9 (b).

Figure 2b shows graphs w(t) for the same pair of MFs, but at fixed stress level $\overline{s }$ = 8 and five different w₀ = 0, 0.1, 0.3, 0.6, 0.9 (curves 0-4). Dashed lines mark their asymptotes w = F ($\overline{s }$). Structuredness increases if w₀ < w_∞ and decreases if w₀ > w_∞. Dotted curves present w(t) graphs at $\overline{s }$ = 0 for comparison. The models considered posess equilibrium structuredness w_∞ = F (0) = (1 + b)^-1 at $\overline{s }$ = 0 which is close to unity and so all w(t) graphs increase rapidly.

Creep curve family equation γ (t; $\overline{s }$, w₀) , generated by the model can be obtained by integrating over (dimensionless) time of the expression for a = $\dot{\gamma }$ (t) / Υ, arising from Eq. (12):

$$\begin{array}{c}\dot{\gamma }=\Upsilon a= \Upsilon \text{exp}\left(1\text{n }\overline{s }-\alpha \left[{w}_{0}-F\left(\overline{s }\right)\right]{e}^{-cB\left(\overline{s }\right)t}-\alpha F\left(\overline{s }\right)\right)=\Upsilon \overline{s}{e }^{-\alpha F\left(\overline{s }\right)}\text{exp}\left(a\left(F\left(\overline{s }\right)-{w}_{0}\right){e}^{-cB\left(\overline{s }\right)t}\right),\\ \gamma \left(t;\overline{s },{w}_{0}\right)=\gamma \left(0;\overline{s },{w}_{0}\right)+\Upsilon \overline{s}{e }^{-\alpha F\left(\overline{s }\right)}Y\left(t;\overline{s },{w}_{0}\right),Y\left(t;\overline{s },{w}_{0}\right)={\int }_{0}^{t}\text{exp}\left(a\left(F\left(\overline{s }\right)-{w}_{0}\right){e}^{-cB\left(\overline{s }\right)\tau }\right)d\tau ,\end{array}$$

(14)

where γ (0; $\overline{s }$, w₀ ) = π / G(w₀) $\overline{s }$ τ_c / (G₀e^βw0) = Υ $\overline{s }$ e^βw0 is the initial shear angle.

It is possible to analyze the general properties of the CC family γ (t; $\overline{s }$, w₀ ) without calculating the integral (14). One can analyze Eqs. (9)-(11) directly. From Eq. (9) follows, that a(t) > 0 , i.e., $\dot{\gamma }$ (t) > 0 , and therefore, for any stress level $\overline{s }$ = 0 CC γ (t; $\overline{s }$, w₀ ) always increases with time (as for all structurally stable materials). Differentiation of Eq. (9) with respect to time gives $\dot{a}$ = -$\overline{s }$ αwe^-αw. The sign of $\ddot{\gamma }$(t) matches the sign of $\dot{\alpha }$ and so inequality $\ddot{\gamma }$(t) > 0 is equivalent to $\dot{w}$ (t) < 0 and $\ddot{\gamma }$(t) < 0 is equivalent to $\dot{w}$ (t) < 0. Due to Eq. (11), $\dot{w}$ (t) = c(1- Bw₀)e^-cBt and the sign of $\dot{w}$(t) (and therefore sgn $\ddot{\gamma }$(t)) doesn’t change in the interval t > 0 and this sign depends only on the sign of the expression 1-w₀B($\overline{s }$) , i. e., on sgn(F ($\overline{s }$) - ):

$$\dot{w}\left(t\right)>0 \&\ddot{ \gamma }\left(t\right)<0 \text{if }F\left(\overline{s }\right)>{w}_{0} \text{and }\dot{w}\left(t\right)<0 \& \ddot{\gamma }\left(t\right)>0 \text{if }F\left(\overline{s }\right)<{w}_{0}.$$

Thus, CC γ (t; $\overline{s }$, w₀) always increases with time for any MF and MPs, has no inflection points, and exactly three cases are possible depending on the values of w₀, $\overline{s }$ and MPs:

• (1) if F ($\overline{s }$) > w₀ (for sufficiently small w₀ and s ), then structuredness increases monotonically to the limit value w_∞ = F ($\overline{s }$) (curves 0-2 in Fig. 2a) and CC γ (t; $\overline{s }$, w₀) is convex up in the interval t > 0 , i.e., CE describes the creep deceleration although the creep rate tends to r = Υ $\overline{s }$ e^{-αF (}$\overline{s }$⁾ as t → ∞ rather than zero (limits a, b, α, c,η₀, G₀ > 0 and r do not depend on β ≥ 0);

• (2) if F ($\overline{s }$) = w₀ , then structuredness does not change at s > 0 ( w(t) = w₀ ) and CC γ (t; s , w₀ ) is a straight line with slope r (integrand in Eq. (14) is equal to 1), i.e., the CE accurately models the steady creep over the interval t > 0 if and only if w₀ and s are linked by eq. w₀ B($\overline{s }$) = 1 (nullifying the right side of the equation (10) at t = 0);

• (3) if F ($\overline{s }$) < w₀ (at sufficiently high s ), then w(t) decreases in the interval t > 0 , has the limit w_∞ = F ($\overline{s }$) and CC γ (t; $\overline{s }$, w₀) is convex down in t > 0 , i.e., the model describes accelerating creep, and the creep rate tends to the limit $\dot{\gamma }$(∞) = Υe^{-αF (s)}.

The intermediate case 2 is realized when $\overline{s }=\widetilde{s}$, where $\overline{s }=\widetilde{s}$ (b, w₀ ) is a solution of the equation F ($\overline{s }$) = w₀ (i.e., w_∞ ($\overline{s }$) = w₀). It is unique for any w₀ ∈(0; (1 + b)^-1) , since the function F ($\overline{s }$) is decreases, its range is (0; (1 + b)^-1] and F ($\overline{s }$) → 0 as $\overline{s }$ → ∞. The equation for $\widetilde{s}$ is easily solved for MF given by Eqs. (6): 1 + be^hs = 1 / w₀, $\widetilde{s}$ = h^-1 ln[(1 – w₀)/ (bw₀)] or 1 + b(1 + (hs)ⁿ) = 1 / w₀, $\widetilde{s}$ = h^-1(1 – w₀ - bw )^1/n (bw₀)^-1/n. But if w₀ ≥ 1 / (1 + b), then the equation has no solutions in the interval $\overline{s }$ > 0, and so the case 3 realizes for any $\overline{s }$. Figure 1a shows the curves w = F (s) separating zones of different behavior of the CCs for the models with specified MFs (6) in the plane ($\overline{s }$, w₀). Every one coincides with the graph of the inverse function for $\widetilde{s}$(w₀) of the specific model.

Therefore, the model (3)-(5) can describe materials with convex down CCs (when w₀ ≥ 1 / (1+ b) ), as well as materials demonstrating evolution of CCs with stress growth from convex up to convex down curves at some level $\overline{s }=\widetilde{s}$. The model is suitable for modeling materials that are prone to steady creep and can describe the change in CC convexity with increasing stress level, but can’t describe CC with inflection points (with all three stages of creep), and materials with limited creep at some (at least small) stress levels.

Figure 3a shows CC families (14) at w₀ = 0.5 and at different stress levels for the same two models with b = 0.001, c = 0.25 , α = 2 , β = 1, G₀ = 100 as in Fig. 2a: (1) the model with g = e^hs, h = 1 (red CC 1-6) at stresses $\overline{s }$ = 3, 5, 7, 8, 9, 10; (2) the model with linear MF g = 1 + hs, h = 100 at $\overline{s }$ = 1, 5, 10, 15, 20 (black CC 1’-5’). Specifying h = 100 makes possible to lower the stress levels by a factor of 100 in order to make them at least comparable with those chosen for exponential MF. With increase in stress $\overline{s }$ creep curves change convexity from convex up to down at $\overline{s }=\widetilde{s}$ (at this level CC is a straight line and w(t) is constant, see curve 3’ in Fig. 2a).

Fig. 3.

Creep curves generated by the models with exponential or linear MF (6): at w₀ = 0.5 and different stress levels (a) and at $\overline{s }$ = 8 and different initial structuredness w₀ = 0, 0.1, 0.3, 0.6, 0.9, 1 (b).

Figure 3b shows CC (Eq. (14)) for the same pair of models but at the fixed stress level $\overline{s }$ = 8 and different values of initial structuredness w₀ = 0, 0.1, 0.3, 0.6, 0.9, 1 (curves 0-5). It will be shown further that every creep curve has an asymptote (15) as t → ∞ and its slope does not depend on w₀.

The existence of the limit $\dot{\gamma }$(∞) = r is necessary for the existence of a CC asymptote, but it is not sufficient: the existence of the limit γ (t) – rt as t → ∞ is also required. Due to Eq. (14) and the formula r = Υ $\overline{s }$ e^-αF($\overline{s }$⁾, this condition is equivalent to convergence of the improper integral $I={\int }_{0}^{\infty }\left[\text{exp}\left(\alpha \left(F\left(\overline{s }\right)-{w}_{0}\right){e}^{-cB\left(\overline{s }\right)\tau }\right)-1\right]d\tau .$ If F($\overline{s }$) = w₀ then the integrand is equal to zero. In other cases, the integral also converges by comparison criterion: the function x(t) = α[F (s ) – w₀]e^-cB $\left(\overline{s }\right)$ ^t tends to zero as t → ∞, it yields exp(α[F ($\overline{s }$) - w₀ ]e^-cBt ) -1 = exp x -1 ~ x(t) and so the integral of the last function over [0, +∞) converges. The integral is positive when F ($\overline{s }$) > w₀, it is zero for $\overline{s }>\widetilde{s}$ and is negative when $\left.\overline{s }>\widetilde{s}\right)$. Therefore, any CC of the model has an oblique asymptote

$$y\left(t;\overline{s }{,w}_{0}\right)=rt+{\gamma }_{0}+rI,{\gamma }_{0}=\Upsilon \overline{s}{e }^{-\beta {w}_{0}},r\left(\overline{s }\right)=\Upsilon \overline{s}{e }^{-\alpha F\left(\overline{s }\right)}.$$

(15)

The slope g = 1 + hs monotonically increases: r′($\overline{s }$) = Υe^-αF($\overline{s }$⁾ (1- α $\overline{s }$ F′($\overline{s }$)) , i.e., r=($\overline{s }$) > Υe^-αF($\overline{s }$⁾ > 0, since F′($\overline{s }$) = -B′ / B² = -bg′(s )/ B² < 0 . For any MF r(0) = 0 and r($\overline{s }$) ~ Υ $\overline{s }$ e⁰ = Υ $\overline{s }$ as $\overline{s }$ → ∞ (the line y = Υs is the asymptote of the graph r(s)).

In the degenerate case, when α = 0 (and the MF g is arbitrary), we have r($\overline{s }$) = Υ $\overline{s }$, and we get from Eq. (14) I (t; $\overline{s }$, w₀) = t and γ (t; $\overline{s }$, w₀) = γ₀ = rt, γ₀ = Υ $\overline{s }$ e^-βw0, i.e., we have creep with constant rate proportional to g(+∞) = +∞ which is specific for the linear Maxwell model. This result is quite expected, since the model with α = 0 decomposes into the classical (linear) Maxwell equation (3) and the additional stress dependent equation (5) for structuredness. It is obvious that a decrease in parameter α weakens the influence of structuredness on the deformation process (because the viscosity and shear modulus in (3), (4) become less sensitive to w(t) ), it gradually decays as α → 0 , and so the CC family differs less and less from the CC of the Maxwell linear model.

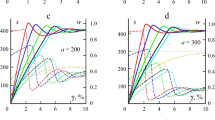
Figure 4 shows CCs (Eq. (14)) and structuredness graphs w(t) (Eq. (11)), generated by two models with b = 0.001 , c = 0.25 , α = 2 , β = 1, G₀ = 100 with the same pair of MFs as in Figs. 2 and 3 at stress levels $\overline{s }$ = 5, 6, 7, 8, 9, 10 and for three values of initial structuredness w₀ = 0, 0.5, 1 (cyan, black dashed and red curves). Figures 4a and 4b present the model with linear MF g = 1+ hs, h = 100, Figures 4c and 4d present the model with exponential MF g = e^hs, h = 1 . Figures 4a and 4c illustrate dependence of creep curves on initial structuredness w₀. At initial section, cyan CCs for w₀ = 0 lie higher than the other (lower structuredness — higher compliance), however red CCs with w₀ = 1 lie lower (lower compliance), but their increase rate rises with time (CCs are convex downwards) in contrast to convex upwards cyan CCs with w₀ = 0 , and after some time CCs with w₀ = 1 catch up and overtake the CCs with w₀ = 0. This is due to the fact that the low initial structuredness quickly increases at selected moderate stresses and the material thickens and hardens (see cyan curves in Figs. 4b and 4d). If w₀ is large, then, as proven above, w(t) decreases under the influence of stress and the faster the higher s (see red curves with w₀ = 1 in Figs. 4b and 4d), and therefore the compliance increases and CCs (with sufficiently large s ) are grow even faster (Fig. 4a and 4c). The higher the stress, the lower the asymptote for w(t) (in Figs. 4b and 4d, the arrow indicates the direction of increase of $\overline{s }$), the higher the steady-state compliance and creep rate (CC asymptote slope angle), the faster the CCs acquire a rectilinear outline, characteristic to steady-state creep (Figs. 4a and 4c).

Fig. 4.

Creep curves and structuredness w(t) at stress levels $\overline{s }$ = 5, 6, 7, 8, 9, 10 and three initial structuredness w₀ = 0, 0.5, 1 (cyan, black dashed and red curves), generated by two models as in Figs. 2 and 3: for linear MF g = 1 + hs , h = 100 (a, b) and for exponential MF g = e^hs, h = 1 (c, d).

The main statements proven are summed up as follows.

THEOREM 3. Let a, b, α, c, η₀, G₀ > 0, β ≥ 0 , w₀ ∈[0;1] , and MF g(s) is continuous and piecewise differentiable on s ≥ 0 , does not decrease and g(0) = 1. If s(t) = $\overline{s }$ const at t > 0 (creep regime), and $\overline{s }$ > 0, then the structuredness evolution w(t; $\overline{s }$, w₀ ) and creep curves γ (t; $\overline{s }$, w₀) are described by the set of differential equations (9), (10), they are expressed by explicit formulas (11) and (14), in which B($\overline{s }$) = 1 + bg($\overline{s }$), F ($\overline{s }$) = 1 / B($\overline{s }$), and have the following properties.

• (1) Structuredness w(t; $\overline{s }$, w₀) is monotonic in time, it decreases in $\overline{s }$ and increases in w₀; as t → ∞, the function (11) has the limit w_∞ = F ($\overline{s }$) (horizontal asymptote), which depends on MP b , MF g(s) and stress level $\overline{s }$ (but does not depend on the initial structuredness η₀) and tends to zero as $\overline{s }$ → ∞.

• (2) Any creep curve γ (t; $\overline{s }$, w₀) (Eq. (14)) monotonically increases in time and has asymptote (15) with the slope r($\overline{s }$) = Υ $\overline{s }$ e^-αF($\overline{s }$⁾ as t → ∞, the steady rate r($\overline{s }$) doesn’t depend on w₀ , increases in s and has the linear asymptote r($\overline{s }$) ~ Υ $\overline{s }$ as $\overline{s }$ → ∞ (Fig. 1b).

• (3) Dimensionless creep rate a(t) is monotonic in time and has the finite limits (Eq. (13)) as t → 0 + or t → ∞; initial rate a(0) is proportional to $\overline{s }$, decreasing in w₀ , but does not depend on the MF, and the steady-state creep rate a(∞) = r / Υ > 0 , as well as equilibrium structuredness w_∞, does not depend on w₀ , but depends on the MF g(s) and stress $\overline{s }$.

• (4) If F ($\overline{s }$) < w₀ (i.e., at sufficiently high $\overline{s }$), then structuredness w(t;, w₀ ) is monotonically decreases and creep curves γ (t; $\overline{s }$, w₀ ) are convex down in interval t > 0 , i.e., the model describes accelerating creep, but the creep rate is bounded and tends to the limit $\dot{\gamma }$(∞) = r as t → ∞.

• (5) If 0 < w₀ < 1 / (1+ b) and $\overline{s }$ = $\widetilde{s}$, $\widetilde{s}$ = $\widetilde{s}$ (b, w₀) is the (unique) solution of the equation F ($\overline{s }$) = w₀ , then structuredness w(t) = w₀ does not change in interval t > 0 and the creep curve (Eq. (14)) is the straight line γ (t) = γ₀ + r($\widetilde{s}$)t , where γ₀ and r are given by the formula (15), i.e., the model (3)-(5) simulates steady-state creep over the interval t > 0 if and only if $\overline{s }=\widetilde{s}.$

• (6) If 0 < w₀ < 1 / (1 + b) and F ($\overline{s }$) > w₀ (i.e., $\overline{s }$ < $\widetilde{s}$ ), then the structuredness increases monotonically, and creep curves γ (t; $\overline{s }$, w₀) are convex up throughout the interval a₁₁ = -e^(β-α)w* (creep rate decreases).

• (7) If w₀ ≥ 1 / (1+ b) , then equation F ($\overline{s }$) = w₀ has no roots in the interval $\overline{s }$ > 0, and the case 4 takes place for any s and all creep curves are convex down.

• (8) The model can describe both materials with convex down creep curves (provided w₀ ≥ 1 / (1+ b)), as well as materials whose creep curves change from convex up to convex down at some level of stress $\overline{s }=\widetilde{s},$ but the model can’t simulate creep curves with inflection points (with all three stages of creep) and materials with limited creep at some (even small) stress levels.

2. Further Prospects for Development of the Basic Model and its Applications.

The model (3)-(5) (after formulation in the 3D case, further study, detailed comparison with experimental data and necessary generalizations, in particular, taking into account the effect of heat release and heat transfer and introducing additional structural parameters and equations to take into account the kinetics of the main physical and chemical processes) will be used to describe testing of bitumens and their modifications with mineral and elastomer fillers, thermoplastic melts (polyethylenes, polyamides, polyphenylene sulfide, polyetheretherketone, etc.), carbon-silicon pastes for 3D printing and for solving boundary problems in polymer processing technologies (in particular, solid phase ram extrusion, filament spinning by melt extrusion and drawing) [19,20,21,22,23, 40,41,42,43,44], problems of creep, accounting for accumulation and healing of damage and the kinetics of chemical transformations under the influence of an aggressive environment, and problems of modeling superplastic deformation of metals and alloys, taking into account the evolution of several structural parameters (the average size, shape and orientation of grains, the proportion of high-angle boundaries, the level of non-equilibrium of grain boundaries, the density of dispersoids, the degree of segregation at the grain boundaries of alloying elements that facilitate grain-boundary sliding, etc.) [45,46,47,48,49,50,51,52,53,54,55,56].

Note that the model (3)-(5) is related to the physically nonlinear CE of Maxwell type

$$\begin{array}{c}{\varepsilon }_{ij}\left(t\right)=\frac{3}{2}\varepsilon \left(t\right)\sigma {\left(t\right)}^{-1}\left[{\sigma }_{ij}\left(t\right)-{\sigma }_{0}\left(t\right){\delta }_{ij}\right]+\frac{1}{3}\theta \left(t\right){\delta }_{ij},\\ \varepsilon \left(t\right)=\mathbf{M}\sigma ={E}^{-1}F\left(\sigma \left(t\right)\right)+{\eta }^{-1}\underset{0}{\overset{t}{\int }}V\left(\sigma \left(\tau \right)\right)d\tau ,\\ \theta \left(t\right)={\mathbf{M}}_{0}{\sigma }_{0}={E}_{0}^{-1}{F}_{0}\left(\sigma \left(t\right)\right)+{\eta }_{0}^{-1}\underset{0}{\overset{t}{\int }}{V}_{0}\left({\sigma }_{0}\left(\tau \right)\right)d\tau ,\end{array}$$

(16)

with four arbitrary (increasing) MF F (x) , V (x) , F₀ (x) , V₀ (x) and parameters E, η, E₀, η ₀ > 0, investigated in a series of articles [8, 35,36,37,38,39] (and others). It connects the history of change of strain ε(t ) and stress σ(t) tensors at a point of the body under the assumption that there is no mutual influence of the spherical and deviatoric parts of the tensors e = ε - ε₀I and s = σ - σ₀I (volumetric strain independence θ (t ) from shear stresses and stress intensity $\sigma ={\left(\frac{3}{2}{S}_{ij}{S}_{ij}\right)}^{0.5}$ while shear strains and strain intensity $\varepsilon ={\left(\frac{2}{3}{e}_{ij}{e}_{ij}\right)}^{0.5}$ does not depend on the average stress σ₀ (t) ) and neglecting the influence of the third invariants of tensors. One dimensional CE prototype (16) is obtained from the classical linear Maxwell model by replacing the linear elastic and viscous elements with nonlinear ones controlled by material functions F (x) and V (x) respectively, i.e., it relies on the decomposition of the total strain into the sum of the elastic and viscoplastic components.

CE (16) generalizes (includes) the classical power models of viscous flow and creep, the Herschel-Bulkley and Shvedov–Bingham rheological models, and special cases of the Sokolovsky–Malvern, Gurevich and VBO models (for an overview and bibliography on these topics, see [8, 35,36,37,38,39]). Nonlinear integral operators M and M₀ control the processes of shape change and development of volumetric deformation (which do not affect each other). Elastic moduli E, E₀ and viscosity coefficients η, η₀ are separated from the MF for the convenience of taking into account the effect of temperature in the form E = E(T ) , η = η (T ) , E₀ = E₀ (T) , η₀ = η₀ (T) [37] and for time nondimensionalization using the parameter τ_r = η / E . In such a general form, CE (16) has not yet been subjected to research before the publication of articles [8, 35,36,37,38,39]. It has been proven that CE (16) (with certain restrictions on several of their MFs) describes well more than a dozen basic effects typical of viscoelastic-plastic solids (and not only for liquid viscoelastic media). In particular, it is suitable for describing loading and unloading curves, cyclic loading, ratcheting, various effects during creep and superplastic deformation. It was discovered in [8, 35,36,37,38,39] that the properties and capabilities of this CE serve as guidelines for further research on the properties of the model (3)-(5) (in particular, the families of SSCs, RCs and CCs that it generates) and its generalizations. In order to expand the class of described effects and the scope of applicability, the model (3)-(5) is convenient to use as an element of more complex hybrid models in combination with CE (16).

Conclusion

The article continues a systematic analytical study of the properties of a nonlinear structural-rheological model for shear flow of thixotropic viscoelastic-plastic media (3)-(5), taking into account the mutual influence of the deformation process and the evolution of the structure proposed and analyzed in [1,2,3,4,5]. A set of two nonlinear differential equations for shear at a constant rate and for stress relaxation is obtained and analyzed. Equation set describing creep is derived, a general solution of the Cauchy problem for the set is constructed in an explicit form (the equations of the families of creep and structuredness curves are derived). For arbitrary six material parameters and an (increasing) material function that govern the model, the basic properties of the stress-strain curve families at constant strain rates (SSCs), stress relaxation curves (RCs), and creep curves (CCs) generated by the model, and features of the evolution of the structure under these conditions (intervals of monotonicity and convexity, extrema, asymptotes, etc.), are analytically studied. Several indicators of the applicability of the model were found, which can be conveniently checked according to test data under these types of loading.

Since the SSC family s(γ; a, w₀) depends on the shear rate a and the initial structuredness of the material w₀ , the RC family γ₀ depends on w₀ and initial stress s₀ (or initial shear angle), and the CC family γ (t; $\overline{s }$, w₀ ) depends on w₀ and on a given stress level $\overline{s }$, the general properties the dependences of SSCs, RCs [2], and CCs were studied not only on the main arguments (shear strain and time), but also with respect to w₀ and the loading parameters a , s₀ , $\overline{s }$, as well as with respect to material parameters and function of the model. It was examined what unusual effects (unusual properties of SSCs, RCs and CCs) are generated by the changing structuredness in comparison with typical properties of SSCs, RCs and CCs of structurally stable materials.

In particular, it has been proven that, for any material parameters and material function governing the model, all stress relaxation curves decrease and have a common zero asymptote as time tends to infinity [2] (as well as RC generated by the linear Maxwell model and the nonlinear model of viscoelasticity of the Maxwell type (16)), and SSCs s(γ; a, w₀) can either increase in γ or have sections of decrease resembling a “yield drop” and damped oscillations, that all SSCs have horizontal asymptotes (steady flow stress) that monotonically depend on the shear rate, and the flow stress strictly increases with increasing shear rate, it has been proven that the instantaneous shear modulus, on the contrary, depends on the initial structuredness, but does not depend on the shear rate [2]. Under certain restrictions on the material parameters, the model is also able to provide a bilinear form of SSC, which is typical an ideal elastoplastic model, but with strain-rate sensitivity. It has been established that the family of SSCs does not have to be increasing either in initial structuredness or in shear rate: in a certain range of shear rates, in which the equilibrium position is a “mature” focus and pronounced SSC oscillations are observed, SSCs with different shear rates can intertwine [2]. Main results on CC properties γ (t; $\overline{s }$, w₀ ) , creep rate and structuredness w(t; $\overline{s }$, w₀ ) are collected in Theorem 3. It was proved that CCs always increase with time and have oblique asymptotes, while structuredness is always monotonic (unlike other loading modes), but it can both decrease and increase depending on the ratio between s and w₀ ; moreover, the same conditions control the convexity of CC up or down: at some critical load $\overline{s }$ = $\widetilde{s},\widetilde{s}$ = $\widetilde{s}$ (b, w₀) CCs change from convexity up (under smaller loads) to convexity down, and structuredness changes from decreasing to increasing. Thus, in particular, it has been proved that the model cannot describe the creep of materials with CCs with inflection points (with all three stages of creep) and materials with limited creep at some (at least small) stress levels.

As a result of the analysis, the ability of the model to describe the behavior of not only liquid-like, but also solid-like (thickening, hardening, hardened) viscoelastic-plastic media was established: effects of creep, relaxation, a number of typical properties of experimental RCs, CCs and SSCs, strain rate and strain hardening, flow at constant loading and other.