Introduction

Both static and cyclic loadings of structural elements often cause, among other things, inelastic strains, and also lead to a material degradation at high stress levels. Number of theories was proposed to describe this type of process [1,2,3,4]. In particular, various degradation measures were introduced [1, 2]:

$$\psi \left(\tau \right)={A}_{eff}\left(\tau \right)/{A}_{0}, \omega \left(\tau \right)=1-\psi \left(\tau \right),$$
(1.1)

where A0 and Aeff are the initial and actual cross-sectional areas, respectively; τ is the time. Then, the true stress is

$${\sigma }_{eff}\left(\tau \right)=\sigma /\left(1-\omega \left(\tau \right)\right).$$
(1.2)

The physical equation for describing the degradation process was adopted in the form [1]:

$$\dot{\omega }=B{\left[\sigma /\left(1-\omega \left(\tau \right)\right)\right]}^{n}, \omega \left(0\right)=0.$$
(1.3)

The failure criteria is

$${\sigma }_{eff}\left({\tau }^{*}\right)={\sigma }^{*},$$
(1.4)

where σ* is the ultimate strength of the material. Sometimes, the condition is used in another version:

$$\omega \left({\tau }^{*}\right)=1.$$
(1.5)

It is often assumed that the formation of microdamages does not affect the rheological processes and vice versa [2]. In the case of a complex stress state, other degradation measures were proposed, including those of fiber reinforced plastics (FRPs) [5,6,7,8,9,10].

The deformation and degradation process of FRPs have the features, depending on the FRP lay-up and type of its components, loading type (in particular, for FRPs formed by [±φ] lay-up, the presence of inelastic strain is characteristic). Therefore, the models used to describe these processes differ from those commonly used for metal structural elements. For example, such models are proposed in [3, 4]. In this case, the type of relationship between stresses and total strain depends on the “load-unloading” states and on the sign of strain. In the axes of orthotropy of the lamina, it is assumed that strain caused by microdamages appear only in tension across the reinforcement and in shear. It is assumed that under compression there are no linear strain caused by FRP degradation, and under shear damage accumulation is considered independent of the sign of shear stresses.

In the general case, the degradation level is taken into account not only when assessing strength, but also in physical relationships describing elastic and rheological processes. For example, the coupled problem of the theory of plastic flow and the theory of damage was considered in [5]. In [1], the physical relations for the damage parameter contain a creep strain.

There are theories in which the intensity of the creep strains accumulated is used as a measure of degradation (see [11]). In [12], for a nonlinear viscoelastic isotropic material, it was proposed to use the relation

$${\varepsilon }_{ij}={\varepsilon }_{ij}^{\left(e\right)}+{\varepsilon }_{ij}^{\left(c\right)}+{\varepsilon }_{ij}^{\left(d\right)},{\varepsilon }_{ij}^{\left(d\right)}=\underset{0}{\overset{\tau }{\int }}{M}_{ijkm}\left(\tau -\theta \right){\psi }^{km}\left(\sigma \left(\theta \right)\right)d\theta ,$$
(1.7)

where \({\varepsilon }_{ij}^{\left(e\right)}\) is the linear elastic strain, \({\varepsilon }_{ij}^{\left(c\right)}\) is the viscoelastic strain, \({\varepsilon }_{ij}^{\left(d\right)}\) is the strain caused by material degradation. The strength criterion was taken in the form:

$$f\left({\varepsilon }^{\left(e\right)}+{\varepsilon }^{\left(d\right)}\right)=1.$$
(1.8)

In [13, 14], the following relationship for the degradation parameter was proposed:

$$\omega \left(\tau \right)=1-\sigma /\left(\sigma +\underset{0}{\overset{\tau }{\int }}M\left(\tau -\theta \right)\sigma \left(\theta \right)d\theta \right).$$
(1.9)

In an integral form, the relationship for the degradation parameter was also proposed in [15]:

$$\omega \left(\tau \right)=\left(1+m\right)\underset{0}{\overset{\tau }{\int }}\frac{{\left(\tau -\theta \right)}^{m}}{{\zeta }^{1+m}}d\theta ,\zeta =\zeta \left[J\left(\sigma \right)\right].$$
(1.10)

In a number of works about cyclic loading, other quantities are also taken as the degradation parameter, for example, the elastic modulus in [16] and the ratio of densities at the current and initial instants of time in [17]. There are proposals to assess the level of degradation by residual stiffness or residual strength [18].

The work [19] was devoted to predicting the behavior of structural elements under conditions of damage accumulation using methods of the theory of probability, in which significant experimental material was presented. In [20], an overview of the works of V. V. Novozhilov was given, in which an approach to the analysis of degradation processes was proposed on the basis of the introduction of the concept of microstresses. Variant of the theory of the endochronic type for describing deformation processes taking into account material degradation is given in [21].

A review of methods for the experimental assessment of the level of material degradation and its evolution can be found, for example, in [22]. In [23], it is concluded that the most practical methods are optical microscopy and acoustic emission (see [24, 25]). The results of a large series of experiments devoted to the analysis of the degradation processes of FRP can be found in [26]. A number of experimental works [27] use the analysis of heat generation caused by irreversible strain.

Some other approaches to the analysis of degradation and failure processes (including numerical methods) can be found, for example, in [28,29,30,31,32,33,34,35,36]. Based on the results of this brief review, the following conclusions can be drawn. As noted above, in a number of works (see, for example, [16, 18, 39]), it is proposed to take the drop of the secant modulus at the current stage of the loading cycle as a damage parameter. However, this can be considered valid only in the case when there is not strain caused by the rheological properties of the composite. The presence of viscoelastic and viscoplastic strains leads to the fact, that the secant modulus at the stage of one loading cycle increases, especially in the initial cycles (this was also found in the author’s experiments for specimens with the cross-ply [±45]2s lay-up during cyclic loading). It turned out that such increase of the modulus, even at low stress, can continue for several hours. Therefore, the magnitude of the drop of the secant modulus, caused by the accumulation of damage, can be determined only with known laws for the rheological strain components. Since even during static tests of the composite material, degradation can occur (most likely, it will take place), it means, that the secant modulus will change in one cycle, also caused by degradation. Therefore, it is doubtful to reduce the problem only to changing the secant modulus in the case consideration the specimens made of CFRP with [±45]2s lay-up under cyclic loading.

Models describing material degradation, for example, based on energy loss (heat release), have similar drawbacks, since these losses are also caused by viscoelastic and viscoplastic strains.

For approaches similar to the classical ones [1, 2] and using effective or equivalent stresses (see, for example, [5,6,7,8,9,10]), it can be noted that they do not take into account the change in material stiffness. However, this can be important in the calculation of structural elements, which are subject to restrictions not only in terms of strength, but also in terms of strains and displacements.

For degradation models based on hereditary type relationships, one can note the disadvantage that they lead to “healing” (i.e., disappearance) of damage over time after the load is removed.

The endochronic theories also have the drawbacks. Regarding the materials, considered in the article (i.e., composites with [±45]2s lay-up), it is known that they exhibit sufficiently strong rheological properties even at not very large loading times and stresses, and creep strain is comparable to elastic strain. Therefore, for such composites, the use of any other models, for example, those using endochronous theories of damage accumulation without taking real time into account, may cause difficulties.

As a conclusion, we can say that any degradation models have both advantages and disadvantages. For some classes of structural materials (including composite ones) and some operating conditions, they lead to good agreement with experiment, but not for others. Therefore, the development of various theories continues, which could lead to less complex experimental procedures or less complex calculation methods.

This paper considers one of the special cases of the degradation process under uniaxial cyclic loading of a laminated composite with cross-ply [±45]2s lay-up (which can be one of the elements of a more complex layered material). Such composites exhibit viscoelastic and viscoplastic properties. In earlier works of the authors of this article, when compiling deformation models and determining the mechanical characteristics, included in these models, a number of wellknown and new hypotheses, approaches and methods were used, described (see, for example, [37]) for static problems. They made it possible to reduce the amount of experiments and obtain good agreement between the calculation and experimental results obtained. As will be seen from the following Sections, these approaches are also applicable when considering cyclic loads, and, moreover, also taking into account the process of damage accumulation. The proposed approach to the determination of mechanical characteristics is also aimed, firstly, at simplifying the task of their identification, and secondly, at reducing the variety and amount of experiments. It is demonstrated on the problem of assessing the level of degradation of these composite specimens only under cyclic uniaxial tension; so the one-dimensional problem of constructing physical relationships is considered in the axes of the specimen.

Experimental Results and Their Theoretical Explanation

To describe the degradation process, as in [3, 4], we introduce a hypothesis about the appearance of additional strain. It also agrees with the idea of the appearance of micropores and microcracks [1, 2], since it can be assumed that microdamages reduce the geometric stiffness of the representative body elements, containing them. Further, only the one-dimensional case of tension is investigated. Then, for total strain, the following relation can be taken:

$$\varepsilon ={\varepsilon }^{el}+{\varepsilon }^{cr}+{\varepsilon }^{v}+{\varepsilon }^{\omega },{\varepsilon }^{el}=\frac{\sigma }{{E}_{0}},$$
(2.1)

where εel is the linear elastic part of strain, E0 is the initial modulus of elasticity, εv is the viscoelastic (heredity elastic) part of strain, εcr is the irreversible creep strain, εω the is strain, caused by the development of microdamages. For εcr and εv components, as in [37], the following relations can be taken:

$$d{\varepsilon }^{cr}/dt={\chi }_{0}\sigma /\left(1+{\chi }_{1}{\left({\varepsilon }^{cr}\right)}^{m}\right),$$
(2.2)
$${\varepsilon }^{v}=\underset{0}{\overset{t}{\int }}f\left(\sigma \right)H\left(t-\tau \right)d\tau , H\left(t-\tau \right)=\frac{B}{\left(t-\tau \right)}, 0<\alpha <1, B>0.$$
(2.3)

When writing the relation for εω, it should be borne in mind, that this strain increases with time and with an increase in the number of cycles, and also depends on both the stresses and the level of this strain. In addition, εω should have different rates of change in tension and compression. Then, the physical relations for εω can be represented in the form:

$$\begin{array}{cc}d{\varepsilon }^{\omega }={F}_{1}\left(\left.\sigma ,\mathrm{sign}\left(\sigma \right),{\varepsilon }^{\omega },t\right)\right)dt+{F}_{2}\left(\left.\sigma ,\mathrm{sign}\left(\sigma \right),{\varepsilon }^{\omega },\theta \right)\right)d\theta ,& \theta =t/T\end{array}$$
(2.4)

where T is the period of cyclic loading. The parameter θ is a variable with which a discrete variable (number of cycles) is replaced with a continuous one.

We note that the adopted relations (2.2)-(2.4) are generalization of Kachanov’s conjecture, which makes it possible to reduce the number of arguments in the functions used in these relations. Namely, it is accepted that the various components of the strain do not affect each other and develop de pending on the stresses and the accumulated strain [37].

Next, let us look at the cyclic tension. For this case, one can take, for example, the following simple form of relation (2.4):

$$d{\varepsilon }^{\omega }={F}_{2}={\left(1+a{\varepsilon }^{\omega }\right)}^{k}{\left(\sigma /{\sigma }_{0}\right)}^{n}d\theta ,k>0,n>0.$$
(2.5)

We can see, that at large n and σ > σ0 sharp increasing of speed of εω occurs.

As in works [3, 4], it is assumed that at full unloading strain εω disappears, but here unloading proceeds according to a nonlinear law. Then for the total value of εel + εω, we can write the relation in the form:

$$\begin{array}{cc}{\varepsilon }^{el}+{\varepsilon }^{\omega }=\sigma /E,& E=\frac{{E}_{0}\sigma }{\sigma +{E}_{0}{\varepsilon }^{\omega }}.\end{array}$$
(2.6)

The parameters σ0, a, k, n are determined by identification methods [38], based on the experimental results. One of the difficulties in solving these problems is the problem of isolating from the experimental data various parts of the strain included in Eq. (2.1). For this, the approach used in [37] can be applied, according to which the hypothesis is accepted that the rates of various inelastic strain cannot always be of the same order at all times of loading, and hence in all cycles. This allows some characteristics to be found at short times (i.e., on the first cycles), but some ones at medium and large times.

Here, we assume that at short times, the strain εω will be much less than the strain εcr + εv. Therefore, the value εω can be neglected in the first few cycles. Further, for the separation of strains εcr and εv, as in [37], we assume that the rate of viscoplastic strain decays faster than the rate of viscoelastic strain. This makes it possible, at considerable time values (in our case, at considerable cycle numbers j1, j2), to assume that the increments of total strain ∆ε mainly consist of increments ∆εv. Then, for large values of the cycles numbers j at some instants of time, which differ by multiples of the period T, the increments of viscoelastic strains ∆εv can be expressed in terms of the experimental values. For example, it is convenient to use those times at which the tension stress reach the maximum value. Then at these instants, we can write the following relations:

$$\begin{array}{c}\Delta {\varepsilon }^{cr}+\Delta {\varepsilon }^{v}\approx \Delta {\varepsilon }^{v}\approx \Delta {\varepsilon }_{\mathrm{exp}}, \Delta {\varepsilon }^{v}={\varepsilon }^{v}\left({j}_{1}T+T/2\right)-{\varepsilon }^{v}\left({j}_{2}T+T/2\right),\\ \Delta {\varepsilon }_{\mathrm{exp}}={\varepsilon }_{\mathrm{exp}}\left({j}_{2}T+T/2\right)-{\varepsilon }_{\mathrm{exp}}\left({j}_{2}T+T/2\right).\end{array}$$
(2.7)

where j1, j2, >> 1 is the number of cycle. Parameters α, B are found from system (2.7) by minimizing its quadratic residual.

After that, for small values j1, j2, the increments ∆εcr can be found:

$$\Delta {\varepsilon }^{cr}\approx \Delta \varepsilon -\Delta {\varepsilon }^{v}\approx \Delta {\varepsilon }_{\mathrm{exp}}-\Delta {\varepsilon }^{v}$$
(2.8)

Since ∆εv can already be found by relation (2.3), then Eq. (2.8) will contain only the required characteristics χ0, χ1, m. They can also be found by the method of minimizing the quadratic residual of the system obtained from Eq. (2.8) for different values j1, j2 ~ 1.

Then, the modulus of elasticity E0 can be determined. To do this, it is necessary to use the stress-strain diagram for any cycle at small values of the cycle numbers j, but taking into account the already found laws of viscoelastic and viscoplastic strains. Then, to determine E0, we can use an expression of the following form:

$$\Delta \left({\varepsilon }^{\mathrm{exp}}-{\varepsilon }^{v}-{\varepsilon }^{cr}\right)=\Delta \sigma /{E}_{0}.$$
(2.9)

At the last stage, the parameters of relation (2.5) can be found. To do this, we can compose the following system of equations for cycles with large numbers j1, j2:

$$\Delta {\varepsilon }^{cr}+\Delta {\varepsilon }^{v}+\Delta {\varepsilon }^{\omega }=\Delta {\varepsilon }_{\mathrm{exp}}, \Delta {\varepsilon }^{\omega }={\varepsilon }^{\omega }\left({j}_{1}T+T/2\right)-{\varepsilon }^{\omega }\left({j}_{2}T+T/2\right).$$
(2.10)

They can also be found by the method of minimizing the quadratic residual of the system obtained from Eqs. (2.10) for large values j1, j2 >> 1.

Experimental Results

Experiments were carried out for two variants of cyclic loading (namely, for cyclic tension) of the CFRP cross-ply specimens with [±45]4 lay-up produced from ELUR-P unidirectional carbon fiber and XT-118 cold curing binder. The average values of thickness and width of specimens are h = 0.56 mm (4 laminas with a thickness of 0.14 mm each) and b = 24.60 mm, respectively, with a gage length of l = 110 mm.

The time dependence of stress on a half-cycle was considered linear. In this case, the values εv and εcr were calculated numerically. As a result of processing test data at σmax = 75 MPa and σmin = 0 MPa (this processing was carried out using the procedure outlined above), the following values of the quantities desired were obtained:

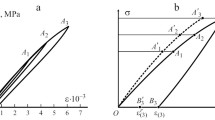
$$\begin{array}{c}{E}_{0}=10100 \mathrm{MPa}, B=2.01\cdot {10}^{-6} {\mathrm{s}}^{\mathrm{\alpha }-1}/\mathrm{MPa}, \alpha =0.68,\\ {\chi }_{0}=0.0116/\left(\mathrm{MPa}\cdot \mathrm{s}\right), {\chi }_{1}=693, m=21.3, \\ {\sigma }_{0}=2.475\cdot {10}^{8} \mathrm{MPa}, n=1, k=4.1, a=101.\end{array}$$
(3.1)

Figures 1 and 2 show the results obtained in the experiment (denoted by round markers), and calculated using the relations (2.1), (2.2), (2.3), and (2.5). Figure 1 also shows the experimental point, which is the value of the residual strain at the instant of unloading after the last cycle. Its numerical value, found in the above-mentioned assumption that the strain εω disappears during unloading, practically coincides with its experimental value, which can be considered a confirmation of this assumption.

Fig. 1.
figure 1

Variation of the total strain (top curve) and the sum of strains εcr + εv + εω (bottom curve), obtained in the test (round markers) depending on the cycle number j for σ = σmax 75 MPa and calculated by relations (3.1), (3.2), (3.3), and (3.5) (solid lines).

Full size image
Fig. 2.
figure 2

Variation of strain εω depending on cycle number j for σ = σmax 75 MPa.

Full size image

Evaluation of the performance of structures has to be carried out on the basis of the strength, stiffness, buckling criteria of their elements. Due to the presence of rheological properties of the material and the accumulation of microdamages over time, as a rule, their stress-strain state changes, as well as a decrease in the strength characteristics of the material. Therefore, in addition to assessing the level of stress-strain state, a large number of works are devoted to the development of the failure criteria of materials, including taking into account the microdamages accumulation (see, for example, in [1, 2, 5,6,7,8,9,10, 13, 34]). When using relations (2.5), as the critical one, we can take the time at which the rate of microdamages accumulation in some elements becomes dangerous (formally, when the curve εω = εω (t) reaches the vertical asymptote).

If we use the approach proposed in [1, 2], then the results above obtained can also be used, assuming that the effective stress can be calculated in terms of the initial elastic characteristics and the sum of strains εel + εω. For example, in the one-dimensional case, as in [12], this condition can be written as follows:

$${\varepsilon }^{el}+{\varepsilon }^{\omega }={\sigma }^{*}/{E}_{0},$$
(3.2)

where σ* is the ultimate strength of the material. However, verification of relation (2.13), on the one hand, was not part of the problem of this study. On the other hand, when carrying out cyclic loading experiments, situations often arose in which the extensometer indicators reached their limit values, after which they could be damaged. Therefore, it was not possible to bring the specimens to failure.

It should be noted that tests of composite specimens with [±45]2s lay-up are carried out, among other things, in order to determine the shear modulus G12 in the plane of the composite reinforcement based on the stress-strain diagram σx(εx). To do this, on the basis of the experimentally obtained dependence σx(εx), the dependence of the secant modulus of elasticity on strain Ex = Ex (εx) in the axes of the specimen is constructed. Further, using the formula G12 = ExC/C (4C –Ex) (C is the experimentally found value), the dependence G12 (γ12) is determined, where the shear strain can be determined with a high degree of accuracy by the simplified formula γ12 ≈ 2εx. The described theoretical-experimental technique is quite simple to implement and allows one to describe the dependence G12 (γ12), which, as shown by numerous studies, is highly nonlinear one.

Conclusion

The review devoted to the problem of describing the degradation processes of FRP shows, that for the experimental assessment of the damage level, as well as for modeling this phenomenon, a large number of methods and constitutive relations were proposed, which are selected depending on both the material and the type of loading. In this study, it is believed, that total strain consists of elastic, viscoelastic, viscoplastic parts, as well as a part formed as a result of material degradation; thus, a phenomenological approach is used to describe all processes. The well-known hypothesis is accepted that the physical relations describing the development of each part of the strain, except for this part itself, include only stress and time. To isolate these parts of the strain in the experimental data, some assumptions were made. Namely, it is believed that strain caused by degradation at short times will be significantly less than other parts of the strain. Therefore, they are neglected in the initial cycles. Further, it is assumed that the rate of viscoplastic strain decays faster than the rate of viscoelastic one. This makes it possible, at considerable time values, to assume that the increments of total strain consist of increments of only viscoelastic strain. The accepted hypotheses make it possible to consistently determine the mechanical characteristics included in the physical relationships. Variants of these ratios are proposed for the above-mentioned parts of strain. The results of solving the problems of identifying the parameters included in the forms of constitutive relations proposed, based on the analysis of the results of cyclic tensile tests, are presented. It is concluded that the hypotheses proposed allow one a fairly good description of the behavior of specimen from the CFRP material under consideration.