Introduction

The deformation and vibrations of structural members connected to an elastic foundation is the subject of many investigations. Behavior of homogeneous beams, plates, and shells were considered as early as in the middle of the last century [1]. In recent decades, composite systems, including three-layer ones, have become widespread. This is due to their special properties, such as the strength and bending stiffness at a minimum weight and good resistance to chemical, thermal, and radiation actions. Various mechanical and mathematical models of elastic three-layer structures were proposed in [2–5]. An analysis of quasi-static deformation of three-layer bars and plates on an elastic foundation was carried out in [6–8]. Vibrations of structural members under impulse actions and thermoradiation impacts were investigated in [9–12]. Unsteady vibrations of an elastic medium bounded by two eccentric spherical surfaces and unsteady wave propagation in an elastic layer were considered in [13–15]. In [16], the resonant vibrations of a circular three-layer plate connected to a Winkler foundation were investigated.

In the present work, small axisymmetric transverse vibrations of an elastic circular plate made of a three-layer composite material and connected to a Winkler foundation are considered under the action of rectangular, sinusoidal, and parabolic impulse loads.

1. Statement of the Problem

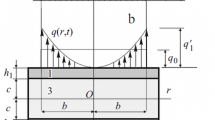
The statement of the problem and its solution is given in the cylindrical coordinates r, φ, and z. The model of a three-layer plate is taken as a basis: the core material is lightweight, i.e., its work in the tangential direction is neglected (ψ = 0 at r = r 1). The external vertical load does not depend on the coordinate φ: q = q(r, t). The reaction of the elastic foundation is applied to the outer face of the second load-carrying layer (Fig. 1). On the plate contour, there is a rigid diaphragm preventing a relative shear of layers. In wiev of symmetry of the problem, there are no tangential displacements in layers, and the deflection w of the plate, the relative shear y in the core, and the radial displacement u of the coordinate surface are functions of the radial coordinate r and time t: u(r, t), ψ (r, t), and w(r, t). Hereafter, we consider these functions as sought ones.

Fig. 1
figure 1

Three-layer circular plate on an elastic foundation.

Full size image

The relation between the reaction of foundation and deflection of the plate is assumed according to the Winkler model:

$$ {q}_R={\kappa}_0w, $$
(1)

where κ 0 is the modulus of subgrade reaction.

The system of differential equations in displacements describing the forced transverse vibrations of a circular three-layer plate connected to an inertialess Winkler foundation, neglecting compression and the rotary inertia of the normal in layers, was obtained in [16]:

$$ \begin{array}{c}\hfill \begin{array}{ll}{L}_2\left({a}_1u+{a}_2\psi -{a}_3w{,}_r\right)=0,\hfill & {L}_2\left({a}_2u+{a}_4\psi -{a}_5w{,}_r\right)=0,\hfill \end{array}\hfill \\ {}\hfill {L}_3\left({a}_3u+{a}_5\psi -{a}_6w{,}_r\right)-{M}_0\overset{\cdot \cdot }{w}-{\kappa}_0w=q.\hfill \end{array} $$
(2)

where M 0 = ρ 1 h 1 + ρ 2 h 2 + ρ 3 h 3 ; ρ k , G k , and K k are the density and elastic moduli of a kth layer; the comma in subscripts, denotes differentiation with respect to the following coordinate; a i are coefficients, and L 2 and L 3 are differential operators:

$$ \begin{array}{c}\hfill {a}_1={\displaystyle \sum_{k=1}^3{h}_k{K}_k^{+}},\kern0.5em {a}_2=c\left({h}_1{K}_1^{+}-{h}_2{K}_2^{+}\right),\kern0.5em {a}_3={h}_1\left(c+\frac{1}{2}{h}_1\right){K}_1^{+}-{h}_2\left(c+\frac{1}{2}{h}_2\right){K}_2^{+},\hfill \\ {}\hfill {a}_4={c}^2\left({h}_1{K}_1^{+}+{h}_2{K}_2^{+}+\frac{2}{3}c{K}_3^{+}\right),\kern0.5em {a}_5=c\left[{h}_1\left(c+\frac{1}{2}{h}_1\right){K}_1^{+}+{h}_2\left(c+\frac{1}{2}{h}_2\right){K}_2^{+}+\frac{2}{3}{c}^2{K}_3^{+}\right],\hfill \\ {}\hfill {a}_6={h}_1\left({c}^2+c{h}_1+\frac{1}{3}{h}_1^2\right){K}_1^{+}+{h}_2\left({c}^2+c{h}_2+\frac{1}{3}{h}_2^2\right){K}_2^{+}+\frac{2}{3}{c}^3{K}_3^{+},\kern1em {K}_k^{+}={K}_k+\frac{4}{3}{G}_k,\hfill \\ {}\hfill {L}_2(g)=\left(\frac{1}{r}(rg){,}_r\right){,}_r\equiv g{,}_{rr}+\frac{g{,}_r}{r}-\frac{g}{r^2},\kern1em {L}_3(g)\equiv \frac{1}{r}\left(r{L}_2(g)\right){,}_r\equiv g{,}_{rrr}+\frac{2g{,}_{rr}}{r}-\frac{g{,}_r}{r^2}+\frac{g}{r^3}.\hfill \end{array} $$

If the plate contour is clamped, the kinematic boundary conditions

$$ u=\psi =w=w{,}_r=0 $$
(3)

have to be satisfied at r = r 1.

At a hinged support of the plate contour and the presence of a rigid diaphragm on it, the conditions

$$ u=\psi =w={M}_r=0 $$
(4)

have to be satisfied at r = r 1, where M r is the generalized internal bending moment expressed in terms of the radial stresses σ (k) r and sought-for displacements:

$$ \begin{array}{c}\hfill {M}_r={\displaystyle \sum_{k=1}^3{\displaystyle \underset{h_k}{\int }{\sigma}_r^{(k)}zdz=\left[{K}_1^{+}{h}_1\left(c+\frac{h_1}{2}\right)-{K}_2^{+}{h}_2\left(c+\frac{h_2}{2}\right)\right]u{,}_r+\left[{K}_1^{-}{h}_1\left(c+\frac{h_1}{2}\right)-{K}_2^{-}{h}_2\left(c+\frac{h_2}{2}\right)\right]\frac{u}{r}}}\hfill \\ {}\hfill +c\left[{K}_1^{+}{h}_1\left(c+\frac{h_1}{2}\right)+{K}_2^{+}{h}_2\left(c+\frac{h_2}{2}\right)+\frac{2}{3}{c}^2{K}_3^{+}\right]\psi {,}_r+\left[{K}_1^{-}{h}_1\left(c+\frac{h_1}{2}\right)+{K}_2^{-}{h}_2\left(c+\frac{h_2}{2}\right)+\frac{2}{3}{c}^2{K}_3^{-}\right]\frac{\psi }{r}\hfill \\ {}\hfill -\left[{K}_1^{+}{h}_1\left({c}^2+c{h}_1+\frac{h_1^2}{3}\right)+{K}_2^{+}{h}_2\left({c}^2+c{h}_2+\frac{h_2^2}{3}\right)+\frac{2}{3}{c}^3{K}_3^{+}\right]w{,}_{rr}\hfill \\ {}\hfill -\left[{K}_1^{-}{h}_1\left({c}^2+c{h}_1+\frac{h_1^2}{3}\right)+{K}_2^{-}{h}_2\left({c}^2+c{h}_2+\frac{h_2^2}{3}\right)+\frac{2}{3}{c}^3{K}_3^{-}\right]\frac{w{,}_r}{r}.\hfill \end{array} $$

The conditions

$$ w\left(r,0\right)\equiv f(r),\kern1em \overset{\cdot }{w}\left(r,0\right)\equiv g(r) $$
(5)

are taken as the initial ones. The problem for search of the functions u(r,t), ψ (r,t), and w(r,t) is closed by adding the boundary and initial conditions Eqs. (3)-(5) to equilibrium equations (2).

2. Solution of the Initial Boundary-Value Problem

The solution can be presented in the series form

$$ \begin{array}{c}\hfill q\left(r,t\right)={M}_0{\displaystyle \sum_{n=0}^{\infty }{\nu}_n{q}_n(t)},\kern0.5em u\left(r,t\right)={b}_1{\displaystyle \sum_{n=0}^{\infty }{\varphi}_n{T}_n(t)},\hfill \\ {}\hfill \psi \left(r,t\right)={b}_2{\displaystyle \sum_{n=0}^{\infty }{\varphi}_n{T}_n(t)},\kern0.5em w\left(r,t\right)={\displaystyle \sum_{n=0}^{\infty }{\nu}_n{T}_n(t)}.\hfill \end{array} $$
(6)

Here, ν n ≡ ν (λ n , r) is the system of orthonormal eigenfunctions satisfying boundary conditions (3) and (4) and the condition of boundedness of the solution at the origin of coordinates [16], namely

$$ {\nu}_n\left({\lambda}_n,r\right)\equiv \frac{1}{d_n}\left[{J}_0\left({\lambda}_nr\right)-\frac{J_0\left({\lambda}_n{r}_1\right)}{I_0\left({\lambda}_n{r}_1\right)}{I}_0\left({\lambda}_nr\right)\right], $$
(7)

where

$$ \begin{array}{c}\hfill {\varphi}_n\left({\lambda}_n,r\right)=\frac{\lambda_n}{d_n}\left[{J}_1\left({\lambda}_n{r}_1\right)r-{J}_1\left({\lambda}_nr\right)+\frac{J_0\left({\lambda}_n{r}_1\right)}{I_0\left({\lambda}_n{r}_1\right)}\left({I}_1\left({\lambda}_n{r}_1\right)r-{I}_1\left({\lambda}_nr\right)\right)\right],\hfill \\ {}\hfill {\lambda}_n^4={\beta}_n^4-{\kappa}^4,\kern0.5em {\beta}^4={M}^4{\omega}^2,\kern0.5em {M}^4={M}_0D,\hfill \\ {}\hfill D=\frac{a_1\left({a}_1{a}_4-{a}_2^2\right)}{\left({a}_1{a}_6-{a}_3^2\right)\left({a}_1{a}_4-{a}_2^2\right)-{\left({a}_1{a}_5-{a}_2{a}_3\right)}^2},\kern0.5em {\kappa}^4={\kappa}_0D.\hfill \end{array} $$

Here, d n are normalizing constants, and J 0 is the zeroth-order Bessel function; I 0 is the modified Bessel function [17] expressed in terms of eigenvalues β n ; ω n are the natural frequencies of the plate.

In the case of clamped contour of the plate, the parameters of λ n are roots of the transcendental equation

$$ {I}_1\left(\lambda {r}_1\right){J}_0\left(\lambda {r}_1\right)+{J}_1\left(\lambda {r}_1\right){I}_0\left(\lambda {r}_1\right)=0. $$

In the case of boundary conditions (4), we find them from the equation

$$ {J}_0\left(\lambda {r}_1\right)\left[{a}_7\left(\lambda {I}_0\left(\lambda {r}_1\right)-\frac{I_1\left(\lambda {r}_1\right)}{r_1}\right)+\frac{a_8}{r_1}{I}_1\left(\lambda {r}_1\right)\right]+{I}_0\left(\lambda {r}_1\right)\left[{a}_7\left(\lambda {J}_0\left(\lambda {r}_1\right)-\frac{J_1\left(\lambda {r}_1\right)}{r_1}\right)+\frac{a_8}{r_1}{J}_1\left(\lambda {r}_1\right)\right]=0, $$

where

$$ \begin{array}{l}{a}_{60}={h}_1\left({c}^2+c{h}_1+\frac{1}{3}{h}_1^2\right){K}_1^{-}+{h}_2\left({c}^2+c{h}_2+\frac{1}{3}{h}_2^2\right){K}_2^{-}+\frac{2}{3}{c}^3{K}_3^{-},\hfill \\ {}{K}_k^{-}\equiv {K}_k-\frac{2}{3}{G}_k,\kern0.5em {a}_7={a}_6-{a}_3{b}_1-{a}_5{b}_2,\kern1em {a}_8={a}_{60}+{a}_3{b}_1+{a}_5{b}_2.\hfill \end{array} $$

The equation for determining the unknown function of time T n (t) follows from the third equation of system (2) after insertion of expressions (6) and (7) into it:

$$ {T}_n+{\omega}_n^2{T}_n={q}_n. $$

The general solution of this equation is

$$ {T}_n(t)={A}_n \cos {\omega}_nt+{B}_n \sin {\omega}_nt+\frac{1}{\omega_n}{\displaystyle \underset{0}{\overset{t}{\int }} \sin {\omega}_n\left(t-\tau \right){q}_n\left(\tau \right)d\tau }. $$
(8)

The coefficients A n and B n are found from initial conditions (5). The parameters of series expansion of the load q n (t) are obtain by multiplying the first of relations (3) by v n and integrating it over the plate area. Due to orthnormality of the system of eigenfunctions (7), we have

$$ {q}_n(t)=\frac{1}{M_0}{\displaystyle \underset{0}{\overset{r_1}{\int }}q\left(r,t\right){v}_nr\mathrm{d}r}. $$
(9)

3. Particular Solutions and Numerical Results

Let us consider several types of local surface loads applied instantantly to the outer surface of the load-carrying layer of a three-layer elastic circular plate.

3.1. Let a local and suddenly applied surface load q(r,t) uniformly distributed inside a circle of radius b ≤ r 1 acts on the plate. Such a loading can be presented by using the Heaviside function H 0 (x):

$$ q\left(r,t\right)={q}_0{H}_0(t){H}_0\left(b-r\right). $$
(10)

Inserting Eq. (10) into Eq. (9), we obtain the integral relation for the parameters q n (t)

$$ \begin{array}{c}\hfill {q}_n(t)=\frac{q_0{H}_0(t)}{M_0{d}_n}{\displaystyle \underset{0}{\overset{r_1}{\int }}{H}_0\left(b-r\right)\left({J}_0\left({\lambda}_nr\right)-\frac{J_0\left({\lambda}_n{r}_1\right)}{I_0\left({\lambda}_n{r}_1\right)}{I}_0\left({\lambda}_n{r}_1\right)\right)r\;\mathrm{d}\;r},\hfill \\ {}\hfill {\displaystyle \underset{0}{\overset{r_1}{\int }}{H}_0\left(b-r\right){J}_0\left({\lambda}_nr\right)rdr}={\displaystyle \underset{0}{\overset{b}{\int }}{J}_0\left({\lambda}_nr\right)r\mathrm{d}r=\frac{b{J}_1\left({\lambda}_nb\right)}{\lambda_n}},\kern1em {\displaystyle \underset{0}{\overset{r_1}{\int }}{H}_0\left(b-r\right){I}_0\left({\lambda}_nr\right)r\;\mathrm{d}\;r=\frac{b{I}_1\left({\lambda}_nb\right)}{\lambda_n}}.\hfill \end{array} $$

As a result, we have

$$ {q}_n(t)=\frac{q_0{H}_0(t)b}{M_0{d}_n{\lambda}_n}\left({J}_1\left({\lambda}_nb\right)-\frac{J_0\left({\lambda}_n{r}_1\right)}{I_0\left({\lambda}_n{r}_1\right)}{I}_1\left({\lambda}_nb\right)\right). $$
(11)

Now, the forced vibrations of the circular three-layer plate are described by relations (6), and the function T n (t) is calculated by formula (8) with account of Eq. (11).

If the intensity of the uniform external load q 0 is constant in magnitude, we have at A n = B n = 0

$$ {T}_n(t)=\frac{q_0b\left(1- \cos \left({\omega}_nt\right)\right)}{M_0{d}_n{\lambda}_n{\omega}_n^2}\left({J}_1\left({\lambda}_nb\right)-\frac{J_0\left({\lambda}_n{r}_1\right)}{I_0\left({\lambda}_n{r}_1\right)}{I}_1\left({\lambda}_nb\right)\right). $$
(12)

Numerical results were obtained for a circular three-layer plate of unit radius consisting of D16-fluoroplastic-D16 layers and clamped along its contour. Its natural frequencies ω n were calculated from formula (7) by using the eigenvalues given in [16] at h 1 = h 2 = 0.01 and c = 0.05. In calculating deflections, the first 15 terms of the series were considered. Adding another 85 following terms changed the result by less than 0.1 %.

The data of Fig. 2 demonstrate the variations of deflection w and relative shear ψ along the radius of the three-layer plate at the instant of time t = 0.026 corresponding to the maximum displacements in the case with local load spots of radii b = 0.5 and 1. Hereinafter, it is assumed that, in the presence of an elastic foundation, q 0 = 7 · 105 Pa and k o = 108 Pa/m, but in the absence of foundation, q 0 = 7 · 103 Pa. Spreading the load over the entire area of plate increased the deflection twice and the relative shear 1.5 times.

Fig. 2
figure 2

Variation in the deflection w and relative shear ψ along the radius r of plate at b = 0.5 (1) and 1 (2).

Full size image

The data of Fig. 3 illustrate the time-dependent deflection of the plate at its center at b = 0.5 and 1 and identical loads. In the absence of foundation, we have a fluctuating stress cycle. A growth in the radius of force circle increases the vibration amplitude. At an average stiffness of foundation κ 0 = 108 Pa/m, an asymmetric cyclic process is observed. On increasing the stiffness of foundation to κ 0 = 109 Pa/m, the graph moves down and approaches the symmetric cycle.

Fig. 3
figure 3

Time-dependent deflections w at the center of plate at b = 0.5 (1) and 1 (2) in the absence of foundation (a) and at κ 0 = 108 (b) and κ 0 = 109 Pa/m (c).

Full size image

A nonlinear growth in the maximum deflection of the plate with increasing radius b of the load spot is illustrated by the data of Fig. 4. The presence of foundation slightly changes the character of the curve. In this case, the deflection of the plate at a load ten times higher is four-fold smaller.

Fig. 4
figure 4

Deflection w at the center of plate vs. the radius b of load spot: without an elastic foundation at t = 0.033 (1) and with an elastic foundation at κ 0 = 108 Pa/m and t = 0.026 (2).

Full size image

3.2. Let us assume that a load uniformly distributed in a ring a ≤ r ≤ b is suddenly applied to the plate:

$$ q\left(r,t\right)={q}_0{H}_0(t){H}_0\left(b-r\right)-{H}_0\left(a-r\right). $$
(13)

Inserting Eq. (13) into formulas (9) and evaluating the integrals, we obtain the parameters q n (t) of series expansion of the load q(r,t) in the form

$$ {q}_n(t)=\frac{q_0{H}_0(t)}{M_0{d}_n{\lambda}_n}\left(b{J}_1\left({\lambda}_nb\right)-a{J}_1\left({\lambda}_na\right)-\frac{J_0\left({\lambda}_n{r}_1\right)}{I_0\left({\lambda}_n{r}_1\right)}\left[b{I}_1\left({\lambda}_nb\right)-a{I}_1\left({\lambda}_na\right)\right]\right). $$

For a load of constant intensity (q 0 = const),

$$ {T}_n(t)=\frac{q_0\left[1- \cos \left({\omega}_nt\right)\right]}{M_0{d}_n{\lambda}_n{\omega}_n^2}\left(b{J}_1\left({\lambda}_nb\right)-a{J}_1\left({\lambda}_na\right)-\frac{J_0\left({\lambda}_n{r}_1\right)}{I_0\left({\lambda}_n{r}_1\right)}\left[b{I}_1\left({\lambda}_nb\right)-a{I}_1\left({\lambda}_na\right)\right]\right). $$
(14)

At a = 0, solution (12) for a circular load spot follows from Eq. (14).

On Fig. 5, variations in the deflection form and values of plates not connected and connected to an elastic foundation in relation to the location of the ring load spot. Its width d = b − a = 0.25 the intensity of load q 0 = 7000 Pa, and the instant of time t = π/ω 0 correspond to the maximum value of function (14).

Fig. 5
figure 5

Variation in the deflection w of plate under a ring load in the case of absence of foundation (a) and at κ 0 = 108 Pa/m (b); a = 0 (1), 0.25 (2), 0.5 (3), and 0.75 (4).

Full size image

In the absence of foundation, the least deflection arises if the load is concentrated at the contour, but the greatest one when the load is distributed in a ring 0.25 ≤ r ≤ 0.5 (see Fig 5a). In the presence of elastic foundation with κ 0 = 108 Pa/m (see Fig. 5b), the maximum deflection decreases in 4.5 times and is reached if the load is distributed in the interval 0.5 ≤ r ≤ 0.75.

Conclusions

For each of the considered cases of local axisymmetric dynamic actions on a three-layer circular plate connected to an elastic foundation, the solutions obtained allows one to investigate its vibrations in relation to the character and magnitude of the load applied and stiffnesses of the elastic foundation and plate.