With the development of industry, much less time is now spent on the fabrication of articles (objects) of complex shape than is needed to monitor their geometric parameters. In aviation, exact correspondence of a part to given dimensions is of exceptional importance, since this affects the functionality and reliability of different mechanisms. Thus, the development of a high-speed, high-precision method for the measurement of the geometric parameters of objects of complex shape is an important problem related to safe operation of aircraft.

Analysis of existing measurement methods. Current widespread methods of measurement are of two types, either contact or noncontact. Contact methods are realized with the use of standard devices and plate-measuring engines. With the use of such devices, it is possible to produce measurements with precision ~(1–9)·10–6 m, though these devices suffer from a number of drawbacks, including low response, high overall dimensions, stationary placement, direct contact of the probe (or template) with the part; and high production cost and high operating costs [1].

Contactless methods utilize laser scanning systems which lack these drawbacks. Through the use of the most recent developments of laser scanning systems, it is possible to achieve measurement precision no less than the precision of contact devices [2], though despite the high rate of measurement of a single individually selected point, the overall response of laser scanners is not adequate. Where the part possesses large dimensions and (or) a set of interface lines that create discontinuities in the functions of the mathematical model, maintenance of a given degree of precision requires tens of millions of measurements. The engine used to deflect the laser beam responsible for scanning the surface is also a drawback of laser measuring engines. Such systems always possess mechanical elements that undergo wear as they are used, which reduces the quality of the measuring engine. Still another drawback derives from the rigorous requirements imposed on the reflection of the beam by the surface of the measured part. Often, laser range finders are unable to measure the distance to an object due to aspects of the reflection properties of the surface or incongruous reflection angles.

In the present article, we will propose a measurement method by means of which we can dispense with the scanning of the object with a laser beam.

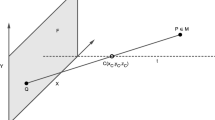
Photoprojection method. The design of the photoprojection method of measuring a three-dimensional (3D) profile of an object is presented in Fig. 1. In the measurement procedure, the object 4 is scanned by a projector of a periodic pattern (coordinate grid) 1. The functional relationships of the variation of the pattern by coordinates X and Y are known. The distance to a single arbitrarily selected point is measured by a laser range finder 2. The reflection spot of the range finder’s laser beam is adopted as the coordinate origin relative to which the set of points of the mathematical model is constructed. The image of the object with projection of the periodic pattern superimposed on it and the light spot of the laser range finder are fixed by the camera 3.

Fig. 1.
figure 1

Block diagram of device for high-speed measurement of shape: 1) projector; 2) laser range finder; 3) camera; 4) object.

Full size image

We adopt the following terms and assumptions: absolute reading point, or exit point of laser beam from the range finder’s optical system; reading point of projector, or focus of optical system of projection; reading point of camera, or point of intersection of the focal axis of the optical system with plane of camera; focal planes of the projection system and the camera coincide and are orthogonal to the beam of the laser range finder; the input-output points of the optical system of the range finder, projector, and camera are coplanar; light propagates rectilinearily; the distance to the object is measured along the Z-axis.

Similar designs have been developed abroad, though these designs utilize illumination of the object by parallel rays of light without positioning of the reference point by the beam of a laser range finder [3].

Procedural foundations. In the general case, the problem of contactless remote measurement of the 3D profile of objects reduces to a determination of the coordinates of a set of points on the surface of the object to which the distance from an absolute reading point and the angles of deviation of the beam of a range finder from the Z-axis are known (Fig. 2). We will propose that measured coordinates n of the check points on the object form a file {P 1, ..., P i }, where i = 0, ..., n. We determine the coordinates of an arbitrary point P i by means of the formulas

$$ \left.\begin{array}{l}{x}_i={D}_i\sin \upalpha; \\ {}{y}_i={D}_i\cos \upalpha \sin \upbeta; \\ {}{z}_i={D}_i\cos \upalpha \cos \upbeta .\end{array}\right\} $$
(1)
Fig. 2.
figure 2

Principle of laser scanning: 1) laser range finder; 2) object.

Full size image

A digital image of an object of complex shape is created in this method. The arbitrary linear dimension, i.e., the distance between points P i and P n on the object, is determined as

$$ {M}_{P_i{P}_n}=\sum \limits_{i=0}^{n-1}\sqrt{{\left({x}_{i+1}-{x}_i\right)}^2+{\left({x}_{i+1}-{y}_i\right)}^2+{\left({z}_{i+1}-{z}_i\right)}^2}=\sum \limits_{i=1}^n\sqrt{\Delta {X_i}^2+\Delta {Y_i}^2+\Delta {Z_i}^2}. $$
(2)

Any curvilinear dimension belonging to the controlled surface is determined as a result of successive summation of its constituent segments, provided that there is a small enough distance between the scanned points. A set of points is needed to create an exact digital image of an object and this is a difficult procedure and requires time and a precision system for the deflection of the beam of a range finder. There now exist high-speed systems [4] by means of which the geometric parameters of objects of simple shape (figures of revolution) may be measured using a small number of reference points. The distinction of the proposed method of measurement of the geometric parameters of objects of complex shape is that it makes it possible to obtain a set of points of the digital image of a test part in a single measurement cycle without the use of mechanical systems to produce a deflection of a laser beam.

Mathematical model of device. Let us consider a projection system consisting of a projector, laser range finder, and planar screen (including the X-axis). We will assume that the plane of the screen and the XY plane of the computational coordinate system are parallel and that the pattern is projected by a diverging light fl ux. Figure 3 (XY plane perpendicular to the plane of figure) shows a geometric model of the photographic measuring engine (projector).

Fig. 3.
figure 3

Geometric model of projection system: 1) projector; 2) laser range finder; 3) camera; 4) object.

Full size image

We select a point S on the X-axis the distance to which is known from the readings of the laser range finder as the coordinate origin. In this case the coordinates X 0 of a point lying on the X-axis and belonging to the terminator line (light separator) of the projected grid may be calculated by the formula

$$ {X}_0=\left(f+D\right)\left[\upsigma /2+{k}_x\left(\uprho +\upsigma \right)\right]/f-L, $$
(3)

where ρ and σ are the dimensions of the dark and light bands of the screen (physical carrier) of the grid (cf. Fig. 3); k x , ordinal number of darkened band counted off from the optical axis of the projector in the direction of the laser range finder (coefficient); D, distance from focal plane of projector to plane of screen; and ƒ, focal distance of lens of projector.

Since the grid is periodic, the coordinate Y 0 may be calculated in similar fashion, but without taking into account the displacement of the reading point along the X-axis:

$$ {Y}_0=\left(f+D\right)\left(\upsigma /2+{k}_y\left(\uprho +\upsigma \right)\right)/f. $$
(4)

Thus, once the distance D is known, it is then always possible to determine the geometric locus of an arbitrary point of the projection of the terminator line on an ideally planar screen. This makes it possible to find an analytic relationship between the absolute coordinate system (X; Y) as a function of the distance to the screen D and the step ρ, σ of the coordinate system of the projector: Y = F(D; σ; ρ), X = F(D; σ; ρ).

Mathematical model of photorecorder. We adopt the following initial conditions: focal plane of optical system of camera and plane of screen are parallel; the axis m of the coordinate system of the projector is collinear with the axis μ of the coordinate system of the photomatrix; and the focal distance ƒ of the optical systems of the projector and the camera are identical. In this case, the axis n of the coordinate system of the projector is parallel to the axis η of the plane of the photomatrix. The coordinates x 0 and μ0 of the points of the terminator on the controlled object and on the photomatrix are connected by the relationship [4]

$$ {\upmu}_0=-f\left(L-{x}_0\right)/D $$
(5)

where the coordinate μ of the point in the plane (μ; η) corresponds to the coordinate x of the point in the plane (X; Y).Substituting in (5) the analytic value (3) derived for a point with coordinate x, we obtain

$$ \upmu =\left[\left(f+D\right)\left(\upsigma /2+{k}_x\left(\uprho +\upsigma \right)\right)-2 fL\right]/\left[\left(f+D\right)m-2 fL\right]/D, $$
(6)
$$ m=\upsigma /2+{k}_x\left(\uprho +\upsigma \right). $$
(7)

Since the directions of the axes n, Y, and η coincide, we may write similar expressions for the axis Y as follows:

$$ \upeta = fy/D=\left(f+D\right)\left(\upsigma /2+{k}_y\left(\uprho +\upsigma \right)\right)/D=\left(f+D\right)n/D; $$
(8)
$$ n=\upsigma /2+{k}_y\left(\uprho +\upsigma \right). $$
(9)

Thus, the known distribution function F(m; n) of the lines of the projector grid is transformed into the computed function F(X; Y) of the lines of the grid on an ideally planar screen and is next transformed into a measured coordinate F(μ; η) for finding the corresponding lines of the grid in the camera matrix. The procedure used to measure the geometric parameters of an object of complex shape begins with selection of a reading point specified by the marker of the laser range finder, which determines the distance D (cf. Fig. 3). We select the point S on the object as the coordinate origin for all three reference systems. In the photomatrix, this point is represented in the form S′ and will correspond to the origin of the scale in the image of the object.

Expressions (3)–(9) determine analytic relationships between the parameters of the coordinate grid specified by the functions F(m; n) and F(X; Y) that depend on the distance to the screen D and F(μ; η), the values of which are computed by the camera matrix. Obviously, where the screen deviates from an ideal form, the observed lines will be shifted relative to the computed positions, Since from the practical point of view any object may be considered a nonideally planar screen, once the displacement of the lines of the projected pattern is fixed, we obtain values ΔX i , ΔY i , ΔZ i for any point found on the terminator line, that is, information about the shape of the study object. The number of measurement points accessible for the construction of a digital image of the object will be equal to the number of pixels in the photomatrix on the lines of the grid.

A block diagram of the photoprojection measuring engine is shown in Fig. 4. It follows from (2) that the solution of the system of equations in (1) relative to an arbitrarily selected point of the surface must be known in order to calculate the dimensions of an object relative to a selected reference point. The coordinates of the points of intersection of the beams of the projector with the imaginary plane (X 0; Y 0) found at a distance D 0 form the terminator line. Any computed point P i situated on these lines has the coordinates X ob, Y ob, Z ob and is represented in the plane of the photomatrix in the form X ob(μ; η), Y ob(μ; η). We write a system of equations for determining the position of the observed points forming a real terminator line on the object relative to the imaginary terminator line, which must occur in the imaginary plane (X 0; Y 0):

$$ \left.\begin{array}{l}\Delta X={X}_0-{X}_{\mathrm{ob}};\\ {}\Delta Y={Y}_0-{Y}_{\mathrm{ob}};\\ {}\Delta \mathrm{Z}={\mathrm{Z}}_0-{\mathrm{Z}}_{\mathrm{ob}}.\end{array}\right\} $$
(10)
Fig. 4.
figure 4

Geometric model of photoprojection measuring engine: 1) projector; 2) pupil of optical system of photorecorder; 3) laser range fi nder; 4, 5) photomatrix and its magnified projection, respectively; 6) object.

Full size image

Viewed from the projector (cf. Fig. 3), the coordinate of any point X 0 of a projected terminator line is determined from (3).

Recalling that

$$ {\displaystyle \begin{array}{c}{X}_{\mathrm{ob}}={\upmu}_{\mathrm{ob}}{D}_{\mathrm{ob}}/f+L;\\ {}\tan \upalpha =\left[\upsigma /2+{k}_x\left(\uprho +\upsigma \right)\right]/f={X}_0/\left({D}_0+f\right)={X}_{\mathrm{ob}}/\left({D}_{\mathrm{ob}}+f\right),\end{array}} $$
(11)

we find

$$ {X}_{\mathrm{ob}}=\left({D}_{\mathrm{ob}}+f\right)\left(\upsigma /2+{k}_x\left(\uprho +\upsigma \right)\right)/f. $$
(12)

Comparing (11) and (12), we write an equation for determining the distance to an observed point D ob, expressed in terms of the parameters of the projector (σ, ρ), and the photomatrix (η, ρ):

$$ \left({D}_{\mathrm{ob}}+f\right)\left(\upsigma /2+{k}_x\left(\uprho +\upsigma \right)\right)=-{\upmu}_{\mathrm{ob}}{D}_{\mathrm{ob}}+ fL. $$

We recall (7) and write

$$ {D}_{\mathrm{ob}}m+{\upmu}_{\mathrm{ob}}{D}_{\mathrm{ob}}= fL- fm;\kern1em {D}_{\mathrm{ob}}=f\left(L-m\right)/\left({\upmu}_{\mathrm{ob}}+m\right). $$

For the Y-axis,

$$ {Y}_{\mathrm{ob}}=\left({D}_{\mathrm{ob}}+f\right)\left(\upsigma /2+{k}_y\left(\uprho +\upsigma \right)\right)/f;\kern0.5em \left({D}_{\mathrm{ob}}+f\right)\left(\upsigma /2+{k}_y\left(\uprho +\upsigma \right)\right)/f={\upeta}_{\mathrm{ob}}{D}_{\mathrm{ob}}/f. $$

Recalling (8), we find

$$ \left({D}_{\mathrm{ob}}+f\right)n=-{\upeta}_{\mathrm{ob}}{D}_{\mathrm{ob}};\kern1em {D}_{\mathrm{ob}}=- fn/\left({\upeta}_{\mathrm{ob}}+n\right). $$

For the Z-axis,

$$ {Z}_0=D;\kern1em {Z}_{\mathrm{ob}}={D}_{\mathrm{ob}}=f\left(L-m\right)/\left({\upmu}_{\mathrm{ob}}+m\right)= fn/\left({\upeta}_{\mathrm{ob}}+n\right). $$

System (10) may be written in the following form:

$$ \left.\begin{array}{l}\Delta X=\left(f+{Z}_0\right)m/f+{\upmu}_{\mathrm{ob}}\left(L-m\right)/\left({\upmu}_{\mathrm{ob}}+m\right)-2L;\\ {}\Delta Y=\left(f+{Z}_0\right)n/f+{\upeta}_{\mathrm{ob}}n/\left({\upeta}_{\mathrm{ob}}+n\right);\\ {}\Delta Z={D}_0-f\left(L-m\right)/\left({\upmu}_{\mathrm{ob}}+m\right)={D}_0- fn/\left({\upeta}_{\mathrm{ob}}+n\right),\end{array}\right\} $$
(13)

where m = σ/2 + k x (ρ + σ), n = σ/2 + k y (ρ + σ) are parameters of the projection grid; k x , k y , node numbers of the projection grid.

The distances between arbitrary points P 0, ..., P i , ..., P n of the surface of the object and points lying on terminator lines of the projected coordinate system may be calculated with the use of the expressions in (13). By determining the set of points of an object of complex form relative to the nodes of the grid, it is possible to increase the precision and speed of the measurements without resorting to continuous scanning of the object.

The errors in the measurements of the geometric parameters of objects of complex shape depend on the precision with which the coordinates of points on the surface of the object is determined. In the present method, the measurement errors are determined by many factors, including the procedure error associated with the step of the projection grid; and the instrument errors of the laser range finder, projection system, and television camera, all of which depend on the resolution of the optical system and the photomatrix. A complete metrological analysis of the new device requires a large number of studies and falls outside the scope of the present investigation. Here, we only wish to indicate a plan of metrological analysis by means of which a technique for determining the general metrological indicators of an article may be created and the requirements imposed on the component parts of equipment, determined based on the concrete requirements imposed on the errors in the measurements of the dimensions of an article.

In the analysis of the geometric parameters of articles of complex shape, we understand by a measurement of linear dimensions a determination not only of the length M jk of a rectilinear segment connecting two arbitrary points P j and P k in the image, but also the length of the line MS jk connecting selected points on a curvilinear surface of the object. In this case, the absolute Δ jk and relative ε jk errors in the measurements are determined correspondingly by the formulas [5]

$$ {\Delta}_{jk}={M}_{jk}^{\mathrm{ref}}-{M}_{jk}\left(\upmu \upeta \right),\kern1em {\upvarepsilon}_{jk}={\Delta}_{jk}/{L}_{jk}^{\mathrm{ref}}, $$
(14)

where \( {M}_{jk}^{\mathrm{ref}} \) is the length of the segment P j P k measured by a reference device, and M jk (μη) is the length of the same segment measured in the image and computed in terms of its coordinate by formula (2) with the use of (13).

In [4, 6], it is shown that in the most unfavorable case, when all the errors in the measurement of the coordinates are of the same sign, the errors in the measurements of the dimensions Δ jk and in the coordinates of the points in space Δco are related by the relationship \( {\Delta}_{jk}=\sqrt{3{\Delta}_{\mathrm{co}}} \). The actual error may be significantly less and in the range \( 0<{\Delta}_{jk}<{\Delta}_{\mathrm{co}}=\sqrt{3} \).

$$ {\Delta}_{\Sigma}=\sqrt{\Delta_{\mathrm{n}}^2+{\Delta}_{\mathrm{c}}^2+{\Delta}_l^2+{\Delta}_{\mathrm{r}}^2,} $$
(15)

where Δn is the error of the projection system of the grid; Δc, error of the camera, which includes the optical distortions produced by the lens and the digitization of the matrix; Δ l , error in the measurement of the ultimate dimension of the laser spot; and Δr, error of laser range finder.

Let us assume that at a distance of 1 m from the laser to the object, the errors are given as Δn = 0.1 mm; Δr = 0.1 mm; Δc = 0.3 mm (matrix 1024 × 1024); and dimension of laser spot Δ l = 0.2 mm, whence by (15) ΔΣ = 0.39 mm.

Preliminary calculations have shown that all the components of the errors are commensurable and depend directly proportionally on the distance from the optical system to the object. The greatest contribution is made by the errors caused by the discreteness of the photomatrix, the parameters of which are being continuously improved. In the measurements it is necessary to reduce the distance to the object, though this leads to significant optical distortions. When processing information, it is best to use the complete screen in the image and to employ special programs for correction of optical distortions. The numerical values of the errors which are obtained are maximally overstated, since they are defined for unfavorable cases, when all the different types of errors are of the same sign and contain the maximum constituent components.

On the whole, whether the required measurement precision can be attained depends on the shape of the object and the components of the equipment employed as well as requiring an individualized approach for different objects and different measurement conditions.

Conclusion. The proposed photoprojection method for the measurement of the geometric parameters of parts of complex shape substantially reduces the time needed for quality control of an article, since it does not require scanning of the surface and enables the determination of an arbitrarily large set of points on a surface found in recognizable elements of the projected coordinate system, such as a terminator line or projection grid. The proposed method does not require systems for the deflection of a laser beam and is less demanding as regards angles and the reflectance of the material of the part, since it utilizes both the illuminated region of the projected grid as well as its darkened part as the information signal. Thus, in view of the substantial capabilities of image processing, it may be asserted that the overall time needed for measurement of the geometric parameters of a part will be equal to the time needed to obtain a single photograph of an object from each of several required approach angles. Through the use of the proposed method, it is possible to significantly increase the rate of inspection of the geometric parameters of articles of complex shape, increase the work efficiency, selectively reject effectively all articles that do not correspond to given dimensions, including those encountered with the use of additive technologies for the production of the parts of machines, engines, and the elements of the structures of aircraft engines.

The present study was carried out with the support of the Ministry of Education and Science of Russia in the framework of the State Assignment (Project No. 8.2297.2017/4.6).