Numerical analyses of rectangular micro-textures in hydrodynamic lubrication regime for sliding contacts

Abstract

Hydrodynamic lubrication of rectangular micro-textures on sliding contact surfaces is investigated using numerical calculation methods. The theoretical models for the slider surface are developed and the film pressure is used to evaluate the hydrodynamic lubrication based on the Reynolds equation. Meanwhile, the geometry and distribution of the rectangular dimples are optimized for maximizing the average film pressure. Results show that the film pressure is dependent on the geometry and distribution of the rectangular micro-dimples. The optimal geometry of the single rectangular dimple is obtained, and the spacing has an important influence on the film pressure. The distribution types of rectangular dimples affect the hydrodynamic lubrication significantly and the interlaced array of the rectangular micro-dimples is beneficial to enhancing the hydrodynamic lubrication. Meanwhile, the rectangular dimples with 72° interlaced angle exhibits the best effectivity.

1 Introduction

Surface textures have proven to be an effective way to enhance the friction and lubrication performances of contact surfaces for many years, and they are used in many mechanical components including bearings [1], piston rings [2], mechanical seals [3], cutting tools [4], gears [5] and cylinder liners [6]. The main functions of the micro-textures are summarized as: capturing wear debris to avoid severe surface damages [7], reducing the actual contact area to decrease the friction coefficient [8], acting as reservoirs to supply micro-lubrication [9] and generating hydrodynamic lubrication to increase the load carrying capacity [10]. Among above functions, the certain improvement of additional hydrodynamic lubrication is regarded as the most dominant mechanism for wide applications of surface textures, which has attracted considerable attention for many years.

Fundamental researches on hydrodynamic lubrication of surface textures have been conducted with experimental and numerical methods [11,12,13,14]. Various results show that the dispersed and closed dimples are beneficial to generating hydrodynamic effect compared to the continuous grooves [15, 16], and the geometry of textures has a profound influence on the hydrodynamic lubrication [11, 17]. For examples, Wang et al. [18] evaluated the hydrodynamic effect of micro-dimples using sliding friction experiments, and it was found that an optimum geometry and distribution of cylinder micro-dimples exists where the load carrying capacity was increased at least twice due to the increasing hydrodynamic pressure. Costa and Hutchings [19] investigated the influence of micro-texture topography (circle, groove and chevron) with various geometries on lubricant film thickness under hydrodynamic lubrication conditions. Experimental results showed that the textures geometrical shapes affected the film thickness and hydrodynamic pressure. Besides, lots of theorical and numerical studies about the hydrodynamic lubrication of textures showed that the texture depth, area ratio, shape, inner structure and location influence the hydrodynamic lubrication and load capacity by evaluating the film pressure [20,21,22,23]. The hydrodynamic pressure generated between textured surfaces was attributed to the convergent wedge-shaped gaps formed by the surface textures [20]; meanwhile, researchers found that the pressure was dependent on the variation of convergence ratio, which was strongly influenced by the geometry of textures [24]. Therefore, the optimization of textures is necessary and important for improving the hydrodynamic effect.

The dimple and groove textures are commonly used in investigations [25, 26], and the rectangular micro-dimple, as a typical shape, is investigated and utilized for reducing friction and increasing the load carrying capacity [27,28,29]. The advantages of rectangular micro-dimples demonstrate potential benefits in improving the hydrodynamic lubrication due to the film pressure generation [30], secondary lubrication [31] and micro-bearing lubrication [20]. Considerable experimental investigations about the rectangular dimples on lubrication and friction were performed, results showed that the rectangular textures had the lower average friction coefficient than circular textures reported by Zhang et al. [32] and the square dimples with a width of 5 µm exhibited lower friction compared to the groove textures under lubricated conditions [26]. Furthermore, Grewal et al. [33] experimentally compared three rectangular micro-textures with different lengths, widths and aspect ratios for enhancing the wettability and friction performance; unfortunately, the geometry of rectangular micro-textures was limited with several parameters. Lu et al. [34] revealed that the square-shaped dimples worked as lubricant reservoirs lowered the friction by secondary lubrication regimes using experimental methods, and the performance depended on the geometry of textures. While the experimental works are time-consuming and limited. Dobrica et al. [35] used numerical analyses to optimize square-textured surface with regard to different plane-inclined sliders and dimple aspects for improving the hydrodynamic lubrication. Further, Papadopoulos et al. [29] used CFD simulations to exhibit that the proper square dimples can improve the load-carrying capacity by increasing the film thickness and film pressure on fluid dynamic lubrication. Considering the inner structures of surface textures, the bottom shape of rectangular micro-textures was studied for stronger film thickness and lubrication enhancement [20]; however, the geometry of rectangular micro-textures was not optimized.

Based on above reviewed literature, it well illustrates that the rectangular micro-textures can improve the lubrication and friction performances due to the increasing hydrodynamic effect, and the geometry of textures has an important effect. However, few studies about the rectangular dimples with different geometries and distribution types are investigated systematically by theoretical analysis on hydrodynamic lubrication. Therefore, efforts are still needed to be continued for selecting the best choice of geometry and distribution of the rectangular dimples for enhancing the hydrodynamic lubrication.

In this paper, numerical analyses are adopted for investigating the effect of rectangular dimples on hydrodynamic lubrication based on the Reynolds equation, and the average film pressure is calculated and regarded as the evaluation criteria for hydrodynamic lubrication. Meanwhile, special attention is focused on the influence of geometry of single rectangular dimple, spacing in array and distribution type of the rectangular dimples. An optimization of the implementation of rectangular textures is performed and the optimal results can provide a guidance for experimental design in order to enhance lubrication and minimize friction.

2 Theoretical analysis

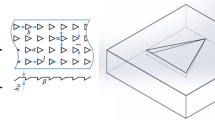
Figure 1 shows the schematic diagram of the sliders with rectangular dimples. The sliding model consisted of two parallel sliders separated with an oil film thickness of h₀ is shown in Fig. 1a. The lower sample is fixed with evenly distributed rectangular dimples, and the upper sample with the smooth surface is sliding with a relative sliding velocity v. The texture geometry and distribution are shown in Fig. 1b, as can be seen that the rectangular dimples with an x-width a, y-width b and depth d are distributed with the x-spacing (horizontal direction) s_x, y-spacing (vertical direction) s_y and array angle φ. Meanwhile, each rectangular dimple is in an imaginary rectangular cell with an x-width l_a and y-width l_b, and the widths of whole distribution zone in x and y directions are l_x and l_y, respectively. The numeral calculations and theoretical models are developed based on the imaginary rectangular cell as a basic unit. Then, the area ratio of single rectangular dimple ε can be expressed as:

$$ \varepsilon = \frac{a}{{l_{a} }} \cdot \frac{b}{{l_{b} }} \times 100\% $$

(1)

Fig. 1

Schematic diagram of the sliders with rectangular dimples

Assuming that the uniform and incompressible lubricants are Newtonian fluid with a constant film thickness, and only the dynamic pressure effect formed by the pressure of the lubricating film is considered. Under these circumstances, the general Reynolds equation can be written as follows [36]:

$$ \frac{\partial }{\partial x}\left( {h^{3} \frac{\partial p}{\partial x}} \right) + \frac{\partial }{\partial y}\left( {h^{3} \frac{\partial p}{\partial y}} \right) = 6v\eta \frac{\partial h}{\partial x} $$

(2)

where h is the local film thickness, p is the local film pressure, and η is the dynamic viscosity of the fluid. Besides, x and y are Cartesian coordinates paralleled and perpendicular to the sliding direction, respectively.

Further, for analyzing the influence of geometry of single rectangular dimple, spacing paralleled to the sliding direction (s_x), spacing perpendicular to the sliding direction (s_y) and the distribution type on hydrodynamic pressure, the values of local film thickness h are divided into four cases:

Case 1: single rectangular dimple

$$ h(x,y) = \left\{ {\begin{array}{*{20}l} {h_{0} + d} \hfill & {{\text{for}}\quad \frac{1}{2}\left( {l_{a} - a} \right) < x < \frac{1}{2}\left( {l_{a} + a} \right)\;{\text{and}}\;\frac{1}{2}\left( {l_{b} - b} \right) < y < \frac{1}{2}\left( {l_{b} + b} \right)} \hfill \\ {h_{0} } \hfill & {{\text{for}}\quad 0 \le x \le \frac{1}{2}\left( {l_{a} - a} \right)\;{\text{or}}\;0 \le y \le \frac{1}{2}\left( {l_{b} - b} \right)\;{\text{or}}\;\frac{1}{2}\left( {l_{a} + a} \right) \le y \le l_{a} } \hfill \\ {} \hfill & {{\text{or}}\;\frac{1}{2}\left( {l_{b} + b} \right) \le y \le l_{b} } \hfill \\ \end{array} } \right. $$

(3)

Case 2: x-direction spacing

$$ h(x,y) = \left\{ {\begin{array}{*{20}l} {h_{0} + d} \hfill & {{\text{for}}\quad ka + \left( {k + \frac{1}{2}} \right)s_{x} \le x \le \left( {k + 1} \right)a + \left( {k + \frac{1}{2}} \right)s_{x} \quad \left( {k = 0,1,2,3,4} \right)} \hfill \\ {} \hfill & {{\text{and}} \frac{1}{2}\left( {l_{b} - b} \right) < y < \frac{1}{2}\left( {l_{b} + b} \right)} \hfill \\ {h_{0} } \hfill & {{\text{for}}\quad 0 \le y \le \frac{1}{2}\left( {l_{b} - b} \right)\;{\text{or}}\;\frac{1}{2}\left( {l_{b} + b} \right) \le y \le l_{b} } \hfill \\ {} \hfill & {{\text{or}}\;ka + \left( {k - \frac{1}{2}} \right)s_{x} \le x \le ka + \left( {k + \frac{1}{2}} \right)s_{x} \quad \left( {k = 1,2,3,4} \right)} \hfill \\ {} \hfill & {{\text{or}}\;l_{a} - \frac{{s_{x} }}{2} \le x \le l_{a} {\text{or}} 0 \le x \le \frac{{s_{x} }}{2}} \hfill \\ \end{array} } \right. $$

(4)

Case 3: y-direction spacing

$$ h(x,y) = \left\{ {\begin{array}{*{20}l} {h_{0} + d} \hfill & {{\text{for}}\quad kb + \left( {k + \frac{1}{2}} \right)s_{y} \le y \le \left( {k + 1} \right)b + \left( {k + \frac{1}{2}} \right)s_{y} \quad \left( {k = 0,1,2,3,4} \right)} \hfill \\ {} \hfill & {{\text{and}}\;\frac{1}{2}\left( {l_{a} - a} \right) < x < \frac{1}{2}\left( {l_{a} + a} \right)} \hfill \\ {h_{0} } \hfill & {{\text{for}}\quad 0 \le x \le \frac{1}{2}\left( {l_{a} - a} \right) {\text{or}} \frac{1}{2}\left( {l_{a} + a} \right) \le x \le l_{a} } \hfill \\ {} \hfill & {{\text{or}}\;kb + \left( {k - \frac{1}{2}} \right)s_{y} \le y \le kb + \left( {k + \frac{1}{2}} \right)s_{y} \quad \left( {k = 1,2,3,4} \right)} \hfill \\ {} \hfill & {{\text{or}}\;l_{b} - \frac{{s_{y} }}{2} \le y \le l_{b} {\text{or}} 0 \le y \le \frac{{s_{y} }}{2}} \hfill \\ \end{array} } \right. $$

(5)

Case 4: surface distribution with different array angles

$$ h(x,y) = \left\{ {\begin{array}{*{20}l} {h_{0} + d} \hfill & {{\text{for}}\quad ka + \left( {k + 1} \right)s_{x} \le x \le \left( {k + 1} \right)a + \left( {k + 1} \right)s_{x} } \hfill \\ {} \hfill & {{\text{and}}\;tb + \left( {t + \frac{1}{2}} \right)s_{y} + \frac{{s_{x} + a}}{{\tan \left( {\varphi /2} \right)}}\left( {\frac{{\left( { - 1} \right)^{t + 1} + 1}}{2}} \right) \le y \le \left( {t + 1} \right)b + \left( {t + \frac{1}{2}} \right)s_{y} + \frac{{s_{x} + a}}{{\tan \left( {\varphi /2} \right)}}\left( {\frac{{\left( { - 1} \right)^{t + 1} + 1}}{2}} \right)} \hfill \\ {} \hfill & {\left( {k = 0,1,2,3,4; t = 0,1,2,3,4} \right)} \hfill \\ {h_{0} } \hfill & {{\text{for}}\quad ka + ks_{x} \le x \le ka + \left( {k + 1} \right)s_{x} } \hfill \\ {} \hfill & {{\text{or}}\;ka + \left( {k + 1} \right)s_{x} \le x \le \left( {k + 1} \right)a + \left( {k + 1} \right)s_{x} \;{\text{and}}\;0 \le y \le \frac{{s_{y} }}{2}{ + }\frac{{s_{x} + a}}{{\tan \left( {\varphi /2} \right)}}\left( {\frac{{\left( { - 1} \right)^{t + 1} + 1}}{2}} \right)} \hfill \\ {} \hfill & {{\text{or}}\;ka + \left( {k + 1} \right)s_{x} \le x \le \left( {k + 1} \right)a + \left( {k + 1} \right)s_{x} } \hfill \\ {} \hfill & {{\text{and}}\;tb + \left( {t - \frac{1}{2}} \right)s_{y} { + }\frac{{s_{x} + a}}{{\tan \left( {\varphi /2} \right)}}\left( {\frac{{\left( { - 1} \right)^{t + 1} + 1}}{2}} \right) \le y \le tb + \left( {t + \frac{1}{2}} \right)s_{y} { + }\frac{{s_{x} + a}}{{\tan \left( {\varphi /2} \right)}}\left( {\frac{{\left( { - 1} \right)^{t + 1} + 1}}{2}} \right)} \hfill \\ {} \hfill & {\left( {k = 0,1,2,3,4; t = 1,2,3,4} \right)} \hfill \\ \end{array} } \right. $$

(6)

The pressure at the textured surface edges can be approximated as ambient pressure p_a, and the textures can be seen a periodical change in y direction that perpendicular to the sliding direction [37]. Thus, pressure distribution of textures is periodical in y direction with a period length of l_b. Meanwhile, to reduce the influence of boundary and ensure the consistency of film pressure of each dimple as far as possible, the pressure gradient with respect to the direction normal to the boundary is kept equal. Therefore, the boundary conditions can be written as:

$$ p(0,y) = p(l_{x} ,y) = p(x,0) = p(x,l_{y} ) = p_{a} $$

(7)

$$ \frac{\partial p}{\partial y}(x,kl_{b} ) = \frac{\partial p}{\partial y}(x,(k + 1)l_{b} )\quad k = 0,1,2,3,4 $$

(8)

From Eq. (8), it can be seen that the boundary condition can be written as: $\frac{\partial p}{\partial y}(x,y = 0) = \frac{\partial p}{\partial y}(x,y = l_{b} )$ with k = 0 for a single dimple (case 1) or the x-spacing distribution (case 2) [38]; for the y-spacing and different array angle distributions (cases 3 and 4), the texture distributions are composed by a series of single row (in x direction) along y direction [21], and for each row (in x direction), the boundary condition can be written with different k. Thus, it is sufficient to consider a periodical boundary condition in y direction, and the single row can be seen the special case.

Meanwhile, considering the cavitation phenomenon will be occurred in the divergent region, Jakobsson–Floberg–Olsson cavitation theory is used as complementary condition in the cavitation zone. The p − θ model presented by Elord is used and which satisfies the mass conservation automatically [39]. Meanwhile, combined with the Elrod algorithm, the partial differential equation with the optimization of a switch function “g” is valid both in full film and cavitation zones [39, 40]. The equation is written as follows:

$$ \frac{\partial }{\partial x}\left( {\beta h^{3} g\frac{\partial \theta }{\partial x}} \right) + \frac{\partial }{\partial y}\left( {\beta h^{3} g\frac{\partial \theta }{\partial y}} \right) = 6v\eta \frac{\partial \theta h}{\partial x} $$

(9)

where β is the lubricant bulk modulus, which is defined as:

$$ \beta { = }\rho \frac{\partial p}{\partial \rho } $$

(10)

θ is the fraction film content, defined as:

$$ \theta { = }\frac{\rho }{{\rho_{c} }} $$

(11)

where ρ is the lubricant density and ρ_c is the lubricant density in cavitation zone.g is the switch function defined as:

$$ g = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\theta \ge 1\quad {\text{full film region}}} \hfill \\ {0,} \hfill & {\theta < 1\quad {\text{cavitation region}}} \hfill \\ \end{array} } \right. $$

(12)

The film pressure can be calculated as below:

$$ p = \left\{ {\begin{array}{*{20}l} {p_{c} + \beta \ln \theta ,} \hfill & {\theta \ge 1} \hfill \\ {p_{c} ,} \hfill & {\theta < 1} \hfill \\ \end{array} } \right. $$

(13)

In order to facilitate calculation, dimensionless processing is conducted, and the dimensionless parameters are defined as follows:

$$ X = \frac{x}{{w_{a} }},\quad Y = \frac{y}{{w_{a} }},\quad H = \frac{h}{{h_{a} }},\quad D = \frac{d}{{h_{a} }},\quad P = \frac{p}{{p_{a} }} - 1 $$

(14)

where w_a is the reference value of the dimple width, h_a is the reference value of the dimple depth, P is the dimensionless film pressure, H is the dimensionless film thickness and D is the dimensionless dimple depth. Additional, X and Y represent the dimensionless Cartesian coordinate system.

Based on above processes, the dimensionless Reynolds equation is given as:

$$ \frac{\partial }{\partial X}\left( {H^{3} g\frac{\partial \theta }{\partial X}} \right) + \frac{\partial }{\partial Y}\left( {H^{3} g\frac{\partial \theta }{\partial Y}} \right) = \frac{{6v\eta w_{a} }}{{h_{a}^{2} p_{a} }}\frac{\partial \theta H}{\partial X} $$

(15)

Accordingly, the dimensionless film thickness for the four cases can be expressed as follows:

Case 1: single rectangular dimple

$$ H(X,Y) = \left\{ {\begin{array}{*{20}l} {H_{0} + D} \hfill & {{\text{for}}\quad \frac{1}{2}\left( {L_{a} - A} \right) < X < \frac{1}{2}\left( {L_{a} + A} \right)\;{\text{and}}\;\frac{1}{2}\left( {L_{b} - B} \right) < Y < \frac{1}{2}\left( {L_{b} + B} \right)} \hfill \\ {H_{0} } \hfill & {{\text{for}}\quad 0 \le X \le \frac{1}{2}\left( {L_{a} - A} \right)\;{\text{or}}\;0 \le Y \le \frac{1}{2}\left( {L_{b} - B} \right)\;{\text{or}}\;\frac{1}{2}\left( {L_{a} + A} \right) \le Y \le L_{a} } \hfill \\ {} \hfill & {{\text{or}}\;\frac{1}{2}\left( {L_{b} + B} \right) \le Y \le L_{b} } \hfill \\ \end{array} } \right. $$

(16)

Case 2: x-direction spacing

$$ H(X,Y) = \left\{ {\begin{array}{*{20}l} {H_{0} + D} \hfill & {{\text{for}}\quad kA + \left( {k + \frac{1}{2}} \right)S_{x} \le X \le \left( {k + 1} \right)A + \left( {k + \frac{1}{2}} \right)S_{x} \quad \left( {k = 0,1,2, \ldots ,n} \right)} \hfill \\ {} \hfill & {{\text{and}}\;\frac{1}{2}\left( {L_{b} - B} \right) < Y < \frac{1}{2}\left( {L_{b} + B} \right)} \hfill \\ {H_{0} } \hfill & {{\text{for}}\quad 0 \le Y \le \frac{1}{2}\left( {L_{b} - B} \right)\;{\text{or}}\;\frac{1}{2}\left( {L_{b} + B} \right) \le Y \le L_{b} } \hfill \\ {} \hfill & {{\text{or}}\;kA + \left( {k - \frac{1}{2}} \right)S_{x} \le X \le kA + \left( {k + \frac{1}{2}} \right)S_{x} \quad \left( {k = 1,2, \ldots ,n} \right)} \hfill \\ {} \hfill & {{\text{or}}\;L_{a} - \frac{{S_{x} }}{2} \le X \le L_{a} \;{\text{or}}\;0 \le X \le \frac{{S_{x} }}{2}} \hfill \\ \end{array} } \right. $$

(17)

Case 3: y-direction spacing

$$ H(X,Y) = \left\{ {\begin{array}{*{20}l} {H_{0} + D} \hfill & {{\text{for}}\quad kB + \left( {k + \frac{1}{2}} \right)S_{y} \le Y \le \left( {k + 1} \right)B + \left( {k + \frac{1}{2}} \right)S_{y} \quad \left( {k = 0,1,2, \ldots ,n} \right)} \hfill \\ {} \hfill & {{\text{and}}\;\frac{1}{2}\left( {l_{a} - A} \right) < X < \frac{1}{2}\left( {L_{a} + A} \right)} \hfill \\ {H_{0} } \hfill & {{\text{for}}\quad 0 \le X \le \frac{1}{2}\left( {L_{a} - A} \right)\;{\text{or}}\;\frac{1}{2}\left( {L_{a} + A} \right) \le X \le L_{a} } \hfill \\ {} \hfill & {{\text{or}}\;kB + \left( {k - \frac{1}{2}} \right)S_{y} \le Y \le kB + \left( {k + \frac{1}{2}} \right)S_{y} \quad \left( {k = 1,2, \ldots ,n} \right)} \hfill \\ {} \hfill & {{\text{or}}\;L_{b} - \frac{{S_{y} }}{2} \le Y \le L_{b} \;{\text{or}}\;0 \le Y \le \frac{{S_{y} }}{2}} \hfill \\ \end{array} } \right. $$

(18)

Case 4: surface distribution with different array angles

$$ H(X,Y) = \left\{ {\begin{array}{*{20}l} {H_{0} + D} \hfill & {{\text{for}}\quad kA + \left( {k + 1} \right)S_{x} \le X \le \left( {k + 1} \right)A + \left( {k + 1} \right)S_{x} } \hfill \\ {} \hfill & {{\text{and}}\;tB + \left( {t + \frac{1}{2}} \right)S_{y} + \frac{{S_{x} + A}}{{\tan \left( {\varphi /2} \right)}}\left( {\frac{{\left( { - 1} \right)^{t + 1} + 1}}{2}} \right) \le Y \le \left( {t + 1} \right)B + \left( {t + \frac{1}{2}} \right)S_{y} + \frac{{S_{x} + A}}{{\tan \left( {\varphi /2} \right)}}\left( {\frac{{\left( { - 1} \right)^{t + 1} + 1}}{2}} \right)} \hfill \\ {} \hfill & {\left( {k = 0,1,2, \ldots ,n; t = 0,1,2, \ldots ,n} \right)} \hfill \\ {H_{0} } \hfill & {{\text{for}}\quad kA + kS_{x} \le X \le kA + \left( {k + 1} \right)S_{x} } \hfill \\ {} \hfill & {{\text{or}}\;kA + \left( {k + 1} \right)S_{x} \le X \le \left( {k + 1} \right)A + \left( {k + 1} \right)S_{x} {\text{ and }}0 \le Y \le \frac{{S_{y} }}{2}{ + }\frac{{S_{x} + A}}{{\tan \left( {\varphi /2} \right)}}\left( {\frac{{\left( { - 1} \right)^{t + 1} + 1}}{2}} \right)} \hfill \\ {} \hfill & {{\text{or}}\;kA + \left( {k + 1} \right)S_{x} \le X \le \left( {k + 1} \right)A + \left( {k + 1} \right)S_{x} } \hfill \\ {} \hfill & {{\text{and }}tB + \left( {t - \frac{1}{2}} \right)S_{y} { + }\frac{{S_{x} + A}}{{\tan \left( {\varphi /2} \right)}}\left( {\frac{{\left( { - 1} \right)^{t + 1} + 1}}{2}} \right) \le Y \le tB + \left( {t + \frac{1}{2}} \right)S_{y} { + }\frac{{S_{x} + A}}{{\tan \left( {\varphi /2} \right)}}\left( {\frac{{\left( { - 1} \right)^{t + 1} + 1}}{2}} \right)} \hfill \\ {} \hfill & {\left( {k = 0,1,2, \ldots ,n;\;t = 1,2, \ldots ,n} \right)} \hfill \\ \end{array} } \right. $$

(19)

The dimensionless film pressure P can be written as the flows:

$$ P = \left\{ {\begin{array}{*{20}l} {P_{c} + \bar{\beta }\ln \theta ,} \hfill & {\theta \ge 1} \hfill \\ {P_{c} ,} \hfill & {\theta < 1} \hfill \\ \end{array} } \right. $$

(20)

where P_c = p_c/p_a is the dimensionless cavitation pressure and $\bar{\beta } = {\beta \mathord{\left/ {\vphantom {\beta \rho }} \right. \kern-0pt} \rho }_{a}$ is the dimensionless lubricant bulk modulus.

The differential equation shown in Eq. (15) is solved by the numerical calculation of the Gauss–Seidel iteration method [41, 42], where the computational domain is meshed with a dense grid with m nodes in x direction and n nodes in y direction, and the interval between two adjacent nodes for all computational domain in x-direction is l_x/m and that in y-direction is l_y/n; meanwhile, to ensure the same calculation accuracy, the same interval value of 0.2 in x direction and y direction is selected considering the computational efficiency and accuracy. Then the dimensionless pressure value P(i, j) at the point (i, j) is acquired based on the values of surrounding four points of P(i − 1, j), P(i + 1, j), P(i, j − 1) and P(i, j + 1), as shown in Eq. (21).

$$ P_{i,j} = K_{1} P_{i - 1,j} + K_{2} P_{i + 1,j} + K_{3} P_{i,j - 1} + K_{4} P_{i,j + 1} + K_{0} $$

(21)

For obtaining and converging the value of P(i, j) quickly, Eq. (22) is adopted:

$$ P_{i,j}^{s + 1} = P_{i,j}^{s} + \left( {P_{i,j}^{s + 1} - P_{i,j}^{s} } \right)w $$

(22)

where s is the number of iterations and w is the relaxation factor of 1.2. The specific iterative processes refer to [43]. The converging condition is shown as Eq. (23).

$$ \frac{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\left| {P_{i,j}^{s + 1} - P_{i,j}^{s} } \right|} } }}{{\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\left| {P_{i,j}^{s + 1} } \right|} } }} \le E_{r} $$

(23)

where E_r represents the error tolerance.

The dimensionless average pressure P_ave in the computational domain is chosen as an indicator to evaluate the load carrying capacity of the dimpled surface and the P_ave can be calculated by Eq. (24).

$$ P_{ave} = \frac{{\int_{0}^{{L_{x} }} {\int_{0}^{{L_{y} }} {P(x,y)dxdy} } }}{{L_{x} L_{y} }} $$

(24)

Based on above theoretical analyses, the effect of geometric parameters and distribution type of the rectangular dimples on the average dimensionless pressure is investigated, and the calculation is performed according to the conditions that in Table 1.

Table 1 Assumed conditions for numerical analyses

3 Results and discussion

3.1 Single rectangular dimple

The effect of the geometry of single rectangular dimple on dimensionless pressure is investigated using the response surface method (RSM) with an L₁₅ array model. Three factors of x-width, y-width, depth of the rectangular dimples and five levels for each factor are selected, and that are shown in Table 2. The dimensionless average pressure is used as the response, and the response surface model established the relationship between the factors and response is built for optimizing the geometry of single rectangular dimple.

Table 2 Factors and levels

3.1.1 Calculated results

The typical morphologies (three-dimensional and two-dimensional) and profiles of the dimensionless pressure distribution and film thickness of the rectangular dimple with x-width of 28 µm, y-width of 82 µm and depth of 40 µm are shown in Fig. 2. As can be seen from Fig. 2a and c that the dimensionless pressure and film thickness are large inside the micro-dimple, and the dimensionless film pressure increases gradually up to a maximum and then reduces sharply. The maximum dimensionless pressure is obtained at the outlet that the fluid shifts to the rectangular dimple (Fig. 2b). It can be explained that the micro-dimple provides the similar effect of the stepped slider and the fluid outlet of micro-dimple forms a convergent contact which builds up the hydrodynamic pressure. The average value of the dimensionless film pressure in the whole surface (Fig. 2) is calculated using as output response and the results based on the L₁₅ array are shown in Table 3.

Fig. 2

Morphologies and profiles of the dimensionless pressure distribution and film thickness of the rectangular dimple (a = 28 µm, b = 82 µm, d = 12 µm). a Three-dimensional (3D) dimensionless pressure distribution; b two-dimensional (2D) dimensionless pressure distribution; c profiles of the dimensionless pressure and film thickness along the A–A

Table 3 Calculated results

3.1.2 Mathematical models

The second-order polynomial response surface mathematical model is adopted to analyze the influence of the rectangular dimple geometry on the dimensionless average pressure, and the general model is expressed as:

$$ f = \alpha_{0} + \sum\limits_{i = 1}^{n} {\alpha_{i} x_{i} } + \sum\limits_{i = 1}^{n} {\alpha_{ii} x_{i}^{2} } + \sum\limits_{i < j} {\alpha_{ij} x_{i} x_{j} } + \xi $$

(25)

where f is the corresponding response, α₀, α_i, α_ii, α_ij are the regression coefficient, x_i and x_j are the coded values of the i^th and j^th parameters, respectively, and ξ is the error.

The objective function for the response of the dimensionless average pressure (P_ave) is built as follows:

$$ P_{ave} = 0.091 - 0.039a - 0.0052b - 0.144d + 0.0059ab + 0.04ad + 0.0068bd - 0.0048a^{2} - 0.0048b^{2} + 0.087d^{2} $$

(26)

where a, b and d represent the x-width, y-width and depth of the rectangular dimple, respectively.

In order to evaluate the adequacy and fitness of the developed model for the response of dimensionless average pressure, the analysis of variance (ANOVA) method is carried out, and the results of ANOVA are shown in Table 4. As can be seen that the model F-value of 11.03 implies the model is significant with a probability of 0.83%. Moreover, the p_r-value less than 0.05 confirms that the developed model is significant with a confidence level of 95%. The “Adeq Precision” that measures the signal to noise ratio is 10.849, which is greater than 4, indicating an adequate signal [44]. Therefore, the model can be used to navigate the dimensionless average pressure.

Table 4 ANOVA for the dimensionless average pressure model

Figure 3 shows the normal probability plot for the residuals. The plot illustrates that the residuals closely follow straight lines, indicating that the errors are in accordance with the normal distribution, thus adequately supports the fitted model. The relation between the actual and predicted dimensionless average film pressure is shown in Fig. 4. As can be seen that scatter of the data points lies near the fitted line, which indicates a good fitness of the predicted and actual values. The above results further prove the adequacy of the developed model.

Fig. 3

Normal probability plot for the residuals

Fig. 4

Relation between the actual and predicted dimensionless average film pressure

3.1.3 Influence of rectangular dimple geometry

Figure 5 shows the variations of dimensionless average pressure with different parameters. As shown in Fig. 5a, with a certain depth of 5 µm, the large dimensionless average pressure is obtained with the small x-width and y-width, and it reduces slightly with respect to the increasing x-width and y-width. Figure 5 b and c shows that the depth has a more profound influence on the P_ave compared to the x-width and y-width. It is also noted that (Fig. 5b), the P_ave decreases firstly and then increases slightly with the increasing depth ranging from 2 to 50 µm, and the largest value of P_ave is obtained with the small depth of 2 µm and x-width of 10 µm. Meanwhile, it can be observed that the P_ave decreases with the increasing x-width in the case of a relatively small depth (e.g. 2 µm) and that increases with the increasing x-width in the case of a relatively large depth (e.g. 50 µm). The results indicate that the P_ave is influenced strongly by a combination of x-width and depth. Figure 5c demonstrates that the P_ave decreases significantly with the increasing depth and that has a minor relationship with the y-width. The results can be explained from Eq. (2), the dynamic pressure effect is reflected by the formula of $6v\eta \frac{\partial h}{\partial x}$, which is strongly affected by the film thickness h and x direction that paralleled to lubricant flow direction. Meanwhile, the film thickness h and x direction are dependent on texture depth and x-width, thus, the film pressure presents a higher correlation with texture depth and x-width than that of texture y-width.

Fig. 5

Variations of dimensionless average pressure with different parameters

3.1.4 Optimal single rectangular dimple

Based on above analyses of RSM, the objective optimization is performed with a purpose of achieving a large dimensionless average pressure, and the optimized parameters of x-width, y-width and depth are 10 µm, 45 µm and 2 µm with a confidence of 95%, respectively. The morphologies and profiles of the film thickness and pressure distribution of the optimal rectangular dimple are shown in Fig. 6. As shown that the film thickness is high inside the texture reflected by the cubic shape of the rectangular dimple. The film pressure increases from the inlet of the rectangular dimple towards to the outlet along the direction of sliding speed and then decreases, and the profile of the section A–A (Fig. 6d) exhibits that the maximum value of film pressure occurs near the outlet of the dimple. The solution for this result is similar to the “step effect” [36, 45]: when the clearance between two sliders has a step change, an additional hydrodynamic pressure can be generated due to the restriction in fluid flow direction cause by the dimple sidewall and reduced clearance. Further, the predicted average film pressure is 1.7353 × 10⁵ Pa that is close to the calculated value of 1.6973 × 10⁵ Pa. Therefore, the predicted error less than 10% can be accepted due to the inherent inaccuracy.

Fig. 6

Morphologies and profiles of the film thickness and film pressure distribution of the optimal rectangular dimple. a 3D film thickness; b 3D film pressure distribution; c 2D film pressure distribution; d profiles of the film thickness and film pressure along A–A

To further verify the optimization results, the average film pressure of rectangular textures is compared with the square textures with the same area ratio, the results are shown in Fig. 7. It is noted that the average film pressure of optimized rectangular textures is slightly higher compared to the square textures with the area ratio of 25% and 11%, which reveals that the optimized rectangular textures have a greater potential in enhancing the hydrodynamic lubrication.

Fig. 7

Comparison of average film pressure of optimized rectangular textures and square textures

3.1.5 Area ratio of single rectangular dimple

To investigate the influence of area ratio of single rectangular dimple on the hydrodynamic lubrication based on the Eq. (1), the average film pressure with different ratios of dimple width to cell width (a/l_a and b/l_b) is calculated and shown in Fig. 8. As seen from Fig. 8a, the average film pressure increases firstly and then reduces with the increasing ratio of a/l_a, which indicates that the increasing area ratio of the single rectangular dimple (induced by the increasing a/l_a) along lubricant flow direction significantly affects the hydrodynamic lubrication, and the area ratio of 15–25% (with a/l_a of 0.3–0.5) generates the relatively large average film pressure. The result is closed to the area ratio of 0.3 reported by Adjemout et al. [46] and Shen and Khonsari [47]. It also indicated that the film pressure is strongly influenced by the end boundaries of the computational domain in the fluid flow direction, thus, the interaction influenced by end boundaries cannot be neglected and the spacing need to be studied. Figure 8b exhibits that the average film pressure increases with the increasing ratio of b/l_b, the results reveal that the increasing area ratio of the single rectangular dimple in y-width direction can enhance the hydrodynamic lubrication.

Fig. 8

Variations of average film pressure with different ratios of dimple width to cell width. a dimple x-width to cell x-width a/l_a (a = 10 µm, b = 45 µm, l_b = 90 µm); b dimple y-width to cell y-width b/l_b (a = 10 µm, b = 45 µm, l_a = 20 µm)

In order to further analyze the interaction of the rectangular dimples, the effect of the horizontal and vertical spacing with 5 rows or 5 columns on the film pressure is investigated, and x-spacing s_x ranging from 2 to 60 µm and y-spacing s_y ranging from 2 to 60 µm for the rectangular dimple (a = 10 µm, b = 45 µm, d = 2 µm) are selected.

3.2 X-direction spacing

Figure 9 shows the morphologies and profiles of the film pressure distribution and film thickness of rectangular dimples with the x-spacing of 10 and 40 µm. As exhibited, with the x-spacing of 10 µm, the significant interaction between the adjacent dimples is occurred shown in zone A (Fig. 9a) compared with the x-spacing of 40 µm in zone B (Fig. 9d). The profiles of the film pressure distribution and film thickness in Fig. 9c along the section A–A exhibit a significant difference compared to that in Fig. 9f along the section B–B. As seen in Fig. 9c that the film pressure increases monotonously with the higher film thickness from the inlet to the outlet of the rectangular dimples and then decreases linearly to the inlet of next dimple. The rising and falling curves seem to be symmetrical due to the equal width of a and s_x. Figure 9d shows that with the x-spacing of 40 µm, the interaction of the adjacent micro-dimples is weakened. The profiles of the film pressure distribution and film thickness in Fig. 9f along the section B–B exhibit that the film pressure increases rapidly up to a maximum at the outlet of the rectangular dimples and then decreases slowly to the inlet of next dimple.

Fig. 9

Morphologies and profiles of the film pressure distribution and film thickness of rectangular dimples (a = 10 µm, b = 45 µm, d = 2 µm) with s_x of 10 and 40 µm. a 3D film thickness, s_x = 10 µm; b 2D film pressure distribution, s_x = 10 µm; c profiles of the film thickness and film pressure along A–A; d 3D film thickness, s_x = 40 µm; e 2D film pressure distribution, s_x = 40 µm; f profiles of the film thickness and film pressure along B–B

The average film pressure of the rectangular dimples with different x-spacing is calculated and that is shown in Fig. 10. As seen that the average film pressure is sensitive to the x-spacing. With the increasing x-spacing ranging from 2 to 60 µm, the average values of the film pressure increase and then continually reduce. The results are consistent with Refs. [45, 48], assuming that each dimple locates in an imaginary rectangular cell, the interaction between two dimples is reduced and even be neglected with the large distance in x-direction. The results exhibit that the optimal value of the x-spacing that maximizes the average film pressure is 10 µm.

Fig. 10

Variations of the average film pressure with the different x-spacing s_x (a = 10 µm, b = 45 µm, d = 2 µm)

3.3 Y-direction spacing

Figure 11 shows the morphologies and profiles of the film pressure distribution and film thickness of rectangular dimples with the y-direction spacing of 10 and 40 µm. It is noted that y-spacing has a significant influence on film pressure distribution. With the small y-spacing of 10 µm (Fig. 11a), there is a remarkable interaction between the adjacent rectangular dimples; and with the y-spacing of 40 µm (Fig. 11d), the film pressure distribution is relatively independent of each dimple. The profiles of film thickness and film pressure along A–A (Fig. 11c) exhibit that the film pressure distribution with the spacing of 10 µm is significantly influenced by the adjacent rectangular dimples compared to that along B–B (Fig. 11f), and then the value of the film pressure on the spacing surface between the dimples with the spacing of 10 µm is larger than that with the spacing of 40 µm, which ascribes to the weakened interaction of the adjacent rectangular dimples with the increasing y-spacing.

Fig. 11

Morphologies and profiles of the film pressure distribution and film thickness of rectangular dimples (a = 10 µm, b = 45 µm, d = 2 µm) with s_y of 10 and 40 µm. a 3D film pressure, s_y = 10 µm; b 2D film pressure distribution, s_y = 10 µm; c profiles of the film thickness and film pressure along A–A; d 3D film pressure, s_y = 40 µm; e 2D film pressure distribution, s_y = 40 µm; f profiles of the film thickness and film pressure along B–B

The average film pressure of rectangular dimples with different y-spacing based on the film pressure distribution (shown as in Fig. 11) is calculated to investigate the influence of y-spacing on the hydrodynamic lubrication, and the results are plotted in Fig. 12. It is observed that the average film pressure reduces with the increasing y-spacing ranging from 2 to 60 µm. The result indicates that the interaction and stepped slider effect induced by the adjacent dimples are weakened with the increasing y-spacing and reduced area density along the y-direction [45], which reduces the hydrodynamic effect; accordingly, the average film pressure is reduced. The results also demonstrate that the strong hydrodynamic lubrication with large average film pressure can be obtained with a small y-spacing as soon as possible.

Fig. 12

Variations of the average film pressure with the different y-spacing s_y (a = 10 µm, b = 45 µm, d = 2 µm)

3.4 Surface distribution with different array angles

The distribution type of the micro-textures on the surface has an important influence on the lubrication, friction and wear [49, 50]. Therefore, surface distribution types of uniform array and interlaced array with 72° of the rectangular dimples are shown in Fig. 13. It is noted that the interaction between the adjacent rectangular dimples in zone B of the interlaced array with 72° is stronger compared to that in zone A of the uniform array with 180°. The two-dimensional morphologies of the film pressure distribution in Fig. 13b and d shows that the film pressure distributes in uniform and interlaced modes, respectively. Meanwhile, the average film pressure of the textured surface with different array angles φ is calculated and shown in Fig. 14. As can be seen that the average film pressure decreases with the increasing array angle ranging from 72° to 180°. The results reveal that the distribution type with the interlaced arrays of the rectangular dimples is beneficial to enhancing the hydrodynamic lubrication by the increased interaction between the adjacent dimples along the fluid flow direction. The array angle of 72° (72° is the special case that the space surface center in the first row of rectangular dimples and the dimple center in the second row of rectangular dimples are on the same horizontal line) exhibits the largest average film pressure, this configuration provides a reference distribution type for promoting the hydrodynamic lubrication and load carrying capacity.

Fig. 13

Three-dimensional and two-dimensional morphologies of the film pressure distribution of rectangular dimples with different distribution types. a and b uniform arrays with 180°; c and d interlaced arrays with 72° (a = 10 µm, b = 45 µm, d = 2 µm, s_x = 10 µm, s_y = 10 µm)

Fig. 14

Variations of the average film pressure with the array angle (a = 10 µm, b = 45 µm, d = 2 µm, s_x = 10 µm, s_y = 10 µm)

3.5 Future research

From these considerable investigates, it is certain that the rectangular dimples have a significant influence on the dimensionless pressure, and the further optimization of rectangular dimples has potential for improving the hydrodynamic lubrication. Therefore, future research can be focused on the situation with randomly distributed dimples with stochastically different positions and shapes, and different film thicknesses and slope angles of two sliders; meanwhile, the experiments can be further studied based on the theoretical results.

4 Conclusions

In this paper, the influence of rectangular micro-textures on hydrodynamic lubrication is studied using numerical analysis. The geometrical parameters and distribution types of the rectangular dimples are optimized in terms of the maximum average film pressure for improving the hydrodynamic lubrication performance. The conclusions are as follows:

• (1) The geometry of the single rectangular dimple has an important influence on the dimensionless pressure. The maximum dimensionless pressure is obtained at the outlet that the fluid shifts to the rectangular dimples due to the divergent contact. The depth of the micro-dimples has a more evident effect compared to the x-width and y-width. The optimized values of x-width (10 µm), y-width (45 µm) and depth (2 µm) are selected for the single rectangular dimple. Meanwhile, the area ratio of single rectangular dimple significantly affects the hydrodynamic lubrication.

• (2) The x-spacing and y-spacing affect the film pressure distribution. The average film pressure increases firstly and then reduces with the increasing x-spacing, and that reduces monotonously with the increasing y-spacing.

• (3) The distribution of the rectangular dimples with an interlaced array exhibits a relatively large value of average film pressure compared to the uniform array, indicating that the interlaced array of the rectangular dimples is beneficial to enhancing the hydrodynamic lubrication. Meanwhile, the interlaced arrays of rectangular dimples with 72° exhibits the best effectivity.