Cessation of Newtonian circular and plane Couette flows with wall slip and non-zero slip yield stress

Abstract

We solve analytically the cessation flows of a Newtonian fluid in circular and plane Couette geometries assuming that wall slip occurs provided that the wall shear stress exceeds a critical threshold, the slip yield stress. In steady-state, slip occurs only beyond a critical value of the angular velocity of the rotating inner cylinder in circular Couette flow or of the speed of the moving upper plate in plane Couette flow. Hence, in cessation, the classical no-slip solution holds if the corresponding wall speed is below the critical value. Otherwise, slip occurs only initially along both walls. Beyond a first critical time, slip along the fixed wall ceases, and beyond a second critical time slip ceases also along the initially moving wall. Beyond this second critical time no slip is observed and the decay of the velocity is faster. The velocity decays exponentially in all regimes and the decay is reduced with slip. The effects of slip and the slip yield stress are discussed.

1 Introduction

The role of wall slip is important in many applications, such as the extrusion of complex fluids, ink jet processes, oil migration in porous media, and in microfluidics. The occurrence of slip has been documented for many fluids both experimentally and theoretically [1, 2]. Experimental studies of wall slip with Newtonian liquids have been reviewed by Neto et al. [3] and Lauga et al. [4]. The occurrence of slip has also been observed in nanoscale experiments [5] and in molecular dynamic simulations [6].

The most common slip equation is Navier’s slip law [7] which relates the wall shear stress, τ _w, to the slip velocity, u _w, defined as the velocity of the fluid relative to that of the wall:

$$\tau_{w} = \beta u_{w} ,$$

(1)

where β is the slip coefficient, which is in general a function of temperature, normal stress and pressure, and the characteristics of the fluid/wall interface [8]. The no-slip boundary condition is recovered when β → ∞. The slip coefficient is related to the so-called slip length b, i.e. β ≡ η/b, where η denotes the viscosity [9]. Different methods have been proposed in order to account for wall slip and improve the rheological characterization of materials for correcting the rheological parameters from Couette rheometers (see [10] and references therein). Works concerned with analytical solutions of Newtonian flows with Navier slip have been reviewed by Kaoullas and Georgiou [11, 12]. Ferrás et al. [13] presented analytical solutions of various Newtonian and inelastic non-Newtonian Couette and Poiseuille flows using a non-linear (power-law) slip equation in addition to Navier slip. Recently, Ng [14] also reported a collection of analytical solutions for starting Newtonian Couette and Poiseuille flows with Navier slip in many different geometries of interest (e.g. in plane, round, annular and rectangular tubes for the latter flow).

In many experimental studies on various fluid systems, it has been observed that wall slip occurs only above a certain critical value of the wall shear stress, known as the slip yield stress, τ _c [15–17]. Spikes and Granick [18] proposed the following two-branch extension of Navier’s slip equation for Newtonian fluid flow:

$$\left\{ {\begin{array}{*{20}l} {u_{w} = 0,} \hfill & {\tau_{w} \le \tau_{c} } \hfill \\ {\tau_{w} = \tau_{c} + \beta u_{w} ,} \hfill & {\tau_{w} > \tau_{c} } \hfill \\ \end{array} .} \right.$$

(2)

A number of other slip equations involving slip yield stress (also referred to as threshold slip equations) have been proposed based on experiments with different materials (see [16] and references therein). The two-branch form of Eq. (2) leads to some interesting theoretical as well as numerical difficulties, analogous to those encountered with the discontinuous Bingham-plastic constitutive model [16, 19]. Different flow regimes are defined by critical values for the occurrence of slip along a wall. For example, in Poiseuille and in simple shear flows, slip occurs only above a critical value of the imposed pressure gradient [11]. Moreover, in 2D and 3D, slip may occur only along unknown parts of the wall which is of interest both physically and numerically [20]. Recently, analytical solutions of steady-state and transient pressure-driven Newtonian flows in various geometries with wall slip governed by Eq. (2) have been derived [11, 12, 17, 21].

A recent work involving a slip equation with non-zero slip yield stress is that of Tauviqirrahman et al. [22] who analyzed the effects of surface texturing and wall slip on the load-carrying capacity of parallel sliding systems. Bryan et al. [23] studied both experimentally and numerically the extrusion flow of a viscoplastic material through axisymmetric square entry dies. They concluded that the linear Navier-slip model (1) is not adequate to describe the experimental flows and that further numerical simulations with slip Eq. (2) are necessary.

The objective of the present work is to derive analytical solutions for the cessation of Newtonian circular and plane Couette flows with wall slip and non-zero slip yield stress. Both flows are standard viscometric flows and their analytical solutions are missing from the recent compilations of Ng [14] and Kaoullas and Georgiou [11, 12]. The circular Couette flow, i.e. the flow between coaxial cylinders one of which is rotating while the other is kept fixed, is widely used for the rheological characterization of complex fluids [24]. Possible sources of error in determining the rheological parameters include end effects, eccentricities, viscous heating, and wall slip [24]. The analytical solutions derived below may be useful in studies involving start up and cessation of steady shear in rheometric and microfluidic devices, in tribology, and in testing numerical codes implementing slip Eq. (2). The steady-state circular and plane Couette flows are analyzed in Sects. 2 and 3, respectively, where the general cases of walls of different properties are also considered and different flow regimes depending on the speed of the moving boundary are identified. In Sect. 4, the solution of the cessation of circular Couette flow is derived and discussed. The cessation of plane Couette flow is investigated in Sect. 5. Finally, the conclusions of this work are provided in Sect. 6.

2 Steady circular Couette flow

We consider the steady circular Couette flow of a Newtonian fluid. The radii of the inner and outer cylinders are κR and R, respectively, where 0 < κ < 1, as illustrated in Fig. 1. The inner cylinder is rotating at an angular velocity Ω and the gravitational acceleration is zero. The two cylinders are assumed to be infinitely long and the flow is axisymmetric.

Fig. 1

Geometry of circular Couette flow

2.1 Navier slip

We first consider the general case in which Navier slip occurs along both the inner and outer cylinders and denote the two slip velocities by u _w1 and u _w2, respectively. We also allow the possibility of different slip coefficients along the two walls so that

$$\tau_{wi} = \beta_{i} u_{wi} ,\quad i = 1,2,$$

(3)

where τ _w1 and τ _w2 are the wall shear stresses along the two walls. The general form of the steady-state azimuthal velocity is [25]:

$$u_{\theta } (r) = c_{1} r + \frac{{c_{2} }}{r}.$$

(4)

The constants c ₁ and c ₂ are determined by applying the boundary conditions

$$u_{\theta } (\kappa R) = \kappa\Omega R - u_{w1}$$

(5)

and

$$u_{\theta } (R) = u_{w2} ,$$

(6)

which gives

$$u_{\theta } (r) = \frac{{\kappa^{2}\Omega R}}{{1 - \kappa^{2} + 2B_{1} + 2\kappa^{3} B_{2} }}\left[ {\frac{R}{r} - (1 - 2\kappa B_{2} )\frac{r}{R}} \right],$$

(7)

where B ₁ and B ₂ are the dimensionless slip numbers defined by

$$B_{i} \equiv \frac{\eta }{{\beta_{i} \kappa R}},\quad i = 1,2.$$

(8)

It should be noted that the slip coefficient appears in the denominator of the slip number. Hence, the no-slip boundary conditions is recovered by setting B _i = 0. For the shear stress τ _rθ  = ηrd(u _θ /r)/dr one finds that

$$\tau_{r\theta } = - \frac{{2\eta \kappa^{2}\Omega R^{2} }}{{1 - \kappa^{2} + 2B_{1} + 2\kappa^{3} B_{2} }}\frac{1}{{r^{2} }}.$$

(9)

Therefore, the two wall shear stresses are

$$\tau_{w1} = \frac{{2\eta\Omega }}{{1 - \kappa^{2} + 2B_{1} + 2\kappa^{3} B_{2} }}$$

(10)

and

$$\tau_{w2} = \kappa^{2} \tau_{w1} .$$

(11)

It should be noted that Eq. (11) holds irrespective of the wall boundary conditions. Finally, for the two slip velocities we find

$$u_{w1} = \frac{{2\kappa B_{1}\Omega R}}{{1 - \kappa^{2} + 2B_{1} + 2\kappa^{3} B_{2} }}\quad {\text{and}}\;u_{w2} = \frac{{B_{2} }}{{B_{1} }}\kappa^{2} u_{w1} .$$

(12)

If the same slip law applies to both cylinders (β ₁ = β ₂ = β), then the velocity is given by

$$u_{\theta } (r) = \frac{{\kappa^{2}\Omega R}}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}}\left[ {\frac{R}{r} - (1 - 2\kappa B)\frac{r}{R}} \right],$$

(13)

where B ≡ η/(βκR). In this case, we have for the two slip velocities

$$u_{w1} = \frac{{2\kappa B\Omega R}}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}} = \frac{{u_{w2} }}{{\kappa^{2} }},$$

(14)

while

$$\tau_{w1} = \frac{{2\eta\Omega }}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}}.$$

(15)

It is clear that setting B ₁ = 0 (and/or B ₂ = 0) the special solution when we have no slip along the inner (and/or the outer) wall is obtained. The various special cases of interest are illustrated in Fig. 2 along with the corresponding expressions of the velocity and the slip velocities.

Fig. 2

Different cases of Navier slip in circular Couette flow with the corresponding solutions

Scaling the azimuthal velocity by κΩR and r by R and denoting dedimensionalized quantities by stars, we can write

$$u_{\theta }^{*} (r^{*} ) = \frac{\kappa }{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}}\left[ {\frac{1}{{r^{*} }} - (1 - 2\kappa B)r^{*} } \right].$$

(16)

In Fig. 3a, we plotted $u_{\theta }^{*}$ for κ = 0.5 and various values of the slip number B. We observe that the velocity at the outer cylinder $u_{\theta }^{*} (1) = u_{w2}^{*}$ increases while $u_{\theta }^{*} (\kappa ) = 1 - u_{w1}^{*}$ decreases with B. Eventually, $u_{\theta }^{*}$ becomes an increasing function of $r^{*}$ and in the limit of infinite B (full slip) $u_{\theta }^{*}$ becomes linear:

$$u_{\theta }^{*} (r^{*} ) \to \frac{{\kappa^{2} }}{{1 + \kappa^{3} }}r^{*} .$$

(17)

Moreover, all velocity profiles have a common point at $r^{*} = \sqrt {1 - \kappa + \kappa^{2} }$. The corresponding plot of the angular velocity $u_{\theta }^{*} /r^{*}$ is shown in Fig. 3b. As expected, the angular velocity is always a decreasing function of $r^{*}$ and becomes flat (solid body rotation) in the limit of full slip. The asymptotic value of the angular velocity is κ ²/(1 + κ ³).

Fig. 3

Velocity profiles in circular Couette flow with Navier slip for κ = 0.5 and various slip numbers: (a) azimuthal velocity; (b) angular velocity

2.2 Slip with non-zero slip yield stress

For simplicity, we consider the case in which the same slip law with a slip coefficient β and a slip yield stress τ _c applies along both cylinders. It is clear that below a critical angular velocity Ω₁ no slip occurs and the expressions of case D in Fig. 2 apply. From Eq. (11) it is deduced that τ _w1 > τ _w2, which implies that if the angular velocity is increased just above Ω₁ slip occurs only along the inner cylinder. The angular velocity Ω₁ corresponds to τ _w1 = τ _c , which gives

$$\Omega _{1} = \frac{{\left( {1 - \kappa^{2} } \right)\tau_{c} }}{2\eta }.$$

(18)

If Ω₂ is the critical angular velocity for the occurrence of slip along the outer cylinder, then when Ω₁ < Ω ≤ Ω₂ slip occurs only along the inner cylinder and the azimuthal velocity is given by

$$u_{\theta } = \frac{{\tau_{c} R\kappa^{2} \left( {\eta\Omega /\tau_{c} + B} \right)}}{{\eta \left( {1 - \kappa^{2} + 2B} \right)}}\left( {\frac{R}{r} - \frac{r}{R}} \right).$$

(19)

The shear stress and the slip velocity at the inner wall are given by

$$\tau_{w1} = \frac{{2\tau_{c} \left( {\eta\Omega /\tau_{c} + B} \right)}}{{1 - \kappa^{2} + 2B}}$$

(20)

and

$$u_{w1} = \frac{{\tau_{c} R\kappa B\left( {2\eta\Omega /\tau_{c} - 1 + \kappa^{2} } \right)}}{{\eta \left( {1 - \kappa^{2} + 2B} \right)}}.$$

(21)

The critical angular velocity Ω₂ corresponds to τ _w2 = τ _c , from which one gets

$$\Omega _{2} = \frac{{\left( {1 - \kappa^{2} } \right)\left( {1 + 2B} \right)\tau_{c} }}{{2\kappa^{2} \eta }}.$$

(22)

In the last regime, Ω > Ω₂, slip occurs along both cylinders and the azimuthal velocity is given by

$$u_{\theta } = \frac{{\tau_{c} R}}{\eta }\left\{ {\frac{{\kappa^{2} \left[ {\eta\Omega /\tau_{c} + \left( {1 + \kappa } \right)B} \right]}}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}}\left[ {\frac{R}{r} - \left( {1 - 2\kappa B} \right)\frac{r}{R}} \right] - \kappa B\frac{r}{R}} \right\}.$$

(23)

For the wall shear stress along the inner cylinder we get

$$\tau_{w1} = \frac{{2\left[ {\eta\Omega /\tau_{c} + \left( {1 + \kappa } \right)B} \right]\tau_{c} }}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}},$$

(24)

while the two slip velocities are given by

$$u_{w1} = \frac{{\tau_{c} R\kappa B\left[ {2\eta\Omega /\tau_{c} - \left( {1 - \kappa^{2} } \right)\left( {1 - 2\kappa B} \right)} \right]}}{{\eta \left[ {1 - \kappa^{2} + 2(1 + \kappa^{3} )B} \right]}}$$

(25)

and

$$u_{w2} = \frac{{\tau_{c} R\kappa B\left[ {2\eta \kappa^{2}\Omega /\tau_{c} - \left( {1 - \kappa^{2} } \right)\left( {1 - 2\kappa B} \right)} \right]}}{{\eta \left[ {1 - \kappa^{2} + 2(1 + \kappa^{3} )B} \right]}}.$$

(26)

In this case, it is more convenient to dedimensionalize the solution by scaling the azimuthal velocity u _θ by τ _c R/η, the angular velocity by τ _c /η, and the shear stress by τ _c . Thus, the two dimensionless critical angular velocities are

$$\Omega _{1}^{*} = \frac{{1 - \kappa^{2} }}{2}$$

(27)

and

$$\Omega _{2}^{*} = \frac{{\left( {1 - \kappa^{2} } \right)\left( {1 + 2B} \right)}}{{2\kappa^{2} }}.$$

(28)

The azimuthal velocity and the inner-cylinder shear stress are given by

$$u_{\theta }^{*} = \left\{ {\begin{array}{*{20}l} {\frac{{\kappa^{2}\Omega ^{*} }}{{1 - \kappa^{2} }}\left( {\frac{1}{{r^{*} }} - r^{*} } \right),} \hfill & {\Omega ^{*} \le\Omega _{1}^{*} } \hfill \\ {\frac{{\kappa^{2} \left( {\Omega ^{*} + B} \right)}}{{1 - \kappa^{2} + 2B}}\left( {\frac{1}{{r^{*} }} - r^{*} } \right),} \hfill & {\Omega _{1}^{*} <\Omega ^{*} \le\Omega _{2}^{*} } \hfill \\ {\frac{{\kappa^{2} \left[ {\Omega ^{*} + \left( {1 + \kappa } \right)B} \right]}}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}}\left[ {\frac{1}{{r^{*} }} - \left( {1 - 2\kappa B} \right)r^{*} } \right] - \kappa Br^{*} ,} \hfill & {\Omega ^{*} >\Omega _{2}^{*} } \hfill \\ \end{array} } \right.$$

(29)

and

$$\tau_{w1}^{*} = \left\{ {\begin{array}{*{20}l} {\frac{{2\Omega ^{*} }}{{1 - \kappa^{2} }},} \hfill & {\Omega ^{*} \le\Omega _{1}^{*} } \hfill \\ {\frac{{2\left( {\Omega ^{*} + B} \right)}}{{1 - \kappa^{2} + 2B}},} \hfill & {\Omega _{1}^{*} <\Omega ^{*} \le\Omega _{2}^{*} } \hfill \\ {\frac{{2\left[ {\Omega ^{*} + \left( {1 + \kappa } \right)B} \right]}}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}},} \hfill & {\Omega ^{*} >\Omega _{2}^{*} } \hfill \\ \end{array} .} \right.$$

(30)

Finally, for the two slip velocities we get:

$$u_{w1} = \kappa B\left\{ {\begin{array}{*{20}l} {0,} \hfill & {\Omega ^{*} \le\Omega _{1}^{*} } \hfill \\ {\frac{{2\Omega ^{*} - \left( {1 - \kappa^{2} } \right)}}{{1 - \kappa^{2} + 2B}},} \hfill & {\Omega _{1}^{*} <\Omega ^{*} \le\Omega _{2}^{*} } \hfill \\ {\frac{{2\Omega ^{*} - \left( {1 - \kappa^{2} } \right)\left( {1 - 2\kappa B} \right)}}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}},} \hfill & {\Omega ^{*} >\Omega _{2}^{*} } \hfill \\ \end{array} } \right.$$

(31)

and

$$u_{w2}^{*} = \kappa B\left\{ {\begin{array}{*{20}l} {0,} \hfill & {\Omega ^{*} \le\Omega _{2}^{*} } \hfill \\ {\frac{{2\kappa^{2}\Omega ^{*} - \left( {1 - \kappa^{2} } \right)\left( {1 + 2B} \right)}}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}},} \hfill & {\Omega ^{*} >\Omega _{2}^{*} } \hfill \\ \end{array} } \right..$$

(32)

It is easily verified that the azimuthal velocity profiles when $\Omega ^{*} =\Omega _{1}^{*}$ and $\Omega _{2}^{*}$ are respectively

$$u_{\theta }^{*} = \frac{{\kappa^{2} }}{2}\left( {\frac{1}{{r^{*} }} - r^{*} } \right)\quad {\text{and}}\;u_{\theta }^{*} = \frac{1}{2}\left( {\frac{1}{{r^{*} }} - r^{*} } \right).$$

(33)

These profiles are independent of the slip number B but it should be noted that $\Omega _{2}^{*}$ varies linearly with it. In Fig. 4, the angular velocities $u_{\theta }^{*} /r^{*}$ for κ = 0.5 corresponding to $\Omega _{1}^{*} ,\Omega _{2}^{*}$, and to $2\Omega _{2}^{*}$ with various slip numbers are plotted. For small values of B (weak slip), the effect of B is more pronounced near the outer wall (where the shear stress is lower).

Fig. 4

Azimuthal velocity profiles in circular Couette flow with κ = 0.5 in the case of non-zero slip yield stress. The profiles for $\varOmega^{*} = \varOmega_{1}^{*}$ and $\varOmega_{2}^{*}$ are independent of the slip number B

3 Steady plane Couette flow

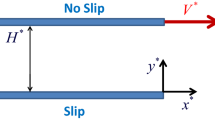
We consider the steady flow of a Newtonian fluid between two infinite parallel plates, placed at a distance H apart, assuming that the upper plate is moving with a speed V while the lower one is fixed, as shown in Fig. 5.

Fig. 5

Geometry of plane Couette flow

3.1 Navier slip

In the general case Navier slip occurs along both walls but with different slip coefficients so that τ _wi  = β _i u _wi , i = 1, 2, where τ _w1 and τ _w2 are the wall shear stresses along the lower and upper walls, respectively. The general form of the steady-state velocity is simply u _x (y) = c ₁ y + c ₂. The constants c ₁ and c ₂ are determined by applying the boundary conditions u _x (0) = u _w1 and u _x (H) = V − u _w2. Thus, the fluid velocity is given by

$$u_{x} (y) = \frac{V}{{1 + B_{1} + B_{2} }}\left( {\frac{y}{H} + B_{1} } \right),$$

(34)

where B _i  ≡ η/β _i H, i = 1, 2. The shear stress τ _xy  = ηdu _x /dy is constant and therefore:

$$\tau_{w1} = \tau_{w2} = \frac{\eta }{{1 + B_{1} + B_{2} }}\frac{V}{H}.$$

(35)

For the two slip velocities one finds

$$u_{w1} = \frac{{B_{1} }}{{1 + B_{1} + B_{2} }}V\quad {\text{and}}\;u_{w2} = \frac{{B_{2} }}{{1 + B_{1} + B_{2} }}V = \frac{{B_{2} }}{{B_{1} }}u_{w1} .$$

(36)

The various special cases of interest are illustrated in Fig. 6 along with the corresponding expressions of the velocity and the slip velocities.

Fig. 6

Different cases of Navier slip in steady plane Couette flow

3.2 Slip with non-zero slip yield stress

As in Sect. 2, we consider only the case in which the same slip law with non-zero slip yield stress applies along both walls. Below a critical velocity V _c of the upper plate no slip occurs (case D in Fig. 6). Setting τ _w  = τ _c we get from Eq. (35)

$$V_{c} = \frac{{H\tau_{c} }}{\eta }.$$

(37)

The velocity is given by

$$u_{x} = \left\{ {\begin{array}{*{20}l} {\frac{y}{H}V,} \hfill & {V \le V_{c} } \hfill \\ {\frac{{V_{c} }}{1 + 2B}\left[ {\left( {V/V_{c} + 2B} \right)\frac{y}{H} + B(V/V_{c} - 1)} \right],} \hfill & {V > V_{c} } \hfill \\ \end{array} .} \right.$$

(38)

The shear stress is constant, and thus the wall shear stress along both plates is

$$\tau_{w} = \left\{ {\begin{array}{*{20}l} {\frac{\eta V}{H},} \hfill & {V \le V_{c} } \hfill \\ {\tau_{c} + \frac{{\frac{{\tau_{c} }}{{V_{c} }}\left( {V - V_{c} } \right)}}{1 + 2B},} \hfill & {V > V_{c} } \hfill \\ \end{array} .} \right.$$

(39)

Obviously, the slip velocities along the two plates are the same:

$$u_{w} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {V \le V_{c} } \hfill \\ {\frac{{B\left( {V - V_{c} } \right)}}{1 + 2B},} \hfill & {V > V_{c} } \hfill \\ \end{array} .} \right.$$

(40)

4 Cessation of circular Couette flow

We consider the cessation of the circular Couette flow of a Newtonian fluid. The steady-state solution serves as the initial condition and at t = 0 the inner cylinder stops rotating. The equation governing the azimuthal velocity u _θ (r, t) is

$$\frac{{\partial u_{\theta } }}{\partial t} = \nu \left( {\frac{{\partial^{2} u_{\theta } }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial u_{\theta } }}{\partial r} - \frac{1}{{r^{2} }}u_{\theta } } \right),$$

(41)

where ν ≡ η/ρ is the kinematic viscosity.

4.1 Navier slip

In the general case in which Navier slip occurs along both cylinders with different slip coefficients, the boundary and initial conditions read:

$$\left. {\begin{array}{*{20}l} {u_{\theta } (\kappa R,t) = \kappa B{}_{1}Rr\left. {\frac{\partial }{\partial r}\left( {\frac{{u_{\theta } }}{r}} \right)} \right|_{r = \kappa R} ,} \hfill & {t > 0} \hfill \\ {u_{\theta } (R,t) = - \kappa B_{2} Rr\left. {\frac{\partial }{\partial r}\left( {\frac{{u_{\theta } }}{r}} \right)} \right|_{r = R} ,} \hfill & {t \ge 0} \hfill \\ {u_{\theta } \left( {r,0} \right) = \frac{{\kappa^{2}\Omega R}}{{1 - \kappa^{2} + 2B_{1} + 2\kappa^{3} B_{2} }}\left[ {\frac{R}{r} - (1 - 2\kappa B_{2} )\frac{r}{R}} \right],} \hfill & {\kappa R \le r \le R} \hfill \\ \end{array} } \right\}.$$

(42)

The solution of the problem (41) and (42) is

$$u_{\theta } (r,t) = \sum\limits_{k = 1}^{\infty } {C_{k} } Z_{1k} \left( {\frac{{\lambda_{k} r}}{R}} \right)e^{{\frac{{ - \lambda_{k}^{2} v}}{{R^{2} }}t}} ,$$

(43)

where (λ _k , γ _k ), k = 1, 2, … are the solutions of the system

$$\left. {\begin{array}{*{20}l} {\kappa B_{1} \lambda_{k} Z_{0k} (\kappa \lambda_{k} ) - (1 + 2B_{1} )Z_{1k} (\kappa \lambda_{k} ) = 0} \hfill \\ {\kappa B_{2} \lambda_{k} Z_{0k} (\lambda_{k} ) + (1 - 2\kappa B_{2} )Z_{1k} (\lambda_{k} ) = 0} \hfill \\ \end{array} } \right\}.$$

(44)

The functions Z _0k and Z _1k are defined by

$$Z_{0k} (r) \equiv J_{0} \left( r \right) + \gamma_{k} Y_{0} \left( r \right),\quad Z_{1k} (r) \equiv J_{1} \left( r \right) + \gamma_{k} Y_{1} \left( r \right),$$

(45)

where J ₁, J ₂ and Y ₀, Y ₁ are Bessel functions of the first and second kind, respectively. The constant C _k is generally given by

$$C_{k} = \frac{{2\kappa^{2} (1 + 2B_{1} )(1 - 2\kappa B_{2} )^{2} Z_{0k} \left( {\kappa \lambda_{k} } \right)\Omega R}}{{\lambda_{k} \left[ {(1 + 2B_{1} )^{2} (1 - 2\kappa B_{2} + \kappa^{2} B_{2}^{2} \lambda_{k}^{2} )Z_{0k}^{2} \left( {\lambda_{k} } \right) - \kappa^{2} (1 - 2\kappa B_{2} )^{2} (1 + 2B_{1} + \kappa^{2} B_{1}^{2} \lambda_{k}^{2} )Z_{0k}^{2} \left( {\kappa \lambda_{k} } \right)} \right]}}.$$

(46)

In the special case that 1 − 2κB ₂ = 0, C _k is simplified as follows:

$$C_{k} = \frac{{2\kappa^{2} (1 + 2B_{1} )Z_{0k} \left( {\kappa \lambda_{k} } \right)\Omega R}}{{\lambda_{k} \left[ {(1 + 2B_{1} )^{2} Z_{1k}^{2} \left( {\lambda_{k} } \right) - \kappa^{2} (1 + 2B_{1} + \kappa^{2} B_{1}^{2} \lambda_{k}^{2} )Z_{0k}^{2} \left( {\kappa \lambda_{k} } \right)} \right]}}.$$

(47)

Various special cases can easily be obtained. Figure 7 illustrates three possibilities for the evolution of the dimensionless velocity (scaled by κΩR) where time is scaled by R ²/ν: (a) the classical no-slip solution obtained by setting B ₁ = B ₂ = 0; (b) the solution when slip occurs only along the inner wall (B ₂ = 0) with B ₁ = 0.5; and (c) the solution when B ₁ = B ₂ = 0.5 (same slip coefficient along the two cylinders). One may observe that cessation becomes slower (the eigenvalues λ _k become smaller) in the presence of slip.

Fig. 7

Cessation of circular Couette flow with κ = 0.5: (a) No-slip along both cylinders (B ₁ = B ₂ = 0); (b) Navier slip only along the inner cylinder (B ₁ = 0.5, B ₂ = 0); (c) Navier slip along both cylinders (B ₁ = B ₂ = 0.5)

4.2 Slip with non-zero slip yield stress

As in Sect. 2.2, we consider the case in which the same slip law applies along both cylinders (B ₁ = B ₂ = B). We have seen that there are three flow regimes defined by the critical angular velocities Ω₁ and Ω₂. We will work with the dimensionless equations hereafter, obtained with the scales used in Sect. 2.2. In addition, time is now scaled by η/τ _c .

4.2.1 No slip ($\Omega ^{*} \le\Omega _{1}^{*}$)

The no-slip solution can be found in many textbooks [25]:

$$u_{\theta }^{*} (r^{*} ,t^{*} ) = \sum\limits_{k = 1}^{\infty } {C_{k} } Z_{1k} \left( {\lambda_{k} r^{*} } \right)e^{{ - \lambda_{k}^{2} t^{*} }} ,$$

(48)

where (λ _k , γ _k ), k = 1, 2, … are the solutions of the system

$$Z_{1k} (\kappa \lambda_{k} ) = Z_{1k} (\lambda_{k} ) = 0$$

(49)

and C _k is given by

$$C_{k} = \frac{{2\kappa^{2}\Omega ^{*} Z_{0k} \left( {\kappa \lambda_{k} } \right)}}{{\lambda_{k} \left[ {Z_{0k}^{2} \left( {\lambda_{k} } \right) - \kappa^{2} Z_{0k}^{2} \left( {\kappa \lambda_{k} } \right)} \right]}}.$$

(50)

4.2.2 Slip only along the inner cylinder ($\Omega _{1}^{*} <\Omega ^{*} \le\Omega _{2}^{*}$)

In this case the boundary and initial conditions read

$$\left. {\begin{array}{*{20}l} {u_{\theta }^{*} (\kappa ,t^{*} ) = \kappa B\left[ {r^{*} \left. {\frac{\partial }{{\partial r{}^{*}}}\left( {\frac{{u_{\theta }^{*} }}{{r^{*} }}} \right)} \right|_{{r^{*} = \kappa }} - 1} \right],} \hfill & {t^{*} > 0} \hfill \\ {u_{\theta }^{*} (1,t^{*} ) = 0,} \hfill & {t^{*} \ge 0} \hfill \\ {u_{\theta }^{*} \left( {r^{*} ,0} \right) = \frac{{\kappa^{2} \left( {\Omega ^{*} + B} \right)}}{{1 - \kappa^{2} + 2B}}\left( {\frac{1}{{r^{*} }} - r^{*} } \right),} \hfill & {\kappa \le r^{*} \le 1} \hfill \\ \end{array} } \right\}.$$

(51)

The solution is then given by

$$u_{\theta }^{*} (r^{*} ,t^{*} ) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{n = 1}^{\infty } {A_{n} } Z_{1n} \left( {\alpha_{n} r^{*} } \right)e^{{ - \alpha_{n}^{2} t^{*} }} - \frac{{\kappa^{2} B}}{{1 - \kappa^{2} + 2B}}\left( {\frac{1}{{r^{*} }} - r^{*} } \right),} \hfill & {t^{*} \le t_{c1}^{*} } \hfill \\ {\sum\limits_{k = 1}^{\infty } {C_{k}^{{}} } Z_{1k} \left( {\lambda_{k} r^{*} } \right)e^{{ - \lambda_{k}^{2} \left( {t^{*} - t_{c1}^{*} } \right)}} ,} \hfill & {t^{*} > t_{c1}^{*} } \hfill \\ \end{array} ,} \right.$$

(52)

where (α _n , δ _n ), n = 1, 2, … are the solutions of the system

$$\left. {\begin{array}{l} {\kappa B\alpha_{n} Z_{0n} (\kappa \alpha_{n} ) - (1 + 2B)Z_{1n} (\kappa \alpha_{n} ) = 0} \\ {Z_{1n} (\alpha_{n} ) = 0} \\ \end{array} } \right\}$$

(53)

with

$$Z_{0n} (r) \equiv J_{0} \left( r \right) + \delta_{n} Y_{0} \left( r \right),\quad Z_{1n} (r) \equiv J_{1} \left( r \right) + \delta_{n} Y_{1} \left( r \right)$$

(54)

and A _n and C _k are respectively given by

$$A_{n} = \frac{{2\kappa^{2} \left( {1 + 2B} \right)\left( {\Omega ^{*} + 2B} \right)Z_{0n} \left( {\kappa \alpha_{n} } \right)}}{{\alpha_{n} \left[ {Z_{0n}^{2} \left( {\alpha_{n} } \right)\left( {1 + 2B} \right)^{2} - \kappa^{2} Z_{0n}^{2} \left( {\kappa \alpha_{n} } \right)\left( {1 + 2B + \alpha_{n}^{2} \kappa^{2} B^{2} } \right)} \right]}}$$

(55)

and

$$C_{k} = \frac{{2Z_{0k} \left( {\kappa \lambda_{k} } \right)}}{{\lambda_{k} \left[ {Z_{0k}^{2} \left( {\lambda_{k} } \right) - \kappa^{2} Z_{0k}^{2} \left( {\kappa \lambda_{k} } \right)} \right]}}\left[ {\sum\limits_{n = 1}^{\infty } {A_{n} \frac{{\kappa \lambda_{k}^{2} }}{{\lambda_{k}^{2} - \alpha_{n}^{2} }}Z_{1n} \left( {\kappa \alpha_{n} } \right)e^{{ - \alpha_{n}^{2} t_{c1}^{*} }} - \frac{{\kappa^{2} B\left( {1 - \kappa^{2} } \right)}}{{1 - \kappa^{2} + 2B}}} } \right].$$

(56)

The critical time $t_{c1}^{*}$, at which slip ceases along the inner wall is the root of the following equation:

$$\sum\limits_{n = 1}^{\infty } {A_{n}^{*} } Z_{1n} \left( {\alpha_{n} \kappa } \right)e^{{ - \alpha_{n}^{2} t^{*} }} = \frac{{\kappa B\left( {1 - \kappa^{2} } \right)}}{{1 - \kappa^{2} + 2B}}.$$

(57)

The slip velocity at the inner cylinder is

$$u_{w1}^{*} (t^{*} ) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{n = 1}^{\infty } {A_{n} } Z_{1n} \left( {\alpha_{n} \kappa } \right)e^{{ - \alpha_{n}^{2} t^{*} }} - \frac{{\kappa \left( {1 - \kappa^{2} } \right)B}}{{1 - \kappa^{2} + 2B}},} \hfill & {t^{*} \le t_{c1}^{*} } \hfill \\ {0,} \hfill & {t^{*} > t_{c1}^{*} } \hfill \\ \end{array} } \right..$$

(58)

4.2.3 Slip along both cylinders ($\Omega ^{*} >\Omega _{2}^{*}$)

In this case the boundary and initial conditions read

$$\left. {\begin{array}{ll} {u_{\theta }^{*} (\kappa ,t^{*} ) = \kappa B\left[ {r^{*} \left. {\frac{\partial }{{\partial r{}^{*}}}\left( {\frac{{u_{\theta }^{*} }}{{r^{*} }}} \right)} \right|_{{r^{*} = \kappa }} - 1} \right],} & {t^{*} > 0} \\ {u_{\theta }^{*} (1,t^{*} ) = - \kappa B\left[ {r^{*} \left. {\frac{\partial }{{\partial r{}^{*}}}\left( {\frac{{u_{\theta }^{*} }}{{r^{*} }}} \right)} \right|_{{r^{*} = 1}} + 1} \right],} & {t^{*} \ge 0} \\ {u_{\theta }^{*} \left( {r^{*} ,0} \right) = \frac{{\kappa^{2} \left[ {\varOmega^{*} + (1 + \kappa )B} \right]}}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}}\left[ {\frac{1}{{r^{*} }} - \left( {1 - 2\kappa B} \right)r^{*} } \right] - \kappa Br^{*} ,} & {\kappa \le r^{*} \le 1} \\ \end{array} } \right\}$$

(59)

and the solution is

$$u_{\theta }^{*} (r^{*} ,t^{*} ) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{m = 1}^{\infty } {A_{m} } Z_{1m} \left( {\mu_{m} r^{*} } \right)e^{{ - \mu_{m}^{2} t^{*} }} - \frac{{\left( {1 - \kappa } \right)\kappa^{2} B}}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}}\left[ {\frac{1}{{r^{*} }} - \left( {1 - 2\kappa B} \right)r^{*} } \right] - \kappa Br^{*} ,} \hfill & {t^{*} \le t_{c1}^{*} } \hfill \\ {\sum\limits_{n = 1}^{\infty } {C_{n} } Z_{1n} \left( {\alpha_{n} r^{*} } \right)e^{{ - \alpha_{n}^{2} \left( {t^{*} - t_{c1}^{*} } \right)}} - \frac{{\kappa^{2} B}}{{1 - \kappa^{2} + 2B}}\left( {\frac{1}{{r^{*} }} - r^{*} } \right),} \hfill & {t_{c1}^{*} < t^{*} \le t_{c2}^{*} } \hfill \\ {\sum\limits_{k = 1}^{\infty } {D_{k} } Z_{1k} \left( {\lambda_{k} r^{*} } \right)e^{{ - \lambda_{k}^{2} \left( {t^{*} - t_{c2}^{*} } \right)}} ,} \hfill & {t^{*} > t_{c2}^{*} } \hfill \\ \end{array} } \right..$$

(60)

Here (μ _m , ɛ _m ), k = 1, 2, … are the solutions of the system

$$\left. {\begin{array}{*{20}c} {\kappa B\mu_{m} Z_{0m} (\kappa \mu_{m} ) - (1 + 2B)Z_{1m} (\kappa \mu_{m} ) = 0} \\ {\kappa B\mu_{m} Z_{0m} (\mu_{m} ) + (1 - 2\kappa B)Z_{1m} (\mu_{m} ) = 0} \\ \end{array} } \right\},$$

(61)

where

$$Z_{0m} (r) \equiv J_{0} \left( r \right) + \varepsilon_{m} Y_{0} \left( r \right),\quad Z_{1m} (r) \equiv J_{1} \left( r \right) + \varepsilon_{m} Y_{1} \left( r \right)$$

(62)

and A _m , C _n and D _k are given by

$$A_{m} = \frac{{2\kappa^{2} \left( {\Omega ^{*} + 2B} \right)Z_{0m} \left( {\kappa \mu_{m} } \right)}}{{\mu_{m} \left( {1 + 2B} \right)\left[ {Z_{0m}^{2} \left( {\mu_{m} } \right)\frac{{\left( {1 - 2\kappa B + \kappa^{2} \mu_{m}^{2} B^{2} } \right)}}{{\left( {1 - 2\kappa B} \right)^{2} }} - \kappa^{2} Z_{0m}^{2} \left( {\kappa \mu_{m} } \right)\frac{{\left( {1 + 2B + \kappa^{2} \mu_{m}^{2} B^{2} } \right)}}{{\left( {1 + 2B} \right)^{2} }}} \right]}},$$

(63)

$$\begin{aligned} C_{n} & = \frac{{2\left( {1 + 2B} \right)^{2} Z_{0n} \left( {\alpha_{n} } \right)}}{{\alpha_{n} \left[ {Z_{0n}^{2} \left( {\alpha_{n} } \right)\left( {1 + 2B} \right)^{2} - \kappa^{2} Z_{0n}^{2} \left( {\kappa \alpha_{n} } \right)\left( {1 + 2B + \alpha_{n}^{2} \kappa^{2} B^{2} } \right)} \right]}} \\ & \quad \times {\kern 1pt} \left\{ {\sum\limits_{m = 1}^{\infty } {A_{m} e^{{ - \mu_{m}^{*2} t_{c1} }} } } \right.\left. {\left[ {\frac{{ - \alpha_{n}^{2} Z_{1m} \left( {\mu_{m} } \right)}}{{\alpha_{n}^{2} - \mu_{m}^{2} }}} \right] + \frac{{\kappa B\left[ {1 - \kappa^{2} + 2\left( {1 + \kappa^{2} } \right)B} \right]}}{{1 - \kappa^{2} + 2\left( {1 + \kappa^{3} } \right)B}}} \right\} \\ \end{aligned}$$

(64)

and

$$D_{k} = \frac{{2Z_{0k} \left( {\kappa \lambda_{k} } \right)}}{{\lambda_{k} \left[ {Z_{0k}^{2} \left( {\lambda_{k} } \right) - \kappa^{2} Z_{0k}^{2} \left( {\kappa \lambda_{k} } \right)} \right]}}\left[ {\sum\limits_{n = 1}^{\infty } {C_{n} e^{{ - a_{k}^{2} \left( {t_{c2}^{*} - t_{c1}^{*} } \right)}} \frac{{\kappa \lambda_{k}^{2} }}{{\lambda_{k}^{2} - \alpha_{n}^{2} }}Z_{1n} \left( {\kappa \alpha_{n} } \right) - \frac{{\kappa^{2} \left( {1 - \kappa^{2} } \right)B}}{{1 - \kappa^{2} + 2B}}} } \right].$$

(65)

The critical time $t_{c1}^{*}$, at which slip no longer occurs along the outer cylinder, and the critical time $t_{c2}^{*}$, at which slip ceases along the inner cylinder are respectively the roots of

$$\sum\limits_{m = 1}^{\infty } {A_{m} } Z_{1m} \left( {\mu_{m} } \right)e^{{ - \mu_{m}^{2} t^{*} }} = \frac{{\kappa B_{2} \left[ {1 - \kappa^{2} + 2\left( {1 + \kappa^{2} } \right)B} \right]}}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}}$$

(66)

and

$$\sum\limits_{n = 1}^{\infty } {C_{n} } Z_{1n} \left( {\kappa \alpha_{n} } \right)e^{{ - \alpha_{n}^{2} \left( {t^{*} - t_{c1}^{*} } \right)}} = \frac{{\kappa \left( {1 - \kappa^{2} } \right)B}}{{1 - \kappa^{2} + 2B}}.$$

(67)

Finally, the two slip velocities are given by

$$u_{w1}^{*} (t^{*} ) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{m = 1}^{\infty } {A_{m}^{{}} } Z_{1m} \left( {\mu_{m} } \right)e^{{ - \mu_{m}^{2} t^{*} }} - \frac{{\kappa B\left[ {1 - \kappa^{2} + 2\left( {1 + \kappa^{2} } \right)B} \right]}}{{1 - \kappa^{2} + 2(1 + \kappa^{3} )B}},} \hfill & {t^{*} \le t_{c1}^{*} } \hfill \\ {0,} \hfill & {t^{*} > t_{c1}^{*} } \hfill \\ \end{array} } \right.$$

(68)

and

$$u_{{w2}}^{*} (t^{*} ) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{{m = 1}}^{\infty } {A_{m} } Z_{{1m}} \left( {\kappa \mu _{m} } \right)e^{{ - \mu _{m}^{2} t^{*} }} - \frac{{\kappa (1 - \kappa )B}}{{1 - \kappa ^{2} + 2(1 + \kappa ^{3} )B}}\left[ {1 - \left( {1 - 2\kappa B} \right)\kappa ^{2} } \right] - \kappa ^{2} B,} \hfill & {t^{*} \le t_{{c1}}^{*} } \hfill \\ {\sum\limits_{{n = 1}}^{\infty } {C_{n} } Z_{{1n}} \left( {\kappa \alpha _{n} } \right)e^{{ - \alpha _{n}^{2} \left( {t^{*} - t_{{c1}}^{*} } \right)}} - \frac{{\kappa \left( {1 - \kappa ^{2} } \right)B}}{{1 - \kappa ^{2} + 2B}},} \hfill & {t_{{c1}}^{*} < t^{*} \le t_{{c2}}^{*} } \hfill \\ {0,} \hfill & {t^{*} > t_{{c2}}^{*} } \hfill \\ \end{array} .} \right.$$

(69)

The evolution of the velocity for κ = 0.5 and B = 0.5 is illustrated in Fig. 8 for three representative values of the angular velocity: (a) $\Omega ^{*} =\Omega _{1}^{*} = 0.375$ such that no slip occurs from $t^{*} = 0$ and the classical cessation solution holds; (b) $\Omega ^{*} =\Omega _{2}^{*} = 3$ such that slip occurs only at the inner cylinder and ceases at $t_{c1}^{*} = 0.0426$; and (c) $\Omega ^{*} = 6 >\Omega _{2}^{*}$ such that initially slip occurs everywhere and ceases along the outer cylinder at $t_{c1}^{*} = 0.0721$ and along the inner cylinder at $t_{c2}^{*} = 0.08$. The evolution of the two slip velocities in the latter case is shown in Fig. 9. Initially the slip velocity $u_{w2}^{*}$ along the outer cylinder appears to be rather constant but later it decays fast and vanishes earlier than $u_{w1}^{*}$. Our calculations showed that $u_{w2}^{*}$ is not necessarily lower than $u_{w1}^{*}$ at all times. One such example is the flow for κ = 0.5 and $\Omega ^{*} = 20$. As shown in Fig. 10, the slip velocity $u_{w1}^{*}$ at the inner cylinder initially decreases faster and becomes lower than $u_{w2}^{*}$ for a while, but then $u_{w2}^{*}$ starts decreasing rapidly and vanishes earlier than $u_{w1}^{*}$.

Fig. 8

Cessation of circular Couette flow with κ = 0.5 and B = 0.5 and different initial conditions: (a) $\varOmega^{*} = \varOmega_{1}^{*} = 0.375$ (no slip initially); (b) $\varOmega^{*} = \varOmega_{2}^{*} = 3$ (slip only at the inner cylinder); and (c) $\varOmega^{*} = 6 > \varOmega_{2}^{*}$ (slip at both cylinders)

Fig. 9

Evolution of the slip velocities in cessation of circular Couette flow for κ = 0.5, B = 0.5, and $\varOmega^{*} = 6 > \varOmega_{2}^{*}$

Fig. 10

Evolution of the slip velocities in cessation of circular Couette flow for κ = 0.5, B = 0.5, and $\varOmega^{*} = 20 > \varOmega_{2}^{*}$

5 Cessation of plane Couette flow

In cessation of plane Couette flow, the upper plate stops moving at t = 0 and the steady-state solution serves as the initial condition. The governing equation is

$$\frac{{\partial u_{x} }}{\partial t} = \nu \frac{{\partial^{2} u_{x} }}{{\partial y^{2} }}.$$

(70)

5.1 Navier slip

In the general case in which Navier slip occurs along both walls with different slip coefficients, the boundary and initial conditions read:

$$\left. {\begin{array}{*{20}c} {u_{x} (0,t) = B_{1} H\left. {\frac{{\partial u_{x} }}{\partial y}} \right|_{y = 0} ,} & {t > 0} \\ {u_{x} (H,t) = - B_{2} H\left. {\frac{{\partial u_{x} }}{\partial y}} \right|_{y = H} ,} & {t \ge 0} \\ {u_{x} (y,0) = \frac{V}{{1 + B_{1} + B_{2} }}\left( {\frac{y}{H} + B_{1} } \right),} & {0 \le y \le H} \\ \end{array} } \right\}$$

(71)

The velocity is given by

$$u_{x} \left( {y,t} \right) = \sum\limits_{k = 1}^{\infty } {C_{k} \left[ {\sin \left( {\frac{{\lambda_{k} y}}{H}} \right) + B_{1} \lambda_{k} \cos \left( {\frac{{\lambda_{k} y}}{H}} \right)} \right]e^{{ - \nu \frac{{\lambda_{k}^{2} }}{{H^{2} }}t}} } ,$$

(72)

where λ _k are the roots of

$$\tan (\lambda_{k} ) = \frac{{\left( {B_{1} + B_{2} } \right)\lambda_{k} }}{{B_{1} B_{2} \lambda_{k}^{2} - 1}}$$

(73)

and the constants C _k are given by

$$C_{k} = \frac{{2V\left( {B_{1}^{2} \lambda_{k}^{2} + 1} \right)\left( {B_{2}^{2} \lambda_{k}^{2} + 1} \right)\cos \lambda_{k} }}{{\lambda_{k} \left( {B_{1} B_{2} \lambda_{k}^{2} - 1} \right)\left[ {\left( {B_{1}^{2} \lambda_{k}^{2} + B_{1} + 1} \right)\left( {B_{2}^{2} \lambda_{k}^{2} + 1} \right) + B_{2} \left( {B_{1}^{2} \lambda_{k}^{2} + 1} \right)} \right]}}.$$

(74)

The evolution of the velocity in various representative cases is illustrated in Fig. 11, where the velocity is scaled by V, lengths by H, and time by H ²/ν, and non-dimensionalized variables are denoted by stars: (a) The classical no-slip solution obtained by setting B ₁ = B ₂ = 0; (b) the solution when slip occurs only along lower wall with B ₁ = 0.5 and B ₂ = 0; (c) the solution when slip occurs only along upper wall with B ₁ = 0and B ₂ = 0.5; (d) the solution when B ₁ = B ₂ = 0.5 (same slip coefficient along the two plates). Since the leading eigenvalue decreases cessation becomes slower as slip is enhanced.

Fig. 11

Cessation of simple shear flow: (a) No-slip along the walls (B ₁ = B ₂ = 0); (b) Navier slip only along the lower wall (B ₁ = 0.5, B ₂ = 0); (c) Navier slip only along the upper wall (B ₁ = 0, B ₂ = 0.5); (d) Navier slip along both walls (B ₁ = B ₂ = 0.5)

5.2 Slip with non-zero slip yield stress

When V ≤ V _c , the standard no-slip solution applies. When V > V _c , the fluid initially slips along both walls. As the velocity is reduced, slip ceases first along the lower plate and then along the upper one. Hence, there is no slip in the final stage of the cessation. The critical times for the cessation of slip along the lower and the upper walls are denoted by t _c1 and t _c2, respectively. For the rest of this section it is more convenient to scale the velocity by V _c, lengths by H, the stress by τ _c, and time by η/τ _c. Again, non-dimensionalized quantities are denoted by stars. Hence, the no-slip case corresponds to $V^{*} \le 1$.

5.2.1 No-slip regime

The boundary and initial conditions read

$$\left. {\begin{array}{ll} {u_{x}^{*} (0,t^{*} ) = u_{x}^{*} (1,t^{*} ) = 0,} & {t^{*} > 0} \\ {u_{x}^{*} (y^{*} ,0) = y^{*} ,} & {0 \le y^{*} \le 1} \\ \end{array} } \right\}$$

(75)

and the solution is given by

$$u_{x}^{*} (y^{*} ,t^{*} ) = \sum\limits_{k = 1}^{\infty } {C_{k}^{*} \sin \left( {\lambda_{k} y^{*} } \right)} e^{{ - \lambda_{k}^{2} t^{*} }} ,$$

(76)

where λ _k  = kπ, k = 1, 2, … and

$$C_{k}^{*} = - \frac{{2V^{*} \cos \lambda_{k} }}{{\lambda_{k} }}.$$

(77)

5.2.2 Slip along both walls ($V^{*} > 1$)

In this case the boundary and initial conditions read

$$\left. {\begin{array}{ll} {u_{x}^{*} (0,t^{*} ) = B\left( {\frac{{\partial u_{x}^{*} }}{{\partial y^{*} }} - 1} \right),} & {t^{*} > 0} \\ {u_{x}^{*} (1,t^{*} ) = - B\left( {\frac{{\partial u_{x}^{*} }}{{\partial y^{*} }} + 1} \right),} & {t^{*} > 0} \\ {u_{x}^{*} (y^{*} ,0) = \frac{1}{1 + 2B}\left[ {\left( {V^{*} + 2B} \right)y^{*} + B(V^{*} - 1)} \right],} & {0 \le y^{*} \le 1} \\ \end{array} } \right\}.$$

(78)

The solution is given by

$$u_{x}^{*} (y^{*} ,t^{*} ) = \left\{ {\begin{array}{*{20}l} {\begin{array}{*{20}c} {\sum\limits_{m = 1}^{\infty } {A_{m}^{*} } \left[ {\sin (\mu_{m} y^{*} ) + B\mu_{m} \cos (\mu_{m} y^{*} )} \right]e^{{ - \mu_{m}^{2} t^{*} }} - B,} & {t^{*} \le t_{c1}^{*} } \\ \end{array} } \hfill \\ {\sum\limits_{n = 1}^{\infty } {C_{n}^{*} } \sin (a_{n} y^{*} )e^{{ - a_{n}^{2} (t^{*} - t_{c1}^{*} )}} - \frac{{By^{*} }}{B + 1},t_{c1}^{*} < t^{*} \le t_{c2}^{*} } \hfill \\ {\begin{array}{*{20}c} {\sum\limits_{k = 1}^{\infty } {D_{k}^{*} } \sin (\lambda_{k} y^{*} )e^{{ - \lambda_{k}^{2} (t^{*} - t_{c2}^{*} )}} ,} & {t^{*} > t_{c2}^{*} } \\ \end{array} } \hfill \\ \end{array} } \right.,$$

(79)

where μ _m and a _n are the roots of

$$\tan \mu_{m} = \frac{{ - 2B\mu_{m} }}{{1 - B^{2} \mu_{m}^{2} }}$$

(80)

and

$$\tan a_{n} = - Ba_{n} ,$$

(81)

respectively. The constants $A_{m}^{*} ,C_{n}^{*}$ and $D_{k}^{*}$ are given by

$$A_{m}^{*} = \frac{{2\cos \mu_{m} (1 + \mu_{m}^{2} B^{2} )(V^{*} + 2B)}}{{\mu_{m} (\mu_{m}^{2} B^{2} - 1)(\mu_{m}^{2} B^{2} + 2B + 1)}},$$

(82)

$$C_{n}^{*} = \frac{ - 2B}{{a_{n} (1 + B\cos^{2} a_{n} )}} - \frac{{2a_{n} B}}{{(1 + B\cos^{2} a_{n} )}}\sum\limits_{m = 1}^{\infty } {\frac{{\mu_{m} A_{m}^{*} e^{{ - \mu_{m}^{2} t_{c1}^{*} }} }}{{\mu_{m}^{2} - a_{n}^{2} }}}$$

(83)

and

$$\begin{aligned} D_{k}^{*} & = \frac{{2B\cos \lambda_{k} }}{{(B + 1)\lambda_{k} }} + 2\lambda_{k} \cos \lambda_{k} \\ & \quad \times \left\{ {\sum\limits_{n = 1}^{\infty } {\frac{{\sin a_{n} e^{{ - a_{n}^{2} \left( {t_{c2} - t_{c1} } \right)}} }}{{a_{n}^{2} - \lambda_{k}^{2} }}\left[ {\frac{ - 2B}{{a_{n} (1 + B\cos^{2} a_{n} )}} - \frac{{2a_{n} B}}{{(1 + B\cos^{2} a_{n} )}}\sum\limits_{m = 1}^{\infty } {\frac{{2\cos \mu_{m} \left( {1 + \mu_{m}^{2} B^{2} } \right)(V^{*} + 2B)e^{{ - \mu_{m}^{2} t_{c1} }} }}{{\left( {\mu_{m}^{2} - a_{n}^{2} } \right)\left( {\mu_{m}^{2} B^{2 - 1} } \right)\left( {\mu_{m}^{2} B^{2} + 2B + 1} \right)}}} } \right]} } \right\}. \\ \end{aligned}$$

(84)

The two slip velocities are given by

$$u_{w1}^{*} (t^{*} ) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{m = 1}^{\infty } {A_{m}^{*} } B\mu_{m} e^{{ - \mu_{m}^{2} t^{*} }} - B,} \hfill & {t^{*} \le t_{c1}^{*} } \hfill \\ 0 \hfill & {t^{*} > t_{c1}^{*} } \hfill \\ \end{array} } \right.$$

(85)

and

$$u_{{w2}}^{*} (t^{*} ) = \left\{ {\begin{array}{*{20}l} {\sum\limits_{{m = 1}}^{\infty } {A_{m}^{*} } \left( {\sin \mu _{m} + B\mu _{m} \cos \mu _{m} } \right)e^{{ - \mu _{m}^{2} t^{*} }} - B,} \hfill & {t^{*} \le t_{{c1}}^{*} } \hfill \\ {\sum\limits_{{n = 1}}^{\infty } {C_{n}^{*} } \sin a_{n} e^{{ - a_{n}^{2} (t^{*} - t_{{c1}}^{*} )}} - \frac{B}{{B + 1}},} \hfill & {t_{{c1}}^{*} < t^{*} \le t_{{c2}}^{*} } \hfill \\ {0,} \hfill & {t^{*} > t_{{c2}}^{*} } \hfill \\ \end{array} .} \right.$$

(86)

The critical times $t_{c1}^{*}$ and $t_{c2}^{*}$ are the roots of

$$\sum\limits_{m = 1}^{\infty } {A_{m}^{*} } B\mu_{m} e^{{ - \mu_{m}^{2} t_{c1}^{*} }} - B = 0$$

(87)

and

$$\sum\limits_{n = 1}^{\infty } {C_{n}^{*} } \sin a_{n} e^{{ - a_{n}^{2} (t_{c2}^{*} - t_{c1}^{*} )}} - \frac{B}{B + 1} = 0,$$

(88)

respectively. Keeping only the first terms of the above summations leads to the following estimates of the critical times:

$$\bar{t}_{c1}^{*} = \frac{1}{{\mu_{1}^{2} }}\ln \left( {A_{1}^{*} \mu_{1} } \right)$$

(89)

and

$$\bar{t}_{c2}^{*} = \bar{t}_{c1}^{*} + \frac{1}{{a_{1}^{2} }}\ln \frac{{(B + 1)C_{1}^{*} \sin a_{1} }}{B}.$$

(90)

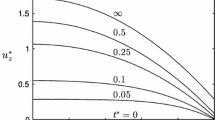
The evolution of the velocity for B = 0.1 and $V^{*} = 1.1,1.5\;{\text{and}}\;2$ is illustrated in Fig. 12. The velocity profiles at $t_{c1}^{*}$ and $t_{c2}^{*}$ are provided in all cases. Figure 13 shows the evolution of the two slip velocities for $V^{*} = 1.1\;{\text{and}}\;1.5$. The lower-plate slip velocity initially appears to be rather constant but eventually it decreases rapidly vanishing at $t_{c1}^{*}$. The upper-plate slip velocity, which is at least one order of magnitude greater, decays very fast initially and then fast to vanish at $t_{c2}^{*} > t_{c1}^{*}$. The effect of $V^{*}$ on the two slip velocities is also illustrated in Fig. 14. In general, slip becomes stronger and cessation becomes slower and therefore the critical times $t_{c1}^{*}$ and $t_{c2}^{*}$ increase as $V^{*}$ is increased. Finally the effect of the slip number B on the two slip velocities is illustrated in Figs. 15 and 16. In Fig. 15, one observes the evolution of the two slip velocities for $V^{*} = 1.5$ and different values of B. The decay of the slip velocities is slower as the slip number B is increased, i.e. when slip is stronger. Figure 16 shows plots of the critical times $t_{c1}^{*}$ and $t_{c2}^{*}$ for the cessation of slip along the lower and upper plates, respectively, versus the slip number B for various values of $V^{*}$. As already discussed the values of the two critical times increase with B. In Fig. 8, the estimates of the stopping times given by Eqs. (89) and (90) are also compared with the exact values. It is shown that the value of $t_{c1}^{*}$ is overestimated while that of $t_{c2}^{*}$ is underestimated. The estimates are improved as the values of B and $V^{*}$ are increased.

Fig. 12

Evolution of the velocity in cessation of simple shear flow with non-zero slip yield stress with B = 0.1: (a) $V^{*} = 1.1$; (b) $V^{*} = 1.5$; (c) $V^{*} = 2$

Fig. 13

Evolution of the slip velocities in cessation of simple shear flow with non-zero slip yield stress with B = 0.1: (a) $V^{*} = 1.1$; (b) $V^{*} = 1.5$

Fig. 14

Evolution of the slip velocities in cessation of simple shear flow with non-zero slip yield stress, for B = 0.1 and various values of $V^{*}$: (a) along the lower plate; (b) along the upper plate

Fig. 15

Evolution of the slip velocity in cessation of plane Couette flow with non-zero slip yield stress for $V^{*} = 1.5$ and various values of B: (a) lower plate; (b) upper plate

Fig. 16

The critical times $t_{c1}^{*}$ and $t_{c2}^{*}$ for the cessation of plane Couette flow with non-zero slip yield stress for various values of $V^{*}$. The dashed lines are the estimates obtained using only the leading term of the corresponding series expansion, i.e. using Eqs. (89) and (90)

6 Conclusions

We have solved both the steady-state and time-dependent circular and plane Couette flows of a Newtonian fluid with wall slip following the two-branch slip equation proposed by Spikes and Granick [18]. The latter involves a non-zero slip yield stress above which the variation of the wall shear stress with the slip velocity is linear. The solutions presented here supplement the analytical solutions reported by Ng [14] and Kaoullas and Georgiou [11, 12] and may be useful in correcting slip effects in Couette rheometry, in checking numerical non-Newtonian simulation codes, and in start up and cessation of steady shear in MEMS devices.

The existence of non-zero slip yield stress results in three steady-state regimes for the circular Couette flow. These are defined by the two critical values of the angular velocity at which slip is triggered along the rotating inner cylinder and the fixed outer one. In cessation of the flow in the last regime where slip is present along both cylinders, it has been shown that slip ceases first finite along the outer cylinder and then along the inner one.

In the case of steady plane Couette flow, there are two flow regimes, since slip occurs only above a critical value of the velocity of the moving upper plate, V _c. Given that the shear stress in the flow domain is constant, the slip velocities u _w1 and u _w2 along the lower and upper plates are equal. In time-dependent flow slip may occur only along one of the two plates. In the case of flow cessation above V _c, there are three flow regimes defined by two critical times t _c1 and t _c2, respectively defined as the times at which slip ceases along the lower and the upper plates. For times after t _c2, the flow decays exponentially with no slip.