On the effectiveness of heuristics for learning nested dichotomies: an empirical analysis

Abstract

In machine learning, so-called nested dichotomies are utilized as a reduction technique, i.e., to decompose a multi-class classification problem into a set of binary problems, which are solved using a simple binary classifier as a base learner. The performance of the (multi-class) classifier thus produced strongly depends on the structure of the decomposition. In this paper, we conduct an empirical study, in which we compare existing heuristics for selecting a suitable structure in the form of a nested dichotomy. Moreover, we propose two additional heuristics as natural completions. One of them is the Best-of-K heuristic, which picks the (presumably) best among K randomly generated nested dichotomies. Surprisingly, and in spite of its simplicity, it turns out to outperform the state of the art.

1 Introduction

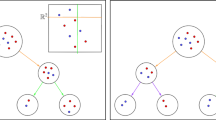
Nested dichotomies (NDs) are known as models for polychotomous data in statistics and used as classifiers for multi-class problems in machine learning (Frank and Kramer 2004). By splitting the set of classes in a recursive way, nested dichotomies reduce the original multi-class problem to a set of binary problems, for which any (probabilistic) binary classifier can be used. For example, the dichotomy shown in Fig. 1 decomposes a problem with five classes into four binary problems.

Fig. 1

Example of a nested dichotomy. The first classifier ($C_1$) is supposed to separate class C from the meta-class $\{A,B,D,E\}$, i.e., the union of classes A, B, D, and E; likewise, the second classifier separates classes $\{A,D\}$ from $\{B,E\}$, the third classifier class A from D, and the fourth B from E

Nested dichotomies are interesting for a couple of reasons. In practice, they have been shown to yield strong predictive accuracy (Frank and Kramer 2004; Leathart et al. 2016; Rodríguez et al. 2010). Moreover, compared to other decomposition techniques, such as all-pairs (Fürnkranz 2002) or one-versus-rest (Rifkin and Klautau 2004), they offer more flexibility in the specification of binary problems. At the same time, the aggregation of individual predictions into an overall (multi-class) prediction can be accomplished in a very natural and consistent manner, based on the chain rule of probability—a property that is specifically appealing in case probabilistic predictions are sought instead of hard class assignments. This is in contrast to other techniques such as error-correcting output codes (Dietterich and Bakiri 1995), which, while being even more flexible, may produce inconsistencies at prediction time.

The flexibility in choosing a structure offers advantages but also comes with the challenge of finding a good decomposition. In fact, the performance of the multi-class classifier eventually produced may strongly depend on the structure of the dichotomy, because the latter specifies the set of binary problems that need to be solved. Obviously, as illustrated in Fig. 2, some of these problems might be much more difficult than others. This is confirmed by Fig. 3, where the distribution of predictive accuracies (on the test data) of nested dichotomies is shown for the datasets pendigits and mfeat-karhunen. As can be seen, depending on the structure chosen, the performance may vary a lot.

Fig. 2

Distribution of 5 classes. Using linear models as base learners (indicated as dashed lines), the nested dichotomy shown in Fig. 1 appears to quite suitable. Starting with a problem such as $\{A,E\}$ versus $\{B,C,D\}$, on the other hand, would lead to much worse performance

Previous work has mostly focused on ensembles of nested dichotomies (Frank and Kramer 2004; Dong et al. 2005; Rodríguez et al. 2010). In that case, structures are typically generated at random, and of course, ensembling reduces the importance of optimizing individual structures. In this paper, however, we are interested in learning a single dichotomy. There are several reasons for why a single model might be preferred to an ensemble, including complexity and interpretability. Indeed, the latter has gained increasing importance in machine learning in recent years. In contrast to an ensemble, a single dichotomy at least offers the chance of interpretability (provided the individual binary classifiers are interpretable). Yet, our main motivation for considering the problem of structure optimization for NDs originates from automated machine learning (Thornton et al. 2013; Feurer et al. 2015). Given a dataset, the goal of AutoML is to select and parametrize a machine learning algorithm (or, more generally, an ML pipeline including data pre- and postprocessing steps) in a most favorable way. If ND is among the (meta) learning techniques the AutoML system can choose from, the search for an optimal decomposition immediately becomes part of the AutoML process. Here, ensembling is not an option, because each of the reduced problems gives rise to a new (and potentially still very complex) AutoML problem. In other words, NDs are indeed used as a means for recursive problem reduction, not merely as a decomposition of a multi-class problem into binary problems, which are all solved in the same way.

Fig. 3

The distribution of predictive accuracy on the pendigits (above) and mfeat-karhunen (below) datasets for 10,000 randomly sampled nested dichotomies with three different classifiers: CART, logistic regression, and decision stumps (CART). Each nested dichotomy is evaluated by the mean accuracy in a 10-fold CV

The problem of ND structure optimization is extremely difficult, mainly because of the huge number of candidate structures. Therefore, several heuristic strategies have been proposed in recent years. In this paper, we analyze and compare the performance of these heuristics in an extensive empirical study. Unlike previous papers, we are not directly focusing on accuracy as a measure for comparison. Instead, what we look at is the position of the selected structure among all structures (sorted by accuracy); statistically, this translates into the quantile that is reached in performance distributions like those in Fig. 3. For reasons that will be explained in more detail further below, we believe this is a more appropriate way of measuring the performance in structure optimization.

In addition, we also introduce two new heuristics, one based on hierarchical clustering and the other on the simple idea of choosing the best among K random structures. To our surprise, the latter turns out to be extremely effective, and even outperforms the current state-of-the-art heuristic. This is one of the most important findings of the paper.

The rest of the paper is organized as follows. In the next section, we introduce nested dichotomies and discuss some of their properties in more detail. In Sect. 3, we address the problem of sampling from the space of ND structures, which is used as an important routine in several heuristics. An overview of existing heuristics is then given in Sect. 4, where we also introduce our new proposals. The empirical study is presented in Sect. 5, prior to concluding the paper in Sect. 6.

2 Nested dichotomies

Given a set of n classes $\mathcal {Y} = \{ y_1, \ldots , y_n \}$, a nested dichotomy (ND) is a recursive separation $(\mathcal {Y}_l, \mathcal {Y}_r)$ of $\mathcal {Y}$ into pairs of disjoint, nonempty subsets. Equivalently, an ND can be defined in terms of a full binary tree on n leaf nodes, which are (uniquely) labeled by the classes; moreover, the $n-1$ inner nodes are labeled by the set of classes in the subtree beneath that node. For example, the ND shown in Fig. 1 corresponds to the recursive separation (C, ((A, D), (B, E))).

To turn a nested dichotomy into a multi-class classifier, a binary classifier is assigned to each inner node. The task of the classifier is to separate the set of classes $\mathcal {Y}_l$ associated with its left successor node (the positive meta-class) from the set of classes $\mathcal {Y}_r$ of its right successor (the negative meta-class). Given a set of training data

$$\begin{aligned} \mathcal {D} = \big \{ (\varvec{x}_i , y_i) \big \}_{i=1}^N \subset \mathcal {X} \times \mathcal {Y}\, , \end{aligned}$$

where $\mathcal {X}$ is the underlying instance space, the binary classifiers are produced by applying a suitable base learner¹ to the corresponding classification problems. We assume the classifier $C_{\mathcal {Y}_l , \mathcal {Y}_r}$ associated with the dichotomy $(\mathcal {Y}_l , \mathcal {Y}_r)$ to be a mapping of the form $\mathcal {X} \longrightarrow [0,1]$, where $C_{\mathcal {Y}_l , \mathcal {Y}_r}(\varvec{x})$ is an estimation of the conditional probability $\mathbf {P}\big ( y \in \mathcal {Y}_l \, | \, y \in \mathcal {Y}_l \cup \mathcal {Y}_r, \varvec{x} \big )$, and hence $1- C_{\mathcal {Y}_l , \mathcal {Y}_r}(\varvec{x})$ an estimation of $\mathbf {P}( y \in \mathcal {Y}_r \, | \, y \in \mathcal {Y}_l \cup \mathcal {Y}_r, \varvec{x} )$. Such a probabilistic classifier is produced by the base learner on the relevant subset of training data $\{ (\varvec{x}_i , y_i) \in \mathcal {D} \, | \, y_i \in \mathcal {Y}_l \cup \mathcal {Y}_r \}$.

2.1 Inference

Once the hierarchy of classifiers required by a nested dichotomy has been trained, a new instance $\varvec{x}$ can be classified probabilistically as follows: For $y_j \in \mathcal {Y}$, let $\mathcal {Y} = \mathcal {Y}_0 \supset \mathcal {Y}_1 \supset \cdots \supset \mathcal {Y}_m = \{ y_j \}$ be the chain of subsets associated with the nodes from the root to the leaf node labeled by $y_j$. Then, by virtue of the chain rule of probability,

$$\begin{aligned} \mathbf {P}(y_j \, \vert \, x) = \prod _{i=1}^{m-1} \mathbf {P}\big ( y_j \in \mathcal {Y}_{i+1} \, \vert \, y_j \in \mathcal {Y}_i, \varvec{x} \big ) , \end{aligned}$$

where $\mathbf {P}( \mathcal {Y}_{i+1} \, \vert \, \mathcal {Y}_i, \varvec{x})$ is given by $C_{\mathcal {Y}_{i+1}, \mathcal {Y}_i \setminus \mathcal {Y}_{i+1}}(\varvec{x})$ if $\mathcal {Y}_{i+1}$ is the left successor of $\mathcal {Y}_i$, and $1-C_{ \mathcal {Y}_{i+1}, \mathcal {Y}_i \setminus \mathcal {Y}_{i+1}}(\varvec{x})$ if $\mathcal {Y}_{i+1}$ is the right successor of $\mathcal {Y}_i$. In other words, the probability $p_j$ of class $y_j$ is obtained by multiplying the predicted probabilities along the path from the root of the ND tree to the leaf node associated with $y_j$ (Frank and Kramer 2004). In case a definite decision in favor of a single class has to be made, the expected loss minimizer can be derived from the probability distribution $(p_1, \ldots , p_n)$; for 0 / 1 loss, this is simply the class $y_j$ for which $p_j$ is highest.

Sometimes, a deterministic approximation of the above inference strategy is used, especially in the case of 0 / 1 loss. Roughly speaking, this strategy consists of submitting $\varvec{x}$ to the root of the dichotomy and following a single path in the tree, instead of exploring all paths. At each inner node, the successor with the higher conditional probability is taken. Note that this strategy can even be realized by any non-probabilistic binary classifier. An example for this type of inference is provided in Duarte-Villaseñor et al. (2012) (see Sect. 4.2 for details). In general, probabilistic and deterministic inference may yield different predictions.

2.2 The choice of base learners

The performance of a ND is of course not only determined by the choice of the decomposition structure, but also by the choice of the base learner, which should be well adapted to the binary problems involved. This can already be seen in the two examples in Fig. 3, where performance differences between classification trees, logistic regression (LR), and decision stumps are clearly visible. Note that these learners exhibit a natural order in terms of their flexibility (as measured, for example, by the VC dimension): classification trees are able to fit highly non-linear models, LR only linear ones, and stumps are even restricted to single axis-parallel splits. While the flexibility of classification trees is obviously useful in the case of pendigits, LR is a better choice for the mfeat-karhunen data.

While the average performance of the base learners is reflected by the location of the corresponding distribution in Fig. 3, one can also observe significant differences in the variance of these distributions. In general, the less flexible the base learner, the higher the variance in performance. This observation can be explained by the fact that flexible models can compensate a suboptimal structure much better than less flexible ones; or, stated differently, the choice of a suitable structure is much more critical when using simple models such as linear discriminants or decision stumps. In the example in Fig. 2, for instance, the ND structure (C, ((A, D), (B, E))) shown in Fig. 1 will yield a good solution when being trained with logistic regression as a base learner. In contrast, a structure such as ((A, E), (B, (C, D))) would lead to very poor performance, because it involves problems that call for highly nonlinear decision boundaries. Using classification trees as a base learner, the difference will be less pronounced, since even nonlinear problems can be solved more or less accurately.

The idea of simplification, and of using simple binary learners, is at the core of decomposition techniques such as nested dichotomies. From this point of view, the use of classification trees as a base learner might be questioned, all the more because classification trees are not restricted to binary problems, and hence could be applied to the original problem right away. Although we could have used non-linear binary methods such as kernelized LR as well, we nevertheless included classification trees as a representative of a non-linear learner in our empirical study, simply because they have also been used in most of the previous studies.

2.3 Performance of nested dichotomies

Formally, one should distinguish between

• (i) a nested dichotomy in the sense of a tree-structure or, equivalently, a recursive decomposition of the set of classes $\mathcal {Y}$, and

• (ii) a nested dichotomy in the sense of a multi-class classifier, that is, the instantiation of a structure through binary classifiers at the inner nodes.

Let $\mathcal {S}_n$ denote the set of all ND structures on n classes. Given a dataset $\mathcal {D}$ and a base learner L, a structure $S \in \mathcal {S}_n$ is instantiated by training all binary classifiers required by S as outlined above. Thus, the classifier $\bar{S}=f(S, \mathcal {D}, L)$ eventually produced depends on the structure, the data, and the learner.

When speaking about the performance of a nested dichotomy, what we actually have in mind is the expected performance of a structure S, where the expectation is taken over the random sample $\mathcal {D}$ used for training. More specifically, let $E(\bar{S})$ denote the generalization performance of the classifier $\bar{S}$, i.e., the expected loss of this classifier on newly generated (test) data. Assuming L to be fixed, $\bar{S}$ depends on the random sample $\mathcal {D}$, and is hence random itself. Therefore, assuming data points $(\varvec{x}, y)$ to be generated according to the distribution P on $\mathcal {X} \times \mathcal {Y}$, we define the performance of a structure S on training data of size N as follows:

$$\begin{aligned} E(S) = E(S,N) = \mathbf {E}_{\mathcal {D} \sim P^N} \big ( E( f(S, \mathcal {D}, L) \big ) , \end{aligned}$$

(1)

where $\mathbf {E}$ denotes the expected value operator. In practice, the performance (1) can of course only be approximated. In our experimental studies, corresponding approximations will be obtained by means of standard cross-validation techniques.

Likewise, the distributions shown in Fig. 3 can be seen as approximations of the distribution of the performance (1) of a structure S drawn uniformly at random from $\mathcal {S}_n$. From the figure and our discussion so far, it is clear that the location and shape of these distributions is strongly influenced by the base learner L. One may wonder, therefore, whether the (numerical) performances E(S) are ideally suited as indicators of the effectiveness of heuristic algorithms for optimizing the structure S.

Alternatively, we may consider the ranking of the $|\mathcal {S}_n|$ structures S according to their performance, where a structure S precedes another one $S'$ if E(S) is better than $E(S')$. Then, one could ask for the position that a structure $S^*=A(\mathcal {D})$ chosen by an algorithm A will reach in this ranking. Normalizing by the length $|\mathcal {S}_n|$ of the ranking, this leads us to the exceedance probability as a measure of performance of an algorithm A:

$$\begin{aligned} p_{exc}(A) = \mathbf {P}\big ( X > e(A) \big ) , \end{aligned}$$

(2)

where

$$\begin{aligned} e(A) = \mathbf {E}(E(S^*)) = \mathbf {E}_{\mathcal {D} \sim P^N} \big ( E(A(\mathcal {D})) \big ) \end{aligned}$$

(3)

is the expected performance of a structure $S^*$ produced by algorithm A (and randomly influenced by the data $\mathcal {D})$, and X is the performance E(S) of a structure chosen uniformly at random from $\mathcal {S}_n$.

Roughly speaking, $p_{exc}(A)$ is the probability that a randomly chosen structure will perform better than a structure produced by A. This measure has a number of appealing properties, especially compared to predictive accuracy as a performance metric. It puts a stronger emphasis on the choice of the structure S, while depending less on the absolute performance of the base learner. Therefore, in contrast to accuracy, it is also comparable across different datasets. Assuming values in [0, 1], the exceedance is well calibrated and has a simple interpretation: Since the extreme value 0 can indeed be assumed, $p_{exc}$ is the “gap” to perfect performance, while 1 / 2 is the performance achieved by a random selection.

3 Uniform random sampling of ND structures

As already mentioned, searching the space $\mathcal {S}_n$ of ND structures for a structure with optimal (estimated) performance (1) is extremely difficult due to the enormous size of this space. In fact, the size of $\mathcal {S}_n$ is finite but grows very quickly with n. It is not difficult to see that this set is equal to the set of unordered complete binary trees on n nodes. The problem of counting this set has been considered in combinatorics (Stanley and Fomin 1999), and its size is known to be

$$\begin{aligned} | \mathcal {S}_n | = 1\cdot 3 \cdot 5 \cdot \cdot \cdot (2n-3) = (2n - 3)!! \end{aligned}$$

(4)

Obviously, this number is prohibitive and excludes an exhaustive search unless n is very small. This is the reason for why sampling techniques are playing an important role in ND structure optimization, and have already been used in several papers (Frank and Kramer 2004; Leathart et al. 2016; Dong et al. 2005). Nevertheless, a concrete algorithm for uniform sampling has never been provided. This is a bit surprising, because the problem is less obvious than it may appear at first sight.

The uniform sampling approach we suggest is based on the one-to-one correspondence between ND structures and rooted full binary trees. In addition, each leaf node in a nested dichotomy is labeled with the corresponding class, a property called “terminally labeled” in the literature on tree algorithms. This labeling uniquely determines the dichotomies at all inner nodes. The problem of generating a nested dichotomy can therefore be divided into two steps: (i) generation of a rooted terminally labeled full binary tree and (ii) propagation of leaf labels towards the root in order to determine the dichotomies at the inner nodes.

For the problem (i), several strategies have been proposed in the literature (Rohlf 1983; Furnas 1984). Here, we provide a two-step procedure for uniform random sampling of rooted terminally labeled full binary trees as suggested by Furnas (1984):

• 1. Generation of an unrooted terminally labeled full binary tree $T_n$. Given is a set of n terminal nodes (leafs).

  • (a) Create a doublet “tree” $T_2$ by connecting nodes 1 and 2 by a single edge.

  • (b) Until all n terminal nodes are connected to the tree, proceed with the following random augmentation:

    • (i) Given a tree $T_k$ on $k < n$ terminal nodes, select an edge of $T_k$ uniformly at random.

    • (ii) On this edge, a new internal node of degree 3 is added and the $(k+1)$st terminal node is connected. The result is a binary tree $T_{k+1}$ on $k+1$ terminal nodes.

• 2. Transformation of $T_n$ into a rooted tree.

  • (a) Choose an edge of $T_n$ randomly with uniform probability.

  • (b) Introduce a new root node of degree 2 on this edge.

Furnas proved that this procedure provides a uniform random sampling of rooted terminally labeled full binary trees. The time complexity of the first step is linear in the number of classes n. The second step can be implemented in constant time, leading to an overall time complexity of O(n).

For the label propagation problem (ii), we suggest the following solution. The leaf node to which class $y_i$ has been assigned is labeled by the number $2^{i}$. The dichotomies at the inner nodes are encoded with a pair of numbers $[d_l, d_r]$, denoting the sum of all leaf labels in the left and right subtree, respectively. Since all leaf nodes are encoded uniquely (with only a single ‘1’ in the corresponding bit string), the encoding is unique. To propagate the leaf labels, we traverse the nested dichotomy in postorder and encode every inner node with the sum of the dichotomies of its child nodes $[d_{l_l} + d_{l_r}, d_{r_l} + d_{r_r}]$. Since the complexity of tree traversal is linear in the number of nodes and the summation, and generating the leaf labels is nearly constant for a usual number of classes,² step (ii) has an overall time complexity of O(n). Using this approach, a single nested dichotomy can be sampled uniformly with the time complexity O(n), i.e., linear in the number of classes in the original problem.

Interestingly, uniform random sampling is likely to produce NDs with a “degenerate” tree structure (deeper trees). To show this, we consider a single inner node of a tree and compute the probability for a split of the remaining classes at this node. We assume $(k,n-k)$-split of $n = | \mathcal {Y}| \ge 2$ classes, where $k \ge 1$ and $k \le n/2$ without loss of generality. According to (4), the probability of observing such a split in the case of uniform random sampling is

$$\begin{aligned} P_{U}(n, k) = \frac{{{n}\atopwithdelims (){k}}T(k)T(n-k)}{T(n)}= \frac{{{n}\atopwithdelims (){k}}(2k-3)!!(2(n-k)-3)!!}{(2n-3)!!} , \end{aligned}$$

(5)

where $T(n) = (2n-3)!!$ is the number of possible distinct NDs rooted at this node, $T(k) = (2k-3)!!$ possible distinct NDs for the left subtree, $T(n-k) = (2(n-k)-3)!!$ for the right subtree, and ${{n}\atopwithdelims (){k}}$ ways to choose k of n classes. The probability distributions is shown in Fig. 4 for $n=20$. It can be seen, that a uniform sampling procedure will tend to produce splits where only a few classes are separated from the rest.

Intuitively, one may wonder whether more balanced tree structures might not be preferable. In particular, one could speculate that a short (average) path length from the root to a leaf of an ND can increase the predictive performance, simply because the fewer the number of binary decisions that are required, the smaller the probability of a mistake.³ On the other side, an imbalanced binary problem might often be easier to solve, because there is a higher chance of separability. In particular, separating a single class from the rest (a problem also solved by the one-vs-rest decomposition) is probably easier than separating a randomly selected subset of several classes from the remaining ones.

Interestingly, the CBND heuristic, to be explained in Sect. 4.3, deliberately produces NDs with perfectly balanced tree structure. This heuristic suggests a quite simple sampling technique that can be used to produce more balanced (and hence non-uniformly distributed) structures: Starting with all classes $\mathcal {Y}$ in the root of a tree structure, the set of classes at each node is randomly decomposed into two subsets. This step is applied recursively until every set contains only a single class. Each decomposition is done by drawing a subset of the given set of classes uniformly at random.⁴ Although every ND can be generated by this procedure, it will yield a biased (non-uniform) distribution. In the case of biased sampling, the corresponding split probability is given by

$$\begin{aligned} P_{N}(n, k) = \left\{ \begin{array}{ll} \frac{{{n}\atopwithdelims (){k}}}{\frac{2^n-2}{2}} = \frac{{{n}\atopwithdelims (){k}}}{2^{n-1}-1}, &{}\quad k < n/2 \\ \frac{\frac{1}{2}{{n}\atopwithdelims (){k}}}{\frac{2^n-2}{2}} = \frac{{{n}\atopwithdelims (){k}}}{2^{n}-2}, &{} \quad k = n/2 \end{array} \right. , \end{aligned}$$

(6)

because ${{n}\atopwithdelims (){k}}$ is the number of ways to choose a subset of size k, and the total number of splits is half the number of (neither empty nor complete) subsets of n classes; the factor of 1 / 2 in the case of $k= n/2$ is to avoid double counting of splits into two subsets of the same size. It can be shown that $P_N(n, k) \ne P_U(n, k)$ as soon as $n > 3$. From the Fig. 4 it is clear that the biased sampling method will more likely produce NDs with balanced tree structure.

Fig. 4

Probability for $(k,n-k)$-splits with $n=20$ for uniform sampling (top) and biased sampling (bottom)

4 Heuristics for ND structure optimization

Several heuristic methods for finding an optimal ND structure $S \in \mathcal {S}_n$ have been proposed in the literature. In this section, we provide an overview of these methods and, moreover, present two additional heuristics that can be seen as a natural completion of the existing ones. Our description of the heuristics is restricted to the step of structure generation—once a structure S is given, the step of turning it into a classifier $\bar{S}$ by training binary classifiers is essentially always the same.

4.1 Random-pair selection (RPND)

The random-pair selection heuristic recently proposed by Leathart et al. (2016) is a randomized top-down heuristic that involves a predefined base learner L. Starting with the set of all classes $\mathcal {Y}' = \mathcal {Y}$ at the root node, the following procedure is applied recursively until sets reduce to singletons:

• 1. A pair of classes $y_l, y_r$ is chosen from $\mathcal {Y}'$ uniformly at random.

• 2. The base learner L is trained on examples of $y_l$ and $y_r$ to obtain a classifier $h:\, \mathcal {X} \longrightarrow \{ y_l, y_r \}$ that discriminates between these two classes.

• 3. Two meta-classes $\mathcal {Y}_{l}'$ and $\mathcal {Y}_{r}'$ are created and initialized with $\{y_l\}$ and $\{y_r\}$, respectively.

• 4. The instances from the remaining classes $\mathcal {Y}' \setminus \{y_l, y_r\}$ are classified using h.

• 5. For each class $y \in \mathcal {Y}' \setminus \{y_l, y_r\}$, it is checked whether the majority of its instances are classified as $y_l$ or $y_r$. In the first case, y is added to the meta-class $\mathcal {Y}_{l}'$, in the second case to $\mathcal {Y}_{r}'$.

• 6. A recursive call is made for $\mathcal {Y}_{l}'$ and $\mathcal {Y}_{r}'$.

As already mentioned, the heuristic itself only determines a structure S, not a classifier $\bar{S}$. Thus, once S has been produced, the random-pair classifiers h are discarded, and the classifiers required for the inner nodes of S are retrained.

4.2 Nested dichotomies based on clustering (NDC)

The structure optimization method suggested by Duarte-Villaseñor et al. (2012) is a clustering-based heuristic. The dichotomies are again generated recursively in a top-down manner, this time based on a (divisive) clustering in the instance space. To this end, the centroids of all classes are computed:

$$\begin{aligned} \bar{\varvec{x}}_i = \frac{1}{|\mathcal {D}_i |} \sum _{(\varvec{x},y) \in \mathcal {D}_i} \varvec{x}, \end{aligned}$$

where $\mathcal {D}_i = \{ (\varvec{x}, y) \in \mathcal {D} \, \vert \, y = y_i \}$. Starting with $\mathcal {Y}' = \mathcal {Y}$, a dichotomy for any remaining (non-singleton) set of classes $\mathcal {Y}'$ is determined based on the following procedure:

• 1. The two maximally remote classes $y_l, y_r$ are chosen from $\mathcal {Y}'$, i.e., the classes with the highest distance $\Vert \bar{\varvec{x}}_l - \bar{\varvec{x}}_r \Vert$ among all pairs of classes.

• 2. Two corresponding meta-classes $\mathcal {Y}_l' = \{y_l\}$ and $\mathcal {Y}_r' = \{y_r\}$ are initialized.

• 3. Every remaining class $y_i \in \mathcal {Y}' \setminus \{y_l, y_r\}$ is added to the closest meta-class, i.e., to $\mathcal {Y}_l'$ if $\Vert \bar{\varvec{x}}_i - \bar{\varvec{x}}_l \Vert < \Vert \bar{\varvec{x}}_i - \bar{\varvec{x}}_r \Vert$, and to $\mathcal {Y}_r'$ otherwise.

• 4. A recursive call is made for $\mathcal {Y}_{l}'$ and $\mathcal {Y}_{r}'$.

4.3 Class-balanced nested dichotomies (CBND)

The CBND heuristic proposed by Dong et al. (2005) is another top-down approach, mainly aiming at creating NDs with a balanced tree structure. To achieve this goal, the dichotomies are obtained by splitting the set of remaining classes $\mathcal {Y}'$ recursively into two roughly equal⁵ parts until $\mathcal {Y}'$ contains only a single class:

• 1. A subset $\mathcal {Y}_l' \subset \mathcal {Y}'$ is chosen from all subsets of size $\lfloor |\mathcal {Y}'|/2\rfloor$ uniformly at random.

• 2. The complement $\mathcal {Y}_r' = \mathcal {Y}' \setminus \mathcal {Y}_l'$ is determined to create a dichotomy.

• 3. A recursive call is made for $\mathcal {Y}_{l}'$ and for $\mathcal {Y}_{r}'$.

Actually, the main motivation for this heuristic is a reduction of the runtime for training a nested dichotomy: Splitting the data in a more balanced way leads to smaller (average) training data per binary problem, and hence to more efficient training of base learners. Moreover, a balanced tree is also advantageous at prediction time, because the (average) path length is only logarithmic (and not linear, as for degenerate trees). Indeed, the empirical results provided by the authors suggest that this heuristic achieves a significant reduction in runtime for ensembles of nested dichotomies while preserving predictive accuracy.

It has not been analyzed in Dong et al. (2005), however, how the heuristic affects the performance of a single nested dichotomy. Yet, as we discussed in Sect. 3, there are reasons to assume that a balanced structure can also have advantages from this point of view.

4.4 The Best-of-K heuristic (BoK)

The first heuristic we additionally propose is a very simple strategy that is also used for many other optimization problems where solutions may vary from run to run (e.g., because of local optima or randomization effects): Produce K candidate solutions and pick the best one. In our case, being equipped with the sampling procedure for nested dichotomies from the previous section, a natural idea for producing candidate solutions is to select them uniformly at random. Thus, we arrive at the following algorithm, referred to as Best-of-K (BoK):

• 1. Sample K structures $S_1, \ldots , S_K \in \mathcal {S}_n$ uniformly at random.

• 2. Train corresponding predictors $\bar{S}_1, \ldots , \bar{S}_K$ on $\mathcal {D}$ using the base learner L.

• 3. Select the (presumably) best structure $\hat{S}_K^* \in \{ S_1, \ldots , S_K \}$ based on performance estimates $\hat{E}(S_k)$, for example the training or validation error of predictors $\bar{S}_k$ (in our implementation, we use the latter).

In spite of its simplicity, this approach has a strong theoretical justification, since the exceedance probability of $S_K^*$, the model with the best generalization performance among all K candidates, follows itself an extreme value distribution:

$$\begin{aligned} \mathbf {P}\left( E(S_K^*) \le x \right)&= 1- \mathbf {P}\left( E(S_K^*)> x \right) \\&= 1 - \prod _{k=1}^K \mathbf {P}\left( E(S_k) > x \right) \\&= 1- (1 - x)^K \end{aligned}$$

Thus, the probability of a high exceedance quickly reduces for increasing K, and the expected exceedance goes to 0 (see Fig. 5).

Fig. 5

Left: Probability density functions of the (theoretical) exceedance of $S_K^*$ for $K \in \{5, 10, 20 \}$. Right: Expected value of exceedance as a function of $K \in \{1, \ldots , 100 \}$

Obviously, this line of reasoning is not completely valid, as it only refers to

$$\begin{aligned} S_K^* = {\text {*}}{argmax} \left\{ E(S_1), \ldots , E(S_K) \right\} , \end{aligned}$$

i.e., the best selection based on the true performances $E(S_k)$. Actually, however, the selection is based on corresponding estimates $\hat{E}(S_k)$, i.e.,

$$\begin{aligned} \hat{S}_K^* = {\text {*}}{argmax} \big \{ \hat{E}(S_1), \ldots , \hat{E}(S_K) \big \} \, . \end{aligned}$$

Depending on how noisy these estimates are, $\hat{S}_K^* = S_K^*$ is therefore not guaranteed. Nevertheless, in spite of this problem of “noisy selection”, the argument of course remains a strong motivation.

4.5 Heuristic based on agglomerative clustering (ACND)

The second heuristic we suggest is based on the concept of agglomerative hierarchical clustering. This approach is mainly motivated by the observation that all previously suggested heuristics are generating nested dichotomies in a top-down manner, i.e., starting with the entire set of classes in the root node and recursively splitting it into subsets. In particular, this also includes the NDC heuristic, which is based on divisive clustering. Thus, applying clustering in the reverse direction, from bottom to top, appears like a rather obvious idea.

Correspondingly, the ACND heuristic works bottom-up and makes use of agglomerative clustering. The classes $\mathcal {Y}$ constitute the leafs that are successively aggregated into a single cluster. The agglomerative approach guarantees that the clusters with the smallest distance to each other will be combined first, thereby shifting the presumably harder classification problems further away from the root of the tree. The heuristic consists of three steps:

• 1. Every class $y_i \in \mathcal {Y}$ is considered to be a pre-defined cluster

  $$\begin{aligned} C_i = \{ \varvec{x} \, \vert \, (\varvec{x}, y_i) \in \mathcal {D} \} \end{aligned}$$

  consisting of those instances in the training data labeled by this class. Correspondingly, the set of initial clusters is $\mathcal {C} = \{ C_1, \ldots , C_n \}$.

• 2. Using the UPGMA algorithm (Sokal 1958), the clusters are iteratively merged until a single cluster remains. In every step, the two clusters that are closest in terms of the (average linkage) distance

  $$\begin{aligned} d(C_i , C_j) = \frac{1}{|C_i||C_j|} \sum _{\varvec{x}_i \in C_i, \varvec{x}_j \in C_j} \Vert \varvec{x}_i - \varvec{x}_j \Vert \end{aligned}$$

  are merged, i.e., the clusters $C_i$ and $C_j$ are removed from $\mathcal {C}$ and replaced by $C_{i,j} = C_i \cup C_j$; the distance to all remaining clusters $C_k \in \mathcal {C}$ is recomputed according to

  $$\begin{aligned} d(C_k, C_{i,j}) = \frac{|C_i|}{|C_i| + |C_j|} d(C_k, C_i) + \frac{|C_j|}{|C_i| + |C_j|} d(C_k, C_j) \, . \end{aligned}$$

• 3. The hierarchical cluster structure is converted into a nested dichotomy. Since each cluster is associated with a class, and in every step exactly two clusters are aggregated, there is a one-to-one correspondence between the cluster structure and the nested dichotomy of classes.

4.6 Complexity

Although complexity is not in the focus of this paper, let us shortly comment on the runtime of the different heuristics. In this regard, it is clear that CBND is the fastest among all heuristics. NDC and ACND are relatively fast, too, because there is no need to solve any classification problem. Yet, the initial computation of pairwise distances $d(C_i,C_j)$ on the level of instances makes ACND a bit less efficient, because this operation scales quadratically with the size of the classes.⁶ RPND and BoK are more costly, because they repeatedly invoke the base learner L on several problems; in both cases, a number of learning problems linear in the number of classes n needs to be solved. Note, however, that the runtime of BoK can be reduced in a rather simple manner. First, since the sampling procedure only depends on the number of classes n, but not on the data itself, it can be carried out in a preprocessing step. Second, the training in the second step can be done independently for each nested dichotomy. Thus, BoK is naturally implemented in a parallel way. If K cores are available for computation, a speedup factor close to K can be achieved in comparison to a standard (sequential) implementation. Then, the runtime reduces to the maximal time needed to train a single ND.

5 Performance comparison

5.1 Data and methods

We compare the performance of the discussed heuristics empirically on 27 standard benchmark datasets mostly from the UCI repository. Table 1 provides a description of these datasets. The datasets used in this study are made available on openml.org⁷ (Vanschoren et al. 2013). Moreover, our Python implementation of the heuristics and the experiments is available at github.⁸

Table 1 The datasets used in the study

We have used three base learners from the scikit-learn framework (ver. 0.19) (Pedregosa et al. 2011): the classification tree learner CART, logistic regression, and decision stumps (CART). These learners are meant to cover the spectrum from very flexible (CART) to very restrictive (decision stumps), with linear models as fit by logistic regression in-between. The hyper-parameters of the base learners were set to default values except for the minimal decrease of the impurity in CART, which was set to .0001 to avoid excessively large trees (with a strong tendency to overfit). For the datasets with missing feature values, we applied imputation with the mean replacement strategy. For categorical features, we adopt a separate class imputation strategy that adds a ‘missing’ feature value. This strategy has been shown to work well in the case of binary classifiers, both for CART and logistic regression (Ding and Simonoff 2010). Since the base learners in scikit-learn are able to deal with numeric features only, all categorical features were converted to numerical ones using one-hot encoding.

5.2 Experimental setting

The experimental study is designed as follows. On every dataset, we perform a 10-fold cross-validation and measure the mean predictive accuracy of every heuristic in combination with every base learner. Each such combination specifies a learning algorithm A, and cross-validated accuracy serves as an estimate $\hat{e}(A)$ of the generalization performance (3) of the corresponding learner. To make the comparison as fair as possible, all heuristics are executed on the same folds. In addition, to stabilize results for randomized heuristics, we repeat the whole experiment ten times and average results. For all heuristics, probabilistic inference is used (Sect. 2.1).

Motivated by our discussion about sampling in Sect. 3, we also evaluate a “biased” version of the Best-of-K heuristic (BBoK). This is a variant of BoK in which ND structures are sampled in a non-uniform way, i.e., with a bias towards more balanced structures. For both BoK heuristics, we use the validation error as a selection criterion. The latter is computed as the mean on a 3-fold CV error on the training data. Once being selected, the best-performing ND is retrained on the whole training data.

Fig. 6

Accuracy distributions estimated from 10,000 randomly sampled nested dichotomies in combination with CART, logistic regression, and decision stumps as base learners on the mfeat-morphological dataset. The (estimated) exceedance probability corresponds to the area under the accuracy distribution to the right of the average performance of the heuristic, which is indicated by a vertical line

For comparing the performance of different heuristics (learners A), we use the exceedance probability (2). More specifically, since the underlying distribution of performances is not known, we approximate this measure by computing the exceedance on an empirical distribution obtained from 10,000 nested dichotomies sampled uniformly at random. The estimated exceedance is then simply given by the fraction of random NDs which, when being trained with the same base learner, yield a performance better than $\hat{e}(A)$. Figure 6 illustrates this approach for the mfeat-morphological dataset.

Table 2 Mean exceedance probability over all datasets

Table 3 Win/tie/loss statistics for CART (Panel A), logistic regression (Panel B), and decision stumps (Panel C) as a base learner (row against column)

One technical remark concerns the learning of NDs for highly imbalanced datasets. When splitting such data for training and testing, it may happen that some classes $y \in \mathcal {Y}$ are not represented in the training data. Obviously, this leads to the problem that, for some binary problems, there will be no examples for a meta-class. To be able to train NDs in such cases, we make use of a default classifier that either predicts probabilities of 0 and 1 (if only one meta-class is absent) or of 0.5/0.5 (if both meta-classes are empty).

5.3 Results

Detailed results of our experiments in terms of exceedance probabilities are provided in “Appendix A”, which, for the sake of completeness, also presents the corresponding predictive accuracies on all datasets. The main summaries of these results are provided in Table 2 in terms of the mean exceedance probability over all datasets, and in Table 3 in terms of pairwise win/tie/loss statistics.

As a first conclusion from these results, we categorize the heuristics into three groups: RPND, BoK and BBoK perform best, the clustering heuristics ACND and NDC are in the middle, and CBND is worst. Interestingly, this ranking is in perfect agreement with the amount of information exploited by the different heuristics or, stated differently, the degree to which they produce ND structures that are tailored for the specific problem at hand:

• On the one extreme, CBND does not exploit any properties of the data, i.e., this heuristic produces ND structures that are completely independent of the current problem.

• On the other extreme, RPND and BoK make use of both the data $\mathcal {D}$ and the base learner L. Thus, the NDs produced by these heuristics are tailored for the problem at hand as well as the algorithms used to learn a predictor.

• The cluster-based heuristics NDC and ACND are in-between in the sense of exploiting the data $\mathcal {D}$ but not the learner L.

Interestingly, the average performance of CBND is even worse than sampling an ND structure at random (which would yield a performance of 0.5). This suggests that, in terms of performance, balanced NDs tend to be worse than more degenerate structures. This observation is also supported by the performance of the BBoK heuristic. It benefits from the Best-of-K selection, but cannot achieve the performance of its unbiased variant BoK.

The heuristics based on clustering in the instance space (ACND and NDC) perform quite comparable on most of the datasets when using CART as a base learner. More interesting is the observation that the performance of these heuristics often strongly differs from each other, which also means that they often “disagree” about the optimal structure of a nested dichotomy. For example, on the dataset mfeat-morphological, the NDC heuristic clearly outperforms ACND, but exactly the opposite is true for the dataset autos. ACND achieves surprisingly strong performance with CART as a base learner, and even outperforms all other heuristics on nine datasets. For weaker base learners, the average performance of NDC tends to improve while the average performance of ACND remains roughly the same. But even in these cases, ACND is a clear winner for some datasets (such as autos). This finding suggests that the optimal choice of a clustering strategy (divisive or agglomerative) used to produce a dichotomy strongly depends on the base learner and on the dataset at hand.

Among the previously proposed heuristics, the best performance is shown by RPND, which is in agreement with earlier studies (Leathart et al. 2016). Yet, the performance of BoK is highly competitive, which is probably the most interesting finding of our analysis. BoK is superior to RPND for all base learners; this already holds for $K=10$ and even more so for $K=50$. The strong performance of BoK may appear surprising at first sight, especially because of the simplicity of this heuristic. On the other side, as explained in Sect. 4.4, BoK does indeed have a solid theoretical foundation.

Finally, we investigated whether the exceedance of a heuristic is influenced by the number of classes in a dataset. Although there is no clear reason for why this should be the case, it appears to be a quite obvious question, especially since standard accuracy measures (such as misclassification rate) are definitely influenced. However, as can be seen in Fig. 7, a strong (statistically significant) correlation is indeed not visible. Note that this result can also be interpreted in favor of exceedance as a performance measure, since this measure tends to be comparable across datasets.

Fig. 7

Exceedance plotted against the number of classes in a dataset. The base learners are marked by different symbols: circle (CART), cross (logistic regression), and plus (decision stumps). For every heuristic, a linear regression model (with 95% confidence band) was fitted

6 Conclusion

In this paper, we addressed the problem of structure optimization for nested dichotomies. If a single nested dichotomy, combined with a certain base learner, is used as a multi-class classifier, its performance can vary a lot depending on how the decomposition structure is chosen. From the point of view of automated machine learning, the ND structure can be seen as a hyper-parameter that is subject to optimization, so as to guarantee the overall best performance. Since an exhaustive search in the space of structures is in general infeasible, several heuristics have been proposed in the literature.

We investigated the performance of these heuristics in an empirical study with 27 multi-class datasets, and completed the repertoire of heuristics with two additional candidates. Moreover, we proposed the exceedance probability as a suitable performance metric. Roughly speaking, the exceedance is the probability that a randomly chosen ND structure will yield a better performance than the structure chosen by the heuristic. Compared to predictive accuracy, this metric is less dependent on the base learner and comparable across different datasets. It assumes values in [0, 1] and has a simple interpretation: Since the extreme value of 0 can indeed be achieved, $p_{exc}$ is the “gap” to perfect performance; moreover, 1 / 2 serves as a calibration point, since this is the performance achieved by a random selection.

As for the approaches existing so far, our study identified the random-pair selection heuristic (RPND) as a clear winner. This is in agreement with earlier studies on ensembles of NDs ( Leathart et al. 2016). More surprising is the strong performance of one of our new proposals, the extremely simple Best-of-K heuristic, which outperforms all other heuristics even for a relative small $K=10$. Together with an efficient algorithm for uniform sampling of nested dichotomies, and an obvious possibility for parallel implementation, this heuristic is highly attractive and clearly worth further investigation.

Appendix A: Detailed experimental results

In the following tables, we show the exceedance probabilities (best value per dataset marked in bold) as well as the mean accuracies (with corresponding ranks) achieved by the heuristics on each dataset, separately for the three base learners. Qualitatively, exceedance and accuracy are in agreement with each other, although there are of course differences on a quantitative level (Tables 4, 5, 6, 7, 8 and 9).

Table 4 Exceedance probability of different heuristics with CART as base learner

Table 5 Mean accuracy and the corresponding rank of different heuristics with CART as base learner

Table 6 Exceedance probability of different heuristics with logistic regression as base learner

Table 7 Mean accuracy and the corresponding ranks of different heuristics with logistic regression as base learner

Table 8 Exceedance probability of different heuristics with decision stumps as base learner

Table 9 Mean accuracy and the corresponding ranks of different heuristics with decision stumps as base learner