Planning in hybrid relational MDPs

Abstract

We study planning in relational Markov decision processes involving discrete and continuous states and actions, and an unknown number of objects. This combination of hybrid relational domains has so far not received a lot of attention. While both relational and hybrid approaches have been studied separately, planning in such domains is still challenging and often requires restrictive assumptions and approximations. We propose HYPE: a sample-based planner for hybrid relational domains that combines model-based approaches with state abstraction. HYPE samples episodes and uses the previous episodes as well as the model to approximate the Q-function. In addition, abstraction is performed for each sampled episode, this removes the complexity of symbolic approaches for hybrid relational domains. In our empirical evaluations, we show that HYPE is a general and widely applicable planner in domains ranging from strictly discrete to strictly continuous to hybrid ones, handles intricacies such as unknown objects and relational models. Moreover, empirical results showed that abstraction provides significant improvements.

1 Introduction

Markov decision processes (MDPs) (Sutton and Barto 1998) are a natural and general framework for modeling probabilistic planning problems. Since the world is inherently relational, an important extension is that of relational MDPs (Wiering and van Otterlo 2012), where the state is represented in terms of first-order logic, that is objects and relations between them. However, while significant progress has been made in developing robust planning algorithms for discrete, relational and continuous MDPs separately, the more intricate combination of those (hybrid relational) and settings with an unknown number of objects have received less attention.

The recent advances of probabilistic programming languages [e.g., BLOG (Milch et al. 2005a), Church (Goodman et al. 2008), ProbLog (Kimmig 2008), Anglican (Wood et al. 2014), distributional clauses (Gutmann et al. 2011)] has significantly improved the expressive power of formal representations for probabilistic models.

While it is known that these languages can express decision problems (Srivastava et al. 2014; Van den Broeck et al. 2010), including hybrid relational MDPs, it is less clear if the inbuilt general-purpose inference system can cope with the challenges (e.g., scale, time constraints) posed by actual planning problems, and compete with existing state-of-the-art planners.

In this paper, we consider the problem of effectively planning in propositional and relational domains where reasoning and handling unknowns may be needed in addition to coping with mixtures of discrete and continuous variables. In particular, we adopt dynamic distributional clauses (DDC) (Nitti et al. 2013, 2014) [an extension of distributional clauses (Gutmann et al. 2011) and based on distribution semantics (Sato 1995)] to describe the MDP and perform inference. In such general settings, exact solutions may be intractable, and so approximate solutions are the best we can hope for. Popular approximate solutions include Monte Carlo methods to estimate the expected reward of a policy (i.e., policy evaluation).

Monte Carlo methods provide state-of-the-art results in probabilistic planners (Kocsis and Szepesvári 2006; Keller and Eyerich 2012). Monte Carlo planners have been mainly applied in discrete domains [with some notable exceptions, such as Mansley et al. (2011), Couetoux (2013), for continuous domains]. Typically, for continuous states, function approximation (e.g., linear regression) is applied. In that sense, one of the few Monte Carlo planners that works in arbitrary MDPs with no particular assumptions is sparse sampling (SST) (Kearns et al. 2002); but as we demonstrate later, it is often slow in practice. We remark that most, if not all, Monte Carlo methods require only a way to sample from the model of interest. While this property seems desirable, it prevents us from exploiting the actual probabilities of the model, as discussed (but unaddressed) in Keller and Eyerich (2012). In this paper we address this issue proposing a planner that exploits the knowledge of the model via importance sampling to perform policy evaluation.

The first contribution of this paper is HYPE: a conceptually simple but powerful planning algorithm for a given (hybrid relational) MDP in DDC. However, HYPE can be adapted for other languages, such as RDDL (Sanner 2010). The proposed planner exploits the knowledge of the model via importance sampling to perform policy evaluation, and thus, policy improvement. Importance sampling has been used in off-policy Monte Carlo methods (Peshkin and Shelton 2002; Shelton 2001a, b), where policy evaluation is performed using trajectories sampled from another policy. We remark that standard off-policy Monte Carlo methods have been used in reinforcement learning, which are essentially model-free settings. In our setting, given a planning domain, the proposed planner introduces a new off-policy method that exploits the model and works, under weak assumptions, in discrete, relational, continuous, hybrid domains as well as those with an unknown number of objects.

The second contribution of this paper is a sample-based abstraction algorithm for HYPE. In particular, using individual samples of trajectories, it removes irrelevant facts from the sampled states with an approach based on logical regression. There exists several exact methods that perform symbolic dynamic programming, that is dynamic programming at the level of abstract states (set of states). Those methods has been successfully used in relational domains (Kersting et al. 2004; Wang et al. 2008). However, abstraction is more challenging in hybrid relational domains, even though some attempts have been made (Sanner et al. 2011; Zamani et al. 2012) in propositional domains, under expressivity restrictions. To overcome the complexity of logical regression in general hybrid relational domains we perform abstraction at the level of sampled episodes. Such an approach carries over the benefits of symbolic methods to sampling approaches. We provide detailed derivations behind this abstraction, and show that it comes with a significant performance improvement.

The first contribution is based on the previous paper Nitti et al. (2015b) and the second contribution on the workshop paper Nitti et al. (2015a). This paper extends previous works with an algorithm for logical regression to abstract samples, a more detailed theoretical justification for abstraction and additional experiments.

2 Background

2.1 Markov decision processes

In a MDP, a putative agent is assumed to interact with its environment, described using a set S of states, a set A of actions that the agent can perform, a transition function $p: S \times A \times S \rightarrow [0,1]$, and a reward function $R: S \times A \rightarrow {\mathbb {R}}.$ That is, when in state $s$ and on doing $a$, the probability of reaching $s'$ is given by $p(s' | s, a)$, for which the agent receives the reward $R(s,a).$ The agent is taken to operate over a finite number of time steps $t = 0, 1, \ldots , T$, with the goal of maximizing the expected reward: ${{\mathbb {E}}}[\sum _{t=0}^T \gamma ^ t R(s_t,a_t)] = {{\mathrm{{\mathbb {E}}}}}[G(E)]$, where $\gamma \in [0,1]$ is a discount factor, $E=<s_0,a_0,s_1,a_1,\ldots ,s_T,a_T>$ is the state and action sequence called episode and $G(E)=\sum _{t=0}^T \gamma ^{t}R(s_t,a_t)$ is the total discounted reward of E.

This paper focuses on maximizing the reward in a finite horizon MDP; however the same ideas are extendable for infinite horizons. This is achieved by computing a (deterministic) policy $\pi : S\times D \rightarrow A$ that determines the agent’s action at state $s$ and remaining steps $d$ (horizon). The expected reward starting from state $s_{t}$ and following a policy $\pi$ is called the value function (V-function):

$$\begin{aligned} V_d^\pi (s_{t})={{\mathrm{{\mathbb {E}}}}}[G(E_{t})|s_{t},\pi ]={\mathbb {E}}\left[ \sum _{k=t}^{t+d} \gamma ^{k-t} R(s_{k},a_{k}) \mid s_{t},\pi \right] , \end{aligned}$$

(1)

where $E_t=<s_t,a_t,s_{t+1},a_{t+1},\ldots ,s_T,a_T>$ is the subset of E from time t. Furthermore, the expected reward starting from state $s_t$ while executing action $a_t$ and following a policy $\pi$ is called the action-value function (Q-function):

$$\begin{aligned} Q_d^\pi (s_{t},a_{t})={{\mathrm{{\mathbb {E}}}}}[G(E_{t})|s_{t},a_{t},\pi ]={\mathbb {E}}\left[ \sum _{k=t}^{t+d} \gamma ^{k-t} R(s_{k},a_{k}) \mid s_{t},a_{t},\pi \right] . \end{aligned}$$

(2)

Since $T=t+d$, in the following formulas we will use T for compactness. An optimal policy $\pi ^*$ is a policy that maximizes the $V$-function for all states. The optimal policy satisfies the Bellman equation:

$$\begin{aligned} V_d^*(s_{t})=max_a\Big ( R(s_{t},a_{t}) +\gamma \int _{s_{t+1}} p(s_{t+1}|s_t,a_t) V_{d-1}^*(s_{t+1})d s_{t+1}\Big ). \end{aligned}$$

(3)

This formula is used to solve the MDP in value iteration methods.

Alternatively, sample-based planners use Monte Carlo methods to solve an MDP and find a (near) optimal policy. Such planners simulate (by sampling) interaction with the environment in episodes $E^m=\langle ^m_0,a^m_0,s^m_1,a^m_1,\ldots ,s^m_T,a^m_T\rangle$, following some policy $\pi$. Each episode is a trajectory of $T$ time steps, and we let $s_t ^ m$ denote the state visited at time $t$ during episode $m.$ (So, after $M$ episodes, $M \times T$ states would be explored). After or during episode generation, the sample-based planner updates $Q_d(s^m_t,a^m_t)$ for each t according to a backup rule, for example, averaging the total rewards obtained starting from $(s^m_t,a^m_t)$ till the end. The policy is improved using a strategy that trades off exploitation and exploration, e.g., the $\epsilon$-greedy strategy. In this case the policy used to sample the episodes is not deterministic; we indicate with $\pi (a_{t}| s_{t})$ the probability to select action $a_{t}$ in state $s_{t}$ under the policy $\pi$. Under certain conditions, after a sufficiently large number of episodes, the policy converges to a (near) optimal policy, and the planner can execute the greedy policy $argmax_a {Q}_d(s_t,a)$.

2.2 Logic programming

In this section we briefly introduce logic programming concepts. See Nilsson and Małiszyński (1996), Apt (1997), Lloyd (1987) for an extensive introduction.

An atomic formula (atom) is a predicate applied to a list of terms that represents objects. A term is a constant symbol, a logical variable or a function (functor) applied to terms. For example, ${\mathtt {inside(1,2)}}$ is an atomic formula, where ${\mathtt {inside}}$ is a predicate, sometimes called relation, and $\mathtt 1, 2$ are terms, in particular constant symbols that refer to objects. A literal is an atomic formula or a negated atomic formula. A clause, in logic programming, is a first-order formula with a head (atom), and a body (a list of literals). For example, the clause

$$\begin{aligned} {\mathtt {inside(A,B)}}\leftarrow {\mathtt {inside(A,C),inside(C,B)}}. \end{aligned}$$

states that for all $\mathtt {A,B}$ and $\mathtt {C}$, $\mathtt {A}$ is inside $\mathtt {B}$ if $\mathtt {A}$ is inside $\mathtt {C}$ and $\mathtt {C}$ is inside $\mathtt {B}$ (transitivity property). $\mathtt {A,B}$ and $\mathtt {C}$ are logical variables, that informally refer to an arbitrary object or value. A clause usually contains non-ground literals, that is, literals with logical variables (e.g., ${\mathtt {inside(A,B)}}$). A clause with logical variables is assumed to be preceded by universal quantifiers for each logical variable, e.g., in the above clause: $\forall {\mathtt{A}},\forall {\mathtt{B}},\forall {\mathtt{C}}$. A substitution $\theta$ replaces the variables with other terms. For example, for $\theta =\{{\mathtt{A=1,B=2,C=3}}\}$ the above clause becomes:

$$\begin{aligned} {\mathtt {inside(1,2)}}\leftarrow {\mathtt {inside(1,3),inside(3,1).}} \end{aligned}$$

and states that if ${\mathtt {inside(1,3)}}$ and ${\mathtt {inside(3,1)}}$ are true, then ${\mathtt {inside(1,2)}}$ is true. We indicate with $\theta ={\mathtt{mgu}}{\mathtt{(}}{\mathtt{A,B}}{\mathtt{)}}$ the most general unifier, i.e. the most general substitution $\theta$ that makes ${\mathtt{A}}\theta ={\mathtt{B}}\theta$.

An Herbrand interpretation I is a set of ground atomic formulas that are assumed to be true. The facts not in I are assumed to be false. In this paper, Herbrand interpretations represent states. For example, $I={\mathtt{\{}}{\mathtt{inside}}{\mathtt{(}}{\mathtt{1,3}}{\mathtt{)}},{\mathtt{inside}}{\mathtt{(}}{\mathtt{2}},{\mathtt{3}}{\mathtt{)}}{\mathtt{\}}}$ represents a world state where 1 and 2 are inside 3, any other fact is false.

In this paper we refer to complete (full) states and partial (abstract) states. In a full state any fact has an assignment true/false, and any other variable has a value. In a partial (abstract) state some of the facts or variables have an assignment. The remaining facts and variables are left undefined. Formally, an abstract state is a conjunctive formula ${\mathcal {F}}$ that represents the set of complete states that satisfies ${\mathcal {F}}$, that is, ${\mathcal {F}} = l_1 \wedge \ldots \wedge l_n$ where all variables are existentially quantified and each literal $l_i$ is either an atom or a negated atom. We will extend the usual notions of substitution, unification and subsumption to these expressions. In addition, an abstract state ${\mathcal {F}}$ subsumes a state s (notation $s \preceq {\mathcal {F}}$) if and only if there exists a substitution $\theta$ such that ${\mathcal {F}}\theta \subseteq s$. For example, the abstract state ${\mathtt{on}}_{\mathtt{t}}{\mathtt{(}}{\mathtt{1,2}}{\mathtt{)}},{\mathtt{not}}{\mathtt{(}}{\mathtt{on}}_{\mathtt{t}} {\mathtt{(}}{\mathtt{2,table}}{\mathtt{)}}{\mathtt{)}}$ represents all the states where object 1 is on top of object 2 and 2 is not on a table. An abstract state might contain logical variables, e.g., ${\mathtt{on}}_{\mathtt{t}}{\mathtt{(}}{\mathtt{1,A}}{\mathtt{)}}$ represents the set of all the states where 1 is on top of an arbitrary object. An example of such state is ${\mathtt{on}}_{\mathtt{t}}{\mathtt{(}}{\mathtt{1,2}}{\mathtt{)}},{\mathtt{on}}_{\mathtt{t}}{\mathtt{(}}{\mathtt{2,3}}{\mathtt{)}}$, subsumed by ${\mathtt{on}}_{\mathtt{t}}{\mathtt{(}}{\mathtt{1,A}}{\mathtt{)}}$: ${\mathtt{on}}_{\mathtt{t}} {\mathtt{(}}{\mathtt{1,2}}{\mathtt{)}},{\mathtt{on}}_{\mathtt{t}}{\mathtt{(}}{\mathtt{2,3}}{\mathtt{)}} \preceq {\mathtt{on}}_{\mathtt{t}}{\mathtt{(}}{\mathtt{1,A}}{\mathtt{)}}$. In this paper we consider only grounded abstract states, that is, without logical variables.

2.3 Relational MDPs

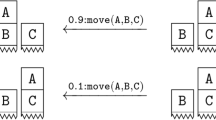
In first-order (relational) MDPs, the state is represented in terms of logic formulas. In particular, in relational MDPs based on logic programming, a state is a Herbrand interpretation and the actions are described as facts. The state transition model and the reward function are compactly defined in terms of probabilistic rules exploiting first-order logic. For example, in a blocksworld we can say that if ${\mathtt{on}}({\mathtt{A,C}}), {\mathtt{clean}}({\mathtt{B}})$ holds then action ${\mathtt{move}}({\mathtt{A,B}})$ will add ${\mathtt{on}}({\mathtt{A,B}})$ with probability 0.9 to the state and remove ${\mathtt{on}}({\mathtt{A,C}}),{\mathtt{clean}}({\mathtt{B}})$, otherwise with probability 0.1 the state will remain unchanged. In addition, it is often convenient to define when an action is applicable in a given state. This can be specified again in terms of rules (clauses). The conditions that make an action applicable are often called preconditions.

A relational MDP can be solved using the Bellman equation applied to abstract states with logical regression, instead of single states individually. This method is called symbolic dynamic programming (SDP), and it has been successfully used to solve big MDPs efficiently (Kersting et al. 2004; Wang et al. 2008; Joshi et al. 2010; Hölldobler et al. 2006). Similar principles have been applied in (propositional) continuous and hybrid domains (Sanner et al. 2011; Zamani et al. 2012). Despite the effectiveness of such approaches, they make restrictive assumptions (e.g., deterministic transition model for continuous variables) to keep exact inference tractable. For more general domains approximations are needed (Zamani et al. 2013). Another issue of SDP is keeping the structures that represent the V-function compact. Despite the recent progress, and the availability of regression methods for inference in hybrid domains (Belle and Levesque 2014), SDP remains a challenging approach in general hybrid relational domains, including MDPs where the number of variables can change over time.

In Sect. 5 we will show how to simplify abstraction by performing regression on the sampled episodes.

3 Dynamic distributional clauses

Standard relational MDPs cannot handle continuous variables. To overcome this limitation we consider hybrid relational MDPs formulated using probabilistic logic programming (Kimmig et al. 2010; Gutmann et al. 2011; Nitti et al. 2013). In particular, we adopt (dynamic) distributional clauses (Nitti et al. 2013; Gutmann et al. 2011), an expressive probabilistic language that supports discrete and continuous variables and an unknown number of objects, in the spirit of BLOG (Milch et al. 2005a).

A distributional clause (DC) is of the form ${\mathtt {h}}\sim {\mathcal {D}} \leftarrow {\mathtt {b_1,\ldots ,b_n}}$, where the ${\mathtt {b_i}}$ are literals and $\sim$ is a binary predicate written in infix notation. The intended meaning of a distributional clause is that each ground instance of the clause $({\mathtt {h}}\sim {\mathcal {D}} \leftarrow {\mathtt {b_1,\ldots ,b_n}})\theta$ defines the random variable ${\mathtt {h}}\theta$ as being distributed according to ${\mathcal {D}}\theta$ whenever all the ${\mathtt {b_i}} \theta$ hold, where $\theta$ is a substitution. Furthermore, a term $\simeq \!\!(d)$ constructed from the reserved functor $\simeq \!\!/1$ represents the value of the random variable d.

Example 1

Consider the following clauses:

$$\begin{aligned}&{\mathtt {n}} \sim {\mathtt {poisson(6)}}. \end{aligned}$$

(4)

$$\begin{aligned}&{{\mathtt {pos(P)}}} \sim {\mathtt {uniform(1,10)}} \leftarrow {\mathtt {between(1,\simeq \!\!(n),P).}} \end{aligned}$$

(5)

$$\begin{aligned}&{\mathtt {left(A,B)}} \leftarrow {\mathtt {\simeq \!\!(pos(A))>\simeq \!\!(pos(B)).}} \end{aligned}$$

(6)

Capitalized terms such as ${\mathtt{P,A}}$ and ${\mathtt{B}}$ are logical variables, which can be substituted with any constant. Clause (4) states that the number of people ${\mathtt {n}}$ is governed by a Poisson distribution with mean 6; clause (5) models the position ${\mathtt {pos(P)}}$ as a random variable uniformly distributed from 1 to 10, for each person ${\mathtt {P}}$ such that $\mathtt{P}$ is between 1 and ${\mathtt {\simeq \!\!(n)}}$. Thus, if the outcome of ${\mathtt {n}}$ is two (i.e., $\simeq \!\!(n)=2$) there are 2 independent random variables ${\mathtt {pos(1)}}$ and ${\mathtt {pos(2)}}$. Finally, clause (6) shows how to define the predicate ${\mathtt {left(A,B)}}$ from the positions of any $\mathtt{A}$ and ${\mathtt{B}}$. Ground atoms such as ${\mathtt {left(1,2)}}$ are binary random variables that can be true or false, while terms such as ${\mathtt {pos(1)}}$ represent random variables that can take concrete values from the domain of their distribution.

A distributional program is a set of distributional clauses (some of which may be deterministic) that defines a distribution over possible worlds, which in turn defines the underlying semantics. A possible world is generated starting from the empty set $S=\emptyset$; for each distributional clause ${\mathtt {h}} \sim {\mathcal {D}} \leftarrow \mathtt {b_1, \ldots , b_n}$, whenever the body $\{\mathtt {b_1}\theta , \ldots , \mathtt {b_n}\theta \}$ is true in the set S for the substitution $\theta$, a value v for the random variable ${\mathtt {h}}\theta$ is sampled from the distribution ${\mathcal {D}}\theta$ and $\simeq \!\!(h\theta )=v$ is added to S. This is repeated until a fixpoint is reached, i.e., no further variables can be sampled. Dynamic distributional clauses (DDC) extend distributional clauses in admitting temporally-extended domains by associating a time index to each random variable.

Example 2

Let us consider an object search scenario (objsearch) used in the experiments, in which a robot looks for a specific object in a shelf. Some of the objects are visible, others are occluded. The robot needs to decide which object to remove to find the object of interest. Every time the robot removes an object, the objects behind it become visible. This happens recursively, i.e., each new uncovered object might occlude other objects. The number and the types of occluded objects depend on the object covering them. For example, a box might cover several objects because it is big. This scenario involves an unknown number of objects and can be written as a partially observable MDP. However, it can be also described as a MDP in DDC where the state is the type of visible objects; in this case the state grows over time when new objects are observed or shrink when objects are removed without uncovering new objects. The probability of observing new objects is encoded in the state transition model, for example:

$$\begin{aligned}&{\mathtt{type}}{\mathtt{(X)}}_{{\mathtt{t+1}}} \sim {\mathtt{val(T)}} \leftarrow \ \simeq \!\!({\mathtt{type(X)}}_{{\mathtt{t}}})={\mathtt{T}},\ {\mathtt{not(removeObj(X))}}. \end{aligned}$$

(7)

$$\begin{aligned}&{\mathtt{num}}{\mathtt{ObjBehind(X)}}_{{\mathtt{t+1}}} \sim {\mathtt{poisson(1)}}\ \leftarrow \ \simeq \!\!({\mathtt{type(X)}}_{{\mathtt{t}}}) ={\mathtt{box,removeObj(X)}}. \end{aligned}$$

(8)

$$\begin{aligned}&{\mathtt{type}}{\mathtt{(ID)}}_{{\mathtt{t+1}}} \sim {\mathtt{finite}}([{\mathtt{0.2:glass,0.3:cup,0.4:box,0.1:can}}]) \leftarrow \nonumber \\&\quad \simeq \!\!({\mathtt{type(X)}}_{{\mathtt{t}}})={\mathtt{box, removeobj(X)}}, \simeq \!\!({\mathtt{numObjBehind(X)}}_{{\mathtt{t+1}}})={\mathtt{N,getLastID(Last)}}_{\mathtt{t}},\nonumber \\&\quad \mathtt \ {\mathtt{NewID}}\ {\mathtt{is}}\ {\mathtt{Last+1}}, {\mathtt{EndNewID}}\ {\mathtt{is}}\ {\mathtt{NewID+N,between(NewID,EndNewID,ID)}}. \end{aligned}$$

(9)

Clause (7) states that the type of each object remains unchanged when we do not perform a remove action. Otherwise, if we remove the object, its type is removed from the state at time $t+1$ because it is not needed anymore. Clauses (8) and (9) define the number and the type of objects behind a box $\mathtt {X}$, added to the state when we perform a remove action on $\mathtt {X}$. Similar clauses are defined for other types. The predicate $\mathtt {getLastID(Last)_t}$ returns the highest object ${\mathtt{ID}}$ in the state and is needed to make sure that any new object has a different ${\mathtt{ID}}$.

DDC can be easily extended to define MDPs. In the previous example we showed how to define a state transition model. To complete the MDP specification we need to define a reward function $R(s_t,a_t)$, the terminal states that indicate when the episode terminates, and the applicability of an action $a_t$ is a state $s_t$ as in PDDL. For objsearch we have:

$$\begin{aligned}&{\mathtt {stop_{t} \leftarrow \simeq \!\!(type(X)_{t})=can. }}\\&\mathtt {reward(20)_{t} \leftarrow stop_{t}. }\\&\mathtt {reward(-1)_{t} \leftarrow not(stop_t). } \end{aligned}$$

That is, a state is terminal when we observe the object of interest (e.g., a can), for which a reward of 20 is obtained. The remaining states are nonterminal with reward $-1$. To define action applicability we use a set of clauses of the form

$$\begin{aligned} \mathtt {applicable(action)_t \leftarrow preconditions_t}. \end{aligned}$$

For example, action $\mathtt {removeobj}$ is applicable for each object in the state, that is when its type is defined with an arbitrary value ${\mathtt{Type}}$:

$$\begin{aligned} \mathtt {applicable(removeobj(X))_t \leftarrow \simeq \!\!(type(X)_t)=Type.} \end{aligned}$$

In DDC a (complete) state contains facts as in standard relational MDPs and statements $\simeq \!\!({\mathtt{variable}})=\mathtt{v}$ (the value of ${\mathtt{variable}}$ is ${\mathtt{v}}$) for continuous or categorical random variables, e.g.: ${\mathtt{on_t(1,2),clean_t(1),on_t(1,table),\simeq \!\!(energy_t)=1.3}}$. All the facts not in the state are assumed false and all variables not in the state are assumed not existent.

4 HYPE: planning by importance sampling

In this section we introduce HYPE (= hybrid episodic planner), a planner for hybrid relational MDPs described in DDC. HYPE is a planner that adopts an off-policy strategy (Sutton and Barto 1998) based on importance sampling and derived from the transition model. Related work is discussed more comprehensively in Sect. 6, but as we note later, sample-based planners typically only require a generative model (a way to generate samples) and do not exploit the model of the MDP (i.e., the actual probabilities) (Keller and Eyerich 2012). In our case, this knowledge leads to an effective planning algorithm that works in discrete, continuous, and hybrid domains, and/or domains with an unknown number of objects under weak assumptions. Moreover, HYPE performs abstraction of sampled episodes. In this section we introduce HYPE without abstraction; the latter will be introduced in Sect. 5.

4.1 Basic algorithm

In a nutshell, HYPE samples episodes $E^m$ and stores for each visited state $s^m_t$ an estimation of the V-function (e.g., the total reward obtained from that state). The action selection follows an given strategy (e.g., $\epsilon$-greedy), where the Q-function is estimated as the immediate reward plus the weighted average of the previously stored V-function points at time $t+1$. This is justified by means of importance sampling as explained later. The essential steps of our planning system HYPE are given in Algorithm 1.

The algorithm realizes the following key ideas:

• $\tilde{Q}$ and $\tilde{V}$ denote approximations of the $Q$ and $V$-function respectively.

• Lines 8 select an action according to a given strategy.

• Lines 9–12 sample the next step and recursively the remaining episode of total length $T$, then stores the total discounted reward $G(E^m_{t})$ starting from the current state $s^m_t$. This quantity can be interpreted as a sample of the expectation in formula (1), thus an estimator of the V-function. For this and other reasons explained later, $G(E^m_{t})$ is stored as $\tilde{V}^m_d(s^m_t)$.

• Most significantly, line 6 approximates the $Q$-function using the weighted average of the stored $\tilde{V}^i_{d-1}(s^i_{t+1})$ points:

  $$\begin{aligned} \displaystyle \tilde{Q}^m_d\left( s^m_t,a\right) \leftarrow R\left( s^m_t,a\right) + \gamma \frac{\sum _{i=0} ^ {m-1} w^i \tilde{V}^i_{d-1}\left( s^i_{t+1}\right) }{\sum _{i=0}^ {m-1} w^i}, \end{aligned}$$

  (10)

  where $w^ i$ is a weight function for episode $i$ at state $s^ i _ {t+1}.$ The weight exploits the transition model and is defined as:

  $$\begin{aligned} \displaystyle w^i=\frac{p\left( s^i_{t+1}\mid s^m_{t},a\right) }{q\left( s^i_{t+1}\right) } \alpha ^{(m-i)}. \end{aligned}$$

  (11)

Here, for evaluating an action $a$ at the current state $s_t,$ we let $w^i$ be the ratio of the transition probability of reaching a stored state $s^i_{t+1}$ and the probability used to sample $s^i_{t+1}$, denoted using $q.$ Recent episodes are considered more significant than previous ones, and so $\alpha$ is a parameter for realizing this. We provide a detailed justification for line 6 below.

We note that line 6 requires us to go over a finite set of actions, and so in the presence of continuous action spaces (e.g., real-valued parameter for a move action), we can discretize the action space or sample from it. More sophisticated approaches are possible (Forbes and Andre 2002; Smart and Kaelbling 2000).

Fig. 1

Left weight computation for the objpush domain. Right a sampled episode that reaches the goal (blue), and avoids the undesired region (red) (Color figure online)

Example 3

As a simple illustration, consider the following example called objpush. We have an object on a table and an arm that can push the object in a set of directions; the goal is to move the object close to a point g, avoiding an undesired region (Fig. 1). The state consists of the object position (x, y), with push actions parameterized by the displacement $\mathtt {(DX,DY)}$. The state transition model is a Gaussian around the previous position plus the displacement:

$$\begin{aligned} \mathtt {pos(ID)_{t+1} \sim \ }&\mathtt { gaussian(\simeq \!\!(pos(ID)_{t})+(DX,DY),cov) \leftarrow push(ID,(DX,DY)). } \end{aligned}$$

(12)

The clause is valid for any object $\mathtt {ID}$; nonetheless, for simplicity, we will consider a scenario with a single object. The terminal states and rewards in DDC are:

$$\begin{aligned} \mathtt {stop_{t}}&\mathtt {\leftarrow dist(\simeq \!\!(pos(A)_{t}),(0.6,1.0))<0.1. }\nonumber \\ \mathtt {reward(100)_{t}}&\mathtt { \leftarrow stop_{t}. }\nonumber \\ \mathtt {reward(-1)_{t}}&\mathtt { \leftarrow not(stop_t),dist(\simeq \!\!(pos(A)_{t}),(0.5,0.8))>=0.2. }\nonumber \\ \mathtt {reward(-10)_{t}}&\mathtt { \leftarrow not(stop_t),dist(\simeq \!\!(pos(A)_{t}),(0.5,0.8))<0.2. } \end{aligned}$$

(13)

That is, a state is terminal when there is an object close to the goal point (0.6, 1.0) (i.e., distance lower than 0.1), and so, a reward of 100 is obtained. The nonterminal states have reward $-10$ whether inside an undesired region centered in (0.5, 0.8) with radius 0.2, and $R(s_t,a_t)=-1$ otherwise.

Let us assume we previously sampled some episodes of length $T=10$, and we want to sample the $m=4$-th episode starting from $s_0=(0,0)$. We compute $\tilde{Q}^m_{10}((0,0),a)$ for each action a (line 6). Thus, we compute the weights $w^i$ using (11) for each stored sample $\tilde{V}^i_{9}(s^i_1)$. For example, Fig. 1 shows the computation of $\tilde{Q}^m_{10}((0,0),a)$ for action $a'=(-0.4,0.3)$ and $a''=(0.9,0.5)$, where we have three previous samples $i=\{1,2,3\}$ at depth 9. A shadow represents the likelihood $p(s^i_1|s_0=(0,0),a)$ (left for $a'$ and right for $a''$). The weight $w^i$ (11) for each sample $s^i_1$ is obtained by dividing this likelihood by $q(s^i_1)$ (with $\alpha =1$). If $q^i(s^i_1)$ is uniform over the three samples, sample $i=2$ with total reward $\tilde{V}^2_9(s^2_1)=98$ will have higher weight than samples $i=1$ and $i=3$. The situation is reversed for $a''$. Note that we can estimate $\tilde{Q}^m_d(s^m_t,a)$ using episodes $i$ that may never encounter $s^{m}_t,a_t$ provided that $p(s^i_{t+1}|s^{m}_{t},a_{t})>0$.

4.2 Computing the (approximate) Q-function

The purpose of this section is to motivate our approximation to the $Q$-function using the weighted average of the $V$-function points in line 6. Let us begin by expanding the definition of the $Q$-function from (2) as follows:

$$\begin{aligned} Q_d^\pi (s_t,a_t)=R(s_t,a_t)+\gamma \int _{s_{t+1:T},a_{t+1:T}} G(E_{t+1}) p(s_{t+1:T},a_{t+1:T}| s_t,a_t,\pi )d s_{t+1:T},a_{t+1:T}, \end{aligned}$$

(14)

where $G(E_{t+1})$ is the total (discounted) reward from time $t+1$ to T: $G(E_{t+1}) = \sum _{k=t+1}^{T} \gamma ^{k-t-1}R(s_{k},a_{k}).$ Given that we sample trajectories from the target distribution $p(s_{t+1:T},a_{t+1:T}| s_t,a_t,\pi )$, we obtain the following approximation to the $Q$-function equaling the true value in the sampling limit:

$$\begin{aligned} \displaystyle Q_d^\pi (s_t,a_t) \approx R(s_t,a_t) + \frac{1}{N}\gamma \sum _i G\left( E^i_{t+1}\right) . \end{aligned}$$

(15)

Policy evaluation can be performed sampling trajectories using another policy, this is called off-policy Monte Carlo (Sutton and Barto 1998). For example, we can evaluate the greedy policy while the data is generated from a randomized one to enable exploration. This is generally performed using (normalized) importance sampling (Shelton 2001a). We let $w^ i$ be the ratio of the target and proposal distributions to restate the sampling limit as follows:

$$\begin{aligned}&Q_d^\pi (s_t,a_t) \approx R(s_t,a_t) +\frac{1}{\sum w^ i} \gamma \sum _i w^ i G\left( E^i_{t+1}\right) . \end{aligned}$$

(16)

In standard off-policy Monte Carlo the proposal distribution is of the form:

$$\begin{aligned} p\left( s_{t+1:T},a_{t+1:T}| s_t,a_t,\pi '\right) = \prod _{k=t}^{T-1} \pi '\left( a_{k+1}| s_{k+1}\right) p\left( s_{k+1}| s_{k},a_{k}\right) . \end{aligned}$$

The target distribution has the same form, the only difference is that the policy is $\pi$ instead of $\pi '$. In this case the weight becomes equal to the policy ratio because the transition model cancels out. This is desirable when the model is not available, for example in model-free Reinforcement Learning. The question is whether the availability of the transition model can be used to improve off-policy methods. This paper shows that the answer to that question is positive.

We will now describe the proposed solution. Instead of considering only trajectories that start from $s_t,a_t$ as samples, we consider all sampled trajectories from time $t+1$ to T. Since we are ignoring steps before $t+1$, the proposal distribution for sample i is the marginal

$$\begin{aligned} p\left( s_{t+1:T},a_{t+1:T}| s_0,\pi ^i\right) =q^i(s_{t+1})\pi ^i(a_{t+1}|s_{t+1}) \prod _{k=t+1}^{T-1} \pi ^i(a_{k+1}| s_{k+1}) p(s_{k+1}| s_{k},a_{k}), \end{aligned}$$

where $q^i$ is the marginal probability $p(s_{t+1}| s_ 0, \pi ^{i})$. To compute $\tilde{Q}^m_d(s^m_t,a)$ we use (16), where the weight $w^i$ (for $0\le i\le m-1$) becomes the following:

$$\begin{aligned}&\frac{p\left( s_{t+1}^i| s^m_{t},a\right) \pi \left( a_{t+1}^i| s_{t+1}^i\right) \prod _{k=t+1}^{T-1} \pi \left( a_{k+1}^i| s_{k+1}^i\right) p \left( s_{k+1}^i| s_{k}^i,a_{k}^i\right) }{ q^i\left( s_{t+1}^i\right) \pi ^i\left( a_{t+1}^i| s_{t+1}^i\right) \prod _{k=t+1}^{T-1} \pi ^i \left( a_{k+1}^i| s_{k+1}^i\right) p \left( s_{k+1}^i| s_{k}^i,a_{k}^i\right) }\nonumber \\&\quad =\frac{ p \left( s_{t+1}^i| s^m_{t},a\right) }{ q^i\left( s_{t+1}^i\right) } \frac{\prod _{k=t}^{T-1} \pi \left( a_{k+1}^i| s_{k+1}^i\right) }{\prod _{k=t}^{T-1} \pi ^i\left( a_{k+1}^i| s_{k+1}^i\right) } \end{aligned}$$

(17)

$$\begin{aligned}&\quad \approx \ \frac{ p\left( s_{t+1}^i|s^m_{t},a\right) }{ q^i\left( s_{t+1}^i\right) } \alpha ^{(m-i)}. \end{aligned}$$

(18)

Thus, we obtain line 6 in the algorithm given that $\tilde{V}^i_{d-1}(s^i_t)=G(E^i_{t+1})$. In our algorithm the target (greedy) policy $\pi$ is not explicitly defined, therefore the policy ratio is hard to compute. We replace the unknown policy ratio with a quantity proportional to $\alpha ^{(m-i)}$ where $0 <\alpha \le 1$; thus, formula (17) is replaced with (18). The quantity $\alpha ^{(m-i)}$ becomes smaller for an increasing difference between the current episode index m and the i-th episode. Therefore, the recent episodes are weighted (on average) more than the previous ones, as in recently-weighted average applied in on-policy Monte Carlo (Sutton and Barto 1998). This is justified because the policy is improved over time, thus recent episodes should have higher weight.

In general, $q^i(s^i_{t+1})$ is not available in closed form; we adopt the following approximation:

$$\begin{aligned} q^i\left( s^i_{t+1}\right) =p\left( s^i_{t+1}|s_0,\pi _{i}\right)&= \int _{s_t,a_t} p\left( s^i_{t+1}|s_{t},a_{t}\right) p \left( s_t,a_t|s_0,\pi _i\right) \nonumber \\&\approx \frac{1}{2D+1} \sum _{j=i-D}^{i+D} p\left( s^i_{t+1}|s^j_{t},a^j_{t}\right) , \end{aligned}$$

(19)

where we are assuming that $\pi ^j\approx \pi ^i$ for $i-D<j<i+D$, and the samples $s^j_{t},a^j_{t}$ refer to episode $E^j$. Each episode $E^j$ is sampled from $p(s_{0:T},a_{0:T}|s_0,\pi _j)$, thus samples $(s^j_t,a^j_t)$ are distributed as $p(s_t,a_t|s_0,\pi _j)$ and are used in the estimation of the integral.

The likelihood $p(s^i_{t+1}|s^m_{t},a)$ is required to compute the weight. This probability can be decomposed using the chain rule, e.g., for a state with 3 variables we have:

$$\begin{aligned} p\left( s^i_{t+1}|s^m_{t},a\right) =p\left( v_3|v_2,v_1,s^m_{t},a\right) p \left( v_2|v_1,s^m_{t},a\right) p \left( v_1|s^m_{t},a\right) , \end{aligned}$$

where $s^i_{t+1}=\{v_1,v_2,v_3\}$. In DDC this is performed evaluating the likelihood of each variable in $v_i$ following the topological order defined in the DDC program. The target and the proposal distributions might be mixed distributions of discrete and continuous random variables; importance sampling can be applied in such distributions as discussed in Owen (2013, Chapter 9.8).

To summarize, for each state $s^m_t$, $Q(s^m_t,a_t)$ is evaluated as the immediate reward plus the weighted average of stored $G(E^i_{t+1})$ points. In addition, for each state $s^m_t$ the total discounted reward $G(E^m_{t})$ is stored. We would like to remark that we can estimate the Q-function also for states and actions that have never been visited, as shown in Example 1. This is possible without using function approximations (beyond importance sampling).

4.3 Extensions

Our derivation follows a Monte Carlo perspective, where each stored point is the total discounted reward of a given trajectory: $\tilde{V}^m_d(s^m_t)\leftarrow G(E^m_{t})$. However, following the Bellman equation, $\tilde{V}^m_d(s^m_t)\leftarrow max_a \tilde{Q}^m_d(s^m_t,a)$ can be used instead (replacing line 11 in Algorithm 1). The Q-function estimation formula in line 6 is not affected; indeed we can repeat the same derivation using the Bellman equation and approximate it with importance sampling:

$$\begin{aligned} Q_d^\pi (s_t,a_t)&= R(s_t,a_t)+ \gamma \int _{s_{t+1}} V_{d-1}^\pi (s_{t+1}) p(s_{t+1}|s_t,a_t) ds_{t+1} \nonumber \\&\approx R(s_t,a) +\gamma \sum \frac{w^i}{\sum w^i} \tilde{V}_{d-1}^i\left( s^i_{t+1}\right) =\tilde{Q}_d^m(s_t,a_t), \end{aligned}$$

(20)

with $w^i=\frac{p(s^i_{t+1}|s_t,a_t)}{q^i(s^i_{t+1})}$ and $s^i_{t+1}$ the state sampled in episode i for which we have an estimation of $\tilde{V}_{d-1}^i(s^i_{t+1})$, while $q^i(s^i_{t+1})$ is the probability with which $s^i_{t+1}$ has been sampled. This derivation is valid for a fixed policy $\pi$; for a changing policy we can make similar considerations to the previous approach and add the term $\alpha ^{(m-i)}$. If we choose $\tilde{V}^i_{d-1}(s^i_{t+1}) \leftarrow G(E^i_{t+1})$, we obtain the same result as in (10) and (18) for the Monte Carlo approach.

Instead of choosing between the two approaches we can use a linear combination, i.e., we replace line 11 with $\tilde{V}^m_d(s^m_t)\leftarrow \lambda G(E^m_{t})+(1-\lambda ) max_a \tilde{Q}^m_d(s^m_t,a)$. The analysis from earlier applies by letting $\lambda = 1$. However, for $\lambda = 0$, we obtain a local value iteration step, where the stored $\tilde{V}$ is obtained maximizing the estimated $\tilde{Q}$ values. Any intermediate value balances the two approaches (this is similar to, and inspired by, $\hbox {TD}(\lambda )$ Sutton and Barto 1998). Another strategy consists in storing the maximum of the two: $\tilde{V}^m_d(s^m_t)\leftarrow max(G(E^m_{t}),max_a \tilde{Q}^m_d(s^m_t,a))$. In other words, we alternate Monte Carlo and Bellman backup according to which one has the highest value. This strategy works often well in practice; indeed it avoids a typical issue in (on-policy) Monte Carlo methods: bad policies or exploration lead to low rewards, averaged in the estimated Q / V-function.

4.4 Practical improvements

In this section we briefly discuss some practical improvements of HYPE. To evaluate the Q-function the algorithm needs to query all the stored examples, making the algorithm potentially slow. This issue can be mitigated with solutions used in instance-based learning, such as hashing and indexing. For example, in discrete domains we avoid multiple computations of the likelihood and the proposal distribution for samples of the same state. In addition, assuming policy improvement over time, only the $N_{{\textit{store}}}$ most recent episodes are kept, since older episodes are generally sampled with a worse policy.

HYPE’s algorithm relies on importance sampling to estimate the $Q$-function, thus we should guarantee that $p>0 \Rightarrow q>0$, where p is the target and q is the proposal distribution. This is not always the case, like when we sample the first episode. Nonetheless we can have an indication of the estimation reliability. In our algorithm we use $\sum w^i$ with expectation equal to the number of samples: ${\mathbb {E}}[\sum w^i]=m$. If $\sum w^i<{\textit{thres}}$ the samples available are considered insufficient to compute $Q^m_d(s^m_t,a)$, thus action $a$ can be selected according to an exploration policy. It is also possible to add a fictitious weighted point in line 6, that represents the initial $Q^m_d(s^m_t,a)$ guess. This can be used to exploit heuristics during sampling.

A more problematic situation is when, for some action $a_{t}$ in some state $s_{t}$, we always obtain null weights, that is, $p(s^i_{t+1}|s_{t},a_{t})=0$ for each of the previous episodes i, no matter how many episodes are generated. This issue is solved by adding noise to the state transition model, e.g., Gaussian noise for continuous random variables. This effectively ‘smoothes’ the V-function. Indeed the Q-function is a weighted sum of V-function points, where the weights are proportional to a noisy version of the state transition likelihood.

5 Abstraction

By exploiting the (relational) model, we can improve the algorithm by using abstract states, because often, only some parts of the state determine the total reward. The idea is to generalize the specific states into abstract states by removing the irrelevant facts (for the outcome of the episode). This resembles symbolic methods to exactly solve MDPs in propositional and relational domains (Wiering and van Otterlo 2012). The main idea in symbolic methods is to apply the Bellman equation on abstract states, using logical regression (backward reasoning). As described in Sects. 2.3 and 6, symbolic methods are more challenging in hybrid relational MDPs. The main issues are the intractability of the integral in the Bellman equation (3), and the complexity of symbolic manipulation in complex hybrid relational domains.

To overcome these difficulties, we propose to perform abstraction at the level of samples. The modified algorithm with abstraction is sketched in Algorithm 2. The main differences with Algorithm 1 are:

• Q-function estimation from abstracted states (line 6)

• regression of the current state (line 11)

• the procedure returns the abstract state and its V-function, instead of the latter only (line 15). This is required for recursive regression.

Fig. 2

Blocksworld with abstraction. Current full state on the right, and a sampled episode on the left. The abstracted states are circled

5.1 Basic principles of abstraction

Before describing abstraction formally, let us consider the blocksworld example to give an intuition. Figure 2 shows a sampled episode from the first state (bottom left) to the last state (top left) that ends in the goal state ${\mathtt{on(2,1)}}$. Informally, the relevant part of the episode is the set of facts that are responsible for reaching the goal, or more generally responsible for obtaining a given total reward. This relevant part is called the abstracted episode. Figure 2 shows the abstract states (circled) that together define the abstract episode. Intuitively, objects 3, 4, 5 and their relations are irrelevant to reach the goal ${\mathtt{on(2,1)}}$, and thus do not belong to the abstracted episode.

The abstraction helps to exploit the previous episodes in more cases, speeding up the convergence. For example, Fig. 2 shows the computation of a weight $w^i$ [using (11)] to compute the Q-function of the (full) state $s^m_t$ depicted on the right, exploiting the abstract state $\hat{s}^i_{t+1}$ indicated by the arrow (from episode i). If the action is moving 4 on top of 5 we have $p(\hat{s}^i_{t+1}|s^m_t,a)>0 \Rightarrow w^i>0$. Thus, the Q-function estimate $\tilde{Q}^m_d(s_t,a)$ will include $w^1\cdot 99$ in the weighted average (line 6 in Algorithm 2), making the action appealing. In contrast, without abstraction all actions get weight 0, because the full state $s^i_{t+1}$ is not reachable from $s^m_t$ (i.e. $p(s^i_{t+1}|s^m_t,a)=0$). Therefore, episode i cannot be used to compute the Q-function. For this reason abstraction requires fewer samples to converge to a near-optimal policy.

This idea is valid in continuous domains. For example, in the objpush scenario, the goal is to put any object in a given region; if the goal is reached, only one object is responsible, any other object is irrelevant in that particular state.

5.2 Mathematical derivation

In this section we formalize sample-based abstraction and describe the assumptions that justify the Q-function estimation on abstract states (line 6 of Algorithm 2).

5.2.1 Abstraction applied to importance sampling

The Q-function estimation (16) can be reformulated for abstract states as follows. For an episode from time $t$, $E_{t}=<s_{t},a_{t}, \ldots , s_T,a_T>$, let us consider an arbitrary partition $E_{t}=\{\hat{E}_{t},E'_{t}\}$ such that $G( E_{t})=G(\hat{E}_{t})$, i.e., the total reward depends only on $\hat{E}_{t}$. The relevant part of the episode has the form $\hat{E}_{t}=<\hat{s}_{t},a_{t}, \ldots , \hat{s}_T,a_T>$, while $E'_{t}=E_{t}\setminus \hat{E}_{t}=< s'_{t}, \ldots , s'_T>$ is the remaining non-relevant part.¹ The partial episode $\hat{E}_{t}$ is called abstract because the irrelevant variables have been marginalized, in contrast $E_{t}$ is called full or complete. The Q-function estimation (16) is reformulated for abstract states marginalizing irrelevant variables:

$$\begin{aligned} Q_d^\pi \left( s^{m}_t,a\right)&=\int _{E_{t} }p\left( E_{t} |s^{m}_t,a,\pi \right) G(E_{t})d E_{t}=\nonumber \\&=\int _{\hat{E}_{t}}\bigg (\int _{E_{t}'} p\left( \hat{E}_{t},E_{t}'|s^{m}_t,a,\pi \right) d E_{t}'\bigg )G\left( \hat{E}_{t} \right) d\hat{E}_{t}=\nonumber \\&=\int _{\hat{E}_{t}} p\left( \hat{E}_{t}|s^{m}_t,a,\pi \right) G\left( \hat{E}_{t}\right) d\hat{E}_{t}=\nonumber \\&=R\left( \hat{s}^{m}_t,a\right) + \gamma \int _{\hat{E}_{t+1}} p\left( \hat{E}_{t+1}|s^{m}_t,a,\pi \right) G\left( \hat{E}_{t+1}\right) d\hat{E}_{t+1}=\nonumber \\&=R\left( \hat{s}^{m}_t,a\right) + \gamma \int _{\hat{E}_{t+1}} \underbrace{\frac{p\left( \hat{E}_{t+1}|s^{m}_t,a,\pi \right) }{q\left( \hat{E}_{t+1}\right) }}_{w\left( \hat{E}_{t+1}\right) } q\left( \hat{E}_{t+1}\right) G\left( \hat{E}_{t+1}\right) d\hat{E}_{t+1}\nonumber \\&\approx R\left( \hat{s}^{m}_t,a\right) + \gamma \frac{1}{\sum _{i=0} ^ {m-1} w\left( \hat{E}^{i}_{t+1}\right) } \sum _{i=0} ^ {m-1} w\left( \hat{E}^{i}_{t+1}\right) G\left( \hat{E}^{i}_{t+1}\right) . \end{aligned}$$

(21)

The above estimation is based on importance sampling just like in the non-abstract case (16), with similar target and proposal distributions. The main difference is the marginalization of irrelevant variables.

5.2.2 Importance weights for abstract episodes

Formula (21) is valid for any partition such that $G( E_{t})=G(\hat{E}_{t})$, but computing the weights $w(\hat{E}_{t+1})$ might be hard in general. To simplify the weight computation let us assume that the chosen partition guarantees the Markov property on abstract states, i.e., $p(\hat{s}_{t+1}| s_{0:t},a_{0:t})=p(\hat{s}_{t+1}| \hat{s}_{t},a_{t})$. To estimate $Q_d^\pi (s^{m}_t,a)$ (episode $m$), the weight for abstract episode $i<m$ becomes the following:

$$\begin{aligned}&w\left( \hat{E}_{t+1}\right) = \frac{p\left( \hat{E}_{t+1}| s^{m}_t,a,\pi \right) }{q^i\left( \hat{E}_{t+1}\right) }=\frac{\int _{E_{t+1}'} p\left( s_{t+1:T},a_{t+1:T}| s^{m}_t,a,\pi \right) dE'_{t+1}}{ \int _{E_{t+1}'}p\left( s_{t+1:T},a_{t+1:T}| s_0,\pi ^{i}\right) d E'_{t+1}}\nonumber \\&\quad =\frac{ p\left( \hat{s}_{t+1:T},a_{t+1:T}| s^{m}_t,a,\pi \right) }{ p\left( \hat{s}_{t+1:T},a_{t+1:T}| s_0,\pi ^{i}\right) }\nonumber \\&\quad =\frac{p\left( \hat{s}_{t+1}| s^{m}_{t},a\right) \pi \left( a_{t+1}| \hat{s}_{t+1}, s^{m}_t,a\right) }{q^i\left( \hat{s}_{t+1}\right) \pi ^i\left( a_{t+1}| \hat{s}_{t+1},s_{0}\right) }\frac{\prod _{k=t+1}^{T-1} \pi \left( a_{k+1}| \hat{s}_{t+1:k+1}, a_{t+1:k},s^{m}_t,a\right) p\left( \hat{s}_{k+1}| \hat{s}_{k},a_{k}\right) }{\prod _{k=t+1}^{T-1} \pi ^i\left( a_{k+1}| \hat{s}_{t+1:k+1},a_{t+1:k}, s_{0}\right) p\left( \hat{s}_{k+1}| \hat{s}_{k},a_{k}\right) }\nonumber \\&\quad =\frac{ p\left( \hat{s}_{t+1}| s^{m}_{t},a\right) }{ q^i\left( \hat{s}_{t+1}\right) } \frac{\prod _{k=t}^{T-1} \pi \left( a_{k+1}| \hat{s}_{t+1:k+1},a_{t+1:k} , s^{m}_t,a\right) }{\prod _{k=t}^{T-1} \pi ^i\left( a_{k+1}| \hat{s}_{t+1:k+1},a_{t+1:k} ,s_{0}\right) } \end{aligned}$$

(22)

$$\begin{aligned}&\quad \approx \frac{ p\left( \hat{s}_{t+1}| s^{m}_{t},a\right) }{ q^i\left( \hat{s}_{t+1}\right) } \frac{\prod _{k=t}^{T-1} \pi \left( a_{k+1}| \hat{s}_{t+1:k+1},a_{t+1:k},s_{0}\right) }{\prod _{k=t}^{T-1} \pi ^i\left( a_{k+1}| \hat{s}_{t+1:k+1},a_{t+1:k},s_{0}\right) } \end{aligned}$$

(23)

$$\begin{aligned}&\quad \approx \ \frac{ p\left( \hat{s}_{t+1}| s^{m}_{t},a\right) }{ q^i(\hat{s}_{t+1})} \alpha ^{(m-i)}, \end{aligned}$$

(24)

where $q^i(\hat{s}_{t+1}) = p(\hat{s}_{t+1}| s_0,\pi ^i)$ and can be approximated with (19) by replacing $s_{t+1}$ with $\hat{s}_{t+1}$. The final weight formula for abstracted states is similar to the non-abstract case. The difference is abstraction of the next state $\hat{s}_{t+1}$, while the state $s^m_t$ in which the Q-function is estimated remains a complete state.

We will now explain the weight derivation and motivate the approximations adopted. Until formula (22) the only assumption made is the Markov property on abstract states. No assumptions are made about the action distributions (policies) $\pi ,\pi ^i$, thus the probability of an action $a_t$ might depend on abstracted states in previous steps. Then (23) is replaced by (22) as discussed later. Finally, the policy ratio in (23) is replaced in (24) as in HYPE without abstraction.

Let us now discuss the approximation introduced in (23). Using (23) instead of (22) is equivalent to using the following target distribution:

$$\begin{aligned} \frac{ p\left( \hat{s}_{t+1}|s^m_{t},a\right) }{ q^i\left( \hat{s}_{t+1}\right) }p\left( \hat{s}_{t+1:T},a_{t+1:T}| s_0,\pi \right) =p\left( \hat{s}_{t+1}|s^m_{t},a\right) p\left( \hat{s}_{t+2:T},a_{t+1:T}|\hat{s}_{t+1}, s_0,\pi \right) , \end{aligned}$$

instead of

$$\begin{aligned} p\left( \hat{s}_{t+1:T},a_{t+1:T}| s^{m}_t,a,\pi \right) =p\left( \hat{s}_{t+1}|s^m_{t},a\right) p\left( \hat{s}_{t+2:T},a_{t+1:T}|\hat{s}_{t+1}, s^m_{t},a,\pi \right) . \end{aligned}$$

(25)

Since the state transition model is the same in both distributions, the only difference is the marginalized action distribution (target policy). The one used in (23) is

$$\begin{aligned} \pi \left( a_{k+1}| \hat{s}_{t+1:k+1},a_{t+1:k} ,s_{0}\right) \end{aligned}$$

(26)

instead of $\pi (a_{k+1}| \hat{s}_{t+1:k+1},a_{t+1:k} , s^{m}_t,a)$ for $k=t,\ldots ,T-1$. It is not straightforward to analyze this result because these actions distributions are obtained from the same policy $\pi$ by applying a different marginalization. Nonetheless, it is worth mentioning that the marginalized target policy (26) does not depend on the specific state $s^{m}_t$, but only on abstract states and on the initial state $s_{0}$. This is arguably a desirable property for the (marginalized) target policy.

Using (26) as target policy, and thus (23) as weight, is useful when the proposal policies are equal to the target policy: $\forall i: \pi =\pi ^i$. In this case the weight is exactly:

$$\begin{aligned} w\left( E^i_{t+1}\right) =\frac{ p\left( \hat{s}_{t+1}^i|s^m_{t},a\right) }{ q^i\left( \hat{s}_{t+1}^i\right) }, \end{aligned}$$

(27)

because the policy ratio cancels out. This formula is also applicable when $\forall i: \pi =\pi ^i$ and $\pi (a|s_t)=\pi (a|\hat{s}_t)$ or at least $\pi (a_{k+1}| \hat{s}_{t+1:k+1},a_{t+1:k} , s^{m}_t,a)=\pi (a_{k+1}| \hat{s}_{t+1:k+1},a_{t+1:k} , s_0)=\pi (a_{k+1}| \hat{s}_{t+1:k+1},a_{t+1:k} )$, that are indeed special cases of (26) and (23). Imposing or assuming $\pi (a|s_t)=\pi (a|\hat{s}_t)$ seems a reasonable choice, even though (26) is a weaker assumption. The optimal policy $\pi ^*$, might depend only on abstract states, thus $\pi ^*(a|s_t)=\pi ^*(a|\hat{s}_t)$. Indeed, we expect that the optimal policy depends only on the relevant part of the state. However, we can neither assume $\pi ^i(a|s_t)=\pi ^i(a|\hat{s}_t)$ nor $\pi ^i(a_{k+1}| \hat{s}_{t+1:k+1},a_{t+1:k}, s_0)=\pi ^i(a_{k+1}| \hat{s}_{t+1:k+1},a_{t+1:k} )$ as proposal policy. This is because the proposal policy $\pi ^i$ used to sample episode i has to explore with a non-zero probability all the actions: abstract states are generally not sufficient to determine the admissible actions. Thus, the dependence on the initial state $s_{0}$ is inevitable. In conclusion, the marginal target policy (26) is one of the weakest assumptions to guarantee a weight (27) for $\forall i: \pi =\pi ^i$. For $\pi \ne \pi ^i$ the weight becomes (23).

Now let us focus on (24) derived from (23). Since the policies $\pi ^i$ used in the episodes are assumed to improve over time, we replaced the policy ratio in (23) with a quantity that favors recent episodes as in the propositional case [formula (18)]. Another way of justifying (24) is estimating for each stored abstract episode i, the Q-function $Q_d^{\pi ^i}(s^{m}_t,a)$, with target policy $\pi =\pi ^i$, and using only the i-th sample. With a marginalized target policy given by (26), the single weight of each estimate $Q_d^{\pi ^i}(s^{m}_t,a)$ is exactly (27). The used Q-function estimate can be a weighted average of $Q_d^{\pi ^i}(s^{m}_t,a)$, where recent estimates (higher index $i$) receive higher weights because the policy is assumed to improve over time. Thus, the final weights are given by (24).

HYPE with abstraction adopts formula (21) and weights (24) for Q-function estimation. Note that during episode sampling the states are complete, nonetheless, to compute $Q_d^\pi (s^{m}_t,a)$ at episode $m$ all previously abstracted episodes $i<m$ are considered. Finally, when the sampling of episode $m$ is terminated, it is abstracted (line 11) and stored (line 14).

5.2.3 Ineffectiveness of lazy instantiation

Before explaining the proposed abstraction in detail, let us consider an alternative solution that samples abstract episodes directly, instead of sampling a complete episode and performing abstraction afterwards. If we are able to determine and sample partial states $\hat{s}^m_t$, we can sample abstract episodes directly and perform Q-function estimation. Sampling the relevant partial episode $\hat{E}_{t}$ can be easily performed using lazy instantiation, where given the query $G(E_t)$, only relevant random variables are sampled until the query can be answered. Lazy instantiation can exploit context-specific independencies and be extended for distributions with a countably infinite number of variables, as in BLOG (Milch et al. 2005a, b). Similarly, Distributional Clauses search relevant random variables (or facts) using backward reasoning, while sampling is performed in a forward way. For example, to prove $R_t$ the algorithm needs to sample the variables $\hat{s}_t$ relevant for $R_t$, $\hat{s}_t$ depends on $\hat{s}_{t-1}$ and the action $a_{t-1}$ depends on the admissible actions that again depend on $\hat{s}_{t-1}$, and so on. At some point variables can be sampled because they depend on known facts (e.g., initial state $s_0$). This procedure guarantees that $G( E_{t})=G(\hat{E}_{t})$, $p(\hat{s}_{t+1}| s_{0:t},a_{t})=p(\hat{s}_{t+1}| \hat{s}_{t},a_{t})$ and $\pi ^i(a|s_t)=\pi ^i(a|\hat{s}_t)$, thus (22) is exactly equal to (23) and it simplifies to $\frac{ p(\hat{s}_{t+1}| s^{m}_{t},a)}{ q^i(\hat{s}_{t+1})} \frac{\prod _{k=t}^{T-1} \pi (a_{k+1}| \hat{s}_{k+1})}{\prod _{k=t}^{T-1} \pi ^i(a_{k+1}| \hat{s}_{k+1})}$. Finally, the approximation (24) can be used. Unfortunately, this method avoids only sampling variables that are completely irrelevant, therefore in many practical domains it will sample (almost) the entire state. Indeed, evaluating the admissible actions often requires sampling the entire state. In other words, the abstract state $\hat{s}_t\subseteq s_t$ that guarantees $\pi ^i(a|s_t)=\pi ^i(a|\hat{s}_t)$ is often equal to $s_t$. The solution adopted in this paper is ignoring the requirement $\pi ^i(a|s_t)=\pi ^i(a|\hat{s}_t)$ and approximate (22) with (23), or equivalently using (26) as marginalized target policy distribution.

5.3 Sample-based abstraction by logical regression

In this section we describe how to implement the proposed sample-based abstraction. The implementation is based on dynamic distributional clauses for two reasons: DDC allow to represent complex hybrid relational domains and provides backward reasoning procedures useful for abstraction as we will now describe.

Algorithm 2 samples complete episodes and performs abstraction afterwards. The abstraction of $\hat{E}_{t}$ from $E_{t}$ (REGRESS function at line 11) is decomposed recursively employing backward reasoning (regression) from the last step $t=T$ till reaching $s_0$. We first regress the query $R(s_T,a_T)$ using $s_T$ to obtain the abstract state $\hat{s}_T=\hat{E}_T$ (computing the most general $\hat{s}_T$ such that $R(\hat{s}_{T},a_{T})=R(s_{T},a_{T})$). For $t=T-1,\ldots ,0$ we regress the query $R(s_t,a_t) \wedge \hat{s}_{t+1}$ using $a_t, s_t\in E_t$ to obtain the most general $\hat{s}_t\subseteq s_t\$ that guarantees $R(\hat{s}_{t},a_{t})=R(s_{t},a_{t})$ and $p(\hat{s}_{t+1}|s_{t},a_{t})=p(\hat{s}_{t+1}|\hat{s}_{t},a_{t})$. Note that $\hat{E}_{t}= \hat{s}_t \cup \ \hat{E}_{t+1}$. This method assumes that the actions are given, thus it avoids determining the admissible actions, keeping the abstract states smaller. For this reason, REGRESS guarantees only $G( E_{t})=G(\hat{E}_{t})$ and $p(\hat{s}_{t+1}| \hat{s}_{0:t},a_{t})=p(\hat{s}_{t+1}| \hat{s}_{t},a_{t})$, in contrast $\pi ^i(a|s_t)=\pi ^i(a|\hat{s}_t)$ is not guaranteed. Those conditions are sufficient to apply (23) and (24) as described in the previous section. Note that derivation (21) assumes a fixed partition, thus exploits only conditional independencies, but the idea can be extended to context-specific independencies.

The algorithm REGRESS for regressing a query (formula) using a set of facts is depicted in Algorithm 3. The algorithm tries to repeatedly find literals in the query that could have been generated using the set of facts and a distributional clause. If it finds such a literal, it will be replaced by the condition part of the clause in the query. If not, it will add the fact to the state to be returned.

Example 4

To illustrate the algorithm, consider the blocksworld example in Fig. 2. Let us consider the abstraction of the episode on the left. To prove the last reward we need to prove the goal, thus $\hat{s}_2={\mathtt{{on(2,1)_{2}}}}$. Now let us consider time step 1, the proof for the immediate reward is ${\mathtt{{not(on(2,1)_{1})}}}$, while the proof for the next abstract state $\hat{s}_2$ is ${\mathtt{{on(2,table)_{1}, clear(1)_{1},clear(2)_{1}}}}$, therefore the abstract state becomes $\hat{s}_1={\mathtt{on(2,table)_{1}, clear(1)_{1},clear(2)_{1}}}$, ${\mathtt{not(on(2,1)_{1})}}$. Analogously, $s'_0 = {\mathtt{{on(1,2)_{0}, on(2,table)_{0}, clear(1)_{0}, not(on(2,1)_{0})}}}$. The same procedure is applicable to continuous variables.

6 Related work

6.1 Non-relational planners

There is an extensive literature on MDP planners, we will focus mainly on Monte Carlo approaches. The most notable sample-based planners include sparse sampling (SST) (Kearns et al. 2002), UCT (Kocsis and Szepesvári 2006) and their variations. SST creates a lookahead tree of depth D, starting from state $s_0$. For each action in a given state, the algorithm samples C times the next state. This produces a near-optimal solution with theoretical guarantees. In addition, this algorithm works with continuous and discrete domains with no particular assumptions. Unfortunately, the number of samples grows exponentially with the depth D, therefore the algorithm is extremely slow in practice. Some improvements have been proposed (Walsh et al. 2010), although the worst-case performance remains exponential. UCT (Kocsis and Szepesvári 2006) uses upper confidence bound for multi-armed bandits to trade off between exploration and exploitation in the tree search, and inspired successful Monte Carlo tree search methods (Browne et al. 2012). Instead of building the full tree, UCT chooses the action a that maximizes an upper confidence bound of Q(s, a), following the principle of optimism in the face of uncertainty. Several improvements and extensions for UCT have been proposed, including handling continuous actions (Mansley et al. 2011) [see Munos (2014) for a review], and continuous states (Couetoux 2013) with a simple Gaussian distance metric; however the knowledge of the probabilistic model is not directly exploited. For continuous states, parametric function approximation is often used (e.g., linear regression), nonetheless the model needs to be carefully tailored for the domain to solve (Wiering and van Otterlo 2012).

There exist algorithms that exploit instance-based methods (e.g. Forbes and Andre 2002; Smart and Kaelbling 2000; Driessens and Ramon 2003) for model-free reinforcement learning. They basically store Q-point estimates, and then use e.g., neighborhood regression to evaluate Q(s, a) given a new point (s, a). While these approaches are effective in some domains, they require the user to design a distance metric that takes into account the domain. This is straightforward in some cases (e.g., in Euclidean spaces), but it can be harder in others. We argue that the knowledge of the model can avoid (or simplify) the design of a distance metric in several cases, where the importance sampling weights and the transition model, can be considered as a kernel.

The closest related works include Shelton (2001a, b), Peshkin and Shelton (2002), Precup et al. (2000), they use importance sampling to evaluate a policy from samples generated with another policy. Nonetheless, they adopt importance sampling differently without knowledge of the MDP model. Although this property seems desirable, the availability of the actual probabilities cannot be exploited, apart from sampling, in their approaches. The same conclusion is valid for practically any sample-based planner, which only needs a sample generator of the model. The work of Keller and Eyerich (2012) made a similar statement regarding PROST, a state-of-the-art discrete planner based on UCT, without providing a way to use the state transition probabilities directly. Our algorithm tries to alleviate this, exploiting the probabilistic model in a sample-based planner via importance sampling.

For more general domains that contain discrete and continuous (hybrid) variables several approaches have been proposed under strict assumptions. For example, Sanner et al. (2011) provide exact solutions, but assume that continuous aspects of the transition model are deterministic. In a related effort (Feng et al. 2004), hybrid MDPs are solved using dynamic programming, but assuming that transition model and reward is piecewise constant or linear. Another planner HAO* (Meuleau et al. 2009) uses heuristic search to find an optimal plan in hybrid domains with theoretical guarantees. However, they assume that the Bellman equation integral can be computed.

For domains with an unknown number of objects, some probabilistic programming languages such as BLOG (Milch et al. 2005a), Church (Goodman et al. 2008), Anglican (Wood et al. 2014), and DC (Gutmann et al. 2011) can cope with such uncertainty. To the best of our knowledge DTBLOG (Srivastava et al. 2014; Vien and Toussaint 2014) are the only proposals that are able to perform decision making in such domains using a POMDP framework. Furthermore, BLOG is one of the few languages that explicitly handles data association and identity uncertainty. The current paper does not focus on POMDP, nor on identity uncertainty; however, interesting domains with unknown number of objects can be easily described as an MDP that HYPE can solve.

Among the mentioned sample-based planners, one of the most general is SST, which does not make any assumption on the state and action space, and only relies on Monte Carlo approximation. In addition, it is one of the few planners that can be easily applied to any DDC program, including MDPs with an unknown number of objects. For this reason SST was implemented for DDC and used as baseline for our experiments.

6.2 Relational planners and abstraction

There exists several modeling languages for planning, the most recent is RDDL [40] that supports hybrid relational domains. A RDDL domain can be mapped in DDC and solved with HYPE. Nonetheless, RDDL does not support a state space with an unknown number of variables as in Example 2.

Relational MDPs can be solved using model-free approaches based on relational reinforcement learning (Džeroski et al. 2001; Tadepalli et al. 2004; Driessens and Ramon 2003), or model-based methods such as ReBel (Kersting et al. 2004), FODD (Wang et al. 2008), PRADA (Lang and Toussaint 2010), FLUCAP (Hölldobler et al. 2006) and many others. However, those approaches only support discrete action-state (relational) spaces.

Among model-based approaches, several symbolic methods have been proposed to solve MDPs exactly in propositional [see Mausam and Kolobov (2012) for a review] and relational domains (Kersting et al. 2004; Wang et al. 2008; Joshi et al. 2010; Hölldobler et al. 2006). They perform dynamic programming at the level of abstract states; this approach is generally called symbolic dynamic programming (SDP). Similar principles have been applied in (propositional) continuous and hybrid domains (Sanner et al. 2011; Zamani et al. 2012), where compact structures (e.g., ADD and XADD) are used to represent the V-function. Despite the effectiveness of such approaches, they make restrictive assumptions (e.g., deterministic transition model for continuous variables) to keep exact inference tractable. For more general domains approximations are needed, for example sample-based methods or confidence intervals (Zamani et al. 2013). Another issue of SDP is keeping the structures that represent the V-function compact. Some solutions are available in the literature, such as pruning or real-time SDP (Vianna et al. 2015). Despite the recent progress, and the availability of regression methods for inference in hybrid domains (Belle and Levesque 2014), SDP remains a challenging approach in general hybrid relational domains.

Recently, abstraction has received a lot of attention in the Monte Carlo planning literature. Like in our work, the aim is to simplify the planning task by aggregating together states that behave similarly. There are several ways to define state equivalence, see Li et al. (2006) for a review. Some approaches adopt model equivalence: states are equivalent if they have the same reward and the probabilities to end up in other abstract states are the same. Other approaches define the equivalence in terms of the V/Q-function. In particular, we take note of the following advances: (a) Givan et al. (2003) who compute equivalence classes of states based on exact model equivalence, (b) Jiang et al. (2014) who appeal to approximate local homomorphisms derived from a learned model, (c) Anand et al. (2015) who extend Jiang and Givan in grouping state-action pairs, and (d) Hostetler et al. (2014) who aggregate states considering the V/Q-function with tight loss bounds.

In our work, in contrast, we consider equivalence (abstraction) at the level of episodes, not states. Two episodes are equivalent if they have the same total reward. In addition, a Markov property condition on abstract states is added to make the weights in (21) easier to compute. Abstraction is performed independently in each episode, determining, by logical regression, the set of facts (or random variables) sufficient to guarantee the mentioned conditions. Note that the same full state $s_t$ might have different abstractions in different episodes, even for the same action $a_t$. This is generally not the case in other works. The proposed abstraction directly exploits the structure of the model (independence assumptions) to perform abstraction. For this reason it relies on the (context-specific) independence assumptions explicitly encoded in the model. However, it is possible to discover independence assumptions not explicitly encoded and include them in the model (e.g., using independence tests).

7 Experiments

This section answers the following questions:

• (Q1) Does HYPE without abstraction obtain the correct results?

• (Q2) How is the performance of HYPE in different domains?

• (Q3) How does HYPE compare with state-of-the-art planners?

• (Q4) Is abstraction beneficial?

The domains used in the experiments are written in DDC; the algorithms were implemented in YAP Prolog and C++, and run on a Intel Core i7 Desktop. We will first describe experiments without abstraction, then compare HYPE with and without abstraction.

7.1 HYPE without abstraction

In this section we consider HYPE without abstraction. The algorithm HYPE and its theoretical foundations are based on approximations (e.g., Monte Carlo). For this reason we tested the correctness of HYPE results in different planning domains (Q1). In particular, we tested HYPE on a nonlinear version of the hybrid mars rover domain (Sanner et al. 2011) (called simplerover1) for which the exact V-function is available. In this domain there is a rover that needs to take pictures. The state consists of a two-dimensional continuous rover position (x, y) and one discrete variable h to indicate whether the picture at a target point was taken. In this simplified domain we consider two actions: move with reward $-1$ that moves the rover towards the target point (0, 0) by 1 / 3 of the current distance, and take-pic that takes the picture at the current location. The reward of take-pic is $max(0,4-x^2-y^2)$ if the picture has not been already taken ($h={\textit{false}}$) and 0 otherwise. In other words, the agent has to minimize the movement cost and take a picture as close as possible to the target point (0, 0). We choose 31 initial rover positions and ran the algorithm with depth $d=3$ for 100 episodes each. An experiment took on average 1.4 s. Figure 3 shows the results where the line is the exact V provided by Sanner et al. (2011), and dots are estimated V points. The results show that the algorithm converges to the optimal V-function with a negligible error.

The domain simplerover1 is deterministic, and so, to make it more realistic we converted it to a probabilistic MDP adding Gaussian noise to the state transition model (with a variance $\sigma ^2=0.0005$ when the rover does not move and $\sigma ^2=0.02$ when the rover moves). The resulting MDP (simplerover2) is hard (if not impossible) to solve exactly. Then we performed experiments for different horizons, number of pictures points (1–4, each one is a discrete variable) and summed the rewards. For each instance the planner searches for an optimal policy and executes it, and after each executed action it samples additional episodes to refine the policy (replanning). The proposed planner is compared with SST which must replan every step. The results for both planners are always comparable, which confirms the empirical correctness of HYPE (Please provide a definition for the significance of [bold, italics, underline, letter a, asterisk] in the table.Table 1).

Fig. 3

$V$-function for different rover positions (with fixed $X=0.16$) in simplerover1 domain (left). A possible episode in marsrover (right) each picture can be taken inside the respective circle (red if already taken, green otherwise) (Color figure online)

Table 1 Experiments without abstraction: d is the horizon used by the planner, T the total number of steps, M is the maximum number of episodes sampled for HYPE, while C is the SST parameter (number of samples for each state and action). Time refers to the plan execution of one instance, from the starting state till the goal or the maximum number of steps is reached, with a timeout of 1800 s. PROST results refer to the IPPC2011 planning competition

To answer (Q2) and (Q3) we studied the planner in a variety of settings, from discrete, to continuous, to hybrid domains, to those with an unknown number of objects. We performed experiments in a more realistic mars rover domain that is publicly available,² called marsrover (Fig. 3). In this domain we consider one robot and 5 picture points that need to be taken. The state is similar to simplerover domains: a continuous two-dimensional position and a binary variable for each picture point. However, in marsrover the robot can move an arbitrary displacement along the two dimensions. The continuous action space is discretized as required by HYPE and SST. The movement of the robot causes a negative reward proportional to the displacement and the pictures can be taken only close to the interest point. Each taken picture provides a different reward.

Other experiments were performed in the continuous objpush MDP described in Sect. 4 (Fig. 1), and in discrete benchmark domains of the IPPC 2011 competition. In particular, we tested a pair of instances of Game of life (called game in the experiments) and sysadmin domains. Game of life consists of a grid X times Y cells, where each cell can be dead or alive. The state of each cell changes over time and depends on the neighboring cells. In addition, the agent can set a cell to alive or do nothing. The reward depends on the number of cells alive. We consider instances with $3 \times 3$ cells, and thus a state of 9 binary variables and 10 actions. The sysadmin domain consists of a network of computers. Each computer might be running or crashed. The probability of a computer to crash depends on how many computers it is connected to. The agent can choose at each step to reboot a computer or do nothing. The goal is to maximize the number of computers running and minimize the number of reboots required. We consider instances with 10 computers (i.e. 10 binary random variables) and so there are 11 actions. The results in the discrete IPPC 2011 domains are compared with PROST (Keller and Eyerich 2012), the IPPC 2011 winner, and shown in Table 1 in terms of scores, i.e., the average reward normalizated with respect to IPPC 2011 results; score 1 is the highest result obtained (on average), score 0 is the maximum between the random and the no operation policy.

As suggested by Keller and Eyerich (2012), limiting the horizon of the planner increases the performance in several cases. We exploited this idea for HYPE as well as SST (simplerover2 excluded). For SST we were forced to use small horizons to keep plan time under 30 min. In all experiments we followed the IPPC 2011 schema, that is each instance is repeated 30 times (objectsearch excluded), the results are averaged and the $95\%$ confidence interval is computed. However, for every instance we replan from scratch for a fair comparison with SST. In addition, time and number of samples refers to the plan execution of one instance.

The results (Table 1) highlight that our planner obtains generally better results than SST, especially at higher horizons. HYPE obtains good results in discrete domains but does not reach state-of-art results (score 1) for two main reasons. The first is the lack of a heuristic, that can dramatically improve the performance, indeed, heuristics are an important component of PROST (Keller and Eyerich 2012), the IPPC winning planner. The second reason is the time performance that allows us to sample a limited number of episodes and will not allow all the IPPC 2011 domains to finish in 24 h. This is caused by a non-optimized Prolog implementation and by the expensive Q-function evaluation; however, we are confident that heuristics and other improvements will significantly improve performance and results. In particular, the weight computation can be performed on a subset of stored V-state points, excluding points for which the weight is known to be small or zero. For example, in the objpush domain, the points too far from the current position plus action displacement can be discarded because the weight will be negligible. Thus, a nearest neighbor search can be used for a fast retrieval of relevant stored V-points.

Moreover, we performed experiments in the objectsearch scenario (Sect. 3), where the number of objects is unknown, even though the domain is modeled as a fully observable MDP. The results are averaged over 400 runs, and confirm better performance for HYPE with respect to SST.

7.2 HYPE with abstraction

To evaluate the effectiveness of abstraction (Q4) we performed experiments with the blocksworld (BW with 4 or 6 objects) and a continuous version of it (BWC with 4 or 6 objects) with an energy level of the agent and object weights. The energy decreases with a quantity proportional to the weight of the object moved plus Gaussian noise. If the energy becomes 0 the action fails, otherwise the probability of success is 0.9. The reward is $-1$ before reaching the goal and $10+{\textit{Energy}}$ if the goal is reached. Then we performed experiments with the objpush scenario. This time we consider multiple objects on the table. We considered different goals: move an arbitrary object in the goal region (domain push1 with 2 objects), and move a specific object in the goal region (push2 and push3 with 3 objects). Finally, we performed experiments with the marsrover domain, with one robot (mars1) or two of them (mars2), and 5 picture points that need to be taken.

Table 2 Experiments with and without abstraction

The current implementation supports negation only for ground formulas. Regression of nonground formulas is possible when the domain is purely relational. However, it becomes challenging when there are continuous random variables and logical variables in a negated formula. If we assume that the domain is fixed (e.g., known number of objects used), logical variables can be replaced with objects in the domain, making the formulas ground. For this reason we will not consider domains with an unknown number of objects, which HYPE without abstraction can solve.

The experiments are shown in Table 2. The rewards are averaged over 50 runs and a $95\%$ confidence interval is computed. The results highlight that abstraction improves the expected total reward for the same number of samples or achieves comparable results. In addition, HYPE with abstraction is always faster. The latter is probably due to a faster weight computation with abstract states and due to the generation of better plans that are generally shorter and thus faster. This suggests that the overhead caused by the abstraction procedure is negligible and worthwhile. We do remark that in domains where the whole state is always relevant, abstraction gives no added value. For example, the reward in Game of life and sysadmin depends always on the full state, thus abstraction is not useful because abstract state and full state coincide. Nonetheless, other type of abstractions can be beneficial. Indeed, the proposed abstraction (Algorithm 3) produces grounded abstract states (i.e., states where the facts do not have logical variables), this is required to allow abstraction in complex domains. In more restricted domains (e.g., discrete) more effective abstractions can improve the performance. For example, abstractions used in SDP (Kersting et al. 2004; Wang et al. 2008; Joshi et al. 2010; Hölldobler et al. 2006) produce abstract states with logical variables.

8 Conclusions

We proposed a sample-based planner for MDPs described in DDC under weak assumptions, and showed how the state transition model can be exploited in off-policy Monte Carlo. The experimental results show that the algorithm produces good results in discrete, continuous, hybrid domains as well as those with an unknown number of objects. Most significantly, it challenges and outperforms SST. Moreover, we extended HYPE with abstraction. We formally described how (context-specific) independence assumptions can be exploited to perform episode abstraction. This is valid for propositional as well as relational domains. A theoretical derivation has been provided to justify the assumptions and the approximations used. Finally, empirical results showed that abstraction provides significant improvements.