Introduction

The investigation of unsteady boundary layer flow is of the utmost significance since a considerable proportion of the flow difficulties that are faced in applied fluid mechanics contain unsteadiness. This sort of flow behavior is now being thoroughly researched to measure the drag caused by friction and to further our understanding of the wide-ranging applications it has in a variety of technical and applied science fields. Over the course of the last several decades, there has been a substantial concentration within the scientific community on understanding the unsteady features of boundary layer flows. This includes the unsteady characteristics of separated stagnation point flows in a variety of situations. Notably, Blasius [1] noted that separation features additionally have a role in the disappearance of skin friction in steady boundary layer flow over a flat plate. This is notable since separation characteristics play a role in the disappearance of skin friction. While this was going on, Abbott et al. [2] proved that the point at which there is no longer any skin friction may not always correspond with the point of separation. In addition to this, they argued that a more in-depth comprehension might be attained by determining a connection between the properties of separation in unsteady flow over fixed surfaces. Researchers have spent a significant amount of time looking into the issue of unstable, separated stagnation point flow. Lok and Pop [3], Dholey [4], and Zainal et al. [5] are just a few of the researchers that have made noteworthy contributions to the field.

The investigation of boundary layer flow in the stagnation area is of critical significance in the context of the manufacturing sector, and more specifically in the context of applications such as the manufacture of polymers and the processes of extrusion. It is essential that continuous progress is made in this area in order to fulfill and maintain these demanding quality requirements [6, 7]. Hiemenz [8] is credited with laying the groundwork for what is now known as the conventional stagnation point flow. In addition, Takhar et al. [9] carried out a thorough examination of unsteady flow that was aimed toward the stagnation zone in a cylindrical shape. The objective of Rafique et al. [10] study is to examine the flow characteristics at a stagnation point across a stretched surface, taking into account the influence of changes in viscosity and aggregation. Ganie and colleagues [11] use the Yamada-Ota model in their research to investigate the unstable and non-axisymmetric magnetohydrodynamic (MHD) Homann stagnation point phenomena of carbon nanotubes as they move across a convective surface. Islam et al. [12] have constructed and investigated the dynamics of an unstable double-diffusive mixed convection flow of nanofluids inside the boundary layer above a vertical area close to a stagnation point. Focusing on the stagnation point flow produced by an extended, heated stretchable sheet, Ali et al. [13] formulate a mathematical model.

The importance of nanofluids has significantly increased over the last several decades as a direct result of the rising need for heating systems that are more energy efficient. The concept of dispersing nanoparticles in a base fluid has since found applications across a wide range of business sectors, according to Choi [14]. Today, thermal transfer devices are essential components in a variety of industries, including the medicinal drug delivery industry, the computer processing industry, aerospace technology, and the heat exchanger system industry (see [15,16,17]). Saleem et al. [18] conducted an investigation into the mathematical interpretation of the electro-osmotically driven flow of Casson nanofluid inside a cylindrical geometry characterized by sinusoidal walls that contract and relax in a regular manner.

Nanoparticles made of aluminum oxide (\({\mathrm{Al}}_{2}{\mathrm{O}}_{3}\)) were selected for this inquiry because of the widespread use of these nanoparticles in a variety of industrial applications [19, 20]. The goal of Ali and colleagues [21] study is to ascertain how variables like the \({\mathrm{Al}}_{2}{\mathrm{O}}_{3}\) nanoparticles’ radius and the inter-particle spacing affect the two-dimensional flow behavior of nanoliquids. In addition, the size of the nanoparticles may have a considerable impact on the amount of skin friction and the rate of heat transfer, which in turn influences the hydrodynamic and thermal behavior of nanofluids in a variety of flow regimes, independent of the regime. In this scenario, the correlation developed by Corcione [22] was used to ascertain both the thermal conductivity and the effective dynamic viscosity of the material. Dogonchi et al. [23] did a study on the magnetohydrodynamic (MHD) flow of \(\mathrm{Cu}/{\mathrm{H}}_{2}\mathrm{O}\) nanofluid across an extended sheet using Corcione’s model. They presented their results in a research article and discussed the implications of their findings. They discovered that an increase in the volume percentage of nanoparticles caused a rise in the Nusselt number. In a later investigation, Selvakumar and Dinakaran [24] discovered that the rate at which the nanofluid removed heat increased in proportion to the reduction in nanoparticle size. Additionally, the findings of their study demonstrated that a reduction in nanoparticle size led to a rise in the enhancement ratio of heat transfer as well as the average Nusselt number. In addition, Ramzan et al. [25] investigated the influence of anisotropic slip on nanofluid flow over a biaxially exponentially stretched sheet using Hall current. Their research made use of Corcione’s correlation. According to the results of their study, increasing the diameter of \({\mathrm{Al}}_{2}{\mathrm{O}}_{3}\) nanoparticles had a favorable impact, which resulted in increased Nusselt numbers and drag force coefficients across a wide range of nanoparticle sizes, especially at greater volume fractions. Mishra et al. [26] created the current model with the primary goal of examining the heating characteristics of \({\mathrm{Al}}_{2}{\mathrm{O}}_{3}/{\mathrm{H}}_{2}\mathrm{O}\) nanofluids and calculating the effective values using the Corcione model.

The transport of heat from one point to another by the movement of fluids is what is referred to as convective heat transfer, sometimes referred to simply as convection. It is referred to as forced convection when the motion of the fluid is driven by an external source. On the other hand, free convection, also known as natural convection, takes place when the motion of the fluid is primarily generated by buoyancy forces because of density differences. On the other hand, what we mean when we talk about mixed convection is the simultaneous activity of both natural and forced convection processes. Researchers have developed a particular interest in the issue of mixed convection flow because of its relevance in a variety of industrial sectors, including solar and nuclear collectors, heat exchangers, and atmospheric boundary layer fluxes [27, 28]. The purpose of the research carried out by Mahmood and Khan [29] is to determine how the aggregation of nanoparticles influences the mixed convective stagnation point flow and porous medium over a permeable, stretched vertical Riga plate. The purpose of the study carried out by Otman and colleagues [30] is to evaluate the factors that have an effect on the behavior of a nanofluid composed of ethylene glycol. These factors include the aggregation of nanoparticles, mixed convection, joule heating, and the presence of a heat source. A study conducted by Amanulla et al. [31] focused on examining the properties of a steady, two-dimensional flow that included a non-Newtonian Prandtl–Eyring fluid flowing around an isothermal sphere. The present research took into account the impact of buoyancy forces and non-Darcy porous media.

Significant temperature shifts occur both inside the surrounding fluid and at the surface in a wide variety of real-world circumstances and industrial applications. It is also important to take into account heat production or absorption, both of which are temperature-dependent, since this factor may have a significant effect on the parameters of heat transmission [32]. Investigations into the influence and significance of heat generation and absorption on boundary layer flow continue to attract a lot of attention. This is especially the case because heat generation and absorption have a wide variety of applications in engineering systems, including thermal insulation, the cooling of nuclear reactors, the extraction of geothermal energy, and many other things [33]. An investigation of the boundary layer flow and heat transmission across a stretched sheet was carried out by Vajravelu and Hadjinicolaou [34], who also took into account the existence of internal heat production. Saleem et al. [35] did research to look into how heat sources and sinks interact in MHD Jeffrey fluid flow system on a cone that spins vertically and has infinite dimensions.

Many processes rely on melting, including the fabrication of semiconductors, the crystallization of hot magma flows, the creation of frozen indefinitely ground, and the thawing of previously frozen ground. Different temperature differences, such as those of the metal, the material being melted, and the surrounding environment in frigid places, provide unique heat transmission issues throughout the melting process. The heat transfer issue of melting-induced laminar steady forced convective flow (FCF) was investigated by Epstein and Cho [36]. Free convective flow (CF) across horizontal and vertical surfaces in a porous medium was studied by Kazmierczak et al. [37], who focused on the effect of melting on CF. Melting process characteristics in the context of a continuous flow and heat transmission toward a stagnation point through a moving sheet were studied by Bachok et al. [38]. Magneto-flow in an electrically conducting, heated liquid next to a melting parallel surface was studied by Venkateswarlu and coworkers [39], who looked into the impacts of heat sources and viscous dissipation. Melting heat transmission and other physical factors associated with a rotating cylinder were also investigated by Khan et al. [40].

Upon conducting a comprehensive analysis of relevant scholarly literature, it becomes evident that the “no-slip boundary condition” has significant importance as a basic notion upon which Navier–Stokes theory is built. Nevertheless, there are circumstances in which this idea may not be applicable. The phenomenon of a liquid displaying incoherent behavior upon departing from a solid boundary condition is often known as the slip velocity boundary condition. The use of slip-type limitations of fluids may be efficiently applied in many applications, such as the cleaning of artificial heart connections and the scouring of internal apertures. In addition, the slip in velocity that occurs on flexible surfaces becomes significant when the liquid goes through particle changes, as is the case in hydrogels, foams, and suspensions. Thompson and Troian [41] conducted research with the presumption that the magnitude of slip is reliant on shear stress to study the generalized slip condition effect (GSCE). An analytical solution to the Navier–Stokes equations was reported by Wang [42] in prior research. This solution took into account the major influence that the slip condition has on a flexible sheet. The hydro-magnetic flow of a viscous fluid with partial slip was investigated in Mukhopadhyay’s work [43]. According to the results of the research, an increase in the degree of slip led to a decrease in velocity, which was followed by a concurrent rise in temperature. This was the case even though the degree of slip had increased. Groşan et al. [44] investigated the Blasius problem in their work by using a semi-infinite plate and taking into consideration the generalized slip condition.

In earlier work that Dholey [45] had carried out, the major emphasis was focused on the investigation of viscous flow; however, there was no incorporation of heat transfer into the mathematical framework. Despite this, recent research, both experimental and computational, has shown evidence that nanofluids have improved heat transfer capabilities in contrast to viscous fluids. Building upon the fundamental contributions made by Dholey [45], the primary objective of this research is to expand the academic examination that he began by incorporating the phenomena of nanofluid flow into the framework of mixed convection within the boundary layer, including the transmission of heat. This will be accomplished by building on the foundation that Dholey [45] has provided. To accomplish this objective, a novel mathematical model for nanofluids is proposed. Moreover, the primary objective of this work is to fill a notable void in the current body of literature, namely in the examination of unsteady, separated stagnation point flow. The present study encompasses an examination of mixed convection phenomena, the influence of heat sources, the impacts of mass suction, and the implications of melting heat. The primary aim of this research is to examine the impact of certain physical factors on the flow and heat transfer characteristics of \({\mathrm{Al}}_{2}{\mathrm{O}}_{3}/{\mathrm{H}}_{2}\mathrm{O}\) nanofluid within the framework of Thompson and Troian’s irregular slip effects. The present study utilizes the Corcione correlation to establish a relationship between the effective dynamic viscosity and thermal conductivity in the context of a moving plate. To fulfill the study goals, the bvp4c scheme provided by the MATLAB package is used. The collected results for a specific example demonstrate a significant congruence between earlier scholarly investigations and the current empirical findings. In general, we argue that there is a need to further investigate unsteady separated stagnation flows and apply mathematical insights to enhance our understanding of their importance in various industrial contexts, such as start-up processes and periodic fluid motion. These endeavors will provide valuable contributions to the continuous progress in enhancing the efficiency, durability, and cost-effectiveness of diverse fluid-dynamic devices, finally resulting in the development of innovative and sophisticated heat transfer technologies.

Description of the problem

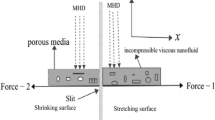
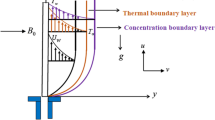
The purpose of this analysis is to investigate the characteristics of an unsteady mixed convective separated stagnation point in a two-dimensional flow. The fluid under consideration is a nanofluid consisting of a mixture of \({\mathrm{Al}}_{2}{\mathrm{O}}_{3}\) nanoparticles and \({\mathrm{H}}_{2}\mathrm{O}\). This concept is exemplified in Fig. 1, whereby the coordinate system utilizes \((x, y)\) as Cartesian coordinates. The x-axis is oriented parallel to the stretching surface, while the y-axis denotes the direction orthogonal to the surface. It is thought that the stretching surface has a velocity shown by \({u}_\text{w}\left(t\right)={u}_{0}(t)\), while the far-field velocity in an inviscid nanofluid flow is shown by \({u}_\text{e}\left(x, t\right)=\alpha \frac{x-{x}_{0}(t)}{{t}_\text{ref}-\beta t}+{u}_{0}(t)\), where \(t\) is the time variable. The temperature at the surface of the sheet, denoted as \({T}_\text{w}\left(x, t\right)\), can be mathematically represented as \({T}_\text{w}\left(x, t\right)={T}_{\infty }+{T}_{0}{\left(x/l\right)}^{2}/{\left(1-\beta t\right)}^{2}\). In this equation, \({T}_{0}\) (which is a positive value) represents the characteristic temperis the time variable. Theature of the sheet, \(l\) represents the characteristic length of the sheet, and \({T}_{\infty }\) represents the temperature of the free stream.

Fig. 1
figure 1

Problem configuration is visually shown

Full size image

The primary premise of this work posits that the stagnation point is reached when the temperature of the plate aligns with the ambient air temperature, denoted as \({T}_\text{w}\left(x, t\right)={T}_{\infty}\). Buoyancy forces in mixed convection fluid flow are generated as a consequence of temperature gradients, leading to differences in fluid density. As a result, the presence of these buoyant forces may result in the development of fluid flow patterns that exhibit asymmetry. The analysis of this work also takes Thompson and Troian’s descriptions of slip’s nonlinear effects into account. Additionally, it is reasonable to assume that the symbol \({T}_\text{m}\) stands for the temperature of the immobile melting surface. This study utilizes a homogeneous fluid consisting solely of a certain sort of nanoparticle, namely alumina (\({\mathrm{Al}}_{2}{\mathrm{O}}_{3}\)). The resulting nanofluid is a composite of \({\mathrm{Al}}_{2}{\mathrm{O}}_{3}\) and \({\mathrm{H}}_{2}\mathrm{O}\), where \({\mathrm{H}}_{2}\mathrm{O}\) acts as the base fluid. In addition, our analysis takes into consideration the impact of heat sources, which have been integrated into the energy equation presented afterward (see Zainal et al. [5]):

$$\frac{\partial u}{\partial \mathrm{x}}+\frac{\partial v}{\partial \mathrm{y}}=0,$$
(1)
$$\frac{\partial u}{\partial \mathrm{t}}+u\frac{\partial u}{\partial \mathrm{x}}+v\frac{\partial u}{\partial \mathrm{y}}=\frac{\partial {u}_\text{e}}{\partial \mathrm{t}}+{u}_\text{e}\frac{{du}_\text{e}}{\mathrm{dx}}+\frac{{\mu }_\text{nf}}{{\rho }_\text{nf}}\left(\frac{{\partial }^{2}u}{\partial {y}^{2}}\right)+\frac{g{\left(\rho \beta \right)}_\text{nf}}{{\rho }_\text{nf}}\left(T-{T}_{\infty }\right)$$
(2)
$$u\frac{\partial \mathrm{T}}{\partial \mathrm{x}}+v\frac{\partial \mathrm{T}}{\partial \mathrm{y}}=\frac{{k}_\text{nf}}{{\left(\rho {C}_\text{p}\right)}_\text{nf}}\left(\frac{{\partial }^{2}T}{\partial {y}^{2}}\right)-\frac{{q}_{0}}{{\left(\rho {C}_\text{p}\right)}_\text{nf}}\left(T-{T}_{\infty }\right).$$
(3)

The slip boundary condition, as formulated by Thompson and Troian (see [41]), is expressed in a generalized form.

$${u}_\text{t}=\beta {\left(1-\gamma {\tau }_\text{w}\right)}^{-1/2}{\tau }_\text{w},$$
(4)

So, the shear stress at the boundary can be shown as a mathematical function that includes the tangential speed (\({u}_\text{t}\)), the inverse of a certain critical rate (\(\gamma\)), the slip length constant from the Navier equation (\(\beta\)), and the shear stress at the wall’s surface (\({\tau }_\text{w}\)).

Consequently, the shear stress within the wall can be characterized as:

$${\tau }_\text{w}={\mu }_\text{nf}{\left(\frac{\partial u}{\partial \mathrm{y}}\right)}_{\text{y} =0}.$$
(5)

The relevant BSBCs of the problem are (see [5, 41]).

$$u = \lambda u_\text{w} + \beta \left( {1 - \gamma \tau_\text{w} } \right)^{ - 1/2} \mu_\text{nf} \left( {\frac{\partial u}{{\partial {\text{y}}}}} \right), v = v_\text{w} , T = T_\text{m} , \rho_\text{nf} \left[ {L + c_\text{s} \left( {T_\text{w} - T_{0} } \right)} \right]v_\text{w} ,\;{\text{at}}\;y = 0,u \to u_\text{e} , T \to T_{\infty } \;{\text{as}}\;y \to \infty$$
(6)

Within the given framework, the symbols \(u\) and \(v\) are utilized to represent the velocity components along the x- and y-axes, respectively. The symbol “\(g\)” denotes the gravitational force, whereas “\({q}_{0}\)” signifies the constant heat source. The velocity of mass transfer at the wall is represented by the symbol \({v}_\text{w}\). A positive value of “\({v}_\text{w}\)” indicates the occurrence of an injection process, while a negative value of “\({v}_\text{w}\)” indicates the occurrence of a suction process. Furthermore, the variable “\(L\)” is used to denote latent heat transmission, while the variable “\({c}_\text{s}\)” represents the heat capacity of the solid surface.

Furthermore, in the present context, there are numerous crucial factors that need to be considered. The variables used in this study are as follows: \({\mu }_\text{nf}\), which represents the dynamic viscosity of the nanofluid; \({\rho }_\text{nf}\), which denotes the density of the nanofluid; \({k}_\text{nf}\), which signifies the thermal conductivity of the nanofluid; \({\left(\rho \beta \right)}_\text{nf}\), representing the thermal expansion of the nanofluid; \({\left(\rho {C}_\text{p}\right)}_\text{nf}\), indicating the heat capacity of the nanofluid; and “\(T\)”, which represents the temperature of the nanofluid. To obtain comprehensive insights into the temperature properties of the conventional fluid comprising \({\mathrm{Al}}_{2}{\mathrm{O}}_{3}\) nanoparticles of interest, we kindly direct your attention to Table 1 for full details.

Table 1 Thermophysical properties of base fluid with nanoparticles (see [25, 46])
Full size table

In this study, we proceed to introduce the suitable similarity factors based on the work of Zainal et al. [5], in the following manner:

$$u=\frac{\alpha \left(x-{x}_{0}(t)\right)}{{t}_\text{ref}-\beta t}{f}{\prime}\left(\eta \right)+{u}_{0}(t), v=-\alpha \sqrt{\frac{{\upsilon }_\text{f}}{{t}_\text{ref}-\beta t}}f\left(\eta \right),$$
$$T={T}_\text{m}+\left({T}_{\infty }-{T}_\text{m}\right)\theta \left(\eta \right), \eta =\frac{y}{{\left[{\upsilon }_\text{f}\left({t}_\text{ref}-\beta t\right)\right]}^{1/2}},$$
(7)

With

$${v}_\text{w}=-\frac{\alpha }{\sqrt{\left({t}_\text{ref}-\beta t\right)}}S,$$
(8)

Within this framework, there exists a fixed value denoted as \(\alpha (>0)\), which is commonly known as the acceleration parameter. The variable \({x}_{0}(t)\) denotes the displacement of the sheet, while \({u}_{0}\left(t\right)=\partial {x}_{0}(t)/\partial t\). The prime symbol is used to indicate differentiation about the variable \(\eta\). Furthermore, the parameter S reflects the continuous mass flux, where \(S>0\) denotes the suction design and \(S<0\) denotes the injection design.

By putting Eq. (7) into Eqs. (2) and (3), a set of ordinary (similarity) differential equations and their related boundary conditions can be derived.

$$\frac{{\mu }_{\text{nf}/{\upmu }_\text{f}}}{{\rho }_\text{nf}/{\rho }_\text{f}}{f}^{{\prime}{\prime}{\prime}}+\alpha f{f}^{{\prime}{\prime}}+\alpha \left(1-{f}^{{\prime}2}\right)-\xi \left({f}{\prime}+\frac{\eta }{2}{f}^{{\prime}{\prime}}-1\right)+\left(\frac{{\left(\rho {\beta }_\text{T}\right)}_\text{nf}/{\left(\rho {\beta }_\text{T}\right)}_\text{f}}{{\rho }_\text{nf}/{\rho }_\text{f}}\right)\delta \theta =0,$$
(9)
$$\frac{1}{Pr}\frac{{k}_\text{nf}/{k}_\text{f}}{{\left(\rho {C}_\text{p}\right)}_\text{nf}/{\left(\rho {C}_\text{p}\right)}_\text{f}}{\theta }^{{\prime}{\prime}}+\left(\alpha f-\xi \frac{\eta }{2}\right){\theta }{\prime}-\Omega \theta =0,$$
(10)
$$\begin{gathered} f\left( 0 \right) = S, f^{\prime}\left( 0 \right) = \lambda + \beta \frac{{\mu_\text{nf} }}{{\mu_\text{f} }}\left( 1 - \gamma \frac{{\mu_\text{nf} }}{{\mu_\text{f} }}f^{\prime\prime}\left( 0 \right)\right)^{ - 1/2} f^{\prime\prime}\left( 0 \right),\frac{{k_\text{nf} /k_\text{f} }}{{\frac{{\rho_\text{nf} }}{{\rho_\text{f} }}}} {\text{Me}}\theta^{\prime}\left( 0 \right) + {\text{Pr}}S = 0, \hfill \\ \quad f^{\prime}\left( \eta \right) \to 1, \theta \left( \eta \right) \to 0,\;{\text{as}}\;\eta \to \infty . \hfill \\ \end{gathered}$$
(11)

Here, \(\mathrm{Pr}=\frac{{\left(\rho {C}_\text{p}\right)}_\text{f}}{{k}_\text{f}}\) is Prandtl number, \(\mathrm{Me}=\frac{{\left({C}_\text{p}\right)}_\text{f}\left({T}_{\infty }-{T}_\text{m}\right)}{L+{c}_\text{s}\left({T}_\text{m}-{T}_{0}\right)}\) is melting parameter, \(S\) is mass suction, \(\beta =a{\mu }_\text{f}\sqrt{\frac{{U}_{0}}{l{\nu }_\text{f}}}\) is velocity slip parameter, \(\delta = {\raise0.7ex\hbox{${{\text{Gr}}}$} \!\mathord{\left/ {\vphantom {{{\text{Gr}}} {{\text{Re}}_{x}^{2} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${{\text{Re}}_\text{x}^{2} }$}}\) indicates the mixed convection parameter where \(\delta >0\) indicates to the assisting flow, \(\delta <0\) represents opposing flow, and \(\delta =0\) indicates pure forced convective flow. Further, \(\mathrm{Gr}=g{\left({\beta }_\text{T}\right)}_\text{f}\left({T}_\text{w}-{T}_{\infty }\right){x}^{3}/{\nu }_{\text{f}^{2}}\) is the Grashof number and \({\mathrm{Re}}_\text{x}=x{u}_\text{e}/{\nu }_\text{f}\) is the local Reynolds number. \(\Omega ={q}_{0}/{a\left(\rho {C}_\text{p}\right)}_\text{f}\) is heat source parameter, and \(\gamma ={\mu }_\text{f}\frac{{U}_{0}b}{l}\sqrt{\frac{{U}_{0}}{l{\nu }_\text{f}}}\) is dimensionless critical shear rate.

This study will primarily examine two prominent physical parameters: the skin friction coefficient, designated as \({C}_\text{f}\), and the local Nusselt number, commonly referred to as \({\mathrm{Nu}}_\text{x}\). Both factors can be precisely delineated in the following manner:

$${C}_\text{fx}=\frac{{\mu }_\text{nf}/{\mu }_\text{f}}{{\rho }_\text{f}{u}_\text{e}^{2}}{\left(\frac{\partial u}{\partial y}\right)}_{\text{y}=0}, {\mathrm{Nu}}_\text{x}=-\frac{x{k}_\text{nf}}{{k}_\text{f}({T}_\text{w}-{T}_{\infty })}{\left(\frac{\partial T}{\partial y}\right)}_{\text{y}=0}.$$
(12)

Hence, using (7) and (12), one obtains

$${\mathrm{Re}}_\text{x}^{1/2}{C}_\text{f}=\frac{{\mu }_\text{nf}}{{\mu }_\text{f}}\frac{1}{{\left[{\upsilon }_\text{f}\left({t}_\text{ref}-\beta t\right)\right]}^{3/2}}\left[{f}^{{\prime}{\prime}}\left(0\right)\right], {\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}=\frac{{k}_\text{nf}}{{k}_\text{f}}\frac{1}{\sqrt{{\upsilon }_\text{f}\left({t}_\text{ref}-\beta t\right)}}\left[-{\theta }{\prime}(0)\right],$$
(13)

where \({Re}_\text{x}={u}_\text{e}/{\nu }_\text{f}\).

Thermal and physical relations for nanofluid

The determination of the thermal conductivity (\({k}_\text{nf}\)) and dynamic viscosity (\({\mu }_\text{nf}\)) of a functional nanoliquid can be achieved by utilizing the Corcione correlation [25], which is expressed as follows:

$$\frac{{k}_\text{nf}}{{k}_\text{f}}=1+4.4{Pr}^{0.66}{\mathrm{Re}}^{0.4}{\left(\frac{T}{{T}_\text{fz}}\right)}^{10}{\left(\frac{{k}_{\text{Al}_{2}{O}_{3}}}{{k}_\text{f}}\right)}^{0.03}{\phi }^{0.66},$$
(14)

A nanoparticle’s Reynolds number can be calculated as:

$$\mathrm{Re}=\frac{{\rho }_\text{f}{u}_\text{B}{d}_\text{p}}{{\mu }_\text{f}},$$
(15)

The term \({u}_\text{B}\), often known as Brownian velocity, may be defined as the ratio of dp to the time interval \({\tau }_\text{D}\) required to traverse the distance [25].

$${\tau }_\text{D}=\frac{{d}_\text{p}^{2}}{6D}=\frac{\pi {\mu }_\text{f}{d}_\text{p}^{3}}{2{K}_\text{b}T},$$
(16)

The formula for Brownian velocity may be stated as follows, taking into consideration the Einstein diffusion coefficient, denoted by \(D\).

$${u}_\text{B}=\frac{2{K}_\text{b}T}{\pi {\mu }_\text{f}{d}_\text{p}^{2}}.$$
(17)

The following relationship about the Reynolds number is obtained by substituting Eq. (17) for Eq. (15):

$$\mathrm{Re}=\frac{2{\rho }_\text{f}{K}_\text{B}T}{{d}_\text{p}\pi {\mu }_\text{f}^{2}}.$$
(18)
$$\frac{{\mu }_\text{nf}}{{\mu }_\text{f}}=\frac{1}{\left(1-34.87{\left(\frac{d\text{p}}{{d}_\text{f}}\right)}^{-0.3}{\phi }^{1.03}\right)},$$
(19)

The density \({\rho }_\text{nf},\) thermal expansion \({\left(\rho {\beta }_\text{T}\right)}_\text{nf}\) and heat capacity \({\left(\rho {C}_\text{p}\right)}_\text{nf}\) of the nanofluids are given as:

$$\frac{{\rho }_\text{nf}}{{\rho }_\text{f}}=\phi \left(\frac{{\rho }_{\text{Al}_{2}{O}_{3}}}{{\rho }_\text{f}}\right)+\left(1-\phi \right),$$
(20)
$${\left(\rho {\beta }_\text{T}\right)}_\text{nf}=\left(1-\phi \right){\left(\rho {\beta }_\text{T}\right)}_\text{f}+\phi {\left(\rho {\beta }_\text{T}\right)}_{\text{Al}_{2}{O}_{3}},$$
(21)
$$\frac{{\left(\rho {C}_\text{p}\right)}_\text{nf}}{{\left(\rho {C}_\text{p}\right)}_\text{f}}=\phi \frac{{\left(\rho {C}_\text{p}\right)}_{{\uprho }_{\text{Al}_{2}{\text{O}}_{3}}}}{{\left(\rho {C}_\text{p}\right)}_\text{f}}+\left(1-\phi \right)$$
(22)

Numerical procedure and code validation

Numerical techniques are used to solve Eqs. (9) and (10), as well as boundary conditions (11), by using the MATLAB tool bvp4c, the finite difference method, and a three-stage Lobatto IIIa formula with a sensitivity of 10−6 (see Zainal et al. [5]). Moreover, the bvp4c technique necessitates the transformation of the issue pertaining to the system of ordinary differential equations into a format of first-order systems to get a solution. To do this, we convert the simplified Eqs. (9) through (10) and their corresponding boundary conditions (11) into a system of first-order differential equations. The conversion of these variables into initial value issues is achieved by the assignment of labels

\({\left(f, {f}{\prime},{f}^{{\prime}{\prime}},\theta , {\theta }{\prime}\right)}^{T}={\left({Z}_{1},{Z}_{1}{\prime}={Z}_{2},{Z}_{2}{\prime}={Z}_{3},{Z}_{4},{Z}_{4}{\prime}={Z}_{5}\right)}^\text{T}.\) In light of the above context, the aforementioned system of equations may be represented in matrix notation in the following manner:

$$\left[ {\begin{array}{*{20}c} {Z_{1}{\prime} } \\ {Z_{2}{\prime} } \\ {Z_{3}{\prime} } \\ {Z_{4}{\prime} } \\ {Z_{5}{\prime} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {Z_{2} } \\ {Z_{3} } \\ { - \frac{{\rho_\text{nf} /\rho_\text{f} }}{{\mu_\text{nf} /\mu_\text{f} }}\left( {\alpha Z_{1} Z_{3} + \alpha \left( {1 - Z_{2}^{2} } \right) - \xi \left( {Z_{2} + \frac{\eta }{2}Z_{3} - 1} \right) + \left( {\frac{{\left( {\rho \beta_\text{T} } \right)_\text{nf} /\left( {\rho \beta_\text{T} } \right)_\text{f} }}{{\rho_\text{nf} /\rho_\text{f} }}} \right)\delta Z_{4} } \right)} \\ {Z_{5} } \\ { - \frac{{Pr\left( {\rho C_{p} } \right)_\text{nf} /\left( {\rho C_\text{p} } \right)_\text{f} }}{{k_\text{nf} /k_\text{f} }}\left( {\left( {\alpha Z_{1} - \xi \frac{\eta }{2}} \right)Z_{5} - {\Omega }Z_{4} } \right)} \\ \end{array} } \right],$$
(23)

Furthermore, the subjects are contingent upon the beginning circumstances.

$$\left[\begin{array}{c}{Z}_{1}\\ {Z}_{2}\\ {Z}_{4}\\ {Z}_{3}\\ {Z}_{5}\end{array}\right]=\left[\begin{array}{c}S\\ \lambda +\beta \frac{{\mu }_\text{nf}}{{\mu }_\text{f}}{\left(1-\gamma \frac{{\mu }_\text{nf}}{{\mu }_\text{f}}{Z}_{3}\right)}^{-1/2}{Z}_{3}\\ -\frac{\frac{{\rho }_\text{nf}}{{\rho }_\text{f}}}{{k}_\text{nf}/{k}_\text{f}Me}PrS\\ 1\\ 0\end{array}\right].$$
(24)

In order to compute a numerical solution for the system of Eqs. (9) and (10) together with the specified boundary conditions (11), we used the bvp4c technique available in the MATLAB software package, as described in the work of Zainal et al. [5]. In order to evaluate the dependability of the findings, a comparative analysis was performed by juxtaposing the obtained results with the data provided in Table 2.

Table 2 Results assessment of \({f}^{{\prime}{\prime}}(0)\) and \(-{\theta }{\prime}(0)\) at \(\phi =\beta =S=\gamma =\delta =\Omega =Me=\xi =0\) and \(\alpha =1.0\) toward \(\lambda\)
Full size table

In the section titled “Results and Discussion,” an analysis is conducted on the influence of several physical factors on the velocity profile \({f}{\prime}(\eta )\), temperature profile \(\theta (\eta )\), skin friction \({\mathrm{Re}}_\text{x}^{1/2}{C}_\text{f}\), and Nusselt number \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\) for assisting flow \(\left(\delta =1.0\right)\) and opposing flow \(\left(\delta =-1.0\right)\).

Results and discussion

The parameters used in the computations are as follows: Non-Newtonian behavior is seen in nanofluids when the volumetric concentration of nanoparticles surpasses 5% to 6%. The present investigation deliberately controlled the volume fraction of alumina nanoparticles within the range of 0.0 to 4% in order to get the desired characteristics, as elucidated in reference [46]. The selected nanoparticle concentration of 4% for this study is regarded as both realistic and of major physical importance. On the other hand, a range of parameters has been chosen by referring to original sources and evaluating the practicality of solutions in the context of the stretching flow such as: \(2.0\le S\le 2.5\) (suction), \(0.0\le \beta \le 0.5\) (velocity ratio parameter), \(0.0\le \gamma \le 1.0\) (critical shear rate parameter), \(0.0\le \lambda \le 1.0\) (stretching parameter), \(0.0\le \mathrm{Me}\le 1.0\) (melting parameter), \(0.0\le \xi \le -1.0\) (unsteadiness parameter), \(0.0\le\Omega \le 1.0\) (heat source) and \(1.0\le \alpha \le 2.0\) (stagnation parameter).

Table 3 presents numerical approximations of wall drag coefficients in the x-direction for various nanoparticle diameter values, namely \({d}_\text{p}\)= 28 nm, 30 nm, and 45 nm, in the presence of both aiding and opposing flow circumstances. The data shown in Table 3 demonstrate that there is a negative correlation between the size of nanoparticles and the wall drag coefficients, indicating that larger nanoparticles result in lower drag coefficients. In addition, augmenting the values of \(\phi\) yields a rise in skin friction, whereas enhancing the values of the velocity slip parameter \(\beta\) produces a contrasting pattern. Moreover, the findings shown in Table 3 demonstrate that the aiding flow scenario displays greater magnitudes in comparison with the opposing flow scenario.

Table 3 Skin friction coefficients are assigned numerical values in relation to certain flow parameters
Full size table

Figure 2A, B displays the impacts of \(\phi =0.01, 0.02, 0.03, 0.04\) which commented as the nanoparticle solid volume fraction and \({d}_\text{p}=45 \mathrm{nm}\) is diameter on the velocity and temperature profiles for assisting \(\left(\delta =1.0\right)\) and opposing \(\left(\delta =-1.0\right)\) flow. The effect that the \(\phi\) has on the velocity profile \({f}{\prime}(\eta )\) is shown in Fig. 2A. The velocity profile of the nanofluid exhibits a decline as the nanoparticle volume fraction increases, owing to the inclusion of nanoparticles inside the fluid medium. As the volume percentage of nanoparticles (\(\phi\)) grows, there is a corresponding increase in the number of nanoparticles that are disseminated throughout the fluid. The presence of nanoparticles may hinder the flow of fluid and provide extra resistance, resulting in a reduction in the total velocity of the stream. The primary reason for the rise in the temperature profile of the nanofluid as the \(\phi\) increases is the augmented thermal conductivity resulting from the nanoparticles’ presence. Nanoparticles often exhibit much greater heat conductivities in comparison with the underlying fluid medium. When the particles are evenly distributed throughout the fluid medium, they exhibit enhanced efficiency in the transmission of thermal energy. Because of this, adding nanofluids makes the heat conduction properties better than the base fluid alone, which leads to higher temperature profiles. The difference between the opposing flow and aiding flow graphs in Fig. 2B could be due to differences in how heat moves between these two flow directions. The presence of opposing flow results in a greater temperature differential and augments heat transfer in comparison with the presence of aiding flow. The observed temperature profiles in counter-current flow demonstrate enhanced heat transfer efficiency, leading to elevated surface temperatures. The impact of this phenomenon may be particularly significant when using nanofluids, owing to their enhanced thermal conductivity. As a result, the increased graphs shown in Fig. 2B may be attributed to the presence of counterflow circumstances.

Fig. 2
figure 2

A, B: Impact of \(\phi =0.01, 0.02, 0.03, 0.04\) on velocity and temperature

Full size image

Figure 3A and B shows the impact of four distinct mass suction values (\(S = 2.1, 2.2, 2.3, 2.4\)) on the velocity \({f}{\prime}(\eta )\) and temperature \(\theta (\eta )\) profiles in the presence of both aiding \(\left(\delta =1.0\right)\) and opposing \(\left(\delta =-1.0\right)\) flow circumstances with \({d}_\text{p}=45 \mathrm{nm}\). The results in Fig. 3A show that there is a strong link between the parameter S and the \({f}{\prime}(\eta )\) profile. This means that when \(S\) goes up, the \({f}{\prime}(\eta )\) profile also goes up proportionally. The observed occurrence may be attributed to the correlation between parameter \(S\) and the extraction of fluid from the boundary layer near the solid surface. The extraction of fluid induces a reduction in the thickness of the boundary layer, hence augmenting the flow characteristics near the surface. Consequently, the fluid’s velocity undergoes augmentation as it approaches the solid surface. In contrast, the temperature profile demonstrates a decrease with an increase in the mass suction parameter, as shown in Fig. 3B, irrespective of whether the flow direction is assisting or opposing. The observed phenomena may be ascribed to the effect of mass suction, which not only affects the velocity of the fluid, but also alters the thermal properties of the flow. The rationale for this is the process of mass suction involves the extraction of fluid from the boundary layer next to the solid surface, including the removal of fluid responsible for heat dissipation from such a surface. When the mass suction rate is increased, a greater volume of fluid is removed from this specific location, leading to a decrease in the quantity of fluid available for heat dissipation. Consequently, a reduction in heat transmission occurs between the surface and the fluid, resulting in decreased temperature profiles.

Fig. 3
figure 3

A, B: Impact of \(S=2.0, 2.1, 2.2, 2.3\) on velocity and temperature

Full size image

The velocity and temperature profiles of the nanofluid under both aiding and opposing flow circumstances are examined in Fig. 4A and B for nanoparticles of \({d}_\text{p}=45 \mathrm{nm}\). The impact of various stagnation parameter values (\(\alpha =0.5, 1.0, 1.5, 2.0)\) on these patterns is seen. Figure 4A demonstrates that the velocity profile exhibits an upward trend as the stagnation parameter values rise. This behavior may be attributed to the fact that the stagnation parameter is directly linked to the flow intensity that impinges on the surface. As the value of the stagnation parameter rises, there is a corresponding increase in the flow velocity at the site of impingement. The elevated impingement velocity contributes to a heightened and swifter flow near the surface, hence causing an augmentation in the velocity profile. In contrast, Fig. 4B demonstrates a reduction in the temperature profile as the stagnation parameter increases. This may be attributed to the heightened flow velocity that accompanies higher stagnation parameters, resulting in an augmented convective heat transfer away from the surface. The fluid exhibits enhanced velocity and efficiency, facilitating a more efficient transfer of heat from the surface. As a result, the surface temperature exhibits a decline due to the increased heat dissipation facilitated by the enhanced fluid flow.

Fig. 4
figure 4

A, B: Impact of \(\alpha =0.5, 1.0, 1.5, 2.0\) on velocity and temperature

Full size image

Figure 5A and B illustrates the dimensionless \({f}{\prime}(\eta )\) and \(\theta (\eta )\) profiles for four distinct values of the unsteadiness parameter, denoted as \(\xi =-0.1, -0.2, -0.3, -0.4\). The profiles provided in this study pertain to the situation of \({d}_\text{p}=45 \mathrm{nm}\), including both aiding and opposing flow circumstances. Negative values of the unsteadiness parameter (\(\xi\)), which indicate a decrease in flow velocity over time, signify decelerating flow. The observed behavior of the velocity and temperature profiles with decreasing values of \(\xi\) in both aiding and opposing flows may be attributed to the following reasons: When the value of the unsteadiness parameter \(\xi\) decreases (i.e., indicating a more pronounced deceleration of flow), it signifies that the rate of decrease in flow velocity is becoming more rapid. In the context of decelerating flows, the reduction in momentum leads to a decline in the velocity profile, resulting in lower velocities. The decrease in flow velocity near the surface leads to the formation of a velocity profile with lower values. Conversely, when the velocity diminishes as a result of deceleration, a longer duration is afforded for the fluid to engage with the solid surface. The extended duration of engagement facilitates enhanced heat transfer from the surface to the fluid, resulting in an elevation of the temperature profile.

Fig. 5
figure 5

A, B: Impact of \(\xi =-0.1, -0.2, -0.3, -0.4\) on velocity and temperature

Full size image

Figure 6A depicts the impact of several velocity slip parameters, namely \(\beta =0.05, 0.1, 0.15, 0.2\) on the velocity profile \({f}{\prime}(\eta )\) under aiding and opposing flow circumstances. The nanoparticles considered in this study have a diameter of \({d}_\text{p}=45 \mathrm{nm}\). The observation may be made that augmenting the value of \(\beta\) results in a notable enhancement in the velocity profile \({f}{\prime}(\eta )\) at a quick rate. This phenomenon occurs due to the existence of velocity slip, which causes the fluid’s velocity to exceed that of the stretched surface. As a result, the disparity in velocities leads to an increase in the velocity of the nanofluid. The observed phenomenon may be attributed to the slip condition, which results in the stretched surface exhibiting a higher rate of movement compared to a scenario where slip is not present. The graph in Fig. 6B shows how different estimates of the critical shear rate parameter change the nanofluid’s velocity profile \({f}{\prime}(\eta )\) when there is both helping and opposing flow. These flow conditions are shown to have a combined effect on the profile. The nanofluid that was investigated for this discovery has nanoparticles with a diameter of 45 nm on average. As the critical shear rate parameter rises, one may see an increase in the velocity profile for both scenarios in which the flow is helping and those in which it is hindering. This phenomenon might be explained by the fact that the critical shear rate parameter acts as a signal of the threshold shear rate at which the nanofluid’s viscosity starts to demonstrate a significant decline in its properties. When the value of this parameter is raised, it shows that the nanofluid displays a sustained viscosity at decreasing shear rates. As a consequence, the nanofluid’s viscosity decreases, even when the flow conditions are slow. An increase in the velocity profile is produced as a consequence of this occurrence. The nanofluid displays a reduction in viscosity at lower shear rates as the value of the critical shear rate parameter increases. This indicates that there is a decrease in the amount of internal resistance that is met during flow, even in situations in which the fluid velocity is quite modest.

Fig. 6
figure 6

A: Impact of \(\beta =0.1, 0.2, 0.3, 0.4\) on velocity. B: Impact of \(\gamma =0.1, 0.2, 0.3, 0.4\) on velocity

Full size image

Figure 7A depicts the effect that the melting parameter, \(\mathrm{Me}\), has on the \(\theta (\eta )\) profile of nanoparticles with a diameter of \({d}_\text{p}=45 \mathrm{nm}\) when the flow direction is either assisting or opposing. Significantly, when the \(\mathrm{Me}\) grows to greater magnitudes, there is a discernible decrease in temperature. The drop in temperature may be attributed to the reduction in frictional forces resulting from the melting process. This reduction in frictional forces leads to a decrease in heat flow, preventing the separation of the boundary layer. As a consequence, an increase in the value of \(\mathrm{Me}\) yields thinner thermal boundary layers, resulting in reduced temperatures inside the boundary layer. The temperature profile of the nanofluid is examined in Fig. 7B, considering different values of the heat source parameters (Ω = 0.2, 0.4, 0.6, 0.8). The nanoparticle diameter (\({d}_\text{p}\)) is set at 45 nm for both aiding and opposing flow circumstances. The temperature profile exhibits an adverse relationship with the heat source parameter since higher values of the heat source parameter indicate a greater influx of thermal energy into the system. This phenomenon results in a reduction in the temperature profile. An increased temperature gradient and enhanced heat dissipation lead to a reduced surface temperature. The drop in the temperature profile may be attributed to the heat source parameter, which results in a more effective cooling of the surface via greater heat convection.

Fig. 7
figure 7

A: Impact of \(Me=0.1, 0.2, 0.3, 0.4, 0.5\) on temperature. B: Impact of \(\Omega =0.1, 0.2, 0.3, 0.4,\) on temperature

Full size image

The fluctuations in skin friction coefficient (\({\mathrm{Re}}_\text{x}^{1/2}{C}_\text{f}\)) and local Nusselt number (\({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\)) for various nanoparticle sizes (\({d}_\text{p}\) = 28 nm, 30 nm, and 45 nm) throughout a range of nanoparticle volume fractions (\(\phi = 0.005, 0.01, 0.02, 0.03, 0.04\)) with stretching \(\lambda\) in an alumina/water nanofluid are shown in Fig. 8A–D. The data also illustrate the impact of the direction of flow, whether it is in the form of assisting or opposing. The skin friction coefficient (\({\mathrm{Re}}_\text{x}^{1/2}{C}_\text{f}\)) for nanofluid, as shown in Fig. 8A and B for assisting and opposing flow, respectively, goes up as the volume fraction of nanoparticles close to a stretched surface goes up. This is because nanoparticles are in the fluid. The occurrence of this phenomenon may be attributed to the following factors: As the volume fraction (\(\phi\)) of nanoparticles rises, a greater number of nanoparticles are spread throughout the nanofluid. The nanoparticles induce changes in the rheological characteristics of the fluid, resulting in an increase in viscosity. The inclusion of nanoparticles in a nanofluid results in a rise in its viscosity. An elevated viscosity level leads to heightened flow resistance, thus resulting in an augmentation of skin friction along the surface. When contemplating the facilitation of flow in a parallel direction to the stretching surface, it is often seen that the flow velocity is elevated near the surface as a result of the stretching phenomenon. Consequently, the heightened skin friction is more evident in this situation. In general, it can be observed that both assisting and opposing flows exhibit an elevation in skin friction as the volume fractions of nanoparticles increase. However, it is important to note that the assisting flow has a more noticeable increase in skin friction. This is because of things like higher local speeds and the possibility of turbulent flow, which we have already talked about. In the present study, the response of the \({Re}_\text{x}^{-1/2}{Nu}_\text{x}\) to changes in nanoparticle volume fraction under different flow circumstances is shown in Fig. 8C and D. These figures specifically demonstrate the impact of stretching on the fluid in both aiding and opposing flow scenarios. The increase in Nusselt number profiles seen in both helping and opposing flow configurations, which is marked by higher nanoparticle volume fractions close to a stretched surface, can be explained by looking at a lot of different factors. In general, nanoparticles have a greater degree of heat conductivity as compared to the underlying fluid medium. The enhancement of the nanofluid’s total thermal conductivity is seen with an increase in the volume percentage of nanoparticles. This improvement enables the flow of heat from the surface to the fluid, resulting in increased \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\). In addition, the inclusion of nanoparticles has the potential to induce a decrease in the thickness of the thermal boundary layer near the surface. A reduction in the thickness of the boundary layer facilitates enhanced heat transfer rates, resulting in elevated \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\). In the context of flow assistance, when the direction of flow aligns parallel to the stretched surface, there is enhanced fluid circulation near the surface. This phenomenon facilitates more effective heat transfer processes. This statement is especially true in cases where the volume proportion of nanoparticles is elevated. In the case of opposing flow, despite the flow direction being counter to the stretched surface, the enhanced thermal conductivity of the nanofluid continues to facilitate the dissipation of heat from the surface, leading to an augmentation in \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\).

Fig. 8
figure 8

A, B: Impact of \(\phi =0.05, 0.01, 0.2, 0.3, 0.4\) and \(\lambda\) against Skin friction, C, D: Impact of \(\phi =0.05, 0.01, 0.2, 0.3, 0.4\) and \(\lambda\) against Nusselt number

Full size image

Figure 9A–D illustrates the impact of different suction rates (\(S = 2.0, 2.1, 2.2, 2.3, 2.4\)) administered to a stretched surface on the profiles of skin friction and \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\) under both aiding and opposing flow circumstances for various nanoparticle sizes (\({d}_\text{p}\) = 28 nm, 30 nm, and 45 nm). The phenomenon of increased skin friction in Fig. 9A and B resulting from larger amounts of mass suction applied to a stretched surface in both aiding and opposing flow scenarios may be attributed to the following factors: The phenomenon of mass suction, sometimes referred to as mass transfer or blowing/suction, induces modifications to the velocity distribution in the vicinity of the surface. When a positive value of \(S\) is applied, suction has the effect of increasing the fluid velocity inside the boundary layer. The augmentation of the velocity gradient in proximity to the surface results in an elevation of skin friction as a consequence of the intensified exchange of momentum between the fluid and the solid surface. Moreover, the phenomenon of mass suction tends to attenuate the boundary layer, hence diminishing its thickness. A reduction in the thickness of the boundary layer necessitates a greater velocity gradient to maintain a consistent flow rate, thereby leading to an elevation in skin friction. The observed augmentation of \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\) profiles in Fig. 9C and D because of elevated mass suction values (positive \(S\) values) implemented on a stretched surface may be attributed to many sources. The phenomenon of mass suction induces changes in the dynamics of the boundary layer in the vicinity of the surface undergoing stretching. The application of suction results in an augmentation in fluid velocity and a reduction in the thickness of the thermal boundary layer. Therefore, there is an increase in the effectiveness of heat transmission from the surface to the fluid, resulting in elevated \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\). Analogous to its impact on skin friction, the application of mass suction has the potential to reduce the thickness of the thermal boundary layer. A reduction in the thickness of the boundary layer facilitates an accelerated rate of heat transmission, resulting in elevated \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\).

Fig. 9
figure 9

A, B: Impact of \(S=2.1, 2.2, 2.3, 2.4, 2.5\) with \(\lambda\) on skin friction, C, D: Impact of \(S=2.1, 2.2, 2.3, 2.4, 2.5\) with \(\lambda\) on Nusselt number

Full size image

Figure 10A–D illustrates the impact of different stagnation parameter \(\alpha =0.5, 1.0, 1.5, 2.0\) values on the profiles of skin friction and \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\) for both aiding and opposing flows over a stretched surface. The presented profiles pertain only to nanoparticles with diameters of 28 nm, 30 nm, and 45 nm. The contrasting patterns seen in the skin friction as a function of the stagnation parameter for aiding and opposing flows in Fig. 10A and B mostly arise from variations in the thickness of the boundary layer and the velocity of the flow near the stretched surface. When aiding flow, the reduction in skin friction is attributed to the presence of a smaller boundary layer and a rise in flow velocity. Conversely, in the case of opposing flow, the increase in skin friction may be attributed to a thicker boundary layer and a higher flow velocity. The thermal efficiency trend shown in Fig. 10C and D follows a clear and methodical pattern. The \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\) gets bigger as the parameter α increases in the nanofluid, which happens for both helping and opposing flow. The findings presented in this study provide strong evidence supporting the notion that increasing the intensity of the stagnation flow within the system results in enhanced efficiency of heat transfer. Moreover, an additional facet of this investigation explores the influence of integrating the unsteadiness attribute represented as \(\xi\) into the nanofluid.

Fig. 10
figure 10

A, B: Impact of \(\alpha =0.5, 1.0, 1.5, 2.0, 2.5\) and \(\lambda\) on Skin friction. C, D: Impact of \(\alpha =0.5, 1.0, 1.5, 2.0, 2.5\) and \(\lambda\) on Nusselt number

Full size image

Figure 11A–D depicts the impact of the unsteadiness parameter \(\xi\), especially decelerating flow \((\xi =-0.1, -0.2, -0.3, -0.4)\), when combined with a stretching surface, on the profiles of skin friction and \({Re}_\text{x}^{-1/2}{Nu}_\text{x}\). These profiles are examined for both aiding and opposing flow situations for nanoparticles of size \({d}_\text{p}\)= 28 nm, 30 nm, and 45 nm. The observed patterns of skin friction in relation to different values of the unsteadiness parameter for both aiding and opposing flow in Fig. 11A and B may be elucidated in the following manner: When considering flow assistance, especially in cases where the flow direction aligns parallel to the stretched surface, it has been shown that the skin friction decreases as the unsteadiness parameter varies. Lower values of the unsteadiness parameter indicate a decrease in flow velocity, which causes the thickness of the boundary layer next to the surface to increase. The presence of a thicker boundary layer results in a reduction of the velocity gradient near the surface. Consequently, this reduction in velocity gradient leads to a drop in skin friction owing to a decrease in the transfer of momentum between the fluid and the surface. When there is opposing flow, the flow is going in the opposite direction of the stretched surface. This makes the skin friction rise as the unsteadiness parameter changes. When the deceleration of the flow occurs, it leads to an augmentation of the flow in proximity to the surface, causing a reduction in the thickness of the boundary layer. The reduction in thickness of the boundary layer results in an amplified velocity gradient near the surface, hence causing an elevation in skin friction owing to enhanced momentum exchange between the fluid and the surface. The \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\) patterns in Fig. 11C and D, on the other hand, correspond to different values of the unsteadiness parameter for helping and opposing flow, and can be explained in the following way: When looking at flow assistance, especially when the flow direction is parallel to the stretched surface, the \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\) tends to go up as the unsteadiness parameter changes. The decelerating flow also tends to diminish the total flow velocity, providing more time for heat transfer and leading to a rise in the \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\). In the case of opposing flow, when the flow direction is counter to the stretched surface, it is observed that the \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\) tends to grow with varying values of the unsteadiness parameter. When there is a decrease in flow velocity, it leads to an increase in flow intensity near the surface, which therefore causes a reduction in the thickness of the thermal boundary layer. The reduction in thickness of the boundary layer results in an amplified temperature gradient at the surface, hence causing an augmentation in heat transfer and a rise in \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\).

Fig. 11
figure 11

A, B: Impact of \(\xi =- 0.1, - 0.2, - 0.3, - 0.4, - 0.5\) and \(\lambda\) on Skin friction. C, D: Impacts of \(\xi =-0.1, -0.2, -0.3, -0.4, -0.5\) and \(\lambda\) on Nusselt number

Full size image

Figure 12A and B illustrates the impact of the velocity slip parameter on both favorable and unfavorable flow scenarios over a stretched surface for nanoparticles with diameters of \({d}_\text{p}\)= 28 nm, 30 nm, and 45 nm. The phenomenon of reduced skin friction in Fig. 12A when the velocity slip parameter increases in the context of helping flow may be elucidated as follows: a greater slip parameter velocity signifies a more pronounced slip phenomenon occurring at the solid surface, where the fluid’s velocity is heightened in comparison with the absence of slip. The drop in relative velocity between the fluid and the surface results in a reduction in shear stress at the surface, subsequently causing a decrease in skin friction. In contrast, the observed phenomenon in Fig. 12B, where skin friction exhibits a dual behavior when the velocity slip parameter increases in opposing flow, may be attributed to the intricate interplay of factors such as boundary layer thickness, shear stress, and flow separation effects. At first, the presence of a thicker boundary layer results in a decrease in skin friction due to certain factors. However, after a certain threshold is surpassed, the detrimental consequences become more prominent, resulting in an escalation of skin friction.

Fig. 12
figure 12

A, B: Impact of \(\beta =0.05, 0.1, 0.15, 0.2, 0.25\) toward \(\lambda\) on skin friction

Full size image

Figure 13A–D depicts the impact of the melting heat and heat source parameter on the profiles of the \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\) for both aiding and opposing flow scenarios over a stretched surface. These figures specifically pertain to nanoparticles with diameters of 28 nm, 30 nm, and 45 nm. In Fig. 13A and B, Nusselt number decreases with increasing values of melting heat parameter. In the heat transfer process, the latent heat of fusion plays a bigger role as the melting heat parameter (\(\mathrm{Me}\)) value rises. This contrasts with the effects of thermal conductivity and temperature difference. This suggests that a greater part of the heat transmission is attributed to the process of phase transition, namely melting, rather than conduction occurring inside the material. As a result, it is seen that the \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\) tends to drop with an increase in the \(Me\), owing to the diminishing influence of conductive heat transmission. In Fig. 13C and D, it can be observed that as the heat source parameter increases in stretching flows, both assisting and opposing, there is an increase in the temperature gradient near the solid surface. This increase in temperature gradient has a detrimental effect on the velocity gradient of the fluid, resulting in a decrease in the convective heat transfer coefficient. Consequently, this decrease in the convective heat transfer coefficient leads to a decrease in the \({\mathrm{Re}}_\text{x}^{-1/2}{\mathrm{Nu}}_\text{x}\) profiles. The observed behavior may be attributed to the intricate interaction between heat transfer and fluid movement inside these systems.

Fig. 13
figure 13

A, B: Impact of \(\mathrm{Me}=0.1, 0.2, 0.3, 0.4, 0.5\) and \(\lambda\) on Nusselt number. C, D: Impact of \(\Omega =0.1, 0.3, 0.5, 0.7, 0.9\) and \(\lambda\) on Nusselt number

Full size image

Conclusions

The present study validates the numerical evaluation of the unstable boundary layer in a separated stagnation point flow, including the effects of mass suction and heat source on both aiding and opposing flow conditions. In addition to the aforementioned factors, the study also considered mass suction, the influence of heat sources, the heat required for melting, as well as the Thomson and Torian slip conditions. A unique mathematical model, which is based on the Corcione correlation, was proposed to simulate the behavior of nanofluids. The research investigated the effects of several control variables on the system. Significantly, the incorporation of a nanoparticle volume fraction concentration was shown to be a successful approach in augmenting heat transfer rates in this study. Nevertheless, it is important to acknowledge that the introduction of the heat source had a similar impact, resulting in a drop in the distribution of temperature profiles and a sudden decline in the rate of heat transfer. The subsequent list delineates the foremost ramifications and outcomes ascribed to the matter:

  • Increasing the Thomson and Troian slip parameters leads to an amplification of the amplitude of the velocity distribution for both flows that assist and oppose.

  • The velocity profiles for both aiding and opposing flows demonstrate an upward trend as the values of suction (\(S\)) and stagnation parameter (\(\alpha\)) rise, but they show a downward trend in response to increased nanoparticle volume fraction (\(\phi\)) and unsteadiness parameter (\(\xi\)).

  • The temperature profile exhibits an increase when manipulating the parameters \(\phi\) and \(\xi\); however, it experiences a reduction when altering the values of \(S, \alpha , \Omega\), and \(\mathrm{Me}\).

  • The skin friction coefficient lowers when the flow is assisted, and this effect is influenced by variations in the unsteadiness parameter. Conversely, the skin friction coefficient rises when the flow is opposed.

  • An augmentation in the particle size of the nanoparticle, denoted as \({d}_\text{p}\), induces an expansion of the skin friction coefficients and concurrently leads to a reduction in the Nusselt number.

Further investigations that build upon the present findings may delve into other models for nanofluids. These models might include factors such as aggregation, effective Prandtl numbers, the influence of particle morphologies, and the Yamada-Ota model. Furthermore, several mathematical analysis approaches, such as Lie-group analysis or entropy generation analysis, show potential for future exploration.