Introduction

The phenomenon that the liquid gravity predominated in natural convection and gradually dissipated in microgravity conditions was found by Marangoni in the middle of the 1860s. Surface tension has an important impact on the gradient of surface tension at the liquid interface. The study of mass and heat transfer in this marvel has garnered a lot of interest due to its numerous uses in the fields of nanotechnology, welding processes, silicon wafers, atomic reactors, thin film stretching, soap films, melting, semiconductor processing, crystal growth, and materials sciences. The solute Marangoni effect (EMS) and the thermal Marangoni effect (EMT) are the two classes into which the Marangoni effects are categorized. The thermal imbalance of the interfacial region, which is primarily based on the temperature gradient and heat source, is that leads to EMT. EMS is caused by the imbalance of the interfacial adsorption, which is due to chemical reactions and the concentration gradient. The modeling of the Marangoni effect was inspired by Pearson [1]. The deposition of thermophoretic particles in Carreau–Yasuda fluid across a chemically reactive Riga plate was studied by Abbas et al. [2]. The Marangoni convection boundary layer flow of a nanofluid is examined by Mat et al. [3]. The Marangoni convection flow and heat transmission properties of water-CNT nanofluid droplets were explored by Al-Sharafi et al. [4]. The pattern of generation of microorganism suspensions, such as bacteria and algae, can be interpreted as bioconvection. The occurrence of these self-moving, motile microbes raises the density of the primary fluid. There are wide range of uses of bioconvection, including organic applications and microsystems, the pharmaceutical industry, biopolymer manufacturing, economical energy sources, microbial progressed oil recovery, biotechnology and biosensor. Khan et al. [5] examined the numerical modeling and analysis of bioconvection on MHD flow due to an upper paraboloid surface of revolution. Chu et al. [6] investigated the study of nanofluid flow over a stretching disks in the presence of gyrotactic microorganisms. For further details, consider [7,8,9,10]. The concept "Arrhenius activation" was first used by Svante Arrhenius in 1889. When potential reactants are present in a chemical system, the least amount of energy is needed to initiate a reaction. The activation energy causes the atoms to move swiftly, which causes a reaction. The idea of activation energy is crucial in the field of chemistry. Many chemically reactive systems, including oil reservoirs and geothermal engineering, exhibit Arrhenius activation energy. A hybrid nanofluid MHD flow and heat transmission over a rotating disk were investigated by Reddy et al. [11] by taking Arrhenius energy into account. The effects of the binary chemical reaction and Arrhenius activation energy on the nanofluid flow were examined by Khan et al. [12].

Non-Newtonian fluids have an extensive range of industrial and technological uses, which causes an increase in researcher’s interest. A number of models of non-Newtonian fluids have been put out in light of their deviations from Newtonian fluids. The most prevalent and fundamental model of non-Newtonian fluids is the Jeffrey fluid, which has a time derivative rather than a general derivative, and provides the best explanation of rheological viscoelastic fluids. Jeffrey fluid is more desirable in the polymer industry due to its linear viscoelastic behavior. Due to its viscoelastic properties, Jeffrey fluid is known to play a significant impact in blood flow and fluid mechanics. Being a considerable generalization of a Newtonian fluid, Jeffrey fluid can be obtained as a special case of Newtonian fluid. Hussain et al. [13] addressed the impacts of the thermal relaxation, double stratification and heat source on Jeffrey fluids flow. The heat transfer phenomena for the Jeffrey fluid flow along a stretched curved surface was solved by Ijaz Khan and Alzahrani [14] by using the shooting approach in the presence of activation energy and entropy minimization. Nanoparticles having sizes between 1 and 100 nm are suspended in a base fluid to develop nanofluids. Nanoparticles continue to have an impact in the varying physical properties of base liquids, such as thermal conductivity, density, electrical conductivity and viscosity. The impact of exponentially varying viscosity and permeability on the Blasius flow of Carreau nanofluid over an electromagnetic plate via a porous media was examined by Hakeem et al. [15]. The effects of nonlinear radiation on magnetic and non-magnetic nanoparticles with various base fluids were studied by Saranya et al. [16] over a flat plate. The flow of nanofluids and its industrial and nuclear applications have attracted the attention of many researchers [17,18,19,20,21,22,23]. In comparison with base liquids and other nanofluids, hybrid nanofluids have a higher thermal conductivity. Hybrid nanofluids have dissimilar applications when compared to nanofluids. By combining two different kinds of nanoparticles with the base liquid, hybrid nanofluids are produced. The numerical simulation of surface tension flow of hybrid nanofluid over an infinite disk with thermophoresis particle deposition was investigated by Abbas et al. [24]. Acharya [25] investigated the magnetized hybrid nanofluid flow and associated thermal boundary conditions within a cube equipped with a circular cylinder. The flow of hybrid nanofluids and its applications have attracted the attention of numerous researchers [26,27,28,29]. Figures 1 and 2 show the applications of nanofluids and hybrid nanofluid respectively. Figure 3 displays the manufacturing process for nanofluids and hybrid nanofluids.

Fig. 1
figure 1

Applications of nanofluids

Full size image
Fig. 2
figure 2

Applications of hybrid nanofluids

Full size image
Fig. 3
figure 3

Manufacturing procedure for nanofluids and hybrid nanofluids

Full size image

The Dufour effect is the term given to the heat transfer induced by a concentration gradient as compared to the Soret effect, which is the term given to the mass transfer caused by temperature gradient. For isotope separation and in a combination of gases with light and medium molecular mass, the Soret effect is used. The impact of Dufour and Soret on mass and heat transmission was examined by Postelnicu [30]. The effects of Dufour and Soret on mixed convection in a non-Darcy porous media saturated with micro-polar fluid were studied by Srinivasacharya and Reddy [31]. As a result, [32,33,34,35] show an exploration of this topic from several physical aspects. The Riga plate is a collection of alternating electrodes as well as permanent magnets that are mounted on a flat surface to guarantee efficient flow within the electromagnetic motor. Riga is a spanwise-replaced permanent magnetization device that is operated by electromagnetics. The Riga plate design generates a Lorentz force that reduces exponentially, which causes the flow to go through the plate. It is the Riga plate that is a great device to stop the separation of the boundary layer and reduce the amount of turbulence. It creates the crossing of electric and magnetic fields which are fixed to an even surface. The non-uniform heat source effects on the 3-D flow of nanoparticles with various base fluids past a Riga plate are examined by Ragupathi et al. [36]. For further details, consider [37,38,39,40,41,42].

The analysis of above literature reveals that none of the studies has been conducted yet to explore the effect of thermo-solutal Marangoni convection on dusty Jeffrey hybrid nanofluid flow across a Riga plate with gyrotactic microorganisms. The present investigation is an extension of Mamatha et al. [43] and fills this gap. The effects of a magnetic field, viscous dissipation, a non-uniform heat source and activation energy are also investigated. Combining \({\text{Fe}}_3 {\text{O}}_4\) and \({\text{Cu}}\) particles with an ethylene glycol \(({\text{C}}_2 {\text{H}}_6 {\text{O}}_2 )\) base fluid is claimed to develop the characteristics of the hybrid nanofluid. Using RKF-45th method, numerical solution is assembled. The purposes of the analysis are as follows:

  • The goal of this research is to ascertain how thermo-solutal Marangoni convection affects the temperature, microbe, flow, and concentration profiles of the dusty Jeffrey hybrid nanofluid.

  • To determine how the thermal boundary layer of Jeffrey hybrid nanofluid and dust particles is impacted by the heat generation/absorption.

  • Examine the impact of the activation energy parameter on the dust and fluid phase concentration profiles.

  • The purpose of this examination is to explore the impacts of Dufour and Soret on the thermal and concentration boundary layer flow of dusty hybrid nanofluid.

Mathematical formulation

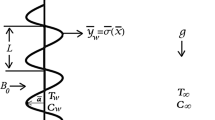
The thermo-solutal Marangoni convective flow of a dusty Jeffrey hybrid nanofluid including microorganisms across a Riga plate has been taken into consideration. The geometric profile of the current model is shown in Fig. 4. The effects of Soret and Dufour have been observed extensively. The present model is described as: (i) Variable thermal conductivity is assumed. (ii) The study is conducted with mixed convection and activation energy. (iii) \(B_0\) is a constant magnetic field that is applied along the \(y -\) axis. (iv) We assume non-uniform heat generation/absorption and viscous dissipation. (v) Dust and nanoparticles, which are spherical in shape, are deliberated to be evenly distributed throughout the fluid. (vi) Thermal properties and correlations of \({\text{Fe}}_3 {\text{O}}_4\) and \({\text{Fe}}_3 {\text{O}}_4 + {\text{Cu}}\) in \({\text{C}}_2 {\text{H}}_6 {\text{O}}_2\). (vii) The dusty fluid moves at a similar velocity as the movable microorganisms. Figures 5 and 6 express the applications chart of \({\text{Cu}}\) and \({\text{Fe}}_3 {\text{O}}_4\) nanoparticles, respectively.

Fig. 4
figure 4

Flow description

Full size image
Fig. 5
figure 5

Applications of Cu nanoparticles

Full size image
Fig. 6
figure 6

Applications of Fe3O4 nanoparticles

Full size image

Riga plate

According to Abbas et al. [2], the Lorentz force \(F\) of the Riga plate is as follows:

$$F = \frac{M_0 J_0 \pi }{8}\exp \left[ { - y\frac{\pi }{p}} \right].$$
(1)

Heat source

In the current model, the term \(q^{{\prime} {\prime} {\prime} }\) is described as a heat source/sink (Obalalu et al. [44]):

$$q^{{\prime} {\prime} {\prime} } = \frac{{K_{{\text{hnf}}} (T)\rho_{{\text{hnf}}} U_0 }}{{2\mu_{{\text{hnf}}} X}}\left[ {A^{*} T_{0 } X^2 f^{\prime} + B^{*} \left( {T - T_\infty } \right)} \right].$$
(2)

Thermal conductivity

The following concept applies to the thermal conductivity (Obalalu et al. [44]):

$$K^* (T) = k_{{\text{hnf}}} \left[ {1 + \varepsilon \left( {\frac{T - T_\infty }{{T_{0 } X^2 }}} \right)} \right]$$
(3)

Marangoni convection

The surface tension \(\sigma_1 = \sigma_0 \left[ {1 - \gamma_{\text{T}} \left( {T - T_\infty } \right) - \gamma_{\text{C}} \left( {C - C_\infty } \right)} \right]\) is supposed to be dependent on linear alternation with solutal and thermal boundaries (see Abbas et al. [2]). Where the surface tension coefficients for concentration \(\gamma_{\text{C}} = - \left. {\frac{\partial \sigma_1 }{{\partial C}}} \right|_{\text{T}}\) and temperature is \(\gamma_{\text{T}} = - \left. {\frac{\partial \sigma_1 }{{\partial T}}} \right|_{\text{C}}\).

Model equations

The constitutive equations of microorganisms, momentum, continuity, concentration and energy for the analysis of the current flow in the fluid phase (Phase-I) and dust phase (Phase-II) are as follows (see Mamatha et al. [43], Gorla [44]):

Fluid phase

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} = 0,$$
(4)
$$\begin{aligned} \rho _{{\text{hnf}}} \left( {~u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}}~} \right) = & \frac{{\mu _{{\text{hnf}}} }}{{1 + \lambda _2 }}\left\{ {\frac{{\partial ^2 u}}{{\partial y^2 }} + \lambda _1 \left( {u\frac{{\partial ^2 u}}{{\partial x\partial y}} - \frac{{\partial u}}{{\partial x}}\frac{{\partial ^2 u}}{{\partial y^2 }} + \frac{{\partial u}}{{\partial y}}\frac{{\partial ^2 u}}{{\partial x\partial y}} + v\frac{{\partial ^2 u}}{{\partial y^2 }}} \right)} \right\}~~ \\ & \quad + KN\left( {u_{\text{p}} - u} \right) - \sigma _{{\text{hnf}}} B_0^2 u + \frac{{\pi j_0 M_0 \exp \left( { - \frac{\pi }{p}y} \right)}}{8} \\ & \quad + g(\rho \beta ^* )_{{\text{hnf}}} \left( {\left( {1 - C_\infty } \right)\left( {T - T_\infty } \right) - \left( {\rho _{\text{p}} - \rho _{\text{f}} } \right)\left( {C - C_\infty } \right) - (\rho _{\text{p}} - \rho _{\text{f}} )\left( {N - N_\infty } \right)} \right), \\ \end{aligned}$$
(5)
$$\begin{aligned} \left( {\rho c_{\text{p}} } \right)_{{\text{hnf}}} \left( {u\frac{{\partial T}}{{\partial x}} + v\frac{{\partial T}}{{\partial y}}} \right) = & \frac{\partial }{{\partial y}}\left( {K^* \left( T \right)\frac{{\partial T}}{{\partial {\text{y}}}}~} \right) + \frac{{16\sigma ^{\text{*}} T_\infty ^3 }}{{3k^{\text{*}} }}\frac{{\partial ^2 T}}{{\partial y^2 }}~ \\ & + \frac{{\rho _{\text{p}C_{\text{m}} } }}{{\tau _{\text{t}} }}\left( {T_{\text{P}} - T} \right) \\ & + \frac{{\rho _{\text{p}} }}{{\tau _{\text{v}} }}\left( {u_{\text{p}} - u} \right)^2 + \left( {\frac{{\rho ~D_{\text{m}} k_{\text{T}} }}{{C_{\text{s}} }}} \right)\frac{{\partial ^2 C}}{{\partial y^2 }} + q^{{\prime} {\prime} {\prime} } \\ & + ~\frac{{\mu _{{\text{hnf}}} }}{{\left( {1 + \lambda _2 } \right)}}\left\{ {\left( {\frac{{\partial u}}{{\partial y}}} \right)^2 + \lambda _1 \left( {u~\frac{{\partial u}}{{\partial y}}~\frac{{\partial ^2 u}}{{\partial y\partial x}} + v~\frac{{\partial u}}{{\partial y}}~\frac{{\partial ^2 u}}{{\partial y^2 }}} \right)} \right\}, \\ \end{aligned}$$
(6)
$$\begin{aligned} u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} = & D_{\text{m}} \frac{\partial^2 C}{{\partial y^2 }} + \frac{{\rho_{\text{p}} }}{{\rho \tau_{\text{C}} }}\left( {C_{\text{p}} - C} \right) \\ & + \frac{{D_{\text{m}} k_{\text{T}} }}{{T_{\text{m}} }}\frac{\partial^2 T}{{\partial y^2 }} - k_{\text{r}}^2 \left( {C - C_\infty } \right){ }\left( {\frac{T}{T_\infty }} \right)^{\text m} \exp \left( {\frac{{ - E_{\text{a}} }}{{k^{\prime} T}}} \right), \\ \end{aligned}$$
(7)
$$u\frac{\partial N}{{\partial x}} + v\frac{\partial N}{{\partial y}} = D_{\text{n}} \frac{\partial^2 N}{{\partial y^2 }} - \frac{{bW_{\text{c}} }}{{\left( {C_{\text{w}} - C_\infty } \right)}}\left[ {\frac{\partial N}{{\partial y}}\frac{\partial C}{{\partial y}} + N\frac{\partial^2 C}{{\partial y^2 }}} \right] + \frac{{\rho_{\text{p}} }}{{\rho \tau_{\text{m}} }}\left( {N_{\text{p}} - N} \right),$$
(8)

Dust phase

$$\frac{{\partial u_{\text{p}} }}{\partial x} + \frac{{\partial v_{\text{p}} }}{\partial y} = 0,$$
(9)
$$u_{\text{p}} \frac{{\partial u_{\text{p}} }}{\partial x} + v_{\text{p}} \frac{{\partial u_{\text{p}} }}{\partial y} = \frac{K}{m}\left( {u - u_{\text{p}} } \right),$$
(10)
$$\rho_{\text{p}} C_{\text{m}} \left( { u_{\text{p}} \frac{\partial T}{{\partial x}} + v_{\text{p}} \frac{\partial T}{{\partial y}} } \right) = \frac{{\rho_{\text{p}} C_{\text{m}} }}{{\tau_{\text{T}} }} \left( { T - T_{\text{P}} } \right),$$
(11)
$$u_{\text{p}} \frac{\partial C_{\text{p}} }{{\partial x}} + v_{\text{p}} \frac{\partial C_{\text{p}} }{{\partial y}} = \frac{1}{\tau_{\text{c}} }\left( {C - C_{\text{p}} } \right),$$
(12)
$$u_{\text{p}} \frac{\partial N_{\text{p}} }{{\partial x}} + v_{\text{p}} \frac{\partial N_{\text{p}} }{{\partial y}} = \frac{1}{\tau_{\text{m}} }\left( {N - N_{\text{p}} } \right),$$
(13)

The following are the possible boundary conditions for this problem (see Abbas et al. [24], Mamatha et al. [43], Gorla [45]):

$$\mu _{{\text{hnf}}} \frac{{\partial u}}{{\partial y}} = {\text{ }}\frac{{\partial \sigma _1 }}{{\partial x}} = {\text{ }} - \sigma _0 \left( {\gamma _{\text{T}} \frac{{\partial T}}{{\partial x}} + \gamma _{\text{C}} \frac{{\partial C}}{{\partial x}}} \right),\quad v = 0,\quad {\text{at}}\quad y = 0,$$
(14)
$$u \to 0,\quad u_{\text{p}} \to 0,\quad v_{\text{p}} \to v,\quad {\text{at}} \quad y \to \infty ,$$
(15)
$$T = T_\infty + T_0 X^2 ,\;{\text{at}}\quad y = 0,T \to T_\infty ,\quad T_{\text{p}} \to T_\infty \;{\text{at}}\quad y \to \infty ,$$
(16)
$$C = C_\infty + C_0 X^2 ,\;{\text{at}}\quad y = 0,\quad C \to C_\infty ,\quad C_{\text{p}} \to C_\infty ,\;{\text{at}}\quad y \to \infty ,$$
(17)
$$N = N_\infty + N_0 X^2 ,\;{\text{at}}\quad y = 0,\quad N \to N_\infty ,\quad N_{\text{p}} \to N_\infty ,\;{\text{at}}\quad y \to \infty .$$
(18)

where this term \(\frac{16\sigma^* T_\infty^3 }{{3k^* }}\frac{\partial^2 T}{{\partial y^2 }}\) in Eq. (6) represents thermal radiation, the term \(\frac{{\rho_{pC_{\text{m}} } }}{{\tau_{\text{t}} }}\left( {T_{\text{P}} - T} \right)\) in Eq. (6) represents two phase flow temperature difference, the term \(\left( {\frac{{\rho D_{\text{m}} k_{\text{T}} }}{{C_{\text{s}} }}} \right)\frac{\partial^2 C}{{\partial y^2 }}\) Eq. (6) represents Dufour effect, term \(q^{{\prime} {\prime} {\prime} }\) in Eq. (6) represents non-uniform heat source, the term \(\frac{{\mu_{{\text{hnf}}} }}{{\left( {1 + \lambda_2 } \right)}}\left\{ {\left( {\frac{\partial u}{{\partial y}}} \right)^2 + \lambda_1 \left( {u \frac{\partial u}{{\partial y}} \frac{\partial^2 u}{{\partial y\partial x}} + v \frac{\partial u}{{\partial y}} \frac{\partial^2 u}{{\partial y^2 }}} \right)} \right\}\) in Eq. (6) \({\text{represents}}\) viscous dissipation, the term \(\frac{{D_{\text{m}} k_{\text{T}} }}{{T_{\text{m}} }}\frac{\partial^2 T}{{\partial y^2 }}\) in Eq. (7) represents Soret effect, the term \(k_{\text{r}}^2 \left( {C - C_\infty } \right)\left( {\frac{T}{T_\infty }} \right)^{\text{m}} \exp \left( {\frac{{ - E_{\text{a}} }}{{k^{\prime} T}}} \right)\) in Eq. (7) represents activation energy term, and the term \(\frac{{\rho_{\text{p}} }}{{\rho \tau_{\text{C}} }}\left( {C_{\text{p}} - C} \right)\) in Eq. (7) represents concentration difference of two phase flow.

Similarity transformations

Introduce the following transformations (see Mamatha et al. [43], Gorla [45]):

$$\begin{aligned} \psi \left( {x,y} \right) = & \nu _{\text{f}} Xf\left( \xi \right), \\ \Psi \left( {x,y} \right) = & \nu _{\text{f}} {\text{X}}g\left( \xi \right), \\ \end{aligned}$$
(19)
$$\begin{aligned} & u = \frac{\partial \psi }{{\partial y}},\quad u_{\text{p}} = \frac{{\partial {\Psi }}}{\partial y}, \\ & v = - \frac{\partial \psi }{{\partial x}}\;{\text{and}}\;v_{\text{p}} = - \frac{{\partial {\Psi }}}{\partial x} , \\ \end{aligned}$$
(20)
$$\begin{aligned} & X = \frac{x}{L}, \xi = \frac{y}{L}, \\ & T\left( {x,y} \right) = T_\infty + T_0 X^2 \theta \left( \xi \right), \\ & T_{\text{P}} \left( {x,y} \right) = T_\infty + T_0 X^2 \theta_{\text{P}} \left( \xi \right), \\ \end{aligned}$$
(21)
$$\begin{aligned} C\left( {x,y} \right) = & C_\infty + C_0 X^2 \phi \left( \xi \right), \\ C_{\text{P}} \left( {x,y} \right) = & C_\infty + C_0 X^2 \phi_{\text{P}} \left( \xi \right), \\ \end{aligned}$$
(22)
$$\begin{aligned} N\left( {x,y} \right) = & N_\infty + N_0 X^2 \Theta \left( \xi \right),~ \\ N_{\text{P}} \left( {x,y} \right) = & N_\infty + N_0 X^2 \Theta _{\text{P}} \left( \xi \right),~\rho _{\text{p}} = m{\text{N}} \\ \end{aligned}$$
(23)

The following fluid and particle phase Eqs. (19–23) can be put into Eqs. (7–21) to obtain the system of ODEs.

Phase-I

$$\begin{aligned} & A_1 \left( {f^{{\prime} {\prime} {\prime} } + \beta \left( {(f^{{\prime} {\prime} } )^2 - ff^{{\prime} {\prime} {\prime} {\prime} } } \right)} \right) + A_2 \left( {f^{{\prime} {\prime} } f - \left( {f^{\prime} } \right)^2 } \right) + \beta_v l\left( {g^{\prime} - f^{\prime} } \right) \\ & - A_3 Mf^{\prime} - + A_4 {\text{Gr}}(\theta + {\text{Gc}} \phi + {\text{Gn}} {\Theta }) + {\text{Q}}e^{ - \beta \eta } = 0, \\ \end{aligned}$$
(24)
$$\begin{aligned} & A_5 \left( {\theta^{{\prime} {\prime} } \left( {1 + \varepsilon {\uptheta }} \right) + \varepsilon ({\uptheta }^{\prime} )^2 } \right) + {\text{Rd}}\theta^{{\prime} {\prime} } + A_6 {\text{Pr}}\left( {f\theta^{\prime} - 2f^{\prime} \theta } \right) + {\text{Pr}}\gamma l\beta_t \left[ {\theta_p - \theta } \right] + {\text{PrEc}}\beta_v l(g^{\prime} - f^{\prime} )^2 \\ &\quad + {\text{PrEc}}A_1 \left( {(f^{{\prime} {\prime} } )} \right.^2 + \beta \left( {\left( {f^{{\prime} {\prime} } } \right)^2 f^{\prime} - ff^{{\prime} {\prime} } f^{{\prime} {\prime} {\prime} } } \right) + {\text{DuPr}}\phi^{{\prime} {\prime} } \\ &\quad + \frac{{A_2 A_5 \left( {1 + \varepsilon {\uptheta }} \right)}}{A_1 }\left( {A^* f^{\prime} + B^* \theta } \right) = 0, \\ \end{aligned}$$
(25)
$$\begin{aligned} & \phi ^{{\prime} {\prime} } + {\text{Le}}\left( {f\phi ^{\prime} - 2f^{\prime} \phi } \right) + {\text{Lel}}\beta _{\text{c}} \left[ {\phi _{\text{p}} - \phi } \right] - {\text{LeRc}}\left( {1 + \delta \theta } \right)e^{\frac{{ - {\text{E}}}}{{\left( {1 + \delta \theta } \right)}}} \phi \\ & \quad + {\text{LeSr}}\theta ^{{\prime} {\prime} } = 0, \\ \end{aligned}$$
(26)
$${\Theta }^{^{\prime\prime}} + {\text{Pe}}\left[ {{\Theta }^{\prime} \phi^{\prime} + \left( {{\Omega } + {\Theta }} \right)\phi^{{\prime} {\prime} } } \right] + Lbf{\Theta }^{\prime} + l\beta_{\text{m}} Lb\left[ {{\Theta }_{\text{p}} - {\Theta }} \right] = 0,$$
(27)

Phase-II

$$gg^{{\prime} {\prime} } - g^{{\prime} 2} + \beta_{\text{v}} \left[ {f^{\prime} - g^{\prime} } \right] = 0,$$
(28)
$$g\theta_{\text{p}}^{\prime} - 2g^{\prime} \theta_{\text{p}} + \beta_{\text{t}} \left[ {\theta - \theta_{\text{p}} } \right] = 0,$$
(29)
$$g\phi_{\text{p}}^{\prime} - 2g^{\prime} \phi_{\text{p}} + \beta_{\text{c}} \left[ {\phi - \phi_{\text{p}} } \right] = 0,$$
(30)
$$g{\Theta }_{\text{p}}^{\prime} - 2g^{\prime} {\Theta }_{\text{p}} + \beta_{\text{m}} \left[ {{\Theta } - {\Theta }_{\text{p}} } \right] = 0.$$
(31)

Boundary conditions

$$f^{{\prime} {\prime} } (0) = - \frac{{2{\text{Mn}}\left( {1 + {\text{Ma}}} \right)}}{A_1 },\quad f\left( 0 \right) = 0,$$
(32)
$$f^{\prime} \left( \infty \right) = 0,\quad f^{{\prime} {\prime} } \left( \infty \right) = 0,\quad g^{\prime} \left( \infty \right) = 0, \quad g\left( \infty \right) = f\left( \infty \right),$$
(33)
$$\theta \left( 0 \right) = 1,\quad \theta \left( \infty \right) = 0,\quad \theta_{\text{p}} \left( \infty \right) = 0,$$
(34)
$$\phi \left( 0 \right) = 1,\quad \phi \left( \infty \right) = 0,\quad \phi_{\text{p}} \left( \infty \right) = 0,$$
(35)
$${\Theta }\left( 0 \right) = 1,\quad {\Theta }\left( \infty \right) = 0,\quad {\Theta }_{\text{p}} \left( \infty \right) = 0.$$
(36)

where magnetic parameter, microorganism mixed convection parameter, fluid-particle interaction parameter, Dufour number, dust particles mass concentration parameter, relaxation time of the dust particles, solutal mixed convection parameter, Marangoni ratio parameter, Marangoni number, Prandtl number, fluid-particle interaction parameter for temperature, Lewis number, fluid interaction parameter for concentration, thermal mixed convection parameter, Peclet number, thermal radiation parameter, fluid interaction parameter for bio-convection, Soret number, microorganisms concentration difference parameter, chemical reaction parameter, specific heat ratio, activation energy parameter, Deborah number, bio-convection Lewis number, Hartman number are given below.

$$\begin{aligned} & M = \frac{{\sigma_{\text{f}} B_0^2 L^2 }}{{\nu_{\text{f}} }},\;{\text{Gn}} = \frac{{\beta_{\text{n}}^* N_0 }}{\beta T_0 },\;\beta_{\text{v}} = \frac{L}{{\tau_{\text{v}} }}, \\ & l = \frac{Nm}{{\rho_{\text{f}} }},\;{\text{Du}} = \frac{{\rho k_{\text{t}} D_{\text{m}} C_0 }}{{C_{\text{S}} C_{\text{p}} T_{\text{o}} }}, \;\tau_{\text{v}} = \frac{m}{K}, \\ & {\text{Gc}} = \frac{{\beta_{\text{c}}^* C_0 }}{\beta T_0 }, \;{\text{Ma}} = \frac{{C_0 \gamma_{\text{c}} }}{{T_0 \gamma_{\text{T}} }},\;{\text{Mn}} = \frac{{\sigma_0 T_0 \gamma_{\text{T}} L}}{{\mu_{\text{f}} \nu_{\text{f}} }} \\ & {\text{Pr}} = \frac{{\mu_{\text{f}} C_{\text{p}} }}{{K_{\text{f}} }},\; {\text{Le}} = \frac{{\alpha_{\text{f}} }}{{D_{\text{m}} }},\; \beta_{\text{c}} = \frac{L^2 }{{\nu_{\text{f}} \tau_{\text{c}} }} \\ & {\text{Gr}} = \frac{{gT_0 L^2 (\rho \beta )_{\text{f}} }}{{\rho_{\text{f}} \nu_{\text{f}} }}, \;\beta_{\text{t}} = \frac{L^2 }{{\nu_{\text{f}} \tau_{\text{t}} }}, \;{\text{Pe}} = \frac{bWc}{{D_{\text{n}} }}, \\ & {\text{Rd}} = \frac{{4\sigma^{*} T_\infty^3 }}{{k^{*} k}}, \;\beta_{\text{m}} = \frac{L^2 }{{\nu_{\text{f}} \tau_{\text{m}} }}, \;{\text{Sr}} = \frac{{k_{\text{t}} D_m T_0 }}{{T_{\text{m}} C_0 }}, \\ & {\Omega } = \frac{N_\infty }{{\left( {N_{\text{w}} - N_\infty } \right)}},\;{\text{Rc}} = \frac{{L^2 K_{\text{r}}^2 }}{{\nu_{\text{f}} }},\;\gamma = \frac{{C_{\text{m}} }}{{C_{\text{p}} }},\; E = \frac{{{\text{Ea}}}}{k^* T_\infty }, \\ & \beta = \frac{{\lambda_1 \nu_{\text{f}} }}{L^2 },{\text{Lb}} = \frac{{\alpha_{\text{f}} }}{{D_{\text{n}} }} {\text{and}}\; Q = \frac{M_0 L^3 \pi J_0 }{{8\nu^2 }}. \\ \end{aligned}$$

Physical curiosity

For non-Newtonian fluid (Jeffrey hybrid nanofluid), the \({\text{Nu}}_{\rm x}\) local rate of heat transfer, \({\text{Nn}}_{\rm x}\) density of motile microorganisms, \({\text{Sh}}_{\rm x}\) local rate of mass transfer and \(C_{{\text{fx}}}\) local skin friction are addressed.

$$\begin{aligned} & C_{{\text{fx}}} = \frac{{\tau _{\text{w}} }}{\rho }~,\;{\text{Nu}}_{\text{x}} = \frac{{xq_{\text{w}} }}{{k_{\text{f}} \left( {T_{\text{w}} - T_\infty } \right)}}~,~ \\ & {\text{Sh}}_{\text{x}} = \frac{{xq_{\text{m}} }}{{D_{\text{m}} \left( {C_{\text{w}} - C_\infty } \right)}}, \\ & {\text{Nn}}_{\text{x}} = \frac{{xq_{\text{n}} }}{{D_{\text{n}} \left( {N_{\text{w}} - N_\infty } \right)}}~, \\ \end{aligned}$$
(37)
$$\tau_{\text{w}} = \frac{{\mu_{{\text{hnf}}} }}{1 + \lambda_2 }\left[ {\frac{\partial u}{{\partial y}} + \lambda_1 \left\{ {u\frac{\partial^2 u}{{\partial y\partial x}} + v\frac{\partial^2 u}{{\partial y^2 }}} \right\}} \right]_{y = 0} ,$$
(38)
$$q_{\text{w}} = - \left[ {k_{{\text{hnf}}} \left( {1 + \varepsilon \left( {\frac{T - T_\infty }{{T_{0 } X^2 }}} \right)} \right) + \frac{{16T_\infty^3 \sigma^{*} }}{{3k^{*} }}} \right]\left. {\frac{\partial T}{{\partial y}}} \right|_{y = 0} ,$$
(39)
$$\begin{aligned} q_{\text{m}} = & - \left. {D_{\text{m}} \frac{\partial C}{{\partial y}}} \right|_{y = 0} , \\ q_{\text{n}} = & - \left. {D_{\text{n}} \frac{\partial N}{{\partial y}}} \right|_{y = 0} , \\ \end{aligned}$$
(40)
$${\text{C}}_{{\text{fx}}} \left( {{\text{Re}}_{\text{x}} } \right)^{ - 0.5} = \frac{A_1 }{{1 + \lambda_2 }}\left( {f^{{\prime} {\prime} } + \beta \left( {f^{\prime} \left( 0 \right)f^{{\prime} {\prime} } \left( 0 \right) - f\left( 0 \right)f^{{\prime} {\prime} {\prime} } \left( 0 \right)} \right)} \right.,$$
(41)
$${\text{Nu}}_{\text{x}} \left( {{\text{Re}}_{\text{x}} } \right)^{ - 0.5} = - \left( {A_5 \left( {1 + \in {\uptheta }} \right) + {\text{Rd}}} \right)\theta^{\prime} \left( 0 \right),$$
(42)
$$\begin{aligned} {\text{Sh}}_{\text{x}} \left( {{\text{Re}}_{\text{x}} } \right)^{ - 0.5} = & & - \phi^{\prime} \left( 0 \right), \\ {\text{Nn}}_{\text{x}} \left( {{\text{Re}}_{\text{x}} } \right)^{ - 0.5} = & - {\Theta }^{\prime} \left( 0 \right). \\ \end{aligned}$$
(43)

The thermo-physical features of hybrid nanofluid are shown in Table 1. The thermo-physical characteristics of base fluid and nanoparticles are displayed in Table 2.

Table 1 Base fluid and nanoparticle thermo-physical characteristics (Unyong et al. [46])
Full size table
Table 2 Represents the thermo-physical aspects of hybrid nanofluid (see Abbas et al. [24])
Full size table

Numerical method

The nonlinear BVP is reduced into a sequence of single-order IVP, and the RKF-45th approach is used to solve the problem. Add the following variables to the equations now:

$$u_1 = f, \quad u_2 = f^{\prime} ,\quad u_3 = f^{{\prime} {\prime} } ,\quad u_4 = f^{{\prime} {\prime} {\prime} } ,\quad u_4^{\prime} = f^{{\prime} {\prime} {\prime} {\prime} } ,$$
(44)
$$u_5 = g,\quad u_6 = g^{\prime} ,\quad u_6^{\prime} = g^{{\prime} {\prime} } ,$$
(45)
$$u_7 = \theta , \quad u_8 = \theta^{\prime} ,\quad u_8^{\prime} = \theta^{{\prime} {\prime} }$$
(46)
$$u_9 = \theta_{\text{p}} ,\quad u_9^{\prime} = \theta^{\prime}_{\text{p}} .$$
(47)
$$u_{10} = \phi ,\quad u_{11} = \phi^{\prime} ,\quad u_{11}^{\prime} = \phi^{{\prime} {\prime} } ,$$
(48)
$$u_{12} = \phi_{\text{p}} ,\quad u_{12}^{\prime} = \phi^{\prime}_{\text{p}} .$$
(49)
$$u_{13} = \Theta ,\quad u_{14} = \Theta^{\prime} ,\quad u_{14}^{\prime} = \Theta^{{\prime} {\prime} } ,$$
(50)
$$u_{15} = {\Theta }_{\text{p}} ,\quad u_{15}^{\prime} = {\Theta }^{\prime}_{\text{p}} .$$
(51)
$$u_1^{\prime} = u_2 ,\quad u_2^{\prime} = u_3 \quad u_3^{\prime} = u_4$$
(52)
$$\begin{aligned} u_4^{\prime} = & \frac{1}{u_1 \beta A_1 } \\ & \quad \left( {A_2 \left( { u_2^2 - u_1 u_3 } \right) + u_3 u_7 \varepsilon _1 e^{ - u_6 \varepsilon _1 } + L\beta_{\text{v}} \left( {u_5 - u_2 } \right) + A_3 Mu_2 + - A_4 {\text{Gr}}} \right. \\ & \quad \left. {\left( {u_7 + {\text{Gc }}u_{10} + {\text{Gn}} u_{13} } \right) + u_4 A_1 + \beta A_1 (u_3 )^3 - Qe^{ - \beta \eta } } \right) \\ \end{aligned}$$
(53)
$$u_5^{\prime} = u_{6 } ,\quad u_6^{\prime} = u_5^{ - 1} \left( {u_6^2 + \beta_{\text{v}} \left( {u_6 - u_2 } \right)} \right. ,$$
(54)
$$u_7^{\prime} = u_8 ,$$
(55)
$$\begin{aligned} u_8^{\prime} = & (A_5 \left( {1 + \varepsilon u_7 } \right) + {\text{Rd}})^{ - 1} ( - \varepsilon A_5 u_8^2 + A_6 \left( {{\text{Pr}}(2~u_2 u_7 - u_1 u_8 } \right) + {\text{PrL}}\gamma \beta _{\text{T}} \left( {u_7 - u_9 } \right) \\ & - {\text{PrLE}}c\beta _{\text{v}} (u_6 - u_2 )^2 - \frac{{A_5 A_2 (1 + \varepsilon u_7 )}}{{A_1 }}\left( {A^* u_2 + B^* u_7 } \right) \\ & - {\text{DuPr}}u_{11}^{\prime} - {\text{PrEc}}A_1 ((u_3 )^2 + \beta \left( {u_2 \left( {u_3 )^2 - u_1 u_3 u_4 } \right)} \right) \\ \end{aligned}$$
(56)
$$u_9^{\prime} = u_5^{ - 1} \left( { 2u_6 u_9 + \beta_{\text{T}} \left( {u_9 - u_7 } \right)} \right),$$
(57)
$$\begin{aligned} u_{10}^{\prime} = & u_{11,} \\ u_{11}^{\prime} = & \left( {\left( {{\text{Le}}(2~u_2 u_{10} - u_1 u_{11} } \right) + {\text{Le}}\beta _C L\left( {z_{10} - z_{12} } \right) - {\text{LeSr}}u_7^{\prime} + {\text{LeRc}}\left( {1 + \delta u_7 } \right)e^{\frac{{ - E}}{{\left( {1 + \delta ~u_7 } \right)}}} } \right. \\ \end{aligned}$$
(58)
$$u_{12}^{\prime} = u_5^{ - 1} \left( { 2u_5 u_{12} + \beta_{\text{T}} \left( {u_{12} - u_{10} } \right)} \right).$$
(59)
$$\begin{aligned} u_{13}^{\prime} = & u_{14,} \\ u_{14}^{\prime} = & \left( {\left( {{\text{Lb}}(2 u_2 u_{13} - u_1 u_{14} } \right) + {\text{Lb}}\beta_{\text{m}} L\left( {u_{13} - u_{15} } \right) + {\text{Pe}}\left( {u_{14} u_{11} + \left( {{\Omega } + u_{13} } \right)u_{11}^{\prime} } \right)} \right., \\ \end{aligned}$$
(60)
$$u_{15}^{\prime} = u_5^{ - 1} \left( { 2u_6 u_{15} + \beta_m \left( {u_{15} - u_{13} } \right)} \right).$$
(61)

Boundary conditions

$$u_1 \left( 0 \right) = 0,~\quad u_2 \left( 0 \right) = n_1 ,~\quad u_3 \left( 0 \right) = - 2\frac{{{\text{Mn}}\left( {1 + {\text{Ma}}} \right)}}{{e^{ - u_6 \varepsilon _1 } A_1 }},\quad ~u_3 \left( 0 \right) = n_2 ,~\quad u_5 \left( 0 \right) = n_3 ,$$
(62)
$$z_6 \left( 0 \right) = n_4 ,\quad u_7 \left( 0 \right) = 1,\quad u_7 \left( 0 \right) = n_5 ,\quad u_9 \left( 0 \right) = n_6 ,$$
(63)
$$u_{10} \left( 0 \right) = 1,\quad u_{10} \left( 0 \right) = n_7 ,\quad u_{12} \left( 0 \right) = n_8 ,$$
(64)
$$u_{13} \left( 0 \right) = 1,\quad u_{13} \left( 0 \right) = n_9 ,\quad u_{15} \left( 0 \right) = n_{10} .$$
(65)

The shooting method is used to estimate the unknowns \(n_1\) to \(n_{10} .\) Figure 7 shows the flow chart of solution.

Fig. 7
figure 7

Flow chart

Full size image

Graphically results and discussion

The main focus is on evaluating dimensionless quantities, such as concentration, velocity, temperature, microorganism \(\left( {\phi \left( \xi \right),\phi_{\text{p}} \left( \xi \right),f^{\prime} \left( \xi \right),g^{\prime} \left( \xi \right),\theta \left( \xi \right),\theta_{\text{p}} \left( \xi \right),\Theta (\xi ) \Theta_{\text{p}} \left( \xi \right)} \right)\) profiles of both phases (I & II) for numerous values of parameters, e.g., \(M,{\text{Gr}}, {\text{Gc}}, {\text{Gn}},\beta\), \({\Phi }_1 , {\Phi }_2 , A^* , B^* , \varepsilon , {\text{Rc}}, {\text{Sr}}, {\text{Pe}}, {\Omega },\) and \({\text{Ma}}\). The range of values for the effective parameters has been chosen by following Mamatha et al. [43], Jawad et al. [47], Khan et al. [48], i.e.,

$$0.1 \le {\text{Pe}} \le 1.0,\;0.1 \le {\Omega } \le 1.0,\; 0.1 \le \beta_{\text{m}} \le 0.5,\; 1 \le {\text{Du}} \le 1.8,\;0.1 \le \beta_{\text{c}} \le 0.5, \; 2 \le {\text{Pr}} \le 6.9,\;0.1 \le M \le 4,\;0.1 \le {\text{Gr}},\;{\text{Gc}},\; {\text{Gn}} \le 1.2,\;0.1 \le \beta_{\text{t}} \le 0.5,\;0.1 \le \beta_{\text{v}} \le 0.5,\; 0.5 \le {\text{Ma}} \le 1.2,\; 0.1 \le {\text{Sr}} \le 1.6,\; 0.1 \le {\text{Rc}} \le 1.0,\; 0.1 \le E \le 5,\;0.1 \le {\text{Le}} \le 0.5, \;0.1 \le {\text{Lb}} \le 0.5.,\;0.1 \le A^* \le 1.0.$$

Figure 8a and b shows variation in flow and thermal profiles of phases (I & II) due to Deborah parameter \(\beta .\) It should be noticed that velocity profiles show a reduction with rising values of \(\beta\). When \(\beta\) increases cause a reduction in velocity but a rise in \(\theta \left( \xi \right),\theta_{\text{p}} \left( \xi \right)\) for both phases (I & II) because Deborah number is proportional to \(\lambda_2\)(relaxation time). Impact of \(M\) on \(f^{\prime} \left( \xi \right)\) and \(g^{\prime} \left( \xi \right)\) profiles of both phases (I & II) is demonstrated in Fig. 9a. It is noted that as \(M\) is increases, the velocity \((f^{\prime} \left( \xi \right)\), \(\left. {g^{\prime} \left( \xi \right)} \right)\) profiles of the Jeffry hybrid nanofluid and particle phase decreases. The application of the transverse magnetic field will result in a drag-like resistive force that tends to slow down the velocity of the fluid flow in both phases. In fact, the increase in magnetic parameter results in the decrease of momentum boundary layer thickness. Figures 9b and 10a and b show the influence of \({\text{Gr}},{\text{Gc}}\) and \({\text{Gn}}\) on velocity profiles of both phases (I & II). For phase-I and phase-II, velocity profiles are improved by increasing the mixed convection parameters. \({\text{Fe}}_3 {\text{O}}_4\) and \({\text{Cu}}\) nanoparticle volume fractions (\(\Phi_1\), \({\Phi }_2\)) to have an impact on both \(f^{\prime} \left( \eta \right),\) \(g^{\prime} (\eta )\) as shown in Fig. 11a and b. A decreasing effect is shown by increased \(\Phi_1\) and \(\Phi_2\). Physically, fluid motion slows down as the concentration of nanoparticles in the fluid exceeds the density of the nanofluid, leading to a decrease in velocity profile. The effects of \(A^{*}\) and \(B^{*}\) on \(\theta \left( \xi \right)\) and \(\theta_{\text{p}} \left( \xi \right)\) distributions of the hybrid nanofluid phase and the dust phase are portrayed in Figs. 12a and b and 13a and b, respectively. It is found that improving the \(A^{*}\) and \(B^{*}\) values leads to improved thermal distributions for both phases (I & II). When the non-uniform heat sources \(A^{*}\) and \(B^{*}\) are considered to have positive values then it indicates that they transfer heat energy into the fluid flow and cause the temperature distribution to become more uniform. While, non-uniform heat sink \(A^{*}\) and \(B^{*}\) are known as heat sinks when they attain negative values. A certain boundary layer's capacity to absorb heat lowers the temperature in both phases. Variation of temperature profile of phases (I & II) against \({\Phi }_1\), \({\Phi }_2\) is shown in Fig. 14a and b. It has been demonstrated that for hybrid nanofluid and nanofluid, the temperatures profiles of both phases (I & II) increase. Physically, more resistance is generated and temperature profiles grow as a result of increasing the values of \(\Phi_1\) and \(\Phi_2\). The impacts of \({\text{Du}}\) and \(\varepsilon\) on \(\theta \left( \xi \right)\) and \(\theta_{\text{p}} \left( \xi \right)\) for the dust and fluid phases, respectively, are shown in Fig. 15a and b. The impact of Du on \(\theta \left( \xi \right)\) and \(\theta_{\text{p}} \left( \xi \right)\) is shown in Fig. 15a. The Dufour effect is used to describe the heat flux caused by a concentration profile. When the Dufour effect is present, the temperature profiles are stronger; while it is absent, it behaves negatively. As the Dufour number rises, the heat boundary layer thickness also dramatically rises, and the boundary layer flow appears to be more active. The impact of \(\varepsilon\) on the thermal profiles is shown in Fig. 15b. Jeffrey hybrid nanofluid and dust phase temperature profiles rise as we raise the value of \(\varepsilon\). By raising the values of the variable thermal conductivity parameter, the heating phenomenon is successfully maintained. It has been discovered that using materials with varied thermal properties may accelerate up heat transfer. The effects of \({\text{Sr}}\) and \({\text{Rc}}\) on \(\phi \left( \xi \right)\) and \(\phi_{\text{p}} \left( \xi \right)\) for both dust and fluid phases, respectively, are shown in Fig. 16a and b. The graph clearly shows that in Fig. 16a, \(\phi \left( \xi \right)\) and \(\phi_{\text{p}} \left( \xi \right)\) drop as \({\text{Rc}}\) increased. The concentration profiles improve when the values of \({\text{Sr}}\) raise. A growth in \(\phi \left( \xi \right)\) is caused by the increasing \({\text{Sr}}\), which exhibits increased molar mass diffusivity. The impacts of \({\Omega }\) and \({\text{Pe}}\) on \({\Theta }(\xi ){ }\) and \({\Theta }_{\text{p}} \left( \xi \right)\) profile of both phases are revealed in Fig. 17a and b. Both the Jeffrey hybrid nanofluid and dust phase microorganism profiles reduced as we raised the \({\text{Pe}}\) and \({\Omega }\) values. The Peclet number \(({\text{Pe}})\) and cell swimming speed \((W_{\text{c}}\)) are directly related to one another and inversely proportional to \(D_{\text{n}}\) (microorganisms diffusivity). The Peclet number affects how quickly advection and diffusion occur. Therefore, a faster rate of advective movement results in a higher \({\text{Pe}}\), which quickly increases the flux of microorganisms. The effects of \({\text{Pe}}\) increases the swimming rate of motile microorganisms, and this property decreases the thickness of the microorganisms close to the surface of Riga. The impacts of \({\text{Ma}}\) on \(\phi \left( \xi \right),\;\phi_{\text{p}} \left( \xi \right),\;f^{\prime} \left( \xi \right),\;g^{\prime} \left( \xi \right),\;\theta \left( \xi \right),\;\theta_{\text{p}} \left( \xi \right),\;{\Theta }(\xi )\) and \({\Theta }_{\text{p}} \left( \xi \right)\) profiles of both the phases (I & II) are illustrated in Figs. 18a and b and 19a and b, respectively. The graph illustrates how raising \({\text{Ma}}\) improves the velocity profiles of both the particles and Jeffrey hybrid nanofluid phase. This portent is based on surface variation. A stronger Marangoni influence will almost always lead to a rise in flow profiles for both the phases (I & II). According to these graphs, the thermal, concentration and microorganism profiles significantly decrease as Ma values rise. Surface tension over the surface is induced by the stronger attraction of the liquid to the particles in the geometry. As a result, as surface tension rises, temperature drops. Thermal gradient declines due to the emergence of the surface molecules. As a result, the thermal gradient decreases. The Sherwood and Nusselt numbers are discussed in Tables 3 and 4 in relation to various emergent constraint values. Table 5 uses the integer case and only common factors to compare the mass and microorganism transfer rates between the current study (RKF-45th and BVP4C) and published research (RKF-45th). The current results and earlier results show great agreement.

Fig. 8
figure 8

a and b Pictogram of \(f^{\prime} \left( \xi \right),\) \(g^{\prime} (\xi ), \;\theta (\xi ),\; \theta_{\text{p}} (\xi )\) against \(\beta\)

Full size image
Fig. 9
figure 9

a and b Pictogram of \(f^{\prime} \left( \xi \right)\) and \(g^{\prime} \left( \xi \right)\) against \(M{ }\) and \({\text{Gr}}\)

Full size image
Fig. 10
figure 10

a and b Pictogram of \(f^{\prime} \left( \xi \right)\) and \(g^{\prime} \left( \xi \right)\) against \({\text{Gc}} {\text{ and Gn}}\)

Full size image
Fig. 11
figure 11

a and b Pictogram of \(f^{\prime} \left( \xi \right)\) and \(g^{\prime} \left( \xi \right)\) against \(\Phi_1 \;{\text{and}}\;\Phi_2\)

Full size image
Fig. 12
figure 12

a and b Pictogram of \(\theta (\xi )\) and \(\theta_{\text{p}} (\xi )\) against \(A^*\)

Full size image
Fig. 13
figure 13

a and b Pictogram of \(\theta (\xi )\) and \(\theta_{\text{p}} (\xi )\) against \(B^*\)

Full size image
Fig. 14
figure 14

a and b Pictogram of \(\theta (\xi )\) and \(\theta_{\text{p}} (\xi )\) against \(\Phi_1 \;{\text{and}}\;\Phi_2\)

Full size image
Fig. 15
figure 15

a and b Pictogram of \(\theta (\xi )\) and \(\theta_{\text{p}} (\xi )\) against \({\text{Du}}\) and \(\varepsilon\)

Full size image
Fig. 16
figure 16

a and b Pictogram of \(\phi (\xi )\) and \(\phi_{\text{p}} (\xi )\) against \({\text{Rc}}\) and \({\text{Sr}}\)

Full size image
Fig. 17
figure 17

a and b Pictogram of \({\Theta }(\xi )\) and \({\Theta }_{\text{p}} (\xi )\) against \({\Omega }\) and \({\text{Pe}}\)

Full size image
Fig. 18
figure 18

a and b Pictogram of \(f^{\prime} \left( \xi \right),\) \(g^{\prime} (\xi ), \theta (\xi )\) and \(\theta_{\text{p}} (\xi )\) against \({\text{Ma}}\)

Full size image
Fig. 19
figure 19

a and b Pictogram of \(\phi \left( \xi \right),\) \(\phi_{\text{p}} (\xi ), {\Theta }(\xi )\) and \({\Theta }_{\text{p}} (\xi )\) against \({\text{Ma}}\)

Full size image
Table 3 Outcome of various parameters on Nusselt number
Full size table
Table 4 Effect of many parameters on Sherwood number
Full size table
Table 5 The comparison results of the present study to earlier published research, with the additional parameters set to zero
Full size table

Conclusions

The thermo-solutal Marangoni convective flow of a dusty MHD Jeffrey hybrid nanofluid including microorganisms with heat source and activation energy over a Riga plate has been examined numerically in the present investigation. The following are the main outcomes of the investigation:

  • The velocity profiles, Nusselt number and Sherwood number enhance due to an increase in Marangoni convection parameter, while converse behavior is found for, thermal, microorganisms and concentration profiles for both phases. The Marangoni number surface tension has a significant impact. Surface tension is a result of a liquid's bulk attraction to the particles in the surface layer on its surface. As a result, the temperature decreases as the surface tension increases, and the bulk magnetism between the surface molecules rises or intensifies.

  • The phases (I&II) of velocity profiles get declined and thermal profiles enhance for higher values of volume friction of nanoparticles. Physically, fluid motion slows down as the concentration of nanoparticles in the fluid exceeds the density of the nanofluid, leading to a decrease in velocity profiles.

  • The concentration profiles decrease as chemical reaction parameter levels rise, while Soret number exhibits the opposite behavior.

  • For larger values of Peclet number, the density of hybrid nanofluid and nanofluid motile microorganisms profiles decreases. The effects of Peclet number increases the swimming rate of motile microorganisms, and this property decreases the thickness of the microorganisms close to the surface of Riga.

  • By increasing the value of Marangoni convection parameter up to \(10\%\) the values of heat transfer and mass transfer enhance up to \(9\%\) and \(7.15\%\), respectively.

Future work

Future research should expand on this work by taking into account thermophoresis particle deposition, convective conditions, variable conditions and trihybrid nanoparticles. These models will be highly helpful in the construction of furnaces, atomic power plants, gas-cooled nuclear reactors, SAS turbines, and unique driving mechanisms for aircraft, rockets, satellites, and spacecraft.