Introduction

Impinging jet is one of the most effective practical techniques used in many industrial applications and thermal treatments, including sheet-form materials e.g., cooling of gas turbine components, drying of textiles, paper, photographic films, heating or cooling of sheets of metal, glass, coated papers, veneer, etc. In the past decades, many studies have been conducted on the effects of impinging jets on the flow and thermal characteristics. For example, Esmailpour et al. [1] investigated the entropy generation of pulsed impinging jet. Guo et al. [2] studied the axisymmetric wall jet development in the confined jet impingement. Hadipour et al. [3] studied the effects of a triangular guide rib on the flow and heat transfer of impingement jet on an asymmetric concave surface. Siddique et al. [4] investigated the heat transfer augmentation of flat target surface under air jet impingement for the varying heat flux boundary condition. Doranehgard et al. [5] investigated the natural-gas diffusion in oil-saturated tight porous media. Hadipour et al. [6] studied the effect of micro-pin characteristics heat transfer of jet impinging to the flat surface. Lytle and Webb [7] investigated the influence of jet-to-plate distance of impinging jet on the Nusselt number distribution at low nozzle-to-surface distances. They proposed a relation based on the jet-to-surface distance for the stagnation point of Nusselt number.

Norbert et al. [8] investigated the temperature and velocity distributions of impinging jet on a semi-confined cavity. The authors found that with a decrease in the jet-to-plate distance, the local Nusselt number increases in the impingement region. The impact of spent air removal on the heat transfer rate at low spacing between the target surface and impinging jet was studied by Singh and Ekkad [9]. They found that low jet-to-surface distance plays an important role in the spent air removal from the system.

Grenson et al. [10] investigated the jet impingement with low jet-to-plate distances. Like previous experiments, they stated that for the low jet-to-surface distances, the distribution of local Nusselt number has a secondary maximum. Glaspell et al. [11] investigated the effect of water jet at small nozzle-to-surface distance on the heat transfer. They found that the stagnation Nusselt number can increase by decreasing the jet-to-plate distance. Choo and Kim [12] observed that for H/D \(\ge\) 5, the features of adiabatic temperature are not contingent on the distance between the jet and target surface. Choo et al. [13] investigated the relation between the stagnation pressure and Nusselt number of the jet impingement for H/D in the range of 0.125 to 40. They observed that the local Nusselt number is dependent on the stagnation pressure. Greco et al. [14] found that the maximum heat transfer rate occurs at a low nozzle-to-plate distance. Zhu et al. [15] studied the transient heat transfer of impinging jet to flat surface at low distance between the jet and target plate. They found that at the low jet-to-jet distance, the heat transfer rate has the best performance. Hadipour and Rajabi [16] examined the temperature and velocity fields of jet impingement on a symmetrical concave surface at low nozzle-to-plate distance. They showed that the jets with very small jet-to-plate distances provide better cooling efficiency. In an experimental investigation, Yu et al. [17] studied the impinging jet heat transfer with two rows of aligned jets.

Many studies have been focused on the impingement of row of jets on a surface. Fregeau et al. [18] examined the rate of heat transfer due to jet impingement for several values of jet-to-target surface distance. They used the Spalart–Allmaras turbulent model and observed the gratifying results for higher jet-to-target plate distances. The flow and heat transfer from the row jets impingement on a concave surface was studied by Craft et al. [19]. In their investigation, the k-ε model together with a wall function was used. They applied a standard wall function for the prediction of the Nusselt number. Sharif and Mothe [20] used various turbulent models for simulating the impinging jet on a concave plate. They observed that better efficiency can be achieved in reproducing the flow features by using the RSM models. Singh et al. [21] performed a numerical investigation on the heat transfer of circular impinging jet. They applied the different nozzle diameters and nozzle-to–target surface distances in their investigation. Their results showed that for all configurations at the impinging zone, all turbulent models over-estimate the Nusselt number. Fenot et al. [22, 23] performed an experimental investigation on a row of jet impingement to the concave and flat surfaces. They investigated the effects of geometric flow and flow parameters. They found that the influence of the near jets on the local Nusselt number is limited to a between jets area. On the other hand, the effectiveness greatly depends on the jet-to-jet distance. Whitaker et al. [24] examined the effects of particle size on the heat transfer due to jet impingement with the dusty air. They found that at high temperatures, air with particles with diameter larger than 10 microns has a higher heat transfer rate. Presley and Christensen [25] measured the thermal conductivity of dusty air. They mentioned that as the particle size of the dust increases, the thermal conductivity increases. Zhang et al. [26] focused on the dust concentration measurement technique based on ultrasonic changes. Their results indicated that the deviation between the experiments and theory is lower than 10% when the dust concentration is varied between 100 and 900 gr m3. In this regard, Aliabadi et al. [27] also reported that using the 0.3% nanofluid flow can enhance the heat transfer coefficient effectively in cooling system.

According to the literature review, decreasing the nozzle-to-surface distance improves the rate of heat transfer and Nusselt number in whole of the target plate. It was found that there is no investigation due to a row jet impinging on a flat plate for low nozzle-to-surface distance for both clean and dusty air. As a result, the present study is focused on the impact of the nozzle distances on the velocity and temperature fields over the heated surface for low different distances. The effects of jet-to-plate distance in the range of 0.1 to 2 and the dust concentration in the range of 0 to 1.8 gr m3 on the flow and heat transfer of row jets impinging have been investigated. Furthermore, the local Nusselt number and velocity distributions achieved by the experiments are compared with those obtained by the numerical simulation.

Experimental apparatus and methodologies

Experimental setup

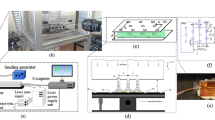
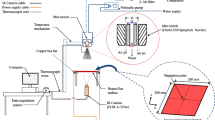
The experimental equipment used in this study is shown in Fig. 1. This system contains the control box, a fan, flow controller valve, thermocouples, IR camera, and a flat surface under the electrical heat flux. The air in the nozzles is supplied by a high-pressure centrifugal fan. To ensure about the fully developed flow conditions at the jet exit, the length of the nozzle is assumed to be more than 20 times of the nozzle diameter.

Fig. 1
figure 1

Experimental apparatus

Full size image

Figures 2 and 3 show the target plate. The length (x-direction) and the width (z-direction) of this plate are 30 cm and 15 cm, respectively.

Fig. 2
figure 2

Schematic of the impingement jet configuration

Full size image
Fig. 3
figure 3

Experimental facility

Full size image

Test model

In this study, the cooling capacity of clean and dusty impinging jets over the flat plate has been evaluated. The test surface with 30*15*10 cm, shown in Figs. 2 and 3, is considered. The top surface is a steel plate with the thickness of 1 mm, which is heated with an electrical (silicone) heater. The jet diameter is 10 mm. In each experiment, first the heat flux of 2 kW.m−2 is provided and the jet velocity was regulated by a calibrated hotwire anemometer. After reaching the steady-state condition, the target surface temperature is measured by an infrared camera. The local Nusselt number is defined by:

$$Nu = \frac{{q^{^{\prime\prime}} }}{{T_{{\text{s}}} - T_{{{\text{jet}}}} }}\frac{{D_{{{\text{jet}}}} }}{k}$$
(1)

where \({D}_{\mathrm{jet}}\) is nozzle diameter (10 mm), \({T}_{\mathrm{s}}\) is target surface temperature and \({T}_{\mathrm{jet}}\) is air temperature at exit jet.

The velocity and temperature fields of the target plate are investigated for the Reynolds numbers of 7000 and 15,000. In addition, three jet-to-target distances of 0.1, 0.5, and 2 are tested. The jet Reynolds number is defined on the basis of the average output velocity of the nozzles and the nozzle diameter as follows:

$${\text{Re}} = \frac{{\rho UD_{{{\text{jet}}}} }}{\mu }$$
(2)

where \(\rho\) is the density, u is the velocity of air at the nozzle exit, \({D}_{\mathrm{jet}}\) is the jet diameter, and \(\mu\) is the dynamic viscosity of the air.

The total uncertainty comprises of many parameters, which affect the experiment in different ways [28]. Consider the value of M, which is dependent on variables x1, x2,..., xN. The uncertainty of M is denoted by U and can be calculated from the following equation:

$$M = F(x_{1} ,x_{2} ,x_{3} , \ldots x_{{\text{n)}}} ,\;U^{2} \left( M \right) = \mathop \sum \limits_{i = 1}^{N} \left[ {\frac{\partial f}{{\partial x_{{\text{i}}} }}} \right]^{2} U^{2} \left( {x_{{\text{i}}} } \right)$$
(3)

where U(xi) is the uncertainty of variable xi. The local Nusselt number as a function of all parameters can be written as:

$$Nu = \frac{{q^{^{\prime\prime}} }}{{T_{\rm s} - T_{\rm j} }}\frac{{D_{{{\text{jet}}}} }}{k}\;{\text{Nu}} = {\text{ F}}\left( {q^{^{\prime\prime}} , T_{\rm s} , T_{\rm j} } \right)$$
(4)

By applying Eqs. (3) and (4), the uncertainty of local Nusselt number can be calculated by:

$$U^{2} \left( {NU} \right) = \left( {\frac{\partial Nu}{{\partial q^{^{\prime\prime}} }}U\left( {q^{^{\prime\prime}} } \right)} \right)^{2} + \left( {\frac{\partial Nu}{{\partial T_{{\text{s}}} }}U\left( {T_{{\text{s}}} } \right)} \right)^{2} + \left( {\frac{\partial Nu}{{\partial T_{{\text{j}}} }}U\left( {T_{{\text{j}}} } \right)} \right)^{2} = \frac{{D_{{{\text{jet}}}} }}{k}\left[ {\left( {\frac{1}{{T_{{\text{s}}} - T_{{\text{j}}} }}U\left( {q^{^{\prime\prime}} } \right)} \right)^{2} + \left( {\frac{{q^{^{\prime\prime}} }}{{\left( {T_{{\text{s}}} - T_{{\text{j}}} } \right)^{2} }}U\left( {T_{{\text{s}}} } \right)} \right)^{2} + \left( {\frac{{q^{^{\prime\prime}} }}{{\left( {T_{{\text{s}}} - T_{{\text{j}}} } \right)^{2} }}\left( {UT_{{\text{j}}} } \right)} \right)^{2} } \right]$$
(5)

It is estimated that the averaged uncertainty values for Nusselt numbers is about ± 8.8% through the Kline and McClintock method [28].

Numerical study

Geometry and boundary conditions

The boundary conditions and geometry of the present work are illustrated in Fig. 4. The computational domain consists of a single circular jet impinging on a flat plate. Three jet-to-surface distances are considered. On the target plate, the constant heat flux with the no-slip condition is used. The air with the standard conditions, temperature of 300 k, thermal conductivity of 0.26 w·mk1\(,\) and viscosity of 1.78 kg·ms1, is used. The air is considered as the Newtonian and incompressible-ideal-gas. The governing equations for simulating the present work are presented in the following section:

Fig. 4
figure 4

Grid generated inside the computational domain

Full size image

3.2 Governing equations

The transport equations in the present study can be expressed as:

$$\frac{{\partial \left( {\rho u_{{\text{i}}} } \right)}}{{\partial x_{{\text{i}}} }} = 0$$
(6)
$$\frac{\partial }{{\partial x_{{\text{j}}} }}\left( {\rho u_{i} u_{j} } \right) = - \frac{\partial P}{{\partial x_{{\text{i}}} }} + \frac{\partial }{{\partial x_{{\text{j}}} }}\left( {2\mu S_{{{\text{ij}}}} - \rho \overline{{\mathop {u_{{\text{i}}} }\limits^{^{\prime}} \mathop {u_{{\text{j}}} }\limits^{^{\prime}} }} } \right)$$
(7)
$$\frac{\partial }{{\partial x_{{\text{j}}} }}\left( {\rho C_{{\text{P}}} u_{{\text{i}}} T} \right) = - \frac{\partial P}{{\partial x_{{\text{i}}} }} + \frac{\partial }{{\partial x_{{\text{i}}} }}\left( {k\frac{\partial T}{{\partial x_{{\text{i}}} }} - \rho C_{{\text{P}}} \overline{{\mathop {u_{{\text{i}}} }\limits^{^{\prime}} \mathop T\limits^{^{\prime}} }} } \right)$$
(8)

Recent studies have shown that the RNG k–ε model has better accuracy as compared with other turbulent models to predict hydrodynamic data in impinging jet flows over target surfaces with a higher convergence speed [3, 20]. The accuracy and high convergence speed of this model are due to some modifications including new constants and existence of an additional term on the right-hand side of the ε equation. It is noted that by using an appropriate mesh near the wall regions, all advantages of the RNG k–ε model can be achieved.

The RNG k–ε turbulent model is employed to simulate the flow and thermal fields [29]. In this model, the transport equations of k and ε are:

$$\rho {\text{u}}_{{\text{j}}} \frac{\partial }{{\partial x_{{\text{j}}} }}\left( {\text{k}} \right) = \frac{\partial }{{\partial x_{{\text{j}}} }}\left[ {\left( {{\upmu } + \frac{{\mu_{{\text{t}}} }}{{\sigma_{{\text{k}}} }}} \right)\frac{\partial k}{{\partial x_{{\text{j}}} }}} \right] + 2\mu_{{\text{t}}} {\text{S}}_{{{\text{ij}}}} {\text{S}}_{{{\text{ji}}}} - \rho$$
(9)
$$\rho u_{{\text{j}}} \frac{\partial }{{\partial x_{{\text{j}}} }}\left( \varepsilon \right) = \frac{\partial }{{\partial x_{{\text{j}}} }}\left[ {\left( {\mu + \frac{{\mu_{{\text{t}}} }}{{\sigma_{\varepsilon } }}} \right)\frac{\partial \varepsilon }{{\partial x_{{\text{j}}} }}} \right] + C_{1\varepsilon } \frac{\varepsilon }{k}{\text{P}}_{{\text{K}}} - C_{2\varepsilon } \rho \frac{{\varepsilon^{2} }}{k}$$
(10)

where Pk can be calculated by:

$${\text{P}}_{{\text{K}}} = \left[ {\mu_{{\text{t}}} \left( {\frac{{\partial U_{{\text{i}}} }}{{\partial x_{{\text{j}}} }}\mu + \frac{{\partial U_{{\text{j}}} }}{{\partial x_{{\text{i}}} }}} \right) - \frac{2}{3}\rho k\delta_{{{\text{ij}}}} } \right]\frac{{\partial U_{{\text{i}}} }}{{\partial x_{{\text{j}}} }}$$
(11)

Theory of dust model

The previous studies showed that the particle size is varied in the range of 5 to 15 microns. \(\rho_{p} = 2650 \left(kg \, m^{-3} \right), \gamma = 0.8 \left(N \, m^{-1} \right), \vartheta_{\rm ARD} = 0.18, BFM = 2 \left( \% \right)\) are the properties of the dust [24].

To achieve the mass flow rate of particles \(\left({W}_{{\rm p} \infty}\right),\) the following equation can be used [30].

$$W_{{{\text{p}}\infty }} = c_{{{\text{mp}}}} \rho_{{{\text{p}}\infty }} \mathop {V_{{{\text{p}}\infty }} }\limits^{.}$$
(12)

The air-particle density can be expressed in the terms of the dust mass concentration \({c}_{\rm mp}\). The dust volume concentration, \({c}_{\rm vp},\) can be calculated by:

$$c_{{{\text{mp}}}} = \frac{1}{{{\raise0.7ex\hbox{${\rho_{\rm f} }$} \!\mathord{\left/ {\vphantom {{\rho_{\rm f} } {c_{{{\text{vp}}}} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${c_{{{\text{vp}}}} }$}} + \left( {1 - {\raise0.7ex\hbox{${\rho_{\rm f} }$} \!\mathord{\left/ {\vphantom {{\rho_{\rm f} } {\rho_{\rm p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\rho_{\rm p} }$}}} \right)}}$$
(13)

For \({\raise0.7ex\hbox{${\rho_{\rm f} }$} \!\mathord{\left/ {\vphantom {{\rho_{\rm f} } {\rho_{\rm p} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\rho_{\rm p} }$}} = 1\), the dust mass concentration is \(c_{{{\text{mp}}}} = {\raise0.7ex\hbox{${c_{{{\text{vp}}}} }$} \!\mathord{\left/ {\vphantom {{c_{{{\text{vp}}}} } {\rho_{f} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\rho_{\text{f}} }$}}.\) Since the air density, \(\rho_{{\text{f}}}\), has the order of 100 Kg m−3, the dust volume concentration can be expressed as follows [30]:

$$c_{{{\text{mp}}}} \approx \frac{{c_{{{\text{vp}}}} }}{{\rho_{\rm f} }}$$
(14)

The chemical and physical properties of dusty air, applied in the present study, are presented in Table1.

Table 1 Chemical and physical properties of dusty air [30, 32, 33]
Full size table

Numerical procedure

In this study, the advection terms of transport equations have been discretized by the second-order scheme. The SIMPLEC algorithm has been adopted for the pressure–velocity coupling [31]. The absolute criteria for the convergence of mass conservation and momentum equations are less than 10–4 and they are lower than 10–7 for the energy equation.

Grid independence test

Figure 4 shows the structured grid generated inside the computational domain. To achieve the independency of the results from the grid sizes, different grids have been generated.

The grid test is performed for four grid numbers and the results are disclosed in Fig. 5. The Nusselt number is calculated at Re = 15,000 and X/D = 0. As shown in Fig. 5, the difference between the Nusselt numbers calculated by the grid sizes of 1,898,367 and 2,436,289 are negligible. Hence, the grid number of 1,898,367 is used for the rest of simulations.

Fig. 5
figure 5

Results of grid independence test

Full size image

Results and discussion

In this work, the impact of jet-to-surface distance, jet-to-jet distance, and Reynolds number for dusty air at low jet-to-surface distance on the flow and thermal characteristics are investigated.

Thermal performance

Figure 6 illustrates the effects of the jet-to-surface distance on the local Nusselt number for two Reynolds numbers of 7000 and 15,000. Note that the local Nusselt number is plotted on the centerline plane (Z/D = 0) in this figure. The results confirm that reducing the jet-to-surface distance (H/D) from 2.0 to 0.1 leads to a significant increase in the local Nusselt number. When a row of jets is used in the jet impingement system, an area between the jets, called the dead area, is formed in which the value of Nusselt number is significantly decreased. This was also observed in the previous studies [19, 22, 23]. Figure 6 shows that by reducing the jet-to-surface distance (H/D) in the range of 2.0 to 0.5, a small increase in the local Nusselt number is achieved. However, as the H/D is decreased from 0.5 to 0.1, the local Nusselt number significantly increases. In other words, for the jet Reynolds number of 7000, the mean Nusselt number increases about 4.2% and the maximum value of Nusselt number increases about 9% as the jet-to-surface distance decreases from 2.0 to 0.5. The average Nusselt number and the maximum value of Nusselt number are increased about 186.7% and 328%, respectively, as the jet-to-plate distance is decreased in the range of 0.5 to 0.1. Both experimental and numerical results are shown in this figure for the comparison. The good agreement between two results can be observed.

Fig. 6
figure 6

Effect of the jet-to-surface distance on the local Nusselt number on the centerline plane (Z/D = 0) for a Re = 7000; b Re = 15,000

Full size image

In general, the increase in the temperature between two jets can be described by the Nusselt number distribution in this area. Figure 7 exhibits the distributions of local Nusselt number on the middle line between the jets (X/D = 2.5) and centerline (X/D = 0) for the Reynolds number of 15,000 and different values of the jet to surface distance. The results show that by placing the nozzles at the lowest jet-to-target plate distance (e.g., H/D = 0.1), the Nusselt number at the region between the jets significantly decreases, while the Nusselt number distribution in the centerline is considerably increased in comparison with other jet-to-surface distances. Although for H/D = 0.1, the local Nusselt number significantly decreases in the dead fluid zone, but still in comparison with other jet-to-surface distances, it has a considerable value in the region between the jets. The main reason for these changes of Nusselt number for the mentioned H/D in different areas of the target surface, is the difference in the flow of coolant fluid on the target surface. In this study, to better understand the reason for these changes of Nusselt number, the fluid flow on the target surface has been investigated.

Fig. 7
figure 7

Nusselt number distribution for different values of H/D and Re = 15,000 on a centerline (X/D = 0); b line between two jets (X/D = 2.5)

Full size image

Effect of air dust on Nusselt number distribution

In recent years, various studies focused on the impact of dust on heat transfer [24, 30, 32,33,34,35]. Most of these studies examined the effect of particle size and concentration of dust on the natural and forced heat convection. In this study, a new attempt was made to investigate the effect of dust on the jet impingement cooling system.

The effects of air dust on the Nusselt number distribution on centerline (X/D = 0) for Re = 15,000 are investigated in Fig. 8. Previous studies have shown that dust particles can greatly enhance the heat transfer process and adding dust to the air can increase the heat transfer coefficient [36, 37]. The results of this study show that the Nusselt number of dusty air is higher than that for the clean air in both stagnation and wall jet regions [38,39,40]. Also, by increasing the dust concentration from 0.32 g m−3 to 1.8 g m−3, the local Nusselt number on throughout the target plate increases. It can be found that the impinging air with the dust concentration of 1.8 g m−3 can increase the maximum Nusselt number by 18% in comparison with that for the clean air jet.

Fig. 8
figure 8

Effect of air dust concentration on Nusselt number distribution at X/D = 0 for Re = 15,000, H/D = 0.1

Full size image

The temperature distributions on the flat plate for different values of the jet-to-surface distance at the Reynolds number of 15,000 and the dust concentration of 0.32 g m−3 are disclosed in Fig. 9. It is observed that the temperature on the flat plate significantly decreases as the jet-to-surface distance is decreased from 2.0 to 0.1. As discussed earlier, due to the higher flow rate for the case of H/D = 0.1, the lower temperature values, varied in the range of 310 to 321 K, can be achieved for this case. Note that the ranges of temperature variation for the cases of H/D = 0.5 and H/D = 2.0 are 318 to 333 K and 319 to 335 K, respectively.

Fig. 9
figure 9

Temperature contour at Re = 15,000 and dust concentration of 0.32 g/m3

Full size image

Figure 10 shows the effect of jet-to-jet distance on the Nusselt number distribution for the Reynolds number of 7000, dust concentration of 0.32 g m−3, and two values of jet-to-target plate distance (H/D = 0.1 and H/D = 2). It can be seen that by reducing the jet-to-jet distance, the Nusselt number increases. This trend is also observed in the previous studies conducted in this field [23, 41]. The previous studies showed that by reducing the jet-to-jet distance, the value of Nusselt number is increased but this increase is not significant [23, 41]. However, the results of this study show that by placing the nozzles at low nozzle-to-surface distance (e.g., H/D = 0.1), the value of Nusselt number significantly increases as the jet-to-jet distance is decreased. Figure 10 also shows that for the case of H/D = 2, the variations of jet-to-jet distance have low effects on the Nusselt number distribution, while the effects of these variations on the Nusselt number value are significant for the case of H/D = 0.1.

Fig. 10
figure 10

Effects of jet-to-jet distance on Nusselt number distribution at Re = 7000 and dust concentration of 0.32 g m−3 for a H/D = 0.1; b H/D = 2

Full size image

Figure 11 shows the impact of jet-to-surface distance on the average Nusselt number along the z-direction for the low jet-to-surface distance. The mean Nusselt number along the z-direction can be calculated as follows:

$$\overline{Nu} \left( x \right) = \frac{1}{14D}\mathop \smallint \limits_{ - 7D}^{7D} Nu\left( {x,z} \right)\rm{d}z$$
(15)
Fig. 11
figure 11

Effect of jet-to-surface distance on average Nusselt number at dust concentration of 0.32 g m−3 at Re = 15,000

Full size image

The results show that by reducing the jet-to-surface spacing, the Nusselt number increases. However, this increase is not significant for the jet-to-surface distance larger than 0.3.

Flow characteristics for dusty air

Figure 12 shows the effects of jet-to-target surface distance on the velocity distribution in the x–y plane. It can be observed that by decreasing the jet-to-plate distance, the velocity magnitude increases around the impingement region. Based on the results reported in this figure, by decreasing the jet-to-plate spacing from H/D = 0.5 to H/D = 0.1, the maximum velocity increases about 253% and 264% for the Reynolds number of 15,000, respectively. This significant increase in the velocity of the fluid increases the turbulent kinetic energy and leads to an increase in the heat transfer rate. The significant decrease in the velocity magnitude can be observed in the region between the jets for all jet-to-surface distances and Reynolds numbers. It should be noted that the velocity reduction between the jets (dead fluid zone) consequences the decrease in heat transfer rate in this region.

Fig. 12
figure 12

Effect of jet-to-plate distance on velocity distribution on the x–y plane at Re = 15,000 and dust concentration of 0.32 g m−3 for a H/D = 0.1; b H/D = 0.5; c H/D = 2

Full size image

Figure 13 shows the impact of jet-to-jet distance on the velocity distribution at different vertical sections, including X/P = 0.1, X/P = 0.2, X/P = 0.3, and X/P = 0.4. As shown in this figure, by reducing the jet-to-jet distance from P/D = 8 to P/D = 5, the value of velocity significantly increases. The considerable velocity increase in the near the wall can be observed for all values of X/P. It should be noted that the velocity increase in the near the wall leads to enhance the heat transfer rate at this region.

Fig. 13
figure 13

Effect of jet-to-jet distance on velocity distribution at Re = 7000 and dust concentration of 0.32 g/m3 for a X/P = 0.1; b X/P = 0.2; c X/P = 0.3; d X/P = 0.4

Full size image

The effects of dust concentration on the average Nusselt number at P/D = 5 are presented in Table 2. In this table, the averaged Nusselt number for the various cases studied is calculated by Eq. 13. It can be found that at the same jet-to-surface spacing (H/D), the increase in jet Reynolds number leads to the enhancement of averaged Nusselt number for both clean and dusty air. Results in Table 2 reveal that for the jet Reynolds number of 7000, the air with the dust concentration of 1.8 gr m3 provides a higher averaged Nusselt number by 18%, 45.8% and 39.5% times more than those for the clean air at the jet-to-surface distances of 0.1, 0.5 and 2, respectively.

Table 2 Effects of dust concentration on average Nusselt number for P/D = 5
Full size table

Conclusions

In the present study, the effects of dust concentration, jet-to-surface distance, and jet-to-jet distance on the flow velocity and Nusselt number distribution from a row impinging jets on the flat surface have been investigated. Constant heat flux of 2.0 kW·m−2 has been used on the flat surface. The predicted local Nusselt numbers by numerical simulation have been compared with the experimental data to benchmark the accuracy of the numerical method. The important results can be summarized as:

  • By placing the nozzles at the low jet-to-target plate distance (e.g., H/D = 0.1), the Nusselt number in the region between the jets significantly decreases, while the value of Nusselt number in whole of the surface is considerably increased.

  • Comparison between the experimental and numerical data confirms that the RNG k-ε turbulent model has the high ability to predict the Nusselt number.

  • By using the nozzle-to-plate distance of H/D = 0.1, the average Nusselt number increases about 251.4% and 278.2% in comparison with the cases of H/D = 0.5 and H/D = 2, respectively.

  • In the region between the jets, the average Nusselt number along z-direction for H/D = 0.1 is 2.03 and 2.46 times larger than those for the cases of H/D = 0.5 and H/D = 2.0, respectively, at Re = 15,000.

  • The Nusselt number of dusty air is higher than that for the clean air in both stagnation and wall jet regions. The impinging air with dust concentration of 1.8 g m−3 increases the maximum Nusselt number by 18% in comparison with the clean air jet.

  • For the jet the Reynolds number of 7,000, the air with dust concentration of 1.8 g m−3, provides a higher averaged Nusselt number by 18%, 45.8% and 39.5% times more than the clean air for jet-to-surface spacing (H/D) of 0.1, 0.5 and 2, respectively.