Introduction

Solar collectors as a technology, compatible with energy and environment, are principal part of solar heating system depending on the implementation location has been produced in different types [1, 2]. The performance of this equipment is such that by absorbing sun’s radiation, the working fluid would be heated. One kind of these collectors is flat plate solar collector (FPSC). FPSC is the most common and the oldest one. Since FPSCs are inherently inefficient, the use of performance enhancement techniques is progressively being felt [3]. The working fluid and the channel are the principal elements of a flat plate collector, which directly affect the performance. Therefore, improving the hydrodynamic and thermal performances of a collector is appealing subjects for researchers to develop and optimize both performances. Correcting the geometry and channel’s material and improvement of working fluid thermo-physical properties is some of techniques to enhance the collector performance [4]. Appropriate thermal characters of open-cell metal foam lead to a hopeful method to correcting the geometry and the material of channel collector. Lansing et al. [5] were one of the group pioneers to employ porous media through the collectors to enhance the performance. Furthermore, for manipulating the thermo-physical properties of working fluid, combining metal nanoparticle to base fluid (like water), which leads to nanofluid formation, is one of the most efficient techniques [6]. After choosing metal porous media as the material of collector’s channel and nanofluid as working fluid, the specific selection of parameters related to these two materials is also significant[7]. In fact, these two types of materials must have the characteristics to achieve the highest efficiency [8].

Entropy generation minimization (EGM) is taken into account as a potent method to maximize the thermal equipment performance [9]. In fact, this approach is a thermodynamic method employing to make an optimization in heat transfer engineering devices from energy yield standpoint [10, 11]. Entropy generation is valuable researchers since it presents a path to specify the quality and the value of energy destruction throughout a proceeding. The scrutiny of second thermodynamics law through EGM for the nanofluid-based systems is considered as an energy saving method [12, 13]. To analyze the second law of thermodynamics through the porous medium, the LTE and LTNE models have different equations for entropy generation analyses [14, 15]. In particular conditions, considerable differences between thermal characteristics of solid and fluid phases lead to a noticeable thermally resistance between two phases [16]. This can lead to a significant difference of temperature between two phases of porous media [17]. Thus, under these conditions, the LTE assumption would be invalidated [18]. In this vein, Javanian Jouybari et al. [19] experimentally studied thermal proficiency and entropy generation in a flat plate collector saturated with metal foam. They found that utilizing media with high porosity rises thermal efficiency and Nusselt number \(\left( {{\text{Nu}}} \right)\). However, the entropy generation analysis illustrates which the irreversibility stem from the fluid flow pressure drop through the porous medium does not play a considerable influence on entropy generation. But compared to an empty channel, there is a direct correlation between pressure drop irreversibility through a collector filled with high porosity medium and the entropy generation. Nasrin and Alim [20] numerically examined the entropy generation due to nanofluid flow with viscosity and variable thermal conductivity through a riser pipe of a horizontal flat plate collector. Their outcomes show using water/Cu nanofluid increases thermal efficiency by about 8%.

Alim et al. [21] in an theoretic work studied the entropy generation, the ability of rising heat transfer and the pressure drop of a conventional FPSC cooled by nanofluid of (Al2O3, CuO, SiO2, TiO2)-water. Based on the analytical results provided by these researchers, comparing nanofluid with pure water in the role of an absorber fluid, employing CuO nanofluid reduces entropy generation to 4.34% as well as improving the HTC or heat transfer coefficient to 22.15%. However, its pumping power increases about 1.58%. Mahian et al. [9] conducted an analytical investigation about the thermal performance and entropy generation of the flow of nanofluid inside a FPSC. During their study, they looked at the effects of pipe roughness, nanoparticle size, and several distinct thermo-physical pattern on \(\left( {{\text{Nu}}} \right)\), HTC, collector output temperature, entropy generation, and Bejan number \(\left( {{\text{Be}}} \right)\). The results of this research represent that with increasing nanofluid concentration, entropy generation falls and pipe roughness increases entropy generation. Parvin et al. [22] checked out thermal performance and entropy generation stem from forced convection heat transfer of copper-pure water flow through direct absorption solar collector. This study’s results show that with increasing nanofluid volume fraction and \({\text{Re}}\), \({\text{Nu}}\) and entropy generation grow up. Further researches in the field of entropy generation through solar devices are provided in [23]. In addition to investigating the entropy generation in solar collectors, the entropy generation in porous media such as microchannels filled with porous medium [24], the porous catalytic microreactor [25, 26], the entropy generation through cooling impinging jet with and without porous medium [27], and the entropy generation of pipes partially saturated with high porosity media have also been studied [28].

So far, few studies have presented the effect of magnetic force on irreversibility through the porous systems [29], specifically with LTNE considerations. In this respect, Torabi and Zhang [30] investigated heat transfer and entropy generation through a horizontal channel saturated by porous media exposed to a magnetic field. These researchers utilized the LTE assumptions and considered two different boundary conditions to temperature distribution. Astanina et al. [31] perused Fe3O4–water free convection and entropy generation through an open trapezoidal enclosure. In this researchers' study, the cavity was accumulated with a substrate of high porosity media as well as a layer of ferrofluid, exposed to a magnetic field. Considering the LTE pattern related to fluid thermal behavior in high porosity medium, they found that increasing the Hartmann number grows the oscillations amplitude of average \({\text{Nu}}\) and average entropy generation. Rabhi et al. [32] conducted a numerical investigation related to irreversibility in a microduct filled with porous media under the condition of LTNE and exposed to magnetic force. Their outcomes demonstrate that the presence of magnetic force causes a strong trace on irreversibility. Other studies on thermal performance and entropy generation of a porous medium can be found in [33, 34].

In recent study, the hydrodynamic and thermal performance of an FPSC is improved by employing a porous metal medium and a hybrid nanofluid. Moreover, using EGM method, the geometric and flow parameters related to the most optimal performance are selected. So far, few research works have been conducted on the entropy generation in a porous media, taking into account the LTNE assumptions between the fluid and solid phases of a porous system. In this study, an accurate analysis is performed by using the thermal non-equilibrium condition. A magnetic force trace on the irreversibility of a porous system is also considered.

Problem configuration and assumptions

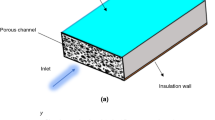
According to Fig. 1, the fluid moves as laminar, incompressible, and fully developed from the hydrodynamics as well as thermal point of view, through the channel of a solar collector. The discussed channel is accumulated by a rigid, homogeneous, and isotropic porous medium. The porous medium is subject to LTNE condition. The longitude of the channel would be shown by \(L\), and its height is \(H\). On an upper absorber plate, a uniform \(q_{{\text{w}}}\) heat flux, indicating the sun's radiation, enters the entire length of the channel. The thickness and optic characteristics of the glass and absorber plate have been ignored. It has been considered that both of these pages have one layer [35, 36]. Hybrid nanofluid with uniform distribution of spherical nanoparticles of uniform size has been selected as the working fluid. The inlet fluid to the channel has a uniform velocity and temperature. Furthermore, the thermo-physical characteristics of the water and nanoparticles are assumed constant with respect to temperature.

Fig. 1
figure 1

Comparison of the present result with: a Xu et al. [37] via dimensionless velocity, b Ting et al. [39] via dimensionless temperature, c Salehpour et al. [47] experimental work via pressure gradient as a function of velocity

Full size image

Mathematical formulation

In accordance with the mentioned assumption in previous section, momentum, energy, entropy generation equations, material characteristics, and the dimensionless conservation equations are presented in five subsections, respectively.

  1. a.

    Hydrodynamic characteristics


For hydrodynamics fully developed flow, the following conditions govern the equations:

$$\frac{\partial \left\langle u \right\rangle }{{\partial x}} = 0,\; v = 0,\; \frac{\partial \left\langle p \right\rangle }{{\partial y}} = 0, \;\frac{{{\text{d}}\left\langle p \right\rangle }}{{{\text{d}}x}} = {\text{constant}}$$
(1)

Therefore, momentum equations through a collector’s channel saturated with a porous medium and is exposed to a magnetic field will be expressed as [37, 38]:

$$0 = - \frac{{{\text{d}}\left\langle p \right\rangle }}{{{\text{d}}x}} + \frac{{\mu_{{{\text{hnf}}}} }}{\varepsilon }\left( {\frac{{\partial^{2} \left\langle u \right\rangle }}{{\partial y^{2} }}} \right) - \left( {\frac{{\mu_{{{\text{hnf}}}} }}{K}} \right)\left\langle u \right\rangle - \left( {\sigma_{{{\text{hnf}}}} B^{2} } \right)\left\langle u \right\rangle$$
(2)

where \(u\), \(p\), \(K\), \(\varepsilon\), \(\mu_{{{\text{hnf}}}}\), \(\sigma_{{{\text{hnf}}}}\), and \(B\) represent state velocity, pressure, permeability, porous, effective hybrid nanofluid dynamic viscosity, hybrid nanofluid electrical conductivity, and magnetic field, respectively. The boundary conditions governing the velocity field would be expressed as follows:

$$\left. {\left\langle u \right\rangle } \right|_{y = 0} = 0, \;\left. {\left\langle u \right\rangle } \right|_{y = H} = 0$$
(3)
  1. b.

    First-law formulations


For thermal fully developed flow, there is a fluid with constant properties as well as a constant condition for heat flux; the temperature gradient is along with \(x\) axis and independent of lateral axis \(y\) [25, 39]:

$$\frac{{{\text{d}}T_{{\text{w}}} }}{{{\text{d}}x}} = \frac{{{\text{d}}\left\langle {T_{{\text{hnf,b}}} } \right\rangle }}{{{\text{d}}x}} = \frac{{\partial \left\langle {T_{{{\text{hnf}}}} } \right\rangle }}{\partial x} = \frac{{\partial \left\langle {T_{{\text{s}}} } \right\rangle }}{\partial x} =\Omega = {\text{constant}}$$
(4)

Therefore, temperature profiles of solid and fluid phases will be stated as [25, 39]:

$$T_{{\text{i}}} \left( {x,y} \right) = f_{{\text{i}}} \left( y \right) +\Omega x,\quad i = hnf, s$$
(5)

By solving Eqs. 8 and 9, \(f_{i} \left( y \right)\) will be obtained. Beneath the boundary constant heat flux condition, energy balance is asserted in the form of [39, 40]:

$$q_{{\text{w}}} .{\text{d}}x = \rho_{{{\text{hnf}}}} .c_{{\text{p,hnf}}} .H.u_{{\text{o}}} .\left\langle {{\text{d}}T_{{\text{hnf,b}}} } \right\rangle$$
(6)

By combining Eqs. 4 and 6, \(\Omega\) is obtained as [39, 40]:

$$\Omega = \frac{{\left\langle {{\text{d}}T_{{\text{hnf,b}}} } \right\rangle }}{{{\text{d}}x}} = \frac{{q_{{\text{w}}} }}{{\rho_{{{\text{hnf}}}} .c_{{\text{p,hnf}}} .H.u_{{\text{o}}} }}$$
(7)

Ultimately, the energy equation for the two phases of high porosity medium considering LTNE is written as [24, 37]:

$$\frac{{q_{{\text{w}}} }}{H}\frac{\left\langle u \right\rangle }{{u_{0} }} = k_{{{\text{fe}}}} \left( {\frac{{\partial^{2} \left\langle {T_{{{\text{hnf}}}} } \right\rangle }}{{\partial y^{2} }}} \right) + h_{{{\text{sf}}}} a_{{{\text{sf}}}} \left( {\left\langle {T_{{\text{s}}} } \right\rangle - \left\langle {T_{{{\text{hnf}}}} } \right\rangle } \right)$$
(8)
$$0 = k_{{{\text{se}}}} \left( {\frac{{\partial^{2} \left\langle {T_{{\text{s}}} } \right\rangle }}{{\partial y^{2} }}} \right) - h_{{{\text{sf}}}} a_{{{\text{sf}}}} \left( {\left\langle {T_{{\text{s}}} } \right\rangle - \left\langle {T_{{{\text{hnf}}}} } \right\rangle } \right)$$
(9)

where \(T_{{\text{s}}}\), \(T_{{{\text{hnf}}}}\), \(k_{{{\text{fe}}}}\), \(k_{{{\text{se}}}}\), \(h_{{{\text{sf}}}}\), and \(A_{{{\text{sf}}}}\) represent solid-phase temperature, fluid-phase temperature effective thermal conductivity of fluid phase, effective thermal conductivity of solid phase, local heat transfer coefficient, and specific surface of porous media. The boundary conditions governing the temperature field are as follows:

$$\begin{aligned} & \left. {\left( {k_{{{\text{se}}}} \frac{{\partial \left\langle {T_{{\text{s}}} } \right\rangle }}{{\partial y}} + k_{{{\text{fe}}}} \frac{{\partial \left\langle {T_{{{\text{hnf}}}} } \right\rangle }}{{\partial y}}} \right)} \right|_{{{\text{y}} = 0}} = 0,~~\left. {\left\langle T \right\rangle _{{\text{s}}} } \right|_{{{\text{y}} = 0}} \\ & \quad = \left. {\left\langle {T_{{{\text{hnf}}}} } \right\rangle } \right|_{{{\text{y}} = 0}} ,\quad \left. {\left\langle {T_{{\text{s}}} } \right\rangle } \right|_{{{\text{y}} = {\text{H}}}} = \left. {\left\langle {T_{{{\text{hnf}}}} } \right\rangle } \right|_{{{\text{y}} = {\text{H}}}} = T_{{\text{w}}} \\ \end{aligned}$$
(10)
  1. c.

    Second-law formulations


In order to investigate the irreversibility of physical processes, the analysis of entropy generation is conducted. Typically, this irreversibility is generated by heat transfer, fluid friction, and so on. Therefore, the volumetric rate of entropy generation in high porosity media is as follows [38, 39]:

$$\dot{s}^{\prime \prime \prime }_{{\text{gen,s}}} = \frac{{k_{{{\text{se}}}} }}{{\left\langle T \right\rangle_{s}^{2} }}\left[ {\left( {\frac{{\partial \left\langle {T_{{\text{s}}} } \right\rangle }}{\partial y}} \right)^{2} + \left( {\frac{{\partial \left\langle {T_{{\text{s}}} } \right\rangle }}{\partial x}} \right)^{2} } \right] - \left[ {\frac{{h_{{{\text{sf}}}} a_{{{\text{sf}}}} \left( {\left\langle T \right\rangle_{{\text{s}}} - \left\langle {T_{{{\text{hnf}}}} } \right\rangle } \right)}}{{\left\langle {T_{{\text{s}}} } \right\rangle }}} \right]$$
(11)
$$\begin{aligned} \dot{s}^{{{\prime \prime \prime }}}_{{\text{gen,hnf}}} & = \frac{{k_{{{\text{fe}}}} }}{{\left\langle {T_{{{\text{hnf}}}} } \right\rangle^{2} }}\left[ {\left( {\frac{{\partial \left\langle {T_{{{\text{hnf}}}} } \right\rangle }}{\partial y}} \right)^{2} + \left( {\frac{{\partial \left\langle {T_{{{\text{hnf}}}} } \right\rangle }}{\partial x}} \right)^{2} } \right] \\ & \quad + \frac{1}{{\left\langle {T_{{{\text{hnf}}}} } \right\rangle }}\left[ {h_{{{\text{sf}}}} a_{{{\text{sf}}}} \left( {\left\langle {T_{{\text{s}}} } \right\rangle - \left\langle {T_{{{\text{hnf}}}} } \right\rangle } \right) + \mu_{{{\text{eff}}}} \left( {\frac{\partial \left\langle u \right\rangle }{{\partial y}}} \right)^{2} } \right. \\ & \quad \left. { + \frac{{\mu_{{{\text{hnf}}}} }}{K}\left( {\left\langle u \right\rangle } \right)^{2} + \left( {\sigma_{{{\text{hnf}}}} B^{2} } \right) \left( {\left\langle u \right\rangle } \right)^{2} } \right] \\ \end{aligned}$$
(12)

in which \(\mu_{{{\text{eff}}}}\) is the effective dynamic viscosity:

$$\mu_{{{\text{eff}}}} = \frac{{\mu_{{{\text{hnf}}}} }}{\varepsilon }$$
(13)

The total entropy generation is calculated from the summation of fluid-phase entropy generation and the solid-phase entropy generation of porous media [38]:

$$\dot{s}^{\prime \prime \prime }_{{\text{gen,tot}}} = \dot{s}^{\prime \prime \prime }_{{\text{gen,hnf}}} + \dot{s}^{\prime \prime \prime }_{{\text{gen,s}}}$$
(14)

By substituting Eqs. 11 and 12 in Eq. 14, the total entropy generation is:

$$\begin{aligned} \dot{s}^{{{\prime \prime \prime }}}_{{\text{gen,tot}}} & = \frac{{k_{{{\text{se}}}} }}{{\left\langle {T_{{\text{s}}} } \right\rangle^{2} }}\left[ {\left( {\frac{{\partial \left\langle {T_{{\text{s}}} } \right\rangle }}{\partial y}} \right)^{2} + \left( {\frac{{\partial \left\langle {T_{{\text{s}}} } \right\rangle }}{\partial x}} \right)^{2} } \right] \\ & \quad + \frac{{k_{{{\text{fe}}}} }}{{\left\langle {T_{{{\text{hnf}}}} } \right\rangle^{2} }}\left[ {\left( {\frac{{\partial \left\langle {T_{{{\text{hnf}}}} } \right\rangle }}{\partial y}} \right)^{2} + \left( {\frac{{\partial \left\langle {T_{{{\text{hnf}}}} } \right\rangle }}{\partial x}} \right)^{2} } \right] \\ & \quad + \left[ {\frac{{h_{{{\text{sf}}}} a_{{{\text{sf}}}} \left( {\left\langle {T_{{\text{s}}} } \right\rangle - \left\langle {T_{{{\text{hnf}}}} } \right\rangle } \right)^{2} }}{{\left\langle {T_{{\text{s}}} } \right\rangle \left\langle {T_{{{\text{hnf}}}} } \right\rangle }}} \right] \\ & \quad + \left[ {\frac{{\mu_{{{\text{eff}}}} \left( {\frac{\partial \left\langle u \right\rangle }{{\partial y}}} \right)^{2} + \frac{{\mu_{{{\text{hnf}}}} }}{K}\left( {\left\langle u \right\rangle } \right)^{2} + \left( {\sigma_{{{\text{hnf}}}} B^{2} } \right) \left( {\left\langle u \right\rangle } \right)^{2} }}{{\left\langle {T_{{{\text{hnf}}}} } \right\rangle }}} \right] \\ \end{aligned}$$
(15)

The two first terms in the right-hand side located in Eq. 15 are the entropy generation of heat transfer resulting from temperature gradient in the two phases of porous media, respectively. The third item of entropy generation of heat transfer stems from convective heat transfer at the interface of two phases. The last sentence is the entropy generation due to friction of the fluid and the magnetic field [32, 39]. Therefore, irreversible components can be described as follows [38, 39]:

$$\dot{s}^{\prime \prime \prime }_{{\text{gen,HT}}} = \dot{s}^{\prime \prime \prime }_{{{\text{gen,HT}}\left( {\text{s}} \right)}} + \dot{s}^{\prime \prime \prime }_{{{\text{gen,HT}}\left( {{\text{hnf}}} \right)}} + \dot{s}^{\prime \prime \prime }_{{{\text{gen,HT}}\left( {{\text{int}}} \right)}}$$
(16)
$$\begin{aligned} \dot{s}^{{{\prime \prime \prime }}}_{{\text{gen,HT}}} & = \frac{{k_{{{\text{se}}}} }}{{\left\langle {T_{{\text{s}}} } \right\rangle^{2} }}\left[ {\left( {\frac{{\partial \left\langle {T_{{\text{s}}} } \right\rangle }}{\partial y}} \right)^{2} + \left( {\frac{{\partial \left\langle {T_{{\text{s}}} } \right\rangle }}{\partial x}} \right)^{2} } \right] \\ & \quad + \frac{{k_{{{\text{fe}}}} }}{{\left\langle {T_{{{\text{hnf}}}} } \right\rangle^{2} }}\left[ {\left( {\frac{{\partial \left\langle {T_{{{\text{hnf}}}} } \right\rangle }}{\partial y}} \right)^{2} + \left( {\frac{{\partial \left\langle {T_{{{\text{hnf}}}} } \right\rangle }}{\partial x}} \right)^{2} } \right] \\ & \quad + \left[ {\frac{{h_{{{\text{sf}}}} a_{{{\text{sf}}}} \left( {\left\langle {T_{{\text{s}}} } \right\rangle - \left\langle {T_{hnf} } \right\rangle } \right)^{2} }}{{\left\langle {T_{s} } \right\rangle \left\langle {T_{{{\text{hnf}}}} } \right\rangle }}} \right] \\ \end{aligned}$$
(17)
$$\dot{s}^{{{\prime \prime \prime }}}_{{\text{gen,FF}}} = \left[ {\frac{{\mu_{{{\text{eff}}}} \left( {\frac{\partial \left\langle u \right\rangle }{{\partial y}}} \right)^{2} + \frac{{\mu_{{{\text{hnf}}}} }}{K}\left( {\left\langle u \right\rangle } \right)^{2} }}{{T_{{{\text{hnf}}}} }}} \right]$$
(18)
$$\dot{s}^{{{\prime \prime \prime }}}_{{\text{gen,MF}}} = \left[ {\frac{{\left( {\sigma_{{{\text{hnf}}}} B^{2} } \right) \left( {\left\langle u \right\rangle } \right)^{2} }}{{\left\langle {T_{{{\text{hnf}}}} } \right\rangle }}} \right]$$
(19)
  1. d.

    Thermo-physical characteristics of hybrid nanofluid and porous media

Throughout this subsection the relation of calculations of hybrid nanofluid properties, thermo-physical characteristics’ values of pure water as well as nanoparticles and relations of porous medium characteristics calculations are listed through Tables 1–3, respectively.

  1. e.

    Dimensionless equations

Table 1 Correlations for the thermo-physical properties of hybrid nanofluid [41, 42]
Full size table
Table 2 Thermo-physical characteristics of water, Cu, and Al2O3 [41, 43]
Full size table
Table 3 Correlations related to porous media factors [44,45,46]
Full size table

To normalize the momentum and energy equations, the dimensionless factors are stated as follows:

$$Y = \frac{y}{H},\;X = \frac{x}{L},\;\theta_{{{\text{hnf}}\left( {\text{s}} \right)}} = \frac{{T_{{{\text{hnf}}\left( {\text{s}} \right)}} - T_{{\text{w}}} }}{{q_{{\text{w}}} H/k_{{{\text{se}}}} }},\;U = \frac{u}{{u_{0} }},\;P = \frac{K}{{\mu_{{{\text{hnf}}}} u_{0} }}\frac{{{\text{d}}p}}{{{\text{d}}x}},$$
(20)

Substituting Eq. 20 to Eqs. 2 and 10 gives the non-dimensional form of momentum, energy equations, and the boundary conditions corresponding to the problem as follows [37]:

$$0 = \frac{{\partial^{2} U}}{{\partial Y^{2} }} - s^{2} U - \frac{\varepsilon }{{{\text{Da}}}}P$$
(21)
$$\left. U \right|_{Y = 0} = 0,\; \left. U \right|_{Y = 1} = 0$$
(22)
$$U = \beta \frac{{\partial^{2} \theta_{{{\text{hnf}}}} }}{{\partial Y^{2} }} + D\left( {\theta_{{\text{s}}} - \theta_{{{\text{hnf}}}} } \right)$$
(23)
$$0 = \frac{{\partial^{2} \theta_{{\text{s}}} }}{{\partial Y^{2} }} - D\left( {\theta_{{\text{s}}} - \theta_{{{\text{hnf}}}} } \right)$$
(24)
$$\begin{aligned} & \left. {\left( {\frac{{\partial \theta _{{\text{s}}} }}{{\partial Y}} + \beta \frac{{\partial \theta _{{{\text{hnf}}}} }}{{\partial Y}}} \right)} \right|_{{{\text{Y}} = 0}} = 0,\;\left. {\theta _{{\text{s}}} } \right|_{{{\text{Y}} = 0}} \\ & \quad = \left. {\theta _{{{\text{hnf}}}} } \right|_{{{\text{Y}} = 0}} ,\quad \left. {\theta _{{\text{s}}} } \right|_{{{\text{Y}} = 1}} = \left. {\theta _{{{\text{hnf}}}} } \right|_{{{\text{Y}} = 1}} = 0 \\ \end{aligned}$$
(25)

where \(P\) parameter in Eq. 21 would be calculated from the mass conservation equation:

$$1 = \mathop \int \limits_{0}^{1} U{\text{d}}Y$$
(26)

The dimensionless numbers appearing in Eqs. 21–25 are expressed as follows:

$${\text{Da}} = \frac{K}{{H^{2} }},\;{\text{Re}} = \frac{{2H\rho_{{{\text{hnf}}}} u_{0} }}{{\mu_{{{\text{hnf}}}} }},\;{\text{Ha}} = {\text{BH}}\sqrt {\left( {\frac{\sigma }{\mu }} \right)_{{{\text{hnf}}}} } ,\;s = \sqrt {\varepsilon \left( {\frac{1}{{{\text{Da}}}} + {\text{Ha}}^{2} } \right)} ,\;\beta = \frac{{k_{{{\text{fe}}}} }}{{k_{{{\text{se}}}} }},$$
$$D = \frac{{h_{{{\text{sf}}}} a_{{{\text{sf}}}} H^{2} }}{{k_{{{\text{se}}}} }}$$
(27)

Furthermore, dimensionless form of the irreversibility terms is presented as [38, 39]:

$$N_{{{\text{HT}}}} = \frac{{\dot{s}^{{{\prime \prime \prime }}}_{{\text{gen,HT}}} H^{2} }}{{k_{{\text{s}}} }},\;N_{{{\text{FF}}}} = \frac{{\dot{s}^{{{\prime \prime \prime }}}_{{\text{gen,FF}}} H^{2} }}{{k_{{\text{s}}} }},\;N_{{{\text{MF}}}} = \frac{{\dot{s}^{{{\prime \prime \prime }}}_{{\text{gen,MF}}} H^{2} }}{{k_{{\text{s}}} }}$$
(28)
$$N_{{{\text{tot}}}} = N_{{{\text{HT}}}} + N_{{{\text{FF}}}} + N_{{{\text{MF}}}}$$
(29)

In Eq. 29, \(N_{{{\text{HT}}}}\) is the dimensionless heat transfer irreversibility. \(N_{{{\text{FF}}}}\) is the dimensionless fluid friction irreversibility, and \(N_{{{\text{MF}}}}\) is representative of dimensionless magnetic field irreversibility. In accordance with Eq. 16, dimensionless heat transfer irreversibility would be expressed as:

$$N_{{{\text{HT}}}} = N_{{{\text{HT,}}\left( {\text{s}} \right)}} + N_{{{\text{HT,}}\left( {{\text{hnf}}} \right)}} + N_{{{\text{HT,}}\left( {{\text{int}}} \right)}}$$
(30)

where \(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\) is irreversibility resulting from heat conduction of the solid phase; \({\mathrm{N}}_{\mathrm{HT},(\mathrm{hnf})}\) presents irreversibility due to heat conduction in the fluid phase; and \(N_{{{\text{HT,}}\left( {{\text{int}}} \right)}}\) shows the irreversibility stems from convective heat transfer in the interface of two porous media phases defining as:

$$N_{{{\text{HT,}}\left( {\text{s}} \right)}} = \frac{{\dot{s}^{{{\prime \prime \prime }}}_{{{\text{gen,HT}}\left( {\text{s}} \right)}} H^{2} }}{{k_{{\text{s}}} }}$$
(31)
$$N_{{{\text{HT,}}\left( {{\text{hnf}}} \right)}} = \frac{{\dot{s}^{{{\prime \prime \prime }}}_{{{\text{gen,HT}}\left( {{\text{hnf}}} \right)}} H^{2} }}{{k_{{\text{s}}} }}$$
(32)
$$N_{{{\text{HT,}}\left( {{\text{int}}} \right)}} = \frac{{\dot{s}^{{{\prime \prime \prime }}}_{{{\text{gen,HT}}\left( {{\text{int}}} \right)}} H^{2} }}{{k_{{\text{s}}} }}$$
(33)

the average total irreversibility and its components on the channel surface are obtained from Eq. 34 and on the whole calculation domain from Eq. 35 [39]:

$$\overline{z} = \mathop \int \limits_{0}^{1} z{\text{d}}Y,\quad z = N_{{{\text{HT}}}} ,N_{{{\text{FF}}}} ,N_{{{\text{MF}}}} ,N_{{{\text{tot}}}}$$
(34)
$$\overline{\overline{z}} = \mathop \int \limits_{0}^{1} \overline{z}{\text{d}}X,\quad z = N_{{{\text{HT}}}} ,N_{{{\text{FF}}}} ,N_{{{\text{MF}}}} ,N_{{{\text{tot}}}}$$
(35)

and the Bejan number is stated as [38]:

$${\text{Be}} = \frac{{\overline{\overline{N}}_{{{\text{HT}}}} }}{{\overline{\overline{N}}_{{{\text{tot}}}} }}$$
(36)

Verification

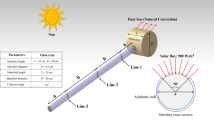
Equations 21, 23 and 24 have been solved via a numerically solution beneath the boundary conditions 22 and 25. For validating the outcomes obtained from recent article, the non-dimensional profile of temperature and velocity is evaluated with other prior works [37, 39]. In this comparison, air is considered as working fluid. The metal porous medium has porosity (\(\varepsilon = 0.9\)) and pores density (\(\omega = 15\,{\text{PPI}}\)). Heat flux received by the sun (\(q_{{\text{w}}} = 10^{3}\) W m−2), channel height (\(H = 0.015\,{\text{m}}\)), its length (\(L = 50\,{\text{H}}\)), and flow velocity (u_(0) = 1 m s−1) is considered.

As can be seen in Fig. 2a, b, it is clear that there is reasonable match between the numerical results provided in references [37] and [39] and the dimensionless profiles of velocity and temperature of this study. Moreover, in accordance with Fig. 2c, the outcomes of the present research have been compared with previous experimental work [47]. In this paper, a rectangular channel filled with copper metal foam is studied. The Reynolds number is considered in the range of 373–1186. The cooling fluid is water, and the permeability and porosity are considered as 1.774 × 10 − 7(m2) and 0.9013, respectively. Moreover, the width (W), height (H), and length (L) are taken as 50 mm, 20 mm, and 430 mm, respectively. According to the figure, there is a good agreement between the results.

Fig. 2
figure 2

Contour plots of heat transfer irreversibility components (pore density effect)

Full size image

When the fluid flows through a normal channel (empty channel), the shear stress resulting from the channel walls causes resistance to the movement of the fluid. But, when a porous medium is added into the channel, more resistive forces are applied to the fluid. These forces are created due to the complex internal structure of the porous medium and the movement of fluid over the solid fibers of the porous medium. At a low velocity, the pressure drop of the channel walls is not negligible against the pressure drop due to the porous medium. At the high velocity, however, the pressure drop of the porous medium is much larger than the pressure drop due to the channel walls. In the present numerical study, just the pressure drop of the porous medium has been calculated, whereas, in the experimental study, the total pressure drop resulting from the porous medium and the walls have been taken into account. Therefore, at very low speeds, there is a difference between the presented numerical results and the experimental results.

Results and discussion

In this section, the effects of different parameters such as porosity, the hybrid nanofluid’s volume fraction, and magnetic force on the distribution of total entropy and its components are studied. In this research, the porous medium has porosity of (ε = 0.9), pores density of (ω = 15 PPI). The heat flux received from the sun (\(q_{{\text{w}}} = 10^{3} {\text{W/m}}^{2}\)) is considered. The height of the channel is (H = 0.015 m) and its length (L = 50 H). The volume fractions of the both materials are considered equal (\(\varphi_{{{\text{p}}1}} = \varphi_{{{\text{p}}2}} = 0.025\)). Reynolds number of the flow is (\({\text{Re}}_{{{\text{bf}}}} = 1000\)), and Hartmann number is presumed (\({\text{Ha}}_{{{\text{bf}}}} = 20\)). It should be noted that in order to check each parameter, all the parameters are constant unless the otherwise is specified and they are equal to the mentioned values. In the following, the outcomes are presented in two general subsections of entropy generation distribution and the average total irreversibility and its components.

Entropy generation distributions

  • Effect of pore density

Figure 3 examines the effect of pore density on the contour of heat transfer irreversibility components (\(N_{{{\text{HT}}}}\)). Figure 3a, b shows the heat conduction irreversibility in the solid phase (\(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\)). As is clear, (\(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\)) has a maximum value on the absorber wall. This phenomenon is due to the fact that heat flux entering the absorber plate causes a temperature gradient in the areas close to the absorber plate and increases (\(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\)) in these areas. By moving away from the absorber plate (in the \(y\) direction) due to the temperature difference decrement (\(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\)) falls down. It should be noted that the (\(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\)) changes along the length of the collector channel are not significant, because based on Eqs. 5 and 7, the temperature gradient is constant in this direction. Comparing the contours of (\(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\)) in ω = 5 PPI and ω = 40 PPI, it can be seen that increasing the pores density does not reduce the maximum value of (\(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\)), but reduces the thickness of this area. In other words, as the distance from the adsorption plate increases, the reduction amplitude rises. Figure 3c, d shows the heat conduction irreversibility in the fluid phase (\(N_{{{\text{HT,}}\left( {{\text{hnf}}} \right)}}\)). The trend of (\(N_{{{\text{HT,}}\left( {{\text{hnf}}} \right)}}\)) changes in the longitudinal and lateral directions of the channel is similar to (\(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\)) except its size is approximately 0.1 times that of (\(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\)). As the pore density grows, the temperature gradient of the fluid phase decreases in areas close to the absorber plate. Therefore, the maximum value of (\(N_{{{\text{HT,}}\left( {{\text{hnf}}} \right)}}\)) is reduced. Figure 3e, f shows the contour of the convection heat transfer irreversibility at the interface of two porous media phases (\(N_{{{\text{HT,}}\left( {{\text{int}}} \right)}}\)). This component of irreversibility is resulted from the LTNE condition. Similar to Fig. 3 (four first graphs), this contour does not change significantly along the length. In the lateral direction, it is almost symmetrical with respect to the line Y = 0.5. Since the temperature of the both porous media phases on the absorber plate and on the insulated wall is equal to each other (Eq. 10), (\(N_{{{\text{HT,}}\left( {{\text{int}}} \right)}}\)) in these areas is zero. In areas close to the plate located in the middle of the collector channel, the temperature difference between two porous media phases rises, and hence, (\(N_{{{\text{HT,}}\left( {{\text{int}}} \right)}}\)) grows. On the other hand, increasing the pore density causes the difference between the both phases temperatures decrease, and thus, (\(N_{{{\text{HT,}}\left( {{\text{int}}} \right)}}\)) goes down.

Fig. 3
figure 3

Contour plots of fluid friction, magnetic field, and total irreversibilities (effect of pore density)

Full size image

Figure 4 investigates the effect of pore density on the contour of fluid friction irreversibility (\(N_{{{\text{FF}}}}\)) contour, the magnetic field irreversibility (\(N_{{{\text{MF}}}}\)), and the total irreversibility (\(N_{{{\text{tot}}}}\)). Figure 4a shows the \(N_{{{\text{FF}}}}\) contour. This contour is symmetrical with respect to the lateral axis of Y = 0.5. In addition, the maximum value of \(N_{{{\text{FF}}}}\) occurs in the areas in the adjacency of absorption plate and the insulated wall. This phenomenon will happen since due to the no-slip condition on the plate and the wall, the velocity gradient in these areas is inherently high. By moving away from this area, the gradient decreases and \(N_{{{\text{FF}}}}\) drops down. On the other hand, close to the plate located in the middle of the channel, the velocity profile goes up; consequently, \(N_{{{\text{FF}}}}\) grows. The more the pore density, the less the permeability of the porous medium, and so, the velocity gradient increases in areas close to the wall, and the velocity becomes uniform earlier. Therefore, as the pore density increases from 5 to 40 PPI, \(N_{{{\text{FF}}}}\) growth rate in the \(y\) direction climbs up.

Fig. 4
figure 4

Contour plots of heat transfer irreversibility components (effect of porosity)

Full size image

Figure 4c, d demonstrates the \(N_{{{\text{MF}}}}\) contour. This contour, similar to the \(N_{{{\text{FF}}}}\) contour, is symmetrical and does not change significantly along the length. Due to the no-slip condition on the insulated wall and the absorber plate, the amount of \(N_{{{\text{MF}}}}\) in these two areas is zero. As pore density rises, velocity becomes uniform at a larger cross-surface of the channel. Due to the fact that the flow in channel input is also constant, so the maximum velocity falls down with pore density rise. Accordingly, as the pore density grows, the maximum of \(N_{{{\text{MF}}}}\) decreases, but the rate of changes in the \(y\) direction would intensify. Figure 4c shows the effect of the pore density on the \(N_{{{\text{tot}}}}\). As can be observed, due to a high-temperature gradient as well as the high friction in the areas close to the absorber plate, maximum \(N_{{{\text{tot}}}}\) occurs in this region. It should be mentioned that owing to the presence of friction in the areas close to the insulated wall, \(N_{{{\text{tot}}}}\) is also large in this area. The \(N_{{{\text{tot}}}}\) decreases with rise of distance from the absorber plate. In addition, as the pore density increases, \(N_{{{\text{tot}}}}\) increases. The reason for this phenomenon can be attributed to the increase in friction caused by the increase in the pore density (see Fig. 4a, b).

  • Effect of porosity

Figures 5 and 6 show the effect of porosity on the total irreversibility contour and all its components. In Fig. 5a, b, the changes of \(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\) and \(N_{{{\text{HT,}}\left( {{\text{hnf}}} \right)}}\) are plotted, respectively. According to this figure, it can be seen that increasing the porosity rises \(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\) and \(N_{{{\text{HT,}}\left( {{\text{hnf}}} \right)}}\). There is a reverse relation between porosity and solid-phase conductivity and a direct relation between porosity and fluid-phase conductivity. From the other aspect, solid conductivity is much larger than fluid conductivity (\(k_{{\text{s }}} \gg k_{{\text{f }}}\)). Therefore, thermal resistance is an increasing function of porosity. By increasing total thermal resistance, conduction decreases in the channel lateral direction. Thus, the temperature difference of both phases of the porous media and temperature of the hot wall goes up, and the heat conduction’s entropy generation increases. Figure 5c also shows the effect of porosity on (\(N_{{{\text{HT,}}\left( {{\text{int}}} \right)}}\)). In this figure, (\(N_{{{\text{HT,}}\left( {{\text{int}}} \right)}}\)) on the insulated wall and the absorber plate is zero. Based on this figure, the porosity change has no effect on (\(N_{{{\text{HT,}}\left( {{\text{int}}} \right)}}\)).

Fig. 5
figure 5

Contour plots of fluid friction, magnetic field, and total irreversibilities (effect of porosity)

Full size image
Fig. 6
figure 6

Contour plots of heat transfer irreversibility components (Hartmann number effect)

Full size image

In Fig. 6a, b the \(N_{{{\text{FF}}}}\) contours are compared in different porosities. In this case, the maximum amount of \(N_{{{\text{FF}}}}\) occurs on the insulated wall and the absorber plate. The \(N_{{{\text{FF}}}}\) distribution is also symmetrical to the Y = 0.5. According to Fig. 6a, b, it can be seen that \(N_{{{\text{FF}}}}\) is a decreasing function of the porosity. Such a reduction could be associated with increment of the high porosity medium permeability due to the porosity rise. Permeability indicates the ability and capability of a porous medium to transfer fluid through itself. Therefore, with increasing permeability, the resistance to fluid flow decreases and leads to a decrement for the \(N_{{{\text{FF}}}}\). In addition, by investigating Fig. 6c, d, it is obvious that porosity changes do not have a significant effect on \(N_{{{\text{MF}}}}\). Figure 6e, f shows the changes in \(N_{{{\text{tot}}}}\) due to the shift of porosity from 0.85 to 0.95. According to this figure, rising the porosity greatly augments the \(N_{{{\text{tot}}}}\). The justification for this augmentation is the increase in heat conduction irreversibility of the porous media phases owing to increase in porosity.

  • Effect of Hartmann number \(\left( {{\text{Ha}}} \right)\)


Figure 7 shows the \({\text{Ha}}\) trace on the heat transfer irreversibility components. As is obvious, by varying the \({\text{Ha}}\), none of the heat transfer irreversibility components change significantly. Figure 8 demonstrates \({\text{Ha}}\) effect on \(N_{{{\text{FF}}}}\), \(N_{{{\text{MF}}}}\), and \(N_{{{\text{tot}}}}\), respectively. According to Fig. 8a, b, \(N_{{{\text{FF}}}}\) has a maximum value in areas close to the insulated wall and absorber plate, as well as a relatively large distribution in the middle plate of the collector channel. The reason of this trend is the high velocity gradient in the areas beside the wall and the absorber plate and the maximum velocity in the middle plate of the channel. In addition, increasing the \({\text{Ha}}\) affects the distribution of \(N_{{{\text{FF}}}}\) and increases it. This phenomenon justification is the increase in velocity gradient due to the growth in \({\text{Ha}}\). On the other hand, as the velocity gradient increases on the wall and plate, the velocity field becomes uniform in more areas of the channel cross section and the maximum velocity decreases. Therefore, with increasing \({\text{Ha}}\), the areas close to the middle plate of the channel no longer have a relatively large distribution (blue area). Based on Fig. 8c, d, increasing the \({\text{Ha}}\) greatly reinforces the \(N_{{{\text{MF}}}}\). This point should be mentioned that the growth of \({\text{Ha}}\) does not change the overall trend of \(N_{{{\text{MF}}}}\) distribution, but rather strengthens the amplitude of the changes. Since \(N_{{{\text{MF}}}}\) is proportional to the hybrid nanofluid motion, the value of this irreversibility component on the absorber plate and the insulated wall is zero and on the middle plate of the channel is maximum. Figure 8e, f demonstrates the effect of \({\text{Ha}}\) on \(N_{{{\text{tot}}}}\). As is clear, increasing the \({\text{Ha}}\) increases the areas where the \(N_{{{\text{tot}}}}\) values are large and increases its changes’ amplitude in the \(y\) direction. The reason for this phenomenon can be attributed to the strengthening of \(N_{{{\text{MF}}}}\) due to the increase in \({\text{Ha}}\).

  • Effect of nanoparticle volume fraction

Fig. 7
figure 7

Contour plots of fluid friction, magnetic field, and total irreversibilities (\({\text{Ha}}\) effect)

Full size image
Fig. 8
figure 8

Contour plots of heat transfer irreversibility components (nanoparticle volume fraction effect)

Full size image

Figures 9 and 10 illustrate that the hybrid nanofluid’s volume fraction influences the total irreversibility contour and its components. In Fig. 9 (first four contours), the changes of \(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\) and \(N_{{{\text{HT,}}\left( {{\text{hnf}}} \right)}}\) are plotted, respectively. According to this figure, it is observed that increasing the volume fraction does not make considerable changes on the contour \(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\) and \(N_{{{\text{HT,}}\left( {{\text{hnf}}} \right)}}\). In the contour of \(N_{{{\text{HT,}}\left( {\text{s}} \right)}}\), growth of volume fraction reduces the area where entropy generation is maximum. There is a reverse trend for the \(N_{{{\text{HT,}}\left( {{\text{hnf}}} \right)}}\) contour. Similarly, increasing the volume fraction has no effect on the \(N_{{{\text{HT,}}\left( {{\text{hnf}}} \right)}}\) contour, and very slightly, it would reduce (see Fig. 9e, f). In accordance with Fig. 10a, b changing the volume fraction of hybrid nanofluid from 0 to 0.1 increases \(N_{{{\text{FF}}}}\). This is because of rise of the effective hybrid nanofluid dynamic viscosity due to the rise in volume fraction. According to Fig. 10c, d \(N_{{{\text{MF}}}}\) is increased imperceptibly due to the increase in electrical conductivity owing to hybrid nanofluid volume fraction increasing. Figure 10e, f reveals the influence of the volume fraction changes of nanoparticles on the \(N_{{{\text{tot}}}}\) contour. Based on this figure, increasing the volume fraction does not affect the maximum value of \(N_{{{\text{tot}}}}\) considerably, but reduces the area with the minimum value for \(N_{{{\text{tot}}}}\) (blue area).

Fig. 9
figure 9

Contour plots of fluid friction, magnetic field, and total irreversibilities (effect of nanoparticle volume fraction)

Full size image
Fig. 10
figure 10

Variation of average total irreversibility and its component in respect of \({\text{Re}}_{{\text{ bf}}}\): a fluid friction, b magnetic field, c heat transfer, d total, and e Bejan number (\({\text{Ha}}\) and φ effects)

Full size image

Average total irreversibility and its component analysis

  • Effect of \({\text{Ha}}\) and φ

Figure 11a represents the effect of Ha and the φ on the average fluid friction irreversibility (\(\overline{\overline{N}}_{{{\text{FF}}}}\)) as with respect to \({\text{Re}}_{{\text{ bf}}}\). As is clear, when the \({\text{Re}}_{{\text{ bf}}}\) increases, \(\overline{\overline{N}}_{{{\text{FF}}}}\) climbs up. The reason for this phenomenon is the strengthening of the velocity field due to the rise of mass flow rate of entering fluid to the collector channel. In addition, the trace of φ is much more significant than the increase in Ha. The increase of the φ causes a significant \(\overline{\overline{N}}_{{{\text{FF}}}}\) increase, specifically in large Reynolds. According to Fig. 11b, the average magnetic field irreversibility (\(\overline{\overline{N}}_{{{\text{MF}}}}\)) augments by increase of \({\text{Re}}_{{\text{ bf}}}\). In respect of this figure, it can be seen that the reinforcing of the magnetic field (in other words, the growth of Ha) leads to a noticeable augmentation in \(\overline{\overline{N}}_{{{\text{MF}}}}\). This increase obviously stems from Eqs. 19 and 28. It is noteworthy that the influence of φ on Ha varies from 5 and 100. In other words, the effect of the φ on small Ha is very small and on large Ha is noticeable.

Fig. 11
figure 11

Variation of average total irreversibility and its component with respect to \({\text{Re}}_{{\text{ bf}}}\): a fluid friction, b magnetic field, c heat transfer, d total, and e Bejan number (porosity and pore density effect)

Full size image

Figure 11c illustrates the effect of the Ha and φ on the average heat transfer irreversibility (\(\overline{\overline{N}}_{{{\text{HT}}}}\)) in respect of \({\text{Re}}_{{\text{ bf}}}\). As is clear, the \({\text{Re}}_{{\text{ bf}}}\) does not significantly change \(\overline{\overline{N}}_{{{\text{HT}}}}\), and this component of the irreversibility regarding to \({\text{Re}}_{{\text{ bf}}}\) is constant; however, increasing the Hartmann number and increasing the nanoparticle volume fraction reduce \(\overline{\overline{N}}_{{{\text{HT}}}}\). This reduction confirms the advantage of using hybrid nanofluid and magnetic fields to reduce the heat transfer irreversibility. Figure 11d shows the variation of average total irreversibility (\(\overline{\overline{N}}_{{{\text{tot}}}}\)) for different values of the Ha and φ as a function of the \({\text{Re}}_{{\text{ bf}}}\). According to this figure, the increase in \({\text{Re}}_{{\text{ bf}}}\) rises \(\overline{\overline{N}}_{{{\text{tot}}}}\), which can be attributed to the strengthening of \(\overline{\overline{N}}_{{{\text{FF}}}}\) and \(\overline{\overline{N}}_{{{\text{MF}}}}\) due to the increase in entering hybrid nanofluid mass flow rate to the collector channel. In addition, Hartmann number effect on increasing \(\overline{\overline{N}}_{{{\text{tot}}}}\) is much greater than that of φ. A special behavior is observed when the Ha is constant at 5 and the φ changes from 0 to 0.1 (black and green diagram). In this case, for \({\text{Re}}_{{\text{ bf}}} < 613\), increasing nanoparticle volume fraction causes a decrease in \(\overline{\overline{N}}_{{{\text{tot}}}}\), and there is a reverse trend for \({\text{Re}}_{{\text{ bf}}} > 613\). Moreover, in the constant \({\text{Ha}}\) = 100, if φ varies from 0 to 0.1 (red and blue diagrams), for \({\text{Re}}_{{\text{ bf}}} < 369.6\), increasing the φ reduces \(\overline{\overline{N}}_{{{\text{tot}}}}\) and it would be an inverse trend for \({\text{Re}}_{{\text{ bf}}} > 369.6\). It should be noted that the lowest \(\overline{\overline{N}}_{{{\text{tot}}}}\) occurs in \({\text{Re}}_{{\text{ bf}}} = 250\), \(\varphi = 0.1\) and \({\text{Ha}}_{{\text{ bf}}} = 5\). To analyze Bejan number (\({\text{Be}}\)), it should be noted that when \(Be > 0.5\), \(\overline{\overline{N}}_{{{\text{HT}}}}\) is greater than the sum of \(\overline{\overline{N}}_{{{\text{MF}}}}\) and \(\overline{\overline{N}}_{{{\text{FF}}}}\), heat transfer irreversibility is dominant, and for \({\text{Be}} < 0.5\), there is a reverse trend. Figure 11e shows the effect of \({\text{Ha}}\) and φ on \({\text{Be}}\) number with respect to the \({\text{Re}}_{{\text{ bf}}}\). It is clear that increasing the \({\text{Re}}_{{\text{ bf}}}\) reduces the \({\text{Be}}\) number. The reason for the decrease can be associated with the strengthening of \(\overline{\overline{N}}_{{{\text{MF}}}}\) and \(\overline{\overline{N}}_{{{\text{FF}}}}\) due to the increase in \({\text{Re}}_{{\text{ bf}}}\). In addition, \({\text{Be}}\) declines as the \({\text{Ha}}\) rises and the φ falls down. Since with increasing \({\text{Ha}}\) and φ of, \(\overline{\overline{N}}_{{{\text{HT}}}}\) decreases and \(\overline{\overline{N}}_{{{\text{MF}}}}\) and \(\overline{\overline{N}}_{{{\text{FF}}}}\) augment.

  • Effect of porosity and pore density

Figure 12a illustrates the influence of porosity and pore density on \(\overline{\overline{N}}_{{{\text{FF}}}}\) in respect of \({\text{Re}}_{{\text{ bf}}}\). Because the growth of \({\text{Re}}_{{\text{ bf}}}\) rises fluid momentum, rise of \({\text{Re}}_{{\text{ bf}}}\) rises \(\overline{\overline{N}}_{{{\text{FF}}}}\). However, there is a point that the effect of \({\text{Re}}_{{\text{ bf}}}\) on \(\overline{\overline{N}}_{{{\text{FF}}}}\) strongly depends on the pore density. In other words, the higher the pore density, the greater the effect of Reynolds number. Increasing the pore density and reducing the porosity dramatically increase \(\overline{\overline{N}}_{{{\text{FF}}}}\). An increase in \(\overline{\overline{N}}_{{{\text{FF}}}}\) can be associated with a decrease in permeability due to increase of pore density and decrement of porosity. Similarly, the effect of reducing porosity on increasing \(\overline{\overline{N}}_{{{\text{FF}}}}\) strongly depends on the pore density. Put it differently, the higher the pore density, the greater the reducing porosity effect on the increasing of \(\overline{\overline{N}}_{{{\text{FF}}}}\). Based on Fig. 12b, increasing the \({\text{Re}}_{{\text{ bf}}}\) climbs up the \(\overline{\overline{N}}_{{{\text{MF}}}}\). In addition, increasing the porosity and decreasing pore density insignificantly rise \(\overline{\overline{N}}_{{{\text{MF}}}}\). Increase in porosity and decrease in pore density reduce the velocity gradient in the areas close to the insulated wall and absorber plate. Therefore, the velocity in the smaller cross section of the channel becomes uniform. On the other hand, by constant input fluid mass flow rate to the channel and according to the mass conservation law, the maximum velocity is reduced. Ultimately, based on Eqs. 19 and 28, \(\overline{\overline{N}}_{{{\text{MF}}}}\) increases. Figure 12c shows the effect of porosity and pore density on \(\overline{\overline{N}}_{{{\text{HT}}}}\) with respect to \({\text{Re}}_{{\text{ bf}}}\). As is clear, \(\overline{\overline{N}}_{{{\text{HT}}}}\) is constant as function of \({\text{Re}}_{{\text{ bf}}}\). In addition, increasing porosity and reducing pore density climb \(\overline{\overline{N}}_{{{\text{HT}}}}\). It is noteworthy that the effect of porosity on \(\overline{\overline{N}}_{{{\text{HT}}}}\) is much greater than pore density. Increasing the porosity rises the thermal resistance of the heat transfer mechanism. As the total heat resistance increases, the heat conduction decreases in the channel lateral direction; subsequently, the heat conduction entropy generation increases. Similarly, reducing pore density reduces the interfacial area of porous media two phases (\(a_{{{\text{sf}}}}\)) and increases the heat conduction entropy generation.

Fig. 12
figure 12

Variation of average total irreversibility and its component with respect to \({\text{Re}}_{{\text{bf}}}\): a fluid friction, b magnetic field, c heat transfer, d total and e Bejan number (porosity and pore density effect)

Full size image

Figure 12d represents the \(\overline{\overline{N}}_{{{\text{tot}}}}\) changes for different values of porosity and pore density in respect of \({\text{Re}}_{{\text{ bf}}}\). Accordingly, for low pore density \(\left( {\omega = 5\,{\text{PPI}}} \right)\), the increase in \({\text{Re}}_{{\text{ bf}}}\) does not play a considerable role on changing of \(\overline{\overline{N}}_{{{\text{tot}}}}\) and in high pore density (ω = 40 PPI) it increases \(\overline{\overline{N}}_{{{\text{tot}}}}\). This phenomenon can be justified by the increment of \(\overline{\overline{N}}_{{{\text{FF}}}}\) due to the increase in Reynolds number in the different pore density. Based on Fig. 12d in a constant porosity, increasing the pore density increases the \(\overline{\overline{N}}_{{{\text{tot}}}}\). When the pore density is small in the pore density of (ω = 5 PPI), the porosity increases \(\overline{\overline{N}}_{{{\text{tot}}}}\). But if the pore density is large (ω = 40 PPI) for \({\text{Re}}_{{\text{ bf}}} < 1205\), \(\overline{\overline{N}}_{{{\text{tot}}}}\) increases with grows of porosity, and for \({\text{Re}}_{{\text{ bf}}} > 1250\), there is a reverse trend. The lowest \(\overline{\overline{N}}_{{{\text{tot}}}}\) occurs at \({\text{Re}}_{{\text{ bf}}} = 250\), ε = 0.85 and ω = 5 PPI. Figure 12e shows the effect of porosity and pore density on the \({\text{Be}}\) with respect to \({\text{Re}}_{{\text{ bf}}}\). It is obvious that increasing \({\text{Re}}_{{\text{ bf}}}\), particularly at high pore density, reduces the \({\text{Be}}\). The reason for the reduction can be attributed to the strengthening of \(\overline{\overline{N}}_{{{\text{FF}}}}\) due to the increase in Reynolds numbers (see Fig. 12a). When the pore density is constant, the increase in porosity due to the strengthening of \(\overline{\overline{N}}_{{{\text{HT}}}}\) causes \({\text{Be}}\) to grow. This point should be mentioned that the higher pore density, the larger the influence of porosity on \({\text{Be}}\). Also, while the porosity is constant, increasing the pore density due to the \(\overline{\overline{N}}_{{{\text{FF}}}}\) reinforcement reduces \({\text{Be}}\).

Conclusions

In this numerical paper, the thermal performance of a FPSC is managed by using entropy generation analysis. The channel of the collector has been completely accumulated by high porosity metal foam and is exposed to a uniform magnetic field. Al2O3–Cu/water hybrid nanofluid has been chosen in the role of the working fluid. The Darcy–Brinkman model has been employed to state the flow of working fluid, and the two-equation model has been used to explain the heat transfer through the high porosity media fluid and solid phases. Eventually, after validating the numerical solution, a precise scrutiny of the effect of pivotal factors on entropy generation is done. Some crucial points of recent article have been stated as:

  • As \({\text{Re}}_{{\text{ bf}}}\) increases, the average fluid friction irreversibility (\(\overline{\overline{N}}_{{{\text{FF}}}}\)) and average total irreversibility \(\overline{\overline{N}}_{{{\text{tot}}}}\) increase and Bejan number \(\left( {{\text{Be}}} \right)\) decreases. But the average heat transfer irreversibility \(\overline{\overline{N}}_{{{\text{HT}}}}\) is almost constant.

  • As \({\text{Ha}}_{{\text{ bf}}}\) increases, \(\overline{\overline{N}}_{{{\text{tot}}}}\) increases and \({\text{Be}}\) and \(\overline{\overline{N}}_{{{\text{HT}}}}\) decreases. Reducing \(\overline{\overline{N}}_{{{\text{HT}}}}\) resulted from the magnetic field confirms the advantage of using this field to reduce the heat transfer irreversibility. \(\overline{\overline{N}}_{{{\text{FF}}}}\) also increases slightly.

  • As φ increases, \(\overline{\overline{N}}_{{{\text{FF}}}}\) increases, \(\overline{\overline{N}}_{{{\text{HT}}}}\) and \(Be\) decreases. Reducing \(\overline{\overline{N}}_{{{\text{HT}}}}\) through the use of hybrid nanofluid confirms the advantage of using these materials to decrease heat transfer irreversibility. Moreover, when magnetic field is weak, for \({\text{Re}}_{{\text{ bf}}} < 613\), increase of φ declines \(\overline{\overline{N}}_{{{\text{tot}}}}\), and a reverse trend for \({\text{Re}}_{{\text{ bf}}} > 613\) is observed. However, if the magnetic field is strong, for \({\text{Re}}_{{\text{ bf}}} < 369.6\), increasing the nanoparticle volume fraction reduces \(\overline{\overline{N}}_{{{\text{tot}}}}\), and the reverse trend for \({\text{Re}}_{{\text{ bf}}} > 369.6\) is observed.

  • Increasing the \(\omega\) increases \(\overline{\overline{N}}_{{{\text{FF}}}}\) and \(\overline{\overline{N}}_{{{\text{tot}}}}\) and decreases \(\overline{\overline{N}}_{{{\text{HT}}}}\). As a result, increasing pore density reduces \({\text{Be}}\).

  • Due to the heat flux absorbed through the adsorption wall, the maximum value of irreversibility due to heat transfer occurs on the adsorption wall.

  • Due to the high shear stress in the areas close to the insulated wall and the adsorption plate, the maximum value of fluid friction irreversibility occurs in the areas close to these solid walls.

  • Since the velocity at the middle plate of the channel is maximum, the maximum value of magnetic field irreversibility occurs on this plate.