Introduction

High share of renewable energy can affect the behavior of global energy matrix [1]. This is, however, somewhat challenging due to a number of technical and economic reasons. For example, wind and solar, which are among the most popular sources, are available on irregular profiles [2]. Of the possible solutions for stabilization of energy output of such systems, the most reliable method is using energy storage systems together with the renewable production plant [3]. This includes both heat and electricity storage systems. Heat storage devices come into the main categories of thermochemical storage and heat storage approaches [4]. Sensible storage method is the one in which the stored energy causes an increase in the temperature of the storage medium, and the latent heat storage method is the approach in which the stored heat leads to a change in the phase of the storage tank [5]. The medium of storage is called PCM and makes this method of heat storage the most effective technique among others due to its great energy density, requiring a smaller volume to store heat [6].

Owing to the variation of phase changing temperatures and good chemical stability, PCMs may be found in many applications [7]. In spite of several outstanding features, PCMs suffer from the main drawback of low conductivity that causes the low performance for unit. Using various ways [8,9,10,11] such as using microencapsulation, heat pump, metallic fins and metal foam, is some of the solutions proposed for overcoming this drawback of PCMs. One of the other effective solutions proposed for enhancing thermal features is nanoparticles, so-called nano-enhanced PCMs (NEPCMs) [12].

Knowing the concept of NEPCM, a large number of investigations were reported to scrutinize the effect of using such materials in various applications. Dadvand et al. [13] accomplished melting phenomena within a tank with various hot plates and concluded that the greatest charging rate occurs when hot plate is situated in the bottom side.

Petrovic et al. [14] scrutinized the effect of nanomaterials in cooling with microchannel. Their outcomes revealed that H2O–NEPCM slurry has greater efficiency than base fluid. Sheikholeslami and Mahian [15] proposed and numerically investigated the augmentation of discharging performance with impose of magnetic force and dispersing nanosized powders. Sheikholeslami et al. [16] analyzed the heat transfer behavior of a NEPCM with insertion of fins and showed favorable impact of fins. In another work, the same group assessed the effect of Hartmann number on NEPCM solidification time within a permeable structured unit [17]. Kumar et al. [18] scrutinized efficiency of heat pipe utilizing NEPCM for unsteady cooling and proved that three Kelvin reduction in surface temperature with the use of heat pipe. Hosseinizadeh et al. [19] scrutinized the unrestrained charging process of a PCM with the use of nanopowders within a spherical tank. Ebrahimi and Dadvand [20] analyzed the melting of NEPCM and found out that the highest liquid fraction is achieved when sinks and sources were consecutively situated on two vertical surfaces.

In one of the latest studies in this framework, Sheikholeslami [21] used a finite element method for numerically scrutinized the discharging of a PCM in the existence of CuO nanoparticles in various shapes and concluded that the greatest rate is achieved for platelet CuO. In another work, Sheikholeslami et al. [22] examined the influence of nanopowders and radiation terms on solidification. Their results showed that solid fraction might be improved with the augment of radiation term. Just in line with two abovementioned works, this study aims at analyzing the second law behavior and entropy generation rate of a porous structured LHTES with a NEPCM under the impact of a magnetic field. The impacts of magnetic force, buoyancy, concentration of nanomaterial on the solid fraction, entropy generation rates (due to thermal effect, friction effect and magnetic effects) and Bejan number are the main parameters examined in this study. Here, Darcy’s law is used for modeling the porous media and the numerical solution method of the Galerkin finite element method is implemented in FlexPDE software.

Problem description

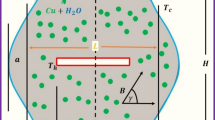
In the current section, the enclosure of the understudy problem is explained. Figure 1 depicts the porous structured tank with a NEPCM instead of a pure PCM. The nanoparticle is employed to reinforce conduction. A horizontal magnetic field is imposed to the NEPCM bed to accelerate the solidification process. The objective is to do a second law analysis of the discharge process (i.e., the solidification process).

Fig. 1
figure 1

2D schematic of porous structured tank

Full size image

The features of the PCM and the CuO particles used for increasing the thermal conductivity of the storage medium are mentioned in Table 1.

Table 1 Characteristics of H2O and particles
Full size table

Formulation

For the solidification process of a NEPCM in a permeable media based on Darcy model, the following equations can be used:

$$ \left( {\mathop g\limits^{ \to } \rho_{\text{nf}} - \nabla p - \mathop B\limits^{ \to } \times \mathop I\limits^{ \to } } \right) = \mathop V\limits^{ \to } \frac{{\mu_{\text{nf}} }}{K} $$
(1)
$$ \nabla \cdot \mathop V\limits^{ \to } = 0 $$
(2)
$$ \left( {\rho C_{p} } \right)_{\text{nf}} \frac{{{\text{d}}T}}{{{\text{d}}t}} = \nabla \left( {k_{\text{nf}} \nabla T} \right) + L_{\text{nf}} \frac{{{\text{d}}S}}{{{\text{d}}t}} $$
(3)
$$ \left\{ {\begin{array}{*{20}l} {S = 2T_{0}^{ - 1} (0.5T_{\text{m}} + T_{0} - 0.5T)} \hfill & {\left( {T_{\text{m}} - T_{0} } \right) < T < \left( {T_{\text{m}} + T_{0} } \right)} \hfill \\ {S = 1} \hfill & {T < T_{\text{m}} - T_{0} } \hfill \\ {S = 0} \hfill & {T > T_{\text{m}} + T_{0} } \hfill \\ \end{array} } \right. $$
(4)
$$ \begin{aligned} & \left( {\mathop V\limits^{ \to } \times \mathop B\limits^{ \to } - \nabla \varphi } \right)\sigma_{\text{nf}} = \mathop I\limits^{ \to } , \\ & \nabla \cdot \mathop I\limits^{ \to } = 0 \\ \end{aligned} $$
(5)

where V is the velocity vector, ρ is the density, k refers to the thermal conductivity, p represents the pressure, μ is the kinetic viscosity, T is the temperature, I is the electrical current, and L, B and S are the length, magnetic force and entropy, respectively.

Neglecting the electric field effect in the above formulation, one might rewrite them as:

$$ \frac{\partial v}{\partial y} + \frac{\partial u}{\partial x} = 0 $$
(6)
$$ u = - \frac{{K\sigma_{\text{nf}} B_{0}^{2} }}{{\mu_{\text{nf}} }}\left( { + v\cos \gamma \sin \gamma - u\sin^{2} \gamma } \right) - \frac{K}{{\mu_{nf} }}\frac{\partial p}{\partial x} $$
(7)
$$ - \frac{K}{{\mu_{\text{nf}} }}\frac{\partial p}{\partial y} - \frac{{\sigma_{\text{nf}} KB_{0}^{2} }}{{\mu_{\text{nf}} }}\left( { - v\cos^{2} \gamma } \right) + {\text{Kg}}\frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\mu_{\text{nf}} }}\left( {T - T_{\text{c}} } \right) = v + u\frac{{B_{0}^{2} }}{{\mu_{\text{nf}} }}K\sigma_{\text{nf}} \cos \gamma \sin \gamma $$
(8)
$$ \left( {\rho C_{\text{p}} } \right)_{\text{nf}} \frac{{{\text{d}}T}}{{{\text{d}}t}} = \nabla \left( {k_{\text{nf}} \nabla T} \right) + L_{\text{nf}} \frac{{{\text{d}}S}}{{{\text{d}}t}} $$
(9)
$$ \left\{ {\begin{array}{*{20}l} {S = 2T_{0}^{ - 1} (0.5T_{\text{m}} + T_{0} - 0.5T)} \hfill & {\left( {T_{\text{m}} - T_{0} } \right) < T < \left( {T_{\text{m}} + T_{0} } \right)} \hfill \\ {S = 1} \hfill & {T < T_{\text{m}} - T_{0} } \hfill \\ {S = 0} \hfill & {T > T_{\text{m}} + T_{0} } \hfill \\ \end{array} } \right. $$
(10)

in which γ is the angle of the imposed magnetic field. The terms (ρcp)nf, ρnf, (ρβ)nf, σnf and (ρL)nf in the above correlations can be calculated as follows:

$$ \left( {\rho C_{\text{p}} } \right)_{\text{nf}} = \left( {\rho C_{\text{p}} } \right)_{\text{f}} (1 - \phi ) + \phi \left( {\rho C_{\text{p}} } \right)_{\text{p}} $$
(11)
$$ \rho_{\text{nf}} = \phi \rho_{\text{p}} + (1 - \phi )\rho_{\text{f}} $$
(12)
$$ \left( {\rho \beta } \right)_{\text{nf}} = \left( {\rho \beta } \right)_{\text{s}} \phi + (1 - \phi )\left( {\rho \beta } \right)_{\text{f}} $$
(13)
$$ \frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }} - 1 = \frac{{ - 3\left( {1 - \frac{{\sigma_{\text{s}} }}{{\sigma_{\text{f}} }}} \right)\phi }}{{\left( {1 - \frac{{\sigma_{\text{s}} }}{{\sigma_{\text{f}} }}} \right)\phi + \left( {2 + \frac{{\sigma_{\text{s}} }}{{\sigma_{\text{f}} }}} \right)}} $$
(14)
$$ \left( {\rho L} \right)_{\text{nf}} = \left( {\rho L} \right)_{\text{f}} (1 - \phi ) $$
(15)

The terms knf and μnf can be estimated via [23]:

$$ \begin{aligned} & g^{{\prime }} \left( {d_{\text{p}} ,T,\phi } \right) = \left( {a_{5} {\text{Ln}}\left( {d_{\text{p}} } \right)^{2} + a_{4} {\text{Ln}}\left( \phi \right){\text{Ln}}\left( {d_{\text{p}} } \right) + a_{2} {\text{Ln}}\left( {d_{\text{p}} } \right) + a_{1} + a_{3} {\text{Ln}}\left( \phi \right)} \right){\text{Ln}}\left( T \right) \\ & \quad \quad \quad \quad \quad \quad + \left( {a_{7} {\text{Ln}}\left( {d_{\text{p}} } \right) + a_{10} {\text{Ln}}\left( {d_{\text{p}} } \right)^{2} + a_{8} {\text{Ln}}\left( \phi \right) + a_{9} {\text{Ln}}\left( \phi \right){\text{Ln}}\left( {d_{\text{p}} } \right) + a_{6} } \right) \\ & \kappa = k_{\text{p}} /k_{\text{f}} ,\frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = 1 - 3\frac{{\left( { - \kappa + 1} \right)\phi }}{{\phi \left( {1 - \kappa } \right) + \left( {2 + \kappa } \right)}} + 5 \times 10^{4} \rho_{\text{f}} g^{{\prime }} (d_{\text{p}} ,T,\phi )\phi \sqrt {\frac{{\kappa_{\text{b}} T}}{{\rho_{\text{p}} d_{\text{p}} }}} c_{{{\text{p}},{\text{f}}}} \\ \end{aligned} $$
(16)
$$ \mu_{\text{eff}} = \left( {1 - \phi } \right)^{ - 2.5} + \frac{{k_{\text{Brownian}} }}{{k_{\text{f}} }} \times \frac{{\mu_{\text{f}} }}{{\Pr_{\text{f}} }} $$
(17)

Table 2 presents the value of constant coefficients that are required for modeling the CuO–water-based nanofluid, in the above formulations.

Table 2 Values of ai in Eq. (16)
Full size table

By employing \( \psi \), with the below format, the shape of equations has been changed:

$$ - \frac{\partial \psi }{\partial x} = v,\;\frac{\partial \psi }{\partial y} = u $$
(18)

Hartman and Rayleigh numbers are defined as:

$$ {\text{Ha}} = \frac{{\sigma_{\text{f}} KB_{0}^{2} }}{{\mu_{\text{f}} }},\;{\text{Ra}} = \left( {\alpha_{\text{f}} \mu_{\text{f}} } \right)^{ - 1} \Delta T\left( {\rho \beta } \right)_{\text{f}} {\text{Lg}}K $$
(19)

Total energy and average temperate are also defined as follows, respectively:

$$ E_{\text{total}} = \int {\left( {\left( {\rho C_{\text{p}} } \right)_{\text{nf}} T + (s)\left( {\rho L} \right)_{\text{nf}} } \right){\text{d}}V} $$
(20)
$$ T_{\text{ave}} = \frac{{\int {T{\text{d}}A} }}{{\int {{\text{d}}A} }} $$
(21)

Finally, the target functions of the current study, i.e., entropy generation rate and Bejan number, could be calculated, respectively, by:

$$ \begin{aligned} S_{\text{gen,total}} = & \underbrace {{\frac{{k_{\text{nf}} }}{{T^{2} }}\left[ {\left( {\frac{\partial T}{\partial x}} \right)^{2} + \left( {\frac{\partial T}{\partial y}} \right)^{2} } \right]}}_{{S_{\text{gen,th}} }} + \underbrace {{\frac{{\mu_{\text{nf}} }}{{T^{2} }}\left[ {\left( {\frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}} \right)^{2} + 2\left( {\left( {\frac{\partial u}{\partial x}} \right)^{2} + \left( {\frac{\partial v}{\partial y}} \right)^{2} } \right)} \right]}}_{{S_{\text{gen,f}} }} \\ & \quad + \underbrace {{\frac{{\sigma_{\text{nf}} }}{{T^{2} }}B_{0}^{2} v^{2} }}_{{S_{\text{gen,M}} }} \\ \end{aligned} $$
(22)
$$ {\text{Be}} = S_{\text{gen,th}} /S_{\text{gen,total}} $$
(23)

Numerical approach and validation

Presenting information about the problem, the governing equations and the study objectives so far, the solution method and tool as well as the verification of the employed model in this article is presented in this section. As mentioned before, the discharging process has been modeled by means of FEM in which mesh refinement was considered (Fig. 2).

Fig. 2
figure 2

Shape of grid in different times at φ = 0.04, Ra = 5 and Ha = 1

Full size image

To show the accuracy of the solution method used in the current work, the outputs were compared with an old study of Ismail et al. [24] in Fig. 3 and proved the simulation and empirical outputs are in good agreement.

Fig. 3
figure 3

Verification of this work with comparing the experimental study by Ismail et al. [24]

Full size image

Various numerical methods were suggested for modeling nanomaterial behavior [25,26,27,28,29,30,31]. An improvement in carrier fluid properties with impose of nanoparticles was mentioned in the recent articles [32,33,34,35,36,37,38,39].

Results and discussion

In this section, the obtained results via the validated solution method were presented and discussed. As mentioned, the study focuses on the investigation of the influences of variation of nanofluid volume fraction (in the range of φ = 0 to 0.04), Ha number (in the range of Ha = 1 to 10) and buoyancy effect (in the range Ra = 10 to 100) on various parameters of the thermal storage unit during a discharge (solidification) process. The target parameters include the solid fraction, entropy generation rate due to various effects and Be number.

Figure 4 illustrates the contours of these four parameters on the storage medium (i.e., solid fraction, Sgen,th, Sgen,f, Sgen,M and Be number) at three different time steps.

Fig. 4
figure 4figure 4

Contours of solid fraction, Sgen,th, Sgen,f, Sgen,M and Be number when Ha = 1, Ra = 5 and φ = 0.04

Full size image

Figure 5 illustrates the contours of these four parameters on the storage medium (solid fraction, Sgen,th, Sgen,f, Sgen,M and Be number) with the aim of investigating the effect of increasing the Ha number and keeping other conditions the same as before. This time φ = 0.04, Ra = 5, and Ha = 10.

Fig. 5
figure 5figure 5

Contours of solid fraction, Sgen,th, Sgen,f, Sgen,M and Be number when Ha = 10, Ra = 5 and φ = 0.04

Full size image

In a similar manner, Fig. 6 depicts the contours of the four focused parameters of this study (i.e., solid fraction, Sgen,th, Sgen,f, Sgen,M and Be number). This time, however, the objective is to see the effect of changing the Ra number from 5 to 50. Thus, for this examination, one has: φ = 0.04, Ha = 1 and Ra = 50.

Fig. 6
figure 6figure 6

Solid fraction, Sgen,th, Sgen,f, Sgen,M and Be number contours at Ra = 50, Ha = 1 and φ = 0.04

Full size image

Figure 7 shows the effects of increasing both the Ha and Ra numbers to the maximum values considered for their ranges in this study, i.e., 10 and 50 respectively, on the contours of the four parameters of Sgen,th, Sgen,f, Sgen,M and Be number when the nanofluid concentration is kept at φ = 0.04 yet.

Fig. 7
figure 7figure 7

Solid fraction, Sgen,th, Sgen,f, Sgen,M and Be number contour plots when Ra = 50, Ha = 10 and φ = 0.04

Full size image

Considering the above four figure sets, one could easily interpret how the four considered parameters of this study (the entropy generation terms and Be number) vary as one or some of the variables (φ, Ha and Ra numbers) change. For making this more readable, the following figure set (Fig. 8) presents a number of plots for the variation of each of these four parameters over time when one of the Ra or Ha numbers is kept constant and other one changes upward. In other words, in these plots, either Ra is constant at 50 and Ha changes from 1 to 10, or Ha is constant at 1 and Ra changes from 5 to 50. In all of these plots, φ is set at 0.04.

Fig. 8
figure 8figure 8

Average solid fraction, Sgen,th, Sgen,f, Sgen,M and Be number variations when one of the Ra or Ha numbers changes while the other is constant

Full size image

According to the figures, the solid fraction increases by almost the same rate over time when Ha number is constant at 1 and Ra number goes up. The same trend can be seen for this parameter (solid fraction) when Ra is constant at 50 and Ha number increases.

The rate of Sgen,th (at a constant Ha number) has a declining trend. This trend is exactly similar for all the Ra numbers during the first 450 s, and thereafter, the effect of increasing the Ra number shows its effect of decreasing the rate of entropy generation. On the other hand, keeping the Ra constant at 50, the descending trend of entropy generation due to the heat transfer effect slows down mildly after t = 450 s when the Ha number is increased from 1 to 10.

Regarding the entropy generation due to the friction effects at the constant Ha number of 1, as can be seen, there is a very big difference between the trend of the graph at low and high Ra numbers. Indeed, when Ra number is set at 5 and 10, the entropy generation profile is almost uniform and close to 0 while this rate increases to the high value of about 250 at t = 0 when Ra = 50 and it gradually decreases as time passes. On the other hand, this term is in a reverse relation to Ha number and it considerably decreases (from about 240 at t = 0 to just above 0) as the Ha number increases from 1 to 10 while Ra is fixed at 50.

With respect to the entropy generation term due to the magnetic field effect, almost similar manner as that observed for the entropy generation due to friction is seen again. This means that as a constant Ha number, the increase in Ra number to 50 significantly increases the entropy generation rate due to the magnetic field effect while for the other two values this rate is almost zero during the entire discharging process. In contrast, as Ra number is fixed at 50 and Ha number increases, the effect is reverse and the entropy generation rate decreases, though even in Ha = 1 and t = 0, Sgen,M is about 2 and it gradually decreases as the discharging process continues. The maximum value of Sgen,M, in this case, is about 7.5 when Ha = 10 and t = 200 s.

Finally, the Be number, which is defined as the ratio of the thermal entropy generation term to the total rate of entropy generation, is investigated in the last couple of plots. The plots show that the increase in the Ra number decreases the Be number and the value of Be number increases with almost the same trend for all Ra values (5, 10 and 50) as time goes forward. And expectedly, as the Ha number increases, in a constant Ra number, the value of Be number goes up significantly. This value, though, increases by the same pace as time passes for both of the cases of Ha = 1 and Ha = 10.

Conclusions

In the current investigation, the improvement in the discharging rate of a NEPCM through a porous structured thermal storage system under a magnetic field effect is investigated. Indeed, dispersing the CuO nanoparticles into H2O and imposing a magnetic field were the two ways which have been employed to expedite the discharging process, and this study considers this process in terms of a second law point of view. Simulation is presented by means of the numerical method of FEM. Here, the influences of active parameters on the solid fraction, and entropy generation rates (due to thermal effect, friction effect and magnetic effects) and Bejan number are the main parameters examined in the current article. The outputs revealed that the solid fraction augments by almost the same rate over time when Ha number is constant and Ra number goes up or Ra is constant and Ha number increases. The rate of Sgen,th has a declining trend with time always where increasing the Ra number decreases this parameter. Sgen,f has a direct relation to Ra number (it goes up as Ra augments) and it gradually decreases as time passes. This term is also in a reverse relation to Ha number, and it decreases as Ha number increases. With respect to the Sgen,M, the increase in Ra number increases the value of this item and in contrast an increase in the table number decreases this term. In the end, the investigations showed that the Be number decreases as Ra number picks up, while as the Ha number increases, the Be number goes up sharply.