Introduction

Heat transfer enhancement is known as one of the most important factors in improving the performance of thermal systems in industries, such as electronics, aerospace and steel. Air tends to be used as a coolant in most heat transfer applications due to its easy availability and low cost. However, air cooling is confined to the application of low heat fluxes and better results could be generated from the fluids with high Prandtl numbers and phase changes (boiling) of the coolant liquid. A need for better heat transfer has obliged researchers to design and perform professional heat treatment methods such as quenching jet impingement. The boiling phenomenon in quenching jet impingement is generally categorized into three boiling regimes based on the superheat of solid surfaces and the type of contact between the solid and fluid. As the heat transfer rate of lower values of wall superheat is high in nucleate boiling regime, it might be an ideal regime for thermal control processes [1, 2].

The fundamentals of jet impingement boiling were first investigated by Copeland [3]. Katto and Kunihiro [4] utilized water jet to remove vapor mass in a pool boiling process. Over the last few decades, a large number of studies into jet impingement boiling have been conducted. Qiu et al. [5] reviewed the development of jet impingement boiling heat transfer in studies already done in the past two decades. Most of the studies in this field were experimental. Liu et al. [6] analytically and numerically studied the boiling heat transfer of water jet impingement on a hot surface to determine local Nusselt number. Mozumder et al. [7] conducted research on quenching during an experiment with water jet impinging on steel, copper and brass blocks with a range of velocities, 3–15 m s−1, subcooling temperature of 50–80 K and initial block temperature of 250–600 °C. The study concluded that maximum heat flux would increase with a rise in water jet velocity and subcooling temperature. Much research has been conducted into influences of hydrodynamic and thermal specifications on the performance of impinging jets. Abo El-Nasr et al. [8] implemented some experimental and numerical research to study the quenching of a hot cylinder with a subcooled, round and perpendicular water jet and examined the effect of initial temperature, water temperature, jet velocity, height and diameter. They observed that when subcooling temperature, jet velocity and jet diameter increase, cooling rate increases. Choi et al. [9] experimentally investigated the convective boiling and local heat transfer characteristics in the process of a jet impingement of dielectric fluid FC-72 in a cross-flow configuration and optimized the heat transfer coefficient for blowing ratio of 1:5. On the other hand, the impacts of impingement surface refinement on heat transfer have been studied by different researchers. Ndao et al. [10] did some experiments on flow boiling heat transfer of R134a jet, impinged on smooth and enhanced surfaces with microstructure, including circular, hydrofoil and square micro-pin-fins. Resulted boiling curves indicated that circular pin-fins showed better thermal performance than others and larger diameters lead to higher heat transfer coefficients. Joshi and Dede [11] worked on two-phase jet impingement cooling of high heat flux wide-band-gap devices using multiscale porous surfaces. Wang et al. [12] conducted a research on the influences of nanoscale surface modification on heat transfer characteristics in high-velocity small slot jet impingement. The results showed that decreasing contact angle of the solid–liquid could enhance the heat transfer coefficient, but decay the critical heat flux.

Unlike the experimental studies, a limited number of numerical studies into jet impingement boiling heat transfer have been reported. Narumanchi et al. [1] investigated nucleate boiling in a submerged jet impingement in power electronics cooling employing the Eulerian multiphase model and Rensselaer Polytechnic Institute (RPI) as a wall-boiling model. They established a tool which can be used for thermal design of two-phase jet impingement cooling systems in the power electronics. Following their study, Abishek et al. [13] used the RPI method to computationally simulate subcooled jet impingement boiling in confined and submerged configurations, but the effect of conjugation was not considered. They found that beyond a threshold value of surface superheat, the heat flux resulted by quenching was the largest contributor to the total heat flux. Qiu et al. [14] used the RPI model to simulate jet impingements in submerged and confined configurations and indicated the great effect of conjugation on boiling heat transfer. Toghraie [15] presented a numerical method using the VOF method to simulate the flow boiling through subcooled water jet, impinged on a heated surface and showed that by increment in water jet velocity, convective heat transfer coefficient at stagnation point increases. Kobayashi et al. [16] defined a CFD model, employing the two-phase Eulerian model, to simulate quenching in a cylindrical water jet impingement and analyzed the quenching process of a moving steel plate by multiple jets. In another numerical study, the influence of patterned target surfaces on jet impingement heat transfer in disparate Reynolds numbers and plate materials was investigated by Dobbertean and Rahman [17]. It was observed that increases in indentation depth of rectangular surfaces, unlike triangular patterns, would lead to a decrease in local heat transfer coefficient.

Hot steel plates with liquid jet impingement are quenched to thermally control the process of steel production or rapidly cool nuclear reactors. Since the block temperature at the beginning of the jet impingement cooling process can be up to 1000 °C, it could be considered a quenching process, if cooled unsteadily over a period of time [7]. Limited studies into jet impingement quenching have been done [18,19,20,21], and some analyses of heat flux, temperature and flow field have been represented so far [22]. Since transported heat in jet impingement quenching tends to be very high, preventing the block distortion caused by non-uniform cooling can be a vital matter; thus, temperature uniformity should be paid attention during the cooling process. Due to the fact that measuring surface temperature directly during quenching is usually impossible [23], numerical simulations for analyzing such problems might be very important. Also, attentions were paid to the numerical analyses of heat transfer and fluid flow characteristics in single- and two-phase configurations with Newtonian and non-Newtonian nanofluid as working fluids in recent years [24,25,26].

Despite some numerical studies on jet impingement quenching, there is still a lack of comprehensive numerical study employing the volume of fluid (VOF) method to simulate the phenomena, since it is the best method to capture the interface of fluid–fluid. The present work made an effort to investigate the effects of two pulsatile nozzle inlets as a Heaviside function of time on a newly defined factor named optimized cooling factor (OCF) and standard temperature uniformity index (STUI) in the solid, during a quenching process. To the knowledge of the authors, no work was found in the literature considering simultaneous pulsating flow of two jets in the quenching process. Also, to simulate the above-mentioned phenomena, the impacts of mass transfer and conjugation are added to a solver in the OpenFOAM open-source code [27] and validated successfully.

Geometry and computational domain

Two subcooled water jets with the jet width of \(D_{\text{j}}\) and jet-to-jet spacing of S perpendicularly are impinged to a superheated block located in a distance of H from nozzle inlets. Length and thickness of the solid are \(t_{\text{wall}}\) and L, respectively. A dimensionless schematic of geometry of the problem is illustrated in Fig. 1.

Fig. 1
figure 1

Geometry and boundary conditions of the problem

Full size image

Since there are no changes in Z-direction, a two-dimensional mesh considering solution time is established. In low Reynolds number jets (500–2000), 2D analysis of impinging jets is expected in order to reach quite accurate results.

As periodic jets induced by pulsating nozzles can disturb the boundary layer and affect the local heat transfer rates, they received increasing research attention for their potential in heat and mass transfer enhancement. Some previous studies have focused on optimizing single-jet configurations, so there is a need to examine the effect of the pulsation on boiling of multiple impinging jets. In this manner, the Heaviside function of time is considered to be applied on the nozzles. In contrary to sinusoidal function, applying this function to nozzle inlets induces high momentum jet for a period of time, after that a periodic break is provided. It also has the advantage of keeping the total liquid consumption constant. The velocities in the inlets are defined in Eq. (1) as:

$$V_{\text{j}} \left( t \right) = \left\{ {\begin{array}{*{20}l} {V \times \left( {H\left( {t - 2n_{\text{st}} P} \right) - H\left( {t - \left( {2n_{\text{st}} + 1} \right)P} \right)} \right)} \hfill & {n_{\text{st}} \ge 0\; {\text{nozzle}}\; 1} \hfill \\ {V \times \left( {H\left( {t - \left( {2n_{\text{st}} - 1} \right)P} \right) - H\left( {t - 2n_{\text{st}} P} \right)} \right)} \hfill & {n_{\text{st}} \ge 1 \;{\text{nozlle }}\;2} \hfill \\ \end{array} } \right.$$
(1)

At every moment of all cases, just one jet is impinged to the surface. The inlet velocity of the second nozzle is inverse of the first one, i.e., when the first jet is on, the second one is off and vice versa. Accordingly, coolant consumption in two-jet and one-jet configurations is equal. H(t) is a Heaviside function of time which is employed in this equation, where V is the constant value of inlet velocity, P is the period of pulse (the time of inlets being open), and \(n_{\text{st}}\) is the step counter and is defined as the number of steps taken to achieve a specific time. Figure 2 displays the variations in both nozzles velocity by time at two different periods of pulse.

Fig. 2
figure 2

Velocity inlet variations as a function of time at different values of period of pulse (P) during 1 s, at: a first nozzle, b second nozzle

Full size image

Jet width \(\left( {D_{\text{j}} } \right)\), solid thickness (\(t_{\text{wall}}\)) and initial solid temperature (\(T_{\text{init}}\)) in all of the cases are constant and equal to 1.6 mm, 5 mm and 1150 K, respectively. In all simulations, only the geometry is altered and the governing equations of the problem remained unchanged.

Mathematical formulation

Governing equations

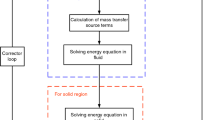
The VOF method first presented by Hirt and Nichols [28] has created a new way to simulate multiphase flows, providing the knowledge of whether the computational cell is occupied by one fluid or the other or both of them. In computational fluid dynamics, VOF is a numerical method which tracks and locates the interface of fluid–fluid, belonging to Eulerian–Eulerian multiphase models. The formulation of VOF is unique because it is based on the assumption that two or more fluids (phases) are immiscible. In this method, the sum of volume fractions of all phases equals the unity in every control volume.

$$\mathop \sum \limits_{i = 1}^{n} \alpha_{i} = 1$$
(2)

where \(\alpha\) represents the volume of one phase to the volume of the cell. When the cell contains vapor, \(\alpha = 0\); when it contains liquid, \(\alpha = 1\); and when the cell contains the interface, it changes from 0 to 1:

$$\alpha_{\text{l}} \left({\vec{x}.t} \right) = \frac{{V_{\text{l}}}}{V} = \left\{{\begin{array}{*{20}l} 1 \hfill & \quad {\vec{x} \;\epsilon \;{\text{liquid}}\;{\text{phase}}} \hfill \\ {0 < \alpha_{\text{l}} < 1 } \hfill & \quad { \vec{x}\;\epsilon \;{\text{interface}}} \hfill \\ 0 \hfill & \quad { \vec{x}\;\epsilon \;{\text{gas}}\;{\text{phase}}} \hfill \\ \end{array}} \right.$$
(3)

Physical properties of vapor and liquid, including density, viscosity, thermal conductivity and specific capacity in the interface, can linearly change based on Eq. (4):

$$\beta = \beta_{\text{l}} \alpha_{\text{l}} + \beta_{\text{g}} \left( {1 - \alpha_{\text{l}} } \right)$$
(4)

where \(\beta\) is representative of such properties. In the phase change process, mass tends to change locally, with total mass remaining unchanged. Therefore, general continuity equation would be as:

$$\frac{\partial \rho }{\partial t} + \nabla \cdot \left( {\rho \vec{U}} \right) = 0$$
(5)

By replacing density from Eq. (4) into Eq. (5), transport equation of the interface locating it at every time step could be:

$$\frac{{\partial \alpha_{\text{l}} }}{\partial t} + \vec{U} \cdot \nabla \alpha_{\text{l}} + \alpha_{\text{l}} \nabla \cdot \vec{U} = - \frac{{\rho_{\text{g}} }}{{\left( {\rho_{\text{l}} - \rho_{\text{g}} } \right)}}\nabla \cdot \vec{U}$$
(6)

In this equation, for incompressible flows including no phase change, however, \(\nabla \cdot \vec{U}\) is defined as:

$$\nabla \cdot \vec{U} = \dot{m}^{\prime \prime \prime } \left( {\frac{1}{{\rho_{\text{g}} }} - \frac{1}{{\rho_{\text{l}} }}} \right)$$
(7)

In processes involving the phase change, by inserting Eq. (7) to Eq. (6), the transport equation of the volume fraction field would be:

$$\frac{{\partial \alpha_{l} }}{\partial t} + \vec{U} \cdot \nabla \alpha_{\text{l}} = \dot{m}^{\prime \prime \prime } \left[ {\frac{1}{{\rho_{\text{l}} }} - \alpha_{\text{l}} \left( {\frac{1}{{\rho_{\text{l}} }} - \frac{1}{{\rho_{\text{g}} }}} \right)} \right]$$
(8)

The momentum equation could be written by:

$$\frac{{\partial \rho \vec{U}}}{\partial t} + \nabla \cdot \left( {\rho \vec{U}\vec{U}} \right) = - \nabla p + \nabla \cdot \left( {\mu \left( {\nabla \vec{U}^{T} + \nabla \vec{U}} \right)} \right) + \overrightarrow {{f_{\text{st}} }} + \overrightarrow {{f_{\text{g}} }}$$
(9)

where the momentum source term \(\overrightarrow {{f_{\text{st}} }}\) is representative of the surface tension force, obtained from the continuous surface force (CSF) model [29], and \(\overrightarrow {{f_{\text{g}} }}\) is gravity force. The surface tension force is generally calculated on the interface and considered perpendicular to it.

$$\overrightarrow {{f_{\text{st}} }} = \sigma \kappa \nabla \alpha_{\text{l}}$$
(10)

In this equation, \(\sigma\) is surface tension, and curvature of the interface is achieved by:

$$\kappa = - \nabla \cdot \left( {\frac{{\nabla \alpha_{\text{l}} }}{{\left| {\left. {\nabla \alpha_{\text{l}} } \right|} \right.}}} \right)$$
(11)

Equation (11) is valid here, since the surface tension is considered constant. The energy equation is defined as Eq. (12), where the source term on the right side of the equation represents the heat transferred by the phase change:

$$\frac{{\partial \rho c_{\text{p}} T}}{\partial t} + \nabla \cdot \left( {\vec{U} \cdot \rho c_{\text{p}} T} \right) = \nabla \cdot \left( {\lambda \nabla T} \right) + \dot{m}^{\prime \prime \prime } h$$
(12)

Mass transfer model

To close the equations, a mass transfer model should be added. Choosing an appropriate mass transfer model would undoubtedly play a crucial role in achieving an exact description of cooling process of the hot surface over the time. The Lee mass transfer model is defined as:

$$\dot{m}_{\text{e}}^{\prime \prime \prime } = r_{\text{e}} \alpha_{\text{l}} \rho_{\text{l}} \frac{{T - T_{\text{sat}} }}{{T_{\text{sat}} }}\quad T > T_{\text{sat}}$$
(13)
$$\dot{m}_{\text{c}}^{\prime \prime \prime } = r_{\text{c}} \left( {1 - \alpha_{\text{l}} } \right)\rho_{\text{g}} \frac{{T - T_{\text{sat}} }}{{T_{\text{sat}} }}\quad T < T_{\text{sat}}$$
(14)

The subscripts e and c state evaporation and condensation, respectively. \(T_{\text{sat}}\) is saturation temperature of fluid and r is an empirical coefficient called mass transfer intensity factor, which in practical cases varies from \(10^{ - 1}\) [30] to \(10^{7}\) [31]. Most of other mass transfer models allow phase change only along the interface, but the Lee model allows phase change both along the interface and within the saturated phase, which is why it is utilized here.

Heat transfer between solid and fluid regions

The heat transfer equation in the solid region is:

$$\frac{{\partial \rho c_{\text{p}} T}}{\partial t} = \nabla \cdot \left( {\lambda \nabla T} \right)$$
(15)

The boundary condition between the fluid and solid regions is defined as:

$$T_{\text{f}} = T_{\text{s}}$$
(16)
$$q_{\text{f}}^{\prime \prime } = q_{\text{s}}^{\prime \prime } \to \lambda_{\text{s}} \frac{{\partial T_{\text{s}} }}{\partial n} = \lambda_{\text{f}} \frac{{\partial T_{\text{f}} }}{\partial n}$$
(17)

Equations (16) and (17) show the continuity of the temperature field and heat flux on the boundary. All the simulations are based on fluid and solid properties, summarized in Table 1.

Table 1 Thermophysical properties
Full size table

In order to discretize the governing equations, the finite volume method, with the QUICK scheme for discretization of convective terms, is used. Temporal terms in equations are discretized, using backward second-order implicit method. To access an appropriate coupling between velocity and pressure, PIMPLE algorithm is applied. OpenFOAM open-source code is employed to solve discretized governing equations. The courant number and convergence criteria for conservation of mass, momentum and energy equations are considered 0.5 and 10−8, respectively.

Standard temperature uniformity index (STUI)

The temperature uniformity of the substrate is considered a key factor during fast cooling processes, since fast cooling in a short period of time may lead to distortion of the substrate and even creation and growth of cracks in it. Thus, the standard temperature uniformity index (STUI), which is known to be a useful tool to evaluate heating uniformity, is used here [32]:

$${\text{STUI}} = \frac{{\mathop \smallint \nolimits_{V}^{ } \sqrt {\left( {T - T_{\text{ave}} } \right)^{2} } {\text{d}}v}}{{\left( {T_{\text{init}} - T_{\text{ave}} } \right)\mathop \smallint \nolimits_{V}^{ } {\text{d}}v}}$$
(18)

Tave is the average temperature in the solid and is calculated by:

$$T_{\text{ave}} = \frac{{\mathop \smallint \nolimits_{V}^{ } T{\text{d}}v}}{{\mathop \smallint \nolimits_{V}^{ } {\text{d}}v}}$$
(19)

where \(T_{ }\) and \(T_{\text{ave}}\) are local and average temperatures inside the plate over the volume (\(V_{\text{vol}}\), m−3), and \(T_{\text{init}}\) is the initial temperature of it before treatment. In a solid plate, a smaller index would correspond to better heating uniformity.

Optimized cooling factor (OCF)

In addition to temperature uniformity, the amount of cooling during the process is substantial. Consequently, a new dimensionless factor named OCF is defined here:

$${\text{OCF}} = \frac{{\frac{{T_{\text{init}} - T_{\text{ave}} }}{{T_{\text{init}} - T_{\text{liq}} }}}}{\text{STUI}}$$
(20)

where \(T_{\text{liq}}\) is liquid temperature at the inlet. According to this relation, as numerator increases (when \(T_{\text{ave}}\) is closer to \(T_{\text{liq}}\)) and STUI value decreases, OCF rises, which results in enhancing cooling efficiency.

Results and discussion

Mesh independency test

Considering the geometry used in this study, a two-dimensional structured non-uniform grid is utilized. Fine gridding is used in the vicinity of the wall to consider sharp gradients. Three different mesh distributions are generated to check the dependency of the mesh on the results. Table 2 shows the influence of the cell size on STUI and OCF. As can be seen, when the number of meshes almost doubled (from 28,283 to 56,160), the results barely changed. Therefore, mesh distribution of the second sample is employed in further simulations. Gridding of the second sample, shown in Fig. 1, was chosen in all simulations.

Table 2 Mesh study
Full size table

Validation

Prior to carrying out the investigations via numerical solution, a validation seems necessary to support the results. Thus, to validate the modified solver in processes involving quenching and two-phase jet impingements with mass transfer, a comparison with an experimental study of Karwa and Stephan [33] was performed. In that experiment, a free surface circular jet of deionized water with the velocity of 2.5 m s−1 was impinged on a flat surface of an AISI-type 314 stainless steel cylinder with the diameter of 50 mm, height of 20 mm and initial temperature of 890 °C. The inlet water jet subcooled temperature was 74.2 °C, jet-to-surface spacing was 97.5 mm, and nozzle diameter was 3 mm. Based on the geometry of the experiment, an axis-symmetrical geometry was used for the simulation. The effect of conjugation and mass transfer was considered in the numerical study. The comparison between the results of the numerical and experimental studies is illustrated in Fig. 3. In this figure, the variation of block temperature with the cylinder radius during 8 s, at 0.085 mm below the impingement surface, is presented. As it is clear, there is a good agreement between the numerical and experimental results.

Fig. 3
figure 3

Comparison of the measured temperature at 0.085 mm below the block surface between the results of Karwa and Stephan [33] and the present study

Full size image

Results

The main goal of this study was to non-dimensionally investigate the effects of velocity inlet function of jets \(V_{\text{j}} \left( t \right)\), jet-to-surface spacing H and jet-to-jet spacing S parameters on the STUI and OCF curves of the solid part. The simulations were performed during 6 s of the fluid flow on the impingement surface. At the end of the solution time, total liquid consumptions of the jets were equal in different configurations due to the equality of periods of pulses of the two jets, e.g., at every moment the net flow rate exiting from the two-jet inlets remains constant. The data were fitted using Spline interpolation to give better insight and understanding into the plots.

The first parameter whose effect on STUI and OCF is studied is velocity inlet function, the influence of which on STUI is represented in Fig. 4. To this aim, three constant inlet velocities, V = 0.4, 0.5 and 1 m s−1, at different periods of pulse, P = 0, 0.02, 0.05, 0.1 and 0.2, are considered. H, S and L contain constant values of \(5 \times D_{\text{j}}\), \(8 \times D_{\text{j}}\) and 40 mm, respectively. As shown in this figure, when the jet inlet velocity decreases, STUI goes up. This can be because of an increase in the momentum of the inlet flow as well as the radius of the wetted region at the stagnation point, at higher velocities, which create a cooled area under jet nozzles. This increase in the radius intensifies the temperature gradient in the block and raises the value of STUI, which is not desirable. With an increase in P, the same results as the results of velocity increment are obtained, which means that with the increase in P, the value of STUI tends to rise. The performance of the OCF against pulse flows can be seen in Fig. 5. In all cases including pulse jets, improvements in the STUI and OCF relative to pulse-free ones can be observed. For example, when V = 0.4 m s−1, OCF peaks at 2 in P = 0.06, which is almost eight times greater than OCF of the pulse-free configuration (OCF = 0.024). As clear in Figs. 4 and 5, although STUI value rises when velocity increases, OCF improves. This can be due to the fact that as the velocity increases, the average block temperature decreases more and reaches the inlet liquid temperature. At all three velocities, at lower values of P, due to more uniform distribution of temperature in both sides of the plate and also continuous destruction of film boiling layers on the surface, OCF reaches its maximum value. At lower velocities, liquid does not have enough momentum and time to transfer the heat at lower P values, so the peaks in plots move toward higher P values. It means when V = 1 m s−1, the optimal OCF is achieved for P = 0.025, but when V = 0.4 m s−1, OCF peaks at P = 0.06. It is worth mentioning that when P = 0.06, first nozzle is open for 0.06 s; after that, it is closed and second inlet will be open for this period of time. This cycle continues to the end of the process time.

Fig. 4
figure 4

Effects of different values of P on the standard temperature uniformity index at various velocities, when \(\frac{H}{{D_{\text{j}} }} = 5\), \(S = 8 \times D_{\text{j}}\) and L = 40 mm (t = 6 s)

Full size image
Fig. 5
figure 5

Optimized cooling factor variations at various velocities, when \(\frac{H}{{D_{\text{j}} }} = 5\), \(S = 8 \times D_{\text{j}}\) and L = 40 mm (t = 6 s)

Full size image

As shown in Figs. 4 and 5, in lower pulse periods, the temperature is distributed more uniformly and the cooling rate is achieved to be higher. By observing the velocity contours in Fig. 6, it can be seen that in lower pulse periods, due to continuous destruction of the vapor layers by the jets, considering the equal velocity at the jet inlets, the flow mixing is performed better on the surface, causing the cooling process to be more uniform and in a higher rate. By increasing P (from 0.02 in Fig. 6a to 0.2 in Fig. 6c), the flow becomes more uniform with less interaction between the two phases of water and vapor.

Fig. 6
figure 6

Velocity contours of the fluid at t = 6 s when V = 1 m s−1, \(\frac{H}{{D_{\text{j}} }} = 5\), \(S = 8 \times D_{\text{j}}\) and L = 40 mm at different P values: aP = 0.02, bP = 0.1, cP = 0.2

Full size image

Contours of volume fraction in fluid domain and temperature distribution of the solid block are simultaneously displayed in Fig. 7. As can be seen, in the contours, disturbance of film boiling layers in the fluid flow, as a result of velocity pulses, causes temperature distribution to be more uniform inside the block, reducing thermal stresses.

Fig. 7
figure 7

Contour of volume fraction in fluid and temperature distribution (in Kelvin) in solid at the same time when V = 0.5 m s−1, P = 0.2, \(\frac{H}{{D_{\text{j}} }} = 5\), \(S = 8 \times D_{\text{j}}\) and L = 40 mm at different times: a 0, b 0.1 s, c 0.22 s, d 2 s and e 6 s

Full size image

Another parameter investigated here is the jet-to-surface spacing. In order to examine the effect of this more accurately, V = 0.5 m s−1, P = 0.05, 0.1 and 0.2 and \(\frac{H}{{D_{\text{j}} }} = 3, \, 5, \, 7\) and 9 were chosen. Constant values of S and L were similar to the previous part. According to the Bernoulli equation, jet velocity and width at the impingement surface would change with the jet inlet velocity and nozzle width as:

$$V_{\text{imp}} = \sqrt {V_{\text{j}}^{2} + 2gH}$$
(21)
$$D_{\text{imp}} = D_{\text{j}} \cdot \frac{{V_{\text{j}} }}{{V_{\text{imp}} }}^{ }$$
(22)

Based on these relations, jet velocity at the impingement surface increases slightly as a function of channel height; however, there is a small decrease in the jet width at the surface. The results of investigating different jet-to-surface spacing are displayed in Figs. 8 and 9. As the figures show, by increasing H, the liquid momentum at the impingement surface rises which results in an increase in the wetted region radius and enhancement of the stagnation point heat transfer. The vapor layers created on the surface in the film boiling region acts like a thermal insulation between the surface and the liquid due to lower thermal conductivity of the vapor in comparison with liquid, so heat transfer rate is less through it. Therefore, an increase in velocity can improve heat transfer from solid to fluid by better disturbing these vapor layers and make the temperature distribution more uniform on the surface. As shown in Fig. 9, when H increases, despite the fluctuations, the enhancement in OCF is observed in a general trend. The presence of these fluctuations might be due to the mutual effects of jet velocity and width parameters on each other at the impingement surface, at various distances from jet nozzles to the surface (H). At lower P values, the effects of changing the height on STUI and OCF are more significant. At P = 0.05, STUI and OCF values change from 0.12 and 1.37 in \(\frac{H}{{D_{\text{j}} }} = 3\) to 0.074 and 2.57 in \(\frac{H}{{D_{\text{j}} }} = 9\) (almost 38% improvement in STUI and 87% in OCF), respectively. However, at higher P values like P = 0.2, OCF is almost constant.

Fig. 8
figure 8

STUI changes in various jet-to-surface spacing \(\left( {\frac{H}{{D_{\text{j}} }}} \right)\) for different P values, when V = 0.5 m s−1, \(S = 8 \times D_{\text{j}}\) and L = 40 mm (t = 6 s)

Full size image
Fig. 9
figure 9

OCF performance as a function of jet-to-surface spacing \(\left( {\frac{H}{{D_{\text{j}} }}} \right)\) for different P values, when V = 0.5 m s−1, \(S = 8 \times D_{\text{j}}\) and L = 40 mm (t = 6 s)

Full size image

The last parameter considered is the distance between the two jets, which can have a considerable impact on the heat transfer performance. Therefore, in order to conduct an accurate and thorough study on jet-to-jet spacing effects, three blocks with L = 40, 50 and 60 mm are employed, when V = 0.5 m s−1, P = 0.5, and \(\frac{H}{{D_{\text{j}} }} = 5\), with different \(\frac{S}{L}\) configurations. As illustrated in Fig. 10, the temperature uniformity (STUI) at the length of 40 mm is lowest among the considered lengths due to more accessibility in the blocks with shorter length and as a result less volume. Based on this figure and Fig. 11, when jet-to-jet spacing decreases (closer to zero), the results of STUI and OCF are closer to the single-jet setting results. By increasing S and placing the jets where the liquid has more time to transfer the heat to the surface before reaching the exit, temperature distribution is achieved more uniform until \(\frac{S}{L} \approx \frac{1}{3}\), where STUI contains the most efficient value followed by OCF reaching the highest one. For example, in the case with the length of 40 mm, when S increases, OCF rises from 0.4 at S = 0 to 2.2 at \(\frac{S}{L} = \frac{1}{3}\). At this point, this result is obtained due to the formation of two stagnation points having the highest heat transfer rate at an appropriate distance from each other. As S rises more, stagnation points move toward the block sides with OCF going down, since the momentum of the liquid in the middle of the plate is low and the liquid is not strong enough to disturb the film boiling layers on the surface.

Fig. 10
figure 10

Variations of STUI with different jet-to-jet spacing \(\left( {\frac{S}{L}} \right)\), at three considered plate lengths, when V = 0.5 m s−1, P = 0.5 and \(\frac{H}{{D_{\text{j}} }} = 5\) (t = 6 s)

Full size image
Fig. 11
figure 11

Effects of different jet-to-jet spacing \(\left( {\frac{S}{L}} \right)\) on OCF, at three considered plate lengths, when V = 0.5 m s−1, P = 0.5 and \(\frac{H}{{D_{\text{j}} }} = 5\) (t = 6 s)

Full size image

Effects of different jet-to-jet spacing on temperature distribution of the steel block with the length of 60 mm are clear in Figs. 12 and 13. The contours in these figures are represented at 2 s and 6 s after the fluid flow impinging on the block surface when the velocity inlet was 0.5 m s−1 with 0.05 period of pulse. According to the figures, there is more uniformity when S = 20 mm, which improves over the solution time.

Fig. 12
figure 12

Temperature distribution (in Kelvin) of the 60-mm steel block after 2 s at V = 0.5 m s−1 and P = 0.05, when: aS = 0, b\(\frac{S}{L} = \frac{1}{6}\), c\(\frac{S}{L} = \frac{1}{3}\) and d\(\frac{S}{L} = \frac{1}{2}\)

Full size image
Fig. 13
figure 13

Temperature distribution (in Kelvin) of the 60-mm steel block after 6 s at V = 0.5 m s−1 and P = 0.05, when a S = 0, b\(\frac{S}{L} = \frac{1}{6}\), c\(\frac{S}{L} = \frac{1}{3}\) and d\(\frac{S}{L} = \frac{1}{2}\)

Full size image

Conclusions

A numerical study was conducted into boiling impinging jets in a quenching process. The effects of phase change and conjugation were implemented to a solver in an open-source code, and the results were validated versus an experimental research. The quenching process of two planar water jets impinging on a highly heated block was then simulated numerically. The liquid–gas interface was tracked by the VOF. In the end, the effects of Heaviside velocity inlet function, jet-to-surface and jet-to-jet spacing on STUI and OCF were non-dimensionally investigated. Significant results are achieved, and most efficient cases from the proposed settings are introduced. According to Results and discussion of this study, the conclusions are summarized as follows:

  • At lower velocities, since the liquid does not have enough momentum and time to transfer the heat for the lower values of P, the peaks in OCF plot moved toward higher P values. For example, when V = 1 m s−1, the maximum OCF was accessible for P = 0.025, but when V = 0.4 m s−1, OCF peaked when P = 0.06.

  • For all of the cases that included pulse jets, enhancements in STUI and OCF relative to pulse-free configurations were obtained; When V = 0.4 m s−1, OCF peaked at 2 in P = 0.06, which was almost eight times greater than OCF of the pulse-free setting (OCF = 0.24).

  • When the jet inlet velocity decreased, STUI rose since at higher velocities, both the momentum of the inlet flow and the radius of the wetted region at the stagnation point increased, creating a cooled area under jet nozzles, which is not desirable. With an increase in the pulse period (P), the results were similar to the results of speed increments.

  • Although STUI tended to rise as velocity increased, OCF improved since the average block temperature decreased more and approached the inlet liquid temperature. At all three velocities, at lower values of P, OCF reached its maximum value due to more uniform distribution of temperature in both sides of the plate and continually destroying film boiling layers generated on the surface as well.

  • More significant results regarding the effect of changing the height on STUI and OCF were observed at lower values of P. When P = 0.05, STUI and OCF values changed from 0.12 and 1.37 in \(\frac{H}{{D_{j} }} = 3\) to 0.074 and 2.57 in \(\frac{H}{{D_{j} }} = 9\) (almost 38% enhancement in STUI and 87% in OCF), respectively.

  • An ideal value for the jet-to-jet spacing was obtained in this research. In all plate lengths, STUI and OCF had the most efficient value, at \(\frac{S}{L} \approx \frac{1}{3}\). For example, in the case with the length of 40 mm, by the S increment, OCF rose from 0.4 at \(\frac{S}{L} = 0\) to 2.2 at \(\frac{S}{L} \approx \frac{1}{3}\).