Local thermal non-equilibrium analysis of conjugate free convection within a porous enclosure occupied with Ag–MgO hybrid nanofluid

Abstract

Current investigation aims to analyze the conjugate free convection inside a porous square cavity occupied with Ag–MgO hybrid nanofluid using the local thermal non-equilibrium (LTNE) model. Hybrid nanofluids are a novel kind of enhanced working fluids, engineered with enhanced thermo-physical and chemical properties. Two solid walls located between the horizontal bounds in two sides of cavity play the role of a conductive interface between the hot and cold walls, and moreover, the top and bottom bounds have been insulated. The governing differential equations are obtained by Darcy model and then for better representation of the results, converted into a dimensionless form. The finite element method is utilized to solve the governing equations. To evaluate the correctness and accuracy of the results, comparisons have been performed between the outcomes of this work and the previously published results. The results indicate that using the hybrid nanoparticles decreases the flow strength and the heat transfer rate. The heat transfer rate augments when R_k rises and the flow strength augments when Ra grows. Enhancing the porosity increases strongly the size and strength of the vortex composed inside the porous medium. When K_r is low, the heat transfer rate is low and by increasing K_r, thermal fields become closer to each other. The effect of hybrid nanoparticles on thermal fields with the thinner solid walls is more than that the thicker ones. An increment in H eventuates the enhancement of heat transfer and hence, the thermal boundary layer thickness. By increasing the volume fraction of the hybrid nanoparticles, Nu_hnf and Nu_s decrease in constant Ra. Besides, increase in Ra enhances the Nu_hnf and Nu_s. For a certain d, the reduction of Nu_s due to using the hybrid nanoparticles is more than that for Nu_hnf. The increment of d lessens Nu_hnf for all values of K_r and has not specific trends for Nu_s. Utilizing hybrid nanoparticles decreases Nu_s (except d = 0.4), rises Nu_s when K_r < 18, while it can increase Nu_s for K_r > 42. In constant d, increment of H, respectively, decreases and boosts Nu_hnf and Nu_s. For all values of d, increment of ε declines Nu_hnf. In low value of d, the increase in ε reduces Nu_s, whereas at higher values, Nu_s has continuously enhancing trend. For different values of d, the increase in ε scrimps Nu_hnf. The increment of d and also ε, and H are, respectively, decreases and increases the heat transfer rate.

Introduction

The conjugate heat exchange in porous media with applying the thermal non-equilibrium (TNE) models is extremely significant area in high-power heat transfer usages [1]. Many researchers have focused on conjugate free convective heat exchange in enclosures due to its significance for a lot of engineering and industrial systems, like heat exchangers, solar collector technology, cooling and storage of radioactive waste containers, flows in microchannels, material processing, electrical units, thermal exchange circuits, and the building energy components [1,2,3]. On the other hand, various engineering and practical usages of local thermal non-equilibrium (LTNE) such as fuel cells, heat pipes and sinks, dryers, computer chips, and catalytic reactors motivate a lot of authors to investigate this model with a goal of precise prediction in the thermal treatment of porous medium [4,5,6,7]. The design of using hybrid nanoparticles as nano-additives can be managed in such usages for multi-objective advantages containing heat transfer enhancement or inhibition. Accordingly, this investigation aims to theoretically analyze the influence of the presence of a hybrid nanofluid in cavity filled by porous media.

Nanofluids are new kind of emended (reinforced) fluids first presented by Choi [8] which contain well-dispersed solid nanometer-sized particles [2, 9,10,11]. Experiments proved that with addition of nanoparticles, physical characteristics of ordinary host fluid including density, viscosity, and thermal conductivity have increased [12, 13]. Thus, nanoparticles existence affects the heat transfer rate and is required in usages. Hybrid nanofluids are newfound category of nanofluids that consist of a small amount of metal nanoparticles (like Zn, Cu, Ag, and Al) and non-metallic nanoparticles (like Al₂O₃, CuO, MgO, and Fe₃O₄). Metallic nanoparticles have high thermal conductivities, whereas they have limitations such as stability and reactivity. On the contrary, non-metallic nanoparticles give lower thermal conductivity compared to the metallic, while they have great number of beneficial properties like stability and chemical inertness. Hence, there is expectation that addition of metallic to non-metallic-based nanofluid able to raise the thermo-physical properties of the final mixture without lessening the stability [14, 15]. Newly, a lot of experimental investigations [16,17,18,19] and numerical studies [15, 20,21,22] have been carried out on hybrid nanofluid as a new conception in technology. Suresh et al. [14] examined the thermal conductivity and viscosity of the alumina–copper/water hybrid nanofluid. Esfe et al. [18, 19] measured and predicted the thermal conductivity of various hybrid nanofluids. Sarkar et al. [23] and Sundar et al. [24] published general reviews about the recent researches and the future challenges in the area of hybrid nanofluids. Heat exchange in an annulus between two confocal elliptic cylinders filled by Cu–Al₂O₃/water hybrid nanofluid conducted numerically by Tayebi and Chamkha [15]. A computational analysis of three various nanofluids (Al₂O₃, TiO₂ and SiO₂) and their hybrids was performed by Minea [25]. Results indicated that thermal conductivity is rising by minimum 12% with adding the nanoparticles.

Convective heat transfer within enclosures occupied with nanofluid considering various conditions is a basic problem and conducted by a lot of authors as an attractive subject [16, 26,27,28,29,30,31,32,33]. Cavities are sometimes filled by porous environment that is saturated with a fluid or nanofluid. Kasaeian et al. [34] investigated recently the progresses in the area of nanofluid flow and heat transfer in a porous medium in format of a comprehensive review. Chamkha and Ismael [29] checked out the free convective heat transfer within a nanoliquid enclosure partially filled with a porous medium. Ghalambaz et al. [32] have considered the existence of viscous dissipation and radiation influences on free convective heat transfer within the porous nanofluid enclosure. Sheikholeslami et al. [35] investigated free convection heat exchange in a region having sinusoidal wall occupied by nanofluid affected by magnetic field. Free and mixed convective heat transfer in a 2-D nanofluid cavity considering multiple pairs of heat source–sinks with simulating the two-phase flow is performed by Garoosi et al. [36]. Most recently, investigation of utilizing a hybrid nanofluid in issues related to cavity has examined by some of the researchers [37,38,39]. Chamkha et al. [37] conducted the melting process of a nanoparticles-enhanced phase change material in a square cavity over a heated horizontal cylinder located in the middle of the enclosure under the influence of both single and hybrid nanoparticles.

Recently, a number of researchers have focused on different thermal boundary conditions in enclosure. One of the most challenging issues in this field is using the LTE (when the fluid and solid temperature are equal) [40] and LTNE (where the fluid and solid temperature are varied) [41, 42] as two well-known models for porous media. Many investigations have utilized the LTE model, whereas LTNE model has not attracted great consideration. Baytas and Pop [43], Kuznetsov and Nield [41], Agarwal and Bhadauria [42] examined an influence of LTNE approach on free convection in different case studies. Lately, Alsabery et al. [1, 44, 45] and Zargartalebi et al. [6] checked out an influence of the LTNE on natural convective heat transfer inside various enclosures filled by nanofluid. Other studies in this field can be found in the literature [46, 47].

Some of researchers focused on conjugate natural convections in enclosures [2, 3, 48,49,50,51,52] for its significant usages in building energy components, electrical parts cooling, collectors of solar energy, material production, etc. Kimura et al. [53] have explained in a review paper that the fundamental hypothesizes about the mathematical approaches of conjugate convection–conduction heat exchange process in porous medium. Influence of natural convective–conductive heat transfer in a cavity bounded by a solid vertical wall of different thermal conductivity ratio is investigated numerically by Kaminski and Prakash [50]. Chamkha and Ismael [2] checked out conjugate heat exchange in a porous cavity saturated by nanoliquids and heated with triangular-shaped thick wall. Mahmoudi et al. [3] investigated the conjugate heat exchange in a cavity with solid walls having Cu–water nanoliquid. It was demonstrated that the divider’s placement affects the heat transfer increment with Rayleigh numbers and solid particles concentration. Sheremet and Pop [48] perused the conjugate free convection in porous nanoliquid cavity by the finite difference method. Free convective–conductive heat exchange in a nanoliquid enclosure having solid partition on various walls is evaluated by Selimefendigil and Öztop [51]. Good references on convective nanofluid flow and heat transfer were presented in the books by Das et al. [54], Nield and Bejan [55], and Shenoy et al. [56] and in the review papers by Buongiorno [57], Kakaç and Pramuanjaroenkij [12], Wong and Leon [58], Wen et al. [59], Mahian et al. [60], and many others.

Due to the presented literature survey and by our best of knowledge, there are no investigations which analyzed natural convective–conductive heat exchange within a porous enclosure saturated with Ag–MgO hybrid nanoliquid with LTNE approach. We believe that this work is noteworthy, and its usefulness for different engineering systems as discussed above motivated us. In hybrid nanofluid usage, it is the first effort to evaluate the conduction–convection effects of natural heat transfer considering the LTNE model within a cavity. The current investigation studies the effects of the Darcy–Rayleigh number, nanoparticles concentration, porosity, interface parameter, modified thermal conductivity ratio, and the width of the solid wall on the nanoliquid flow and thermal fields. The governing differential equations are written using the Darcy model and then transformed into a non-dimensional form. Solution of the boundary-value problem has been performed using the finite element method. Several examinations are performed to find out the accuracy of the present model. The numerical data are validated using the results available in the literature.

Description and formulation of the model

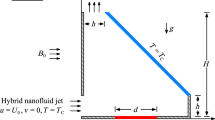
A simple schematic view of the under study conjugate free convection problem is observed in Fig. 1. Two solid walls which have the finite thickness of d* are located between the horizontal bounds in two sides of a square cavity with size L. Indeed, these solid walls play the role of a conductive interface between the hot and cold walls with constant temperatures of T_h and T_c, respectively, and the porous entity occupied by Ag–MgO hybrid nanofluid. The top and bottom bounds have been thermally insulated. It should be mentioned that all of the walls are fully impermeable. Here, the volumetric heat exchange between the hybrid nanofluid and porous matrix is finite and nonzero. This specific type of the heat transfer is considered using the LTNE model. The hybrid nanoparticles always remain suspended in the pores of the cavity. There is no contact resistance in the interface boundary between the solid walls and porous medium. In addition, the dynamic and thermal slips between nanoparticles and host liquid are negligible. Only body force applied is gravity force that acts in reverse direction of y-axis. During the process of the natural convection, all the characteristics of the host liquid and nanoparticles are unchangeable except for the density in the buoyancy term in momentum equation where its variation will be modeled using Boussinesq approximation.

Fig. 1

A simple schematic of the problem

Using the aforementioned assumptions to derive the equations leads to the following formulations

$$\frac{{\partial u_{\text{hnf}}^{*} }}{{\partial x^{*} }} + \frac{{\partial v_{\text{hnf}}^{*} }}{{\partial y^{*} }} = 0,$$

(1)

$$0 = - \frac{{\partial p^{*} }}{{\partial x^{*} }} - \frac{{\mu_{\text{hnf}} }}{K}u_{\text{hnf}}^{*} ,$$

(2)

$$0 = - \frac{{\partial p^{*} }}{{\partial y^{*} }} - \frac{{\mu_{\text{hnf}} }}{K}v_{\text{hnf}}^{*} - \left( {\rho \beta } \right)_{\text{hnf}} \left( {T_{\text{hnf}}^{*} - T_{0} } \right){\mathbf{g}}_{\text{y}} ,$$

(3)

$$\left( {\rho C_{\text{p}} } \right)_{\text{hnf}} \left( {u_{\text{hnf}}^{*} \frac{{\partial T_{\text{hnf}}^{*} }}{{\partial x^{*} }} + v_{\text{hnf}} \frac{{\partial T_{\text{hnf}}^{*} }}{{\partial y^{*} }}} \right) = \varepsilon k_{\text{hnf}} \left( {\frac{{\partial^{2} T_{\text{hnf}}^{*} }}{{\partial x^{*2} }} + \frac{{\partial^{2} T_{\text{hnf}}^{*} }}{{\partial y^{*2} }}} \right) + h\left( {T_{\text{s}}^{*} - T_{\text{hnf}}^{*} } \right),$$

(4)

$$0 = \left( {1 - \varepsilon } \right)k_{\text{s}} \left( {\frac{{\partial^{2} T_{\text{s}}^{*} }}{{\partial x^{*2} }} + \frac{{\partial^{2} T_{\text{s}}^{*} }}{{\partial y^{*2} }}} \right) + h\left( {T_{\text{hnf}}^{*} - T_{\text{s}}^{*} } \right).$$

(5)

The energy equation without considering convection term and heat absorption or generation for the solid wall will be summarized as follows

$$0 = \frac{{\partial^{2} T_{\text{w}}^{*} }}{{\partial x^{*2} }} + \frac{{\partial^{2} T_{\text{w}}^{*} }}{{\partial y^{*2} }}.$$

(6)

The boundary conditions subjected in dimensional x* and y* coordinates are

$$\begin{aligned} T_{\text{w}}^{*} = & T_{\text{h}}^{*} \quad {\text{on}}\quad x^{*} = 0 , { 0} \le y^{*} \le L, \\ T_{\text{w}}^{*} = & T_{\text{c}}^{*} \quad {\text{on}}\quad x^{*} = L , { 0} \le y^{*} \le L, \\ \end{aligned}$$

(7-a)

$$\begin{aligned} u_{\text{hnf}}^{*} = & v_{\text{hnf}}^{*} = 0 ,\quad \frac{{\partial T_{\text{s}}^{*} }}{{\partial y^{*} }} = \frac{{\partial T_{\text{hnf}}^{*} }}{{\partial y^{*} }} = 0\quad {\text{on}}\quad y^{*} = 0 ,\;d^{*} \le x^{*} \le L - d^{*} ,\\ u_{\text{hnf}}^{*} = & v_{\text{hnf}}^{*} = 0 ,\quad \frac{{\partial T_{\text{s}}^{*} }}{{\partial y^{*} }} = \frac{{\partial T_{\text{hnf}}^{*} }}{{\partial y^{*} }} = 0\quad {\text{on}}\quad y^{*} = L ,\;d^{*} \le x^{*} \le L - d^{*} ,\\ \end{aligned}$$

(7-b)

$$\frac{{\partial T_{\text{w}}^{*} }}{{\partial y^{*} }} = 0\quad {\text{on}}\quad 0\le x^{*} \le d^{*} ,\;L - d^{*} \le x^{*} \le L ,\;y^{*} = 0 ,\;y^{*} = L.$$

(7-c)

At the solid wall–porous medium interface, we have the following conditions:

$$\, \left. \begin{aligned} u_{\text{hnf}}^{*} = v_{\text{hnf}}^{*} = 0 , { }T_{\text{hnf}}^{*} = T_{\text{s}}^{*} = T_{\text{w}}^{*} \hfill \\ k_{\text{w}} \frac{{\partial T_{\text{w}}^{*} }}{{\partial x^{*} }} = \varepsilon k_{\text{hnf}} \frac{{\partial T_{\text{hnf}}^{*} }}{{\partial x^{*} }} + \left( {1 - \varepsilon } \right)k_{\text{s}} \frac{{\partial T_{\text{s}}^{*} }}{{\partial x^{*} }} \hfill \\ \end{aligned} \right\}{\text{on}}\quad x^{*} = d^{*} ,\;x^{*} = L - d^{*} \;{\text{and}}\; 0\le y^{*} \le L.$$

(7-d)

At the present time, the model which can accurately give the thermal conductivity and dynamic viscosity of the hybrid nanoliquids has not been provided. Hence, this study applies the experimental values of these two thermo-physical properties in [18] to do a realistic analysis. Esfe et al. [18] experimentally determined the thermal conductivity and viscosity of the MgO–Ag hybrid nanoliquid in which the diameters of Ag and MgO particles were 25 and 40 nm, respectively. The volume fraction of each nanoparticle was evenly 50% of the total volume fraction. They represented the new relations to calculate the thermal conductivity (Eq. 8) and viscosity (Eq. 9) of the MgO–Ag hybrid nanoliquid by curve fitting on the empirical results. The empirical data of Table 1 are the values that the curve fitting have been performed based on them and are utilized to represent the results. Additionally, in Table 1, M and α_r are two dimensionless functions of the volume fractions and will be introduced in the following.

Table 1 Experimental data for thermal conductivity and viscosity of hybrid MgO–Ag/water nanoliquid.

There are excellent correspondences between empirical data and models proposed by Esfe et al. [18]. The other thermo-physical properties employed in this study (shown in Table 2) are obtained using the classical models that are mostly in good coincidence with the empirical results. Here φ_hnp is the total volume fraction which equals the summation of the volume fractions of Ag and MgO.

$$\begin{aligned} k_{\text{hnf}} = & \left( {\frac{{0.1747 \times 10^{5} + \varphi_{\text{hnp}} }}{{0.1747 \times 10^{5} - 0.1498 \times 10^{6} \varphi_{\text{hnp}} + 0.1117 \times 10^{7} \varphi_{\text{hnp}}^{2} + 0.1997 \times 10^{8} \varphi_{\text{hnp}}^{3} }}} \right)k_{\text{bf}} , \\ & \quad 0\le \varphi_{\text{hnp}} \le 0.03 \\ \end{aligned}$$

(8)

$$\begin{aligned} \mu_{\text{hnf}} = & \left( {1 + 32.795\varphi_{\text{hnp}} - 7214\varphi_{\text{hnp}}^{2} + 714600\varphi_{\text{hnp}}^{3} - 0.1941 \times 10^{8} \varphi_{\text{hnp}}^{4} } \right)\mu_{\text{bf}} . \\ & \quad 0\le \varphi_{\text{hnp}} \le 0.02 \\ \end{aligned}$$

(9)

Table 2 Applied relations for hybrid nanofluid properties.

To eliminate the pressure terms from momentum equations, the cross differencing can be applied for the momentum equations along x and y directions:

$$\frac{{\mu_{\text{hnf}} }}{K}\left( {\frac{{\partial u_{\text{hnf}}^{*} }}{{\partial y^{*} }} - \frac{{\partial v_{\text{hnf}}^{*} }}{{\partial x^{*} }}} \right) = - g\left( {\rho \beta } \right)_{\text{hnf}} \frac{{\partial T_{\text{hnf}}^{*} }}{{\partial x^{*} }},$$

(10)

Now, a function should be defined that corresponds to the continuity equation and the velocity components $u_{\text{hnf}}^{*}$ and $v_{\text{hnf}}^{*}$ can be obtained by partial differentials of that function. In fact, this function is same as the stream function that is written as:

$$u_{\text{hnf}}^{*} = \frac{{\partial \psi^{*} }}{\partial y}\text{,}\quad v_{\text{hnf}}^{*} = - \frac{{\partial \psi^{*} }}{\partial x}\text{,}$$

(11)

To have a dimensional parametric analysis, the non-dimensional parameters are employed to transfer the equations and boundary conditions from dimensional x*–y* coordinates to dimensionless x–y coordinates:

$$\begin{aligned} x = & {{x^{*} } \mathord{\left/ {\vphantom {{x^{*} } L}} \right. \kern-0pt} L},\quad y = {{y^{*} } \mathord{\left/ {\vphantom {{y^{*} } L}} \right. \kern-0pt} L},\quad \psi = {{\psi^{*} } \mathord{\left/ {\vphantom {{\psi^{*} } {\alpha_{\text{bf}} }}} \right. \kern-0pt} {\alpha_{\text{bf}} }},\quad T_{\text{hnf}} = {{\left( {T_{\text{hnf}}^{*} - T_{\text{c}}^{*} } \right)} \mathord{\left/ {\vphantom {{\left( {T_{\text{hnf}}^{*} - T_{\text{c}}^{*} } \right)} {\left( {T_{\text{h}}^{*} - T_{\text{c}}^{*} } \right)}}} \right. \kern-0pt} {\left( {T_{\text{h}}^{*} - T_{\text{c}}^{*} } \right)}}, \\ T_{\text{s}} = & {{\left( {T_{\text{s}}^{*} - T_{\text{c}}^{*} } \right)} \mathord{\left/ {\vphantom {{\left( {T_{\text{s}}^{*} - T_{\text{c}}^{*} } \right)} {\left( {T_{\text{h}}^{*} - T_{\text{c}}^{*} } \right)}}} \right. \kern-0pt} {\left( {T_{\text{h}}^{*} - T_{\text{c}}^{*} } \right)}},\quad H = \frac{{hL^{2} }}{{\varepsilon k_{\text{bf}} }},\quad K_{r} = \frac{{\varepsilon k_{\text{bf}} }}{{\left( {1 - \varepsilon } \right)k_{\text{s}} }}. \\ \end{aligned}$$

(12)

So, the final non-dimensional equations can be rewritten:

$$\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial y^{2} }} = - Ra \cdot M \cdot \frac{{\partial T_{\text{hnf}} }}{\partial x},$$

(13)

$$\frac{1}{\varepsilon }\left( {\frac{\partial \psi }{\partial y}\frac{{\partial T_{\text{hnf}} }}{\partial x} - \frac{\partial \psi }{\partial x}\frac{{\partial T_{\text{hnf}} }}{\partial y}} \right) = \alpha_{\text{r}} \left( {\frac{{\partial^{2} T_{\text{hnf}} }}{{\partial x^{2} }} + \frac{{\partial^{2} T_{\text{hnf}} }}{{\partial y^{2} }}} \right) + \frac{{\left( {\rho C_{\text{p}} } \right)_{\text{bf}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{hnf}} }}H\left( {T_{\text{s}} - T_{\text{hnf}} } \right),$$

(14)

$$0 = \left( {\frac{{\partial^{2} T_{\text{s}} }}{{\partial x^{2} }} + \frac{{\partial^{2} T_{\text{s}} }}{{\partial y^{2} }}} \right) + K_{\text{r}} H\left( {T_{\text{hnf}} - T_{\text{s}} } \right),$$

(15)

$$0 = \left( {\frac{{\partial^{2} T_{\text{w}} }}{{\partial x^{2} }} + \frac{{\partial^{2} T_{\text{w}} }}{{\partial y^{2} }}} \right).$$

(16)

In Eq. (13), Ra is the abbreviation of the Darcy–Rayleigh number which is defined as $Ra = {{gK\left( {\rho \beta } \right)_{\text{bf}} \left( {T_{\text{h}} - T_{\text{c}} } \right)L} \mathord{\left/ {\vphantom {{gK\left( {\rho \beta } \right)_{\text{bf}} \left( {T_{\text{h}} - T_{\text{c}} } \right)L} {\left( {\alpha_{\text{bf}} \mu_{\text{bf}} } \right)}}} \right. \kern-0pt} {\left( {\alpha_{\text{bf}} \mu_{\text{bf}} } \right)}}.$Two dimensionless numbers M and α_r are also introduced as $M = \left( {{{\left( {\rho \beta } \right)_{\text{hnf}} } \mathord{\left/ {\vphantom {{\left( {\rho \beta } \right)_{\text{hnf}} } {\left( {\rho \beta } \right)_{\text{bf}} }}} \right. \kern-0pt} {\left( {\rho \beta } \right)_{\text{bf}} }}} \right)\left( {{{\mu_{\text{bf}} } \mathord{\left/ {\vphantom {{\mu_{\text{bf}} } {\mu_{\text{hnf}} }}} \right. \kern-0pt} {\mu_{\text{hnf}} }}} \right)$ and $\alpha_{\text{r}} = {{\alpha_{\text{hnf}} } \mathord{\left/ {\vphantom {{\alpha_{\text{hnf}} } {\alpha_{\text{bf}} }}} \right. \kern-0pt} {\alpha_{\text{bf}} }}$. The thermal and dynamic boundary conditions of the model have been listed below:

$$\begin{aligned} T_{\text{w}} = & 1\quad {\text{on}}\quad x = 0 , { 0} \le y \le 1, \\ T_{\text{w}} = & 0\quad {\text{on}}\quad x = 1 , { 0} \le y \le 1, \\ \end{aligned}$$

(17-a)

$$\begin{aligned} \psi = 0 ,\quad \frac{{\partial T_{\text{s}} }}{\partial y} = \frac{{\partial T_{\text{hnf}} }}{\partial y} = 0\quad {\text{on}}\quad y = 0 ,\;d \le x \le 1 - d ,\hfill \\ \psi = 0 ,\quad \frac{{\partial T_{\text{s}} }}{\partial y} = \frac{{\partial T_{\text{hnf}} }}{\partial y} = 0\quad {\text{on}}\quad y = 1 ,\;d \le x \le 1 - d ,\hfill \\ \end{aligned}$$

(17-b)

$$\frac{{\partial T_{\text{w}} }}{\partial y} = 0\quad {\text{on}}\quad 0\le x \le d ,\; 1- d \le x \le 1 ,\;y = 0 ,\;y = 1,$$

(17-c)

$$\left. \begin{aligned} &\psi = 0 , T_{\text{hnf}} = T_{\text{s}} = T_{\text{w}} \hfill \\ &\frac{{\partial T_{\text{hnf}} }}{\partial x} = R_{\text{k}} \frac{{k_{\text{bf}} }}{{k_{\text{hnf}} }}\frac{{\partial T_{\text{w}} }}{\partial x} - K_{\text{r}}^{ - 1} \frac{{k_{\text{bf}} }}{{k_{\text{hnf}} }}\frac{{\partial T_{\text{s}} }}{\partial x} \hfill \\ \end{aligned} \right\}\quad {\text{on}}\quad x = d,\;x = 1 - d\;{\text{and}}\; 0\le y \le 1.$$

(17-d)

Parameter appeared in the last boundary conditions, R_k, is named as the thermal conductivity ratio and introduced as:

$$R_{\text{k}} = \frac{{k_{\text{w}} }}{{\varepsilon k_{\text{bf}} }},$$

(18)

To evaluate the heat transfer rate through the porous cavity, the average Nusselt number of the solid and liquid phases of the porous medium at the porous-wall interface bounds is defined as follows:

$$Nu_{\text{hnf}} = \int\limits_{0}^{1} {\left( {\frac{{\partial T_{\text{hnf}} }}{\partial x}} \right)}_{x = d} \;{\text{d}}y,$$

(19)

$$Nu_{\text{s}} = \int\limits_{0}^{1} {\left( {\frac{{\partial T_{\text{s}} }}{\partial x}} \right)}_{x = d} {\text{d}}y,$$

(20)

Further, the rate of heat exchange across the walls can be obtained using the weighted sum of the aforesaid average Nusselt numbers such as the following:

$$Q_{\text{w}} = R_{\text{k}}^{ - 1} Nu_{\text{hnf}} + R_{\text{k}}^{ - 1} K_{\text{r}}^{ - 1} Nu_{\text{s}} ,$$

(21)

or

$$Q_{\text{wall}} = \frac{{q_{\text{w}} L}}{{k_{\text{w}} }} = \int\limits_{0}^{1} {\left( {\frac{{\partial T_{\text{w}} }}{\partial x}} \right)}_{x = 0} \;{\text{d}}y,$$

(22)

Numerical approach, grid sensitivity test and validation

The formulated Eqs. (12)–(15) are nonlinear and coupled; therefore, the finite element method can be more effective for the present study. The details of the used finite element method can be found in [62]. To have an accurate solution which is independent of the number of the elements, it needs to do the grid independency test. The grid independency examination is performed based on assessing the variations of Nu_hnf, Nu_s and |ψ|_max with the grid size. From Table 3, the maximum error because of the variations of grid size, belonged to |ψ|_max, is 0.3% when grid size enhances from 50 × 50 to 100 × 100. This means that a 50 × 50 mesh can give very satisfactory outcomes. However, to receive the grid independence results at all cases, the grid of 100 × 100 nodes is confidently employed to discretize the computational domain. The accuracy of the outcomes of the present work is evaluated via comparing these results and those reported by Sun and Pop [30], Sheremet et al. [28] and Saeid [63] in Tables 4 and 5. The excellent agreements found between the data of the present work and reported in the literature certify the accuracy of present modeling and simulating.

Table 3 Grid independency test for Ra = 10³, H = 100, K_r = 10, R_k = 1, d = 0.1, ε = 0.6, φ_Ag = φ_MgO = 0.0

Table 4 Average Nusselt number in a porous triangular cavity for different Rayleigh numbers and nanoparticles volume fraction

Table 5 Data of the present numerical solution and those performed by Saeid [63] at Ra = 10³, d = 0.1, K_r = H=1

Results and discussion

This part has focused on influences of parameters appeared in the equations and boundary conditions such as Darcy–Rayleigh number Ra = 10–1000, porosity ε = 0.1–0.9, interface parameter H = 1–1000, K_r = 0.1–10, volume fraction of the hybrid nanofluid φ_hnf = 0–0.02 and the width of the solid wall d = 0.1–0.4 on the nanoliquid flow and thermal fields as well as the rates of heat exchange through the solid walls, the solid and liquid phases of the porous medium.

The set of images shown in Fig. 2 illustrates the dependency of streamlines, isotherms of the liquid and solid phases of the porous medium on R_k at constant parameters Ra = 10³, ɛ = 0.5, d = 0.1, K_r = H=1. In the figures, the solid and dash lines are indicants of the pure fluids and Ag–MgO hybrid nanofluids, respectively. It is visible that the use of the Ag–MgO hybrid nanoparticles decreases the strength of the fluid flow. Indeed, using the Ag–MgO hybrid nanoparticles amplifies the dynamic viscosity of the base fluid which acts as a resistant force against the buoyancy effects. The increment of the density of the isotherms attributed to each of the phases by increasing R_k bodes that the heat transfer rate through the porous region raises when R_k increases. Comparing the isotherms of the fluid and solid phases at low and high values of R_k indicates that when R_k is low, the influences of the presence of the hybrid nanoparticles on the temperatures fields are more than those compared to the high values of R_k, while the relative decrease in the strength of the flow for the high value of R_k is more than that for the low value of R_k. These relative decreases are 4.8 and 8.0% for R_k = 0.1 and 10, respectively.

Fig. 2

Effects of R_k on the flow, fluid temperature T_hnf and solid temperature T_s fields at Ra  = 10³, ɛ  = 0.5, d  = 0.1, K_r = H = 1, aR_k = 0.1, bR_k = 1 and cR_k = 10

From Fig. 3, it is apperceived that a weak circular-shaped vortex is appeared in the center of the porous cavity when Ra = 10. In this case, the parallelism of the isotherms attributed to the fluid phase of the porous medium with vertical bounds reflects the heat conduction dominance on the thermal convection mechanism during the heat transfer process. As Ra enhances, the strength and the size of the formed vortices becomes more as a result of increasing the buoyancy effects. In addition, it is visible that the hybrid nanoparticles more impress the thermal fields, when Ra is low.

Fig. 3

Effects of Ra on the flow, fluid temperature T_hnf and solid temperature T_s fields at R_k = 1, ɛ  = 0.5, d  = 0.1, K_r = H = 10, aRa  = 10, bRa  = 100 and cRa  = 1000

From Fig. 4, the increment of porosity ε increases strongly the size and the strength of the vortex created within the porous media. Indeed, when the porosity ε increases, the dynamic resistance resulting from the solid matrix, which was modeled by Darcy term in the momentum equation, is reduced. It is found that the elongation of isotherms along horizontal bounds decreases as ε increases; however, the effect of ε on the solid matrix temperature field is not so perceptible.

Fig. 4

Effects of ε on the flow, fluid temperature T_hnf and solid temperature T_s fileds at Ra  = 10³, d  = 0.1, R_k = K_r = H = 10, aε  = 0.1, bε  = 0.5 and cε  = 0.9

Efficacies of modified thermal conductivity ratio K_r on the velocity and temperatures patterns have been illustrated in Fig. 5. For this analysis, other characteristics are kept constant so that Ra  = 10³, d  = 0.1, R_k = H = 10 and ε  = 0.5. At first, when K_r augments from 0.1 to 1, the intensity of the recirculating flow formed in the porous enclosure slightly increases. Then, the augmentation of K_r from 1 to 10 declines this characteristic of the flow. This trend can literally be seen in Saied’s work [63]. According to the definition of the K_r, the ability of the fluid phase for heat transfer enhances as K_r increases. When K_r is low, the thermal resistance of the fluid occupying the pores of the porous medium is high; hence, the heat exchange rate between the fluid and solid phases of the porous matrix is low. This fact eventuates a drastic TNE condition between the fluid and solid phases of the porous matrix. The difference of the configurations of the isotherms ascribed to two phases at the low value of K_r vouches the above statements. Then, it is observed that these thermal fields become closer to each other by increasing K_r. According to the above description, it is clear that this trend is a result of decreasing thermal resistance of the fluid phase when K_r enhances.

Fig. 5

Effects of K_r on the flow, fluid temperature T_hnf and solid temperature T_s fields at Ra  = 10³, d  = 0.1, R_k =  H = 10, ε = 0.5, aK_r = 0.1, bK_r = 1 and cK_r = 10

The efficacies of the solid wall thickness on the flow and temperatures patterns are shown in Fig. 6. With the constant parameters, Ra = 100, R_k = K_r = 10, H = 100, ε = 0.5, the strength and the size of the recirculation formed in the porous cavity decreases as the solid wall thickness rises. One argument says that since the wall thermal conductivity is limited, the thermal resistance of the wall is completely related to the thickness of the wall and increases with a growth of the wall thickness. Consequently, when the wall is thick, less heat can reach the porous media from the hot bound. Decreasing trend of the fluid convection with being thicker solid wall reduces the share of the convection mode in the heat transfer mode and mutually amplifies the share of the conduction mode in the heat transfer process by the fluid phase. Comparing the isotherms of the pure fluid and hybrid nanofluid in a certain case to each other clarifies that the influence of the presence of the hybrid nanoparticles on the temperature fields at the cavity with the thinner solid walls is more than that for the cavities with the thicker solid walls.

Fig. 6

Effects of d on the flow, fluid temperature T_hnf and solid temperature T_s fields at Ra = 100, R_k = K_r = 10, H = 100, ε = 0.5, ad = 0.02, bd = 0.2 and cd = 0.4

The LTNE conditions between the fluid and solid phases of the porous matrix, which are deputized by the Nield number H, make the different temperature fields for these two phases as can be observed in Fig. 7. In fact, H is a criterion of the heat exchange rate microscopically between the fluid and solid phases of the porous matrix. An increment in H augments the heat transfer between the fluid and solid phases of the porous medium. Accordingly, it is said that the thickness of the thermal boundary layer rises with H. A detailed look at the fluid temperature field affirms this claim. Additionally, the increment of the interface parameter H causes a more elongation for the isotherms of the solid phase. Indeed, the growth of the heat exchange between these two phases arising from enhancing H directs both the thermal fields to a unique thermal field. It is visible that the influences of using hybrid nanoparticles on the isothermal fields of the solid phase are significant at high values of H (H = 100 and 1000). It should be noted that the influence of the hybrid nanoparticles on the reduction of the local temperatures difference of two phases reduces with an increment in H.

Fig. 7

Effects of H on the flow, fluid temperature T_hnf and solid temperature T_s fields at, Ra = 10³, K_r = R_k = 1, d = 0.1, aH = 1, bH = 10, cH = 100 and dH = 1000

The variations of Nu_hnf and Nu_s according to Ra for various values of the concentration of Ag–MgO hybrid nanoparticles are illustrated in Fig. 8. As shown, using Ag–MgO hybrid nanoparticles declines the rate of heat exchange through the components forming the porous entity. As stated previously, the thermal conductivity and the dynamic viscosity of the host liquid boost by raising the concentration of the Ag–MgO hybrid nanoparticles suspended. The increment of thermal conductivity and dynamic viscosity of the host liquid with the nanoparticles concentration are known as desirable and undesirable results at the natural convection, respectively. From Table 1, it is seen that the increment of the desirable parameter is significantly less than that of undesirable parameter. Hence, the suspension of the Ag–MgO hybrid nanoparticles in the host liquid to raise the heat transfer rate cannot be a deliberated operation. In addition, Fig. 8a shows that a growth of Ra enhances the heat transfer rate carried by fluid phase of the porous medium. However, it can be seen that the increment of Ra has not significant effects on the Nu_s when Ra > 600.

Fig. 8

Variations of Nu_hnf (a) and Nu_s (b) according to the Ra numbers at various values of φ when ε  = 0.5 and R_k =  H = K_r = 10

In Fig. 9a, b, the variations of Nu_hnf and Nu_s versus R_k are reported at different values of d when Ra = 10³, ε = 0.5, K_r = H=100. It is visible that the increment of R_k increases the heat transfer rates through the fluid and solid phases. This trend is due to that fact that increasing R_k deals with the increment of the heat exchange through the walls. Additionally, it is observed that whatever the solid wall thickness is less, the heat exchange rate through the solid and fluid phases of the porous medium is more. As said previously, the thermal resistance of the solid wall is completely related to the thickness of the wall and increases with a growth of the wall thickness. Consequently, when the wall is thick, less heat can reach the porous media from the hot bound. It is worth noting here that for a certain thickness of the wall the reduction of Nu_s due to the use of the hybrid nanoparticles is more than for Nu_hnf.

Fig. 9

Variations of Nu_hnf (a) and Nu_s (b) according to d at different values of R_k when Ra  = 10³, ε  = 0.5, K_r = H=100

Figure 10a, b displays the influences of the thickness of the solid wall on Nu_hnf and Nu_s as functions of K_r. It can be concluded that the heat rate carried by hybrid nanofluid occupying the pores (Nu_hnf) is increasing when K_r increases from 0.1 to 3, after which this rate approximately remains constant with a growth of K_r. In addition, the heat exchange rate through the solid phase Nu_s increases as K_r is increasing, while retaining the solid wall thickness fixed. It is obviously seen that the increment of the thickness lessens Nu_hnf for all the values of K_r. This is despite the fact that the decreasing behavior Nu_s with the increase in the thickness d only can be seen for thicknesses of less than or equal to 0.2. As shown in Fig. 10b, depending on the value of K_r, an increase in the wall thickness to 0.4 can increase or decrease Nu_s. Here it can also be seen that dispersing Ag–MgO hybrid nanoparticles declines Nu_s with the exception d = 0.4. Using the hybrid nanoparticles slightly raises Nu_s when K_r < 18, while the nanoparticles can enhance Nu_s for K_r > 42.

Fig. 10

Variations of Nu_hnf (a) and Nu_s (b) according to d at different values of K_r when Ra  = 10³, ε  = 0.5, R_k = H = 10

From Fig. 11a, b, the increase in H declines and elevates Nu_hnf and Nu_s, respectively, keeping the thickness of solid wall constant. The increment in H augments the heat transfer between the fluid and solid phases of the porous medium, consequently, the thickness of thermal boundary layer increases. Hence, the temperature gradient inside the boundary layer declines which means the reduction of Nu_hnf. As illustrated in Fig. 11b, it can be observed that Nu_s increases when H grows. This result can easily be justified due to this fact that the temperature gradient of the porous matrix near the vertical bounds amplifies as a result of the enhancement of H. For a cavity with d = 0.4 and H < 300, dispersing the hybrid nanoparticles Ag–MgO in the host fluid can amplify the heat transfer rate through the solid phase. However, if H > 300, the use of the nanoparticles debilitates this rate.

Fig. 11

Variations of Nu_hnf (a) and Nu_s (b) according to d at various values of H when Ra = 10³, ε = 0.5, R_k = 10 and K_r = 1

The results represented in Fig. 12a illustrate that for different values of d, the increase in porosity ε scrimps Nu_hnf. Nevertheless, as shown in Fig. 12b, the different trends can be observed for the variations of Nu_s versus porosity ε as the thickness of solid wall varies. Although in the low value of d (d  = 0.02), the increase in porosity declines Nu_s, when d  = 0.2 or 0.4, Nu_s continuously augments with increasing ε. Further, there is no a certain trend for the variations of Nu_s with increasing ε when d  = 0.05 and 0.1.

Fig. 12

Variations of Nu_hnf (a) and Nu_s (b) according to d at different values of ε when Ra  = 10³, R_k = H = K_r = 10

Figure 13 shows the variations of heat transfer rate across the solid wall Q_w versus H for various values of d when Ra = 10³, ε = 0.5, R_k = 10 and K_r = 1. According to the above presented results, it is expected that the increment of the solid wall thickness declines the heat exchange rate Q_w. This fact has obviously been illustrated in Fig. 13. Also Q_w increases with the increment of H. It is clear that the effect of H on the increase in the rate of Q_w is more essential when the solid wall thickness is low. Figure 14 displays the variations of heat transfer rate across the solid wall Q_w versus ε for various values of d when Ra = 10³, R_k = H=K_r = 10. As shown, the increment in ε strongly declines Q_w. In addition, it can be said that the decreasing trend Q_w by using the Ag–MgO hybrid nanoparticles is more essential at high values of ε.

Fig. 13

Variations of Q_w according to d at various values of H for Ra = 10³, ε = 0.5, R_k = 10 and K_r = 1

Fig. 14

Variations of Q_w according to d at different values of ε when Ra  = 10³, R_k = H = K_r = 10

Conclusions

Current investigation studies the conjugate natural convection inside a porous enclosure filled with Ag–MgO hybrid nanofluid using LTNE model. Two solid walls located in two sides of cavity introduced as conductive interface between hot and cold walls, and besides, the top and bottom bounds have been insulated. The governing differential equations are written using the Darcy law and then transformed into a non-dimensional form for better representation of the results. Governing equations have been solved by the finite element method. Various amounts of the Darcy–Rayleigh number (Ra = 10–10³), volume fraction of hybrid nanoparticles (φ_hnf = 0–0.02), porosity (ε = 0.1–0.9), interface parameter (H = 1–10³), thermal conductivity ratio (K_r = 0.1–10), and the width of the solid wall (d = 0.1–0.4) are examined to perform calculations. The most significant findings are listed below:

• Using the hybrid nanoparticles decreases the flow strength. The heat transfer rate increases when R_k rises. When R_k is low, the influences of the hybrid nanoparticles on the temperatures fields and the relative decreasing of the flow strength are, respectively, more and less than those compared to the high values of R_k,

• As Ra enhances, the flow strength becomes more. When Ra is low, the hybrid nanoparticles more impress the thermal fields. Besides, increment of ε, increases strongly the size and the strength of the vortex created within the porous media.

• When K_r augments from 0.1 to 1, the strength of recirculation formed slightly increases, whereas the augmentation of K_r from 1 to 10 declines that. When K_r is low, the heat transfer rate is low and by increasing K_r, thermal fields become closer to each other. The strength and size of the recirculation formed decreases as d increases. The effect of hybrid nanoparticles on thermal fields with the thinner solid walls is more than that the thicker ones.

• An increment in H leads to the heat exchange enhancement. The influences of hybrid nanoparticles on the solid phase isothermal fields are significant at high magnitudes of H and on the reduction of two phases temperatures difference reduces with increasing H.

• Using hybrid nanoparticles declines the heat exchange rate. By raising the hybrid nanoparticles concentration, Nu_hnf and Nu_s decreased for constant Ra. Besides, increase in Ra enhances the Nu_hnf and Nu_s. The increment of R_k and d augment the heat transfer. For a certain d, the reduction of Nu_s due to using the hybrid nanoparticles is more than that for Nu_hnf. Growth of Ra enhances the heat exchange rate. However, the increment of Ra has not significant influences on Nu_s when Ra > 600.

• Nu_hnf enhances when K_r increases from 0.1 to 3, after which this rate approximately remains constant. Moreover, Nu_s increase with augment of K_r, while d retaining fixed. The increment of d lessens Nu_hnf for all values of Kr and not has specific trends for Nu_s. Dispersing hybrid nanoparticles declines Nu_s except for d = 0.4, raises Nu_s when K_r < 18, while it can enhance Nu_s for K_r > 42.

• The increase in H, respectively, declines and elevates Nu_hnf and Nu_s, keeping d constant. For all values of d, the increase in ε scrimps Nu_hnf. Although in low value of d (d = 0.02), the increase in ε declines Nu_s, but at higher values, Nu_s continuously augments.

• For different values of d, the increase in ε scrimps Nu_hnf; however, various trends can be seen for the variations of Nu_s versus ε as d varies. The increment of d and also ε declines the heat transfer rate. In addition, Q_w increases with the increment of H.