An Efficient Approximation Technique for Solving a Class of Fractional Optimal Control Problems

Abstract

In this paper, we discuss a class of fractional optimal control problems, where the system dynamical constraint comprises a combination of classical and fractional derivatives. The necessary optimality conditions are derived and shown that the conditions are sufficient under certain assumptions. Additionally, we design a well-organized algorithm to obtain the numerical solution of the proposed problem by exercising Laguerre polynomials. The key motive associated with the present approach is to convert the concerned fractional optimal control problem to an equivalent standard quadratic programming problem with linear equality constraints. Given examples illustrate the computational technique of the method together with its efficiency and accuracy. Graphical representations are provided to analyze the performance of the state and control variables for distinct prescribed fractions.

1 Introduction

Fractional calculus has captured the attention of researchers during the last few decades due to its applicability in the diverse field of applied mathematics and engineering such as continuum mechanics, fluid mechanics, signal processing, bioengineering, etc. This apparent modernization inspires us to look for admissible applications and physical properties unattended by integer-order operators (integral/differential). Starting with a remarkable application in the tautochronous problem, continuing with applications in viscoelasticity, diffusion and wave propagation, control theory: Fractional calculus appears to be suitable for modeling purposes as the previous set of data is associated.

The classical optimal control problem is extended to the fractional optimal control problem (FOCP) by means of fractional calculus. The deviation exists in dynamical constraints that contain fractional-order derivatives in place of classical derivatives. The existence theorem on FOCPs was first introduced by Bhatt in [1]. Some of the recent work done on FOCP include Hamiltonian formulation [2], central difference numerical scheme [3], a numerical scheme using modified Jacobi polynomials [4], FOCP with free terminal time [5].

In this paper, we present a class of FOCPs and further investigate it for necessary and sufficient optimality conditions. In the literature, orthogonal polynomials like Chebyshev polynomials [6], Jacobi polynomials [4, 7], Legendre polynomials [8], have already practiced while handling FOCPs. The representation of a function in terms of the series expansion by orthogonal polynomials is a fundamental concept in approximation and optimization. The presence of orthogonality is sufficient in scaling down the complexity by reducing it to a simpler system of algebraic equations. We adopt the Laguerre polynomials to approximate the state, control variable and thus the objective function. The concerned problem is then transformed to an equivalent standard quadratic programming problem with linear equality constraints. A solution to the latter problem corresponds to a solution of the original FOCP.

2 Problem Statement

Consider a class of FOCPs, designed to find the optimal control u(t), that minimizes the given performance index J

$$\begin{aligned} \mathbf{(P)}\quad \quad \quad \mathrm{Minimize}\quad \quad J=\int _{0}^{1}\,F(x,u,t)\,\mathrm{d}t, \end{aligned}$$

(1)

subject to the system dynamic constraints

$$\begin{aligned} G_1\left( x'(t),\,{}_0D^{\alpha }_t x(t)\right) =G_2(x,u,t),\,\,\alpha \in ]0,1[, \end{aligned}$$

(2)

and the initial condition

$$\begin{aligned} x(0)=x_0, \end{aligned}$$

(3)

where x(t) is the state variable known as the optimal trajectory.

• The functions F and $G_2$ are assumed to be continuously differentiable in all the three arguments.

• To generalize a class of FOCPs already present in the literature (see, e.g., [9, 10]), the function $G_1$ is considered to be a combination of classical and fractional-order derivatives.

• By taking $G_1\equiv {}^c_0D^{\alpha }_t x(t)$, (P) reduces to the problem originally introduced by Agrawal [11]. Further investigations for solution schemes are made by many researchers like Baleanu [2], Dehghan [4], Lotfi [12].

Our aim is to obtain the necessary and sufficient conditions, together with a solution scheme for the proposed problem (P).

3 Preliminaries

In this section, we give some basic definitions of fractional-order derivatives [13,14,15] and Laguerre polynomials, which will be needed in the sequel.

Fractional-Order Derivatives Let $f\in C^n [a, b];n\in \mathbb {N}$, where $C^n [a, b]$ is the space of n times continuously differentiable functions defined over [a, b].

Definition 3.1

For all $t\in [a, b], n-1\le \alpha <n$, left Riemann–Liouville fractional derivative of order $\alpha$ is defined as

$$\begin{aligned} {}_aD_t^{\alpha }f(t)=\frac{1}{\varGamma (n-\alpha )}\left( \frac{\mathrm{d}}{\mathrm{d}t}\right) ^n\int _a^t (t-\tau )^{n-\alpha -1}f(\tau )\mathrm{d}\tau . \end{aligned}$$

Definition 3.2

For all $t\in [a, b] , n-1\le \alpha <n$, left Caputo fractional derivative of order $\alpha$ is defined as

$$\begin{aligned} {}^c_aD_t^{\alpha }f(t)=\frac{1}{\varGamma (n-\alpha )}\int _a^t \left( t-\tau \right) ^{n-\alpha -1}f^n(\tau )\mathrm{d}\tau . \end{aligned}$$

Definition 3.3

(Integration by parts) If f, g,  and the fractional derivatives $_aD_t^{\alpha }g, {}_t D_b^{\alpha }f$ are continuous at every point $t \in [a, b]$, then

$$\begin{aligned} \int _a^bf(t)\,{}_aD_t^{\alpha }g\, \mathrm{d}t=\int _a^b g(t)\,{}_tD_b^{\alpha }f\,\mathrm{d}t,\quad \alpha \in ]0,1[. \end{aligned}$$

Laguerre Polynomials The Laguerre polynomials $L_n(x)$ (see [16] and references therein), are solutions of a second-order linear differential equation $xy''+(1-x)y'+ny=0,\,n\in \mathbb {N}.$

• The power series representation for Laguerre polynomials is given by

  $$\begin{aligned} L_n(x)=\sum _{k=0}^n \, \frac{(-1)^k}{k!}\, {\large {{}^nc_k}}\, x^k, \quad \mathrm{where}\,\,{}^nc_k=\frac{n!}{k!(n-k)!}. \end{aligned}$$

  (4)

• Orthogonal property in $[0,\infty [$ with $e^{-x}$ as the weight function

  $$\begin{aligned} \int _0^{\infty }L_n(x)L_m(x)\, e^{-x}\mathrm{d}x= \delta _{nm}=\left\{ \begin{array}{ll} 1 &{}\quad \mathrm{if}\,\, n=m, \\ 0 &{}\quad \mathrm{otherwise.} \end{array} \right. \end{aligned}$$

  (5)

• In the interval ]0, 1[, the orthogonality relation can be viewed as

  $$\begin{aligned} \int _0^{1}L_n\left( -\ln (x)\right) L_m\left( -\ln (x)\right) \, \mathrm{d}x= \delta _{nm}=\left\{ \begin{array}{ll} 1 &{}\quad \mathrm{if}\,\, n=m, \\ 0 &{}\quad \mathrm{otherwise.} \end{array} \right. \end{aligned}$$

  (6)

4 Necessary and Sufficient Conditions

In this section, we derive the necessary optimality conditions of the problem (P). Under appropriate assumptions, it is shown that the obtained necessary optimality conditions become sufficient.

Theorem 4.1

(Necessary conditions) If u is an optimal control of the problem $\mathbf{(P)}$, then u satisfies the necessary conditions given by

$$\begin{aligned} G_1(x'(t),\,{}_0D^{\alpha }_t x(t))= & {} G_2(x,u,t),\\ \frac{\partial G_1}{\partial ({}_0D^{\alpha }_t x)}\,{}_tD^{\alpha }_1 \lambda -\frac{\partial G_1}{\partial (x')}\,\frac{\mathrm{d}\lambda }{\mathrm{d}t}= & {} \frac{\partial F}{\partial x}+\lambda \frac{\partial G_2}{\partial x},\\ \frac{\partial F}{\partial u}+\lambda \frac{\partial G_2}{\partial u}= & {} 0, \end{aligned}$$

with terminal conditions, $x(0)=x_0$ and $\lambda (1)=0.$

Proof

To find the optimal control u(t), define the modified performance index

$$\begin{aligned} \bar{J}(u)=\int _0^1 F(x,u,t)+\lambda \left[ G_2(x,u,t)-G_1(x'(t),\,{}_0D^{\alpha }_t x(t))\right] \,\mathrm{d}t, \end{aligned}$$

where $\lambda$ is a Lagrange multiplier also known as the costate or adjoint variable. Taking the first variation of the modified performance index $\bar{J}(u)$, we get

$$\begin{aligned} \delta \bar{J}(u)= & {} \int _0^1\left[ \frac{\partial F}{\partial x}\delta x+\frac{\partial F}{\partial u} \delta u+\delta \lambda (G_2-G_1)\right. \\&+\left. \lambda \left( \frac{\partial G_2}{\partial x}\delta x+\frac{\partial G_2}{\partial u}\delta u-\frac{\partial G_1}{\partial (x')}\delta (x')- \frac{\partial G_1}{\partial ({}_0D^{\alpha }_t x)}\delta ({}_0D^{\alpha }_t x)\right) \right] \mathrm{d}t, \end{aligned}$$

where $\delta x,\delta u$ and $\delta \lambda$ are the variations of x, u and $\lambda$, respectively, with the specified terminal conditions. Using integration by parts, we obtain

$$\begin{aligned} \int _0^1 \lambda (t) \, \delta ({}_0D^{\alpha }_t x(t))\,\mathrm{d}t= & {} \int _0^1\delta x(t)\, ({}_tD^{\alpha }_1 \lambda (t))\, \mathrm{d}t,\\ \mathrm{and} \quad \int _0^1 \lambda (t) \, \delta (x'(t))\,\mathrm{d}t= & {} -\int _0^1\delta x(t)\, \lambda '(t)\, \mathrm{d}t, \end{aligned}$$

provided $\delta x (0) =0$ or $\lambda (0) =0$, and $\delta x(1)=0$ or $\lambda (1)=0$. As x(0) is specified, we take $\delta x (0) =0$. Since x(1) is not specified, we require $\lambda (1)=0$. Thus,

$$\begin{aligned} \delta \bar{J}(u)= & {} \int _0^1\left[ (G_2-G_1)\delta \lambda + \left( \frac{\partial F}{\partial x}+\lambda \frac{\partial G_2}{\partial x}+\frac{\partial G_1}{\partial ( x')}\,\lambda '(t)-\frac{\partial G_1}{\partial ({}_0D^{\alpha }_t x)}\,{}_tD^{\alpha }_1 \lambda \right) \delta x\right. \nonumber \\&+\left. \left( \frac{\partial F}{\partial u}+\lambda \frac{\partial G_2}{\partial u}\right) \delta u\right] \,\mathrm{d}t. \end{aligned}$$

(7)

To minimize $\bar{J}(u)$, we need the first variation $\delta \bar{J}(u)$ to be zero, i.e., the coefficients of $\delta x,\delta u$ and $\delta \lambda$ in Eq. (7) have to be zero. Thus,

$$\begin{aligned} G_1(x'(t),\,{}_0D^{\alpha }_t x(t))= & {} G_2(x,u,t), \end{aligned}$$

(8)

$$\begin{aligned} \frac{\partial G_1}{\partial ({}_0D^{\alpha }_t x)}\,{}_tD^{\alpha }_1 \lambda -\frac{\partial G_1}{\partial (x')}\,\frac{\mathrm{d}\lambda }{\mathrm{d}t}= & {} \frac{\partial F}{\partial x}+\lambda \frac{\partial G_2}{\partial x},\end{aligned}$$

(9)

$$\begin{aligned} \frac{\partial F}{\partial u}+\lambda \frac{\partial G_2}{\partial u}= & {} 0,\end{aligned}$$

(10)

$$\begin{aligned} \mathrm{with} \quad x(0)= & {} x_0 \quad \mathrm{and}\quad \lambda (1)=0. \end{aligned}$$

(11)

Equations (8)–(11) represent necessary optimality conditions for the posed problem (P). We may mark that, once the costate variable $\lambda$ is obtained by solving (8) and (9), the control variable u(t) can easily be obtained by (10). $\square$

Particular Cases

• For $G_1={}_0D^{\alpha }_t x(t)$, the problem (P) reduces to the simplest (FOCP) given by Agrawal in 1989 (see [11]).

• For $G_1=Ax'(t)+B{}_0D^{\alpha }_t x(t)\,;\, A,B\in \mathbb {R}$, the necessary conditions reduce to

  $$\begin{aligned} A\,x'(t)+B\,{}_0D^{\alpha }_t x(t)= & {} G_2(x,u,t),\\ B\,{}_tD^{\alpha }_1 \lambda -A\,\frac{d\lambda }{dt}= & {} \frac{\partial F}{\partial x}+\lambda \frac{\partial G_2}{\partial x},\quad \mathrm{and}\quad \frac{\partial F}{\partial u}+\lambda \frac{\partial G_2}{\partial u}=0, \end{aligned}$$

  with terminal conditions (11). For solution schemes and sufficient optimality conditions of this problem, we refer the reader to [5, 17].

Note that, $G_1$ involves left Riemann–Liouville fractional derivative. Similar results are obtained by taking Caputo’s fractional-order derivatives, as shown in the next theorem.

Theorem 4.2

If u is an optimal control of performance index (1) subject to the system dynamical constraint $G_1(x'(t),\, {}^c_0D_t^{\alpha }x(t))=G_2(x,u,t),$ and terminal conditions (3), then u satisfies the necessary conditions given by

$$\begin{aligned} G_1(x'(t),\,{}^c_0D^{\alpha }_t x(t))= & {} G_2(x,u,t),\\ \frac{\partial G_1}{\partial ({}^c_0D^{\alpha }_t x)}\,{}_tD^{\alpha }_1 \lambda -\frac{\partial G_1}{\partial (x')}\,\frac{\mathrm{d}\lambda }{\mathrm{d}t}= & {} \frac{\partial F}{\partial x}+\lambda \frac{\partial G_2}{\partial x},\\ \frac{\partial F}{\partial u}+\lambda \frac{\partial G_2}{\partial u}= & {} 0, \end{aligned}$$

with terminal conditions (11).

In the next theorem, we shall show that the necessary optimality conditions (Theorem 4.1) become sufficient under suitable conditions.

Theorem 4.3

(Sufficient conditions) Let $(x^*,u^*,\lambda ^*)$ be a triplet satisfying necessary conditions (8)–(10) of the fractional optimal control problem $(\mathbf{P})$. Moreover, assume that

• (i) f and $G_2$ are convex in the arguments x and u.

• (ii) $\lambda (t)\ge 0,$ for all $t\in [0,1]$ or $G_2$ is linear in x and u.

Then $(x^*,u^*)$ is an optimal solution.

Proof

Since $(x^*,u^*,\lambda ^*)$ satisfies necessary conditions (8)–(10).

Refereing to (8), we get

$$\begin{aligned} x'\,\frac{\partial G_1}{\partial x'}+{}_0D_t^{\alpha }x\, \frac{\partial G_1}{\partial {}_0D_t^{\alpha }x}=x\,\frac{\partial G_2}{\partial x}+u\,\frac{\partial G_2}{\partial u}. \end{aligned}$$

(12)

By (9) and (10), we have

$$\begin{aligned} \frac{\partial F}{\partial x}= & {} \frac{\partial G_1}{\partial ({}_0D^{\alpha }_t x)}\,{}_tD^{\alpha }_1 \lambda -\frac{\partial G_1}{\partial (x')}\,\frac{\mathrm{d}\lambda }{\mathrm{d}t} -\lambda \frac{\partial G_2}{\partial x}, \end{aligned}$$

(13)

$$\begin{aligned} \mathrm{and }\quad \frac{\partial F}{\partial u}= & {} -\lambda \frac{\partial G_2}{\partial u}. \end{aligned}$$

(14)

Let (x, u) be an admissible solution of the problem (P). For $(x^*,u^*)$ to be an optimal solution, it is left to show that $J(x^*,u^*)\le J(x,u)$. According to Eqs. (13) and (14), we observe that

$$\begin{aligned} J(x,u)-J(x^*,u^*)= & {} \int _0^1 \left[ F(x,u,t)-F(x^*,u^*,t)\right] \mathrm{d}t\\\ge & {} \int _0^1\left[ (x-x^*)\,\frac{\partial F}{\partial x}+ (u-u^*)\,\frac{\partial F}{\partial u}\right] \, \mathrm{d}t,\\= & {} \int _0^1\left[ (x-x^*)\,\frac{\partial G_1}{\partial ({}_0D^{\alpha }_t x)}\,{}_tD^{\alpha }_1 \lambda -(x-x^*)\,\frac{\partial G_1}{\partial (x')}\,\frac{\mathrm{d}\lambda }{\mathrm{d}t} \right. \\&-\,\lambda \, (x-x^*)\, \frac{\partial G_2}{\partial x} -\left. \lambda \, (u-u^*)\,\frac{\partial G_2}{\partial u}\right] \,\mathrm{d}t.\quad \end{aligned}$$

Using integration by parts, we arrive at

$$\begin{aligned} J(x,u)-J(x^*,u^*)\ge & {} \int _0^1\left[ \lambda \, \frac{\partial G_1}{\partial ({}_0D^{\alpha }_t x)}\,{}_0D^{\alpha }_t(x-x^*)+\lambda \, \frac{\partial G_1}{\partial (x')}\,(x-x^*)' \right. \\&-\lambda \, (x-x^*)\, \frac{\partial G_2}{\partial x} -\left. \lambda \, (u-u^*)\,\frac{\partial G_2}{\partial u}\right] \mathrm{d}t,\\\ge & {} \int _0^1\left[ \lambda \, (x-x^*)\, \frac{\partial G_2}{\partial x} +\lambda \, (u-u^*)\,\frac{\partial G_2}{\partial u}\right. \\&-\lambda \, (x-x^*)\, \frac{\partial G_2}{\partial x} -\left. \lambda \, (u-u^*)\,\frac{\partial G_2}{\partial u}\right] \mathrm{d}t, \quad \mathrm{by}\,\,(12)\\= & {} \mathbf{0}. \end{aligned}$$

$J(x,u)\ge J(x^*,u^*)$ implies that $(x^*,u^*)$ is an optimal solution of the problem (P), which concludes the proof. $\square$

5 Mathematical Formulation of Solution Scheme: Algorithm

We explore the Laguerre polynomials to obtain a solution scheme for FOCPs and analyze its effectiveness practically. These polynomials are used to approximate more complicated functions into a linear or nonlinear system of algebraic equations. The formulation of the solution scheme for FOCP starts with parameterizing the state variable with a polynomial of degree N, and hence u(t) can be determined by lesser number of parameters that minimizes the performance index J.

Let $Q\subset C[0,1]$ be the set of all functions satisfying initial condition (3), and $Q_N\subset Q$ be the class of all Laguerre polynomials of degree up to N.

Numerical Scheme

• State parameterization Parameterize the state variable as a linear combination of Laguerre polynomials of degree up to N.

  $$\begin{aligned} x(t)\approxeq x_N(t)=\sum _{k=0}^N a_k\,L_k(t),\quad N=1,2,3... \end{aligned}$$

  where $L_k$s are Laguerre polynomials of degree k and $a_k$s are the unknown coefficients to be determined.

• Expression of the control variable Dynamical constraint (2) assists in rewriting the control variable as a function (say $\phi$) of time t, parameterized state variable $x_N(t)$, and fractional derivative ${}^{c}_0D_t^{\alpha }x_N(t)$. For $\alpha ,\beta \in ]0,1[,$

  $$\begin{aligned} u(t)\approxeq u_N(t)= & {} \phi \left( t,x_N(t),{}^{c}_0D_t^{\alpha }x_N(t)\right) ,\\= & {} \phi \left( t,\sum _{k=0}^N a_k L_k(t),\sum _{k=0}^{N}a_k\,{}^{c}_0D^{\alpha }_t L_k(t)\right) . \end{aligned}$$

• Approximation of performance index Transform performance index (1) to a function of $N+1$ unknowns $a_i\,(i=0,1,2,...N)$.

  $$\begin{aligned} \hat{J}[a_0,...,a_N]= & {} \int _{t_0}^{t_1}F\left( t,\sum _{k=0}^N a_k L_k(t),\phi \left( t,\sum _{k=0}^N a_k L_k(t),\sum _{k=0}^{N}a_k{}^{c}_0D^{\alpha }_t L_k(t)\right) \right) dt,\nonumber \\ \end{aligned}$$

  (15)
  $$\begin{aligned}&\mathrm{subject}\,\mathrm{to}\quad x_0\approxeq x_N(t_0)=\sum _{k=0}^N a_k\, L_k(t)\,{\large {|}_{t=t_0}}\,. \end{aligned}$$

  (16)

• Transformation to standard programming problem With quadratic performance index, the problem (P) is converted into a quadratic function (15) of unknown parameters $a_i$ with equality constraints (16) described below in the equivalent matrix form.

  $$\begin{aligned} {Minimize } \,\, \left( \frac{1}{2}\,a'Ha+G'a\right) ,\quad a\in \mathbb {R}^{N+1}, \end{aligned}$$

  (17)

  subject to the linear equality constraints

  $$\begin{aligned} Ba=C, \end{aligned}$$

  (18)

  where $a=[a_0\,\,a_1...\,a_N]'$, $B=[L_0(t_0)\,\,L_1(t_0)...\,L_N(t_0)]$, and $C=[x_0]$.

• Obtain the optimal value We now find the optimal value $a^*$ to solve quadratic programming problem (17)–(18) as follows

  $$\begin{aligned} a^*=-H^{-1}\,(G+B'\lambda ^*), \quad \mathrm{where} \quad \lambda ^*=-(BH^{-1}B')^{-1}(C+BH^{-1}G). \end{aligned}$$

• Expression for approximated state and control variable Using $a^*$, we write the expressions for $x_N(t)$, $u_N(t)$ and the optimal value of $\hat{J}$ that approximates the original performance index J.

Proposed Algorithm

• 1. Parameterize the state variable x(t) by $x_N(t)$, using Laguerre polynomials.

• 2. Approximate u(t) by $u_N(t)$, as a function of $x_N(t)$ and ${}^c_{0}D^{\alpha }_t x_N(t)$.

• 3. Obtain H, G: Approximate J by $\hat{J}$, write $\hat{J}=a'Ha+G'a$.

• 4. Obtain B, C: Write the linear equality constraints as $Ba=C$.

• 5. Determine $\lambda ^*$ and $a^*$.

• 6. Deduce $x_N(t)$, $u_N(t)$ and find the optimal value of $\hat{J}$ that approximate J.

We have used Mathematica to perform all the numerical and graphical segments. One can also use MATLAB software to solve a quadratic programming problem with linear equality constraints by providing the matrices $H,\,G,\,B,\,C\,$ as input and extracting the column matrix a as output.

6 Laguerre Orthogonal Approximation: Convergence Criterion

In this section, we compute the $\alpha {\mathrm{th}}$-order fractional derivative of Laguerre polynomials for $\alpha \in ]0,1[$, followed by an approximation formula for the fractional derivative of the state variable. Afterward, we discuss the convergence analysis of the designed approximation.

Theorem 6.1

For $\alpha \in ]0,1[$, the fractional derivative of Laguerre polynomials of order $\alpha$ is given by

$$\begin{aligned} {}^c_0D_t^{\alpha }L_n(t)= & {} L_n^{\alpha }(t), \end{aligned}$$

(19)

$$\begin{aligned} where\quad L_n^{\alpha }(t)= & {} \sum _{k=[\alpha ]}^n \, \frac{(-1)^k}{k!}\, {\large {{}^nc_{_k}}}\, \frac{t^{k-\alpha }}{\varGamma (k-\alpha +1)}. \end{aligned}$$

(20)

Proof

By Eq. (4), we have $L_n(t)=\sum _{k=0}^n \, \frac{(-1)^k}{k!}\, {\large {{}^nc_k}}\, t^k\,$.

For Caputo’s derivative, we know that

$$\begin{aligned} {}^c_0D_t^{\alpha } K= & {} 0, \quad K\, \mathrm{is}\,\, \mathrm{a}\,\,\mathrm{constant},\\ \Rightarrow \quad {}^c_0D_t^{\alpha } t^p= & {} \left\{ \begin{array}{ll} \frac{\varGamma (p+1)}{\varGamma (p-\alpha +1)}\,t^{p-\alpha } &{} \quad \mathrm{for}\quad p>0, \\ 0 &{}\quad \mathrm{for}\quad p\le 0. \end{array}\right. \end{aligned}$$

We clearly observe that,

$$\begin{aligned} L_n^{\alpha }(t)= & {} {}^c_0D_t^{\alpha }L_n(t)= {}^c_0D_t^{\alpha }\left( \sum _{k=0}^n \, \frac{(-1)^k}{k!}\, {\large {{}^nc_k}}\, t^k\right) ,\\= & {} \sum _{k=[\alpha ]}^n \, \frac{(-1)^k}{k!}\, {\large {{}^nc_{_k}}}\, \frac{t^{k-\alpha }}{\varGamma (k-\alpha +1)}. \end{aligned}$$

$\square$

Next, we parameterize the state variable x(t) as a linear combination of Laguerre polynomials of degree N with unknowns $\{a_k\}_{k=0}^{N}$,

$$\begin{aligned} x(t)\approxeq x_N(t)=\sum _{k=0}^{N}a_k\,L_k(t)\,,\quad N=1,2,3... \end{aligned}$$

(21)

where $L_k$s are Laguerre polynomials of degree k. Using (21) and (6),

$$\begin{aligned} a_j= & {} \int _0^{\infty } x_N(t)\,L_j(t)\,e^{-t}\,dt,\quad j=0,1,...N. \nonumber \\ \mathrm{Or,}\quad a_j= & {} \int _0^{1} x_N(-ln(t))\,L_j(-ln(t))\,\mathrm{d}t,\quad j=0,1,...N. \quad \mathrm{by}\,\mathrm{(5)} \end{aligned}$$

(22)

Remark 6.1

In (20), one may observe that $t^{k-\alpha }$ can be expressed approximately in terms of Laguerre polynomials, which is given by

$$\begin{aligned} t^{k-\alpha }\approxeq \sum _{j=0}^{N}c_{_{kj}}L_j(t), \end{aligned}$$

where $c_{_{kj}}$ can be obtained from (22) with $x_N(t)=t^{k-\alpha }\,$.

Theorem 6.2

For $\alpha \in ]0,1[$, the approximation formula for fractional derivative of the state variable is given by

$$\begin{aligned} {}^c_0D_t^{\alpha }x(t)\approxeq {}^c_0D_t^{\alpha }x_N(t)=\sum _{k=[\alpha ]}^{N}a_k\,L_k^{\alpha }(t)\,,\quad N=1,2,3... \end{aligned}$$

(23)

where $L_k^{\alpha }(t)$ is given by Eq. (20). Or,

$$\begin{aligned} {}^c_0D_t^{\alpha }x(t)\approxeq \sum _{k=[\alpha ]}^{N}a_k\sum _{j=[\alpha ]}^{k}\frac{(-1)^j}{j!}\,{}^kc_{_j}\,\frac{t^{j-\alpha }}{\varGamma (j-\alpha +1)}. \end{aligned}$$

Proof

Using (21), we approximate ${}^c_0D_t^{\alpha }x(t)$ as

$$\begin{aligned} {}^c_0D_t^{\alpha }x(t)\approxeq {}^c_0D_t^{\alpha }x_N(t)= & {} {}^c_0D_t^{\alpha }\left( \sum _{k=0}^{N}a_k\,L_k(t)\right) =\sum _{k=[\alpha ]}^{N}a_k\,L_k^{\alpha }(t),\\= & {} \sum _{k=[\alpha ]}^{N}a_k\sum _{j=[\alpha ]}^{k}\frac{(-1)^j}{j!}\,{}^kc_{_j}\,\frac{t^{j-\alpha }}{\varGamma (j-\alpha +1)}. \end{aligned}$$

$\square$

We shall now explain the convergence analysis of the proposed algorithm, ensured by the Weierstrass approximation theorem.

Theorem 6.3

(Weierstrass approximation theorem [18]) Let $f\in C([a, b], \mathbb {R})$. Then, there is a sequence of polynomials $P_n(x)$ that converges uniformly to f(x) on [a, b].

Theorem 6.4

(see [6]) If $\xi _n = \mathrm{inf}_{Q_n}J,\, n\in \mathbb {N}$, where $Q_n$ is a subset of Q, consisting of all polynomials of degree at most n. Then, $\mathrm{lim}_{n\rightarrow \infty }\xi _n=\xi$, where $\xi = \mathrm{inf}_QJ$.

Theorem 6.5

If J has continuous first-order derivatives, and for $n\in \mathbb {N}, \beta _n=\mathrm{inf}_{Q_n}J$. Then, $\mathrm{lim}_{n\rightarrow \infty }\beta _n=\beta$, where $\beta =\mathrm{inf}_QJ$.

Proof

Let us define the sequence, $\beta _n=\mathrm{min}_{a_n\in \mathbb {R}^{n+1}}J(a_n).$

Since $a_n^*\in \mathrm{Argmin}\{J(a_n);\,a_n\in \mathbb {R}^{n+1}\}$, that implies, $\beta _n=J(a_n^*).$

Again, let $x_n^*\in \mathrm{Argmin}\{J(x(t));\,x(t)\in Q_n\}$

$$\begin{aligned} \Rightarrow J(x_n^*(t))=\mathrm{min}_{x(t)\in Q_n}J(x(t)), \end{aligned}$$

in which $Q_n$ is a class of combinations of Laguerre polynomials in t, of degree n, so $\beta _n = J(x_n^*(t))$. Additionally $Q_n\subset Q_{n+1}$, thus we have

$$\begin{aligned} \mathrm{min}_{x(t)\in Q_{n+1}}J(x(t)) \le \mathrm{min}_{x(t)\in Q_n} J(x(t))\Rightarrow \beta _{n+1}\le \beta _n, \end{aligned}$$

which shows that $(b_n)$ is a nonincreasing sequence. Theorem 6.4 concludes the proof, that is, $\mathrm{lim}_{n\rightarrow \infty }\beta _n = \mathrm{min}_{x(t)\in Q} J(x(t))\,.$ $\square$

Note Theorem 6.5 is proved when $Q_n$ is a class of combinations of Chebyshev polynomials, Boubaker polynomials (see, e.g., [6, 19]).

7 Computational Segment: Examples

In this section, we exhibit the applicability of the formulated numerical scheme by considering the time-varying and time-invariant FOCPs. The efficiency and accuracy of the strategy are observed by plotting the absolute error functions, state, and control variable as a function of time t.

Example 7.1

(see [3]) Find the optimal control u(t) that minimizes the time-invariant FOCP with quadratic performance index

$$\begin{aligned} J^*=\frac{1}{2}\,\int _{0}^{1}\,[x^{2}(t)+ u^{2}(t)]\,\mathrm{d}t, \end{aligned}$$

(24)

subject to the system dynamical constraints

$$\begin{aligned} ^{c}_0D_t^{\alpha }\,x(t)=-x(t)+ u(t),\quad \alpha \in ]0,1[\,, \end{aligned}$$

(25)

and the initial condition

$$\begin{aligned} x(0)=1. \end{aligned}$$

(26)

As elaborated in the proposed algorithm (Sect. 5), we parameterize the state variable x(t) by Laguerre polynomials ($L_k$’s) of degree up to $N=5$, i.e.,

$$\begin{aligned} x(t)\approxeq x_5(t)= & {} \sum _{k=0}^5 a_k\,L_k(t),\nonumber \\= & {} \sum _{k=0}^5 a_k-\left( \sum _{k=1}^5k\,a_k\right) \,t+\left( \frac{a_2}{2}+\frac{3a_3}{2}+3a_4+5a_5\right) \,t^2\nonumber \\&-\left( \frac{a_3}{6}+\frac{2a_4}{3}+\frac{5a_5}{3}\right) \,t^3+ \left( \frac{a_4}{24}+\frac{5a_5}{24}\right) \,t^4-\frac{a_5}{120}\, t^5, \end{aligned}$$

(27)

where $a_k$s ($k=0,1,...,5$) are the unknown coefficients to be determined. Using initial condition (26), we get

$$\begin{aligned} x_5(0)=1=a_0+a_1+a_2+a_3+a_4+a_5. \end{aligned}$$

(28)

We materialize system dynamical constraint (25) to approximate the control variable u(t) by $u_5(t)$. Thus, $u(t)\approxeq u_5(t)$ is considered as a function of $x_5(t)$ and its $\alpha {\mathrm{th}}$-order Caputo derivative ${}^{c}_0D_t^{\alpha }\,x_5(t)$, that is,

$$\begin{aligned}&u(t)\approxeq u_5(t)=x_5(t)+{}^{c}_0D_t^{\alpha }x_5(t),\\&\quad =1-\sum _{k=1}^5ka_k \,t+\left( \frac{a_2}{2}+\frac{3a_3}{2}+3a_4+5a_5\right) t^2-\left( \frac{a_3}{6}+\frac{2a_4}{3}+\frac{5a_5}{3}\right) t^3\\&\qquad +\,\left( \frac{a_4}{24}+\frac{5a_5}{24}\right) t^4-\frac{a_5}{120}t^5-\left( a_1+2a_2+3a_3+4a_4+5a_5\right) \frac{t^{1-\alpha }}{\varGamma (2-\alpha )}\\&\qquad +\,\left( a_2+3a_3+6a_4+10a_5\right) \,\frac{t^{2-\alpha }}{\varGamma (3-\alpha )}-\left( a_3+4a_4+10a_5\right) \,\frac{t^{3-\alpha }}{\varGamma (4-\alpha )}\\&\qquad +\,\left( a_4+5a_5\right) \,\frac{t^{4-\alpha }}{\varGamma (5-\alpha )}-a_5 \,\frac{t^{5-\alpha }}{\varGamma (6-\alpha )}. \end{aligned}$$

In order to make the mechanism evident, we choose $\alpha =0.99$.

$$\begin{aligned} u_5(t)= & {} 1-(a_1+2a_2+3a_3+4a_4+5a_5)t+\left( \frac{a_2}{2}+\frac{3a_3}{2}+3a_4+5a_5\right) t^2\\&-\,\left( \frac{a_3}{6}+\frac{2a_4}{3}+\frac{5a_5}{3}\right) t^3 +\,\left( \frac{a_4}{24}+\frac{5a_5}{24}\right) t^4-\frac{a_5}{120} t^5\\&-\,(1.00571 a_1+ 2.01141 a_2+ 3.01712 a_3+ 4.02283 a_4+5.02853 a_5)t^{0.01}\\&+\,(0.995749 a_2+ 2.98725 a_3 + 5.97449 a_4 + 9.95749 a_5)t^{1.01}\\&-\,(0.495398 a_3-1.98159 a_4-4.95398 a_5)t^{2.01}\\&+\,(0.164584 a_4 + 0.822919 a_5 )t^{3.01}- 0.0410434 a_5\, t^{4.01}. \end{aligned}$$

Use $x_5(t)$ and $u_5(t)$ to approximate the performance index $J^*$ in Eq. (24),

$$\begin{aligned} \hat{\mathbf{J}}^*[{\mathbf{a_0,a_1,...,a_5}}]= & {} a_0^2 + 0.00425096 a_0 a_1-1.16277a_0a_2-1.74897a_0a_3\\&-\,1.94457a_0a_4 - 1.89303a_0a_5 + 0.333742a_1^2\\&+\,0.91581a_1a_2+0.898313a_1a_3 \\&+\,0.725467 a_1a_4 + 0.477065a_1a_5+1.00625 a_2^2\\&+\,2.44028 a_2a_3+2.43648 a_2a_4\\&+\,2.17755 a_2a_5+1.60254 a_3^2\\&+\,3.44524 a_3a_4+3.3518a_3a_5+1.97683 a_4^2\\&+\,4.11856 a_4a_5+2.28776a_5^2\mathbf {\,\,=\,\frac{1}{2} a'Ha}, \end{aligned}$$

where

$$\begin{aligned} \quad \mathbf{H}= & {} \left( \begin{array}{cccccc} 2 &{} 0.00425096 &{}-1.16277 &{}-1.74897 &{} -1.94457 &{} -1.89303 \\ 0.00425096 &{}0.667485 &{} 0.915817 &{} 0.898313 &{} 0.725467&{}0.477065 \\ -1.16277 &{}0.915817 &{} 2.0125 &{} 2.44028 &{}2.43648 &{}2.17755 \\ -1.74897 &{}0.898313 &{} 2.44028 &{} 3.20509 &{}3.44524 &{} 3.3518 \\ -1.94457 &{}0.725467 &{} 2.43648&{} 3.44524 &{} 3.95965 &{}4.11856 \\ -1.89303&{}0.477065&{} 2.17755 &{} 3.3518 &{}4.11856 &{} 4.57551 \end{array} \right) . \end{aligned}$$

Finally, fractional optimal control problems (24)–(26) are converted into a quadratic programming problem described below:

$$\begin{aligned} \mathrm{Minimize}\quad \hat{J}^*= & {} \frac{1}{2}a'Ha, \end{aligned}$$

subject to $Ba=C$, where $a=[a_0\,a_1\,a_2\,a_3\,a_4\,a_5]', B=[1\, 1\,1\,1\,1\,1]$, and $C=[1]$.

On simplifying the equivalent quadratic programming problem with linear equality constraints, $\mathbf{a}=[1.59173\,\,-3.9641\,\,4.19967\,\,1.9204\,\,-4.98458\,\,2.23688]'.$ At last, we figure out the approximated state $x_5(t)$ and optimal control $u_5(t)$ as a function of time t.

$$\begin{aligned} x_5(t)= & {} 1-1.44252\,t+1.2111\, t^2-0.725147\,t^3+0.258326\,t^4-0.0186407\,t^5,\\ u_5(t)= & {} x_5(t)-1.45075t^{0.01}+2.41189t^{1.01}-2.15542t^{2.01}\\&+\,1.02029t^{3.01}-0.0918091t^{4.01}, \end{aligned}$$

and the approximate minimum value of $J^*=1.19155077$.

For $\alpha =1$, the classical case is widely investigated and the analytic solution for this system is given as (see [7] and references therein)

$$\begin{aligned} x(t)= & {} \beta \, e^{\sqrt{2}\,t}+(1-\beta )\,e^{-\sqrt{2}\,t}, \end{aligned}$$

(29)

$$\begin{aligned} u(t)= & {} \beta \,\left( \sqrt{2}\,t+1\right) e^{\sqrt{2}\,t}-(1-\beta )\,\left( \sqrt{2}-1\right) e^{-\sqrt{2}\,t},\end{aligned}$$

(30)

$$\begin{aligned} J= & {} \frac{e^{-\sqrt{2}t}}{2}\left( \left( \sqrt{2}+1\right) \left( e^{4\sqrt{2}}-1\right) \beta ^2+\left( \sqrt{2}-1\right) \left( e^{2\sqrt{2}}-1\right) \left( 1-\beta \right) ^2\right) ,\nonumber \\ \end{aligned}$$

(31)

where $\beta =\frac{2\sqrt{2}-3}{-e^{\sqrt{2}}+2\sqrt{2}-3}$. The exact solution for the performance index in this case is $J=0.1929092978$. Using $5{\mathrm{th}}$-order Laguerre approximation, we obtain the approximate solution for $\alpha =1$ as $J=0.1929115932$. The approximated state $x_5^*(t)$ and control variable $u_5^*(t)$ of order 5 ($\alpha =1$) are given as

$$\begin{aligned} x_5^*(t)= & {} 1 - 1.379561t + 0.955479t^2 - 0.362649t^3 + 0.072987t^4 - 0.004296t^5,\\ u_5^*(t)= & {} -\,0.379561+0.531398t-0.132468t^2-0.070699t^3\\&+\,0.051507t^4-0.004296t^5. \end{aligned}$$

Example 7.2

(see [5]) Find the optimal control u(t) that minimizes the time-varying (FOCP) with quadratic performance index

$$\begin{aligned} M=\int _{0}^{1}\,\left( t\,u(t)-(\alpha +2)\,x(t)\right) ^2\,\mathrm{d}t, \end{aligned}$$

(32)

subject to the system dynamic constraints

$$\begin{aligned} x'(t)+{}^{C}_0D_t^{\alpha }\,x(t)= u(t)+t^2,\quad \alpha \in ]0,1[, \end{aligned}$$

(33)

and the boundary conditions

$$\begin{aligned} x(0)=0,\quad { \mathrm and}\quad x(1)=\frac{2}{\varGamma (3+\alpha )}. \end{aligned}$$

(34)

The analytical solution for this problem is

$$\begin{aligned} (x^*(t),u^*(t))=\left( \frac{2\,t^{\alpha +2}}{\varGamma (\alpha +3)}\,,\,\frac{2\,t^{\alpha +1}}{\varGamma (\alpha +2)}\right) . \end{aligned}$$

(35)

Following the same way as in Example 7.1, we parameterize the state variable $x(t)\,\left( \approxeq x_5(t)\right)$ by Laguerre polynomials (see Eq. (27)) with the initial condition given in (34). The approximated control variable $u(t)\,\left( \approxeq u_5(t)\right)$ can be determined by Eq. (33), that is,

$$\begin{aligned} u(t)\approxeq u_5(t)= x'_5(t)+{}^{C}_0D_t^{\alpha }\,x_5(t)-t^2\,. \end{aligned}$$

Choose $\alpha =0.6$, and substitute the approximated state and control variable into the performance index M. Problems (32)–(34) are now transformed into a quadratic programming problem described below

$$\begin{aligned} \mathrm{Minimize}\quad {\hat{M}}= & {} \frac{1}{2}a'Ha+G'a+ k,\\ \mathrm{subject\,\, to}\quad Ba= & {} C, \end{aligned}$$

where $a=[a_0\,\,a_1\,\,a_2\,\,a_3\,\,a_4\,\,a_5]'{\small B=\left[ \begin{array}{cccccc} 1 &{} 1 &{} 1 &{} 1 &{} 1 &{} 1 \\ 1 &{} 0 &{} -\frac{1}{2} &{} -\frac{2}{3} &{} -\frac{5}{8} &{} -\frac{7}{15} \\ \end{array} \right] }$, $C=[0\,\,\, 0.538065]'$, $G'=[1.3\,\,\,1.07743\,\,\,0.703284\,\,\,0.287267\,\,\,-0.0989874\,\,\,-0.412705]$, $k=0.142857$, and

$$\begin{aligned} H= & {} \left( \begin{array}{cccccc} 13.52 &{} 11.802 &{} 9.37269 &{} 6.71526 &{} 4.15709 &{} 1.90549 \\ 11.802 &{} 10.33764&{} 8.28318 &{} 6.03844 &{} 3.87478 &{} 1.96436 \\ 9.37269 &{} 8.28318 &{} 6.80524 &{} 5.1974 &{} 3.63693 &{} 2.23805 \\ 6.71526 &{} 6.03844 &{} 5.1974 &{} 4.29346 &{} 3.39926 &{} 2.56466 \\ 4.15709 &{} 3.87478 &{} 3.63693 &{} 3.39926 &{} 3.13726 &{} 2.84063 \\ 1.90549 &{} 1.96436 &{} 2.23805 &{} 2.56466 &{} 2.84063 &{} 3.00638 \\ \end{array} \right) . \end{aligned}$$

On simplifying the above quadratic programming problem, we get

$$\begin{aligned} {\mathbf{a}}=[2.382743\,\,\,-6.712458\,\,6.253306\,\,\,-1.918213\,\,\,-0.0041420\,\,\,-0.001237]'. \end{aligned}$$

Using a, the approximated state variable $x_5(t)$ and control variable $u_5(t)$ can now be obtained as a function of time t. The approximate value of performance index is $M=0.000035032$, for $\alpha =0.6$.

Table 1 Optimal value of performance index $J^*$ and M, for $N=5$

Fig. 1

Absolute error function of state and control variable for $N=5$ (Example 7.1)

Fig. 2

$x_5(t)$ and $u_5(t)$ as a function of time t (Example 7.1)

Fig. 3

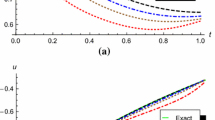
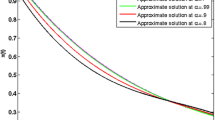
State and control variable, for $\alpha =0.9, 0.99,1.0$ (Example 7.1)

Fig. 4

Absolute error function of state and control variable for $N=5$ (Example 7.2)

Fig. 5

$x_5(t)$ and $u_5(t)$ as a function of time t (Example 7.2)

Fig. 6

State and control variable (exact and approximated), for $\alpha =1$ (Example 7.2)

Discussion on Graphical Representation We display the approximate value of optimal performance index $J^*,\,M$ for different values of $\alpha \in ]0,1[$, and $N=5$ (Table 1). One can review the absolute error of state and control variable (i.e., $|x(t)-x_5^*(t)|$ and $|u(t)-u_5^*(t)|$) in Fig. 1 (Example 7.1) and Fig. 4 (Example 7.2). To monitor the action of parameterized state $x_5(t)$ and control variable $u_5(t)$ for different values of $\alpha$, we plot these as a function of time t. The graphs presented are essential to outlook the nature of state and control variable for different values of $\alpha$. We see that the edges come closer as $\alpha$ approaches 1 and meet the exact solution for $\alpha =1$. To make the comments clear, dotted line in Fig. 2 corresponds to the exact solution, whereas pink and orange correspond to $\alpha =1$ and $\alpha =0.99$, respectively. In order to have a nice interpretation, one may look at Fig. 3 (Example 7.1) which gives the exact and approximate plots of state and control variable at one place, Figs. 5 and 6 (Example 7.2).

8 Conclusions

We have investigated a class of FOCPs for necessary and sufficient optimality conditions along with a solution scheme. The presented computational technique is advantageous as we can easily convert the original FOCP to a quadratic programming problem. We extract the state and control variables as a continuous function of time to obtain the minimum value of the performance index. The technique is systematically executed for both time-invariant and time-varying FOCPs. Error analysis corresponding to other orthogonal polynomials will be an issue of future research of the authors.

Appendix: Singular Fractional Optimal Control Problem

We wish to address some control problems where the performance index is either linear or independent of the control function u. For example, consider the FOCP to find an optimal control u(t) that minimizes the performance index

$$\begin{aligned} J[u]=\frac{1}{2}\int _0^1 \,x^2(t)\,\mathrm{d}t \end{aligned}$$

(36)

subject to the system dynamic constraints

$$\begin{aligned} {}^{C}_0D_t^{\alpha }\,x(t)= u(t),\quad \alpha \in ]0,1[\,, \end{aligned}$$

(37)

and the initial condition $x(0)=1$. One can clearly observe that:

• The integrand of J is independent of the control function u.

• Necessary optimality conditions (Theorem 3.1) reduce to ${}_0D_t^{\alpha }x=u$, ${}_tD_1^{\alpha }\lambda =x(t)$ and $\lambda (t)=0$. The condition $\lambda (t)=0$ complicates the system to further look for some control function, and hence the control problem is termed as singular.

If $\alpha =1$, the problem stated above corresponds to the classical singular optimal control problem (see [20] and references therein). An independent investigation by researchers has to be carried out for such problems.