Bootstrapping Topological Properties and Systemic Risk of Complex Networks Using the Fitness Model

Abstract

In this paper we present a novel method to reconstruct global topological properties of a complex network starting from limited information. We assume to know for all the nodes a non-topological quantity that we interpret as fitness. In contrast, we assume to know the degree, i.e. the number of connections, only for a subset of the nodes in the network. We then use a fitness model, calibrated on the subset of nodes for which degrees are known, in order to generate ensembles of networks. Here, we focus on topological properties that are relevant for processes of contagion and distress propagation in networks, i.e. network density and k-core structure, and we study how well these properties can be estimated as a function of the size of the subset of nodes utilized for the calibration. Finally, we also study how well the resilience to distress propagation in the network can be estimated using our method. We perform a first test on ensembles of synthetic networks generated with the Exponential Random Graph model, which allows to apply common tools from statistical mechanics. We then perform a second test on empirical networks taken from economic and financial contexts. In both cases, we find that a subset as small as 10 % of nodes can be enough to estimate the properties of the network along with its resilience with an error of 5 %.

1 Introduction

The reconstruction of statistical properties of a network when only partial information is available is one of the outstanding and unresolved problems in the field of statistical physics of networks [4, 13]. Addressing this issue has many concrete applications.

A paramount example is the case of financial networks where nodes represent financial institutions and edges are various types of financial ties such as loans or derivative contracts. These ties result in dependencies among institutions and constitute the ground for the propagation of financial distress across the network. The resilience of the system to the default or the distress of one or more institutions depends on the topological structure of the whole network [1, 2]. In contrast, due to confidentiality issues, the information that regulators are able to collect on the mutual exposures among institutions is very limited.

Typically the analysis of systemic risk has been done by trying to reconstruct the unknown links in the network using the so-called Maximum Entropy (ME) algorithm. This method assumes that the network is fully connected (for this reason this class of approaches is called “dense reconstruction methods”). The weights of the links are then obtained via a “maximum homogeneity” principle. This means that each node is assumed to bear a similar level of dependence from all other nodes. After that, the method proceeds by looking for the matrix that minimizes the distance from the uniform matrix (in which every entry has the same value), while satisfying certain constraints (imposed in this case by the budget of the individual banks). Such a matrix is found using the Kullback-Leibler divergence as the objective function to minimize [5, 14, 16].

However, the hypothesis that the network is fully connected is a strong limitation of the ME algorithm, since empirical networks show instead a largely heterogeneous degree distribution. Moreover, such “dense reconstruction” leads to an underestimation of the systemic risk [13, 14]. In Ref. [13] a “sparse reconstruction” algorithm has been proposed, that allows to minimize the Kullback-Leibler divergence obtaining a matrix with an arbitrary level of heterogeneity given certain constraints. The latter approach is more reliable but leaves open the question of what value of heterogeneity would be appropriate to choose. Moreover, the density of connections must be specified ex-ante and it is not recovered by the algorithm.

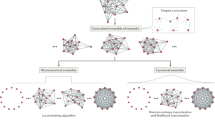
To overcome these problems, in this paper we introduce a new general method that we name Bootstrapping Method (BM). We investigate if it is possible to estimate both the topological properties of a network and its resilience to distress propagation starting from limited information. Notice that differently from previous work—e.g. [4], our method does not aim at reconstructing individual missing links, but aims instead at estimating global properties. We study how the accuracy of the estimation depends upon the size of the subset of nodes for which the information is available. In more detail, among all the possible topological properties, we focus on those that in the literature have been shown to play an important role in contagion processes and in the propagation of distress, i.e., the network density [1] and the k-core structure [12]. For the resilience, we focus on a recently introduced notion, DebtRank [2], which measures the systemic impact of an initial shock on one or more nodes, whenever the links in the network represent the financial dependencies among nodes.

In our method, the allocation of the links among nodes is carried out using the fitness model [3, 11]. Differently from other network generation models, the fitness model generates a network structure starting from a non-topological variables (fitness) associated to the nodes. This approach has been used in the past to reproduce the topological properties of several empirical economical networks, including the network of equity investments in the stock market [10], the interbank market [6], and the WTW [9].

To validate our method we use both synthetic networks as well as examples of real economic systems. In all these cases, we have full information on the system and we evaluate the accuracy of our method by using only part of the information. The two empirical cases of study are (1) the World Trade Web (WTW), i.e. the network in which nodes are countries and links are trade volumes (in US dollars) among them, and (2) the interbank loan network of the so-called e-mid interbank money market. The result of our analysis is that information on the degree of a relatively small fraction of nodes is sufficient to estimate with good approximation the above mentioned topological properties, as long as the fitness of all nodes is known. For instance, with only about 7 % of the nodes (10 out of 185) we have a relative error of about: 7 % on the density, 10 % on the average degree of the main core, 7 % on the size of the main core. Similarly, we find that with about 7 % of the nodes the resilience can be estimated with a relative error within 10 %.

At a first thought, it can be surprising that a small fraction of nodes enables to reconstruct so well global emerging properties of the network. However, one should bear in mind that in the method, while the degrees are known only for a subset of nodes, the fitness is assumed to be known for all the nodes. Therefore, a limitation of this method could arise when considering different topological properties as strong community structure or assortativity. Possibly, in these situations the method would probably require a larger initial information to obtain the same results. Investigation of these situations is left for future research. Overall, our method can be applied to any network representing a set of dependencies among components in a complex system and it is thus of general interest in the field of complex networks and statistical physics.

2 Exponential Random Graph and Fitness Model

We start by briefly describing the Exponential Random Graph Model (ERGM) and the associated fitness model. In order to generate ensembles of complex networks, both a dynamic and a static approach can be utilized. In the dynamic case, nodes and/or links are added step by step using for instance a “preferential attachment” algorithm. In the static case, instead, the number of nodes is fixed and the links are assigned at once according to some statistical or deterministic criterion. ERGM is one of the most studied network generation models [7, 15]. The model can be described using the powerful mathematical formalism of the equilibrium statistical mechanics [15].

As a specific example, we will consider the so-called fitness or hidden variables models, where the network topology is determined by an intrinsic property (called fitness) associated with each node of the network [3]. Through this scheme we can define a framework to investigate those networks where the topology is driven, at least in part, by non-topological properties of the nodes. With the fitness model it is possible to study several economical networks, ranging from the WTW (where the fitness of the model are the GDP of the various countries) [9], to the financial networks (where fitness are, for instance, the market capitalization of each institution) [6, 10].

Given a set of network properties, {C _a } the ERG is defined as the ensemble Ω of maximally random networks with {C _a } constrained to some statistical properties. More specifically, let us suppose that the ensemble averages of {C _a } are fixed:

$$ \langle C_a \rangle_{\varOmega} \equiv\sum _G P (G) C_a(G) = C_a^* \quad \forall a. $$

(1)

It has been shown that Ω can be defined through a set of control parameters {θ _a }, the values of which depend on the set of constraining values $\{C^{*}_{a}\}$ [7, 15]. Furthermore the probability P(G) of a network G to occur in Ω is given by P(G)=e ^−H(G)/Z, where we introduced the graph Hamiltonian H(G)≡∑ _a θ _a C _a (G), and the partition function Z≡∑ _G exp(−H(G)). {θ _a } is the set of Lagrange multipliers associated to the constraints $\{C^{*}_{a}\}$. The fitness model can be seen as a specific case where the set of properties {C _a } is the degree sequence {k _i } _i=1,…N of the nodes of the network, that is the values of 〈k _i 〉 for all nodes i are fixed. In the following, unless differently specified, we consider undirected graphs. In this case, the partition function, H=∑ _i θ _i k _i , is exactly computable and each node can be identified by its control parameter (or Lagrange multiplier) θ _i . Fixing the values of {θ _i } is equivalent to fix the mean values of {k _i }. In order to further clarify the role of {θ _i } in controlling the topology, let us define $x_{i} \equiv e^{-\theta_{i}}$. It is possible to show [15] that knowing the set {θ _} for all nodes, the ensemble is such that, for each network in Ω, two nodes i and j are connected with a probability given by:

$$ p_{ij}=\frac{x_ix_j}{1+x_ix_j} . $$

(2)

Therefore, x _i can be considered as a sort of fitness of the node i and it is related to the ability of i to create links to other nodes.

The average in Ω of several topological properties of the network can be expressed in terms of appropriate compositions of the linking probabilities p _ij for every i and j. For instance, we can write the degree k _i as

$$ \langle k_i \rangle= \sum_{j (\neq i )=1}^{N}p_{ij} ; $$

(3)

the average nearest neighbor degree $K^{nn}_{i}$ as

$$ \bigl \langle k_{i}^{nn} \bigr \rangle =\frac{\sum_{j\neq i}\sum_{k\neq j}p_{ij}p_{jk}}{\langle k_{i}\rangle} ; $$

(4)

and the clustering coefficient C _i as

$$ \langle C_{i}\rangle=\frac{\sum_{j\neq i}\sum_{k\neq j,i}p_{ij}p_{jk}p_{ki}}{\langle k_{i}\rangle[\langle k_{i}\rangle -1 ]}. $$

(5)

In the limit of small values of fitnesses (and therefore small connectivity), x _i is proportional to the desired degree of the node i. Indeed, in this limit we can assume 〈k _i 〉≃∑ _j x _i x _j ∝x _i .

3 Bootstrapping Method

The estimation of the linking probability, p _ij , between node i and node j is the initial step in order to develop a network bootstrapping method. Let us suppose to have incomplete information about the topology of a given network (say G ₀). In particular, we assume to know the degree k _i only for a subset I of the nodes. Moreover, we assume to know, for all the nodes, a non-topological property, denoted as y _i , that is correlated to some statistical properties of the degree k _i of the nodes by a known relation as clarified below. For instance, in the World Trade Web y _i could be the country GDP, while in financial networks it can be the operating revenue of the firm i. Given these constraints, we formulate a statistical procedure to find the most probable estimate of the value s(G ₀) of a topological property S(G ₀) of the network G ₀ compatible with the constraints. We assume two important hypotheses:

• 1. the network G ₀ can be seen as drawn from an ensemble of ERGM, that we call Ω. From the statistical mechanics of networks we know that the value s(G ₀) of the property S in G ₀, typically varies within the range $\langle S \rangle_{\varOmega} \pm\sigma_{S}^{\varOmega}$ where $\sigma _{S}^{\varOmega}$ is the standard deviation, and 〈S〉 _Ω the average of the property S estimated on the whole ensemble Ω.

• 2. each known value of the non-topological property y _i is assumed to be proportional to the fitness, denoted as x _i (because a generic property of the network can be used as a fitness variable) of the node i in the ensemble Ω, through a universal unknown parameter z: $\sqrt{z}y_{i}=x_{i}$. Therefore Eq. (2) becomes:

  $$ p_{ij}=\frac{zy_iy_j}{1+zy_iy_j}. $$

  (6)

With these hypotheses, we map the problem of evaluating s(G ₀) into the one of choosing the optimal ERGM ensemble Ω compatible with the constraints on G ₀ (knowledge of y _i for all nodes and k _i for the subset I). Once Ω is determined (it is univocally defined by the set of {x _i }), we can use the average 〈S〉 _Ω as a good estimation for s(G ₀) and $\sigma _{S}^{\varOmega}$ as the typical statistical error. More precisely, the question to address is what ensemble Ω, belonging to the class ERGM, is the most probable to extract the real network G ₀, given we that know only partial information, i.e. {y _i } and k _i for the subset I of the nodes. Since we know {y _i }, i.e. the rescaled fitness values (a non topological property of the network), the problem becomes to find the most likely value of z. For this reason we use the notation Ω(z) for the desired ensemble.

If we knew not only {y _i }, but the entire topology of the network, z could be found by means of a maximum likelihood argument (Ref. [9]) comparing the average number of links of a network in the ensemble Ω(z) with the total number of links L ₀ in G ₀:

$$ \langle L \rangle\equiv\frac{1}{2} \sum_{i=1}^{N} \langle k_i \rangle\equiv\frac{1}{2} \sum _{i=1}^{N} \sum_{j \neq i} p_{ij} = L_0, $$

(7)

where p _ij contains the unknown parameter z through Eq. (6). Since {y _i } and L ₀ are known, the last equality of Eq. (7) defines an algebraic equation in z from which one can evaluate the real fitnesses $x_{i}=\sqrt{z}y_{i}$. Let us call z ₀ the estimate of z calculated in this way, and Ω(z ₀) the respective ERGM ensemble. However, in our case we assume to ignore the complete topology of the network and to know only the degrees of the nodes in a subset I. Let n be the number of nodes of I. In this case, we cannot apply Eq. (7) to estimate z. Nevertheless, we can still apply the maximum likelihood principle through the following relation in which the first equality comes from the ERGM and the second one is the application of the constraint on the knowledge of the degrees for the nodes in the subset I [15]:

$$ \sum_{i \in I} \langle k_i \rangle\equiv \sum_{i \in I} \sum_{j \neq i} p_{ij} = \sum_{i \in I} k_i, $$

(8)

where the degrees k _i are calculated in the original network G ₀. For a generic subset I of the nodes of the network the estimation is less precise than the one given by the last equality of Eq. (7) and the two equations coincides only when I is the whole set of nodes in the network. However, even with just the knowledge of the degree of a single node, the Eq. (8) yields an estimation of z, and finally of X(G ₀). In the following, we show that the accuracy can be good even with a rather small subset I.

The network bootstrap of a network G ₀ is defined by the above equations using the following procedure. Let us assume to know the non topological property y _i of all N nodes of the system and the links of a subset I of n<N nodes.

• Given the topological information of the links in the subset I, we compute the sum of all known degrees of these n nodes in G ₀: ∑ _i∈I k _i .

• This sum is substituted into the Eq. (8) to obtain the relative value of z, denoted as z′, that is an approximation of the “real” value z ₀.

• Through the value of z′ and the knowledge of every y _i we extract all the links in the network according to the linking probability of Eq. (6).

It is important to estimate the accuracy of the network bootstrap method both for topological and non-topological properties. To this end, we first apply the method to a synthetic network generated using the fitness model (see Sect. 4). We then apply the method to an empirical case, i.e. the WTW and the e-mid (see Sect. 5). In the second case, we test how well we can estimate a global and non-topological property such as the resilience of the network to distress propagation (see Sect. 6).

4 Test of BM: Synthetic Networks

Let be {I _α }, with α=1,…,M, an ensemble of subsets of the network G ₀, each of them containing n nodes, for which we know the degree k _i . In order to test how much our BM estimate of the property S is precise, we will proceed in the following way:

• Evaluate z for each subset I _α from Eq. (8), and call such estimate z _α ;

• Use the value z _α to estimate, through the relation $\sqrt{z}y_{i} = x_{i}$, the average property $\langle S \rangle_{\alpha } \equiv \langle S \rangle_{\varOmega(z_{\alpha}) \equiv I}$ from the corresponding ensemble $\varOmega_{z_{\alpha}}$;

• Repeat the calculation for all other sets I _α′ with α′=1,…,M, accumulate the values of 〈S〉 _α and compute the arithmetic average $\overline{ \langle S \rangle}$ of these quantities and the associated standard deviation with respect to the “real” value of S(G ₀) across all the realizations of I _α , for fixed n.

The property S is then estimated by averaging the 〈S〉 computed for each subset I. Notice that each value 〈S〉 is by itself also an estimation of the true, unknown, property S.

In order to study the accuracy of the reconstruction, we study how the root mean square error varies as a function of the size n of the subset of nodes for which information is available. Using the fitness model and all the available information, we generate an ensemble of networks G each one of size N and we compute several properties like the network density, the size of the main core and the average degree of the main core. These values will be our benchmarks to test how good is the reconstruction of the statistical and topological properties of the network with the BM.

More precisely, we test the BM by focusing on the following three topological quantities, which were chosen because they have been found to play a role in the distress propagation and contagion processes and therefore are relevant to the resilience of the network to systemic risk (see Sect. 1). Further properties will be studied in future work.

• 1. density of links D, which is the ratio between the actual number of links in the network and the maximal one compatible with the number of nodes N (i.e. N(N−1)/2) for an undirected graph;

• 2. degree of the main core, k ^main. In a network/graph, the k-core is defined as the “largest subgraph whose nodes have at least k connections (within this subgraph, of course)” [7]. The main core is the k-core with the highest possible degree, k ^main;

• 3. size of the main core, S ^main, i.e. its number of nodes.

Each of these measures will play the role of the property X in the previous notation. In order to use a real-world fitness, we take as reference the WTW (in year 2000) which contains 185 nodes. We thus generate networks of size N=185 and we use as fitness y _i the GDP from the WTW. For each of these properties we carry out the procedure described here below.

• 1. Choose a value for the variable z ₀ (compatible with the fitness model for WTW, where the fitness is the GDP of a country). We start with z ₀=10⁴;

• 2. By using as fitness the GDP of a country, create 50 realizations of the networks from the corresponding ERGM that we call ensemble Ω _N . Compute on the this set the average link density D _e ;

• 3. Use a 51st network from the Ω _N ensemble as reference network, call it G ₀, this will be the network to reconstruct;

• 4. Start from the knowledge of the degree k of a randomly chosen set of n nodes (we start with n=1) and of the GDP y _i for all the nodes in the network to compute an estimation of z, say z′, from Eq. (8);

• 5. Using the new value z′ create a new ERGM ensemble $I_{1}^{(n)}$ of 50 networks;

• 6. Consider another set of randomly chosen n nodes of the network, generate again 50 networks from this set, and repeat this operation 100 times each time with a different set $I_{\alpha}^{(n)}$ (α=1,…,100) of n nodes;

• 7. In each of the 100 ensembles of 50 networks at fixed n, I _α estimate the average density 〈Dα〉;

• 8. Compute the root mean square error: $\sigma_{d} = 1/100 \sum_{\alpha} \sqrt{ ( \langle D_{\alpha} \rangle- D_{e} )^{2}}$. The difference is between the average density of the reconstructed networks 〈D _α 〉 and the original average link density D _e ;

• 9. Compute and plot σ _d /D _e ;

• 10. Repeat the points from 4 to 9 using a different values of n.

The entire procedure is repeated for the quantities S ^main and k ^main, and the results are shown in Fig. 1 for 3 different values of z ₀, corresponding to different values of density. We observe that in all cases there is a rapid decrease of the relative error as the number of nodes n, used to reconstruct the topology, increases. This is an indication of the goodness of the estimation provided by the BM. Even with a single node, plus the information on the fitnesses y _i of all nodes (here, we used the GDP of the countries), we are able to estimate the topological properties of the network with a relative error of about 13 % for the main core average degree k ^main, about 18 % for the network density D, and about 10 % for the size of main core S ^main.

Fig. 1

Esitmation of network properties as a function of the size n of the subset of nodes used for calibration. (a) Relative error $\sigma^{\mathrm{main}}_{k} /k^{\mathrm{main}}_{e}$ obtained with three different values of the parameter z ₀. (b) Relative error of the S-main core size. (c) Relative error of the density D of the links. In all the 3 plots it is evident how the quality of the reconstruction increases with the number of nodes used to generate the network ensemble (Color figure online)

As expected, if we have a denser network (Fig. 1 (d)–(f)) the relative error is smaller because the network has more links from which the BM can reconstruct the topology. The same trend in the decrease of the relative error is found for all the examined topological quantities.

5 Test of BM: World Trade Web and E-mid

We now test the method on the empirical network of the WTW and the e-mid on the same topological properties as in the previous case. The main difference is that now instead of using a reference network generated with the fitness model and an average measure over this network class (generated in the ensemble Ω _N ), the reference is now the empirical WTW network or the e-mid network. As fitness we use: (1) in the case of the WTW, the GDP of the countries, and (2) in the case of e-mid, the out-strength of the nodes, that is the total lending of each bank.

For the WTW, we use the trade volume data for the year 2000. For the e-mid, we initially looked at daily snapshot of loans among banks. However, we found that the a high volatility of the links at this time scale prevented a robust estimation of the network properties. Therefore, we focus on snapshots of loans aggregated at a monthly scale, as done also in other works on the e-mid [6]. In the following, we report the results related to the snapshot for February 1999. We performed the same analysis also for other monthly snapshots and we found comparable results.

Similar to what presented above, we perform the test with the following procedure:

• 1. Compute the “real” value z ₀ of the model parameter z.

• 2. From the complete network compute the “true” density of links, D _WTW and D _emid ;

• 3. Start from the knowledge of the degree k of a randomly chosen set of n nodes (we start with n=1) and from the knowledge of the fitness y _i of all the nodes in the network to compute an estimation of z, say z′, from Eq. (8);

• 4. Using the new value z′ create a new ERGM ensemble $I_{1}^{(n)}$ of 50 networks;

• 5. Choose another set of randomly chosen n nodes of the network, generate again 50 networks from this set, and repeat this operation 100 times each time with a different set $I_{\alpha}^{(n)}$ (α=1,…,100) of n nodes;

• 6. In each of the 100 ensembles $I_{\alpha}^{(n)}$ of 50 networks, with fixed n, estimate the average density 〈Dα〉;

• 7. Compute the root mean square error: $\sigma_{d} = 1/100 \sum _{\alpha}\sqrt{ (\langle D_{\alpha} \rangle- D_{\mathit{WTW}} )^{2}}$, taking the difference between the reconstructed networks 〈D _α 〉 and the original WTW link density D _WTW . Similarly, for the e-mid.

• 8. Compute and plot σ _d /D _WTW and σ _d /D _emid

• 9. Repeat the points from 4 to 9 using a different value of n.

The same test is carried out for the other quantities k ^main and S ^main. Results are shown in Fig. 2 for the WTW network and in Fig. 3 for the e-mid network.

Fig. 2

WTW network. The plots from top left represent respectively: (a) the relative error in the estimation of average degree of the main core $\sigma_{k}^{\mathrm {main}} / k_{\mathit{WTW}}^{\mathrm{main}}$ computed with real WTW network following the procedure described in the previous paragraph (b) same as in (a) but for the relative error in the size of main core (c) same as in (a) but for the density of the links D. In all the 3 plots it is evident how the goodness of the reconstruction of the WTW network increases with the number of nodes used to generate the network ensemble

Fig. 3

E-mid network. The plots from top left represent respectively: (a) the relative error in the estimation of average degree of the main core $\sigma_{k}^{\mathrm {main}} / k_{\mathit{WTW}}^{\mathrm{main}}$ computed with a e-mid network following the procedure described in the previous paragraph (b) same as in (a) but for the relative error in the size of main core (c) same as in (a) but for the density of the links D. In all the 3 plots it is evident how the goodness of the reconstruction of the e-mid network increases with the number of nodes used to generate the network ensemble

6 Test of BM: DebtRank a Measure of Systemic Risk

In order to estimate the resilience of the networks we use DebtRank (DR) a recently introduced measure of the systemic impact of the distress of one or more nodes to the rest of the network [2]. In particular, we also use Group DebtRank (GDR), which measures the impact caused by a small shock on all the nodes in the network, due to the reverberations across links in the network. The method consists in computing the impact of the shock in a recursive way from the matrix of the link weights, given an initial shock ψ to one node in the case of DR and to all nodes in the case of GDR. The rescaling factor 0<α<1 determines the scale of the impact along each link in the network.

Let us focus on the WTW network. Our goal is to test how well DR and GDR are estimated by the network bootstrap method. We make several tests for different values of initial shock ψ and impact rescaling factor α. Both DebtRank and Group DebtRank depend strongly on the link weights, which are assumed to be unknown in the simulations. In fact the fitness model reconstructs the degree sequence, but not the weights of the links. We then use a value for each link with two rules:

• Compute the average weight by averaging the elements of the W _ij matrix associated to the n<N nodes. Use this value as homogeneous weight for all nodes.

• Assign to each node a weight similarly to what done in a gravity model (see [8]) where the link l _ij has a weight proportional to the product of the GDPs GDP _i ⋅GDP _j .

We want to consider the impact in case a distress in a country (i.e. a delay in the payments) propagates to the others. Since the adjacency matrix represents the economic value of the goods sold (the links are in the opposite direction), we transpose the WTW matrix normalize the rows imposing a row stochastic condition ∑ _j w _ij =1.

The procedure to compute the GDR in the case of the WTW is the following. Results are shown in Fig. 4. The procedure to compute the GDR in the case of the e-mid is completely analogous, with out-strength values instead of GPDs. For the e-mid network, results are shown in Fig. 5

• 1. Compute the reference Group DebtRank on the original WTW network with an initial shock ϕ=0.1. Keep this value as reference (green dashed line in the plots).

• 2. Bootstrap the networks from subsets of size n<N using homogeneous weights (computed as average of the weights of the only nodes that we start from in the simulation), compute the average GDR on 50 bootstrapped networks with homogeneous weights. Repeat the operation 100 times changing the starting set of nodes during the generation of the 50 networks, obtaining for each n an average value with error (blue dots). It is important to point out that each bootstrap network is an undirected network, whereas the GDR in the real WTW is computed using the original, directed topology. Therefore we calculate the GDR on directed versions of the boostrap networks, obtained simply changing each link in two directed links.

• 3. In the non homogeneous case (green dots), bootstrap the networks using weights according to a gravity model, where the weight of the link is the product of the GDPs of each node. In order to add a “perturbation” on such a network, we estimate empirically from the plot of W _ij vs GDP _i ⋅GDP _j the average variation of the weight W _ij as a function of the GDP’s product. We then alter the corresponding adjacency matrix $W'_{ij}$ by imposing, for each weight, a random normal error: $w'_{ij} = w_{ij} + \sigma N(0,1)$, where σ is a standard deviation computed on w _ij for the corresponding fixed value of GDP _i ⋅GDP _j . The new perturbed weight matrix is then transformed to maintain the row stochasticity.

Fig. 4

WTW network. The plots represent respectively: Group DebtRank computed on the original WTW network with empirical weights (green dashed line); the average Group DebtRank on the 100 bootstrapped networks with weights obtained using gravity model (green dots) and respective errors; the Group DebtRank on the original WTW network with homogeneous weights (blue dashed line); the average Group DebtRank on the 100 bootstrapped networks with homogeneous weights (blue dots) and respective errors. The impact rescaling factor is set as follows: (a) α=0.1, (b) α=0.3, (c) α=0.5, (d) α=0.7, (e) α=0.9 (Color figure online)

Fig. 5

E-mid network. The plots represent respectively: Group DebtRank computed on the original e-mid network with empirical weights (green dashed line); the average Group DebtRank on the 100 bootstrapped networks with weights obtained using gravity model (green dots) and respective errors; the Group DebtRank on the original e-mid network with homogeneous weights (blue dashed line); the average Group DebtRank on the 100 bootstrapped networks with homogeneous weights (blue dots) and respective errors. The impact rescaling factor is set as follows: (a) α=0.1, (b) α=0.3, (c) α=0.5, (d) α=0.7, (e) α=0.9 (Color figure online)

In Fig. 4, we plot the GDR for various α values, ranging from 0.1 to 0.9, in all cases the initial shock is ψ=0.1, 10 % of the value of the trade of every country. From the pictures we can draw the following conclusions:

• There is a significant difference when using homogeneous weights or heterogeneous weights. Using a constant value for the weight of each link leads to underestimating the value of systemic risk as measured by Group DebtRank, for both WTW and e-mid network.

• The reconstruction of the DebtRank values is relatively good even for small subsets of nodes in the network.

• Using a gravity model (even if simplified) improves the estimate of the GDR of both the WTW and e-mid network.

• The gap between the homogeneous GDR and the empirical one increases for larger values of the impact rescaling factor α. This can be interpreted as follows: when the network effects are important the use of homogeneous weights in the dynamics leads to a larger error. Conversely when the network effects (reverberation) are less important the homogeneous weights are not so far from the true value of the GDR.

From this analysis we can conclude that the BM performs fairly well in allowing to estimate a global non-topological property such as the Group DebtRank. However, in order to achieve this goal one has to chose careful the weights of links because the use of an average value leads to inaccurate estimates, especially if the network effects are relevant.

The impact of shocks on individual nodes (DR) is shown in Table 1 for the WTW network. The impact rescaling factor is set as α=0.5 and the initial shock as ψ=1. As expected, the biggest is the GDP the biggest is the corresponding DebtRank but with some variation due to network effects. Consider for instance a country like Canada, a big exporter of oil and minerals, its impact on the WTW will be larger than Germany that is a strong exporter of final goods. This analysis shows as the DebtRank measure is important to assess the distress propagation yielding results that are not trivially contained in the size of the countries.

Table 1 The values of DebtRank and the GDP rank (year 2000) for the 20 biggest countries in the WTW network. Notice that the ranking according to DebtRank agrees only in part with the ranking by the GDP. Depending on the size of the exports volume, each country can be more or less affected by a shock on the others countries. The values are obtained setting α=0.5 and ψ=1

7 Conclusions

In this paper we proposed a novel Bootstrap Method (BM) to estimate topological properties of a network by using only partial information from its connections and an auxiliary non-topological property, interpreted as the fitness associated to each node. This method is particularly useful to overcome the lack of topological information which often hampers the estimation of systemic risk in financial networks. We tested the method both on synthetic and empirical networks. We have studied how well it is possible to estimate some topological properties relevant to systemic risk (as mentioned in the introduction) such as the network density, the size and the average degree of the main core, as well as the a measure of the resilience of the network to the propagation of distress.

We found that, by using about 5 % of the nodes, the density of the links, the size of the main core, the average degree of the main core are estimated with a tolerance varying between 1 % and 10 %, depending on the property examined. An interesting finding is that the denser is the network the better is the estimation. We also checked how the accuracy of the estimation increases with the size of the subset of nodes used for which information is available. We found that this strongly depends on the accuracy of the fitness model. In the case of the WTW, the fitness model is fairly accurate in describing how links are formed across countries depending on their GDP and geographical distance. In the e-mid the fitness model is less accurate but still useful.

Furthermore, the BM method was tested against a non-topological property, namely Group DebtRank, a recently introduced measure of the systemic impact of a shock on the nodes of the network. We found that, both for WTW and e-mid network, the method allows to evaluate fairly well this property even starting from a small number of nodes.

In particular, we compared the results obtained using link weights derived from the gravity model of the WTW (this means that the weight of a link is proportional to the product of the GDPs of each node) with those obtained using homogeneous weights (taken as the average of the original weights). In the latter case, the BM estimates a value of Group DebtRank that is lower than the real one. This means that when the network is simulated using an average value for the weight, there is a systematic bias in the evaluation of systemic risk as measured by DebtRank. Conversely, in the case of non homogeneous weights, imposing more realistic values from the WTW fitness (gravity) model we obtain a more accurate estimation of the Group DebtRank. Finally we notice that the bigger is the impact factor α in rescaling the nodes the greater is the distress propagation in the network captured by the Group DebtRank. We observed the above results for both WTW and e-mid networks.

Further work is needed to address several issues that remain open. One could test the accuracy of estimation obtained with the Bootstrap Method on other topological and non-topological properties. In particular, one could try and extend the method in order to take into account degree-degree correlations and other higher order properties.