1 Introduction

Foamed materials demonstrate extraordinary properties such as light weight, high strength, good sound absorbency, and excellent thermal resistance [1–4]. These properties are of immense technological importance to different branches of science and technology, such as photon emission, chemical sensors, metallurgy, machinery, building blocks for traffic and aerospace applications [5, 6]. The detectable properties of porous substances remain no longer constant as they do in the ideal bulk material but change with the concentration and size (L) of the pores. For instance, the Young modulus (Y) [7–11], melting point (T m), and the thermal conductivity (k) [12–19] of the foamed specimens are tunable by changing their porosities. However, mechanism behind the porosity effect remains its infancy.

In order to understand the tunable behavior of nanostructure, numerous models have been proposed from various perspectives. Among them, the size-induced Y elevation is generally interpreted using the models of surface tension, surface relaxation, and surface reconstruction [20, 21]. The size-depressed T m is described using liquid-shell nucleation and growth, liquid-drop formation, and surface-phonon instability models [22, 23]. Little has yet been known about the size effect on the thermal conductivity, for the foamed materials in particular. In a word, some materials with large surface-to-volume ratio, such as foamed materials and nanostructured materials [24], show some fantastic properties. While the pore size (L) or particle size (K) governs their surface-to-volume ratio (γ i ).

In this communication, we attempted to clarify, correlate, formulate and quantify the porosity effect on the unusual behavior, such as Y, T m, and k, of the foamed materials from the perspective of three-component media premise and bond order-length-strength (BOLS) correlation notion [25, 26] that atom undercoordination induce local bond relaxation. Consistency between predictions and observations confirms that the pore size (L) effect of these seemingly irrelevant properties of the foamed materials originate from the broken-bond-induced local bond contraction and the associated change of bond energy in the negatively curved skins.

2 Principles

2.1 BOLS Correlation

The core content of BOLS correlation is that the undercoordinated atom causes the decrease of the bond length of residual bond of the atom, d i  = c i d 0, and the increase of the bond energy, E i  = c −m i E b, with respect to the bulk counterpart, where the subscript i is the number of atomic layers which counted from the outmost atomic layer up to three inwards of the surface, as no bond order loss occurs for i > 3. c i (z i ) = 2/{1 + exp[(12 –z i )/(8z i )]} is the bond contraction coefficient that varies only with the effective coordination number (CN) z i of an atom in the ith atomic layer of surface that varies with curvature and the relations is follow as:

$$\left\{ {\begin{array}{*{20}l} {z_{1} = \left\{ \begin{aligned} 4(1 \pm 0.75/K)\quad curved - surface \hfill \\ 4\quad \quad \quad \quad \quad \quad flat - surface \hfill \\ \end{aligned} \right.} \hfill \\ \begin{aligned} z_{2} = z_{1} + 2 \hfill \\ z_{3} = z_{2} + 6{\kern 1pt} \hfill \\ \end{aligned} \hfill \\ \end{array} } \right.$$
(1)

where K is the number of atoms lined along the radius of material and approximately equals R/d 0. The index m is the bond nature parameter that is not freely adjustable for a given material.

2.2 Three-component media premise

For a foamed substance, its properties depend on the ratio of three parts that bulk, surface skin of volume and pore. In the BOLS correlation, the undercoordination atoms induced local bond relaxation of surface skin of volume and pore lead to their properties different from bulk. While the distinguishing curvature between volume and pore induced a difference on their effective coordination number, which result in the extent of locality. Therefore, the properties of porous materials are determined by the proportion of atom of each component.

2.3 Surface-to-volume ratio

The surface-to-volume ratio (γ i ) is the volume ratio of surface skin and bulk, and equal to the ratio of number of atom, \(\gamma_{i} = \frac{{V_{i} }}{V} = \frac{{N_{i} }}{N}\), that can characterize the influence of each part to a detectable quantity.

Due to the existence of pores, the surface-to-volume ratio (γ i ) of the foamed materials is more complex than the bulk material. Figure 1 is a unit of the ideal foamed material with the radius K which contains many sphere pores with the same size L and evenly distributed. Therefore, the volume of the matrix (V 0), the volume of the surface atoms of matrix and pore (V i ), and the surface-to-volume ratio (γ i ) of the foamed material could be calculated as follows [26]:

$$\begin{aligned} V_{0} & = \frac{{4\uppi}}{3}\left[ {K^{3} - \frac{{4\uppi}}{3}\left( {n + \frac{1}{2}} \right)^{3} L^{3} } \right] \\ V_{i} & = 4\uppi\left[ {K^{2} C_{{{\text{S,}}i}} + \frac{{4\uppi}}{3}\left( {n + \frac{1}{2}} \right)^{3} L^{2} C_{{{\text{P,}}i}} } \right] \\ \gamma_{i} (n,L,K) & = \frac{{V_{i} }}{{V_{0} }} = \frac{{4\uppi\left[ {K^{2} C_{{{\text{S,}}i}} + \frac{{4\uppi}}{3}\left( {n + \frac{1}{2}} \right)^{3} L^{2} C_{{{\text{P,}}i}} } \right]}}{{\frac{{4\uppi}}{3}\left[ {K^{3} - \frac{{4\uppi}}{3}\left( {n + \frac{1}{2}} \right)^{3} L^{3} } \right]}} \\ & = \frac{{3\left\{ {{{\left[ {C_{{{\text{S,}}i}} + \frac{{4\uppi}}{3}\left( {n + \frac{1}{2}} \right)^{3} L^{2} C_{{{\text{P,}}i}} } \right]} \mathord{\left/ {\vphantom {{\left[ {C_{{{\text{S,}}i}} + \frac{{4\uppi}}{3}\left( {n + \frac{1}{2}} \right)^{3} L^{2} C_{{{\text{P,}}i}} } \right]} {K^{2} }}} \right. \kern-0pt} {K^{2} }}} \right\}}}{{K\left\{ {1 - {{\left[ {\frac{{4\uppi}}{3}\left( {n + \frac{1}{2}} \right)^{3} L^{3} } \right]} \mathord{\left/ {\vphantom {{\left[ {\frac{{4\uppi}}{3}\left( {n + \frac{1}{2}} \right)^{3} L^{3} } \right]} {K^{3} }}} \right. \kern-0pt} {K^{3} }}} \right\}}} \\ \end{aligned}$$
(2)

where (n + 1/2) is the number of sphere pores along the radius K which contains half a pore at the centre. L is the number of absent atoms lined along the radius of a pore, C S,i and C P,i are the bond contraction coefficient of the outside surface of the foamed material and inside surface of pores, respectively.

Fig. 1
figure 1

Illustration of a unit of the foamed material with sphere pores

Full size image

Besides, there is a relationship between (n + 1/2), L and K that 2L (n + 1/2) ≤ K [26]. Usually, the porosity of foamed substance is up to more than 90 %. Once pore is small enough, we can get n + 1/2 = K/(2L) approximately. Then, we simplified Eq. (2) as:

$$\gamma_{i} \left( {n,L,K} \right) = \frac{{V_{i} }}{{V_{ 0} }}\; = \frac{6}{{6 -\uppi}}\left( {\frac{{3C_{{{\text{S,}}i}} }}{K} + \frac{{\uppi\,C_{{{\text{P,}}i}} }}{2L}} \right)$$
(3)

Among them, the first part is the ratio of outside surface, while the second part is the ratio surface of pore. For a fixed size of K, the surface-to-volume (γ i ) is just depends on the pore size (L).

2.4 Pore size effect

Based on the scaling relationship [25, 26] the pore size (L) dependence of detectable physical quantity Q (L) = (N– N i ) q 0 + N i q i can be expressed as,

$$\frac{\Delta Q\left( L \right)}{Q\left( 0\right)} = \frac{Q\left( L \right) - Q\left( 0\right)}{Q\left( 0\right)} = \sum\limits_{i \le 3} {\gamma_{i} } \left( {\Delta q_{i} /q_{ 0} } \right)$$
(4)

where Q(0) = Nq 0 is the known quantity of ideal bulk material, q 0 and q i are the Q value of per atomic volume of the bulk material and the ith surface layer of pore in the foamed materials. N and N i are the number of atoms, in the foamed material and the ith atomic layer of the pore surface. While V and V i are volume of the foamed material and atoms of the ith atomic layer in the pore surface, respectively.

According to the BOLS theory, it can be derived that the T m is proportional to z i E i (the atomic cohesive energy per discrete atom) [27] that equals to the multiplication of the bond energy of the remaining bonds; the Y is proportional to E i /d 3 i (the cohesive energy density) [28]. Equation (3) [29] is the formula of the thermal conductivity k and the relative parameters. α is thermal diffusion coefficient, ρ is the density, C is the thermal capacity, kB is the Boltzmann constant, T is the temperature, θ D is the Debye temperature, ħ is the reduced Planck constant, ω m and ω m,i is the maximum phonon vibration frequency of an atom in material and an atom at the ith atomic layer of surface, respectively.

$$\left\{ {\begin{array}{*{20}l} {k =\upalpha\rho C} \hfill \\ {C = \frac{12}{5}\uppi^{ 4} N{\text{k}}_{\text{B}} \left( {\frac{T}{{\theta_{\text{D}} }}} \right)^{ 3} \quad (T < \theta_{\text{D}} )} \hfill \\ {\theta_{\text{D}} = \frac{{\hbar \omega_{\text{m}} }}{{{\text{k}}_{\text{B}} }}} \hfill \\ {\omega_{m,i} \propto \frac{{z_{i} E_{i}^{{\frac{ 1}{ 2}}} }}{{d_{i} }}} \hfill \\ \end{array} } \right.$$
(5)

According to Eq. (5), we can infer that the k is proportional to d 3 i /(z 3 i E 3/2 i ). So T m, Y, and k can be expressed as functional dependence on the bond order (z i ), length (d i ) and energy (E i ) as displayed in Eq. (6):

$$\left\{ {\begin{array}{*{20}l} {T_{m,i} \,\infty\, z_{i} E_{i} } \hfill \\ {Y_{i}\, \infty\,E_{i} /d_{i}^{3} } \hfill \\ {{{k_{i}\, \infty \,d_{i}^{3} } \mathord{\left/ {\vphantom {{k_{i} \infty d_{i}^{3} } {\left( {z_{i}^{3} E_{i}^{{\frac{3}{2}}} } \right)}}} \right. \kern-0pt} {\left( {z_{i}^{3} E_{i}^{{\frac{3}{2}}} } \right)}}} \hfill \\ \end{array} } \right.$$
(6)

Letting Q (0) in Eq. (4) be the T m (0), Y (0), and k (0). Combining Eqs. (3), (4), and (6), we correlate these seemingly irrelevant quantities in the form of Eq. (7). Among them, z ib = z i /zb while z bi  = zb/z i . zb is the CN of an atom in bulk materials, and usually zb = 12.

$$\left. {\begin{array}{*{20}c} {\frac{{\Delta T_{m} (L)}}{{T_{m} (0)}}} \\ {\frac{\Delta Y(L)}{Y(0)}} \\ {\frac{\Delta k(L)}{k(0)}} \\ \end{array} } \right\} = \frac{6}{6 - \pi }\sum\limits_{i \le 3} {\left( {\frac{{3C_{S,i} }}{K} + \frac{{\pi C_{P,i} }}{2L}} \right)} \left\{ {\begin{array}{*{20}c} \begin{aligned} \left( {z_{ib} C_{P,i}^{ - m} - 1} \right) \hfill \\ \left( {C_{P,i}^{ - m + 3} - 1} \right) \hfill \\ \end{aligned} \\ {} \\ {\left( {z_{bi}^{3} C_{P,i}^{{3 + \frac{3}{2}m}} - 1} \right)} \\ \end{array} } \right.$$
(7)

Equation (7) indicate that the pore size induced variation of different properties for a unit foamed substance all originate from interaction between undercoordinated atoms in the surface of pores skin up to three atomic layers. The magnitude of the pore size (L) effect is determined by the surface-to-volume ratio (γ i ).

3 Results and discussion

With the parameters d 0, Y, T m, k of ideal bulk material shown in Table 1, combine Eqs. (1, 6, 7) calculated, we plotted and compared the theoretical curves with measured date of Y, T m and k.

Table 1 The parameters for calculation of ideal bulk materials
Full size table

By making a general survey of Figs. 2, 3, and 4, the exceedingly good match between the theoretical predictions and the experimental results shows that the Y increased, while T m and k decreased with the decreasing of L. And the smaller the L, the more obvious the variation will be.

Fig. 2
figure 2

Theoretical reproduction of the pore size-enhanced Y for a Mg [7, 10], b Ni [9], c NiTi [11], and d Al [8] foams. Ni-1 and Ni-2 are obtained under 5 and 9 mN

Full size image
Fig. 3
figure 3

Theoretical reproduction of the pore size-depressed T m of a C6H12 [13], CCl4 [13], C6H12NO2 [14] and b Si [12] foams

Full size image
Fig. 4
figure 4

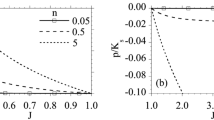
Theoretical reproduction of the pore size-depressed k of a Bi [19], Si [15], and b opened-cell and closed-cell Al [17, 18] and Fe [16] alloys. Bi-1 and Bi-2 are tested under 220 and 300 K, respectively. Si-1 and Si-2 are tested under 44 and 150 K, respectively. O–Al-1(2, 3) is the results of samples which are stretched, untreated, and rammed, respectively. Fe-1 and Fe-2 are tested under 550 and 650 K, respectively

Full size image

As we know, the properties of surface and inner of material are different. The ratio of surface determines the properties of the foamed material which has large pore surface. According to Eq. (3), the surface-to-volume ratio (γ i ) depends on pore size (L). As a result, with the change of L, the γ i will change too, which further influences the properties of the whole material. The different variation trend of each property is governed by its correlation with bond nature parameters.

By observing Fig. 2a–d respectively, we can also get some more information. For Fig. 2b, during test, a different load causes different Y for the same sample and the variation is more obvious when the load is higher. The reason is that the applied load will reshape the materials and its pores and change the surface-to-volume ratio (γ i ) slightly. Usually, the larger the load, the more serious the deformation will be. From Fig. 2d, it can be seen that after processing, such as annealing, fabricating, strengthening or ramming, the Y of the sample will change, which is the same with the effects of deformation. Besides, some of these processing will reconstruct its organization, which determines the properties. In a word, the processing will influence properties directly or indirectly.

For Fig. 4, it’s shown that the variation of k is greater for foamed pure metal than non-mental or alloy and also greater for closed-cell metal than opened-cell metal, respectively. The main reason is that m is different for different kind of materials. One can imagine that there is overlapped between the pores of opened-cell foam which lead to lower surface-to-volume ratio than closed-cell foam. From Fig. 4b, it can also be seen that the k of the sample that after processing will change too.

In a word, all these unusual phenomena result from different surface-to-volume ratio which leads to different proportion of the undercoordinated atoms in pore surface for different foamed materials. The inner mechanism is all because the bond length of residual bond decreases and bond energy increases for an undercoordinated atom. These seemingly irrelevant quantities are thus uniquely reconciled under the three-component media and the BOLS premise, which indicates that the pore size dependence of quantities originate from the relaxation of the bond in the pore surface skin up to three atomic layers. The reproduction of these quantities confirms the importance of the surface, which favors the proposals that the origin of these novel properties is merely skin thick [27, 28].

The actual shape and size of pores are different to each other, and the arrangement of pores of the foamed material is not organized too. These issues will affect the accuracy of the calculations and the obtained m value, which may lead to some deviation of the theoretical predictions from the observations, but have nothing to do with the nature, the origin, the trend, and the pore size dependence of these quantities.

4 Conclusion

In conclusion, from the perspective of BOLS correlation and three-component media premise, we have been able to clarify, formulate and correlate the porosity effect on Young modulus (Y), melting point (T m), and thermal conductivity (k) of the foamed materials. It has been found that the mechanisms behind the porosity effects are the atomic CN imperfection reduced atomic cohesive energy (E i ) and the energy density gain per unit volume. Reproduction of the reported pore size (L) dependence of these quantities evidences the validity of the general rule behind the pore size (L) trends of these properties for the foamed material. Theoretical reconciliation of the observed pore size (L) dependence of these physical quantities not only confirms the theory expectations but also provides guidelines for preparation of the foamed materials and device design.