1 Introduction

Thickness is one of the important parameters affecting the quality of plate metal during manufacturing and service [1]. Non-destructive testing methods such as eddy current testing, laser testing, ultrasonic testing, and radiographic testing are used to detect the thickness of metal plates to ensure their quality [2,3,4]. Eddy current testing is one of the most commonly used methods for on-line thickness measurement of metal plates due to its non-contact, easy automation and low cost [5,6,7,8,9]. When the thicknesses of metal plates are less than the standard penetration depth, eddy currents with different amplitude will be generated in metal plates with different thicknesses, which affects the impedance of the detection coil. Therefore, the thickness can be characterized by the impedance change.

At present, the main methods used to measure the thickness of metal plates are single-frequency eddy current testing, swept-frequency eddy current testing and pulsed eddy current testing. Pulsed eddy current testing contains rich detection information and has the feature of a large measurement range than harmonic eddy current testing [10, 11]. Yang et al. [12] used the peak value of the response signal of the pulsed eddy current to characterize the thickness of the tested piece. Fan et al. [13,14,15] found that the features of the phase and lift-off intersection (LOI) in the pulsed eddy current testing were not affected by lift-off and used these two features to measure the thickness of metal plates. Because the signal of pulsed eddy current testing is easily affected by noise, it is not widely used in practical testing. Swept-frequency eddy current testing can obtain information of different depths of the specimen using continuously broadband frequency. Mao et al. [16] obtained the thickness of a single-layer metal tube by the inverse problem of swept-frequency eddy current testing. Takahashi et al. [17] used swept-frequency eddy current testing to measure the thickness of Ni-based alloy coating on 304 Austenite stainless steel. Yin et al. [18] investigated that the peak frequency of the imaginary part of the coil inductance was inversely proportional to the thickness of the specimen. Although the swept-frequency eddy current testing can obtain more information, it is not efficient for on-line detection. As the most widely used eddy current technology, single-frequency eddy current testing is adopted by many scholars to measure the thickness of the test piece through the inversion algorithm. Based on the model of impedance change derived by Dodd-Deed [19], Moulder et al. [20] inversely deduced the conductivity and thickness of the specimens by the least square method. Mizukami et al. [21] measured the conductivity of a carbon fiber reinforced plastic plate by inversion algorithm. Yu et al. [22] proposed to use the inversion algorithm to simultaneously detect the conductivity and thickness of the conductive coating. Fan et al. [23] found that the lift-off effect could be eliminated by the model-based inversion algorithm, and the accuracy of inversion results was improved. It needs a large amount of calculation to reverse the thickness of the plate, and the smaller input error will cause a large error for the inversion result.

Traditionally, the thickness of a specimen is usually predicted by the linear calibration curve in single-frequency eddy current testing. And, the linear calibration curve for thickness measurement is obtained by fitting the experimental data of two standard samples. It is very important to find a linear calibration curve with high linearity for thickness measurement because the linearity of the linear calibration curve is the key factor to determine the accuracy of the predicted thickness. The linear relationship between thickness and impedance change can be deduced by an equivalent transformer model. Li et al. [24,25,26] studied that the tangent value of the phase angle of impedance change was proportional to the thickness through the equivalent transformer model, which was known as the approximate linear method (ALM). Their work’s focus was to design a fast and efficient circuit detection system to measure the thickness of aluminum foil and copper foil according to ALM, and also to study the influence of temperature on the detection accuracy. The influence of ALM on detection accuracy has not been studied. However, it is found that the accuracy of ALM is not very good, especially when the thickness of the specimen is very thin compared with standard penetration depth. In addition, ALM was obtained on the basis of equivalent approximation, and the factors that affect the accuracy of the linear calibration curve are not to be investigated in physics and evaluated quantitatively.

In order to solve this problem, the relationship between the thickness and the impedance change based on the Dodd-Deed model is derived [19], and according to the characteristics of derivative of tangent of phase to thickness, the log–log method (LLM) is obtained. LLM has the characteristics of high linearity and accurate prediction result, and its slope is less affected by the change of excitation frequencies and lift-offs. The outline of this paper is organized as follows: In Sect. 2, in order to improve the accuracy of thickness measurement, the new LLM is acquired through the numerical simulation. In Sect. 3, the numerical simulations for LLM with different excitation frequencies, lift-offs and conductivities are carried out. It is shown that LLM has a good linearity and highly predicted accuracy. In Sect. 4, advantages of LLM for thickness measurement are verified by experiments, that is, its slope of linear calibration curve is affected minimally by the change of excitation frequencies and lift-offs, and the precision of the predicted thickness is high. Finally, some conclusions are obtained in Sect. 5.

2 Theoretical analysis of eddy current testing for thickness measurement

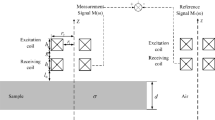
The schematic diagram of detecting the thickness of a single-layer metal plate by a hollow coil is shown in Fig. 1.

Fig. 1
figure 1

Schematic diagram of the testing model

Full size image

The model of impedance change for a single layer plate derived by Dodd-Deed can be expressed as [19]

$$ \begin{gathered} \Delta Z = \pi j\omega \mu_{0} n_{cd}^{2} \int_{0}^{\infty } {\phi (\alpha )P(\alpha )L(\alpha )} d\alpha \hfill \\ \phi (\alpha ) = \frac{{ - \alpha_{1}^{2} \mu_{0}^{2} + \alpha^{2} \mu^{2} }}{{2\alpha \alpha_{1} \mu_{0} \mu \coth (d\alpha_{1} ) + \left( {\alpha_{1}^{2} \mu_{0}^{2} + \alpha^{2} \mu^{2} } \right)}} \hfill \\ P(\alpha ) = [\int_{{r_{e1} }}^{{r_{e2} }} r J_{1} (\alpha r)dr]^{2} \hfill \\ L(\alpha ) = \frac{{\left( {{\text{e}}^{{ - \alpha z_{e1} }} - {\text{e}}^{{ - \alpha z_{e2} }} } \right)^{2} }}{{\alpha^{2} }} \hfill \\ \alpha_{1} { = }\sqrt {\alpha^{2} + j\omega \mu \sigma } \hfill \\ n_{cd} = \frac{N}{{(z_{e2} - z_{e1} )(r_{e2} - r_{e1} )}} \hfill \\ \end{gathered} $$
(1)

where, \(\Delta Z\) represents the impedance change, \(\omega\) is the angular frequency, \(\sigma\) and \(\mu\) are the conductivity and permeability of the metal plate, \(d\) is the thickness of the metal plate, \(\mu_{0}\) represents the permeability of air; \(r_{e1}\) and \(r_{e2}\) are the inner diameter and outer diameter of the coil, \(z_{e2} - z_{e1}\) is the height of coil, \(z_{e1}\) is lift-off, \(N\) represents the number of turns of the coil, \(n_{cd}\) stands for the turn density of the coil, \(\alpha\) is an integration variable, \(J_{1} (\alpha r)\) is a first-order Bessel function of the first kind, and \(j\) is an imaginary unit.

The model of impedance change (Eq. 1) is a generalized integral, and it is difficult to obtain the original function of the integral. Generally, the integration interval is truncated first, and the numerical results are obtained after numerical integration on the truncated interval. It is found that the accuracy of the calculation results is very high when the integral variable \(\alpha\) is truncated at 2000 [27]. Therefore, the generalized integral of impedance change can be converted into definite integral and the integral interval is [0 2000].

In eddy current testing, it is difficult to use a simple mathematical model to describe the thickness of the conductor due to the uneven distribution of the eddy current density [24]. Using the equivalent transformer model is a method to solve this problem. Li et al. [24,25,26] derived the approximate formula based on the equivalent transformer model

$$ \tan \theta = \left| {\frac{{{\text{Im}} (\Delta Z)}}{{{\text{Re}} (\Delta Z)}}} \right| \propto sd $$
(2)

where, \(s\) is the slope, \(\tan \theta\) is the tangent of the phase angle of impedance change.

The method of thickness measurement by Eq. (2), also known as the approximate linear method (ALM), can be used to measure the specimen whose thickness is less than the standard penetration depth (\(\delta\)). The measured thickness is normalized, and the relationship between \(\tan \theta\) and \(d/\delta\) is simulated by Eq. (1). The parameters of the coil and specimen in the numerical simulation are shown in Table 1.

Table 1 Parameters of the coil and specimen
Full size table

In the numerical simulation, the lift-off of the coil is 0.25 mm, and the exciting frequency is 30 kHz. The numerical simulation results are linearly fitted, and the relative error between the predicted thickness of linear calibration curves and the actual thickness is defined as

$$ R_{e} = \left| {\frac{{d_{a} - d_{p} }}{{d_{a} }}} \right| \times 100\% $$
(3)

where, \(d_{a}\) represents the actual thickness and \(d_{p}\) is the predicted thickness.

The numerical simulation and linear fitting results between \(\tan \theta\) and \(d/\delta\) are shown in Fig. 2.

Fig. 2
figure 2

Linear fitting curve (a) and the relative errors of the predicted thicknesses (b)

Full size image

It can be seen from Fig. 2b that when the thickness of the specimen is thin, the relative error of the predicted thickness obtained by linear fitting curve is large, especially the relative error of the predicted thickness measurement in the interval \([0,0.1d/\delta ]\) is very large. It can also be seen that when the thickness is greater than \(0.8\delta\), the relative errors of the predicted thickness also increases. This shows that the linear fitting results of ALM by Eq. (1) is not perfect.

A new fitting method is needed. For this purpose, the first and second order derivatives of \(\tan \theta\) to \(d/\delta\) are calculated as shown in Fig. 3.

Fig. 3
figure 3

The derivatives of \(\tan \theta\) to \(d/\delta\)

Full size image

As can be seen from Fig. 3, the first derivative is greater than 0 and the second derivative is less than 0. This is consistent with the power function whose exponent is greater than 0 and less than 1. Therefore, the trend of \(\tan \theta\) with \(d/\delta\) can be fitted by a power function \(\tan \theta { = }12.25 \times (d/\delta )^{0.8345}\).The fitting curves of two method and the relative errors of the predicted thicknesses are shown in Fig. 4.

Fig. 4
figure 4

Fitting curves (a) and the relative errors of the predicted thicknesses (b)

Full size image

Figure 4b shows that the relative error of the thickness predicted by the power fitting curve is smaller, especially better than that of linear fitting results of ALM in the interval \([0,0.1d/\delta ]\). Taking \(R_{e} < 5\%\) as the measurable interval, it can be seen from Fig. 4b that the power fitting curve can be used to measure the thickness in the interval \([0.1d/\delta, \;d/\delta ]\). In the interval \([0, 0.1d/\delta ]\), the relative error of predicted thickness is large, so this method is no longer applicable.

The fitting curve is used as the calibration curve. In order to make the calibration curve more accurate in the detection range, linear fitting and power fitting are used again in the interval \([0.1d/\delta, \;d/\delta ]\). The results after re-fitting are shown in Fig. 5.

Fig. 5
figure 5

Re-fitting curves (a) and the relative errors of the predicted thicknesses (b)

Full size image

It can be seen from Fig. 5b that the prediction accuracy of power fitting is significantly better than that of linear fitting in the interval \([0.1d/\delta, \;d/\delta ]\). Taking \(R_{e} < 5\%\) as the measurable interval, the measurement range of power fitting results is \( [0.1d/\delta, \;d/\delta ]\), while that of linear fitting results is \( [0.2d/\delta, \;d/\delta ]\).

For the convenience of calculation, the log–log method (LLM) is obtained by taking logarithm of power fitting equation

$$ \ln (\tan \theta ){ = }k\ln d + c $$
(4)

where, \(k\) represents the slope and \(c\) is the intercept.

Thus, the linear regression equation of the LLM is obtained. LLM uses Eq. (4) to get the linear calibration curve through the least square method. The results of power fitting can be represented as linear calibration curves of LLM, which is shown in Fig. 6.

Fig. 6
figure 6

Linear calibration curves of LLM

Full size image

3 Analysis of influencing factors in detection

Under the condition that the coil parameters, excitation frequency and material parameters of the test piece are known, the impedance change of different thicknesses is calculated according to Eq. (1) to obtain \(\tan \theta\). Then, the slope and intercept of Eq. (4) can be obtained by linear fitting the \(\ln (\tan \theta )\) with \(\ln d\) to get the linear calibration curve. In actual testing, the experimental results can be brought into the linear calibration curve to deduce the thickness of the tested piece.

3.1 Influence of excitation frequency

According to the formula of standard penetration depth, the influence of the excitation frequency on thickness measurement is very important. Generally, the thickness range of the tested piece should be estimated to select the appropriate excitation frequency. For the thinner specimen, the higher excitation frequency should be selected, and for the thicker specimen, the lower excitation frequency should be selected.

In the numerical simulation, the parameters of the specimen are shown in Table 1. The excitation frequencies are 10 kHz, 15 kHz, 20 kHz, 25 kHz and 30 kHz, and the corresponding standard penetration depths are 0.9091 mm, 0.7423 mm, 0.6429 mm, 0.5750 mm and 0.5249 mm, respectively. The lift-off of the coil is 0.25 mm. Linear calibration curves of LLM with different excitation frequencies are numerically simulated as shown in Fig. 7.

Fig. 7
figure 7

Linear calibration curves of LLM with different excitation frequencies

Full size image

In order to evaluate the influence of excitation frequencies, the slopes and correlation coefficients of linear calibration curves of LLM are shown in Fig. 8.

Fig. 8
figure 8

The correlation coefficients and slopes of LLM with different frequencies

Full size image

As shown in Fig. 8, the variations of excitation frequencies have little influence on the correlation coefficients, and the correlation coefficients of linear calibration curves of LLM are obviously close to 1. It can also be seen that with the increase of the excitation frequency, the slopes of linear calibration curves of LLM increase slightly.

Subsequently, the relative errors between the actual thicknesses and the predicted thicknesses are calculated according to Eq. (3), as shown in Fig. 9.

Fig. 9
figure 9

Relative errors of the predicted thicknesses with different excitation frequencies

Full size image

As can be seen from Fig. 9, the maximum relative error between the actual thickness and the predicted thickness of LLM is only 4% with different excitation frequencies.

3.2 Influence of lift-off

In eddy current testing of metal plate thickness, the influence of the lift-off effect on the result is an unavoidable problem. This is mainly due to the fact that the eddy current generated by the coil in the test piece is rapidly attenuated as the lift-off increases. In the numerical simulation, the lift-offs of the coil are 0 mm, 0.25 mm, 0.5 mm, 0.75 mm, and 1 mm. Results of LLM with different lift-offs in the numerical simulation are shown in Fig. 10.

Fig. 10
figure 10

Linear calibration curves of LLM with different lift-offs

Full size image

To evaluate the influence of lift-off, the slopes and correlation coefficients of linear calibration curves of LLM are shown in Fig. 11.

Fig. 11
figure 11

The correlation coefficients and slopes of LLM with different lift-offs

Full size image

As illustrated in Fig. 11, the changes of lift-offs have little effect on the correlation coefficients of LLM. It can also be known that with the increase of lift-offs, the slopes of linear calibration curves of LLM increase slightly.

Subsequently, the relative errors between the actual thicknesses and the predicted thicknesses are calculated as shown in Fig. 12.

Fig. 12
figure 12

Relative errors of the predicted thicknesses with different lift-offs

Full size image

Figure 12 shows that when lift-off changes, the maximum relative error between the actual thickness and the predicted thickness of LLM is 4.2%.

3.3 Influence of conductivity

LLM is also suitable for other non-ferromagnetic materials. Assuming that the electrical conductivities of the material are 4.032MS/m, 14.46MS/m, 30.65MS/m and 51.5MS/m, the range of measuring thickness is \( [0.1d/\delta, \;d/\delta ]\). The numerical simulation results of LLM are shown in Fig. 13.

Fig. 13
figure 13

Linear calibration curves of LLM with different conductivities

Full size image

To evaluate the influence of conductivities, the slopes and correlation coefficients of linear calibration curves of LLM are shown in Fig. 14.

Fig. 14
figure 14

The correlation coefficients and slopes of LLM with different conductivities

Full size image

As illustrated in Fig. 14, the changes of conductivities have little effect on the correlation coefficients of LLM. It can also be seen that with the increase of conductivities, the slopes of linear calibration curves of LLM increase slightly.

Subsequently, the relative errors between the actual thicknesses and the predicted thicknesses are calculated as shown in Fig. 15.

Fig. 15
figure 15

Relative errors of the predicted thicknesses of LLM with different conductivities

Full size image

As can be seen from Fig. 15, the max relative error of the predicted thickness of LLM is no more 4%.

It can be known from the numerical simulations that linear calibration curves of LLM have excellent linearity with different excitation frequencies, lift-offs and conductivities, which also means that LLM has a high measurement accuracy.

4 Experiments

4.1 Experimental Systems

The experimental system is composed of PC, impedance analyzer and coil, as shown in Fig. 16. The parameters of the coil are shown in Table 1. The impedance analyzer, whose type is WK65120B (made by Wayne Kerr Electronics), has an excitation frequency range from 20 Hz to 120 MHz and 0.05% basic measurement accuracy. The PC is connected to the impedance analyzer by LAN. The specimen in the experiment is aluminum strip, whose electrical conductivity is 30.65 MS/m and the size is \(100{\text{mm}} \times 100{\text{mm}} \times 0.1{\text{mm}}\). The specimens of aluminum plate with thickness of 0.1 mm, 0.2 mm, 0.3 mm, 0.4 mm and 0.5 mm are simulated by pressing aluminum strip with thick glass plate.

Fig. 16
figure 16

Experimental system

Full size image

4.2 Verification of Method with Different Excitation Frequencies

According to the condition \(d \le \delta\), it can be obtained from the formula of standard penetration depth that the excitation frequency should not be greater than 30 kHz. When the lift-off of the coil is 0.25 mm, the linear calibration curves and experimental results of LLM with different excitation frequencies are shown in Fig. 17.

Fig. 17
figure 17

Linear calibration curves (lines) and experimental results (markers) with different excitation frequencies

Full size image

Figure 17 shows that the experimental results are in good agreement with the linear calibration curves when the excitation frequencies are different. This figure also shows that the fixed thickness measurement can be moved left or right on the calibration linear curve by selecting different excitation frequencies. According to the results of Fig. 9, when the data with the excitation frequency of 20 kHz is in the middle of the calibration curve, the relative errors of the predicted thickness are smaller than that of the other two excitation frequencies. The experimental values in Fig. 17 have been taken into the linear calibration curves of LLM to calculate the predicted thickness of the specimens. Subsequently, relative errors between the predicted thickness of experimental results and the actual thickness are calculated, as shown in Fig. 18.

Fig. 18
figure 18

Relative errors between actual thicknesses and predicted thicknesses with different excitation frequencies

Full size image

Figure 18 indicates that the relative errors between actual thicknesses and predicted thicknesses with different excitation frequencies are small, and the maximum relative error is no more than 3%.

4.3 Verification of Method with Different Lift-Offs

From the analysis of Sect. 4.2, it can be known that the excitation frequency of 20 kHz is suitable for the aluminum plate with thickness of 0.1 mm–0.5 mm. The linear calibration curves and experimental results of LLM can be obtained with different lift-offs, as shown in Fig. 19.

Fig. 19
figure 19

Linear calibration curves (lines) and experimental results (markers) with different lift-offs

Full size image

Figure 19 shows that the experimental results are in good agreement with the linear calibration curves when the lift-offs are different. Subsequently, relative errors between predicted thickness and the actual thickness of the specimen are calculated, as shown in Fig. 20.

Fig. 20
figure 20

Relative errors between actual thicknesses and predicted thicknesses with different lift-offs

Full size image

Figure 20 illustrates that the relative errors between actual thicknesses and predicted thicknesses with different lift-offs vary slightly and the maximum relative error is no more than 3%. The inconsistency between the experimental and simulation results is mainly caused by the following reasons. First of all, there are some errors between LLM method and Dodd-Deed model. Then, the analytical model (Eq. 1) ignores the capacitance of the coil. Last but not least, the winding process of the coil can not ensure that the coil in the experiment is consistent with the simulated coil.

5 Conclusion

As a commonly used method for measuring thickness, ALM is obtained by approximating the equivalent transformer model of eddy current testing. Therefore, the linearity of ALM is not high. In this paper, LLM is proposed whose linear calibration curve has the characteristics of high linearity and accurate prediction results. In addition, linearity and slope of the linear calibration curve of LLM remain stable with the change of excitation frequencies, lift-offs and conductivities. The results of numerical simulations and experiments demonstrate that the maximum relative error of LLM is no more than 3% with different excitation frequencies and lift-offs. In the actual detection, attention should be paid to selecting the appropriate excitation frequency so that the detection range of the specimen is in the middle of \( [0.1d/\delta, \;d/\delta ]\). Thus, adopting LLM can obtain higher detection accuracy. In future work, LLM will be used to detect metal plates with different conductivities.