Study on the Shielding Effect of Claddings with Transmitter–Receiver Sensor in Pulsed Eddy Current Testing

Abstract

The shielding effect caused by the cladding has a serious influence on pulsed eddy current testing (PECT) of ferromagnetic metallic structures. To analyze the shielding effect and reveal the essence for reducing the shielding effect, a non-coaxial transmitter–receiver sensor (TR sensor) is used, and the influence of the shielding effect caused by the cladding on the TR sensor is studied theoretically in this paper. Firstly, an analytical model for the TR sensor with rectangular cross-section coils is conducted by using the first integral mean value theorem. Then, on the basis of the analytical model, the expression of the shielding effectiveness is derived to quantitatively evaluate the shielding effect and the spatial frequency spectra is utilized to research the characteristics of the sensor. Based on these, the performances of the TR sensor for reducing the shielding effect are studied. Results show the TR sensor which is more sensitive to the smaller radial spatial frequency can be used to reduce the shielding effect caused by the galvanized steel sheet.

1 Introduction

Wall thinning caused by erosion or corrosion is one of the threats to the ferromagnetic metallic structures such as pipes or vessels which are widely used in petrochemical and power generation industries. To guarantee the continued safe operation, the non-destructive testing (NDT) methods are necessary [1, 2]. As one of the powerful NDT methods, pulsed eddy current testing (PECT) has attracted a great deal of attention for its advantages of non-contact and acquisition of information at various depths in one excitation process [3, 4], and it has been employed to measure wall thickness of the ferromagnetic metallic structures. While in petrochemical and power generation industries, ferromagnetic metallic structures are always wrapped with insulations and externally protected metal claddings. The cladding made of galvanized steel unavoidably causes the shielding effect which adversely affects PECT [5], thus it is a difficult problem to be settled.

Attempts have been made to reduce the shielding effect. Cheng [6] used an Anisotropic Magneto Resistive (AMR)-sensor-embedded differential detector to measure the time-varying magnetic field signal, and found that the signal’s decay behavior was almost independent of the shielding effect over some time after switching off the excitation current. Xu et al. [7] reduced the shielding effect based on the saturation magnetization, a probe with a U-shaped magnetizer was designed. However, neither of them has quantitatively analyzed the shielding effect and revealed the essence for reducing the shielding effect.

To solve these problems, the transmitter–receiver (TR) sensor is used and the influence of the shielding effect caused by the cladding on the TR sensor is studied in this paper. The TR sensor which consists of non-coaxial transmitter and receiver coils has a number of advantages, such as the lift-off independence, the deep penetration depth, the improved signal-to-noise ratio etc. [8]. And it has already been used in ECT and PECT. Kojima et al. [9] presented a preventive maintenance methodology by using the TR sensor. Rosell [10] studied the probability of detection for ECT with the TR sensor. Xie et al. [11] utilized the TR sensor to study the inversion algorithm for the three-dimensional profile reconstruction of the wall thinning defect. However, most of the studies are not directly towards ferromagnetic metallic structures with claddings, the influence of the shielding effect caused by the cladding on the TR sensor has not been studied. Meanwhile, as a useful tool to reveal the essence and predict the signal, the analytical model for the TR sensor was also presented [12,13,14]. Rybachuk [12] and Yin [13] obtained the solution of the coil impedance for TR sensor by considering the cross-section of the receiver coil to be infinitesimal. While it is not suitable for the receiver coil with a large cross-section. Cao [14] gave the solution for the receiver coil with a cross-section, while it is expressed by the complex improper integral of Bessel functions and cosine function which is cumbersome and complex for numerical analysis.

The purpose of this paper is to quantitatively analyze the shielding effect and study the performances of the TR sensor for reducing the shielding effect. Firstly, the analytical model of PECT for the TR sensor with rectangular cross-section coils located above an insulated ferromagnetic metallic structures is established, and its calculation is simplified by using the first integral mean value theorem [15]. Then after analyzing the physical meanings of the parameters in the solution, the shielding effect is evaluated through the shielding effectiveness and the characteristics of the TR sensor are studied by analyzing the spatial frequency spectra. Results show the TR sensor which is more sensitive to the smaller radial spatial frequency can be used to reduce the shielding effect. The rest of this paper is organized as follows. In Sect. 2, the analytical model for the TR sensor is conducted. In Sect. 3, experiments are performed to verify the analytical model. In Sect. 4, the shielding effect caused by the cladding and the characteristics of the TR sensor for reducing the shielding effect are analyzed. In Sect. 5, the performances of the TR sensor for reducing the shielding effect are examined under different conditions. Finally, a brief conclusion is given in Sect. 6.

2 Analytical Model

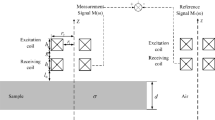
To simplify the calculation, the insulated ferromagnetic metallic structure is approximated by a four-layered structure shown in Fig. 1. Layers from 1 to 4 represent the air in the metallic structure, the metallic structure wall, the insulation and the cladding, respectively. Mediums of the four-layered structure are assumed to be linear, homogeneous and isotropic. Their relative magnetic permeability and electrical conductivity are denoted by μ_rk and σ_k (k = 1, 2, 3, 4), respectively. The layer over the cladding is considered to be the layer 5. It can be divided as three subregions shown in Fig. 1. The TR sensor which consists of non-coaxial transmitter and receiver coils with rectangular cross-section is located in subregion I–II. The sensor in polar coordinates is shown in Fig. 2.

Fig. 1

A TR sensor over a four-layered structure

Fig. 2

A TR sensor in polar coordinates

2.1 Induced Voltage of Receiver Coil with a Rectangular Cross-section

As the square-wave excitation current of PECT is theoretically represented by superimposing a series of sinusoidal harmonics in the frequency domain, the PECT signal can be derived from a sum of harmonic responses in the frequency domain by using an inverse Fourier transform (IFT). For each frequency component, according to the general equation given by Dodd and Deeds [16], the voltage induced of the receiver coil with a rectangular cross-section can be expressed as

$$ U = \frac{{n_{R} }}{{ (r_{2R} - r_{1R} ) (l_{2R} - l_{1} )}}\iint\limits_{\text{Receiver Coil section}} {U_{\text{Single Loop}} {\text{d}}r_{0R} {\text{d}}z} = \frac{{n_{R} }}{{ (r_{2R} - r_{1R} ) (l_{2R} - l_{1} )}}\int\limits_{{r_{1R} }}^{{r_{2R} }} {\int\limits_{{l_{1} }}^{{l_{2R} }} {U_{\text{Single Loop}} {\text{d}}r_{0R} {\text{d}}z} } $$

(1)

where l₁ is the lift off of the sensor, n_R is the number of the receiver coil turns, r_1R, r_2R, (l_2R− l₁) are the inner radius, the outer radius and the height of the receiver coil, respectively, U_{Single Loop} denotes the induced voltage for the receiver coil with a single loop of radius r_0R. According to [12, 13], it satisfies

$$ \begin{aligned} U_{\text{Single Loop}} = & j\omega \int {{\mathbf{A}}^{{{\text{I}} - {\text{II}}}} \cdot d{\mathbf{s}}} = j\omega \int\limits_{0}^{2\pi } {\cos (\phi )A^{{{\text{I}} - {\text{II}}}} r_{0R} d\theta } = \frac{{j\omega \mu_{0} n_{T} I(\omega )}}{{2 (r_{2T} - r_{1T} ) (l_{2T} - l_{1} )}} \times \int\limits_{0}^{\infty } {\frac{{Int (\alpha r_{1T} ,\alpha r_{2T} )}}{{\alpha^{3} }}J_{1} (\alpha r )r_{0R} } \\ \, & \times \int\limits_{0}^{2\pi } {\cos \left( {\theta - {\text{tg}}^{ - 1} \left( {\frac{{r_{0R} \sin (\theta )}}{{D + r_{0R} \cos (\theta )}}} \right)} \right)d\theta } \times \left[ {2 - e^{{\alpha \left( {z - l_{2T} } \right)}} - e^{{ - \alpha \left( {z - l_{1} } \right)}} + e^{ - \alpha z} (e^{{ - \alpha l_{1} }} - e^{{ - \alpha l_{2T} }} )R^{\prime}_{5,4} (\alpha )} \right]d\alpha \\ \end{aligned} $$

(2)

$$ Int(x_{1} ,x_{2} ) = \int_{{x_{1} }}^{{x_{2} }} {xJ_{1} (x)} {\text{d}}x $$

(3)

where j is the imaginary unit, μ₀ is the permeability of vacuum, J₁(x) denotes the first-order Bessel function of the first kind, α can be understood as the radial spatial frequency [17]. ω is the angular frequency of the harmonic excitation current, I(ω) is the amplitude of the harmonic excitation current. A^I–II is the magnetic vector potential in the subregion I–II, φ = θ-tg⁻¹(r_0Rsinθ/(D + r_0Rcosθ)), r = ((D + r_0Rcosθ)² + (r_0Rsinθ)²)^1/2, θ is the angle between x-axis and ds shown in Fig. 2. n_T is the number of the transmitter coil turns, r_1T, r_2T, (l_2T−l₁) are parameters of the transmitter coil shown in Fig. 1, D is the center distance between the transmitter coil and the receiver coil. R’_5,4(α) is the generalized reflection coefficient [18, 19] of the four-layered structure which is calculated from the ratio of the amplitude of the reflected wave to the amplitude of the incident wave in layer 5. It can be written as

$$ R^{\prime}_{5,4} (\alpha ) = \frac{{R_{5,4} (\alpha ) + R^{\prime}_{4,3} (\alpha )e^{{ - 2\beta_{4} \left( {d_{3} - d_{4} } \right)}} }}{{1 + R_{5,4} (\alpha )R^{\prime}_{4,3} (\alpha )e^{{ - 2\beta_{4} \left( {d_{3} - d_{4} } \right)}} }} $$

(4)

where

$$ R_{k + 1,k} (\alpha ) = \frac{{\mu_{rk} \beta_{k + 1} - \mu_{r(k + 1)} \beta_{k} }}{{\mu_{rk} \beta_{k + 1} + \mu_{r(k + 1)} \beta_{k} }} \, k = 1,2,3,4 $$

(5)

$$ R^{\prime}_{k + 1,k} (\alpha ) = \frac{{R_{k + 1,k} (\alpha ) + R^{\prime}_{k,k - 1} (\alpha )e^{{ - 2\beta_{k} \left( {d_{k - 1} - d_{k} } \right)}} }}{{1 + R_{k + 1,k} (\alpha )R^{\prime}_{k,k - 1} (\alpha )e^{{ - 2\beta_{k} \left( {d_{k - 1} - d_{k} } \right)}} }} \, k = 1,2,3 $$

(6)

R_k+1,k(α) (k = 1,2,3,4) is the single reflection coefficient at the interface between layers k + 1 and k. R’_k+1,k(α) (k = 1,2,3) is the generalized reflection coefficient of layer k + 1, R’_2,1(α) = R_2,1(α), β_k= (α² + jωμ₀μ_rkσ_k)^1/2, (d_k−1 − d_k) denotes the thickness of the layer k.

Substituting Eq. (2) into Eq. (1), and using partial integration method [16], the expression of the voltage induced for the receiver coil with a rectangular cross-section is obtained.

$$ U = \frac{{j\pi \omega \mu_{0} n_{T} n_{R} I(\omega )}}{{ (r_{2T} - r_{1T} ) (l_{2T} - l_{1} ) (r_{2R} - r_{1R} ) (l_{2R} - l_{1} )}} \, \times \int\limits_{0}^{\infty } {\frac{1}{{\alpha^{6} }}} Int (\alpha r_{1T} ,\alpha r_{2T} )Int_{P} (\alpha r_{1R} ,\alpha r_{2R} ) { } \times \{ 2\alpha (l_{2R} - l_{1} )+ \frac{1}{\alpha } [e^{{\alpha (l_{1} - l_{2T} )}} - e^{{\alpha (l_{2R} - l_{2T} )}} + e^{{ - \alpha (l_{2R} - l_{1} )}} - 1] \, + [ (e^{{ - \alpha l_{2R} }} - e^{{ - \alpha l_{1} }} ) (e^{{ - \alpha l_{2T} }} - e^{{ - \alpha l_{1} }} )R^{\prime}_{5,4} (\alpha ) ] \} {\text{d}}\alpha $$

(7)

where

$$ Int_{P} (\alpha r_{1R} ,\alpha r_{2R} )= \frac{1}{2\pi }\int\limits_{0}^{2\pi } {\int\limits_{{r_{1R} }}^{{r_{2R} }} {\cos (\theta - tg^{ - 1} (\frac{{r_{0R} \sin \theta }}{{D + r_{0R} \cos \theta }} ) )} } \times \alpha r_{0R} J_{1} (\alpha [ (D + r_{0R} \cos \theta )^{2} + (r_{0R} \sin \theta )^{2} ]^{1/2} ) {\text{d}}\alpha r_{0R} {\text{d}}\theta $$

(8)

Int_P(αr_1R, αr_2R) contains the parameters of the receiver coil and the center distance between the transmitter coil and the receiver coil, it can be used for coil optimizing. Therefore, it is important. Meanwhile, Int_P(αr_1R, αr_2R) is the key equation for getting the solution of Eq. (7) as it contains complex expressions of the Bessel function and the cosine function which are hard to be solved. In [12, 13], Int_P(αr_1R, αr_2R) is simplified by considering the cross-section of the receiver coil to be infinitesimal. While, the infinitesimal cross section approximation makes the accuracy of the solution reduced and it is not suitable for the receiver coil with a large cross-section. Thus a new method is introduced in this paper by using the first integral mean value theorem [15].

Making D and α × r_0R in Eq. (8) equal to d_f × r_0R and x, respectively. We get

$$ Int_{P} (\alpha r_{1R} ,\alpha r_{2R} )= \frac{1}{2\pi }\int\limits_{0}^{2\pi } {\cos \left( {\theta - tg^{ - 1} \left( {\frac{\sin \theta }{{d_{f} + \cos \theta }}} \right)} \right)\int\limits_{{\alpha r_{1R} }}^{{\alpha r_{2R} }} x J_{1} (x [ (d_{f} + \cos \theta )^{2} + (\sin \theta )^{2} ]^{1/2} ) {\text{d}}x{\text{d}}\theta } $$

(9)

where the integral $\int\nolimits_{{\alpha r_{1R} }}^{{\alpha r_{2R} }} x J_{1} (x [ (d_{f} + \cos \theta )^{2} + (\sin \theta )^{2} ]^{1/2} ) {\text{d}}x$ can be solved first. As in the range [αr_1R, αr_2R], J₁(x[(d_f+ cosθ)² + (sinθ)²]^1/2) is continuous, x is continuous and its values are always greater than 0, the first integral mean value theorem $\int\nolimits_{{a}}^{{b}} f(x)g(x){\text{d}}x=f({\varepsilon})\int\nolimits_{{a}}^{{b}}g(x){\text{d}}x$ can be utilized. Considering ε approximately equals to αr_0R, we get

$$ \int\limits_{{\alpha r_{1R} }}^{{\alpha r_{2R} }} x J_{1} (x [ (d_{f} + \cos \theta )^{2} + (\sin \theta )^{2} ]^{1/2} ) {\text{d}}x \approx \frac{{\alpha^{ 2} (r_{2R}^{2} - r_{1R}^{2} )}}{ 2}J_{1} (\alpha r_{0R} [ (d_{f} + \cos \theta )^{2} + (\sin \theta )^{2} ]^{1/2} ) $$

(10)

Substituting Eq. (10) into Eq. (9) gives

$$ Int_{P} (\alpha r_{1R} ,\alpha r_{2R} )= \frac{{\alpha^{ 2} (r_{2R}^{2} - r_{1R}^{2} )}}{ 2}J_{1} (\alpha r_{0R} ) \times \int\limits_{0}^{2\pi } {\frac{{\cos (\theta - tg^{ - 1} (\frac{\sin \theta }{{d_{f} + \cos \theta }} ) )J_{1} (\alpha r_{0R} [ (d_{f} + \cos \theta )^{2} + (\sin \theta )^{2} ]^{1/2} )}}{{2\pi J_{1} (\alpha r_{0R} )}}{\text{d}}\theta } $$

(11)

Using characteristics of Bessel functions, the integral of θ in Eq. (11) can be simplified as J₀(α × d_f × r_0R). Since J₀(α × d_f × r_0R) = J₀(αD), Eq. (11) becomes

$$ Int_{P} (\alpha r_{1R} ,\alpha r_{2R} )= \frac{{\alpha^{ 2} (r_{2R}^{2} - r_{1R}^{2} )}}{ 2}J_{1} (\alpha r_{0R} )J_{0} (\alpha D ) $$

(12)

As Int(x₁, x₂) shown in Eq. (3) can be approximated by ($x_{2}^{2}$ −$x_{1}^{2}$)/2 × J₁(αr_0R) with the same method presented in Eq. (10), to unify the expression form, α²($r_{{2{\text{R}}}}^{2}$ − $r_{{1{\text{R}}}}^{2}$)/2 × J₁(αr_0R) in Eq. (12) is considered to be Int(αr_1R,αr_2R). Thus Eq. (12) becomes

$$ Int_{P} (\alpha r_{1R} ,\alpha r_{2R} )= Int (\alpha r_{1R} ,\alpha r_{2R} )J_{0} (\alpha D ) $$

(13)

Then Int_P(αr_1R, αr_2R) is solved.

Applying Eq. (13) into Eq. (7), the solution of the analytical model for the receiver coil with the rectangular cross-section excited by a sinusoidal harmonic is obtained as

$$ \begin{aligned} U = & \frac{{j\pi \omega \mu_{0} n_{T} n_{R} I(\omega )}}{{ (r_{2T} - r_{1T} ) (l_{2T} - l_{1} ) (r_{2R} - r_{1R} ) (l_{2R} - l_{1} )}} \, \times \int\limits_{0}^{\infty } {\frac{1}{{\alpha^{6} }}} Int (\alpha r_{1T} ,\alpha r_{2T} )Int (\alpha r_{1R} ,\alpha r_{2R} )J_{0} (\alpha D ) { } \\ \, & \times \{ 2\alpha (l_{2R} - l_{1} )+ [e^{{\alpha (l_{1} - l_{2T} )}} - e^{{\alpha (l_{2R} - l_{2T} )}} + e^{{ - \alpha (l_{2R} - l_{1} )}} - 1] \, + [ (e^{{ - \alpha l_{2R} }} - e^{{ - \alpha l_{1} }} ) (e^{{ - \alpha l_{2T} }} - e^{{ - \alpha l_{1} }} )R^{\prime}_{5,4} (\alpha ) ] \} {\text{d}}\alpha \\ \end{aligned} $$

(14)

2.2 Series Expression of Induced Voltage Change for PECT

The induced voltage U in Eq. (14) is expressed in the integral of Bessel functions which is cumbersome and complex to be solved. In order to improve the calculation efficiency, the Truncated Region Eigenfunction Expansion (TREE) method [20] is used in this paper. The TREE method is available to get the solution in the form of series by imposing a field boundary at an appropriate distance from center of the transmitter coil. For the proposed analytical model, setting the distance of the field boundary equals to h, as shown in Fig. 1, then the induced voltage U shown in Eq. (14) is rewritten as

$$ \begin{aligned} U = & \frac{{j2\pi \omega \mu_{0} n_{T} n_{R} I(\omega )}}{{ (r_{2T} - r_{1T} ) (l_{2T} - l_{1} ) (r_{2R} - r_{1R} ) (l_{2R} - l_{1} )}} \times \sum\limits_{i = 1}^{\infty } {\frac{1}{{[\alpha_{i} hJ_{0} (\alpha_{i} h)]^{2} \alpha_{i}^{5} }}} Int (\alpha_{i} r_{1T} ,\alpha_{i} r_{2T} )Int (\alpha_{i} r_{1R} ,\alpha_{i} r_{2R} )J_{0} (\alpha_{i} D ) { } \\ \, & \times \{ 2\alpha_{i} (l_{2R} - l_{1} )+ { [}e^{{\alpha_{i} (l_{1} - l_{2T} )}} - e^{{\alpha_{i} (l_{2R} - l_{2T} )}} + e^{{ - \alpha_{i} (l_{2R} - l_{1} )}} - 1] + [ (e^{{ - \alpha_{i} l_{2R} }} - e^{{ - \alpha_{i} l_{1} }} ) (e^{{ - \alpha_{i} l_{2T} }} - e^{{ - \alpha_{i} l_{1} }} )R^{\prime}_{5,4} (\alpha_{i} ) ] \}\\ \end{aligned} $$

(15)

where the discrete eigenvalue α_i is the i-th positive root of J₁(α_ih) and the generalized reflection coefficient R’_5,4(α_i) is obtained by applying α_i into Eqs. (4)–(6).

The induced voltage U in Eq. (15) is the sum of the induced voltage U₀ and the induced voltage change △U. Where U₀ is directly resulted from the excitation current in the transmitter coil and △U is produced by the eddy current induced in the layered structure. And only △U can be used to evaluate the thickness of the metallic structure wall. Separating △U from U, we get

$$ \Delta U = j2\pi \omega \mu_{0} I(\omega ) \times \sum\limits_{i = 1}^{\infty } {\frac{{\alpha_{i} }}{{[\alpha_{i} hJ_{0} (\alpha_{i} h)]^{2} }}e^{{ - 2\alpha_{i} l_{1} }} S(\alpha_{i} )} R^{\prime}_{5,4} (\alpha_{i} ) $$

(16)

$$ S(\alpha_{i} ) = n_{T} n_{R} J_{0} (\alpha_{i} D )\frac{{Int (\alpha_{i} r_{1T} ,\alpha_{i} r_{2T} )}}{{\alpha_{i}^{2} (r_{2T} - r_{1T} )}}\frac{{Int (\alpha_{i} r_{1R} ,\alpha_{i} r_{2R} )}}{{\alpha_{i}^{2} (r_{2R} - r_{1R} )}}\frac{{ (e^{{ - \alpha_{i} (l_{2R} - l_{1} )}} - 1 )}}{{\alpha_{i} (l_{2R} - l_{1} )}}\frac{{ (e^{{ - \alpha_{i} (l_{2T} - l_{1} )}} - 1 )}}{{\alpha_{i} (l_{2T} - l_{1} )}} $$

(17)

where S(α_i) is the spatial frequency spectra of the TR sensor. It is determined by the parameters of the transmitter coil, the parameters of the receiver coil and the distance D between them, so it can be used to study the characteristics of the sensor.

Considering the induced voltage as a function of time is needed, IFT is applied to Eq. (16). Then, △U excited by a square-wave excitation current is recovered from the superposition of all time-domain fields in the function of frequency harmonics. Thus the PECT signal in time domain is acquired as

$$ \Delta U[s] = \frac{1}{N}\sum\limits_{m = 1}^{N} {e^{{j\frac{2\pi }{N}(s - 1)(m - 1)}} \Delta U[\omega_{m} ]} , \, s = 1,2, \ldots ,N $$

(18)

where m denotes the m-th sinusoidal harmonic, N is the number of sampling point.

3 Experimental Verification

Experiments are performed in this section to verify the proposed analytical model. Figure 3 illustrates the experimental set-up. A step wedge 16Mn steel plate with the thicknesses of 21.5 mm, 20.0 mm and 14.8 mm is applied as the metallic structure wall. A 40 mm-thick plastic plate and a 0.5 mm-thick galvanized steel sheet are attached on the 16Mn steel plate to simulate the insulation and the cladding, respectively. The TR sensor which consists of a transmitter coil and a receiver coil is placed over the cladding. A square-wave voltage signal is generated by a function generator, and then it is converted to a current signal and amplified by a power amplifier. The amplified square-wave current signal is provided to the transmitter coil. The induced voltage of the receiver coil is amplified by a preamplifier, then digitized by a data acquisition card. The computer is used to dispose the induced voltage for subtracting the signal U₀ and display the final induced voltage change △U. In this work, the parameters of the TR sensor are listed in Table 1. The amplitude, duty cycle and period of the square-wave current are set to be 4 amps, 50% and 1 s, respectively. The TR sensor and the square-wave current used in this section are also used in the following sections of this paper.

Fig. 3

Experimental set-up for PECT with TR sensor

Table 1 Parameters of the TR sensor

The calculations based on the analytical model are conducted using the same parameters with the experiments. The relative magnetic permeability and conductivity of the 16Mn steel plate are 500 and 1.6 MS/m, respectively. The relative magnetic permeability and conductivity of the galvanized steel sheet are 300 and 2.0 MS/m, respectively. Figure 4 presents the results of the analytical model and the experiments. The correspondences of △U from the two results are good, which indicates the analytical model for the TR sensor which consists of transmitter and receiver coils with rectangular cross-section is correct. Furthermore, the signals of 16Mn steel plate with the thicknesses of 21.5 mm, 20.0 mm and 14.8 mm can be easily distinguished, which indicates that the TR sensor can be used for wall thickness measurement, and its accuracy is (21.5-20.0)/21.5 × 100% = 7.5%.

Fig. 4

The results of the analytical model and experiments

4 Shielding Effect and Its Influence on the TR Sensor

The verified analytical model provides a theoretical foundation for the discussion of the essence for reducing the shielding effect. As Eq. (16) shows, the solution of △U is determined by the generalized reflection coefficient R’_5,4(α_i) and the spatial frequency spectra S(α_i). R’_5,4(α_i) which is determined by the reflection and transmission in the four layered structure is related to the shielding effect caused by the cladding, S(α_i) is decided by the parameters of the TR sensor. Thus by analyzing the reflection and transmission in the four layered structure and the features of S(α_i), the shielding effect and the characteristics of the TR sensor are studied. Furthermore, the essence for reducing the shielding effect is revealed.

4.1 Shielding Effectiveness of the Cladding

Since shielding effectiveness SE_dB [21] is a parameter that can be used to quantitatively evaluate the shielding effect, SE_dB is used in this section. SE_dB is defined as SE_dB= 20log₁₀(H₀/H_s), where H₀ and H_s represent the incident magnetic field and the transmission magnetic field through a conducting barrier, respectively. That is to say SE_dB is related to the ratio of the incident wave and the transmitted wave, thus the process of reflection and transmission in the four-layered structure is analyzed to derive the expression of SE_dB for the cladding.

Firstly, a simplified model, as shown in Fig. 5, is considered. The layer 4 is the cladding with the thickness (d₃−d₄), the layer 5 is the air above the cladding, and the layer 3 is the insulation below the cladding. Different from the four-layered structure shown in Fig. 2, the thickness of the layer 3 is considered to be infinite.

Fig. 5

Reflections and transmissions for the model with infinite thick insulation

To get the expression of SE_dB for the simplified model, the reflection and transmission of the simplified model are studied. And as the thickness of the cladding is finite, the multiple reflections and transmissions in the cladding cannot be ignored. The schematic diagram is shown in Fig. 5. To simplify the analysis, the amplitude of the incident wave in the layer 5 is set to be 1, then R_5,4, T_5,4R_4,3T_4,5η², T_5,4R²_4,3R_4,5T_4,5η⁴, … are the reflections from the interface between the layer 5 and the layer 4. T_5,4, T_5,4R_4,3R_4,5η², … are the multiple transmissions in the cladding. T_5,4R_4,3η, T_5,4R²_4,3R_4,5η³, … are the multiple reflections in the cladding. And T_5,4T_4,3η, T_5,4T_4,3R_4,3R_4,5η³, … are the transmissions through the cladding. Where $\eta={e^{-\beta}}_4({^d}_3-{^d}_4)$; R_k+1,k and T_k+1,k denote the single reflection coefficient and the single transmission coefficient from the interface between the layer k + 1 and the layer k (k = 4,3), respectively.

According to the definition of the generalized reflection coefficient R’_k+1,k(α_i) in [18, 19], the generalized transmission coefficient T’_k+1,k(α_i) can be defined as the ratio of the amplitude of the transmitted wave to the amplitude of the incident wave. In this way, the multiple transmissions in the cladding can be expressed as T’_5,4(α_i) which is derived from

$$ T^{\prime}_{k + 1,k} (\alpha_{i} ) = \frac{{T_{k + 1,k} (\alpha_{i} )}}{{1 - R_{k,k - 1} (\alpha_{i} )R_{k,k + 1} (\alpha_{i} )e^{{ - 2\beta_{k} (d_{k - 1} - d_{k} )}} }} $$

(19)

Then the reflection in the cladding is ${T^{\prime}}_{5,4}(\alpha_{i})R_{4,3}(\alpha_{i}){e^{-\beta}}_4({^d}_3-{^d}_4)$ and the transmission through the cladding is ${T^{\prime}}_{5,4}(\alpha_{i})T_{4,3}(\alpha_{i}){e^{-\beta}}_4({^d}_3-{^d}_4)$, thus based on the definition of SE_dB in [21], the shielding effectiveness SE_dB of the cladding in the simplified model shown in Fig. 5 can be expressed as

$$ SE_{dB} (\alpha_{i} ) = 20\log_{10} \frac{1}{{T^{\prime}_{5,4} (\alpha_{i} )T_{4,3} (\alpha_{i} )e^{{ - \beta_{4} (d_{3} - d_{4} )}} }} = 20\log_{10} \frac{1}{{\frac{{T_{5,4} (\alpha_{i} )T_{4,3} (\alpha_{i} )e^{{ - \beta_{4} (d_{3} - d_{4} )}} }}{{1 - R_{4,3} (\alpha_{i} )R_{4,5} (\alpha_{i} )e^{{ - 2\beta_{4} (d_{3} - d_{4} )}} }}}} $$

(20)

While for the four-layered structure studied in this paper, as the thickness of the layer 3 is finite, there are also multiple reflections and transmissions in the layer 3, the expression of SE_dB is more complex. The generalized reflection coefficient and the generalized transmission coefficient can be used to simplify the analysis. Replace R_4,3(α_i) and T_4,3(α_i) in Eq. (20) with R’_4,3(α_i) and T’_4,3(α_i), respectively, SE_dB for the cladding in the four-layered structure is acquired as

$$ SE_{dB} (\alpha_{i} ) = 20\log_{10} \frac{1}{{\frac{{T_{5,4} (\alpha_{i} )T^{\prime}_{4,3} (\alpha_{i} )e^{{ - \beta_{4} (d_{3} - d_{4} )}} }}{{1 - R^{\prime}_{4,3} (\alpha_{i} )R_{4,5} (\alpha_{i} )e^{{ - 2\beta_{4} (d_{3} - d_{4} )}} }}}} $$

(21)

Substituting T’_4,3(α_i) derived from Eq. (19) into Eq. (21), and using the fact that T_5,4 = 1 + R_5,4, R_4,5 = −R_5,4, we get

$$ SE_{dB} (\alpha_{i} ) = 20\log_{10} \frac{{(1 + R^{\prime}_{4,3} (\alpha_{i} )R_{5,4} (\alpha_{i} )e^{{ - 2\beta_{4} (d_{3} - d_{4} )}} )(1 + R^{\prime}_{3,2} (\alpha_{i} )R_{4,3} (\alpha_{i} )e^{{ - 2\beta_{3} (d_{2} - d_{3} )}} )}}{{(1 + R_{5,4} (\alpha_{i} ))(1 + R_{4,3} (\alpha_{i} ))e^{{ - \beta_{4} (d_{3} - d_{4} )}} }} $$

(22)

Finally the expression of the shielding effectiveness SE_dB for the cladding in the four-layered structure is obtained. Meanwhile, as shown in Eqs. (5) and (6), R_5,4(α_i), R_4,3(α_i), R’_4,3(α_i) and R’_3,2(α_i) are related to the metallic structure wall and the material of the cladding, ${e^{-2\beta}}_4({^d}_3-{^d}_4)$ is decided by the thickness of the cladding, and ${e^{-2\beta}}_3({^d}_2-{^d}_3)$ is effected by the thickness of the insulation, so SE_dB is determined by the material and the thickness of the cladding, the insulation as well as the metallic structure wall. Furthermore, SE_dB is also related to the radial spatial frequency α_i and the angular frequency of the harmonic excitation current.

To study the shielding effect specifically, a four-layered structure with 0.5 mm-thick galvanized steel sheet, 21.5 mm-thick metallic structure wall, 40 mm-thick insulation is taken as an example. The result is shown in Fig. 6, of which the x-axis denotes the radial spatial frequency α_i, the y-axis denotes the angular frequency of the harmonic excitation current, the color density denotes the value of SE_dB, and the line denotes the contour line whose value is marked aside. Figure 6 shows that SE_dB of the 0.5 mm-thick galvanized steel is almost independent with the angular frequency of the harmonic excitation current, while it increases with α_i. When α_i is smaller, SE_dB is smaller, the shielding effect is relatively less. When α_i is larger, the shielding effect is obvious. For example, when α_i is about 50, SE_dB is more than 40, which means the incident wave has been reduced by a factor of 100. That indicates the shielding effect caused by the 0.5 mm-thick galvanized steel sheet will adversely affect PECT.

Fig. 6

The shielding effectiveness SE_dB for the 0.5 mm-thick galvanized steel sheet, calculated by Eq. (22) with 21.5 mm-thick wall and 40 mm-thick insulation

4.2 The Characteristics of the TR Sensor for Reducing the Shielding Effect

To reduce the shielding effect, the sensor is required to go through the cladding and get the information of the metallic structure wall. As mentioned above, when α_i is smaller, the shielding effect caused by the galvanized steel sheet is relatively less. Therefore, the sensor which is sensitive to the smaller α_i can be used to reduce the shielding effect. As the spatial frequency spectra S(α_i) of the sensor denotes the amplitude of the contribution as a function of α_i [17, 22], S(α_i) can be used to study the sensitivity of the sensor to α_i. In this section, S(α_i) for the TR sensor and the common used coaxial sensor are researched, and the characteristics of the two sensors for reducing the shielding effect are studied.

Figure 7a gives S(α_i) for the TR sensor used in Sect. 3 and the coaxial sensor with the same parameters except that the center distance of the transmitter coil and receiver coil D is 0 mm. Figure 7a illustrates that (1) S(α_i) is a oscillating attenuation curve, (2) the attenuation characteristics of S(α_i) of the TR sensor are different with those of the coaxial sensor. For TR sensor, the amplitude of S(α_i) is smaller and it goes down to zero faster, which indicate that the sensitivity of the TR sensor to α_i is different with that of the coaxial sensor.

Fig. 7

a The spatial frequency spectra S(α_i) for the coaxial sensor and the TR sensor and b the radial spatial frequency response range for the coaxial sensor and the TR sensor

To quantitatively analyze the sensitivity of the two sensors to α_i, the radial spatial frequency response range is defined. Its limit inferior is considered to be 0 and its limit superior is regarded as the value of α_i when S(α_i) is reduced to 1/e times of its amplitude. Furthermore, as S(α_i) is an oscillating attenuation curve, there are more than one α_i whose corresponding S(α_i) are equal to 1/e times of its amplitude, and some of them maybe negative. Thus to simplify the analysis, take the absolute value of S(α_i) firstly, and then select the maximum value of α_i to be the limit superior of the radial spatial frequency response range. Taken the radial spatial frequency response range of the coaxial sensor as an example, as shown in Fig. 7b, the amplitude for the absolute value of S(α_i) is 248.5, and the 1/e times of the amplitude is 91.4 which marked with “□” in Fig. 7b, thus its radial spatial frequency response range is 0–77. In this way, the radial spatial frequency response range for the TR sensor is 0–43, which is about half smaller than that of the coaxial sensor. According to Fig. 6, the values of SE_dB in 0–43 are small, therefore the TR sensor is suitable for reducing the shielding effect.

To illustrate that the TR sensor is suitable for reducing the shielding effect caused by the galvanized steel sheet, the characteristics of the coaxial sensor and the TR sensor are studied. Figure 8a and b give the induced voltage changes △U of the four-layered structure used in Sect. 4.1 obtained by the coaxial sensor and the TR sensor, respectively. Results show that (1) the amplitude of △U for the TR sensor is smaller than that of the coaxial sensor, that is because the amplitude of S(α_i) for the TR sensor is smaller than that of the coaxial sensor. (2) The difference of △U with and without the galvanized steel sheet obtained by the coaxial sensor is larger than that obtained by the TR sensor. Define the difference as

$$ \xi_{\text{cladding}} = (\Delta U_{\text{with - cladding}} - \Delta U_{\text{without - cladding}} )/\Delta U_{\text{without - cladding}} $$

(23)

where △U_{with-cladding} and △U_{without-cladding} are obtained with and without the cladding, respectively.

Fig. 8

Induced voltage change △U with and without the galvanized steel sheet. a Results obtained by the coaxial sensor and b results obtained by the TR sensor

Results are shown in Fig. 9, of which the oscillatory in the later time is caused by the ‘Gibbs Phenomenon’ in the calculation of △U [18]. $\xi_{\text{cladding}}$ obtained by the coaxial sensor is larger than 50% while the one obtained by the TR sensor is less than 10%, that proves the TR sensor can largely reduce the shielding effect. Experimental signals shown in Fig. 10 give another evidence, and they also show that the signal-to-noise ratio of the TR sensor is higher than that of the coaxial sensor, thus the TR sensor can be used in the case when the electromagnetic noise is large. In conclusion, the discussion made above proves that the sensor which is sensitive to the smaller α_i can be used to reduce the shielding effect caused by the galvanized steel sheet.

Fig. 9

$\xi_{\text{cladding}}$ obtained by the coaxial sensor and the TR sensor

Fig. 10

The experimental signals obtained by the coaxial sensor and the TR sensor

5 Discussion

Except for the galvanized steel sheet, the aluminum alloy sheet and the stainless steel sheet are also usually used as the cladding. Furthermore, the thickness of the cladding, the thickness of the insulation and the thickness of the metallic structure wall are not fixed. As shown in Eq. (22), the factors mentioned above all affect the shielding effect, and then affect the performances of the TR sensor, thus the performances of the TR sensor with different parameters should be researched.

The 0.5 mm-thick galvanized steel sheet, 0.5 mm-thick aluminum alloy sheet and 0.5 mm-thick stainless steel sheet are taken as examples to study the performances of the TR sensor with different materials of the cladding. Based on Eq. (22), SE_dB for the three claddings are obtained. The relative magnetic permeability and conductivity of the aluminum alloy sheet is set to be 1 and 21.6 MS/m, respectively; the relative magnetic permeability and conductivity of the stainless steel sheet is set to be 1 and 1.35 MS/m, respectively. Figure 6 has given SE_dB for the 0.5 mm-thick galvanized steel sheet and Fig. 11 gives SE_dB for the 0.5 mm-thick aluminum alloy sheet and 0.5 mm-thick stainless steel sheet. Results show that for aluminum alloy sheet and stainless steel sheet, the values of SE_dB increase with α_i, meanwhile, they are also sensitive to the angular frequency. Those lead to that SE_dB of the aluminum alloy sheet is larger than that of galvanized steel sheet when α_i and angular frequency are smaller. While in most cases, SE_dB for the aluminum alloy sheet and stainless steel sheet is smaller than that of the galvanized steel sheet, and SE_dB of the stainless steel sheet is the smallest. That means the shielding effect caused by the galvanized steel sheet is the worst.

Fig. 11

The shielding effectiveness SEdB for the claddings with different materials. a The aluminum alloy sheet and b the stainless steel sheet, calculated by Eq. (22) with 21.5 mm-thick wall and 40 mm-thick insulation

To research the influence of the shielding effect caused by the aluminum alloy sheet and stainless steel sheet on the TR sensor, Fig. 12a and b give $\zeta_{\text{cladding}}$ for the 0.5 mm-thick stainless steel sheet and the 0.5 mm-thick aluminum alloy sheet, respectively. As Fig. 12 shows, $\zeta_{\text{cladding}}$ obtained by the TR sensor is bigger than that of the coaxial sensor, especially in the early time of the signal. That mostly because SE_dB of the aluminum alloy sheet and stainless steel sheet are sensitive to the angular frequency, and SE_dB obtained with smaller angular frequency maybe even larger than that of the galvanized steel sheet. As the smaller angular frequency mainly contribute to the signal in the early time, thus $\zeta_{\text{cladding}}$ obtained by the TR sensor is bigger than that of the coaxial sensor especially for the aluminum alloy sheet.

Fig. 12

$\xi_{\text{cladding}}$ for the claddings with different materials. a The stainless steel sheet and b the aluminum alloy sheet

Furthermore, as Fig. 12 shows, the shielding effect caused by the stainless steel sheet is rather small which can be ignored; the shielding effect caused by the aluminum alloy sheet is larger than 100% in the early time, while it becomes less in the later time, thus it can be reduced by using the characteristic in the later time of the signal. However, the shielding effect caused by the galvanized steel sheet is the most difficult problem and the TR sensor is a favorable method to settle it.

As the thickness of the galvanized steel sheet is not fixed, the applicability of the TR sensor with different thicknesses of the galvanized steel sheet should be analyzed. The commonly used galvanized steel sheet is located in 0.3–0.7 mm thick, thus the 0.3 mm-thick, 0.5 mm-thick and 0.7 mm-thick galvanized steel sheet are used as examples. Figure 6 has given SE_dB for the 0.5 mm-thick galvanized steel sheet and Fig. 13 gives SE_dB for the 0.3 mm-thick and 0.7 mm-thick galvanized steel sheet. Results show SE_dB increases with the thickness of the cladding, while the change is small. ζ_cladding for the galvanized steel sheet shown in Fig. 14 further proves that conclusion. Furthermore, as the maximum ofζ_cladding is less than 20%, the TR sensor is suitable for galvanized steel sheet with different thicknesses.

Fig. 13

The shielding effectiveness SE_dB for the galvanized steel sheets with different thicknesses. a 0.3 mm-thick and b 0.7 mm-thick, calculated by Eq. (22) with 21.5 mm-thick wall and 40 mm-thick insulation

Fig. 14

$\xi_{\text{cladding}}$ for the galvanized steel sheets with different thicknesses

To study the performances of the TR sensor with different thichnesses of the metallic structure wall, the 21.5 mm-thick wall and the 30.0 mm-thick wall are used, and the thickness of the galvanized steel sheet is 0.5 mm, the thickness of the insulation is 40 mm. The corresponding $\zeta_{\text{cladding}}$ is shown in Fig. 15a. It indicates that the thickness of the metallic structure wall has a negligible effect on the TR sensor for reducing the shielding effect. Meanwhile, Fig. 15b gives $\zeta_{\text{cladding}}$ variation with insulation thicknesses for the 21.5 mm-thick wall and 0.5 mm-thick galvanized steel sheet. It states that $\zeta_{\text{cladding}}$ increases with the thickness of the insulation, that is to say the shielding effect is sensitive to the insulation, thus the thickness of the insulation must be considered in PECT with the TR sensor.

Fig. 15

a $\xi_{\text{cladding}}$ variation with different thicknesses of the metallic structure wall and b $\xi_{\text{cladding}}$ variation with different thicknesses of the insulation

6 Conclusions

The shielding effect and the essence for reducing the shielding effect are analyzed in this paper. Firstly, the analytical model for the TR sensor which consists of coils with rectangular cross-section is conducted by using the first integral mean value theorem to expose the essence and predict the signal. Then, the expression of the shielding effectiveness SE_dB for the cladding of the insulated ferromagnetic metallic structure is derived to quantitatively evaluate the shielding effect and the spatial frequency spectra S(α_i) is utilized to research the characteristics of the sensor. Finally, based on the analysis above, performances of the TR sensor with different parameters are studied. Results show that compared with the aluminum alloy sheet and the stainless steel sheet, the shielding effect caused by the galvanized steel sheet is the most obvious and it is also the most difficult to be reduced. As the TR sensor is more sensitive to the smaller radial spatial frequency α_i, it is an available method to reduce the shielding effect caused by the galvanized steel sheet. Furthermore, the performances of the TR sensor is sensitive to the thickness of the insulation, thus the insulation must be considered in PECT with the TR sensor. The research proposed in this paper can be used for the sensor design which will contribute to PECT for ferromagnetic metallic structures with claddings in petrochemical and power generation industries.