Abstract
We present and analyze a uniquely solvable and unconditionally energy stable numerical scheme for the ternary Cahn-Hilliard system, with a polynomial pattern nonlinear free energy expansion. One key difficulty is associated with presence of the three mass components, though a total mass constraint reduces this to two components. Another numerical challenge is to ensure the energy stability for the nonlinear energy functional in the mixed product form, which turns out to be non-convex, non-concave in the three-phase space. To overcome this subtle difficulty, we add a few auxiliary terms to make the combined energy functional convex in the three-phase space, and this, in turn, yields a convex-concave decomposition of the physical energy in the ternary system. Consequently, both the unique solvability and the unconditional energy stability of the proposed numerical scheme are established at a theoretical level. In addition, an optimal rate convergence analysis in the \(\ell ^\infty (0,T; H_N^{-1}) \cap \ell ^2 (0,T; H_N^1)\) norm is provided, with Fourier pseudo-spectral discretization in space, which is the first such result in this field. To deal with the nonlinear implicit equations at each time step, we apply an efficient preconditioned steepest descent (PSD) algorithm. A second order accurate, modified BDF scheme is also discussed. A few numerical results are presented, which confirm the stability and accuracy of the proposed numerical scheme.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Cahn-Hilliard (CH) flow, which models spinodal decomposition and phase separation in a binary fluid [2, 14, 15], is one of the most well-known gradient flows. In the CH family of models, sharp interfaces are replaced by narrow diffusive transition layers, which often leads to models that are simpler and more theoretically tractable than their sharp interface counterparts. Most existing works for the CH flow are based on the two-phase model, including both the isotropic and anisotropic ones [17, 24, 29, 36, 39, 62], etc. Meanwhile, if three or even more phase components are involved in the physical system, an interaction of these components has to be taken into consideration; see the related works [3,4,5,6,7, 10, 12, 13, 37, 38, 65].
There have been many different choices of free energy for the ternary CH system. In this article, we focus on the following three-phase free energy [13], which is of polynomial pattern:
where \(F(\varphi _1,\varphi _2,\varphi _3) = \sum _{i=1}^{3}\frac{\Sigma _i}{2}\varphi _i^2(1-\varphi _i)^2 + \Lambda \varphi _1^2\varphi _2^2\varphi _3^2\) with \(\Lambda \) large enough to make F nonnegative. The domain \(\Omega \in {\mathbb {R}}^d,\ d=2,3\) is open bounded and connected. The three unknowns \(\varphi _i, \ i=1,2,3\) are the order parameters subject to a constraint \(\varphi _1 + \varphi _2 + \varphi _3=1\). The triple constant parameters \(\Sigma =(\Sigma _1,\Sigma _2,\Sigma _3)\) and the interface width \(\varepsilon \) are constants. Note that the coefficients \(\Sigma _i\) are not assumed to be positive in the physical literature, \(-\Sigma _i\) is called the spreading coefficient of the phase i at the interface between another two. If one of coefficients \(\Sigma _i\) is negative, the spreading is said to be total, otherwise, it’s said to be partial. For total spreading case, the following conditions are assumed to ensure the well-posedness of system:
In particular, it was proved in [13] that, the existence of a \(\underline{\Sigma }>0\) such that \(\forall n\ge 1,\ (\xi _1,\xi _2,\xi _3)\in ({\mathbb {R}}^n)^3\) with \(\xi _1+\xi _2+\xi _3=0\),
is equivalent to condition (1.2).
In fact, making use of the mass conservation constraint \(\varphi _2 = 1 - \varphi _1 - \varphi _3\), we are able to rewrite the energy functional as
In turn, the chemical potential is defined as
As a result, the mass conservative dynamic equations of the three-phase CH model are given by
where \(M_0(\varvec{\varphi })\) is a diffusion coefficient called mobility which may depend on \(\varvec{\varphi }\triangleq (\varphi _1,\varphi _2,\varphi _3)\).
With periodic boundary condition imposed, and taking inner product with (1.7) by \(\mu _1,\mu _3\), we get the energy dissipation law of the three-phase CH model:
Note that the above inequality also holds for total spreading case under the conditions (1.2) since there can only be one negative coefficient \(\Sigma _i\) among \(\Sigma \) (say \(\Sigma _2<0\)). Thus we can replace the order parameter with respect to the negative coefficient by another two.
In fact, such a substitution (to represent \(\varphi _2\) in terms in \(\varphi _1\) and \(\varphi _3\) by the mass conservation constraint) reduces the three-variable system to a two-variable one. While the symmetry between \(\varphi _2\) and \((\varphi _1, \varphi _3)\) has been broken, that between \(\varphi _1\) and \(\varphi _3\) is kept intact. In contrast, a Lagrange multiplier approach has also been reported in a few other related works [65, 68]. In this approach, a three-component physical energy structure is preserved, while an average of the nonlinear chemical potentials (for each phase component) is subtracted from each equation, which plays a Lagrange multiplier role to enforce the mass conservation identity. To make a comparison between these two different ideas to enforce such an identity, each approach has its own advantages. Our approach, formulated as (1.4), (1.5)–(1.7), avoids the degeneracy in the PDE system. In addition, the PDE formulation (1.7) is more natural, since there is no reasonable physical explanation for the Lagrange multiplier terms. Also see the related discussions in the pioneering work [13].
Among the existing numerical works for the ternary CH model, theoretical analysis for the energy stability is very limited, due to the challenge associated with the three-phase nature of the nonlinear energy functional. This issue has been extensively discussed in [13] for a wide class of numerical schemes of various CH models; meanwhile, the stability analysis for the ternary system with the energy (1.1) depends on a convex-concave decomposition, which has not been available at a theoretical level, because of the non-convex, non-concave nature of the mixed product part. In a more recent work [65], an invariant energy quadratization (IEQ) approach is studied for the ternary flow, and a stability analysis has been provided for a numerically modified energy. Meanwhile, we point out that a uniform in time bound for the energy functional (1.1), in terms of the original phase variable, is not theoretically available in this approach. A related work [68] has been reported for a coupled system of ternary CH flow with incompressible fluid motion. In addition, the scalar auxiliary variable (SAV) approach has also been applied to the ternary model [66, 67], in which a constant-coefficient linear scheme was proposed, and the stability was proved for an SAV-induced energy functional. An extension of the IEQ idea to multi-component phase model, with an arbitrarily high order temporal accuracy, has also been reported in a recent work [45].
In this article, we propose and analyze a uniquely solvable, energy stable numerical scheme for the ternary CH system (1.5)–(1.7), with the stability in terms of the original energy functional (1.4). To assure both the unique solvability and unconditional energy stability, we look for a convex-concave decomposition of the physical energy (1.4). The convexity structures of \(\varphi _1^2 (1 - \varphi _1)^2\), \(\varphi _3^2 (1 - \varphi _3)^2\) and \( (\varphi _1 + \varphi _3)^2 (1 - \varphi _1 - \varphi _3)^2\) are standard, following that for the two-phase CH model. The key difficulty has been associated with the convexity analysis for the mixed product term, namely, \(\varphi _1^2 \varphi _3^2 (1 - \varphi _1 - \varphi _3 )^2\), which turns out to be non-convex, non-concave in the three-phase field \((\varphi _1, \varphi _2, \varphi _3)\). To overcome this well-known difficulty, we observe that the detailed expansion of a convex function \((\varphi _1^2 + \varphi _2^2 + \varphi _3^2)^3\) contains a multiple of the mixed product term, namely, \(6 \varphi _1^2 \varphi _2^2 \varphi _3^2\). Subsequently, we add and subtract a few non-trivial auxiliary terms in the energy functional, so that a convex-concave decomposition for the three-phase energy becomes available. In turn, we derive a numerical scheme which treats the convex terms implicitly and concave terms explicitly, and the unconditional unique solvability and unconditional energy stability follow immediately. To our knowledge, this scheme is the first to preserve both properties at a theoretical level.
As a result of the proposed numerical scheme, a challenging discrete nonlinear system for \((\varphi _1, \varphi _3)\) appears at each time step. We apply an efficient PSD solver, recently proposed and analyzed in [42], to solve the nonlinear system. The main idea is to use a linearized version of the nonlinear operator as a pre-conditioner, or in other words, as a metric for choosing the search direction. Only two constant-coefficient linear equations need to be solved in the preconditioning process, one for \(\varphi _1\), one for \(\varphi _3\), and these two solvers could be efficiently implemented via FFT-based computations. On the other hand, the mixed product term is explicitly treated at each iteration stage, and the convexity of the constructed energy functional assures the geometric convergence of the PSD iteration sequence. In practice, this approach greatly improves the numerical efficiency over Newton-type methods as reported in [42].
In addition, the convergence analysis of any numerical scheme applied to the ternary CH system has been an open problem for a long time. In this article, we perform an optimal rate convergence analysis for the proposed numerical scheme, in the \(\ell ^\infty (0,T; H_N^{-1}) \cap \ell ^2 (0,T; H_N^1)\) norm. The energy stability in turn leads to a uniform in time \(H_N^1\) analysis of the numerical solution. Such an \(H_N^1\) estimate is sufficient to ensure a discrete \(\ell ^8\) bound for the 2-D flow, by making use of discrete Sobolev inequality. For the 3-D flow, a direct estimate is not available any more, while an \(\ell ^8\) bound for the numerical solution could still be obtained with the help of inverse inequality, combined with the discrete \(\ell ^6\) bound (coming from the \(H_N^1\) estimate and the discrete Sobolev inequality) and a standard linear mesh requirement: \(D_1 h \le {\Delta t}\le D_2 h\) with \(D_1,D_2\) positive constants. To our knowledge, it is the first such result in this area.
The convexity analysis technique could also be applied to derive a second order accurate, energy stable scheme. We make use of a modified backward differentiation formula (BDF) approach, instead of the modified Crank-Nicolson approach, for the sake of nonlinear structure. In more details, the second order BDF concept is applied to obtain second order temporal accuracy, while the concave diffusion term is treated by an explicit extrapolation. Such an explicit treatment for the concave part of the chemical potential terms (for \(\varphi _1\), \(\varphi _3\), respectively) ensures the unique solvability of the scheme. And also, an additional second order Douglas-Dupont-type regularization is added (for both \(\varphi _1\) and \(\varphi _3\)), for the sake of energy stability. For simplicity of presentation, we only present the numerical algorithm in this article; the theoretical analysis is more complicated and will be left to future works.
In the spatial discretization, we choose the Fourier pseudo-spectral approximation. The advantage of this method is associated with the fact that all the numerical variables, such as the phase variable and its Laplacian, are evaluated at the regular grid points; no staggered finite difference mesh points are needed in the numerical implementation. And also, the summation by parts formulae enable one to perform the theoretical analysis for the fully discrete scheme, including the unique solvability, energy stability, and optimal rate convergence estimates.
This article is organized as follows. In Sect. 2, we provide a convexity analysis for the nonlinear energy functional. The numerical schemes are formulated in Sect. 3, where the unique solvability and energy stability are established. An optimal rate convergence analysis for the first order accurate scheme is presented in Sect. 4. Moreover, the preconditioned steepest descent solver is formulated in Sect. 5. Some numerical results are presented in Sect. 6, and concluding remarks are made in Sect. 7.
2 Convexity Analysis for the Physical Energy
As mentioned in the introduction section, the following four nonlinear energy functionals are non-convex, non-concave in terms of \(\varvec{\varphi } = (\varphi _1, \varphi _2, \varphi _3)\):
where
The treatment of \(E_{nl,(i)}\) for \(1 \le i \le 3\) follows similar ideas as in the two-phase CH model, since only one phase variable is involved in each term. The following analysis is needed in the numerical design.
Lemma 1
For each \(1 \le i \le 3\), \(E_{nl,(i)}\) has the following convex-concave decomposition:
Moreover, for the nonlinear functional \(E_{nl,(4)}\), in which a triple product is involved, the following estimate is valid. Its proof is based on the confirmation of the non-negative definite property of the corresponding Hessian matrix (in terms of \(\varvec{\varphi } = (\varphi _1, \varphi _2, \varphi _3)\)); the technical details are left to interested readers.
Lemma 2
The energy functional \(E_{nl,(4)}\) has a convex-concave decomposition: \(E_{nl,(4)}= H_{nl,(4)} + H_{nl,(4)}^*\), in which \(H_{nl,(4)}\) is convex, \(H_{nl,(4)}^*\) is concave with respect to \(\varvec{\varphi }\):
where
As a result, if we rewrite \(H_{nl,(4)}\) as a functional of \(\varphi _1\) and \(\varphi _3\), by making use of \(\varphi _2 = 1 - \varphi _1 - \varphi _3\), it is also convex in terms of \((\varphi _1, \varphi _3)\):
Therefore, the following convex-concave decomposition is available for the partial spreading case, i.e., \(E(\varphi _{1},\varphi _{3}) = E_1 (\varphi _{1},\varphi _{3}) - E_2 (\varphi _{1},\varphi _{3})\), with
in which \(\varphi _2=1-\varphi _1-\varphi _3\) has been used.
Similarly, for the total spreading case, the convex-concave decomposition becomes
3 The Fully Discrete Numerical Schemes
Based on the convex-concave decomposition (2.6)–(2.7) for the physical energy \(E(\varphi _1, \varphi _3)\), the convex splitting method could be derived; an extension to a modified BDF temporal discretization will also be discussed. On the other hand, the spatial discretization is carried out with Fourier collocation spectral method [11, 46, 54]. The standard Sobolev space notation follows from [1].
Let N be a positive integer and \(\Omega = (0,L)^d\). We focus on the difficult case \(d=3\) which can be trivially modified for \(d=2\). Divide the space uniformly with \(N^3\) grid points \((x_i,y_j,z_k)\), where \(N=2K+1\), \(x_i=ih,y_j=jh,z_k=kh, h=L/N, 0\le i,j,k \le 2K\). For a fixed \(T\in {\mathbb {R}}^{+}\) and \(N_t \in {\mathbb {N}}^{+}\), we denote time step size by \({\Delta t}= T/N_t\). In this paper, we denote C a generic positive constant independent of \(h,{\Delta t}\) and \(\varepsilon \). Let \({\mathcal {G}}\) be the periodic grid function space. We assume the discrete Fourier expansion of a periodic grid function f given by
where \({\hat{f}}_{\ell , m, n}^{N} = h^3\sum _{i,j,k=0}^{2K} f_{i,j,k}\exp (-\frac{2\pi \mathrm {i} }{L}(\ell x_i + m y_j + n z_k))\) with \(\mathrm {i}=\sqrt{-1}\) represents the discrete Fourier coefficients. The spectral derivatives of f are formulated as
and \({\mathcal {D}}_{y}, {\mathcal {D}}^2_{y}, {\mathcal {D}}_{z}, {\mathcal {D}}^2_{z}\) can be defined in the same manner. Furthermore, the discrete Laplacian, gradient and divergence operators become
at the point-wise level. Given \(f\in {\mathcal {G}}\), its discrete \(\ell ^p\) norm is defined as
For \(p=2\), we can also define the discrete \(\ell ^2\) inner product:
The summation-by-parts formulas have been discussed in [25, 28, 47, 48]:
In the following analysis, the discrete \(H^{-1}\) norm will be needed. We introduce a discrete operator \((-\Delta _{N})^{-p}(p>0)\) for mean-free grid function \(f\in \mathring{{\mathcal {G}}} :=\{u\in {\mathcal {G}} \ | \ (u,1)_2 = 0 \}\):
In turn, the discrete \(H^{-1}\) norm and inner product are defined as
Recall the spectral interpolation operator \({\mathcal {I}}_N\) onto \({\mathcal {P}}_N\) and Fourier projection operator \(\pi _N: L^2(\Omega )\rightarrow {\mathcal {P}}_N\) where \({\mathcal {P}}_N\) represents the space of trigonometric polynomials of degree at most N:
with \({\tilde{f}}_{\ell ,m,n} = \int _{\Omega } f(x,y,z) \exp \left( \frac{-2\pi \mathrm {i}}{L}(\ell x + my+nz) \right) \text{ d }{} \mathbf{x} \) the continuous Fourier coefficients. Some relevant properties of the two operators are recalled.
Lemma 3
[48, Lemma 1] Let \(f\in {\mathcal {P}}_{k N}\) in d-dimension space, we obtain
Lemma 4
[16, Theorem 1.2] Suppose f and \(\partial ^{\alpha }f(|\alpha | \le m)\) are continuous and periodic, then
Lemma 5
[16, Theorem 1.1] Let \(f\in H^{m}\) and be periodic on \(\Omega \), then
To facilitate the analysis in later sections, we introduce a discrete average: \(\overline{f}:= \frac{1}{| \Omega | } ( f , \mathbf{1} )_2\), for any \(f \in {\mathcal {G}}\). Furthermore, a discrete version of the physical energy \(E (\varphi _1, \varphi _3)\) (given by (1.4)) is defined as
In addition, we also need some auxiliary techniques to derive the error analysis; the proof of Lemma 6 will be provided in Appendix A.
Lemma 6
We have
Lemma 7
( [30]) Let \(f\in \mathring{{\mathcal {G}}}\), we have
For simplicity of presentation, we focus on the constant mobility case, \(M_0(\varvec{\varphi }) \equiv M_0\), for the rest of this article, for both the theoretical analysis and numerical simulations. An extension to a general mobility \(M_0(\varvec{\varphi })\) could be carefully carried out, and the details may be reported in a future paper.
3.1 The First Order Scheme
3.1.1 The Convex Splitting for the Partial Spreading
Based on the decomposition (2.6)–(2.7) for the physical energy \(E(\varphi _1, \varphi _3)\), our first order convex splitting scheme for the partial spreading system (1.7) is formulated as: find \(\varphi _{i}^{k+1} \in {\mathcal {G}} \ (i=1,3)\) for \(0\le k \le N_t\) such that
with
in which the notation of \(\varphi _2 = 1 - \varphi _1 - \varphi _3\) is used. In particular, we observe that, all the diffusion coefficients are positive: \(\Sigma _i > 0\), \(1 \le i \le 3\). Thus, all of the surface diffusion energy contributions are convex. This fact leads to an implicit treatment for all the surface diffusion terms in the numerical algorithm (3.22)–(3.24).
Theorem 8
The proposed numerical scheme (3.22)–(3.24) is uniquely solvable and unconditionally energy stable: \(E_h (\varphi _1^{k+1},\varphi _3^{k+1}) \le E_h (\varphi _1^k,\varphi _3^k)\). In addition, we have a uniform in time \(H_N^1\) bound for the numerical solution:
with \(C_0^*\) only dependent on \(\Sigma _i\) (\(1 \le i \le 3\)), \(\Lambda \) and the initial data, independent on \({\Delta t}\), h and the final time.
Proof
The existence and unique solvability follows from standard convexity analysis of \(E_1 (\varphi _1,\varphi _3)\) and \(E_2 (\varphi _1,\varphi _3)\), given by (2.6) and (2.7). For the energy decay property, taking discrete \(\ell ^2\) inner-product with the two terms in (3.22) by \(\mu _1^{k+1}\) and \(\mu _{3}^{k+1}\), respectively, we get
In turn, an application of induction argument implies that
Meanwhile, by the expansion of the discrete energy given by (3.15), we see that
On the other hand, the mass conservative property of the numerical solution (3.22) reveals that
In turn, an application of the discrete Poincaré inequality (3.17) (stated in Lemma 6) leads to
for any \(k \ge 0\), with the estimate (3.28) recalled. Therefore, a combination of (3.28) and (3.30)–(3.31) yields the desired \(H_h^1\) estimate (3.25), with \(C_0^*:= C (|\beta _1^{(0)} | + | \beta _3^{(0)} | + ( \frac{8 C_0}{3 \varepsilon \Sigma _0})^{1/2})\). \(\square \)
3.1.2 The Convex Splitting for Total Spreading
When \(\Sigma _2<0\), a total spreading ternary CH system is presented. The first order convex splitting scheme for system (1.7) becomes: find \(\varphi _{i}^{k+1} \in {\mathcal {G}} \ (i=1,3)\) for \(0\le k \le N_t\) such that
where
Again, the identity \(\varphi _2 = 1 - \varphi _1 - \varphi _3\) has to be repeatedly used. In the total spreading case, since the diffusion coefficient \(\Sigma _2\) is negative, \(\Sigma _2 <0\), the surface diffusion energy for the component \(\varphi _2\) is concave. As a result, we treat the corresponding diffusion terms explicitly to ensure the energy stability. This is the primary difference between this numerical scheme and the one for the partial spreading case, as given by (3.22)–(3.24).
Similar to the partial spreading case, the unique solvability and energy stability could be established in a similar manner; the proof is skipped for the sake of brevity, and the details are left to interested readers.
Theorem 9
The proposed numerical scheme (3.32)–(3.34) is uniquely solvable and unconditionally energy stable: \(E_h (\varphi _1^{k+1},\varphi _3^{k+1}) \le E_h (\varphi _1^k,\varphi _3^k)\). And also, a uniform in time \(H_N^1\) bound (3.25) is available for the numerical solution.
Remark 10
The convex splitting framework, initiated by Eyre’s pioneering work [40], has been successfully applied to various gradient models, such as the phase field crystal (PFC) equation and the modified version [8, 9, 34, 55, 60, 63]; epitaxial thin film growth models [18, 20, 22, 27, 56, 58, 59]; non-local gradient model [49,50,51]; phase field model coupled with fluid flow [19, 21, 31, 32, 44, 57, 61]; functionalized CH and Willmore model [24, 41]; phase field with Flory-Huggins energy potential [23, 35], etc. In this approach, the unique solvability and energy stability could be established via a variational framework.
Meanwhile, we observe that an application of the convex splitting idea to the ternary CH system (1.5)–(1.7) is highly challenging, due to the fact that the mixed product term \(\varphi _1^2 \varphi _2^2 \varphi _3^2\) is non-convex, non-concave in the three-phase field. In addition, the multi-component, multi-chemical potential feature makes a theoretical analysis even more complicated. To overcome this well-known difficulty, we include such a mixed product term into a convex multi-variable function \(( \varphi _1^2 + \varphi _2^2 + \varphi _3^2 )^3\), and subtract the additional terms, which turn out to be also convex in the three-phase field. In turn, the unique solvability and energy stability could be proved via a convexity analysis in the three-phase field.
3.2 The Second Order Scheme
3.2.1 A Modified BDF2 Method for the Partial Spreading Case
An energy stable BDF2 scheme for system (1.7) could be formulated as: find \(\varphi _{i}^{k+1} \in {\mathcal {G}} \ (i=1,3)\) for \(1\le k \le N_t\) such that
where
where \(A_1\) is a positive constant and the notation of \(\varphi _2 = 1 - \varphi _1 - \varphi _3\) has been used.
3.2.2 A Modified BDF2 Method for the Total Spreading Case
When \(\Sigma _2<0\), a total spreading ternary CH system has to be considered. The corresponding energy stable BDF2 scheme for system (1.7) becomes: find \(\varphi _{i}^{k+1} \in {\mathcal {G}} \ (i=1,3)\) for \(1\le k \le N_t\) such that
where
Similar to the first order schemes, since all the diffusion coefficients are positive in the partial spreading case, an implicit treatment has been taken for all the surface diffusion terms in the corresponding numerical algorithm (3.35)–(3.37). In comparison, since \(\Sigma _2 <0\) in the total spreading case, the diffusion terms associated with \(\varphi _2\) have to be updated explicitly to ensure the energy stability, which turns out to be the primary difference between (3.35)–(3.37) and (3.38)–(3.40).
Remark 11
There have been various second order accurate, energy stable schemes reported for the standard two-phase CH model, based on either the Crank-Nicolson [33, 52, 53] or the modified BDF2 approach [26, 64]. For the ternary CH system with a mixed product, we believe that the modified BDF2 approach would bring more convenience in the theoretical justification of both the unique solvability and energy stability.
The unique solvability for the proposed second order schemes, either (3.35)–(3.37) or (3.38)–(3.40), follows exactly the same analysis for the first order schemes. The energy stability is more involved, and the details will be left to future investigations.
Remark 12
The physical systems comprised of a phase field model coupled with a fluid motion model, such as the Cahn-Hilliard-Hele-Shaw system and the Cahn-Hilliard-Navier-Stokes system, have attracted much attention in the scientific computing community, due to their potential applications. There have been a great deal of numerical works in this area, some of which address stability and convergence analysis [21, 31, 32, 57], et cetera. Meanwhile, most of these existing works have been focused on the two-phase flows. For the ternary CH model coupled with various fluid motion, the physical system is expected to be well-posed, and the total energy (composed of the phase field energy and the kinematic energy) dissipation law is also expected. The idea of convex-concave decomposition for the phase field energy and the corresponding numerical treatment for the nonlinear convection part will lead to a uniquely solvable, energy stable numerical scheme for the whole physical system, and such an energy stability is in terms of the energy functional in the original phase variables. No essential difficulty is expected, while the technical details are very involved, and will be left to the future works.
4 Convergence Analysis and Error Estimate
In this section, we provide the convergence analysis and error estimate of the first-order energy stable scheme. For simplicity of presentation, we only focus on the algorithm (3.22)–(3.24) for the partial spreading case; the one for the total spreading could be analyzed in a similar manner. We denote \(\varphi _{e,k}(t)\) the exact solution of (1.7), \(1 \le k \le 3\). With sufficiently regular initial data, we could assume that the exact solution has regularity of class \({\mathcal {R}}\):
Define \(\varphi _{N,k} (\, \cdot \, ,t) := \pi _N \varphi _{e,k} (\, \cdot \, ,t)\), \(1 \le k \le 3\), the (spatial) Fourier projection of the exact solution into \(\mathcal{B}^K\), the space of trigonometric polynomials of degree to and including K (with \(N=2K +1\)). The following projection approximation is standard: if \( \varphi _{e,k} \in L^\infty (0,T;H^\ell _\mathrm{per}(\Omega ))\), for some \(\ell \in {\mathbb {N}}\),
By \(\varphi _{N,j}^n\), \(\varphi _{e,j}^n\) we denote \(\varphi _{N,j} (\, \cdot \, , t_n)\) and \(\varphi _{e,j} (\, \cdot \, , t_n)\), respectively, with \(t_n = n {\Delta t}\). Since \(\varphi _{N,j} \in \mathcal{B}^K\), the mass conservative property is available at the discrete level:
On the other hand, the solution of (3.22)–(3.24) is also mass conservative at the discrete level:
As indicated before, we use the mass conservative projection for the initial data: \(\varphi _j^0 = {\mathcal {P}}_h \varphi _{N,j} (\, \cdot \, , t=0)\) where \({\mathcal {P}}_h:\mathcal{B}^K \rightarrow {\mathcal {G}}\) represents taking value on grid point, that is
The error grid function is defined as
Therefore, it follows that \(\overline{{\hat{e}}_{\varphi _j}^n} =0\), for any \(n \in \left\{ 0 ,1 , 2, 3, \cdots \right\} \), \(j=1, 3\), so that the discrete norm \(\left\| \, \cdot \, \right\| _{-1,N}\) is well defined for the error grid function.
The following theorem is the main result of this section.
Theorem 13
Given initial data \(\varphi _1, \varphi _3 (\, \cdot \, ,t=0) \in C^6_\mathrm{per}(\Omega )\), suppose the exact solution for ternary CH flow (1.7) is of regularity class \({\mathcal {R}}\). Then, provided \({\Delta t}\) and h are sufficiently small, and under the linear refinement requirement \(D_1 h \le {\Delta t}\le D_2 h\), we have
for all positive integers n, such that \(t_n=n{\Delta t}\le T\), where \(C>0\) is independent of n, \({\Delta t}\), and h.
The truncation error analysis for the numerical discretization can be obtained by using straightforward Taylor expansions, as well as the estimate (4.2) for the projection solution:
where
With repeated application of the consistency estimates in Lemmas 3-5, we obtain
Notice that we have introduced \(\varphi _{N,2} := 1 - \varphi _{N,1} - \varphi _{N,3}\). In addition, we denote \({\hat{e}}_{\varphi _2}^n := {\mathcal {P}}_h \varphi _{N,2}^n - \varphi _2^n\), and it is clear that \({\hat{e}}_{\varphi _2}^n = - {\hat{e}}_{\varphi _1}^n - {\hat{e}}_{\varphi _3}^n\).
Before the detailed convergence analysis, the following two preliminary results are needed, which provide an \(\ell ^8\) bound of the numerical solution.
Proposition 14
For numerical scheme (3.22)–(3.24) applied to the 2-D ternary CH flow (1.7), the following \(\ell ^8\) bound is always available:
with \({\tilde{C}}_1\) independent of \({\Delta t}\), h and the final time.
Proof
A combination of the discrete Sobolev inequality (3.19) (stated in Lemma 6) and the uniform in time \(H_N^1\) estimate (3.25) (as derived in Theorem 8) yields the desired \(\ell ^8\) bound (4.12), with \({\tilde{C}}_1 := C_5 C_0^*\). \(\square \)
Proposition 15
Consider the numerical solution (3.22)–(3.24) for the 3-D ternary CH flow (1.7). Under the following a-priori assumption for the numerical error function at the previous time step:
as well as the linear refinement requirement \(D_1 h \le {\Delta t}\le D_2 h\), an \(\ell ^8\) bound becomes available:
with \({\tilde{C}}_2\) independent of \({\Delta t}\), h and the final time.
Proof
Since \(\overline{{\hat{e}}_{\varphi _1}^n} =0\), we apply the discrete Sobolev inequality (3.18) in Lemma 6 and obtain
Subsequently, an application of inverse inequality (3.16) implies that
provided that \(h \le ( C C_4 ( D_2^{1/4} + 1) )^{-8}\). Also notice that we have made use of the requirement \({\Delta t}\le D_2 h\) in the derivation. As a consequence, the following \(\ell ^8\) estimate for the numerical solution \(\varphi _1^n\) is available, with the help of triangle inequality:
The corresponding estimate for \(\Vert \varphi _3^n \Vert _8\) could be derived in the same fashion. This completes the proof of Proposition 15.
Now we proceed into the proof of Theorem 13. \(\square \)
Proof
Subtracting the numerical solution (3.22)–(3.24) from the truncation error estimate (4.8)–(4.10) leads to
where
Taking a discrete \(\ell ^2\) inner product with the error equation (4.18) by \(2 (-\Delta _N)^{-1} {\hat{e}}_{\varphi _1}^{n+1}\), \(2 (-\Delta _N)^{-1} {\hat{e}}_{\varphi _3}^{n+1}\), respectively, we get
in which we have repeatedly applied the summation by parts formula
The derivation of the following identities are based on summation by parts formulas:
For the term \(( \mathcal{R}_{1,1} , {\hat{e}}_{\varphi _1}^{n+1} )_2\), it is observed that \(( \varphi _{N,1}^{n+1} - \frac{1}{2} )^3\) is the gradient of a convex function \(\frac{1}{4} ( \varphi _{N,1}^{n+1}- \frac{1}{2} )^4\). This in turn indicates that
Similarly, we also have
Moreover, we observe that \(( \varphi _1^{n+1} - \varphi _2^{n+1} ) \left( (\varphi _1^{n+1}) ^2 + (\varphi _2^{n+1})^2 + (\varphi _3^{n+1})^2 \right) ^2\) and \(( \varphi _3^{n+1} - \varphi _2^{n+1} ) \cdot \)\( \left( (\varphi _1^{n+1}) ^2 + (\varphi _2^{n+1})^2 + (\varphi _3^{n+1})^2 \right) ^2\) are the gradient of the following convex function, in terms of \(\varphi _1^{n+1}\), \(\varphi _3^{n+1}\), respectively:
with \(\varphi _2^{n+1} = 1 - \varphi _1^{n+1} - \varphi _3^{n+1}\). Therefore, the sum of the following two discrete inner products turns out to be non-negative:
On the right hand side of (4.37), the two terms associated with the truncation error could be controlled by the Cauchy inequality:
In addition, the Cauchy inequality could be applied to bound the linear error growth terms on the right hand side:
For the nonlinear error growth on the right hand side, we focus on \(\mathcal{R}_{1,4}\); the other terms could be analyzed in a similar fashion. We begin with the following decomposition:
If we make the a-priori assumption (4.13) for the numerical error function at time step \(t^n\), an application of (4.14) of Proposition 15 reveals that
In turn, an application of discrete Hölder inequality leads to
with \({\tilde{C}}_3:= C ( (C^*)^4 + {\tilde{C}}_2^4 +1 ) \). A similar estimate could be derived for the other error term contained in \(\mathcal{R}_{1,4}\):
Then we arrive at
The other nonlinear error growth terms on the right hand side of (4.37) could be analyzed in a similar manner; the details are skipped for the sake of brevity.
Therefore, a substitution of (4.38)–(4.43), (4.44), (4.45)–(4.48), (4.53) and (4.54)–(4.56) into (4.37) results in
To facilitate the calculation below, we denote \({\tilde{C}}_4 = 6 \Sigma _1 + 12 \Sigma _2\), \({\tilde{C}}_5 = 6 \Sigma _3 + 12 \Sigma _2\), \({\tilde{C}}_6 = C_8 {\tilde{C}}_3 \Lambda \). Furthermore, with an application of (3.20), (3.21) in Lemma 7 (as cited in [30]), we have the following estimates:
Notice that the Young’s inequality has been repeatedly applied in the derivation. Then we arrive at
Consequently, an application of discrete Gronwall inequality yields the desired error estimate (4.7):
in which the fact that \(\Vert {\mathcal {R}}_{N,1} \Vert _{-1,N}, \Vert {\mathcal {R}}_{N,1} \Vert _{-1,N} \le C ({\Delta t}+ h^m)\) has been applied.
Finally, we have to recover the a-priori assumption (4.13) at the next time step \(t^{n+1}\). The convergence estimate (4.67) implies that
provided that \({\Delta t}\ge h^{2m -1}\). In addition, it is observed that the a-priori assumption (4.13) is valid at the next time step \(t^{n+1}\) under the following constraint for \({\Delta t}\) and h:
This completes the proof of Theorem 13. \(\square \)
Remark 16
Because of the nonlinear decomposition (4.49), which comes from a mixed product energy term \(\varphi _1^2 \varphi _2^2 \varphi _3^2\), an \(\ell ^8\) bound for the numerical solution is necessary for the nonlinear error estimate, as derived in (4.51). In comparison, for the two-phase CH flow, only a fourth degree polynomial appears in the double-well potential. In turn, only an \(\ell ^6\) bound for the numerical solution is needed for the convergence analysis of the two-phase flow, as reported in a related work [64].
For the 2-D ternary CH flow (1.7), an application of Proposition 14 gives a uniform in time \(\ell ^8\) bound for the numerical solution, so that the convergence analysis of (3.22)–(3.24) for 2-D ternary CH flow is unconditional; no linear refinement requirement is needed in the 2-D case.
Remark 17
In the proof of Theorem 13, we only focus on the convergence analysis for the partial spreading case (\(\Sigma _j >0\), \(1 \le j \le 3\)), for simplicity of presentation. In the total spreading case (\(\Sigma _1 >0\), \(\Sigma _3 >0\), \(\Sigma _2 <0\)), the well-posedness condition (1.2) assures the desired inequality (1.3) needed in the error estimates for the surface diffusion terms. In combination with the analysis for the nonlinear parts, which could be handled in a similar fashion as in the proof for the partial spreading case, we are able to obtain the convergence result. The technical details are skipped for the sake of brevity.
5 The Preconditioned Steepest Descent Solver
In this section, we describe a preconditioned steepest descent (PSD) algorithm for the proposed numerical schemes (3.22), (3.32), (3.35) and (3.38), based on the theoretical framework in [42, 43]. We take the first order schemes (3.22), (3.32) for instance and others likewise.
5.1 PSD for the First Order Scheme of Partial Spreading Case
The numerical scheme (3.22) at time \(k+1\) can be expressed as
with
Note that (5.1) can be recast as a minimization problem with energy functional that involves the discrete \(H^{-1}\) norm. In particular, we see that
Now we use a linearized version of the nonlinear operator as a preconditioner:
which is used to find an appropriate search direction. Given the current iterate \((\varphi _1^{k+1,n},\varphi _3^{k+1,n})\), the search direction can be computed by solving the equation \(\mathcal {L}(d_1^n,d_3^n) = (f_1 - \mathcal {N}_1, f_3 - \mathcal {N}_3)^T\). In this way, the search directions \(d_1,\ d_3\) are also mean-free according to the periodic boundary condition. With the current iterate and search direction on hand, the next iteration is updated as
where \(\alpha _n\in {\mathbb {R}}\) satisfies
5.2 PSD for the First Order Scheme of Total Spreading Case
The numerical scheme (3.32) at time \(k+1\) can be expressed as
with
Note that (5.5) can be recast as a minimization problem with energy functional that involves the discrete \(H^{-1}\) norm. In particular, we have
The linearized operator becomes
Given the current iterate \((\varphi _1^{k+1,n},\varphi _3^{k+1,n})\), the search direction can be computed by solving the equation \(\widetilde{\mathcal {L}}(d_1^n,d_3^n) = (\widetilde{f}_1 - \widetilde{\mathcal {N}}_1, \widetilde{f}_3 - \widetilde{\mathcal {N}}_3)^T\). With the current iteration and search direction on hand, the next iterate is updated as
where \(\alpha _n\in {\mathbb {R}}\) satisfies
6 Numerical Results
In this section, we provide some numerical results for the numerical method proposed in the previous sections and make some comparisons with pure BDF schemes. For brevity, we denote the first-order, second-order convex-concave schemes by CC1 and CC2 respectively, the implicit-Euler by BDF1 and the second-order implicit backward differential formula by BDF2. Some numerical examples have been described in [13]. In the presented numerical experiments, the approximate solutions are visualized through the isolines of the function:
The stability and convergence estimates presented in the previous sections are valid for both the 2-D and 3-D models. In this section, we focus on the numerical simulation of the 2-D examples, since the 2-D results will be sufficient to illustrate the complicated structures of the ternary flow. Because the numerical ideas are independent of the dimension, as demonstrated in the earlier theoretical analysis, an extension of these numerical implementations to the 3-D ternary flow is expected to be standard, though they require sophisticated high-performance computing (HPC) techniques.
6.1 Three-Phase: Partial Spreading
6.1.1 Convergence Test
For the partial spreading case, the coefficients \(\Sigma _i\) are positive, thus the potential \(F_0 = \sum _{i=1}^{3}\frac{\Sigma _i}{2}\varphi _i^2(1-\varphi _i)^2\) is bounded by zero from below, then we can choose \(\Lambda =0\). Some other parameters are given by
and the domain \(\Omega =[-X/2,X/2]^2\) is divided uniformly with step size \(h = X/128\). An artificial term on the right hand side has to be added to make the exact solution satisfies the equations:
First we perform the convergence test at the final time \(T=0.5\). The temporal convergence rates in the discrete \(\ell ^2\) norm (i.e., \(\Vert \varvec{\varphi }(\cdot ,T)-\varvec{\varphi }_N^{\Delta t,h}\Vert \)) are displayed in Tables 1, 2, for the first and second order numerical schemes, respectively. Both the CC schemes and pure BDF schemes are accurate.
6.1.2 Energy Decay
In the energy decay test, the same parameters are used, except that we let \(\varepsilon =0.01\), and the domain is taken as \(\Omega =[-0.3,0.3]\times [-0.25,0.25]\). Besides, the artificial terms are removed and we set the initial data \(\varvec{\varphi }^{0}\) as
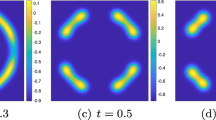
The energy decay plots are presented in Fig. 1, computed by the first order scheme (3.22)–(3.24) and the second order BDF one (3.35)–(3.37). It is believed that the dotted line, which stands for the energy plot computed by the second order scheme, is more accurate than the solid line, the one by the first order scheme. This fact is verified by both the formal Taylor expansion and the numerical comparison with the results computed by finer time step sizes. In addition, the evolution of the interface position is observed through the isolines of the transformed variables (6.1) and the corresponding results are displayed in Fig. 2. Also, we separately depict the phase states of the three order parameters at four different times in Fig. 3.
6.2 Three-Phase: Total Spreading
6.2.1 Convergence Test
For the total spreading case, the coefficients \(\Sigma _i\) can be negative, thus the potential \(F_0 = \sum _{i=1}^{3}\frac{\Sigma _i}{2}\varphi _i^2(1-\varphi _i)^2\) could be unbounded, while there exists \(\Lambda _0>0\) such that for all \(\Lambda \ge \Lambda _0\) the potential F is non negative, and we can choose \(\Lambda =7\). Some other parameters are given by
and the domain \(\Omega =[-X/2,X/2]^2\) is divided uniformly with step size \(h = X/128\). In this case, the following exact solution is chosen, and the corresponding artificial terms have to be added on the right hand side
Similarly, the convergence test is performed at the final time \(T=0.5\). The temporal convergence rates in the discrete \(\ell ^2\) norm are displayed in Tables 3, 4, for the first and second order schemes, respectively. The errors of pure BDF scheme are lower than that of CC scheme by one or two orders of magnitude. This is due to the convex-concave decomposition for the mixed product term in which some additional explicit terms are involved, resulting in certain numerical errors. Nevertheless, the convergence performances of CC scheme are still significant.
6.2.2 Energy Decay
In the energy decay study, the same parameters are used, except that we take \(\varepsilon =0.01\), and the domain is given by \(\Omega =[-0.3,0.3]\times [-0.25,0.25]\). Again, the artificial terms are removed, and the following initial data \(\varvec{\varphi }^0\) are taken:
Similarly, the energy decay plots are presented in Fig. 4, computed by the first order scheme (3.32)–(3.34) (corresponding to the dotted line) and the second order BDF one (3.38)–(3.40) (corresponding to the solid line). Again, it is believed that the dotted line is more accurate than the solid line, which could be verified by both the formal Taylor expansion and the numerical comparison with the results computed by finer time step sizes. Moreover, the snapshot evolution of the interface (in terms of the isolines of the functions (6.1)) is displayed in Fig. 5 and the phase states of the three order parameters at different times are shown in Fig. 6.
7 Concluding Remarks
In this article, we propose and analyze a uniquely solvable and unconditionally energy stable numerical scheme for the ternary CH system. The total mass constraint leads to effective equations for two components, and the physical energy could be appropriately rewritten. However the nonlinear energy functional in the mixed product form, which turns out to be non-convex, non-concave in the three-phase space, turns out to be highly challenging. To overcome this difficulty, we make a key observation that, such a mixed product term is included in \((\varphi _1^2 + \varphi _2^2 + \varphi _3^2)^3\), a convex function in the three-phase space. As a consequence, a convex-concave decomposition of the physical energy in the ternary system becomes available, and the numerical scheme could be appropriately constructed. Both the unique solvability and the unconditional energy stability of the proposed numerical scheme are theoretically proved. With a careful estimate of a discrete \(\ell ^8\) bound for the numerical solution, an optimal rate convergence analysis is derived for the proposed numerical scheme, which is the first such result in this area. The implicit terms in the resulting scheme are highly nonlinear, while they are the gradient of certain convex functional in the three-phase space; we present detailed descriptions of an efficient preconditioned steepest descent (PSD) algorithm to solve the corresponding nonlinear systems, with Fourier pseudo-spectral spatial approximation. A second order accurate, modified BDF scheme is also discussed in this article. A few numerical results have also been presented in this work, including the convergence test, simulation results for both partial and total spreading models.
References
Adams, R., Fournier, J.F.: Sobolev Spaces, vol. 140. Elsevier, New York (2003)
Allen, S.M., Cahn, J.W.: A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 27, 1085 (1979)
Barrett, J., Blowey, J.: Finite element approximation of a model for phase separation of a multi-component alloy with non-smooth free energy. Numer. Math. 77, 1–34 (1997)
Barrett, J., Blowey, J.: Finite element approximation of a model for phase separation of a multi-component alloy with a concentration-dependent mobility matrix. IMA J. Numer. Anal. 18, 287–328 (1998)
Barrett, J., Blowey, J.: An improved error bound for a finite element approximation of a model for phase separation of a multi-component alloy. IMA J. Numer. Anal. 19, 147–168 (1999)
Barrett, J., Blowey, J.: An improved error bound for a finite element approximation of a model for phase separation of a multi-component alloy with a concentration dependent mobility matrix. Numer. Math. 88, 255–297 (2001)
Barrett, J., Blowey, J., Garcke, H.: On fully practical finite element approximations of degenerate Cahn-Hilliard systems. M2AN Math. Model. Numer. Anal. 35, 286–318 (2001)
Baskaran, A., Hu, Z., Lowengrub, J., Wang, C., Wise, S.M., Zhou, P.: Energy stable and efficient finite-difference nonlinear multigrid schemes for the modified phase field crystal equation. J. Comput. Phys. 250, 270–292 (2013)
Baskaran, A., Lowengrub, J., Wang, C., Wise, S.: Convergence analysis of a second order convex splitting scheme for the modified phase field crystal equation. SIAM J. Numer. Anal. 51, 2851–2873 (2013)
Blowey, J.F., Copetti, M.I.M., Elliott, C.M.: Numerical analysis of a model for phase separation of a multi-component alloy. IMA J. Numer. Anal. 16, 111–139 (1996)
Boyd, J.: Chebyshev and Fourier Spectral Methods. Dover, New York (2001)
Boyer, F., Lapuerta, C.: Study of a three-component Cahn-Hilliard flow model. M2AN Math. Model. Numer. Anal 40, 653–687 (2006)
Boyer, F., Minjeaud, S.: Numerical schemes for a three component Cahn-Hilliard model. M2AN Math. Model. Numer. Anal 45(4), 697–738 (2011)
Cahn, J.W.: On spinodal decomposition. Acta Metall. 9, 795 (1961)
Cahn, J.W., Hilliard, J.E.: Free energy of a nonuniform system. I. interfacial free energy. J. Chem. Phys 28, 258–267 (1958)
Canuto, C., Quarteroni, A.: Approximation results for orthogonal polynomials in sobolev spaces. Math. Comput. 38(157), 67–86 (1982)
Chen, C., Yang, X.: Fast, provably unconditionally energy stable, and second-order accurate algorithms for the anisotropic Cahn-Hilliard model. Comput. Methods Appl. Mech. Eng. 351, 35–59 (2019)
Chen, W., Conde, S., Wang, C., Wang, X., Wise, S.M.: A linear energy stable scheme for a thin film model without slope selection. J. Sci. Comput. 52(3), 546–562 (2012)
Chen, W., Feng, W., Liu, Y., Wang, C., Wise, S.M.: A second order energy stable scheme for the Cahn-Hilliard-Hele-Shaw equation. Discrete Contin. Dyn. Syst. Ser. B 24(1), 149–182 (2019)
Chen, W., Li, W., Luo, Z., Wang, C., Wang, X.: A stabilized second order ETD multistep method for thin film growth model without slope selection. Math. Model. Numer. Anal. 54, 727–750 (2020)
Chen, W., Liu, Y., Wang, C., Wise, S.M.: An optimal-rate convergence analysis of a fully discrete finite difference scheme for Cahn-Hilliard-Hele-Shaw equation. Math. Comp. 85, 2231–2257 (2016)
Chen, W., Wang, C., Wang, X., Wise, S.M.: A linear iteration algorithm for a second-order energy stable scheme for a thin film model without slope selection. J. Sci. Comput. 59(3), 574–601 (2014)
Chen, W., Wang,C., Wang, X., Wise, S.M.: Positivity-preserving, energy stable numerical schemes for the Cahn-Hilliard equation with logarithmic potential. J. Comput. Phys.: X, 3:100031 (2019)
Chen, Y., Lowengrub, J.S., Shen, J., Wang, C., Wise, S.M.: Efficient energy stable schemes for isotropic and strongly anisotropic Cahn-Hilliard systems with the Willmore regularization. J. Comput. Phys. 365, 57–73 (2018)
Cheng, K., Feng, W., Gottlieb, S., Wang, C.: A Fourier pseudospectral method for the “Good” Boussinesq equation with second-order temporal accuracy. Numer. Methods Partial Differ. Equ. 31(1), 202–224 (2015)
Cheng, K., Feng, W., Wang, C., Wise, S.M.: An energy stable fourth order finite difference scheme for the Cahn-Hilliard equation. J. Comput. Appl. Math. 362, 574–595 (2019)
Cheng, K., Qiao, Z., Wang, C.: A third order exponential time differencing numerical scheme for no-slope-selection epitaxial thin film model with energy stability. J. Sci. Comput. 81(1), 154–185 (2019)
Cheng, K., Wang, C.: Long time stability of high order multi-step numerical schemes for two-dimensional incompressible Navier-Stokes equations. SIAM J. Numer. Anal. 54, 3123–3144 (2016)
Cheng, K., Wang, C., Wise, S.M.: A weakly nonlinear, energy stable scheme for the strongly anisotropic Cahn-Hilliard equation and its convergence analysis. J. Comput. Phys., Submitted and in review (2019)
Cheng, K., Wang, C., Wise, S.M., Yue, X.: A second-order, weakly energy-stable pseudo-spectral scheme for the Cahn-Hilliard equation and its solution by the homogeneous linear iteration method. J. Sci. Comput. 69(3), 1083–1114 (2016)
Diegel, A., Feng, X., Wise, S.M.: Convergence analysis of an unconditionally stable method for a Cahn-Hilliard-Stokes system of equations. SIAM J. Numer. Anal. 53, 127–152 (2015)
Diegel, A., Wang, C., Wang, X., Wise, S.M.: Convergence analysis and error estimates for a second order accurate finite element method for the Cahn-Hilliard-Navier-Stokes system. Numer. Math. 137, 495–534 (2017)
Diegel, A., Wang, C., Wise, S.M.: Stability and convergence of a second order mixed finite element method for the Cahn-Hilliard equation. IMA J. Numer. Anal. 36, 1867–1897 (2016)
Dong, L., Feng, W., Wang, C., Wise, S.M., Zhang, Z.: Convergence analysis and numerical implementation of a second order numerical scheme for the three-dimensional phase field crystal equation. Comput. Math. Appl. 75(6), 1912–1928 (2018)
Dong, L., Wang, C., Zhang, H., Zhang, Z.: A positivity-preserving, energy stable and convergent numerical scheme for the Cahn-Hilliard equation with a Flory-Huggins-deGennes energy. Commun. Math. Sci. 17, 921–939 (2019)
Elliot, C.M., Stuart, A.M.: The global dynamics of discrete semilinear parabolic equations. SIAM J. Numer. Anal 30, 1622–1663 (1993)
Elliott, C.M., Garcke, H.: Diffusional phase transitions in multicomponent systems with a concentration dependent mobility matrix. Physica D 109, 242–256 (1997)
Elliott, C.M., Luckhaus, S.: A generalized diffusion equation for phase separation of a multi-component mixture with interfacial free energy. IMA Preprint Ser. 887, 242–256 (1991)
Elliott, C.M., Stuart, A.M.: Viscous Cahn-Hilliard equation. II. Anal. J. Differ. Eq. 128, 387–414 (1996)
Eyre, D.: Unconditionally gradient stable time marching the Cahn-Hilliard equation. In: Bullard, J.W., Kalia, R., Stoneham, M., Chen, L.Q. (eds.) Computational and Mathematical Models of Microstructural Evolution, vol. 53, pp. 1686–1712. Materials Research Society, Warrendale (1998)
Feng, W., Guan, Z., Lowengrub, J.S., Wang, C., Wise, S.M., Chen, Y.: A uniquely solvable, energy stable numerical scheme for the functionalized Cahn-Hilliard equation and its convergence analysis. J. Sci. Comput. 76(3), 1938–1967 (2018)
Feng, W., Salgado, A., Wang, C., Wise, S.M.: Preconditioned steepest descent methods for some nonlinear elliptic equations involving p-Laplacian terms. J. Comput. Phys. 334, 45–67 (2017)
Feng, W., Wang, C., Wise, S.M., Zhang, Z.: A second-order energy stable Backward Differentiation Formula method for the epitaxial thin film equation with slope selection. Numer. Methods Partial Differ. Equ. 34(6), 1975–2007 (2018)
Feng, X., Wise, S.M.: Analysis of a fully discrete finite element approximation of a Darcy-Cahn-Hilliard diffuse interface model for the Hele-Shaw flow. SIAM J. Numer. Anal. 50, 1320–1343 (2012)
Gong, Y., Zhao, J., Wang, Q.: Arbitrarily high-order linear energy stable schemes for gradient flow models. J. Comput. Phys., Submitted and in review (2020)
Gottlieb, D., Orszag, S.A.: Numerical Analysis of Spectral Methods. Theory and Applications. SIAM, Philadelphia, PA (1977)
Gottlieb, S., Tone, F., Wang, C., Wang, X., Wirosoetisno, D.: Long time stability of a classical efficient scheme for two dimensional Navier-Stokes equations. SIAM J. Numer. Anal. 50, 126–150 (2012)
Gottlieb, S., Wang, C.: Stability and convergence analysis of fully discrete Fourier collocation spectral method for 3-d viscous Burgers equation. J. Sci. Comput. 53(1), 102–128 (2012)
Guan, Z., Lowengrub, J.S., Wang, C.: Convergence analysis for second order accurate schemes for the periodic nonlocal Allen-Cahn and Cahn-Hilliard equations. Math. Methods Appl. Sci. 40(18), 6836–6863 (2017)
Guan, Z., Lowengrub, J.S., Wang, C., Wise, S.M.: Second-order convex splitting schemes for nonlocal Cahn-Hilliard and Allen-Cahn equations. J. Comput. Phys. 277, 48–71 (2014)
Guan, Z., Wang, C., Wise, S.M.: A convergent convex splitting scheme for the periodic nonlocal Cahn-Hilliard equation. Numer. Math. 128, 377–406 (2014)
Guo, J., Wang, C., Wise, S.M., Yue, X.: An \(H^2\) convergence of a second-order convex-splitting, finite difference scheme for the three-dimensional Cahn-Hilliard equation. Commu. Math. Sci. 14, 489–515 (2016)
Han, D., Brylev, A., Yang, X., Tan, Z.: Numerical analysis of second order, fully discrete energy stable schemes for phase field models of two phase incompressible flows. J. Sci. Comput. 70(3), 965–989 (2017)
Hesthaven, J., Gottlieb, S., Gottlieb, D.: Spectral Methods for Time-Dependent Problems. Cambridge University Press, Cambridge (2007)
Hu, Z., Wise, S., Wang, C., Lowengrub, J.: Stable and efficient finite-difference nonlinear-multigrid schemes for the phase-field crystal equation. J. Comput. Phys. 228, 5323–5339 (2009)
Li, W., Chen, W., Wang, C., Yan, Y., He, R.: A second order energy stable linear scheme for a thin film model without slope selection. J. Sci. Comput. 76(3), 1905–1937 (2018)
Liu, Y., Chen, W., Wang, C., Wise, S.M.: Error analysis of a mixed finite element method for a Cahn-Hilliard-Hele-Shaw system. Numer. Math. 135, 679–709 (2017)
Shen, J., Wang, C., Wang, X., Wise, S.M.: Second-order convex splitting schemes for gradient flows with Ehrlich-Schwoebel type energy: Application to thin film epitaxy. SIAM J. Numer. Anal. 50, 105–125 (2012)
Wang, C., Wang, X., Wise, S.M.: Unconditionally stable schemes for equations of thin film epitaxy. Discrete Contin. Dyn. Sys. A 28, 405–423 (2010)
Wang, C., Wise, S.M.: An energy stable and convergent finite-difference scheme for the modified phase field crystal equation. SIAM J. Numer. Anal. 49, 945–969 (2011)
Wise, S.M.: Unconditionally stable finite difference, nonlinear multigrid simulation of the Cahn-Hilliard-Hele-Shaw system of equations. J. Sci. Comput. 44, 38–68 (2010)
Wise, S.M., Kim, J.S., Lowengrub, J.S.: Solving the regularized, strongly anisotropic Chan-Hilliard equation by an adaptive nonlinear multigrid method. J. Comput. Phys. 226, 414–446 (2007)
Wise, S.M., Wang, C., Lowengrub, J.S.: An energy stable and convergent finite-difference scheme for the phase field crystal equation. SIAM J. Numer. Anal. 47, 2269–2288 (2009)
Yan, Y., Chen, W., Wang, C., Wise, S.M.: A second-order energy stable BDF numerical scheme for the Cahn-Hilliard equation. Commun. Comput. Phys. 23, 572–602 (2018)
Yang, X., Zhao, J., Wang, Q., Shen, J.: Numerical approximations for a three-component Cahn-Hilliard phase-field model based on the invariant energy quadratization method. Math. Models Methods Appl. Sci. 27(11), 1993–2030 (2017)
Zhang, J., Yang, X.: Decoupled, non-iterative, and unconditionally energy stable large time stepping method for the three-phase Cahn-Hilliard phase-field model. J. Comput. Phys. 404, 109115 (2020)
Zhang, J., Yang, X.: Unconditionally energy stable large time stepping method for the L2-gradient flow based ternary phase-field model with precise nonlocal volume conservation. Comput. Meth. Appl. Mech. Eng. 361, 112743 (2020)
Zhao, J., Li, H., Wang, Q., Yang, X.: Decoupled energy stable schemes for a phase field model of three-phase incompressible viscous fluid flow. J. Sci. Comput. 70(3), 1367–1389 (2017)
Acknowledgements
This work is supported in part by the Grants NSFC 11671098, 91630309, a 111 Project B08018 (W. Chen), NSF DMS-1418689 (C. Wang), NSF DMS-1715504, NSFC 11871159, Guangdong Key Laboratory 2019B030301001 (X. Wang) and NSF DMS-1719854 (S. Wise). C. Wang also thanks the Key Laboratory of Mathematics for Nonlinear Sciences, Fudan University, for support during his visit.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
A Proof of Lemma 6
A Proof of Lemma 6
To prove the inverse inequality (3.16), we begin with the following observation:
due to the fact that \(\frac{q}{p} \ge 1\). This is equivalent to
In turn, we get
which is exactly (3.16), because of the fact that \(h = \frac{L}{2K+1}\).
For the rest three inequalities, we assume the periodic grid f has the discrete Fourier transformation as given by (3.1). For simplicity of presentation, we also assume that \(L=1\). In addition, we denote its extension to a continuous function as
The following estimates could be derived with the help of the Parseval’s identity; also see the related analysis in [30, 42, 43, 52]:
As a result, the discrete Poincaré inequality (3.17) is a direct consequence of its continuous version:
combined with the identities (A.5)–(A.7).
On the other hand, we recall a key estimate given by Lemma A.2 in an existing work [43]:
In addition, such an analysis could also be extended to the 3-D case
For the 3-D discrete Sobolev inequality (3.18), we begin with the observation that
Subsequently, an application of the 3-D estimate (A.10) results in
in which a continuous Sobolev embedding has been applied in the second step, due to the fact that \(\int _\Omega \, f_{\mathbf{F}} d \mathbf{x} =0\).
Similarly, for the 2-D discrete Sobolev inequality (3.19), we apply the estimate (A.9) and obtain
Again a continuous Sobolev embedding has been applied in the second step, and the last step is based on the identities (A.5), (A.7).
Rights and permissions
About this article
Cite this article
Chen, W., Wang, C., Wang, S. et al. Energy Stable Numerical Schemes for Ternary Cahn-Hilliard System. J Sci Comput 84, 27 (2020). https://doi.org/10.1007/s10915-020-01276-z
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-020-01276-z
Keywords
- Ternary Cahn-Hilliard system
- Convexity analysis
- Energy stability
- Optimal rate convergence analysis
- Fourier pseudo-spectral approximation
- Partial and total spreading