An a Posteriori Error Estimate for Scanning Electron Microscope Simulation with Adaptive Mesh Refinement

Abstract

The intensity variation in a scanning electron microscope is a complex function of sample topography and composition. Measurement accuracy is improved when an explicit accounting for the relationship between signal and measurand is made. Because the determinants of the signal are many, the theoretical understanding usually takes the form of a simulator. For samples with nonconducting regions that charge, one phase of the simulation is finite element analysis to compute the electric field. The size of the finite element mesh, and consequently computation time, can be reduced through the use of adaptive mesh refinement. We present a new a posteriori local error estimator and adaptive mesh refinement algorithm for the scanning electron microscope simulation. This error estimate is designed to minimize the error in the electron trajectories, rather than the energy norm of the error that traditional error estimators minimize. Using a test problem with a known exact solution, we show that the adaptive mesh can achieve the same error in electron trajectories as a carefully designed hand-graded mesh while using 3.5 times fewer vertices and 2.25 times less computation time.

1 Introduction

Interaction of electrons with condensed matter is the basis for many useful methods in science and engineering, including electron microscopy for measuring the form and dimensions of sample features down to the nanometer scale [7], x-ray microanalysis for mapping sample composition at micrometer spatial resolution [7], electron beam lithography [11], radiation-induced modification of materials [5, 10], and many others. A theoretical understanding of the relevant interaction mechanisms is crucial to obtaining the best performance in the most demanding of these applications. For example, owing to scattering and other effects, the intensity variation in a scanning electron microscope (SEM) is a complex function of sample topography and composition. Measurement accuracy, e.g., for feature size and shape, is improved when an explicit accounting for the relationship between signal and measurand is made [17]. Because the determinants of the signal are many, including electron/nuclear scattering, secondary electron generation, charging, phonon scattering, electron trapping, traversal of potential energy steps at material boundaries, beam and detector properties, etc., the theoretical understanding usually takes the form of a simulator (e.g., the National Institute of Standards and Technology’s Java MONte Carlo Simulator for Secondary ELectrons, or JMONSEL [15, 17]) that predicts the signal that would be produced by a sample of given composition and shape under specified imaging conditions.

Inclusion of the effects of charging in the model is important for samples that are entirely or partly insulating. The insulating parts charge, and the captured charge generates electric fields that influence the trajectories of subsequent electrons. Charging continues until a steady-state condition is reached, wherein the charge distribution and resulting fields exhibit statistical fluctuations about stationary averages. In good insulators the steady-state fields can be strong enough to deflect or slow an incoming beam of electrons, thereby altering the location and depth of the region where the electron beam interacts with the sample for all of the above mentioned sample analysis or sample modification techniques. This is particularly important for secondary electrons (SE) because these have low kinetic energy, less than 50 eV at formation and often less than 5 eV for those that escape the sample. They are therefore strongly affected by the fields. In JMONSEL, simulations that involve charging are performed within a tetrahedral mesh to facilitate solution of the fields by finite element analysis (FEA). There is a trade-off, with speed and economy of memory favoring a coarse mesh and accuracy favoring a fine one.

This trade-off can be optimized through the use of adaptive mesh refinement. The goal of adaptive mesh refinement is to automatically generate a mesh that is fine in the regions where small elements are needed to accurately resolve the solution, and coarse in regions where large elements suffice. This is done by solving the differential equation on a coarse mesh, computing local a posteriori error estimates, and refining elements that have large error estimates. This process is repeated until the solution is sufficiently accurate or a resource limitation is reached.

Apart from an early start by Grella and coworkers [8, 9] that was followed by a long hiatus, inclusion of charging effects in electron trajectory simulators is a fairly recent phenomenon [4, 16]. Electron trajectories may have curvature on the order of nanometers where the fields are high, but they must be tracked from sample to detector, a distance of the order of a centimeter. Since the memory cost of making all mesh elements as small as required in the most sensitive regions would be prohibitive, charging implementations to date reserve the smallest elements for locations deemed important according to an a priori model. In this paper we instead present an adaptive mesh refinement algorithm for SEM simulations. Key to this algorithm is a new a posteriori error estimate designed to minimize the error in electron trajectories, rather than the electric field, since this is what one ultimately cares about in a SEM simulation.

The remainder of the paper is organized as follows. In Sect. 2 the model for simulating scanning electron microscopes is described. Section 3 contains the algorithm for adaptive mesh refinement in the finite element method including the new a posteriori error estimate for SEM simulations. Section 4 contains numerical computations to demonstrate the effectiveness of adaptive mesh refinement and the new error estimate for SEM simulations. Finally, Sect. 5 contains the conclusions.

2 Scanning Electron Microscope Simulation

A typical simulation begins with definition of an electron gun, a sample, and detectors. The gun generates a specified number of electrons with an initial energy aimed with specified accuracy in a given direction (e.g., electrons converging first toward and then away from a Gaussian best-focus spot). In a simulation that involves charging, the sample is represented by a tetrahedral mesh. Regions within the mesh are assigned different materials (e.g., vacuum, various metals or insulators). Each material is associated with material properties including elemental constituents and their stoichiometry, a density, a dielectric constant, and a scattering model. The scattering model includes a list of scattering mechanisms, each of which is characterized by an energy-dependent scattering probability and a probability distribution of outcomes for scattering events. The scattering mechanisms generally include both elastic ones, such as electron scattering from an atomic nucleus, and inelastic ones such as generation of SE or phonons. They may also include electron traps. The simulation for each electron proceeds in a series of Monte Carlo steps. At the beginning of a step, the electron occupies a particular tetrahedral element of the mesh and has an initial direction of motion and energy (its energy at the end of the previous step or, if this is its first step, its energy at creation by an electron gun or SE generation process). An electron’s free path is the distance it traverses before a scattering event. The electron’s inverse mean free path (IMFP, the sum of the IMFPs of the individual scattering mechanisms) determines a Poisson probability distribution of possible free paths. A free path is chosen according to this distribution. The distance to the nearest boundary of its tetrahedron along its unscattered path is also determined. The electron is moved the shorter of the two distances. Its energy and direction of motion are adjusted to account for the effect of the electric field within the tetrahedron occupied by the electron. If the boundary distance was shorter, the electron undergoes a boundary crossing event into the next tetrahedron, possibly with a change of energy and trajectory, or even a reflection, if the materials are dissimilar. Otherwise the electron scatters. In either case, the outcome (the electron’s new energy and direction of motion, possible generation of a secondary electron) is determined Monte Carlo style, randomly according to the relevant model-specified probability distribution. Details of the available scattering mechanisms and their associated probability distributions are published elsewhere [17]. The scattering or boundary crossing event concludes the trajectory step. If the electron does not satisfy a stopping criterion (e.g., it undergoes a trapping event, its energy falls below a model-prescribed level, it is captured by a detector, or it exits the “chamber”) execution proceeds to the current electron’s next step. Otherwise, simulation proceeds to the next electron. Any SE generated by scattering mechanisms are processed in the same way.

When charging effects are simulated, an integer count of elementary charges is maintained for each tetrahedral element of the mesh. When an SE is generated in an element, the count is incremented by 1. When an electron’s trajectory ends within an element, that element’s count is decremented by 1. If an element’s count is n, its charge is therefore ne, with $e \approx 1.602 \times 10^{-19}\, \hbox {C}$ the magnitude of the electron’s charge. After every N electrons from the electron gun, the scattering simulation described above pauses while a fresh FEA solution is performed for the then extant charge distribution together with boundary conditions supplied

by the user. N is an adjustable parameter. Its value determines a speed/accuracy trade-off. The electric field estimate at any given time is determined by the most recent FEA solution. Smaller N means less change to the charge distribution between estimates, but it also increases the frequency of time-consuming FEA solutions.

At the end of a simulation, detectors that were assigned at the beginning are polled to determine simulated signals. For example, a detector is generally assigned to electrons that leave the chamber, arbitrarily defined as a radius 0.1 m sphere. Electrons that get this far from the sample are binned into energy and angular histograms, counted, and then dropped from further simulation. Other detectors may be assigned to specific regions within the chamber. They may count detected electrons, measure energy deposited in the sample, create trajectory plots, detailed logs of simulated events, etc. Simulations like these may be placed in a loop, for example with the electron gun aimed each time at a new position in a raster scan with low energy ($E < 50 \, \hbox {eV}$) or higher energy ($E \ge 50 \, \hbox {eV}$) electron yields recorded at each position to simulate images.

The FEA computes the electrostatic potential, $\phi$, given by

$$\begin{aligned} -\nabla \epsilon \nabla \phi = \rho \end{aligned}$$

(1)

where $\epsilon = \epsilon _r \epsilon _0$, $\epsilon _r$ is the material dependent dielectric constant, $\epsilon _0$ is the permittivity of free space, and $\rho$ is the charge density. This equation is solved on a meshed region or combination of regions specified by the user. For example, the sample might have one or more thin insulating regions on a conducting substrate which is in contact with a metal grounded sample holder. The electron microscope raster-scans the beam over a rectangular area of the sample with a size of a few micrometers. The sample and its holder are in a vacuum chamber with the electron gun and lens column above the sample. Some SEMs impose a background electric field in the vicinity of the sample to direct the slower moving secondary electrons toward a detector located in the lens column. A reasonable way to simulate this is to mesh a cylindrical region centered on the scanned area, which is where the charges will accumulate as electrons or holes become trapped in the insulator. The cylinder axis is parallel to the electron beam’s average direction. Its bottom coincides with the underlying grounded conductor, justifying a Dirichlet boundary condition with $\phi =0 \, \hbox {V}$ on that surface. Its dimensions (radius and height) should be large enough that the electric field (i.e., the gradient of $\phi$) produced by the accumulated charges should be approaching 0 at the boundary, justifying a Neumann boundary condition of 0 on the cylinder wall and $-\nabla \phi$ equal to the externally imposed electric field on the top surface.

In this paper, a single FEA is considered, i.e., Eq. 1 is solved for a given charge density.

3 Adaptive Mesh Refinement

3.1 Finite Element Method

An approximate solution to Eq. 1 is computed by the usual Galerkin finite element method. A mesh, M, consisting of tetrahedral elements $\{T_i, i=1,N_e\}$ with vertices $\{v_i, i=1,N_v\}$ covers the domain. The volume of $T_i$ is $V_i$, and the diameter is defined to be $h_i = \root 3 \of {V_i}$. The approximation space of continuous piecewise linear functions over M is spanned by the basis $\{B_i : B_i(v_j) = \delta _{i,j}, i,j=1,N_v\}$ where $\delta _{i,j}$ is the Kronecker delta function. Discretization produces the linear system of equations

$$\begin{aligned} \mathbf{Ax}=\mathbf{b} \end{aligned}$$

(2)

where

$$\begin{aligned} A_{i,j}&= \int \varepsilon \nabla B_i \cdot \nabla B_j \end{aligned}$$

(3)

$$\begin{aligned} b_i&= \int \rho B_i. \end{aligned}$$

(4)

The solution $\mathbf{x}=[\alpha _1 \alpha _2 \dots \alpha _{N_v}]^\mathrm {T}$ contains the coefficients of the approximate solution

$$\begin{aligned} \phi _M = \sum _{i=1}^{N_v} \alpha _i B_i. \end{aligned}$$

(5)

Before solving Eq. 2 the coefficients corresponding to vertices on the Dirichlet part of the boundary are set from the boundary conditions and eliminated from the linear system.

Fig. 1

Newest vertex bisection refinement of a tetrahedron

3.2 Tetrahedron Refinement

A critical component of adaptive mesh refinement is a method for refining elements and maintaining a valid finite element mesh. We refine a tetrahedron by the method of newest vertex bisection [12] as illustrated in Fig. 1. One edge of the tetrahedron is selected as the refinement edge, which is the edge to be bisected. With newest vertex bisection, the refinement edge will always be opposite the most recently created vertex, but with tetrahedra there is more than one choice for the refinement edge. We use the method of Arnold et al. [2] to select the refinement edge. The tetrahedron is then bisected by connecting the midpoint of the refinement edge to the two vertices that are not contained in the refinement edge. The element that was refined is called the parent, and the two new elements are called the children.

To maintain a valid finite element mesh, one must enforce compatibility. A tetrahedral mesh is said to be compatible if the intersection of any two elements is empty, a common vertex, a common edge or a common face. Compatibility can be maintained by simultaneously refining all elements that contain the refinement edge as in Fig. 2. The set of elements to be refined simultaneously are called mates, and the set of elements created by refining the mates are siblings.

However, it is possible that one (or more) of the elements that contains the refinement edge has a different edge as its refinement edge. In that case, that element (or those elements) must first be refined by its refinement edge. It can be shown that within two levels of refinement all the descendants that contain the refinement edge have that edge as their refinement edge.

An element that was created by refinement can be coarsened (unrefined) provided none of the siblings have been refined. The element to be coarsened and its siblings are simply rejoined to recreate the parent and mates.

Fig. 2

Simultaneous refinement of all four tetrahedra that share a common refinement edge to maintain compatibility of the mesh

3.3 Standard Error Estimate

Another critical component of adaptive mesh refinement is the a posteriori local error estimate, which is used as an error indicator to determine which elements should be refined and which should be coarsened, and for computing a global error estimate.

There are many methods for computing an a posteriori error estimate. See for example [1, 14]. Most methods estimate the energy norm of the error over one or a few elements, and the goal of adaptive mesh refinement with these methods is to create a mesh that equidistributes the error over the domain.

As an error estimate of this type we choose a frequently used method due to Bank and Weiser [3]. For a piecewise constant function f, let $\left[ f \right]$ denote the magnitude of the jump discontinuity in f across the boundary of an element. The local residual problem

$$\begin{aligned} -\nabla \varepsilon \nabla e_k&= \rho + \nabla \varepsilon \nabla \phi _M&\mathrm {in}~~T_k \end{aligned}$$

(6)

$$\begin{aligned} \varepsilon \frac{\partial e_k}{\partial n}&= -\frac{1}{2} \left[ \varepsilon \frac{\partial \phi _M}{\partial n} \right]&\mathrm {on}~~\partial T_k \end{aligned}$$

(7)

is solved to obtain an estimate of the error, $e_k$, over element $T_k$ by the finite element method using quadratic basis functions associated with the edges of $T_k$ (but not the linear bases associated with the vertices). Note that although the continuous solution of Eqs. 6 and 7 is not unique, the omission of the linear bases essentially imposes an additional Dirichlet boundary condition that the solution is 0.0 at the vertices of $T_k$, so that the approximate solution is well defined. The local error estimate for $T_k$ is $\eta _k = ||e_k||$ where the norm is the energy norm over $T_k$. The global error estimate for M, $\eta _M$, is given by

$$\begin{aligned} \eta _M^2 = \sum _{i=1}^{N_e} \eta _i^2 \end{aligned}$$

(8)

3.4 Error Estimate for SEM Simulation

To provide a rationale for our error estimate, it is useful to consider electrons in three groups: (1) those that emerge and then escape from the sample, (2) those that scatter within the sample, and (3) those that emerge from the sample but return. Errors in the FEA solution affect the trajectories of electrons in all three groups, but the importance of the effects differ owing to the iterative nature of the charging simulation, as described in Sect. 2. Electrons that escape the sample (group 1) do not charge the sample so there are no associated errors in the electric field that propagate to subsequent iterations. Electrons that scatter within the sample have relatively short range due to rapid slowing caused by inelastic collisions, and their paths may be considered random or diffusive because of frequent strong deflections in elastic collisions with heavy nuclei. Errors in the electric field act over a relatively short time so cause only small errors in the electrons’ final positions. Group 3 exists when the sample charges positively under electron bombardment. Low energy electrons that emerge from the sample are attracted by the positive charge and return. Since these electrons are not slowed by collisions within the sample, their paths are relatively long and errors in their trajectories have more time to accumulate. Their erroneous final positions once they are trapped upon return to the sample produce errors in the next iteration’s computed electric field. These electrons thus represent a worst case. In choosing to minimize their errors, we will also minimize errors due to electrons in group 2.

Thus we wish to approximate how much the error in the solution in an element contributes to the error in the trajectory of an average electron, rather than estimating the energy norm of the error in the electric potential as a traditional error indicator would do, and ideally generate a mesh that equidistributes the contributions over the elements. There are significant uncertainties in the computation of trajectory error because, as we will see below, the errors depend upon such things as the electron range and energy and the volume of the simulated space sampled by the trajectories. These depend upon such things as sample materials, their distribution and topography, the beam energy, and the extent of sample charge (which changes over the course of the simulation). For this reason, our derivation is in the spirit of a “back of the envelope” calculation. We will freely ignore factors of 2 and $\pi$ or the difference between a sphere and a tetrahedron. The goal is two-fold: on the one hand an order of magnitude approximation of the expected trajectory errors associated with an FEA solution, and on the other hand a good understanding of how those errors scale with our choice of element size.

Consider an electron with initial velocity $\mathbf{v}$ which travels a distance R before reaching a final position. We begin with the error in the electric field averaged over the electron’s path, $C_k$, through element $T_k$, given by

$$\begin{aligned} \left\langle \nabla \phi _M - \nabla \phi \right\rangle _k = \frac{1}{h_k}\int _{C_k}\nabla \phi _M - \nabla \phi . \end{aligned}$$

(9)

where $h_k$, the diameter of element $T_k$, approximates the length of $C_k$. The magnitude of the error in the force on the electron in element $T_k$ is thus $e \left| \left\langle \nabla \phi _M - \nabla \phi \right\rangle _k \right|$ where e is the magnitude of the charge of the electron. Dividing the error in the force by the mass of the electron, m, gives the error in acceleration. If we approximate the time spent in the element by $h_k$ divided by the electron’s initial speed $v=|\mathbf{v}|$, then the estimate of the contribution of element k to the error in the electron’s speed, given by the error in acceleration times the time spent in the element, is

$$\begin{aligned} \frac{eh_k}{mv} \left| \left\langle \nabla \phi _M - \nabla \phi \right\rangle _k \right| \end{aligned}$$

(10)

The estimate of the contribution of element $T_k$ to the error in position at the end of the trajectory is given by the contribution to the error in speed times the remaining time of the trajectory after passing through element $T_k$. Here we consider an electron that spends most of the time outside the sample, where the speed can be approximated as constant. Then the time to traverse the entire trajectory is approximately $\frac{R}{v}$. (If we consider an electron that spends most of the time inside the sample and assume constant deceleration until the electron stops at the end of the trajectory, the average velocity is v / 2, so the time to traverse the trajectory is $\frac{R}{v/2}$, though R is on average much smaller in this case.) Since $T_k$ is equally likely to be anywhere along the trajectory, the average time over the remaining part of all trajectories of length R with initial speed v is half that, or $\frac{R}{2v}$. Thus the estimate of the contribution of element $T_k$ to the error in position is

$$\begin{aligned} \frac{R}{2v}\frac{eh_k}{mv} \left| \left\langle \nabla \phi _M - \nabla \phi \right\rangle _k \right| = \frac{eRh_k}{4T} \left| \left\langle \nabla \phi _M - \nabla \phi \right\rangle _k \right| \end{aligned}$$

(11)

where $T=\frac{1}{2}mv^2$ is the electron’s initial kinetic energy.

Fig. 3

Volume swept out by a spherical volume element in the electron’s reference frame. An electron position within the swept volume is equivalent to the electron trajectory intersecting the volume element

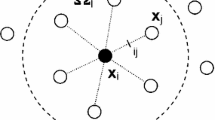
Equation 11 assumes the trajectory passes through element $T_k$, but a trajectory will only pass through some elements. The probability that an arbitrary electron’s trajectory passes through $T_k$ can be determined by considering the electron’s frame of reference, i.e., let the electron’s position be fixed and the tetrahedron be in motion. For simplicity, we approximate the tetrahedron by a sphere of diameter $h_k$. Then $T_k$ sweeps out a curved cylinder of length R and diameter $h_k$ as illustrated in Fig.  3. The trajectory of $T_k$ in this frame of reference, shown as a black curve down the center of the curved cylinder, is the same as that of the electron in the original frame of reference, except for being shifted to $T_k$’s position and moving in the opposite direction. The probability that an arbitrary electron’s trajectory intersects $T_k$ is then the volume of the curved cylinder divided by the volume, V, of the region containing all electron trajectories, which is approximately $Rh_k^2/V$. To get the estimate of this element’s contribution to the position error of an average randomly chosen trajectory, multiply by that probability, giving

$$\begin{aligned} \eta _k = \frac{eR^2h_k^3}{4TV} \left| \left\langle \nabla \phi _M - \nabla \phi \right\rangle _k \right| \end{aligned}$$

(12)

The local error estimate in Eq. 12 is element $T_k$’s contribution to the error in the final position of a randomly chosen trajectory. The total error in that position is given by the sum of all such contributions, and we divide by R to get the relative position error. Thus the global error estimate is

$$\begin{aligned} \eta _M = \frac{1}{R}\sum _{k=1}^{N_e} \eta _k = \sum _{k=1}^{N_e} \frac{eRh_k^3}{4TV} \left| \left\langle \nabla \phi _M - \nabla \phi \right\rangle _k \right| \end{aligned}$$

(13)

An estimate of $\left| \left\langle \nabla \phi _M-\nabla \phi \right\rangle _k \right|$ is computed by using the local residual problem of the standard error estimate. First note that the path $C_k$ in Eq. 9 is not known, but it is equally likely to be anywhere within the element. To compute the average error in the electric field we can, instead, compute the integral of the gradient of the error over the entire element and divide by the volume of the element,

$$\begin{aligned} \left\langle \nabla \phi _M-\nabla \phi \right\rangle _k \approx \frac{1}{V_k}\int _{T_k}\nabla \phi _M -\nabla \phi = \frac{1}{V_k}\int _{T_k}\nabla \left( \phi _M-\phi \right) . \end{aligned}$$

(14)

The error $\phi _M - \phi$ is estimated by solving Eqs. 6–7 for $e_k$. The gradient of $e_k$ can be computed and integrated over $T_k$ to obtain the estimate in Eq. 14. This is a vector of length 3, and the absolute value is given by its Euclidean norm.

For the global error estimate to be used as a termination criterion and an indication of the accuracy of the solution, an estimate of $\frac{eR}{4TV}$ is needed. Unfortunately, this is a problem dependent quantity and there is no general purpose way to estimate it. It depends on factors such as the size of the scan region, initial energy of secondary electrons, and properties of the sample. It is up to the user to provide an estimate of this quantity based on knowledge of the particular problem being solved. In the results of Sect. 4.4 we use actual R, T and V from the simulation (which would not be known in a real problem) to show that a fairly good error estimate can be obtained if $\frac{eR}{4TV}$ is well estimated.

However, e, R, T and V are constants with respect to the elements of the mesh. When determining which elements to refine, only the relative size of the local error estimates matters. So as an elemental error indicator to guide adaptive refinement in the algorithm in Sect. 3.5, it suffices to use the mesh-dependent part of $\eta _k$, $h_k^3 \left| \left\langle \nabla \phi _M - \nabla \phi \right\rangle _k \right|$.

This estimate and the more customary energy norm error estimate are similar inasmuch as for each the global error is a sum of elemental contributions in the form of an elemental integral of a function of the error. The difference is that the function is quadratic in the electric field (gradient of $\phi$) error for the conventional estimator and linear for Eq. 13. The linear weighting is motivated by the linear effect of electric field errors on position errors.

Fig. 4

Algorithm for adaptive mesh refinement

3.5 Adaptive Mesh Refinement Algorithm

   The adaptive mesh refinement algorithm is shown in Fig. 4. There are many variations on adaptive mesh refinement; this section describes the methods used in this paper.

One begins with a coarse initial mesh and discretizes and solves on this mesh. A mark-refine-solve loop is then performed until some termination criterion is met. Typical termination criteria are having the global error estimate, $\eta _M$, smaller than a given tolerance, or a limit on some resource, for example a maximum number of elements in the mesh. For the results in Sect. 4.4, a limit of 10 million elements was imposed.

The first step in the loop is to mark elements for refinement or coarsening. An error indicator (the local error estimate of Sect. 3.3 or 3.4), $\eta _k$, is computed for each element. The maximum error indicator is denoted $\eta _\mathrm {max}$. The elements with a sufficiently large error indicator are marked for refinement, and those with a sufficiently small error indicator are marked for coarsening. An error indicator is considered to be sufficiently large if it is larger than some fraction of the maximum error indicator, $\eta _\mathrm {max}/f_r$, and is sufficiently small if it is smaller than some smaller fraction $\eta _\mathrm {max}/f_c$. For the results in Sect. 4.4, $f_r=10$ and $f_c=100$.

Next, elements that are marked for coarsening and are coarsenable are coarsened. As per the definition of coarsening in Sect. 3.2, an element is not coarsenable if it is in the initial mesh or any of the siblings have been refined or are marked for refinement.

Elements that are marked for refinement are then refined. An element is deemed to be not refinable if the diameter of the element is less than some designated minimum size. For the results in Sect. 4.4 a minimum size of 1 nm was used.

Finally Eq. 1 is discretized and solved on the new mesh, and the loop is repeated until the termination criterion is satisfied.

4 Numerical Computations

4.1 Test Problem

To compare the effectiveness of adaptive refinement for SEM simulation to the use of a non-adaptive mesh, and of the new error estimate to the standard error estimate, we use a test problem for which the exact solution is known. Space is divided into upper and lower infinite half-spaces by a horizontal plane at $z=H_0$. The upper half space is a vacuum, with $\varepsilon _1 = 1$. The lower half space is $\mathrm {SiO}_2$ with $\varepsilon _2 = 3.9$. Any number, $N_c$, of point charges with charges $c_i e,~i=1,N_c$, may be embedded in a finite bounded region at positions $(x_i,y_i,z_i)$ in the lower half-space. The boundary condition is $\phi =0$ at infinity. $e \approx 1.602\mathrm {x}10^{-19}$ C is the magnitude of the charge of an electron. Let

$$\begin{aligned} r_i = \sqrt{(x-x_i)^2+(y-y_i)^2+(z-z_i)^2}. \end{aligned}$$

(15)

Then the exact solution is

$$\begin{aligned} \phi = {\left\{ \begin{array}{ll} {\sum }_{i=1}^{N_c} \frac{c_i e}{4\pi \varepsilon _0\varepsilon _2} \left( \frac{1}{r_i}- \frac{\varepsilon _1-\varepsilon _2}{(\varepsilon _1+\varepsilon _2) \sqrt{(x-x_i)^2+(y-y_i)^2+(2h-z-z_i)^2}}\right) , &{} \mathrm {if}~z<H_0 \\ {\sum }_{i=1}^{N_c} \frac{c_i e}{2\pi \varepsilon _0}\frac{1}{(\varepsilon _1+\varepsilon _2)r_i}, &{} \mathrm {otherwise.} \end{array}\right. } \end{aligned}$$

(16)

Here $\varepsilon _0 \approx 8.854 \times 10^{-12} \frac{\mathrm {C}}{\mathrm {Vm}}$ is the permittivity of free space.

The infinite region is truncated to a cylinder of radius $R_0=20\, 000$ nm and height $H=10\, 000 \, \hbox {nm}$ with the bottom at $z=0\, \hbox {nm}$ and central axis at $(x,y)=(0,0)\, \hbox {nm}$. The interface between vacuum and $\mathrm {SiO}_2$ is at $H_0=5000\, \hbox {nm}$. The boundary conditions are modified to be Dirichlet on all sides and are set to the exact solution.

Fig. 5

Slice of a typical hand-graded mesh in the x-y plane at $z=5000\, \hbox {nm}$

For the charges we used 5000 negative charges ($c_i=-1$) randomly distributed in the box $(-1000,1000)\times (-1000,1000)\times (4750,4900)\, \hbox {nm}$, and 5500 positive charges ($c_i=1$) randomly distributed in $(-1000,1000)\times (-1000,1000) \times (4950,4999)\, \hbox {nm}$. The random numbers were given by the Fortran intrinsic RANDOM_NUMBER function with seed=314159.

4.2 Hand-Graded Mesh

As a means of comparison with the mesh generated by adaptive mesh refinement, we designed a hand-graded mesh appropriate for the problem in Sect. 4.1. The mesh is uniform over the charged region since there is no a priori knowledge of the location of the charges within that region, and outside the charged region the elements increase in size like $r^{3/2}$ where r is the distance from the center of the charged region. This growth rate is chosen to approximately equalize the root mean square average error of the piecewise linear approximation to the potential, which is assumed to behave like $\frac{1}{r}$. Figure 5 shows a slice of a typical hand-graded mesh in the x–y plane at $z=5000\, \hbox {nm}$.

The meshes are generated by the freely-available mesh generator Gmsh [6]. Gmsh allows specifying mesh element sizes by defining what they call a field. For this mesh we define two fields and then define the field to use as the pointwise minimum of the two.

The first field is of type “MathEval” in the Gmsh terminology, which defines a field with an explicit mathematical function. To get a mesh that increases in size like $r^{3/2}$, the function is

$$\begin{aligned} S\left( h_\mathrm {min}+\left( \frac{(x-x_0)^4}{s_x^2+(x-x_0)^2} + \frac{(y-y_0)^4}{s_y^2+(y-y_0)^2}+\frac{(z-z_0)^4}{s_z^2+(z-z_0)^2} \right) ^{3/4} \right) \end{aligned}$$

(17)

where $h_\mathrm {min}=1\, \hbox {nm}$ ensures elements do not get too small, $(x_0,y_0,z_0)=(0,0,4875)\, \hbox {nm}$ is the center of the charged region, and $(s_x,s_y,s_z)=(2000, 2000, 250)\, \hbox {nm}$ is the size of the charged region. S is a scale factor which allows generating meshes of different sizes.

The second field is of type “Box” which specifies the size of elements inside and outside a parallelpiped. We use $S\, \hbox {nm}$ inside the charged region and 10 000 nm outside. These values ensure the first field is used outside the charged region, and the second field is used inside.

To generate a sequence of meshes to examine the convergence of the error with respect to the mesh size, we begin with $S=100/\root 6 \of {2}$, which gives a mesh with 11174 vertices, and use a sequence of values of S that decrease by factors of $\root 6 \of {2}$ until $S=12.5\sqrt{2}$, which gives a mesh with 1 270 010 vertices. This sequence of S approximately increases the number of vertices in each mesh of the sequence by a factor of $\sqrt{2}$, and produces meshes in the range of 10 000 to 1.5 million vertices.

Fig. 6

The initial mesh for adaptive mesh refinement

The initial mesh for adaptive mesh refinement, shown in Fig. 6, is created with the same input to Gmsh using $S=800$ and contains 123 vertices.

4.3 Error Metric

As indicated in Sect. 3.4, for this application the quantity of interest is the error in an electron’s trajectory (which is caused by the error in the electrostatic potential). So rather than measuring some norm of the error $\phi _M-\phi$, a metric for the error in an average electron trajectory is needed. For this we generate a set of reference trajectories using the exact solution of the test problem and measure the error at a particular point in the trajectories obtained with the approximate solution.

A set of trajectories was generated by scanning the simulated beam over a 1400 nm $\times$ 1400 nm square centered in the charged area. The first 3000 beam electrons and all secondary electrons produced in their cascade were logged in a text file. Of the logged electrons, 273 were in group 3 of Sect. 3.4, i.e., electrons that leave the sample and return. These electrons were isolated for analysis.

Given an approximate solution $\phi _M$, approximate trajectories are computed using the position, direction of motion, and energy of the electrons of the reference trajectories at the point where the electron leaves the $\mathrm {SiO}_2$ slab. The error of an approximate trajectory is taken to be the relative error in the landing position where the electron returns to the $\mathrm {SiO}_2$ slab, i.e., the Euclidean norm of the distance between the landing position of the reference trajectory and the landing position of the approximate trajectory divided by the range of the reference trajectory. The range is approximated by the length of a piecewise linear interpolation of the reference trajectory using 100 nodes. Approximate trajectories for which the electron escapes are discarded (there were typically fewer than 10 for the results reported in Sect. 4.4) and the error metric is the average of the errors in the remaining approximate trajectories.

4.4 Numerical Results

The methods described in this paper have been implemented in the adaptive finite element program PHAML [13]. PHAML Version 1.17.1 was compiled with Intel Parallel Studio XE Composer Edition for Fortran Linux 2017¹ on a Dell Precision 7710 with four Intel Core i7-6820HQ cpus clocked at 2.70 GHz and 64 Gbyte of memory, operating under the CentOS 7.3 distribution of Linux.

The test problem was solved using the adaptive refinement algorithm of Fig. 4 with the standard error estimate and with the new error estimate. The error metric is computed using the mesh and solution at the end of each time through the mark-refine-solve loop, and the number of vertices in the mesh and computation time so far are associated with that error. The test problem was also solved using each of the hand-graded meshes, and the same data recorded.

Fig. 7

Comparison of the error as a function of mesh size for adaptive refinement with the new error indicator and standard error indicator, and for the hand graded mesh

The graph in Fig. 7 shows the error in landing position as a function of the number of vertices in the mesh, $N_v$, for each of the three methods. The symbols show the data points. The solid lines are a least squares fit of the form $\mathrm {error} = aN_v^b$ to the data after the asymptotic rate of convergence is reached. The dashed lines are the extension of the solid line to the preasymptotic region. Since this error is based on an integral of the gradient of the error in the solution, as in Eqs. 9 and 14, one would expect the error to converge like $O(h)=O(N_v^{-1/3})$, the same as the theoretical convergence rate of the energy or $H^1$ norm of the error in the solution. Thus Fig. 7 also contains a line to show the slope of perfect $O(N_v^{-1/3})$ convergence.

Adaptive refinement with the new error indicator, shown with circles, has near perfect $O(N_v^{-1/3})$ convergence with the least squares slope $b=-\,0.33275$. The hand-graded mesh, shown with triangles, is also near perfect with $b=-\,0.33452$. For a given error, the hand-graded mesh requires about 3.5 times as many vertices as the adaptive mesh with the new error estimate. Adaptive refinement with the standard error indicator, shown with squares, fails to achieve the proper order of convergence, exhibiting $b=-\,0.19614$, which is close to $O(\sqrt{h})$. However, it is not surprising that it fails under this unusual error metric since it is intended to optimize the mesh for minimizing the energy norm of the error in the potential.

Fig. 8

Comparison of the error as a function of computation time for adaptive refinement with the new error indicator and the hand graded mesh

Figure 8 compares the error versus computation time for adaptive refinement with the new error estimate and the hand-graded mesh. The computation time includes the time to generate the mesh, either by the algorithm of Fig. 4 for adaptive refinement or by Gmsh for the hand-graded mesh, and the time to discretize and solve the differential equation. It does not include the time to compute the error metric. These graphs have slopes of − 0.30249 and − 0.29665, respectively. The slightly less than optimal rate of convergence is due to the time to solve the linear system, which is $O(N^{3/2})$ rather than the optimal O(N). The hand-graded mesh takes about 2.25 times longer than the adaptive mesh to achieve a given error.

Fig. 9

Comparison of the error estimate to the error

Figure 9 presents the error estimates as a function of $N_v$ for the adaptive mesh and the hand-graded mesh. The least squares fit of the error is taken from Fig. 7. The constant $\frac{eR}{4TV}$ is determined from the simulation data. The range, $R_i$ and initial kinetic energy, $T_i$ are known for each of the 273 trajectories. The ratio $R_i/T_i$ is computed for each trajectory and these are averaged to get $R/T=3.34\mathrm {x}10^{-6}/\mathrm {m}^2\mathrm {V}$. The volume, V, is the volume of the region bounded by the scan area ($1400 \, \hbox {nm} \times 1400 \, \hbox {nm}$) and the maximum vertical displacement of an electron in the 273 trajectories (4800 nm). The error estimates do not quite obtain the optimal order of convergence, having slopes of − 0.24717 for the adaptive mesh and − 0.28768 for the hand-graded mesh. However, they are within an order of magnitude of the error. In the asymptotic range, the error estimate for the adaptive mesh is about 4.4–5.0 times larger than the error, and that of the hand-graded mesh is about 3.1–3.5 times larger than the error.

5 Conclusion

In this paper we presented an algorithm for adaptive mesh refinement for the finite element analysis phase of a model for scanning electron microscope simulation. This algorithm includes a new a posteriori local error estimate which is designed to optimize the mesh to minimize the error in the electron trajectories, as opposed to minimizing the energy norm of the error in the solution like most a posteriori error estimates. The new estimate consists of a mesh size and FEA solution dependent part that is useful to guide mesh refinement, and a mesh independent prefactor for which there is only an order of magnitude estimate. We demonstrated the algorithm using a test problem with 10 500 point charges. The global error estimate was a good ballpark estimate of the error, overestimating it in this test problem by about a factor of 3 to 5. Compared to a hand-graded mesh, there was a 3.5X reduction in number of vertices and 2.25X reduction of computation time to achieve a given error. Both the adaptive mesh with the new error estimate and the hand-graded meshes achieve O(h) convergence. Adaptive mesh refinement using a conventional error estimator failed to achieve O(h) convergence, probably because it is designed to optimize the mesh for a different error metric.