1 Introduction

In recent years, the diffuse-interface or phase-field model has been used successfully in many fields of science and engineering to describe multiphasic materials and emerged as one of the effective modeling and computational tools to study interfacial phenomena (cf. [1, 8, 14–16, 19, 21, 23, 37–39], and the references therein). The essential idea in the phase field model, which can be traced back to the pioneering work of [27, 32], is to use continuous phase field variables to describe multiple phases in multiphasic material systems, where the interfaces are represented by thin, smooth transition layers. When the phase field model is derived from an energetic variational formalism coupled with the Onsager principle, the governing system of equations is normally well-posed and satisfies an energy dissipation law. As the result, one can carry out mathematical analyses to show solution existence and uniqueness in appropriate function spaces and then develop efficient numerical schemes to approximate the equations in the model that possess an analogous energy dissipation property discretely.

To model a two-phase system using the phase field approach, one phase variable is needed to label the two distinctive components at two distinct values. Such a phase variable is a smooth function with a steep change at the interface, controlled by an interfacial thickness parameter. The free energy for the binary material system usually consists of (i) a double-well bulk part which promotes either of the two phases in the bulk, yielding a hydrophobic contribution to the free energy; (ii) a conformational entropic term that promotes hydrophilicity in the multiphasic material system. The competition between the hydrophilic and hydrophobic part in the free energy forms the mechanism for the coexistence of two distinctive phases in the binary system. Based on the generalized Onsager principle [25, 26, 35, 36], dynamics of the interfaces can be governed either by the Allen–Cahn equation or the Cahn–Hilliard equation. The Cahn–Hilliard equation is a fourth-order equation which conserves the integral of the phase variable, normally linked to the volume of the material in one phase. It is relatively harder to solve numerically however. The Allen–Cahn equation on the other hand is a second-order equation, which is easier to solve numerically but does not conserve the volume of the material in any phase. However, it can be modified by adding a Lagrangian multiplier [31, 33] or a penalty term to the free energy [11] to force the model to conserve the volume approximately. Such a phase-field model has been well studied for instance in [1, 14, 15, 21]).

For three-phase (ternary) systems, two models are proposed in [3, 18] using three phase variables governed by Cahn–Hilliard equations. In [18], the free energy of the system is simply a summation of the original biphasic energy for each phase variable in binary models. To conserve the volume by applying the Lagrangian multiplier, one phase variable and its transport equation is actually redundant and is therefore neglected. However, such a system is not well posed for the total spreading case and some nonphysical instabilities at interfaces may occur, that is shown in [3]. Therefore, a sixth order polynomial potential is added to the free energy that can make the system well-posed. But such term makes the three phase variables nonlinearly coupled together. The authors in [3] also developed several energy stable schemes for the model. We note that the schemes are all nonlinear and quite complicated, which requires some efficient iterative methods in their implementations. In fact, all difficulties about how to develop easy-to-implement (linear) numerical schemes while maintaining the energy-stability for the ternary model in [3], lie in the sixth order polynomial potential term, and it remains an open problem.

Many phase field models available so far satisfy total energy dissipation, especially, the ones derived using the generalized Onsager principle. While developing numerical schemes to solve the phase field models, it is especially desirable to preserve such an energy dissipation law at the discrete level. On the one hand, the preservation of the energy law is critical for the numerical schemes to capture the correct long time dynamics of the system. On the other hand, the energy-law preserving schemes provides flexibility for dealing with the stiffness issue in phase-filed models. In particular, the dynamics of the coarse-graining (macroscopic) process may undergo rapid changes near the interface, so the non-compliance of energy dissipation laws may lead to spurious numerical solutions if the grid and time step sizes are not carefully chosen.

In this paper, we consider a new ternary phase field model proposed in [5], which is not originated from the addition of biphasic free energies derived in [3, 18]. In the traditional approach [3, 18], the authors introduce three phase variables which add up to be 1. Although one can always eliminate one phase variable during numerical simulations. However, we note that, after elimination, the transport equations may be quite complicated. For the model in [5], only two phase variables are introduced to describe the three fluid components, where the two phase variables are coupled nonlinearly in the free energy functional and the free energy functional as well as the resulting transport equations for the phase variables are simpler. This allows us to develop elegant numerical schemes to solve the equations in this paper. It is remarkable that analogous approaches have been used to study the multiphasic fluid mixture of liquid crystals and viscous fluids [31, 34, 37, 40], where the liquid crystal phase is introduced in the similar way through a nonlinear coupling with the phase variable. In addition, to conserve the volume of each phase, we modify the free energy functional in the model derived in [5] by adding two penalty terms (cf. [11]).

The model in [5] is proposed for three phase fluid systems in which two pairs of the surface tension coefficients between adjacent fluid phases are identical. The phase variables in this model should be called label functions more appropriately. When the transport equation is formulated using the Allen–Cahn equation, the total volume of the fluid mixture is naturally conserved. In contrast, one has to imposed a penalty functional to enforce the constrain using the traditional three phase model when formulating using the Allen–Cahn equation. In addition, the transport equation in this model is simpler compared to the equations of the traditional three-phase model after one phase variable is eliminated in [3, 18]. Aside from the triple point where all three phases meet, the model and the traditional three phase model all give a reasonably good approximation to the surface energy in the mixture system. This prompted us to develop an efficient numerical approximation to the new model and use it to study interfacial dynamics of three-phase fluid mixtures.

One of the objectives of this paper is to construct efficient numerical schemes to solve the coupled three-phase hydrodynamic model that (i) is stable, (ii) satisfies a discrete energy dissipation law, and (iii) leads to linear and decoupled elliptic equations to solve at each time step. This is by no means an easy task due to the nonlinear couplings among the velocity, the pressure and the multiple phase variables. The second objective is to implement the scheme to simulate three multiphasic phenomena involving multiphasic fluids of three distinct viscous fluid components. First, we simulate how a pair of encapsulated binary fluid drops merge into a single one. Second, we simulate a liquid lens situated at the interface between two distinct viscous fluids. Third, we simulate a rising fluid bubble through a stratified viscous fluid layer. The simulations reveal many details during the complex interfacial dynamical processes, which has not been exposed before via numerical simulations.

The rest of the paper is organized as follows. In the next section, we describe the three-phase field model and derive the associated energy dissipation law. In Sect. 3, we construct the decoupled, linear, energy stable numerical scheme to solve the coupled nonlinear partial differential equation system and prove its energy stability. In Sect. 4, we benchmark the convergence rate of the model and perform numerical simulations on three applications to illustrate the efficiency of the proposed scheme and to reveal details of the three non-equilibrium interfacial dynamical processes. In Sect. 5, we give the concluding remark.

2 Phase-Field Model for Three-Phase Viscous Fluid Mixtures

In the traditional framework of the phase-field method for two-phase fluid flows, one needs a labeling function or phase variable \(\phi (x,t)\) to identify the two distinct fluid phases, namely

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi =1, &{} \text {for fluid I},\\ \phi =-1, &{} \text {for fluid II}. \end{array}\right. } \end{aligned}$$
(2.1)

where a thin smooth transitional layer of finite thickness connects the two fluids so that the interface of the two phase fluid is described by the zero level set \(\Gamma _t=\{x: \phi (x,t)=0\}\). Thereafter, the motion of the free moving interface is automatically tracked by dynamics of the diffusive interface model. Hence, the mixing energy functional is defined as follows:

$$\begin{aligned} E^{bi}_{mix}= \int _\Omega \lambda \left( \frac{\varepsilon }{2}|\nabla \phi |^2+ F(\phi )\right) dx, \end{aligned}$$
(2.2)

where \(\Omega \in \mathbb {R}^3\) is a smooth domain, \(F(\phi )=\frac{1}{4\varepsilon }(\phi ^2-1)^2\) is the Ginzburg–Landau double-well potential, \(\lambda \) is the surface tension parameter and \(\varepsilon \) is a parameter describing the interfacial thickness. The two parts of the energy functional represents the “hydrophilic” and the “hydrophobic” tendency of the two fluids, respectively.

Extending the approach for modeling the two phase case, a model for three-phase fluids is developed by introducing an additional labeling variable \(\psi (x,t)\) in [5]. Specifically, a single phase is characterized by \(\{\psi =1\}\) where \(\phi \) is not defined. In the region represented by \(\{\psi =-1\}\), there are two phases distinguished by different values of \(\{\phi =1\}\) and \(\{\phi =-1\}\), namely

$$\begin{aligned} {\left\{ \begin{array}{ll} \psi =1, &{} \text {for fluid I},\\ \psi =-1, \phi =1, &{} \text {for fluid II },\\ \psi =-1, \phi =-1, &{} \text {for fluid III }. \end{array}\right. } \end{aligned}$$
(2.3)

Then, the mixing free energy is defined as follows:

$$\begin{aligned} \begin{aligned} E^{tri}_{mix}&=\int _\Omega W(\phi ,\psi ,\nabla \phi ,\nabla \psi )dx\\&= \int _\Omega \bigg (\lambda _1(\phi )\left( \frac{1}{ 2} |\nabla \psi |^2+F_1(\psi ) \right) +\lambda _{23}\left( \frac{\psi -1}{2}\right) ^2\left( \frac{1}{ 2} |\nabla \phi |^2+F_2(\phi ) \right) \bigg )d{\mathbf x}, \end{aligned} \end{aligned}$$
(2.4)

where \(F_1(\psi )=\frac{1}{4\varepsilon (\phi )^2}(\psi ^2-1)^2\) and \(F_2(\phi )=\frac{1}{4\varepsilon _{23}^2}(\phi ^2-1)^2\). \(\varepsilon (\phi )\) and \(\varepsilon _{23}\) are model parameters describing interfacial thickness along different phases, \(\lambda _1(\phi )\) and \(\lambda _{23}\) measure surface tensions at the interfaces, where \(\varepsilon (\phi )=\varepsilon _{12} \) if \(\phi =1\), \(\varepsilon (\phi )=\varepsilon _{13} \) if \(\phi =-1\); \(\lambda _1(\phi )=\lambda _{12} \) if \(\phi =1\) and \(\lambda _1(\phi )=\lambda _{13} \) if \(\phi =-1\). One particular choice is given as

$$\begin{aligned} \lambda _1(\phi ) = \lambda _{12} \frac{(1+ \phi )^2}{2} + \lambda _{13} \frac{(1-\phi )^2}{2}, \quad \varepsilon (\phi ) = \varepsilon _{12} \frac{(1+\phi )^2}{2} + \varepsilon _{13} \frac{(1-\phi )^2}{2}. \end{aligned}$$
(2.5)

In other words, \((\lambda _{12},\varepsilon _{12})\), \((\lambda _{13},\varepsilon _{13})\) and \((\lambda _{23},\varepsilon _{23})\) are the surface tension parameter and interfacial parameter along the interface of fluid I and II, I and III, II and III, respectively. Notice that the coefficient \((\frac{\psi -1}{2})^2\) is used to ensure that the interaction between two different phases (fluid II and III) do not directly influence the bulk of fluid I. Figure 1 illustrates the model parameters and the three fluid components labeled by the two phase variables \(\psi \) and \(\phi \), respectively.

Fig. 1
figure 1

A schematic illustration of the three components and model parameters distinguished/labeled by two phase variables

Full size image

The total energy of the three-phase fluid system is a sum of the kinetic energy \(E_{kin}\) and the mixing energy \(E^{tri}_{mix}\) [5]:

$$\begin{aligned} \begin{aligned} E&=E_{kin}+E^{tri}_{mix}=\int _\Omega \left( \frac{1}{2}\rho |{\mathbf u}|^2+ W(\phi ,\psi ,\nabla \phi ,\nabla \psi )\right) d{x}, \end{aligned} \end{aligned}$$
(2.6)

where \(\rho \) is the density of the fluid system, \(\varvec{u}\) is the average fluid velocity. In this model, we assume \(\rho \) is a constant.

Assuming a solenoidal velocity field and following the generalized Onsager principle, in which the flux associated to the labeling function is proportional to the gradient of the chemical potential [7, 12, 21, 22, 36], one derives the following Allen–Cahn type transport equations for the phase variables coupled with the momentum transport equation:

$$\begin{aligned} \psi _t+(\varvec{u}\cdot \nabla )\psi= & {} -M_1\mu _1,\quad \mu _1=\frac{\delta E}{\delta \psi }, \end{aligned}$$
(2.7)
$$\begin{aligned} \phi _t+(\varvec{u}\cdot \nabla )\phi= & {} -M_2\mu _2, \quad \mu _2=\frac{\delta E}{\delta \phi }, \end{aligned}$$
(2.8)
$$\begin{aligned} \rho (\varvec{u}_t+(\varvec{u}\cdot \nabla ) \varvec{u})+\nabla p= & {} \nabla \cdot \sigma _{v}-\mu _1\nabla \psi -\mu _2\nabla \phi , \end{aligned}$$
(2.9)
$$\begin{aligned} \nabla \cdot \varvec{u}= & {} 0, \end{aligned}$$
(2.10)

where p is the hydrostatic pressure, \(M_1\) and \(M_2\) are the reciprocals of two relaxation time coefficients, \(\sigma _{v}=\nu (\frac{\nabla \varvec{u}+(\nabla \varvec{u})^T}{2})\) is the viscous stress with the viscosity \(\nu \) [20].

In the formulation, we notice that the volume of each phase is not automatically conserved even if one adopts the Cahn–Hilliard type equations. In fact, the volume \(V_i, i=1,2,3\) for each phase is given by

$$\begin{aligned} \begin{aligned}&V_1(\psi )= \int _\Omega \frac{1+\psi }{2} dx, \\&V_2(\psi ,\phi )= \int _\Omega \frac{(1-\psi )}{2} \frac{(1+\phi )}{2} dx, \\&V_3(\psi ,\phi ) = \int _\Omega \frac{(1-\psi )}{2} \frac{(1-\phi )}{2} dx, \end{aligned} \end{aligned}$$
(2.11)

in which two integrands are nonlinear. The following identity always holds though,

$$\begin{aligned} V_1(\psi ) + V_2(\psi ,\phi ) + V_3(\psi ,\phi ) = |\Omega |. \end{aligned}$$
(2.12)

Thus, we modify the free energy functional by adding two penalty terms to conserve \(V_1(\psi )\) and \(V_2(\psi ,\phi )\), then \(V_3(\psi ,\phi )\) is automatically conserved. To this end, the modified free energy reads as follows.

$$\begin{aligned} E = E_{kin}+E^{tri}_{mix} + A_1 (V_1(\psi ) -\alpha )^2 + A_2 (V_2(\psi ,\phi ) - \beta )^2, \end{aligned}$$
(2.13)

where \(\alpha =V_1(\psi _0),\beta =V_2(\psi _0,\phi _0)\), \(A_1,A_2\) are two positive model parameters or Lagrange multipliers.

Remark 2.1

There is an alternative way to conserve the volume instead of modifying the free energy functional. For example, one can add a scalar Lagrange multiplier in (2.7) and (2.8) directly to enforce this conservation property (cf. [33]). However, due to nonlinear degeneracy of phase variable \(\phi \) and the nonlinearity of \(V_2\) and \(V_3\), such a formulation may be very complicated, which we will not pursue in this paper.

Remark 2.2

Notice that this model automatically satisfies the constraints that the volume fraction of each phase adds up to be 1, where the original approaches [3, 18] require a Lagrange multiplier to enforce that. This indicates that the model conserves the total volume of the material system, but not that of each phase. The later has to be enforced by penalizing potentials.

Remark 2.3

This model is an alternative way to formulate a phase field model for three-phase material systems using labeling functions. Assuming label \(\phi \) does not vary rapidly across the interface where \(\psi \) has a transitional layer, the model does provide a method to yield the surface tension approximating the sharp interface limit across all three phase boundaries. This is certainly valid in the case where each phase occupies a reasonably large domain and away from the triple point. A detailed comparison with the three phase model used in [3, 18] is perhaps in order. But, that is certain beyond the scope of this paper.

For simplicity, we consider in this paper where the three fluids have matching densities and viscosities i.e., \(\rho _1=\rho _2=\rho _3=1\) and \(\nu _1=\nu _2=\nu _3=\nu \). When the three fluids have different densities with a relative small density ratio, one can use the Boussinesq approximation to derive an approximation which models the effect of different densities by a gravitational force [21, 33]. The case of different viscosities can usually be dealt with in a straightforward manner by assuming the viscosity is a linear or harmonic average of the phase functions.

We also assume that \((\lambda _{12},\lambda _{13},\lambda _{23})=(\lambda _1,\lambda _1,\lambda _2)\) and \((\varepsilon _{12},\varepsilon _{13},\varepsilon _{23})=(\varepsilon _1,\varepsilon _1,\varepsilon _2)\) for simplicity as well. The case of \(\lambda _{12}\ne \lambda _{13}\) will bring more complexities induced by nonlinear couplings in the system, which will be investigated in the future. With the assumptions, the simplified energy becomes

$$\begin{aligned} \begin{aligned} E^{tri}_{mix}&=\int _\Omega \left( \lambda _1\left( \frac{1}{ 2} |\nabla \psi |^2+F_1(\psi )\right) +\lambda _{2}\left( \frac{\psi -1}{2}\right) ^2\left( \frac{1}{ 2} |\nabla \phi |^2+F_2(\phi ) \right) \right) dx. \end{aligned} \end{aligned}$$
(2.14)

Then, the system (2.7)–(2.10) reduces to the following in the dimensionless form,

$$\begin{aligned}&\psi _t+(\varvec{u}\cdot \nabla )\psi =-M_1\mu _1, \end{aligned}$$
(2.15)
$$\begin{aligned}&\mu _1=\lambda _1(-\Delta \psi +f_1(\psi ))+\lambda _2\left( \frac{\psi -1}{2}\right) \left( \frac{|\nabla \phi |^2}{2}+F_2(\phi )\right) +A_1(V_1(\psi )-\alpha )\nonumber \\&\quad \qquad -\,A_2(V_2(\psi ,\phi )-\beta )\left( \frac{1+\phi }{2}\right) , \end{aligned}$$
(2.16)
$$\begin{aligned}&\phi _t+(\varvec{u}\cdot \nabla ) \phi =-M_2\mu _2, \end{aligned}$$
(2.17)
$$\begin{aligned}&\mu _2=\lambda _2\left( -\nabla \cdot \left( \frac{\psi -1}{2}\right) ^2\nabla \phi +\left( \frac{\psi -1}{2}\right) ^2 f_2(\phi )\right) +A_2(V_2(\psi ,\phi )-\beta )\left( \frac{1-\psi }{2}\right) ,\nonumber \\ \end{aligned}$$
(2.18)
$$\begin{aligned}&\varvec{u}_t+(\varvec{u}\cdot \nabla ) \varvec{u}+\nabla p=\nu \Delta \varvec{u}-\mu _1\nabla \psi -\mu _2\nabla \phi , \end{aligned}$$
(2.19)
$$\begin{aligned}&\nabla \cdot \varvec{u}=0. \end{aligned}$$
(2.20)

Throughout the paper, we adopt the following boundary conditions

$$\begin{aligned} \varvec{u}|_{\partial \Omega }=0,\partial _n \phi |_{\partial \Omega }=0,\partial _n \psi |_{\partial \Omega }=0. \end{aligned}$$
(2.21)

Since the above system is consistent with the generalized Onsager principle, it can be readily established that the total energy of the system (2.7)–(2.10) is dissipative. Namely, taking the inner product of (2.7) with \(\frac{\delta E}{\delta \psi }\), (2.8) with \(\frac{\delta E}{\delta \phi }\), and (2.9) with \(\varvec{u}\), and then summing up these equalities, we obtain the following energy dissipation law:

$$\begin{aligned} \frac{d}{dt} E=-\int _\Omega \left( \nu |\nabla \varvec{u}|^2+ M_1\Big |\frac{\delta E}{\delta \psi }\Big |^2+ M_2\Big |\frac{\delta E}{\delta \phi }\Big |^2\right) dx\le 0. \end{aligned}$$
(2.22)

We notice that the nonlinear terms in \(\frac{\delta E}{\delta \psi }\) and \(\frac{\delta E}{\delta \phi }\) involve second order derivatives so that it is not convenient to use them as test functions in numerical approximations, making it difficult to obtain the energy dissipation law in the fully discrete level. To overcome this difficulty, we have to reformulate the system (2.17)–(2.20) in an alternative form which is convenient for numerical approximations. We denote the material derivative by

$$\begin{aligned} \dot{\psi }=\psi _t+(\varvec{u}\cdot \nabla ) \psi ,\dot{\phi }=\phi _t+(\varvec{u}\cdot \nabla )\phi . \end{aligned}$$
(2.23)

The momentum equation (2.19) can be rewritten as follows:

$$\begin{aligned} \varvec{u}_t+(\varvec{u}\cdot \nabla ) \varvec{u}-\nu \Delta \varvec{u}+\nabla p+\frac{\dot{\phi }}{M_2}\nabla \phi +\frac{\dot{\psi }}{M_1}\nabla \psi =0. \end{aligned}$$
(2.24)

To derive the energy law, we take the inner products of (2.15) with \(\frac{\psi _t}{M_1}\), (2.17) with \(\frac{\phi _t}{M_2}\), and (2.24) with \(\varvec{u}\) to arrive at

$$\begin{aligned}&\frac{\Vert \dot{\psi }\Vert ^2}{M_1}-\left( \frac{\dot{\psi }}{M_1},(\varvec{u}\cdot \nabla )\psi \right) =\lambda _1\partial _t\left( \frac{\Vert \nabla \psi \Vert ^2}{2}+(F_2(\psi ),1)\right) \nonumber \\&\quad +\,\lambda _2\left( \left( \frac{\psi -1}{2}\right) \left( \frac{|\nabla \phi |^2}{2}+F_2(\phi )\right) ,\psi _t\right) \nonumber \\&\quad +A_1(V_1(\psi )-\alpha ,\psi _t)-A_2\left( \left( V_2(\psi ,\phi )-\beta \right) \left( \frac{1+\phi }{2}\right) ,\psi _t\right) ,\end{aligned}$$
(2.25)
$$\begin{aligned}&\frac{\Vert \dot{\phi }\Vert ^2}{M_2}-\left( \frac{\dot{\phi }}{M_2},(\varvec{u}\cdot \nabla )\phi \right) =\lambda _2\left( -\nabla \cdot \left( \frac{\psi -1}{2}\right) ^2\nabla \phi +\left( \frac{\psi -1}{2}\right) ^2 f_2(\phi ),\phi _t\right) \nonumber \\&\quad +\,A_2\left( (V_2(\psi ,\phi )-\beta )\left( \frac{1-\psi }{2}\right) ,\phi _t\right) , \end{aligned}$$
(2.26)

and

$$\begin{aligned} \frac{1}{2}\partial _t\Vert \varvec{u}\Vert ^2+\nu \Vert \nabla \varvec{u}\Vert ^2+ \left( \frac{\dot{\psi }}{M_1}\nabla \psi ,\varvec{u}\right) + \left( \frac{\dot{\phi }}{M_2}\nabla \phi , \varvec{u}\right) =0. \end{aligned}$$
(2.27)

Here, the inner product of the function f(x) and g(x) and \(L^2\) norm \(\Vert f\Vert \) is defined as follows:

$$\begin{aligned} (f,g)=\int _{\Omega } f(x)g(x) dx, \qquad \Vert f\Vert =(f,f)^{\frac{1}{2}}. \end{aligned}$$
(2.28)

We notice that the following identities hold.

$$\begin{aligned}&\partial _t\left( \left( \frac{\psi -1}{2}\right) ^2\left( \frac{|\nabla \phi |^2}{2}+F_2(\phi )\right) , 1\right) =\left( \left( \frac{\psi -1}{2}\right) ^2\nabla \phi , \nabla \phi _t\right) +\left( \left( \frac{\psi -1}{2}\right) ^2f_2(\phi ), \phi _t\right) \nonumber \\&\quad +\,\left( \left( \frac{\psi -1}{2}\right) \left( \frac{|\nabla \phi |^2}{2}+F_2(\phi )\right) , \phi _t\right) , \end{aligned}$$
(2.29)
$$\begin{aligned}&\qquad \,\partial _t((V_2(\psi ,\phi )-\beta )^2, 1) =-\left( V_2(\psi ,\phi )-\beta , \left( \frac{1+\phi }{2}\right) \psi _t \right) \nonumber \\&\quad +\,\left( V_2(\psi ,\phi )-\beta , \left( \frac{1-\psi }{2}\right) \phi _t\right) , \end{aligned}$$
(2.30)

and

$$\begin{aligned} \partial _t((V_1(\psi )-\alpha )^2, 1)=(V_1(\psi )-\alpha , \psi _t). \end{aligned}$$
(2.31)

Summing up the above equalities (2.25)–(2.27) and applying (2.29)–(2.31), we arrive at the following result:

Lemma 2.1

Solutions of (2.15)–(2.20) satisfy the following energy law:

$$\begin{aligned} \begin{aligned} \frac{d}{dt} E&=\frac{d}{dt} \int _\Omega \bigg \{\frac{1}{2}|\varvec{u}|^2+\lambda _1 \left( \frac{|\nabla \psi |^2}{2}+F_1(\psi ),1\right) +\lambda _2\left( \left( \frac{\psi -1}{2}\right) ^2,\frac{|\nabla \phi |^2}{2}+F_2(\phi )\right) \\&\quad +A_1(V_1(\psi )-\alpha )^2+A_2(V_2(\psi ,\phi )-\beta )^2\bigg \}dx \\&=-\int _\Omega \left( \nu |\nabla \varvec{u}|^2+\frac{|\dot{\psi }|^2}{M_1}+\frac{|\dot{\phi }|^2}{M_2}\right) dx\le 0. \end{aligned} \end{aligned}$$
(2.32)

We note that the above derivation is suitable in a finite dimensional approximation since test functions \(\phi _t\), \(\psi _t\) are in the same subspaces as \(\phi \) and \(\psi \). Hence, it allows us to design numerical schemes which satisfy a discrete energy law.

3 Decoupled Semi-discretized Scheme in Time

The coupled nonlinear partial differential equation system (2.15)–(2.20) presents many challenges for algorithm design, implementation as well as numerical analysis. In particular, one has to overcome the following difficulties:

  • the coupling of the velocity and the pressure through the incompressible condition;

  • nonlinear couplings among the equations through convection terms and the nonlinear stress.

  • the stiffness in the phase transport equations as well as the nonlinear coupling between the two phase variables.

It is widely believed that the compliance of discrete energy dissipation laws usually serves as the justification of fine numerical approximations and results, when no benchmark solutions are available. In addition, use of energy stable schemes usually enables the use of relatively large time steps, the size of which is dictated only by accuracy considerations. Therefore, in this paper, the emphasis of our algorithm development is placed on designing numerical schemes that are not only easy-to-implement, but also satisfy a discrete energy dissipation law.

We now construct an energy stable scheme based on a stabilization strategy [29] for a double well potential to avoid nonlinear iterations. The convex splitting technique can be applied as well, but the resulted scheme is nonlinear. So, we will not pursue in this study. To this end, we shall assume that \(F_1(\psi )\) and \(F_2(\phi )\) satisfy the following conditions: there exist constant \(L_1\) and \(L_2\) such that

$$\begin{aligned} \max _{|\psi |\in \mathbb R}|F_1''(\psi )|\le L_1,\quad \max _{|\phi |\in \mathbb R}|F_2''(\phi )|\le L_2. \end{aligned}$$
(3.1)

One immediately notices that this condition is not satisfied by the usual Ginzburg–Landau double-well potential. However, since it is well-known that the Allen–Cahn equation satisfies the maximum principle (for Cahn–Hilliard equation, a similar result is established in [6]), it is common practice that one truncates this fourth order polynomial to quadratic growth outside of an interval \([-M,M]\) without affecting the solution if the maximum norm of the initial condition \(\phi _0\) is bounded by M. Therefore, one can (cf. [9, 17, 29]) consider the Allen–Cahn and Cahn–Hilliard equations with a truncated double-well potential \(\tilde{F}_1(\phi ), \tilde{F}_2(\psi )\). It is then obvious that there exist \(L_i, i=1,2\) such that (3.1) is satisfied with \(F_i\) replaced by \(\tilde{F}_i, i=1,2\).

The new numerical scheme reads as follows.

Algorithm: Given the initial conditions \(\phi ^0\), \(\psi ^0\), \(\varvec{u}^0\) and \(p^0=0\), having computed \(\phi ^n\), \(\psi ^n\), \(\varvec{u}^n\) and \(p^n\) for \(n> 0\), we compute \((\phi ^{n+1},\psi ^{n+1},\tilde{\varvec{u}}^{n+1}, \varvec{u}^{n+1},p^{n+1})\) by

Step 1:

$$\begin{aligned} \left\{ \begin{aligned}&{C^n}(\phi ^{n+1}-\phi ^n)+\frac{1}{M_2}\dot{\phi }^{n+1}=\lambda _2\nabla \cdot \left( \frac{\psi ^{n}-1}{2}\right) ^2\nabla \phi ^{n+1}-\lambda _2\left( \frac{\psi ^{n}-1}{2}\right) ^2f_2(\phi ^{n})\\&-A_2(V_2(\psi ^n,\phi ^n)-\beta )\left( \frac{1-\psi ^n}{2}\right) ,\\&\frac{\partial \phi ^{n+1}}{\partial n}|_{\partial \Omega }=0, \end{aligned} \right. \end{aligned}$$
(3.2)

with

$$\begin{aligned} \dot{\phi }^{n+1}=\frac{\phi ^{n+1}-\phi ^n}{\delta t}+\left( \varvec{u}^{n}_{\star }\cdot \nabla \right) \phi ^n,\quad \varvec{u}^n_{\star }=\varvec{u}^n-\delta t\frac{\dot{\phi }^{n+1}}{M_2}\nabla \phi ^n. \end{aligned}$$
(3.3)

Step 2:

$$\begin{aligned} \left\{ \begin{aligned}&{S^n}(\psi ^{n+1}-\psi ^n)+\frac{1}{M_1}\dot{\psi }^{n+1} =\lambda _1(\Delta \psi ^{n+1}-f_1(\psi ^{n}))-\lambda _2\left( \frac{\psi ^{n+1}-1}{2}\right) W(\phi ^{n+1})\\&-A_1(V_1(\psi ^n)-\alpha )+A_2(V_2(\psi ^n,\phi ^n)-\beta ) \left( \frac{1+\phi ^{n+1}}{2}\right) \\&\frac{\partial \psi ^{n+1}}{\partial n}|_{\partial \Omega }=0, \end{aligned} \right. \!\!\!\nonumber \\ \end{aligned}$$
(3.4)

with

$$\begin{aligned} \dot{\psi }^{n+1}=\frac{\psi ^{n+1}-\psi ^n}{\delta t}+( \varvec{u}^{n}_{\star \star }\cdot \nabla )\psi ^n, \varvec{u}^n_{\star \star }=\varvec{u}^n_\star -\delta t\frac{\dot{\psi }^{n+1}}{M_1}\nabla \psi ^n. \end{aligned}$$
(3.5)

and

$$\begin{aligned} W(\phi ^{n+1})=\frac{|\nabla \phi ^{n+1}|^2}{2}+F_2(\phi ^{n+1}). \end{aligned}$$
(3.6)

Step 3:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\tilde{\varvec{u}}^{n+1}-\varvec{u}^n}{\delta t}+(\varvec{u}^n\cdot \nabla )\tilde{\varvec{u}}^{n+1}-\nu \Delta \tilde{\varvec{u}}^{n+1}+\nabla p^n+\frac{\dot{\psi }^{n+1}}{M_1}\nabla \psi ^n+\frac{\dot{\phi }^{n+1}}{M_2}\nabla \phi ^n=0,\\&\tilde{\varvec{u}}^{n+1}|_{\partial \Omega }=0, \end{aligned} \right. \nonumber \\ \end{aligned}$$
(3.7)

Step 4:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\varvec{u}^{n+1}-\tilde{\varvec{u}}^{n+1}}{\delta t}+\nabla (p^{n+1}-p^n)=0,\\&\nabla \cdot \varvec{u}^{n+1}=0, \\&n\cdot \varvec{u}^{n+1}|_{\partial \Omega }=0. \end{aligned} \right. \end{aligned}$$
(3.8)

In the above, \(C^n\) and \(S^n\) are two stabilizing parameters to be determined in simulations.

The above scheme is constructed by combining several effective approaches in the approximation of Allen–Cahn equation [29], Navier–Stokes equations [13] and phase-field models [4, 24, 30].

For the new scheme, we give several remarks as follows.

  • A pressure-correction scheme [13] is used to decouple the computation of the pressure from that of the velocity in step 4.

  • We recall that nonlinear terms \(f_1\) and \(f_2\) both take the form like \(\frac{1}{\varepsilon ^2}\phi (\phi ^2-1)\), so the explicit treatment of this term usually leads to a severe restriction on the time step \(\delta t\) when \(\varepsilon \ll 1\). Thus we introduce in (3.2) and (3.4) two linear “stabilizing” terms to improve the stability while preserving simplicity. It allows us to treat the nonlinear term explicitly without suffering from any time step constraint [28–30]. Note that this stabilizing term introduces an extra consistent error of order \(O({\delta t})\) in a small region near the interface, but this error is of the same order as the error introduced by treating it explicitly, so the overall truncation error is essentially of the same order with or without the stabilizing term. It is noticeable that the truncation error of the stabilizing approach is exactly same as the convex splitting method.

  • Inspired by [4, 24, 31], which deal with a phase-field model of three-phase viscous fluids, we introduce two new, explicit, convective velocities \(\varvec{u}_{\star }^n\) and \(\varvec{u}^n_{\star \star }\) in the phase equations. \(\varvec{u}_{\star }^n\) and \(\varvec{u}^n_{\star \star }\) can be computed directly from (3.3) and (3.5), i.e.

    $$\begin{aligned} \varvec{u}^n_\star= & {} \left( I+\frac{\delta t}{M_2} \left( \nabla \phi ^n\right) ^T\nabla \phi ^n\right) ^{-1}\left( \varvec{u}^n-\frac{1}{M_2}(\phi ^{n+1}-\phi ^n)\nabla \phi ^n\right) , \end{aligned}$$
    (3.9)
    $$\begin{aligned} \varvec{u}^n_{\star \star }= & {} \left( I+\frac{\delta t}{M_1}(\nabla \psi ^n)^T\nabla \psi ^n\right) ^{-1}\left( \varvec{u}^n_\star -\frac{1}{M_1}(\psi ^{n+1}-\psi ^n)\nabla \psi ^n\right) . \end{aligned}$$
    (3.10)

    It is easy to get \(det(I+c(\nabla \phi )^T\nabla \phi )=1+c\nabla \phi \cdot \nabla \phi \), thus the above matrix is invertible.

  • The scheme (3.2)–(3.8) is a totally decoupled, linear scheme. Indeed, (3.2), (3.4) and (3.7) are respectively (decoupled) linear elliptic equations for \(\phi ^{n+1}\), \(\psi ^{n+1}\) and \(\tilde{\varvec{u}}^{n+1}\), and (3.8) can be reformulated as a Poisson equation for \(p^{n+1}-p^n\). Therefore, at each time step, one only needs to solve a sequence of decoupled elliptic equations which can be solved very efficiently.

  • As we shall show below, the above scheme is energy stable. To the best of the authors’ knowledge, this is the first such scheme for a model of ternary phase field model that has the linear and decoupling properties at the same time.

Theorem 3.1

Under condition (3.1) and

$$\begin{aligned} C^n\ge & {} \frac{1}{2}\lambda _2L_2\Big \Vert \frac{\psi ^n-1}{2}\Big \Vert _\infty ^2+A_2|\Omega |\Big \Vert \frac{1-\psi ^n}{2}\Big \Vert _\infty ^2,\\ S^n\ge & {} \frac{1}{2}\lambda _1L_1+\frac{A_1}{4}|\Omega |+A_2|\Omega |\Big \Vert \frac{1+\phi ^{n+1}}{2}\Big \Vert ^2_\infty , \end{aligned}$$

the scheme defined by (3.2)–(3.8) admits a unique solution satisfying the following discrete energy dissipation law:

$$\begin{aligned} \begin{aligned} \frac{1}{2}\Vert \varvec{u}^{n+1}\Vert ^2&+E_1^{n+1}+E_2^{n+1}+\frac{\delta t^2}{2}\Vert \nabla p^{n+1}\Vert ^2 +\bigg \{\nu \delta t\Vert \nabla \tilde{\varvec{u}}^{n+1}\Vert ^2 +\delta t\left( \frac{|\dot{\psi }^{n+1}|^2}{M_1}+\frac{|\dot{\phi }^{n+1}|^2}{M_2}\right) \bigg \}\\&\le \frac{1}{2}\Vert \varvec{u}^{n}\Vert ^2+E_1^{n}+E_2^{n}+\frac{\delta t^2}{2}\Vert \nabla p^{n}\Vert ^2, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} E^{n}_1=\lambda _1\left( \frac{1}{2}\Vert \nabla \psi ^{n}\Vert ^2+(F_1(\psi ^{n}),1)\right) , \quad E^{n}_2=\lambda _2\left( \left( \frac{\psi ^{n}-1}{2}\right) ^2, \frac{|\nabla \phi ^{n}|^2}{2}+F_2(\phi ^{n})\right) .\nonumber \\ \end{aligned}$$
(3.11)

Proof

From the definition of \(\varvec{u}^n_\star \) and \(\varvec{u}^n_{\star \star }\) in (3.3) and (3.5), we rewrite the momentum equation (3.7) as follows

$$\begin{aligned} \begin{aligned}&\frac{\tilde{\varvec{u}}^{n+1}-\varvec{u}^n_{\star \star }}{\delta t}+(\varvec{u}^n\cdot \nabla )\tilde{\varvec{u}}^{n+1}-\nu \Delta \tilde{\varvec{u}}^{n+1}+\nabla p^n=0. \end{aligned} \end{aligned}$$
(3.12)

Taking the inner product of (3.12) with \(2\delta t \tilde{\varvec{u}}^{n+1}\) and using the identity

$$\begin{aligned} (a-b,2a)=|a|^2-|b|^2+|a-b|^2, \end{aligned}$$
(3.13)

we obtain

$$\begin{aligned} \begin{aligned}&\Vert \tilde{\varvec{u}}^{n+1}\Vert ^2-\Vert \varvec{u}^n_{\star \star }\Vert ^2+\Vert \tilde{\varvec{u}}^{n+1}-\varvec{u}^n_{\star \star }\Vert ^2+2\nu \delta t\Vert \nabla \tilde{\varvec{u}}^{n+1}\Vert ^2+2\delta t(\nabla p^n, \tilde{\varvec{u}}^{n+1})=0. \end{aligned} \end{aligned}$$
(3.14)

To deal with the pressure term, we take the inner product of (3.8) with \(2\delta t^2\nabla p^n\) to derive

$$\begin{aligned} \begin{aligned} \delta t^2\left( \Vert \nabla p^{n+1}\Vert ^2-\Vert \nabla p^{n}\Vert ^2-\Vert \nabla p^{n+1}-\nabla p^n\Vert ^2\right) =2\delta t (\tilde{\varvec{u}}^{n+1},\nabla p^n). \end{aligned} \end{aligned}$$
(3.15)

Taking the inner product of (3.8) with \(\varvec{u}^{n+1}\), we obtain

$$\begin{aligned} \begin{aligned} \Vert \varvec{u}^{n+1}\Vert ^2+\Vert \varvec{u}^{n+1}-\tilde{\varvec{u}}^{n+1}\Vert ^2=\Vert \tilde{\varvec{u}}^{n+1}\Vert ^2. \end{aligned} \end{aligned}$$
(3.16)

We also derive from (3.8) directly that

$$\begin{aligned} \begin{aligned} \delta t^2\Vert \nabla p^{n+1}-\nabla p^n\Vert ^2=\Vert \tilde{\varvec{u}}^{n+1}-\varvec{u}^{n+1}\Vert ^2. \end{aligned} \end{aligned}$$
(3.17)

Combining all identities above, we obtain

$$\begin{aligned} \begin{aligned}&\Vert \varvec{u}^{n+1}\Vert ^2-\Vert \varvec{u}^n_{\star \star }\Vert ^2+\Vert \tilde{\varvec{u}}^{n+1}-\varvec{u}^n_{\star \star }\Vert ^2+\delta t^2 (\Vert \nabla p^{n+1}\Vert ^2-\Vert \nabla p^n\Vert ^2)\\&\quad +2\nu \delta t\Vert \nabla \tilde{\varvec{u}}^{n+1}\Vert ^2=0. \end{aligned} \end{aligned}$$
(3.18)

Next, we derive from (3.3) and (3.5) that

$$\begin{aligned} \frac{\varvec{u}_\star ^n-\varvec{u}^n}{\delta t}=-\frac{\dot{\phi }^{n+1}}{M_2}\nabla \phi ^n, \end{aligned}$$
(3.19)
$$\begin{aligned} \frac{\varvec{u}_{\star \star }^n-\varvec{u}_\star ^n}{\delta t}=-\frac{\dot{\psi }^{n+1}}{M_1}\nabla \psi ^n. \end{aligned}$$
(3.20)

Taking the inner product of (3.19) with \(2\delta t \varvec{u}_\star ^n\), of (3.20) with \(2\delta t \varvec{u}_{\star \star }^n\) , we obtain

$$\begin{aligned} \Vert \varvec{u}_\star ^n\Vert ^2-\Vert \varvec{u}^n\Vert ^2+\Vert \varvec{u}^n_\star -\varvec{u}_n\Vert ^2=-2\delta t\left( \frac{\dot{\phi }^{n+1}}{M_2}\nabla \phi ^n,\varvec{u}_\star ^n\right) , \end{aligned}$$
(3.21)
$$\begin{aligned} \Vert \varvec{u}_{\star \star }^n\Vert ^2-\Vert \varvec{u}_\star ^n\Vert ^2+\Vert \varvec{u}^n_{\star \star }-\varvec{u}^n_\star \Vert ^2=-2\delta t\left( \frac{\dot{\psi }^{n+1}}{M_1}\nabla \psi ^n,\varvec{u}_{\star \star }^n\right) . \end{aligned}$$
(3.22)

Then, by taking the inner product of (3.2) with \(2(\phi ^{n+1}-\phi ^n)\), we obtain

$$\begin{aligned}&{2C^n}\Vert \phi ^{n+1}-\phi ^n\Vert ^2+2\delta t\frac{\Vert \dot{\phi }^{n+1}\Vert ^2}{M_2}-2\delta t \left( \frac{\dot{\phi }^{n+1}}{M_2}, \left( \varvec{u}_\star ^{n}\cdot \nabla \right) \phi ^n\right) \nonumber \\&+\,2\lambda _2\left( \left( \frac{\psi ^{n}-1}{2}\right) ^2\nabla \phi ^{n+1}, \nabla \phi ^{n+1}-\nabla \phi ^n\right) +2\lambda _2\left( \left( \frac{\psi ^{n}-1}{2}\right) ^2f_2(\phi ^n),\phi ^{n+1}-\phi ^n\right) \nonumber \\&+\,2A_2\left( (V_2(\psi ^n,\phi ^n)-\beta )\left( \frac{1-\psi ^n}{2}\right) ,\phi ^{n+1}-\phi ^n \right) =0. \end{aligned}$$
(3.23)

By taking the inner product of (3.4) with \(2(\psi ^{n+1}-\psi ^n)\), we arrive at

$$\begin{aligned} \begin{aligned}&{2S^n}\Vert \psi ^{n+1}-\psi ^n\Vert ^2+2\delta t\frac{\Vert \dot{\psi }^{n+1}\Vert ^2}{M_1}-2\delta t \left( \frac{\dot{\psi }^{n+1}}{M_1},(\varvec{u}_{\star \star }^{n}\cdot \nabla ) \psi ^n\right) \\&\quad +2\lambda _1\left( \frac{\Vert \nabla \psi ^{n+1}\Vert ^2}{2}-\frac{\Vert \nabla \psi ^n\Vert ^2}{2}+\frac{\Vert \nabla \psi ^{n+1}-\nabla \psi ^n\Vert ^2}{2}\right) \\&\quad +2\lambda _1(f_1(\psi ^{n}),\psi ^{n+1}-\psi ^n)+2\lambda _2\left( \left( \frac{\psi ^{n+1}-1}{2}\right) W(\phi ^{n+1}), \psi ^{n+1}-\psi ^n\right) \\&\quad +2A_1((V_1(\psi ^n)-\alpha ),\psi ^{n+1}-\psi ^n)\\&\quad -2A_2\left( (V_2(\psi ^n,\phi ^n)-\beta )\left( \frac{1+\phi ^{n+1}}{2}\right) ,\psi ^{n+1}-\psi ^n\right) =0. \end{aligned} \end{aligned}$$
(3.24)

Combining (3.18), (3.21), (3.22), (3.23), and (3.24), we arrive at

$$\begin{aligned} \begin{aligned}&\Vert \varvec{u}^{n+1}\Vert ^2-\Vert \varvec{u}^n\Vert ^2+\Vert \tilde{\varvec{u}}^{n+1}-\varvec{u}^n_{\star \star }\Vert ^2+\Vert \varvec{u}^{n}_{\star \star }-\varvec{u}^n_{\star }\Vert ^2+\Vert \varvec{u}^{n}_{\star }-\varvec{u}^n\Vert ^2\\&\qquad +\delta t^2(\Vert \nabla p^{n+1}\Vert ^2-\Vert \nabla p^n\Vert ^2)\\&\qquad +2\nu \delta t\Vert \nabla \tilde{\varvec{u}}^{n+1}\Vert ^2+2\delta t\frac{\Vert \dot{\phi }^{n+1}\Vert ^2}{M_2}+2\delta t\frac{\Vert \dot{\psi }^{n+1}\Vert ^2}{M_1}\\&\qquad +2\lambda _1\left( \frac{\Vert \nabla \psi ^{n+1}\Vert ^2}{2}-\frac{\Vert \nabla \psi ^n\Vert ^2}{2}+\frac{\Vert \nabla \psi ^{n+1}-\nabla \psi ^n\Vert ^2}{2}\right) \\&\qquad +{2S^n}\Vert \psi ^{n+1}-\psi ^n\Vert ^2+{2C^n}\Vert \phi ^{n+1}-\phi ^n\Vert ^2\\&\qquad +2\lambda _1(f_1(\psi ^{n}),\psi ^{n+1}-\psi ^n)\qquad (\text {:Term } A)\\&\qquad +2\lambda _2\left( \left( \frac{\psi ^{n+1}-1}{2}\right) W(\phi ^{n+1}),\psi ^{n+1}-\psi ^n\right) \qquad (\text {:Term } B)\\&\qquad +2\lambda _2\left( \left( \frac{\psi ^{n}-1}{2}\right) ^2\nabla \phi ^{n+1}, \nabla \phi ^{n+1}-\nabla \phi ^n\right) \qquad (:\text {Term } C)\\&\qquad +2\lambda _2\left( \left( \frac{\psi ^{n}-1}{2}\right) ^2f_2(\phi ^{n}),\phi ^{n+1}-\phi ^n\right) \qquad (:\text {Term } D)\\&\qquad +2A_2\left( (V_2(\psi ^n,\phi ^n)-\beta )\left( \frac{1-\psi ^n}{2}\right) ,\phi ^{n+1}-\phi ^n\right) \qquad (:\text {Term } E)\\&\qquad -2A_2\left( (V_2(\psi ^n,\phi ^n)-\beta )\left( \frac{1+\phi ^{n+1}}{2}\right) ,\psi ^{n+1}-\psi ^n\right) (:\text {Term } F)\\&\qquad +2A_1(V_1(\psi ^n)-\alpha ,\psi ^{n+1}-\psi ^n) \qquad (:\text {Term } G)\\&\quad =0. \end{aligned} \end{aligned}$$
(3.25)

We deal with the terms A, B, C, D, E, F, G as follows.

For Term A, we apply the Taylor expansions to obtain

$$\begin{aligned} \begin{aligned} A=2\lambda _1 (F_1(\psi ^{n+1})-F_1(\psi ^n),1)- 2\lambda _1 \left( \frac{f_1'(\xi )}{2},(\psi ^{n+1}-\psi ^n)^2\right) . \end{aligned} \end{aligned}$$
(3.26)

For Term B, we have

$$\begin{aligned} B= & {} 4\lambda _2\left( W(\phi ^{n+1})\left( \frac{\psi ^{n+1}-1}{2}\right) ,\left( \frac{\psi ^{n+1}-1}{2}\right) - \left( \frac{\psi ^n-1}{2}\right) \right) \nonumber \\= & {} 2\lambda _2\left( W(\phi ^{n+1}), \left( \frac{\psi ^{n+1}-1}{2}\right) ^2-\left( \frac{\psi ^{n}-1}{2}\right) ^2\right) +2\lambda _2\left( W(\phi ^{n+1}),\left( \frac{\psi ^{n+1}-\psi ^n}{2}\right) ^2\right) .\nonumber \\ \end{aligned}$$
(3.27)

For Term C, we have

$$\begin{aligned} \begin{aligned} C=2\lambda _2\left( \left( \frac{\psi ^{n}-1}{2}\right) ^2, \frac{|\nabla \phi ^{n+1}|^2}{2}-\frac{|\nabla \phi ^{n}|^2}{2}\right) +2\lambda _2\left( \left( \frac{\psi ^{n}-1}{2}\right) ^2, \frac{|\nabla \phi ^{n+1}-\nabla \phi ^n|^2}{2}\right) .\qquad \end{aligned} \end{aligned}$$
(3.28)

For term D, we apply the Taylor expansion to obtain

$$\begin{aligned} \begin{aligned} D=2\lambda _2\left( \left( \frac{\psi ^{n}-1}{2}\right) ^2,F_2(\phi ^{n+1})-F_2(\phi ^n)-\frac{f_2'(\eta )}{2}(\phi ^{n+1}-\phi ^n)^2\right) . \end{aligned} \end{aligned}$$
(3.29)

For term E and term F, we have

$$\begin{aligned} E+F= & {} 4A_2\left( (V_2(\psi ^n,\phi ^n)-\beta )\left( \frac{1-\psi ^n}{2}\right) , \left( \frac{1+\phi ^{n+1}}{2}\right) -\left( \frac{1+\phi ^{n}}{2}\right) \right) \nonumber \\&+\,4A_2\left( (V_2(\psi ^n,\phi ^n)-\beta )\left( \frac{1+\phi ^{n+1}}{2}\right) , \left( \frac{1-\psi ^{n+1}}{2}\right) -\left( \frac{1-\psi ^{n}}{2}\right) \right) \nonumber \\= & {} 4A_2\left( V_2(\psi ^n,\phi ^n)-\beta ,(V_2(\psi ^{n+1},\phi ^{n+1})-\beta )-(V_2(\psi ^n,\phi ^n)-\beta )\right) \nonumber \\= & {} 2A_2\left( (V_2(\psi ^{n+1},\phi ^{n+1})-\beta )^2-(V_2(\psi ^{n},\phi ^{n})-\beta )^2\right) \nonumber \\&-\,2A_2\left( V_2(\psi ^{n+1},\phi ^{n+1})-V_2(\psi ^n,\phi ^n)\right) ^2. \end{aligned}$$
(3.30)

For Term G, we derive

$$\begin{aligned} \begin{aligned} G&=2A_1(V_1(\psi ^n)-\alpha ,\psi ^{n+1}-\psi ^n)\\&=4A_1\bigg (V_1(\psi ^n)-\alpha ,\left( \frac{1+\psi ^{n+1}}{2}\right) - \left( \frac{1+\psi ^{n+1}}{2}\right) \bigg )\\&=4A_1\bigg (V_1(\psi ^sn)-\alpha ,\left( V_1(\psi ^{n+1})-\alpha \right) -\left( V_1(\psi ^n)- \alpha \right) \bigg )\\&=2A_1\left( \left( V_1(\psi ^{n+1})-\alpha \right) ^2-\left( V_1(\psi ^n)-\alpha \right) ^2\right) -2A_1\left( V_1(\psi ^{n+1})-V_1(\psi ^n)\right) ^2. \end{aligned} \end{aligned}$$
(3.31)

Finally, combining (3.25), (3.26)–(3.29), and dropping some positive terms, we obtain

$$\begin{aligned} \begin{aligned}&\Vert \varvec{u}^{n+1}\Vert ^2-\Vert \varvec{u}^n\Vert ^2+\delta t^2\left( \Vert \nabla p^{n+1}\Vert ^2-\Vert \nabla p^n\Vert ^2\right) +2\nu \delta t\Vert \nabla \tilde{\varvec{u}}^{n+1}\Vert ^2\\&\qquad +2\delta t\left( \frac{|\dot{\psi }^{n+1}|^2}{M_1}+\frac{|\dot{\phi }^{n+1}|^2}{M_2}\right) \\&\qquad +2\lambda _1\left( \frac{\Vert \nabla \psi ^{n+1}\Vert ^2}{2}-\frac{\Vert \nabla \psi ^n\Vert ^2}{2}\right) +2\lambda _1\left( F(\psi ^{n+1})-F(\psi ^n),1\right) \\&\qquad +2\lambda _2\left( W(\phi ^{n+1}),\left( \frac{\psi ^{n+1}-1}{2}\right) ^2\right) -2\lambda _2\left( W(\phi ^n),\left( \frac{\psi ^{n}-1}{2}\right) ^2\right) \\&\qquad +2A_1\left( (V_1(\psi ^{n+1})-\alpha )^2-(V_1(\psi ^{n})-\alpha )^2\right) \\&\qquad +2A_2\left( (V_2(\psi ^{n+1},\phi ^{n+1})-\beta )^2-(V_1(\psi ^{n},\phi ^n)-\beta )^2\right) \\&\qquad +({2S^n}-\lambda _1L_1)\Vert \psi ^{n+1}-\psi ^n\Vert ^2 +\left( 2C^n-\lambda _2 L_2\Big \Vert \left( \frac{\psi ^n-1}{2}\right) ^2\Big \Vert _\infty \right) \Vert \phi ^{n+1}-\phi ^n\Vert ^2\\&\quad \le 2A_1\left( V_1(\psi ^{n+1})-V_1(\psi ^n)\right) ^2+2A_2\left( V_2(\psi ^{n+1},\phi ^{n+1})-V_2(\psi ^n,\phi ^n)\right) ^2. \end{aligned} \end{aligned}$$
(3.32)

The last two terms on the right are estimated as follows.

$$\begin{aligned} (V_1(\psi ^{n+1})-V_1(\psi ^n))^2= & {} \frac{1}{4}\left( \int _\Omega (\psi ^{n+1}-\psi ^n)dx\right) ^2\le \frac{1}{4}|\Omega |\Vert \psi ^{n+1}-\psi ^n\Vert ^2. \nonumber \\ \end{aligned}$$
(3.33)
$$\begin{aligned} (V_2(\psi ^{n+1},\phi ^{n+1})-V_2(\psi ^n,\phi ^n))^2= & {} \Bigg (\int _\Omega \left( \frac{1-\psi ^{n+1}}{2}-\frac{1-\psi ^n}{2}\right) \left( \frac{1+\phi ^{n+1}}{2}\right) dx\nonumber \\&+\int _\Omega \left( \frac{1-\psi ^{n}}{2}\right) \left( \frac{1+\phi ^{n+1}}{2}-\frac{1+\phi ^{n}}{2}\right) dx\Bigg )^2\nonumber \\= & {} \Bigg (-\frac{1}{2}\int _\Omega (\psi ^{n+1}-\psi ^n)\left( \frac{1+\phi ^{n+1}}{2}\right) dx\nonumber \\&+\frac{1}{2} \int _\Omega \left( \frac{1-\psi ^n}{2}\right) (\phi ^{n+1}-\phi ^n)dx\Bigg )^2\nonumber \\\le & {} \frac{1}{2} \left( \int _\Omega (\psi ^{n+1}-\psi ^n)\left( \frac{1+\phi ^{n+1}}{2}\right) dx\right) ^2\nonumber \\&+\frac{1}{2}\left( \int _\Omega \frac{1-\psi ^n}{2}(\phi ^{n+1}-\phi ^n)dx\right) ^2\nonumber \\\le & {} \frac{1}{2}\Big \Vert \frac{1+\phi ^{n+1}}{2}\Big \Vert _\infty ^2\left( \int (\psi ^{n+1}-\psi ^n)dx\right) ^2\nonumber \\&+\frac{1}{2}\Big \Vert \frac{1-\psi ^{n}}{2}\Big \Vert _\infty ^2\left( \int _\Omega (\phi ^{n+1}-\phi ^n)dx\right) ^2\nonumber \\\le & {} \frac{1}{2}\Big \Vert \frac{1+\phi ^{n+1}}{2}\Big \Vert _\infty ^2|\Omega |\Vert \psi ^{n+1}-\psi ^n\Vert ^2\nonumber \\&+\frac{1}{2}\Big \Vert \frac{1-\psi ^{n}}{2}\Big \Vert _\infty ^2|\Omega |\Vert \phi ^{n+1}-\phi ^n\Vert ^2. \end{aligned}$$
(3.34)

Therefore, the terms from (3.33) and (3.34) can be absorbed into the corresponding stabilizing terms of \(C^n\) and \(S^n\), we obtain the desired result.

Remark 3.1

The stability condition of \(C^n\) only depends on the solution of \(\psi ^n\) that is known at \(t=t^n\). More significantly, in spite of the fact that the stability condition of \(S^n\) depends on the solution of \(\phi ^{n+1}\) at \(t=t^{n+1}\) step, but \(\phi ^{n+1}\) is already known from step 1 while computing step 2.

4 Numerical Results and Discussion

In this section, we conduct some numerical experiments using the numerical scheme constructed in Sect. 3 to illustrate its efficiency in resolving interfacial dynamics of three-phase viscous fluid flow problems. In all numerical simulations, after we pre-assign the interfacial thickness parameters \(\varepsilon _i, i=1,2\), the grid resolution is determined to ensure that the interfaces are fully resolved, and the time step is set small enough to attain the desired accuracy.

We note that a detailed parameter study is essential for investigating the physical properties of the proposed three-phase field model. However, in this paper, our focus is to illustrate the efficiency of our proposed energy stable numerical scheme. Therefore, we will use a fixed set of model parameters.

4.1 Spatial Discretization and GPU Implementation

For the spatial operators in the scheme, we use second-order central finite difference methods to discretize them over a uniform grid, where the velocity fields are discretized at the center of mesh surface, and pressure p, phase variables (\(\phi \) and \(\psi \)) are discretized at the cell center, as shown in Fig. 2. The boundary conditions are handled by ghost cells.

Fig. 2
figure 2

Variable locations on the 3-D staggered grid

Full size image

The fully discretized equations in the scheme are implemented on GPUs (graphic processing units) in 3D space for high-performance computing. To better utilize the performance of the GPU, we store all variables in the global memory and store all parameters and mesh information (which do not change during the simulation) in the constant memory such that it drastically reduces the latency of data access.

One advantage of using GPUs is their virtual allocations of processors (we can claim as many thread labors as we desire, even if it is beyond the existing number of multiprocessors on the physical device). Therefore, in our implementation, we allocate as many processors as the degrees of freedom allow.

4.2 Convergence Test in 2D

We first test the convergence rate of the proposed scheme in a 2D domain for time discretization, where \(L_x=L_y=1\), and we choose \(\varepsilon _1=\varepsilon _2=0.01\). In order to eliminate the disturbance from the space discretization, we use \(512 \times 512\) grids in space. We set the exact solution as follows by modifying the governing system of equations through adding appropriate forcing terms.

$$\begin{aligned} \begin{aligned}&\psi (t,x,y)=2+\mathrm{sin}(t)\mathrm{cos}(\pi x)\mathrm{cos}(\pi y),\nonumber \\&\phi (t,x,y)=2+\mathrm{cos}(t)\mathrm{cos}(\pi x)\mathrm{cos}(\pi y),\nonumber \\&u(t,x,y)=\pi \mathrm{sin}(2\pi y)\mathrm{sin}^2(\pi x) \mathrm{sin}(t),\nonumber \\&v(t,x,y)=-\pi \mathrm{sin}(2\pi x)\mathrm{sin}^2(\pi y) \mathrm{sin}(t),\nonumber \\&p(t,x,y)=\mathrm{cos}(\pi x)\mathrm{sin}(\pi y) \mathrm{sin}(t).\nonumber \end{aligned} \end{aligned}$$

In Fig. 3, we show the \(L^1,L^2\) and \(L^\infty \) error at \(t=1\) using the time step size \(\delta t = 2\times 10^{-3}\), \(10^{-3}\), \(5 \times 10^{-4}\), and \(2.5 \times 10^{-4}\), for \(\psi ,\phi , u\) and v, respectively. We observe that the accuracy of our numerical scheme is at least first-order accurate in time.

Fig. 3
figure 3

Temporal convergence rates. The error plots are taken in the norms of \(L_1\), \(L_2\), \(L_\infty \) for phase variables \(\psi \), \(\phi \) and velocity field \(\varvec{u}=(u,v)\), respectively. The slopes of all error curves are close to 1. a The error plot for phase variable \(\psi \). b The error plot for phase variable \(\phi \). c The error plot for velocity component u. d The error plot for velocity component v

Full size image
Fig. 4
figure 4

Dynamics of coalescence of two kissing bubbles. Snapshots are taken at \(t=0, 0.5, 1, 2, 3, 4, 5, 6, 7\), respectively. The color in blue (ambient fluid), red (smaller bubbles) and yellow (bigger bubbles) represent fluids I, II, and III respectively (Color figure online)

Full size image
Fig. 5
figure 5

Discrete energy plot with time during the coalescence process in Example 2

Full size image
Fig. 6
figure 6

3D view and 2D cut-off plane of the initial profile of the liquid lens between stratified fluids in Example 3

Full size image
Fig. 7
figure 7

The steady state of the liquid lens between two stratified fluids for different surface tension parameters. The color in yellow (lens), red (upper half) and blue (lower half) represent fluids I, II, and III respectively. a 3D view and 2D cut-off plane of the liquid lens for \((\lambda _1,\lambda _2,\lambda _3)=(1,1,1)\). b 3D view and 2D cut-off plane of the liquid lens for \((\lambda _1,\lambda _2,\lambda _3)=(2,2,1).\) c 3D view and 2D cut-off plane of the liquid lens for \((\lambda _1,\lambda _2,\lambda _3)=(1,1,2)\) (Color figure online)

Full size image
Fig. 8
figure 8

Dynamics of a rising bubble. Snapshots are taken at \(t=0, 1, 2, 4, 5, 6, 7, 8\). The color in yellow (bubble), blue (lower half) and red (upper half) represent fluids I, II, and III respectively (Color figure online)

Full size image

4.3 Numerical Examples in 3D

The 3D computational domain is set at \(\Omega =[0, L_x] \times [0, L_y] \times [0, L_z]\) where \(L_x, L_y, L_z\) are the domain lengths along the x, y, z axis, respectively. The time step \(\delta t\) is set to be small enough to ensure the obtained numerical results are approximate solutions of the system. In all the numerical studies presented below, we set following parameter values at

$$\begin{aligned} \delta t = 10^{-3}, \quad \varepsilon _1=\varepsilon _2 = 0.01, \quad M_1=M_2 = 10^{-3}. \end{aligned}$$
(4.1)

Next, we present three numerical examples in 3-dimensional space to illustrate the usefulness of the three-phase model and the efficiency of the numerical method.

Example 1

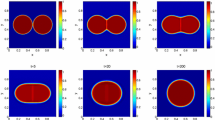
Coalescence of two kissing bubbles We simulate the dynamic coalescent process of two kissing bubbles, each of which is of the core-shell structure of two different viscous fluids. The computational domain is set at \(L_x= L_y= L_z=1\). A \(128\times 128\times 128\) spatial grid is used. Surface tension parameters are set at \(\lambda _1=\lambda _2=1\). Initially, two identical bubbles with the same size and same internal core-shell structure are placed next to each other. In the core-shell structure, the core, a smaller bubble with half of the radius of the larger one is situated at the center inside the larger bubble. We set the fluid outside the bigger bubble as fluid I, the fluid inside the smaller bubble as fluid II, and the rest as fluid III. With this initial setup, we simulate dynamics of the bubbles and depict the dynamical process of coalescence in Fig. 4. At the beginning, it is the fluid in the shell first to merge. At about \(t=4\), the two smaller bubbles collide and start to further coalesce. At \(t=7\), the merging process completes and the final steady state is one bigger bubble enclosing a smaller bubble at the center, a whole new core-shell structure. This dynamical process is the combination of the surface tension effect and the elastic effect from the stress. To illustrate that our numerical scheme indeed respects the discrete energy dissipation law proved in the last section, we plot in Fig. 5 the evolution of the discrete total energy during the coalescence process. We observe from this plot that the discrete energy indeed decays with time.

Example 2

Liquid lens between two stratified fluids. In the second example, we simulate the steady state of a liquid lens which is initially spherical sitting at the interface between two other immiscible viscous fluids shown in Fig. 6. The computational domain is once again \(L_x=L_y=L_z=1\), in which \(128\times 128\times 128\) spatial grids are used. We set the fluid drop or the lens as fluid I, the upper half as fluid II and the lower half as fluid III. In the numerical experiments, we compare the steady states for different surface tension parameters in Fig. 7. When the surface tension among all three components are identical, the steady state shape of the liquid lens is shown in Fig. 7a. When the surface tension between the liquid lens and the neighboring fluid is larger than that between the adjacent fluids (II and III), the lens becomes thicker, shown in Fig. 7b. When the surface tension between the liquid lens and the neighboring fluid is smaller than that between the adjacent fluids, the liquid lens tends to be thinner, shown in Fig. 7c. The numerical results are quantitatively consistent with the “partial spreading” case simulated by the three-component Cahn–Hilliard phase field model proposed in [3, 18]. This shows that the new three-phase model can model the phenomenon as well as the traditional three-phase model.

Example 3

A rising bubble through a stratified viscous fluid layer. In the third example, we simulate a viscous fluid bubble rising up through a stratified fluid layer composed of two viscous fluids driven by a gravity force, where we set the gravity pointing to the upward direction. We consider the case where the density difference of the viscous drop and other ambient fluids is small so that we can use the Boussinesq approximation [5, 21] in the momentum equation as follows:

$$\begin{aligned} \rho _0 (\varvec{u}_t+(\varvec{u}\cdot \nabla )\varvec{u})+\nabla p=\nabla \cdot \sigma _{vis}-\mu _1\nabla \psi -\mu _2\nabla \phi +f_{gty}e_z, \end{aligned}$$
(4.2)

where \(e_z=(0,0,1)\) and the external force is given as

$$\begin{aligned} f_{gty} = -\frac{1+\psi }{2}(\rho _1 - \rho _0) g_0 -\frac{1-\psi }{2} \left( \frac{1+\phi }{2} (\rho _2 - \rho _0) + \frac{1-\phi }{2}(\rho _3 - \rho _0) \right) g_0, \end{aligned}$$
(4.3)

where \(\rho _0\) is the background density, \(\rho _1, \rho _2, \rho _3\) are the densities for each phase, and \(g_0\) is the gravity acceleration. We set \(\rho _0=\rho _2=\rho _3=1, \rho _1=2\), \(\lambda _1=\lambda _2=1\) and \(g_0=80\). The computational domain is \(L_x=L_y=1, L_z=2\), with \(128\times 128 \times 256\) spatial grids.

Figure 8 shows the upward motion of a viscous fluid bubble (Fluid I with \(\psi =1\)) that penetrates a fluid–fluid interface (Fluid II: lower, Fluid III: upper). At \(t=0\), the bubble is immersed in the lower fluid, where the fluid–fluid interface is horizontal and all phases are at rest. Due to the gravity force, as time evolves, the bubble starts to rise up, and then penetrates through the fluid interface with a long and thin filament trapped behind at \(t=7\). Even after the filament pinches off, a small amount of fluid II is still trapped at the lower surface of the bubble at \(t=8\). Qualitatively, this is consistent to the simulations obtained using the sharp interface model in [2, 10].

5 Concluding Remarks

We have developed an energy stable numerical scheme for the three-phase field model consisting of Allen–Cahn type phase-field models coupled to the Navier–Stokes equation proposed in [5]. We first modified the free energy functional in the model to conserve the volume of each phase and satisfies total energy dissipation, then reformulated the model to a form which is suitable for numerical approximations. We then constructed a numerical scheme based on a stabilization technique. The scheme possesses the following properties: (i) it leads to completely decoupled elliptic equations in space to solve at each time step; (ii) it is stable and obeys a discrete energy law; and (iii) all elliptic equations are linear so that fast solvers can be employed. Hence, the numerical scheme is extremely efficient.

This is the first numerical scheme for phase-field models of three-phase viscous fluid flows that decouples the computations of all phase field variables, the velocity, and the pressure leading to linear, elliptic equations at each time step. Our mesh refinement tests confirm the convergence rate. We then presented three numerical examples to illustrate the usefulness of the three-phase field model and the efficiency of the proposed scheme.