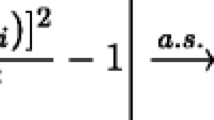The wavelet transforms and statistical models for near infrared spectra analysis

Abstract

Often extensive spectral data is collected on multiple samples with the goal of predicting one or more properties of the sample. For example, measurements can be made at hundreds of wavelengths along with the more expensive assay values. The predictor variables are often highly correlated and it is expected that only small sections of the wave are pertinent to the measured analytes. There is a need to simplify or compress the predictors to both save data storage and possibly de-noise the data prior to making predictive models. Our idea is to use a factorial design (a two-step frame work) to explore two wavelet transformations, Haar wavelets and Daubechies wavelets, with progressively better approximation to the raw data curves in combination with several statistical prediction methods, including stepwise regression, principal component regression, ridge regression and partial least squares regression. The plan is to study prediction quality using Haar-Step, Haar-PCR, Haar-PLS, Haar-Ridge, Daubechies-Step, Daubechies-PCR, Daubechies-PLS and Daubechies-Ridge. Often PLS and stepwise regression can predict substance concentrations equally well. In such situations, the preferred statistical method should be the simplest method. From our studies, we conclude that the type of wavelet is unimportant, the number of wavelets should be large enough to capture most of the variability in the wave forms, and the choice of the statistical method depends on the analyte.

1 Introduction

A major goal of analytical chemistry is to find cost effective ways to determine the amount of analytes in samples. Relatively simple spectral methods are often used as substitutes for more expensive methods. To that end, it is important to have sound statistical methods to calibrate spectral methods. Spectral methods typically produce a large number of highly correlated predictors. A large number of predictors can lead to overly optimistic predictions as some of the predictors can, by chance, fit noise in the system and as noise will change with new samples, the predictions from the training set will not fit new observations. Correlated predictors present their own problems. If simple multiple linear regression is used, the regression coefficients are unstable. There are three standard methods used for data of this type, principal components regression (PCR), ridge regression (RR), and partial least squares (PLS). To these standard methods we add stepwise regression (Step). PLS is the method of choice among most analytical chemist [1].

Our experimental plan is to conduct a factorial design (two-step framework) to look at multiple aspects of statistical prediction using spectral data. We look at two types of wavelets, the Haar wavelet and the Daubechies 4 tap wavelet. These wavelets, described in more detail later, are small curves that can be used to approximate a more complex wave form. The approximation can be made as exact as one wants, up to giving back the original curve. We examine up to two levels of approximation in the first example, and five levels of approximation in the last two examples. Note that approximation can actually improve the prediction as noise is typically removed when the wave form is approximated. In our approximation, we select the wavelet coefficients within each sample wave form or globally over all the samples. We examine four statistical prediction methods: stepwise regression (Step), principle components regression (PCR), partial least squares (PLS), and ridge regression (Ridge). From the four main methods, we examine multiple settings for each method and use some methods in combination: Haar-Step, Haar-PCR, Haar-PLS, Haar-Ridge, Daubechies-Step, Daubechies-PCR, Daubechies-PLS and Daubechies-Ridge. Here Haar-Step is the combination of the Haar wavelets with stepwise regression for building prediction equations for the data. All these methods were designed for situations where the number of predictors is large relative to the number of samples and the predictors are themselves correlated. Note that it is tacitly assumed that the number of “real” predictors is small relative to the number of samples.

Finally, this factorial design, two wavelet types by four analysis methods, is executed using three separate data sets to get some sense of how the effects seen hold up with different data sets.

2 Materials and methods

The original data sets were spectra data where each observation was represented by amplitude and frequency and the levels of the material of interest were noted. In this format, it is typical for the number of observations to be far less than the number of predictors. The three datasets, Baltic Sea dataset, biscuit dataset, and urine dataset, analyzed in this paper will be described next.

2.1 Baltic sea data

Pollution can be harmful to fish and can be found in the Baltic Sea. Therefore, researchers were interested in creating an inexpensive test to monitor the contents of water. They investigated fluorescent spectroscopy for samples including lignin sulfonate, humic acids, and a detergent. Lignin sulfonate is a product of pollution from the pulp industry, and humic acids are a natural forest product. These substances along with detergents have severe spectral overlap and there is no spectral region where only a single emitting compound is present [2].

Man-made water samples were created to simulate typical ranges for concentrations of lignin sulfonate, humic acid, and detergents found in Swedish seawaters. The original data set consists of 18 observations, but the published data set contained 16 different concentration combinations. The emission spectra readings from 27 equidistant wavelengths were recorded using a Perkin-Elmer Model 512 double beam fluorescence spectrometer.

2.2 Biscuit data

The data was acquired in hopes of finding a nondestructive method for quality control on the production line using near infrared spectral analysis on raw biscuit dough. Responses were the percent of fat, flour, sucrose, and water in the raw dough. The variations of the percentages of the response variables were further restricted such that the end combination of substances would result in an edible biscuit if cooked [3]. Brown [4] had deleted one observation as measurement error, so we deleted the same observation in our analysis. Therefore, the dataset consists of 79 observations and the raw data is composed of 700 readings.

2.3 Urine data

Data was acquired to evaluate less expensive methods for urine analysis which provides insight into patient’s health. Mid-IR absorption spectra were obtained by averaging the results from two duplicate dried urine films using a Bio-Rad FTS-40A Fourier transform IR spectrometer to evaluate mid-IR spectroscopy in determining urine urea, creatinine, and total protein for 200 samples [5].

The dataset has one observation where the measurements of the response variables were unknown, so this observation was deleted from the analysis. Therefore, the dataset consists of 199 usable observations and the raw data is composed of 2,178 readings. The urine dataset is the only dataset in the study that was not created in a lab as actual urine samples were analyzed.

2.4 Wavelet data

We use two types of wavelet filters to transform the spectra data into wavelet coefficients. The first is the Haar wavelet and the second is the Daubechies 4 tap wavelet. Both of these wavelets are orthogonal wavelets. We use the default wavelet decomposition function ‘wavedec.m’ of the wavelet package of Matlab toolbox to compute our data. This function performs a multilevel one-dimensional wavelet analysis using either a specific wavelet or a specific wavelet decomposition filter. We use the maximal decomposition level which is related to the length of input data and the length of the filter to compute our wavelet coefficient.

2.5 Wavelets coefficient selection

For each spectra data, we did not adjust the length of data by adding zero elements or truncate any data to reset the length of data to power of 2. We just use the Matlab default function to perform the wavelet transform and computed the wavelet decomposition for each series, giving a nxp matrix. For each of the $p$ columns, we looked at the sum of the squares of the wavelet coefficients and kept the $k$ largest components and set other components to be zero. These calculations were done for both the Daubeches 4 tap wavelet, and the Haar wavelet.

2.6 Statistical analysis methods

When the number of potential predictors is large and/or there are high correlations among the predictors, there are a number of numerical and statistical problems. The simplest prediction method is stepwise linear regression. Special methods designed for situations where the sample size is smaller than the number of parameters to be estimated (the so-called $n\ll p$ or High Dimension, Low Sample-size problem) include Principle Component Regression, Partial Least Squares Regression, Ridge Regression. We will give a brief description of these methods in the next; for more details, see for example, Frank and Friedman [6].

2.7 Stepwise regression

Stepwise regression was introduced by Efroymson [7] and is designed for statistical models selection when large numbers of explanatory variables are available. This method consists of two steps: forward selection and backward elimination. At each step of the algorithm, based on the criteria, e.g. residual sum of squares (SSR), the forward selection selects the most important variable which is not yet in the model to enter, and the backward elimination selects the variable (among all variables that are already in the model) that contributes least to be removed from the model based on the criteria of SSR. The algorithm stops when there is no variable to enter the model based on the criteria.

Two settings were established for our use of stepwise regression. For the case defined as ‘Strict Step’, the required $p$ value to enter into the model is $<$0.01 and the required F ratio statistic $p$ value to exit from the model is $>$0.15. For the case defined as ‘Step’, the default SAS selection criteria was used, the F ratio statistic $p$ value to enter into the model is $<$0.15 and the F ratio statistic $p$ value to exit from the model is $>$0.15.

After selecting the variables in the model, multiple linear regression was performed using the selected variables to obtain parameter estimates. These parameter estimates were used to score the observation or cluster of observations that was removed from the model (the holdout set used for model validation). This was repeated for all observations or clusters. It is noted that as different observations or clusters were deleted, different variables were selected to be included in the model.

When considering a transformation, the transformation was restricted to be the same transformation for all observations, and only applied to the leave one out case. Box–Cox transformations were calculated for the case that includes all observations and that transformation was applied to the case where each observation was removed. After transforming the response, forward stepwise regression was again performed to select predictor variables to enter in to the equation. This second model in the transformed scale was also examined and compared to the original untransformed model as discussed in the evaluation section.

2.8 Principal component regression (PCR)

Principal component regression was introduced by Massy [8] and has been widely used in statistical analysis since then. The main idea of this method is to begin with the covariance matrix $V$ and its eigenvector decomposition, $V=\sum \nolimits _{k=1}^{p}e_{k}^{2}v_{k}v_{k}^{T}$ where $\{\nu _1 ,\nu _2 ,\ldots ,\nu _{\mathrm{p}}\}$ are the eigenvalues of $V$ in the descending order, and $\{e_{1} ,e_{2} ,\ldots ,e_p \}$ are the corresponding eigenvectors. PCR generates $\hat{{y}}_k =\sum \nolimits _{k=0}^K {[average(yv_k^T x)/e_k^2 ]v_k^T x}$, $\hbox {K}=1, 2,\ldots ,\hbox {R}$, where R is the rank of V. Then the PCR picks the one with the lowest mean square error.

After removing either one observation or one cluster, the principle components of the predictors were calculated. To simplify calculations, the number of principal components was restricted to be the same as different observations or clusters were removed. Therefore, as different observations or clusters were removed, different principal components were calculated, but the number of principal components was held constant. However, the results for a variety of number of principal components were calculated and the number of principal components that produced the best results was retained. The required number of principal components for all observations was used as a starting point. Then, principal components were added and subtracted so that all results can be compared to each other.

Combining stepwise and principal components was utilized, by performing stepwise regression on the principal components. As each observation or cluster was removed, the principal components were calculated. Then, stepwise regression was performed to select the principal components to be included into the model. Finally, multiple linear regression was performed to obtain parameter estimates that were used to score the observation or cluster that was removed. This was repeated for what was called ‘PCR Step’ and ‘PCR Strict Step’. Once the principal components were selected, PCR Step used the default settings to perform stepwise selection. PCR Strict Step utilized the stricter settings on the stepwise selection as defined in the stepwise section. Since stepwise regression was to be done last, generally, a larger number of principal components were kept before performing the stepwise regression. Therefore, the principal components were selected to account for at least 99 % of the variability in the predictors before stepwise regression was performed. However, there are still some limitations of PCR, as discussed in the paper of Hadi and Ling [9].

2.9 Partial least squares regression (PLS)

Partial Least Squares was proposed by Wold [1] and has been used widely in chemical applications where the number of predictors is larger than the number of observations. PLS looks like PCR, but the scores and loadings are computed differently, left and right factoring vectors. The first vector of loading are computed by first centering Y and normalizing each column of X by subtracting the mean and dividing by the standard deviation, then regressing each column of X on Y. It is standard to normalize the loadings by dividing each by the sum of the squares of the elements. The linear combination of the columns of X is used to estimate Y and the estimated Y becomes the first vector of scores. The outer product of the scores and loadings are used to approximate X, and the residuals are then subject to the same analysis, producing a second pair of vectors, loadings and scores. This process is continued until the number of vector pairs is k. Like PCR, PLS produces a series of models $\{\hat{{y}}_1 ,\hat{{y}}_2,\ldots ,\hat{{y}}_k \}$ where $\{\hat{{y}}_1 ,\hat{{y}}_2 ,\ldots ,\hat{{y}}_k \}$ are the fitted values in the models. The best value of k is determined through the ordinary cross-validation [10].

PLS decomposes both $X$ (explanatory variable matrix) and $Y$ (response vector) as a product of a common set of orthogonal factors. $X$ is decomposed as $X=QP^{T}$ with $Q^{t}Q=I$. PLS can be performed on one response at a time or by looking at all responses at as a group [11]. For our examples, partial least squares was applied to each response separately.

In this paper, we computed both the original PLS and the SIMPLS de Jong’s 1993 version of partial least squares [12]. The two versions produced the same result out to two decimal places in all cases except one, so the original version was reported in all cases. Detail algorithms can be found in the book of Hastie et al. [22] and some other references [6, 13–17].

2.10 Ridge regression

Ridge regression was introduced by Hoerl and Kennard [18] and is especially for the case of highly correlated predictors, a situation that is problematic in ordinary least-squares regression. The basic idea is to take the coefficients of the linear regression as the solution of the penalized lease squares criterion.

$\hat{{a}}_\lambda = \arg \min [average(y-a^{T}x)^{2}+\lambda a^{T}a]=(V+\lambda I)^{-1}average(yx),$ where $a$ is a vector of the coefficients of the linear regression: $y_j =a_j^T x$, and $\lambda >0$ is a tuning parameter, which controls the strength of the penalty term.

This project used ridge regression as both a variable selection technique (Ridge Select) and as a technique to obtain parameter estimates (Ridge All). For variable selection, ridge regression produces ridge coefficients for each ridge constant. As the ridge constants increase, all ridge coefficients converge to zero, but the variables with ridge coefficients that converge to zero the slowest can be considered as the variables to include in the model. After looking at multiple ridge constants, 0.9 was selected as the ridge constant where the ridge coefficients were stable. Therefore the best x variable model, is the model that includes x variables with the largest absolute value of the ridge coefficient where the ridge constant is 0.9. Multiple linear regression was performed to obtain parameter estimates that were used to score the one observation or cluster that was removed. This process was repeated for all observations or clusters. Then the best two variable model was selected and applied after removing each observation or cluster. This was repeated until all variables were exhausted or the data matrix became singular. Finally all models were compared and the model with the lowest Root Mean PRESS was selected.

Using ridge regression to obtain parameter estimates simply takes the ridge coefficients for all variables as the parameter estimates. After removing one observation or cluster, ridge regression was used to obtain the parameter estimates that we utilized to score the observation or cluster that was removed. This was repeated for nine ridge coefficients: 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, and 0.9. The model with the lowest Root Mean PRESS (defined later) was selected.

2.11 Root mean predicted residual error sum of squares (Root Mean PRESS)

Since our primary purpose is prediction, the Root Mean Predicted Residual Error Sum of Squares (Root Mean PRESS) was examined. Here the Root Mean PRESS is defined as the follows.

$$\begin{aligned} \hbox {Root Mean PRESS} = \frac{\sqrt{\sum \nolimits _{i=1}^N (Y_i -Y_{i\Pr ed})^{2}}}{N}, \quad \hbox {where} \quad (Y_{i}-Y_{i\Pr ed})\,\,\hbox {is the deleted residual}. \end{aligned}$$

The deleted residual was calculated by removing an observation from the dataset, performing the statistical method on the remaining observations, scoring the deleted observation with the calculated parameters from the statistical method, and calculating the residual. This residual is called the deleted residual. When appropriate, residual diagnosis was performed to suggest Box–Cox transformations on the response variable. In cases where a transformation was performed, the comparison between the original model and the transformed model need to be performed so that the statistics are the same scale. Once the statistic is in the same scale, the model with the lowest Root Mean PRESS was selected.

In order to evaluate the statistics in the same scale, the transformations need to be performed such that the inverse of the transformation is defined as real numbers for all values of each observation’s predicted value. For example, the total protein content of urine is an example of this concern. In the case where $f^{-1}(y_{i\Pr ed}^{*})$ does not exist, an alternate transformation is considered. For example if $y^{*}=y^{2}=.01$

and $y_{i\Pr ed}^{*}=-.2$ then $f^{-1}(y_{i\Pr ed}^{*})$ does not exist. This is overcome searching for transformation on ($y+k$) for some constant k such that the inverse transformation is defined as real numbers for all values of each observation’s predicted value.

2.12 k-Fold cross-validation

Due to the fact that identical and very similar data points were found, the validity of the Root Mean PRESS statistic to perform as expected was suspect. Any method that can “memorize” a data set would use the very similar observations to fit the data and produce an unrealistically good prediction. Therefore, k-fold cross-validation was used to create another evaluation method [19]. Clusters were found using Ward’s methods. For each cluster, the statistical procedure was done by leaving that cluster out. The calculated parameters were used to score the cluster that was left out, and the residuals were found. This was repeated for all clusters, and the reported statistic was the square root of the mean squared predicted error. Here the k-fold cross-validation is defined as

$$\begin{aligned} \hbox {k-fold} \,\, \hbox {cross-validation}=\frac{\sqrt{\sum \nolimits _{c=1}^k {\sum \nolimits _{i=1}^{Nc} {\mathop {\left( {\mathop y\nolimits _i - \mathop y\nolimits _{i \Pr ed}} \right) }\nolimits ^2 } } }}{N}, \end{aligned}$$

where k is the number of clusters and Nc is the number of observations in cluster number c.

Note that transformations were not performed when calculating the k-fold cross-validation statistic.

Since the purpose of creating the clusters was to ensure that like or very similar observations were not used in creating the parameter estimates for observations held out to be scored from those parameter estimates, k was taken to be the same across all datasets as the minimum reasonable number of clusters. It was found that ten [10] clusters accomplished this task, so this paper performed tenfold cross-validation.

2.13 Wavelets

Wavelets are a well-established tool for compressing and de-noising data, such as those arising from time series and images. Unlike the Fourier transform, wavelet function is compact supported and the wavelet coefficient only showed the frequency of local region. Hence wavelet transforms have advantages over traditional Fourier transforms for representing functions that contains discontinuities or sharp peaks.

For a detailed description of the Discrete Wavelet Transform, we recommend the reader consider the book “Introduction to wavelets and wavelet transforms: A Primer” by Burrus et al. [20]. A detailed description of the algorithms used would take too much space for this paper, so we will instead give a brief introduction of discrete wavelet transform here. The basic idea behind the discrete wavelet transform is the structure of multi-resolution analysis. Because the father wavelet is a scaling function, it can be reconstructed by the finite two-scale formula $\phi (x)=\sum \nolimits _{n=1}^{N}c_{n} \phi (2x-n)$, where $c_{n}$ is called the scaling coefficient. If $\phi (x)$ is compactly supported, then the support of $\phi (x)$ is contained in the finite interval [0,N]. A multi-resolution analysis is a sequence $\{V_{j}\}$ of a subspaces of $L^{2}(R)$ such that

• (1) $\cdots \subset V_{-1} \subset V_0 \subset V_1 \subset \cdots$

• (2) $\overline{\cup _{j\in Z} V_j } =L^{2}(R),\cap _{j\in Z} V_j =\{0\}$

• (3) $f(x)\in V_j \Leftrightarrow f(2x)\in V_{j+1}$

• (4) $f(x)\in V_0 \Leftrightarrow f(x-n)\in V_0 ,\forall n\in Z$

Let $\phi (x)$ be a scaling function in $L^{1}(R)\cap L^{2}(R)$, define $V_j =span\{\sqrt{2^{j}}\phi (2^{j}x-n)|n\in Z\},\forall j\in Z$ The complement space of $V_{j}$ in $V_{j+1}$ is $W_{j}$ which is defined by $W_j =span\{\sqrt{2^{j}}\psi (2^{j}x-n)|n\in Z\},\forall j\in Z$ where $\psi (x)$ the mother wavelet function. For the discrete wavelet transform of data $\{a_{n}\}$, it assumed that there exists a function $f\in V_{j}$ for some j such that f(x) can be represented by $f(x)\!=\!\sum a_{n}\phi (2^{j}x\!-\!n)$.

Because $V_{j-1} \oplus W_{j-1}=V_{j}$, we are looking for the representation of f(x) in the low filter space $V_{j-1}$ and the high filter space $W_{j-1}$. Then f(x) is represented by $f(x)=\sum a_{n}^{j-1} \phi (2^{j-1}x-n)+\sum b_{n}^{j-1} \psi (2^{j-1}x-n)$.

The coefficient $\{a_{n}^{j-1}\}$ is the low pass coefficient of $\{a_{n}\}$ and $\{b_{n}^{j-1}\}$ is the high pass coefficient of $\{a_{n}\}$. By the definition of multi-resolution analysis, $\{a_{n}^{j-1}\}$ is corresponding to another function belongs to $V_{j-1}$. Then we can transform $\{a_{n}^{j-1}\}$ into the next level by $\{a_{n}^{j-2}\}$ and $\{b_{n}^{j-2}\}$. The collection of $\{\{b_{n}^{j-k}\}_{k=1}^{p}\}$ is the multi-level wavelet coefficients.

The simplest wavelet is the Haar wavelet, given by $f(x)=\left\{ {\begin{array}{l} 1\{0\le x<1/2\} \\ -1\{1/2\le x<1\} \\ 0\{otherwsie\} \\ \end{array}} \right.$. The scaling coefficient of Haar function is {1,1} and the wavelet coefficient of Haar function is {1,$-$1}. So the discrete wavelet transform by Haar basis is down sampling of the pair-wise average to the low pass space and down sampling of the pair-wise difference to the high pass space.

For our analysis, we also used the Daubechies 4 tap wavelet, which, while more complicated, is continuous. The scaling coefficient of Daubechies 4 tap wavelet is $\frac{1\,+\,\sqrt{3}}{4\sqrt{2}}\frac{3\,+\,\sqrt{3}}{4\sqrt{2}}\frac{3\,-\,\sqrt{3}}{4\sqrt{2}}\frac{1\,-\,\sqrt{3}}{4\sqrt{2}}$.

The Haar basis can represent step function perfectly. When the function is a high order function, only the constant component is vanish to the high pass filter. The Daubechies 4 tap wavelet has vanishing moment of order 2, then the constant component and the linear component vanish for the high pass filter. That is using the high order vanishing moment wavelet to represent the high order function gets the better and efficiency representation.

A nice feature of the Discrete Wavelet Transform is that it makes data-driven denoising and compression of signals straightforward. Donoho and Johnstone [21] suggested applying a soft thresholding rule. The noise level would be estimated from the data, and this would be used as the threshold. Each coefficient would then be reduced by this amount k. That is, $Y_{m,n}^*(t)=sgn(Y_{m,n} )\max (|Y_{m,n} |-k,0)$, where $\hbox {sgn}()$ denotes the sign (1 or $-$1) of the argument, and $Y_{m,n}^{*}$ is the shrunk coefficient.

To estimate the noise level, Donoho and Johnstone suggested looking at the highest resolution wavelet coefficients, figuring little signal would be present at this level. They suggested using 1.48*MAD$\backslash$sqrt{2*log(n)}, where MAD refers to the Median Absolute Deviation (Median[abs(observation-Median[observations])]), a more robust measure of spread than the standard deviation, and n is the length of the data series.

We found the Donoho and Johnstone bound too tight. Instead we experimented by keeping a fixed number of wavelet coefficients, and tested how well each method used with these wavelet coefficients as predictors. When adjusting shrinkage methods to work on multiple series at once, we ranked the wavelet coefficients by which was the largest (in sum-of-squares sense), and chose the k largest. The rest were set to zero. This provided for reasonably construction, and about an 80+% compression of the data. Alternatives to this scheme are certainly possible; we chose this approach because (a) it provided reasonable reconstructions, (b) optimal selection of wavelet coefficients is ancillary to the point we are trying to make, and (c) it requires no training data where the response of interest is known. The implications of dropping the last two requirements will be explored in future work.

3 Results

3.1 Baltic Sea data

The Baltic Sea data is considered a very small dataset for spectral data, but there have been many published papers on this dataset. The data set is the result of a planned experiment and the concentration combinations were selected, so that the predictors had little correlation; the values of responses were spread across the range for each variable. Three pure samples were constructed such that only one response, analyte, was present in each of these samples. There is not much correlation between the various response variables, and there do not appear to be any outliers when projected down to two dimensions. From the original data, we learned that the measured levels of detergents are very much different than the levels of the other responses so the responses were analyzed separately.

In this small dataset, we exam two wavelet transformations with two degrees of compression: 8 Haar, 16 Haar, 8 Daubechies and 16 Daubechies wavelet coefficients. The leave one out statistic for the Baltic Sea for all analyses are listed in Table S-1 in Supplement. In order to compare the performance of the different combinations of wavelets compression and statistical methods, we show detailed patterns from the Table S-1 in Supplement for each individual response in Figs. 1, 2 and 3. The lines do not actually exist and only exist to help show the trend. The dots represent the statistic for each response for all the available number and types of wavelets plus the raw spectra data. Moving from the left to the right, the number of wavelets increases, the type of wavelets alternates and the last one is for the raw data. In Fig. 1, we see multiple analyses perform very similar on the 16 Daubechies wavelet data, and only Ridge All performs differently with a value close to 0.4. For the 16 Haar coefficient wavelet data, we see the PCR Step has a much larger value, close to 1, than all other analyses.

Fig. 1

The leave one out performance on the response lignin sulfonate in Baltic data

Fig. 2

The leave one out performance on the response humic acids in Baltic data

Fig. 3

The leave one out performance on the response detergents in Baltic data

From Fig. 1, the variance of all analyses lignin sulfonate appears to be smaller on the Daubechies wavelets when compared to the Harr wavelets or the raw data. Figures 2 and 3 also show the leave one out statistic for humic acids and detergents. For humic acids in Fig. 2, PCR Step and PCR Strict Step using Haar wavelets appear deteriorate as more wavelet coefficients are introduced into the data. Otherwise, the analyses performed similar to each other, and the analysis performed similarly across all types of wavelets, number of coefficients, and even the raw data. For detergents in Fig. 3, PLS clearly out performs the other analyses across all datasets. Except for PCR Step and PCR Strict Step on the raw data, the remaining analyses perform similar for all datasets. From Figs. 1, 2 and 3 we found that the PLS out performs the other methods. However, many other analyses perform similar for the other responses. There does appear to be an effect for the number of wavelets and type of wavelets for some analyses and responses, but there does not appear one setting that is best for all analytes. Since the Baltic Sea data is so small, the analyses on the wavelet data did not complete faster than when performed on the raw data, and the performance on the raw data was very similar to the performance on wavelet data.

3.2 Biscuit data

The responses of interest account for about 98 % of the total ingredients of the samples, so the remaining 2 % of materials in the biscuit dough will be treated as noise. The substances were varied such that percentages of each response were spread evenly across the range. From the basic statistics of the original data, we see that the percent of flour is generally much different than the percent of the other responses. From the correlation study, we see some large negative correlations where the most notable is the negative correlation between sucrose and flour while water is correlated with all other three responses. Therefore, techniques that examine all the responses at the same time might have an advantage over techniques that examine one response at a time.

Table S-2 in the Supplement lists the leave one out statistic for the biscuit data for all analysis. With 700 spectra readings, the analyses on the wavelet data completed much faster when compared to when they were applied to the raw data. For example, PCR using the raw data was not able to complete using the available computational resources. These values from the Table S-2 for each response are plotted in Figs. 4, 5, 6 and 7 separately. Again, the lines do not actually exist and only exist to help show the trend. The dash line links to a point representing the case that the method forms poorly due to the computational demands. From the results, it shows that as more wavelets are introduced into the data, both Haar and Daubechies wavelets with PCR, PCR Step, and PCR Strict Step start to have difficulty predicting the response. However, with fewer wavelet coefficients, these analyses do as well as with the other methods.

Fig. 4

The leave one out performance on the response fat % in the biscuit data

Fig. 5

The leave one out performance on the response flour % in the biscuit data

Fig. 6

The leave one out performance on the response sucrose % in the biscuit data

Fig. 7

The leave one out performance on the response water % in the biscuit data

For the Haar wavelets and Daubechies waveles, all analyses perform well even using only 25 wavelet coefficients. In fact, for both wavelets, all analyses perform well when the number of coefficients is smaller than 100. The Daubechies wavelets perform better than Haar wavelets when 100 wavelet coefficients are introduced.

3.3 Urine data

Urine will contain more compounds than was included in the previous examples and that may create more noise in the system. The responses are the levels of creatinine, urea, and total protein in the urine samples. In this dataset there are responses that appear to be separated from others. Most samples should only have trace amounts of protein. Hence, it is expected that total protein consists mostly of observations at or near zero with a few larger observations. From the basic statistics of the original data, we see that the 95 % decile of total proteins is much smaller than the maximum value. It is also noted that the measured levels of urea are very much different than the levels of the other responses; therefore, comparing error sums of squares across the responses will be avoided. From the correlation study, there is a strong correlation between creatinine and urea while total proteins are not correlated with either urea or creatinine. With two correlated responses, techniques that examine all the responses together may have an advantage over techniques that examine one response at a time, but we do not use a combined PLS analysis.

Table S-3 in the Supplement shows the leave one out statistic for the urine data for all analysis. PCR, PCR Step, PCR Strict Step, and Ridge All cannot be performed on the raw data using the available computational resources. Figures 8, 9 and 10 shows the leave one out statistic for creatinine, all analyses perform similarly while PLS on the individual responses has a small advantage. Only creatinine shows lower error as the number of wavelets increase. The analyses on the wavelet data took considerably less time to complete and many of the analyses could not complete given the available computational resources. In the Creatinime performance plot in Fig. 8, most analyses perform quite invariantly to the number and types of wavelet, but they perform poorly on the raw data due to computational demands.

Fig. 8

The leave one out performance on the response creatinine in the urine data

Fig. 9

The leave one out performance on the response total protein in the urine data

Fig. 10

The leave one out performance on the response urea in the urine data

In addition, Table S-4 in the Supplement lists the leave one cluster out statistic for the Biscuit data for all analysis and the subsequent Figs. 11, 12, 13 and 14 plot these values. All other analyses seem to perform similarly with very low errors when the number of wavelets coefficients is small. PLS appears to either be either the best or equally well for the remaining analysis for different responses. Once at least 100 wavelet coefficients are used, the performance of PCR Step and PCR Strict Step start to degrade. PCR was not able to be computed on the raw data using the available computational resources.

Fig. 11

The leave one cluster out performance on the response Fat% in the biscuit data

Fig. 12

The leave one cluster out performance on the response Flour % in the biscuit data

Fig. 13

The leave one cluster out performance on the response Sucrose% in the biscuit data

Fig. 14

The leave one cluster out performance on the response Water% in the biscuit data

The Table S-5 in the Supplement lists the leave one cluster out statistic for the urine data for all analysis and the subsequent Figs. 15, 16 and 17 plot these values. PLS performs worst when looking at responses creatinine and urea. PCR performs worst in total protein. The other analyses appear to perform similarly over the number of wavelets. Again, some methods perform poorly on the raw data due to the computational demands.

Fig. 15

The leave one cluster out performance on the response creatinine in the urine data

Fig. 16

The leave one cluster out performance on the response total protein in the urine data

Fig. 17

The leave one cluster out performance on the response urea in the urine data

4 Discussion and conclusions

When the number of predictors is large and the predictors are correlated, there are a number of numerical and statistical problems. In such a case, there is a need to simplify or compress the predictors to save data storage and de-noise the data. Working with wavelets was effective; usually the wavelets were better predictors than the raw data in all three of our examples. The dimension reduction from the wavelet analysis has additional computational advantages as some statistical methods take considerably more processing time on the raw data than on the wavelet data. For example, according to the SAS logs, it would have taken four days to complete the k-fold CV analysis for ridge regression on the raw urine data, but at 50 wavelet coefficients the process completed very quickly.

Stepwise regression has a distinct interpretability advantage for spectral data because the procedure would identify either wavelengths or locations and granularities that are important in describing the response. Often PLS and stepwise regression can predict substance concentrations equally well, the preferred statistical method should be the simplest method, step-wise regression.

In this paper, we conclude that factorial experimentation, computing the analysis using multiple combinations of analysis settings, can be used to determine the factor settings for a given type of analysis problem. From our studies, we propose to use a two-step framework to analyze spectral data. When the dataset is small, such as the Baltic data, data compression is also necessary because it can reduce the error when build up prediction equations. When the number of predictors is large, wavelets offer many advantages: dimension reduction, noise reduction, and the ability to point to informative regions of the wave form.

For the Baltic Sea data set, PLS on the raw data was effective relative to wavelets. The number of predictors was not large. For the other two data sets, wavelets were more effective than raw data. For the biscuit data set, all statistical methods worked well as long as the number of wavelets was 50 or smaller. For 100 or more wavelets a number of methods appeared to break down.

The urine data set was the most complex data set. The number of predictors was large and the chemical composition was more complicated. There were some erratic results where the model fit was not good. We removed one outlier observation (200 Haar, Urea, PCR Step) that have a very large prediction error of 799.2. After this observation was removed from consideration, there are some general comments that can be made. The type of wavelet had relatively little effect on the prediction error. For Cretinine and Total Protein, the number of wavelets was not important. For all three analytes 100–150 wavelets were able to capture the information in the wave forms. For Total Protein all statistical methods performed well, with PCR Step and PLS performing best. For Urea, there was more variability among the statistical methods with Ridge All performing best.

Having said all that, finding a good set of analysis conditions appears to require checking many conditions for the data set at issue. The type of wavelet was relatively unimportant. The number of wavelets should be large enough to capture most of the variability in the wave forms. The choice of the best statistical method depended on the analyte.