Vibrating Microwire Resonators Used as Local Probes of Quantum Turbulence in Superfluid $^{4}$He

Abstract

We report the use of a 60 $\upmu$m thick superconducting NbTi vibrating wire resonator as a local probe of quantum turbulence in superfluid $^{4}$He (He II). Wire resonance is driven via magneto-motive force, exclusively in the laminar hydrodynamic regime. For the detection of quantized vortices, changes in the probe resonant frequency and peak amplitude are measured in reaction to the applied external counterflow. Calibration of the device response is obtained in thermal counterflow in the temperature range from 1.45 to 2.1 K against second sound attenuation data. The main motivation of this work is the development of local probes of quantum turbulence suitable for use in non-homogeneous systems such as flows with spherical or cylindrical symmetry. The frequency response of the devices is described with good accuracy at lower temperatures by considering the balance between viscosity and mutual friction and its effect on the boundary layer. Under the experimental conditions, the fluid–structure interaction cannot be modeled reliably by an effective turbulent viscosity and agrees better with a model of the boundary layer modified by mutual friction. The obtained results may be extended to the interaction of nanoscale devices with sufficiently dense vortex tangles.

1 Introduction

Following the discovery of superfluidity, this captivating phenomenon akin to superconductivity in solids inspired numerous scientists to devote their time and effort to its deeper study and continues to be an important part of low-temperature physics research today. Soon after the first models of superfluid helium formulated by Landau and Tisza were tested experimentally with significant success, it became apparent that superfluids had yet another trick up their sleeve: quantum turbulence.

The existence of quantized vortices in superfluid helium, first suggested by Onsager and confirmed experimentally by Vinen [1] using vibrating wires in the superfluid phase of $^4$He (He II), changed the situation dramatically. It became clear that new and more advanced models of superfluidity were required, while continually improved experimental techniques provided new insights. Today, the range of theoretical, numerical and experimental methods is quite certainly beyond the hopes of the founders of this field, yet many questions remain unanswered, and with more detailed understanding, new ones frequently emerge.

It is then perhaps no surprise that more than 60 years after Vinen’s famous experiment [1], vibrating structures such as superconducting wires or their nanomechanical counterparts are still used in the research of quantum turbulence (QT). In this work, we return to some of the original questions—how do solid structures interact with a quantum-turbulent flow? Can a small vibrating device be used for local detection of a tangle of quantized vortices in He II?

Due to the two-fluid character of He II, which consists of a normal viscous fluid and an inviscid superfluid component, we have to account for two types of turbulence rather than one: classical-like turbulent flow of normal component, and a very specific turbulent flow of superfluid component which consists only of quantized vortices—topological line defects with circulation $\kappa \approx 10^{-7}$ m$^{2}$s$^{-1}$. At temperatures between $\approx$1 K and 2.17 K, where the superfluid transition occurs, both types of turbulent flow may exist based on which flow experiences the first instability [2, 3], but typically soon after the transition, both forms of turbulence are present, as energy and momentum transfer between the two components is mediated by pressure or the mutual friction force.

While experimental detection of quantized vortices is generally quite challenging, many different techniques exist today. It is possible to directly visualize them with the use of frozen hydrogen particles illuminated by a laser sheet [4,5,6] or by helium excimers [7]. Second sound attenuation [8] represents a thoroughly tested technique allowing indirect quantification of the amount of quantized vortices, giving the average vortex line density, L, i.e., total length of vortex line per unit volume in the probed region. To allow the conversion of the second sound signal to L, typically, homogeneity and isotropy of the probed flows are assumed.

Recent numerical and experimental works discussing non-homogeneous tangles of quantized vortices generated in thermal counterflow in various geometries (oscillatory counterflow, cylindrically or spherically symmetric counterflow) [3, 9,10,11] showcased the need for new local detectors of QT. Local probes using second sound [12] represent a highly interesting choice, offering excellent spatial resolution and little or no parasitic effects, but limits are imposed on their sensitivity by the relatively lower resonance quality factor that can be obtained in an open geometry.

Vibrating wire resonators, in the form of superconducting NbTi loops, already proved as useful QT detectors close to 1 K and at sub-kelvin temperatures [13, 14], where the density of normal component of superfluid helium is negligible. Here, we report the use of a 60 $\upmu$m thick superconducting NbTi vibrating wire resonator, driven via the magneto-motive scheme exclusively in its laminar hydrodynamic regime. For the detection of quantized vortices, changes in its resonant frequency and amplitude in reaction to the applied external flow are analyzed. The probes are tested and evaluated in a well-understood system represented by thermal counterflow turbulence [15], with a pair of second sound sensors placed at the position of each probe, allowing their in situ characterization.

2 Experimental Method

All experiments were conducted in a helium bath cryostat with thermal PID temperature stabilization to the level of 1 mK. Bath temperature was measured with Microsensor TTR-G type [16] of Ge on GaAs film thermometer calibrated to saturated vapor pressure. Two brass channels were employed, each with a manganin resistive heater at its closed end, open to the bath on the other side, see Fig. 1.

Fig. 1

Photographs of long and short channel assemblies together with their schematics. Left: Second sound ports in the long channel are displayed facing the viewer, while oscillators are installed from the bottom side. Permanent magnets are placed over the long channel assembly using separate plastic holders. Right: The circular cut-out in the short channel body serves for direct installation of permanent magnets with grooves provided for gluing vibrating wire leads

The first channel with inner square cross section 7 mm $\times$ 7 mm and length of 167.5 mm included slots for both types of used QT detectors: second sound capacitive sensors [8] and vibrating wires. Vibrating wires were constructed from d = 60 $\upmu$m thick bare NbTi wire in the shape of a semicircular loop with leg spacing D of 3 mm (varnish and Cu matrix were stripped in HNO$_{3}$) and glued with 2850FT Stycast to a brass holder, see Fig. 2. The wire holders were constructed in a way that the top of the loop was positioned close to the center of the flow channel, with 0.5 mm uncertainty. Pairs of sensors were installed at two different positions, 65 mm (for wire “L2” and sensors 3,4) and 115 mm (wire “L3” and sensors 1,2) from the channel inlet in such a manner that each vibrating wire was placed in a volume probed by the second sound sensors, see Fig. 1. The wire L2 was oriented so that its plane was perpendicular to the counterflow direction while L3 was parallel. The resonant frequencies of the wires L2 and L3 when immersed in superfluid helium were 6314 Hz and 5365 Hz, respectively, with a very small temperature-dependent variation of order 1 Hz. An additional TTR-G thermometer was installed 90 mm from the inlet, exactly midway between the positions of the two wires and close to the channel wall, for direct measurement of the thermal gradient inside the counterflow channel.

Fig. 2

Photographs of the vibrating wire detectors installed on custom holders compatible with “long” channel (left) and “narrow” channel (right). The middle photograph shows a close-up view of a sample vibrating wire resonator

The second channel with inner square cross section 4 mm $\times$ 4 mm and length of 40 mm included two vibrating wires, both oriented perpendicularly to the counterflow direction, at positions 12 mm (wire M2) and 20 mm (wire M1) from the channel inlet, see Fig. 1. A Ge thermometer was mounted at a distance of 16 mm, exactly midway between the wires. In this channel, no second sound sensors were installed. This channel was used to generate more intense vortex tangles at higher counterflow velocities obtained with the same heater power. The resonant frequencies of the wires M1 and M2 were 5830 Hz and 7250 Hz, respectively.

A driving static magnetic field B of order of 100 mT was applied for each wire by the pair of FeNdB permanent magnets. Relations between the driving force F and the driving alternating current I as well as between the induced Faraday voltage U and the wire velocity V that satisfy the conservation of energy are given for semicircular geometry [2] as:

$$\begin{aligned} F(\omega ) = 0.690\,I(\omega )\textrm{DB} ; V(\omega ) = \frac{U(\omega )}{0.690\,\textrm{DB}}. \end{aligned}$$

(1)

Minor discrepancies may result from deviations of the real geometry from a perfect semi-circle.

Due to a universal scaling of drag forces by the normal component acting on oscillators operated in high Stokes number regime [2], one can calibrate the real low-temperature value of the magnetic field from resonance measurements in laminar flow using:

$$\begin{aligned} B = \sqrt{ \frac{\xi \rho _{w} \Delta f \pi ^3 d^2 U_{p}}{4 \times 0.690^2\,\textrm{D I}_{p}} }, \end{aligned}$$

(2)

where $\xi$ = 0.396 represents an effective mass prefactor for the fundamental resonant mode [2], $\rho _{w}$ is the density of the wire material, and $\Delta$f, U$_p$, I$_p$ are the resonant width, the measured peak amplitude of the Faraday voltage and the peak amplitude of the applied driving current, respectively. Both numerical prefactors 0.690 for the force–current relationship and 0.396 for the effective mass are obtained by integration along the length of the wire, of the driving force projected onto the resonant mode profile, or of the squares of the local amplitudes of motion, respectively, see Ref. [2].

We have performed experiments at temperatures ranging from 1.45 to 2.1 K, covering a wide range of normal-to-superfluid component ratios of He II. QT was generated by thermally driven counterflow in a slow pulse sequence at various powers ranging between 1 and 500 mW in ascending order. The resulting counterflow velocity v$_{ns}$ for the applied heat flux $\dot{q}$ is given as:

$$\begin{aligned} v_\textrm{ns}=\frac{\dot{q}}{sT\rho _s}, \end{aligned}$$

(3)

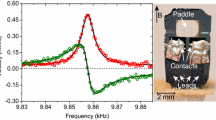
where s and $\rho _{\textrm{s}}$ are the specific entropy and the density of superfluid component, respectively, taken at temperature T. One heater power step consisted of two repetitions of heater-ON and heater-OFF states with a duration of order 100 s for each state. During the power series, time evolution of the resonant amplitude and frequency of both second sound and vibrating wire signals was measured for all detectors. For this purpose, resonance was tracked with the use of a PID algorithm stabilizing the quadrature signal component to zero (after background correction obtained from a full frequency sweep). In Fig. 3, we show a representative measurement of rescaled amplitudes for one pair of detectors during the power series. The decrease of both signal amplitudes is caused by additional damping due to the generation of QT in counterflow and its interaction with the wires and the second sound wave.

Fig. 3

Left: Measured time series of second sound and vibrating wire L3 amplitude at 1.65 K as the heater power is gradually stepped up. The heater is switched on/off twice at each given power. The microwire is visibly less sensitive than the second sound technique, as expected for a local, but fairly large, mechanical probe. Right: Changes in the resonant frequency of the microwire L3 at 1.65 K. For comparison, changes in second sound frequency reach units of percent at the highest applied powers despite operating near the local maximum in the dependence of second sound velocity on temperature. The insets show details of the individual heater switching events

The data show that the vibrating wire detects successfully only the highest applied powers and its sensitivity is less than that of second sound. Data such as those in Fig. 3 can be used for calibration of the wire response to a given vortex line density. The resonant frequency of the wires also shifts, as shown in the right panel of Fig. 3. In the following, we analyze the wire response in more detail, estimate its magnitude from HVBK equations [17] and evaluate the response that could be expected for finer (nano-)mechanical structures.

3 Results and Discussion

First of all, it is useful to convert the observed resonance frequency shifts to changes in the resonator effective mass, $\Delta m_{\textrm{eff}}$, and then express the extra damping due to counterflow as an inverse quality factor $Q^{-1}_{\textrm{cf}}$ using

$$\begin{aligned} \frac{\Delta m_{\textrm{eff}}}{m_{\textrm{eff}}} = \left( \frac{f_{0}^{2}}{f^{2}}-1\right) ; Q^{-1}_{\textrm{cf}} = \frac{\Delta f_0}{f_0} \left( \frac{A_{0}}{A}-1\right) , \end{aligned}$$

(4)

where $f_{0}$ and f denote resonance frequencies without and with the counterflow applied, respectively, and similarly $A_{0}$ and A represent the amplitudes of the resonant peak, with $\Delta f_0$ standing for the resonant linewidth in the absence of counterflow. The obtained values of $\Delta m_{\textrm{eff}}$ are much lower than the effective mass of the resonator, comparable to the mass of the viscous boundary layer of the normal fluid attached to its surface. Similarly, the excess damping is usually lower than the combined background damping due to viscosity and intrinsic dissipation in the device. For these reasons, it is important to provide suitable corrections for parasitic effects. These include most notably variations of local temperature when the counterflow is applied, as the viscous damping scales with $\sqrt{\rho _{\textrm{n}}(T) \eta (T)}$, where $\eta (T)$ is the dynamic viscosity and $\rho _{\textrm{n}}(T)$ the density of the normal component. At the same time, the effect of overheating by about 10 mK (see below) on the observed resonance frequency is negligible except very close to the lambda point.

The temperature gradient in the channel was measured using sensitive TTR-G thermometers and follows the prediction of Eq. (5) below, derived from the HVBK equations [17] assuming that the mutual friction force dominates in thermal counterflow over both turbulent and viscous drag and that the vortex line density is given by $L = \gamma ^2 \left( {v_\textrm{ns}}^{2}-{v_\textrm{crit}}^2\right)$, which in our case fits the data slightly better than $L = \gamma ^2 \left( {v_\textrm{ns}}-{v_\textrm{crit}}\right) ^{2}$. The leading role of mutual friction among dissipative phenomena in counterflow experiments is expected from simple estimates and is found to be in agreement with a more detailed analysis performed for spherical geometry in Ref. [18]. For the purposes of comparison, the gradient $\nabla T$ given by

$$\begin{aligned} \nabla T = \frac{ B_{\textrm{mf}} \kappa \rho _n\gamma ^2\left( {v_\textrm{ns}}^{2}-{v_\textrm{crit}}^2\right) }{2s\rho }v_\textrm{ns}, \end{aligned}$$

(5)

with $B_{\textrm{mf}}$ being the dissipative mutual friction coefficient and $\rho$ being total helium density is converted to a finite temperature difference using the distance of the thermometer from the open bath, see Fig. 4, left panel. The agreement is quite remarkable, considering the simplifications involved in the derivation.

Subsequently, we can account for thermally induced changes of the viscous damping $Q^{-1}_{\textrm{th}}$ at the positions of the wires using

$$\begin{aligned} Q^{-1}_{\textrm{th}} = Q_{\textrm{hd}}^{-1} \left( \sqrt{\frac{\rho _\textrm{n}(T)\eta (T)}{\rho _{\textrm{n}}(T_0)\eta (T_0)} } - 1 \right) \end{aligned}$$

(6)

where $Q_{\textrm{hd}}^{-1}$ is the total hydrodynamic viscous damping in the absence of external counterflow and the temperature $T_0$ is that of the helium bath, while T is the inferred temperature at the wire locations using the gradient obtained from Eq. (5). The damping due to quantum turbulence may thus be expressed as $Q^{-1}_{\textrm{QT}} = Q^{-1}_{\textrm{cf}} - Q^{-1}_\textrm{th}$. We note that at all heater powers where the wire detects an excess damping, the thermally induced contribution is always at least an order of magnitude lower than the one due to quantum turbulence, for both counterflow channels used. The resulting values of $Q^{-1}_{\textrm{QT}}$ are shown in the right panel of Fig. 4.

Fig. 4

Left: Temperature rise inside the channel when the heater driving the counterflow is switched on. Right: Corrected microwire excess damping $Q^{-1}_{\textrm{QT}}$ vs. counterflow velocity

Additionally, second sound measurements were performed in the same channel, allowing us to establish an approximately linear calibration between the wire response and vortex line density, as is summarily shown in Fig. 5. It is evident that the wire sensitivity is a limiting factor here and that mechanical probes of this size are useful only in highly turbulent tangles. The wires detect no (measurable) additional damping at vortex line densities lower than the threshold given by the comparison of the mean intervortex distance with the characteristic dimension—wire diameter $d = 60$ $\upmu$m.

Fig. 5

Left: Vortex line density obtained from second sound measurement in the long channel. The observed $\gamma$ factors in Eq. (5) are consistent with earlier work [19, 20], see also Table 1. Right: Calibration of microwire response against the vortex line density L. The solid blue line shows a linear relationship which is observed only in the upper decade of L. The mean intervortex distance $\delta _{\textrm{L}} = L^{-1/2}$ becomes equal to the diameter of the wire at $L = 2.78 \times 10^8$ m$^{-2}$, indicated by the vertical dashed line

To test the linearity of the calibration relationship at higher L, we repeated the experiment in the second channel of smaller cross section, where tangles of higher density could be easily produced. The $\gamma$ factors from the above measurements were used to deduce vortex line density here, as direct measurement was not available. The $\gamma$ values are summarized in Table 1, and the results are shown in Fig. 6. The plot shows two regimes which differ by the temperature dependence of the observed damping. At lower L, the proportionality constant c in the relation $Q^{-1}_{\textrm{QT}} = c L$ depends systematically on temperature and appears to scale approximately with the superfluid density, $\rho _{\textrm{s}}$ (showing a notable deviation only at 1.45 K), while at higher L the temperature dependence is mostly suppressed, see also Table 1.

Table 1 Values of $\gamma$ used for calculation of vortex line density in the small channel, together with the parameter c relating the inverse quality factor and the vortex line density by $Q^{-1}_\textrm{QT} = c L$. The last column contains a theoretical value for $c/\rho _{\textrm{s}}$ based on Eq. (23) below for wire M1

Fig. 6

Microwire damping vs. vortex line density L in the narrow channel. The solid lines depict linear relationships $Q^{-1}_{\textrm{QT}} = c L$. Two distinct regimes are observed. First, at lower L, the damping is temperature dependent. For the values of the prefactors c, see Table 1. At higher L, the temperature dependence is suppressed; the linear relationship between damping and vortex line density appears with $c \approx 2 \times 10^{15}$ m$^{2}$

3.1 Interpretation

When the heater is switched on and thermal counterflow is generated, the oscillating wire changes its resonant frequency as well as the damping, as discussed above. Importantly, the frequency increases in all observed instances.

The resonant frequency $\omega _0 = 2\pi f_0$ is determined by the effective hydrodynamic mass, $m_{\textrm{eff}}$, of the device and by its spring constant, $k_{\textrm{s}}$. The resonant frequency defined as the frequency at which maximum power is absorbed from a drive mechanism, or equivalently, maximum velocity (rather than displacement) amplitude is reached, is given by $\omega _0^2 = k_{\textrm{s}}/m_\textrm{eff}$, irrespective of the magnitude of the linear damping. Generally speaking, the observations in the right panel of Fig. 3 may be explained either by an increase in the spring constant, or by a decrease of the effective mass.

The spring constant could change, e.g., due to vortices pinned between the loop of the wire and its base, as long as they are not directed exactly parallel to the direction of motion, in which case only a constant vortex tension would act on the wire. For straight vortices attached to the wire going directly toward a pinning site at its base, the total force projected on the direction of motion would be given by:

$$\begin{aligned} F_{\textrm{QV}}= & {} f N F_{\textrm{1}} \, 2x/D, \end{aligned}$$

(7)

$$\begin{aligned} F_{1}= & {} \frac{\rho _{\textrm{s}} \kappa ^2}{4 \pi } \ln \frac{b}{a_0}, \end{aligned}$$

(8)

$$\begin{aligned} N= & {} L d D, \end{aligned}$$

(9)

where $F_{1}$ stands for the force acting due to one quantized vortex (vortex tension), $a_0$ is the vortex core size, b being a cutoff distance (intervortex spacing in the case of many vortex problem), N denotes the estimated number of attached vortices, x is the immediate displacement of the wire and f is a geometric factor of order unity. This would yield an enhancement to the spring constant due to quantized vortices $k_{\textrm{QV}}$, and its relative magnitude can be estimated as:

$$\begin{aligned} \frac{k_{\textrm{QV}}}{k_{\textrm{s}}} = \frac{\rho _{\textrm{s}} \kappa ^2 L d}{2 \pi m_{\textrm{eff}} \omega _0^2} \ln (b/a_0). \end{aligned}$$

(10)

For $T = 1.65$ K and $L = 3 \times 10^9$ m$^{-2}$, this gives $k_\textrm{QV}/k_{\textrm{s}} \simeq 10^{-8}$, i.e., three orders of magnitude too small to explain the frequency shift observed in Fig. 3.

Similarly, following Ref. [21], one may consider quantized circulation around the NbTi wire itself interacting with its mirror image reflected through the plane of the base (as per boundary conditions). This interaction produces a static Magnus force, attracting the wire toward its base and changing its tension. However, a semicircular loop with diameter significantly exceeding that of the wire is under tension only due to its curvature. In a situation without vortices, from the neutral line passing through the center of the wire inside, the tension felt by the wire material is negative, while toward the outside it is positive. An integral of the tension taken over the full cross section of the wire in equilibrium position would yield zero. Circulation trapped around the wire may, in principle, affect this balance of tension forces, but in effect, such a tiny change¹ of the tension due to curvature could not contribute significantly toward the spring constant, which is determined mostly by the elastic modulus of the material itself, seeing as the curved half-loop behaves essentially like a cantilever. We therefore consider it a valid approximation to neglect these effects for our device.

As we cannot justify the observed frequency shift by considering elastic effects, in the following, we analyze the results under the assumption that it is the effective mass that is changing rather than the spring constant. This requires that at high counterflow velocities, the effective mass of the device, or rather, its hydrodynamic enhancement, decreases appreciably. In an ideal fluid (superfluid component), the hydrodynamic mass enhancement of an oscillating object is given in terms of the potential backflow. In a viscous fluid, the same effect exists and additionally, the mass of the viscous boundary layer moving with the object [22, 23] must be considered. For an oscillating body, the backflow contribution is constant regardless of any externally applied stationary flow, we are thus most likely seeing effects related to the viscous boundary layer in the normal component. Generally, for an oscillating body in an external stationary viscous flow, two types of boundary layers need to be considered: (i) a stationary Blasius-type boundary layer, and (ii) a periodically changing Stokes-type boundary layer. The interaction of these two types of boundary layers is presently not understood in its entirety and represents a challenging topic with relevance, e.g., in the treatment of waves in shallow water [24] or to some extent in aeronautics, via Interacting Boundary Layer models.

At zero counterflow, the effective mass of the device is given by [2, 23]:

$$\begin{aligned} m_{\textrm{eff}} = \xi m + \beta \rho V + \beta ' S \rho _{\textrm{n}} \delta _{\textrm{n}}, \end{aligned}$$

(11)

where the first term expresses the effective mass of the device in vacuum (differing from its gravitational mass due to the profile of the resonant mode), the second term represents the ideal backflow and the last term is the boundary layer mass, with V and S being the volume and surface area of the body, respectively, $\delta _{\textrm{n}} = \sqrt{2 \eta / \rho _{\textrm{n}} \omega }$ is the Stokes boundary layer thickness and the $\beta$ and $\beta '$ are constants of order unity determined by the exact geometry of the body.

In the following, we consider only the Stokes boundary layer, as it is relevant to the oscillating motion of the device which we are measuring, whereas the Blasius-type boundary layer would only affect its steady state characteristics, which are not probed experimentally. Specifically, for an oscillating cylinder, the mass of the Stokes boundary layer, $m_{\textrm{bl}}$, given by the last term on the RHS of Eq. (11) can be expressed as:

$$\begin{aligned} m_{\textrm{bl}} = \frac{\pi ^2}{2} \rho _{\textrm{n}} D \delta _{\textrm{n}} \left( d + \delta _{\textrm{n}} \right) , \end{aligned}$$

(12)

and may be used to normalize the observed change of the effective mass. Naively, one might expect that once the counterflow is switched on and turbulence is created in the main flow, vortices will interact with the Stokes boundary layer and cause mixing. This would, in turn lead to partial boundary layer separation, reducing its contribution to the effective mass. The left panel of Fig. 7 shows the mass decrease obtained from the resonant frequency change plotted as a fraction of $m_{\textrm{bl}}$ against L. First of all, we find that the mass change is lower than (but comparable to) the boundary layer mass, making this effect a likely explanation of the experimental data and deserving a closer analysis.

Fig. 7

Left: Change in effective mass normalized by the mass of the Stokes boundary layer plotted against counterflow velocity. The solid lines are calculated using the ratio of effective masses $(a-b)$ as obtained from Eq. (22), showing remarkable agreement with the data. Right: Ratio of extra drag due to quantum turbulence, $Q_{\textrm{QT}}^{-1}$, to the hydrodynamic viscous drag in zero counterflow, $Q_{\textrm{hd}}^{-1}$. The solid lines are obtained using the ratios $(a+b)$ from Eq. (22). The data show higher damping than predicted, see text

Before proceeding further, let us turn for a moment to the origin of the additional damping. First, let us consider this excess damping due to turbulent motion of both fluids for a moment as if it were a manifestation of some effective dynamic viscosity, $\eta _{\textrm{eff}}$, mediating an excess force acting on the oscillator. To begin with, let us state that this notion of an effective viscosity is conceptually different from the usual definition based on turbulent energy dissipation given by $\epsilon = \nu _{\textrm{eff}} (\kappa L)^2$, as the latter relates to dissipation of the kinetic energy of the externally driven turbulent flow, whereas in our case we are interested in the dissipation of the kinetic energy of the mechanical resonator via fluid–structure interaction. A viscous-like behavior would correspond to a situation, where quantized vortices exist in sufficient density to effectively exchange momentum between layers of fluid adjacent to the body. This requires vortex spacing lower than the boundary layer thickness, which may be estimated from Ref. [2], Eq. (9) in the high Stokes number limit, reprinted here for convenience using the present notation:

$$\begin{aligned} Q^{-1}_{\textrm{QT}} = \frac{\alpha \rho S_r \delta _{\textrm{eff}}}{2 m}, \end{aligned}$$

(13)

where $\alpha = 2$ is the flow enhancement factor for a cylinder, $S_r$ is the effective surface area incorporating roughness, $\delta _{\textrm{eff}} = \sqrt{2\eta _{\textrm{eff}} / \rho \omega }$ is the effective viscous penetration depth and m stands for the (full, not effective) mass of the resonator. The surface area can be approximated by that of a smooth semicircular loop of wire giving $S_r \simeq \pi ^2 d D/2$, while the mass of the NbTi wire is given by $m = \rho _{\textrm{w}} \pi ^2 d^2 D/8$ with $\rho _{\textrm{w}} = 6550$ kg m$^{-3}$. Finally, we arrive at:

$$\begin{aligned} Q^{-1}_{\textrm{QT}} = \frac{4 \rho \delta _{\textrm{eff}}}{\rho _{\textrm{w}} d}, \end{aligned}$$

(14)

which could be used to extract the experimental effective penetration depth $\delta _{\textrm{eff}}$ and hence the effective dynamic viscosity $\eta _{\textrm{eff}}$. The high Stokes number limit manifests by the requirement $\delta _{\textrm{eff}} \ll d$ here, with the wire diameter $d = 60$ $\upmu$m. The values of $\delta _{\textrm{eff}}$ obtained from our data always fall below 1 $\upmu$m, requiring $L>10^{12}$ m$^{-2}$ in order for this scenario to work, which is not satisfied in our experiments. In view of this evidence, we rule out dissipation by an effective viscous-like transfer of momentum via interactions with quantized vortices, although the possibility remains that at higher drives beyond those investigated here, this mechanism may yet come into play.

Here we must consider that while quantized vortices cannot mediate a viscous-like dissipation directly (and should be treated either ballistically, or better, within detailed numerical simulations of the vortex filament model), they may still have a nonzero net effect on the viscous boundary layer via the mutual friction force. As the vortex spacing exceeds the boundary layer thickness, vortices interact with the BL only sporadically. Thus, in a similar fashion to Reynolds decomposition in classical fluids, one may define an mean vortex line density in the boundary layer $\langle L \rangle$ and separate the HVBK equations of motion into steady and fluctuating parts. As the experimental data obtained using the lock-in technique are in any case averaged over thousands periods of oscillation of the device, we must assume that the measurements, in fact, correspond to the mean value $\langle L \rangle$. The question arises: How is the Stokes boundary layer effectively modified in the presence of mutual friction? In the following, we re-derive its properties, extending Stokes’ second problem—in-plane oscillations of a planar infinite boundary—to superfluid helium.

3.2 Stokes Boundary Layer with Mean Mutual Friction

Setting the pressure and temperature gradients to zero and neglecting the vortex tension in the HVBK equations [17], we start from

$$\begin{aligned} \rho _{\textrm{n}} \frac{\partial v_{\textrm{n}}}{\partial t}= & {} - \frac{\rho _{\textrm{n}} \rho _{\textrm{s}}}{2 \rho } B \kappa L v_{\textrm{ns}} + \eta \Delta v_{\textrm{n}}, \end{aligned}$$

(15)

$$\begin{aligned} \rho _{\textrm{s}} \frac{\partial v_{\textrm{s}}}{\partial t}= & {} + \frac{\rho _{\textrm{n}} \rho _{\textrm{s}}}{2 \rho } B \kappa L v_{\textrm{ns}}, \end{aligned}$$

(16)

where $v_{{{\text{ns}}}} = v_{{\text{n}}} - v_{{\text{s}}}$. We seek solution in the form

$$\begin{aligned} v_{\textrm{n}}= & {} v_{\textrm{n0}} + v_{\textrm{n1}} e^{i (kz - \omega t)}, \end{aligned}$$

(17)

$$\begin{aligned} v_{\textrm{s}}= & {} v_{\textrm{s0}} + v_{\textrm{s1}} e^{i (kz - \omega t)}, \end{aligned}$$

(18)

where z is the distance from the plane, and we require $\Im (k) > 0$ to obtain vanishing solutions at infinity. Both velocities oscillate in the same direction as the plane, i.e., we are dealing with a 2D flow, see, e.g., Ref. [22] for a classical hydrodynamical treatment. It follows that the nonlinear terms are identically zero due to symmetry of the problem. The superfluid component is expected to be set in motion by the mean mutual friction force, and the relation between $v_{\textrm{n}}$ and $v_{\textrm{s}}$ is obtained from the second equation in Eqs. (16). The vortex line density may be expressed as $L = \langle L \rangle + \tilde{L}$, where $\tilde{L}$ represents both random fluctuations in the turbulent flow and oscillations at the frequency of the resonator, $\omega$. Focusing only on terms that oscillate with the frequency $\omega$, neglecting the product $(v_{\textrm{n0}} - v_\textrm{s0}) \tilde{L}$ in comparison to $(v_{\textrm{n1}} - v_{\textrm{s1}}) \langle L \rangle$ as the oscillator is not expected to generate turbulence of its own at low drive, we arrive at the condition for the wavenumber k

$$\begin{aligned} (k \delta _{\textrm{n}})^2 = 2 i \, \frac{(2 \rho \omega )^2 + \rho _{\textrm{n}} \rho (B \kappa \langle L \rangle )^2 + 2 i \rho \rho _{\textrm{s}} \omega B \kappa \langle L \rangle }{(2 \rho \omega )^2 + (\rho _{\textrm{n}} B \kappa \langle L \rangle )^2}, \end{aligned}$$

(19)

where we use the usual viscous penetration depth of the normal component $\delta _{\textrm{n}}^2 = 2 \eta / (\rho _{\textrm{n}}\omega )$. Note that the expression $B \kappa \langle L \rangle /2 \equiv \tau _\textrm{mf}^{-1}$ represents a mean inverse relaxation time associated with mutual friction. For $\langle L \rangle = 10^{10}$ m$^{-2}$, the relaxation time is $\tau _{\textrm{mf}} \approx 2$ ms, meaning that mutual friction is sufficiently fast to act in the experimental window given by the lock-in time constant typically of order 100 ms, but certainly cannot follow each oscillation of the device with a characteristic time given by $\omega ^{-1} \approx 30$ $\upmu$s; hence observation of a “mean-field effect” on the boundary layer is indeed expected. Introducing a dimensionless quantity $w = (\omega \tau _{\textrm{mf}})^{-1}$ analogical to the Weissenberg number used for dilute classical gases, the above expression may be simplified to

$$\begin{aligned} (k \delta _{\textrm{n}})^2 = 2 i \, \frac{1 + x_{\textrm{n}} w^2 + i x_{\textrm{s}} w}{1 + (x_{\textrm{n}} w)^2}, \end{aligned}$$

(20)

where $x_{\textrm{n}} = \rho _{\textrm{n}} / \rho$ and $x_{\textrm{s}} = \rho _\textrm{s} / \rho$. The argument of the complex quantity in the fraction is always between 0 and $\pi /2$ and one may take the positive square root in Eq. (19) to obtain

$$\begin{aligned} k \delta _{\textrm{n}} = (1 + i) (a + i b) = a-b + i(a+b), \end{aligned}$$

(21)

with $a \ge 1 \ge b \ge 0$, satisfying the requirement that $\Im (k) > 0$. The wavenumber k may be substituted in Eq. (18) to obtain the exact velocity profiles satisfying the boundary condition that the normal fluid moves together with the oscillating plane at $z = 0$. The viscous stress at the boundary will be then given by

$$\begin{aligned} \sigma = \eta \frac{\partial v_{\textrm{n}}}{\partial z} \bigg |_{z = 0} = \left[ -\left( a+b\right) + i\left( a-b\right) \right] \frac{\eta v_{\textrm{p}}}{\delta _{\textrm{n}}} e^{-i \omega t}, \end{aligned}$$

(22)

where $v_{\textrm{p}} \exp (-i \omega t)$ is the velocity of the planar surface. Comparison of this result with the classical treatment in Ref. [22] shows that the viscous dissipation will be rescaled by the factor $a+b > 1$ compared to the case without counterflow (and thus without mutual friction) while the added mass will be rescaled by $a-b$, in agreement with the observations of increased damping and decreased effective mass ($a-b < 1$ for our experimental conditions). We also note specifically that the phase shift between the viscous force and the plane velocity generally differs from $\pi /4$ that is obtained in the case without mutual friction [22], and is restored here in the limit $L \rightarrow 0$. It may be also noted that in order for an effective viscosity to describe this problem correctly, the two prefactors $a+b$ and $a-b$ would have to be identical, contrary to both this simple model and experimental observations.

In linear approximation, the prefactors may be expanded in terms of L with

$$\begin{aligned} a \approx 1; \,\,\, b \approx \frac{1}{2} w x_{\textrm{s}} = \frac{\rho _{\textrm{s}}}{\rho } \frac{B \kappa L}{4 \omega }. \end{aligned}$$

(23)

In the case of flow past a circular cylinder, a similar treatment holds as for the planar surface if $\delta _{\textrm{n}}<< d$ and we may approximate its surface by planar elements. Both terms in the stress tensor in Eq. (22) would further contain the flow enhancement factor $\alpha = 2$ expressing the ratio between the velocity of the cylinder surface and that of the potential flow around it, but the comparison to the case without counterflow would yield the same ratios $a+b$, and $a-b$ for the dissipation and the effective mass, respectively.

The modification of the Stokes boundary layer by mutual friction is not the only mechanism responsible for additional dissipation in our experiment. Additionally, one should consider direct momentum transfer from collisions with quantized vortices impacting on the device. While a rough estimate may be obtained from a simplistic model of ballistic vortex ring propagation that agrees in order of magnitude with the observed additional damping, it cannot be formulated precisely without a detailed knowledge of the distribution of sizes of vortex rings, and a thorough analysis would require running numerical simulations that would be heavily influenced by the boundary conditions at the device surface. The experimental data follow the same temperature dependence as given by Eq. (22), which exhibits scaling with $\rho _\textrm{s}$ in linear approximation, see the right panel of Fig. 7, but the data are consistently higher than the theoretical prediction. Thus, we expect that direct momentum transfer from impacting vortex rings will also contribute to the dissipation significantly. The results indicate that the frequency shift is indeed a safer way to measure the vortex line density with similar devices.

Although we cannot ascertain that the presented crude model is fundamentally correct and further studies using different techniques are certainly required, let us, for a moment, consider its implications for measurements with nanoscale devices. The sensitivity of the nanodevice would be again given by the prefactors expressed in Eqs. (22,23), which will be to some extent influenced by the detailed geometry of the device and its density, but for a wire-like geometry, it will be always inversely proportional to the resonance frequency. This result may be used to design the approximate dimensions and frequencies of devices with a given sensitivity to quantized vortices present in flows of superfluid helium. For example, one may expect nanomechanical beams resonating at MHz frequencies to display a lower relative change in frequency, while the absolute frequency shift would be approximately the same. Thus, if suitable demodulation techniques are used in the high frequency measurements, the nanoscale devices would operate equally well as far as sensitivity to the average vortex line density L is concerned. However, due to their reduced size, they would perform two or three orders of magnitude better in terms of spatial resolution, or equivalently, the total length of vortex line that they can detect locally in comparison to the current, rather large, superconducting wire. Finally, we note that detection of quantized vortices stably attached to nanodevices will behave differently from the model presented here, as both the dissipation and the frequency shifts will be dominated by different mechanisms than discussed here.

4 Conclusion

We have tested several NbTi superconducting microwires as probes of quantum turbulence in thermal counterflow of He II generated in the two-fluid regime above 1 K. The devices respond to the counterflow, displaying changes in damping and resonant frequency. In both cases, the effect is proportional to the vortex line density and the observations can be approximately described by considering a net effect of quantized vortices modifying the Stokes boundary layer due to mutual friction. The observed dissipation displays two regimes differing by their temperature dependence and agrees within an order of magnitude with that given by the above model, but exceeds it systematically, leaving momentum transfer by collisions with vortex rings as a likely additional dissipative mechanism. On the other hand, the observed frequency shift corresponds quite well to the modified Stokes boundary layer model, allowing a local quantification of the mean vortex line density, especially after device calibration in a well-characterized flow. This is a promising advance in view of studies of inhomogeneous flows such as cylindrically or spherically symmetrical thermal counterflow and may be extended to modern nanomechanical devices. We hope that our results will stimulate further work both theoretical and experimental and that the simple model presented will help to provide a basic understanding of fluid–structure interactions in turbulent superfluids.