1 Introduction

The counterintuitive concept of supersolidity can only be understood in terms of extremely quantum matter. The simultaneous existence of spatial solid order, characteristic of the solid state, and superfluidity, property that in principle requires of mass movement without friction, is hardly understandable in usual solids. The natural candidate for this fascinating possibility has been along the time always the same, solid 4He. The solid phase of 4He is not a normal solid, in the classical meaning of this term. 4He atoms have so small mass and shallow interaction that its stable condensed phase, in the limit of zero temperature, is a liquid and thus a finite pressure is required to crystallize it. Even in the crystal phase, the zero-point motion of the 4He atoms is not fully depressed as it is explicitly quantified by its large Lindemann ratio and impressively large kinetic energy, with respect to typical classical values. Furthermore, the exchange frequency, which is absolutely absent in classical solids, is low but not zero. Altogether makes the study of a quantum solid a very interesting topic, the possibility of a supersolid scenario being one of its more stimulating possibilities.

The recent experimental findings by Kim and Chan [1, 2] on the existence of a non-zero fraction of non-classical moment of inertia (NCRI) in torsional oscillator measurements have revived this topic that emerged in the past as an hypothetical theoretical conjecture. This unexpected result has been corroborated by other laboratories, although the dispersion in the size of the effect is large [3]. From the very beginning, it was clear that the way in which the crystal is produced, the annealing during its growth and the purity of the 4He sample were, among others, relevant parameters which introduce changes of the NCRI fraction of an order of magnitude. The decoupling of a part of the mass, measured in the torsional oscillator, is observed at an onset temperature which also depends on the particular conditions of the experiment, but its fluctuation is sizeably smaller than the one obtained for the NCRI fraction (superfluid fraction). Very close to the onset temperature for supersolidity it has been observed an increase in the shear modulus of hcp 4He, its temperature dependence being similar in shape to the one of NCRI [4]. The interplay between this anomalous elastic behavior and the NCRI effect observed in torsional oscillators has been object of theoretical debate: it seems clear that part of the NCRI effect can be attributed to elasticity but probably not all.

To date, there is not a complete theoretical understanding of the observed phenomena. A point in which the community working in this field has reached an overall agreement is the absence of any supersolid signal in a perfect crystal, i.e., a crystal where the number of particles and the number of sites matches exactly. The supersolidity is then attributed to alterations of the perfect crystal due to the disorder introduced by defects, that inevitably appear during its growing process from the liquid phase. The major role has been assigned to dislocations and their mobility in relation with the pining/depining of 3He impurities to them. But, even if dislocations can be in the origin of experimental NCRI they can not be the only explanation since the superfluidity of hcp 4He in bulk or in vycor is nearly the same, whereas the dislocation density is reasonably expected to be very different. Another possibility, that has been theoretically explored from long time is the presence of a fraction of point defects, i.e., vacancies.

Vacancies were originally proposed by Andreev and Lifshitz [5] as a mechanism for creating a supersolid phase in solid helium. This scenario was rebuked by experimental and theoretical findings showing that vacancies are energetically too expensive to be created by thermal activation. However, Rossi et al. [6] showed using a variational estimate that wavefunctions that are able to describe well the equation of state of solid 4He support a finite vacancy concentration between 10−6 and 10−3. This possibility is yet to be tested with first principles calculations, as the number of helium atoms that corresponds to such low concentrations is still too large to handle. Even such low vacancy concentrations should be experimentally significant, given the observed influence of sub-ppm concentrations of 3He [7]. Notice that as a quasiparticle in hcp 4He, a vacancy is in many ways similar to a 3He impurity.

Even if thermal activation of vacancies seems improbable at very low temperature it is reasonable to consider that a significant number of vacancies can be introduced into solid samples during their growth. Eventually, some of them can disappear by migrating to dislocations or grain boundaries but one cannot exclude a priori that a tiny fraction of vacancies can dissolve into the bulk crystal. It was, however, argued [8] that even if initially vacancy-rich, solid hcp 4He would phase separate into a vacancy-rich phase and a perfect, insulating crystal and therefore any growth-introduced vacancies will be effectively removed from the experimental samples. On the other hand, our detailed studies with several vacancies show no sign of vacancy clustering [9, 10].

In this work, we report recent results on the properties of vacancies in a fully quantum crystal like 4He obtained using different quantum Monte Carlo methods. In Sect. 2, we describe the microscopic methods used in the present analysis. In Sect. 3, we present PIMC results on the one-body density matrix of hcp solid 4He as a function of temperature, showing the onset temperature where both Bose-Einstein condensation and vacancy delocalization appear. Section 4 comprises results of the shear modulus at zero temperature and as a function of the pressure. Finally, an account of the main conclusions of the present work is included in Sect. 5.

2 Quantum Monte Carlo Methods in the Study of Solid 4He

A quantitatively accurate study of solid 4He is demanding due to the high density of the system and strong interparticle correlations. If a microscopic approximation to the system is pursued, the most powerful tool is quantum Monte Carlo with several methods to deal properly with zero or finite temperature simulations. The final goal is to get relevant microscopic information, on both energy and structure, starting directly from the Hamiltonian of the system. The helium interatomic potential is accurately known and there are several models that are able to describe its equation of state very well. In the present work, we have used an Aziz potential [11] that has proven to be very accurate in the reproduction of the equation of state P(ρ) in both liquid and solid 4He.

Calculations at zero temperature have been performed with diffusion Monte Carlo (DMC). DMC is a zero-temperature first-principles method which can access exactly the ground state of bosonic systems. It is a form of Green’s Function Monte Carlo which samples the projection of the ground state from the initial configuration with the operator . Here, is the system Hamiltonian, E 0 is a norm-preserving adjustable constant and τ is the variable which corresponds to imaginary time. The simulation is performed by advancing in τ via a combination of diffusion, drift and branching steps on walkers (sets of 3N coordinates) representing the wavefunction of the system.

One of the advantages of DMC lies in the convenient incorporation of the importance sampling. The imaginary time evolution of the walkers is “guided” during the drift stage by a guiding wavefunction ϕ G , which is usually a good guess for the wavefunction of the system. When a guiding wavefunction is used, the expectation value of an operator computed with DMC results in a value equal to , where ϕ 0 is the ground state wavefunction of the system. This leads to a common misunderstanding regarding the bias resulting from the choice of ϕ G . In fact, it is straightforward to show that for the Hamiltonian and any operator commuting with it, the expectation value is computed exactly within statistical error. That is, if , then for any ϕ G such that 〈ϕ 0|ϕ G 〉≠0. In practice, one usually demands that the DMC results are not sensitive to small changes in parameters describing ϕ G , if the parameters are sufficiently close to the optimal values. The use of the importance sampling is the reason why DMC results agree so precisely with a wide range of energetic and structural experimental data, both for liquid and solid 4He.

The wavefunction that we use for the importance sampling of solid helium is a symmetrization of the well-known Nosanow–Jastrow [12] wavefunction. The symmetrized version has the form

$$\phi_{\mathrm{SNJ}}= \Biggl(\prod_{i<j}^{N_{p}} f\bigl(\vert \boldsymbol{r}_i-\boldsymbol{r}_j\vert \bigr) \Biggr) \Biggl( \prod_{k}^{N_{s}} \sum _i^{N_{p}} g \bigl(\vert \boldsymbol{r}_i-\boldsymbol{l}_k\vert \bigr) \Biggr). $$
(1)

The first term in ϕ SNJ is the McMillan product of pair correlation functions f(r)=exp[−1/2 (b/r)5]. The second term describes the lattice structure. Here r and l describe respectively positions of the N p atoms and N s lattice sites. The localizing function g(r) is set to a Gaussian, g(r)=exp(−1/2 γr 2). The two parameters, b and γ, are obtained from optimization of the unsymmetrized form of the function, as described in Ref. [13]. This allows for excellent convergence, including insensitivity of results with respect to changes in the parameters, as described above.

The symmetrized wavefunction of Eq. (1) is an excellent and, at the same time, simple description of a quantum crystal. Already on the variational level, this wavefunction is capable of predicting the solid-to-liquid transition for 4He (optimized γ experiences a discontinuous jump to γ=0, corresponding to the liquid phase), which by itself is a very remarkable result. The second lattice term in ϕ SNJ is a product of sums over all particles. The product is maximized when the smallest possible number of the sums is vanishingly small. This corresponds to largest possible number of lattice sites being occupied. The product therefore includes all possible permutations of atoms on the lattice, but the atoms are more likely to occupy maximum number of sites in each permutation. Interstitials are allowed but have a built-in probability penalty, as it should be. Exchanges between atoms are allowed by construction. Vacancies may be introduced by using N p <N s , which only changes the norm of ϕ SNJ. Structural defects may be created by perturbing the set of the lattice sites {l}. This wavefunction was first introduced and tested with DMC for quantum solids by Cazorla et al. [14] and has been since then applied to a range of problems including elasticity [15] and point defects [10, 13] in solid 4He, and even quantum crystals of atoms excited to the Rydberg states [16].

We are also interested in the behavior of vacancies in solid 4He at finite temperature. In this case, the appropriate theoretical tool is the path integral Monte Carlo (PIMC) method. Starting from the Hamiltonian and the temperature T=(k B β)−1 of the system, it is possible to rewrite the partition function Z making use of the convolution property that the thermal density matrix \(\rho(\mathbf{R}',\mathbf{R};\beta)=\langle\mathbf{R}' \vert e^{-\beta\hat{H}} \vert\mathbf{R} \rangle\) satisfies,

(2)

with ε=β/M, and the boundary condition R M+1=R 1.

PIMC describes the quantum N-body system considering M different configurations R j of the same system, whose sequence constitutes a path in imaginary time. This means that the N-body quantum system is mapped onto a classical system of N ring polymers, each one composed by M beads. The different beads can be thought as a way to describe the delocalization of the quantum particle due to its zero-point motion.

For sufficiently large M, we recover the high-temperature limit for the thermal density matrix, where it is legitimate to separate the kinetic contribution from the potential one (primitive action). In this way, it is possible to reduce the systematic error due to the analytical approximation for ρ below the statistical uncertainties and therefore to recover “exactly” the thermal equilibrium properties of the system. However, the primitive action is too simple for studying extreme quantum matter and a better choice for the action is fundamental to reduce the complexity of the calculation and ergodicity issues. Using the Chin action [17, 18], we are able to obtain an accurate estimation of the relevant physical quantities with reasonable numeric effort even in the low temperature regime, where the simulation becomes harder due to the large zero-point motion of particles.

An additional problem we have to deal with when approaching the low temperature limit with PIMC simulations arises from the indistinguishable nature of 4He atoms. In the path integral formalism, the exchanges between L different particles are represented by long ring polymer composed by L×M beads. If we study a bosonic system, the indistinguishability of the particles does not affect the positivity of the integrand function in Eq. (2) and thus the symmetry of Z can be recovered via the direct sampling of permutations between the ring polymers. A very efficient sampling scheme that we have used in the present study is provided by the Worm Algorithm [19].

The formation of long permutation cycles is a frequent event at very low temperature and polymers which close themselves winding the periodic boundary conditions of the simulation box can appear in the PIMC configurations. The winding number, that is the net number of times the paths of the polymers wind around the periodic cell, is an important quantity since it is related to the superfluid fraction of the system [20]. In particular, the appearance of polymers presenting non-zero winding numbers in PIMC configurations gives indication of superfluidity in the simulated system.

3 Vacancies at Finite Temperature

The presence of vacancies in solid 4He produces at zero temperature the emergence of supersolidity, even when the vacancy concentration is very small. The influence of vacancies in solid 4He is reasonably expected to change with temperature, but an accurate estimation of temperatures at which supersolidity appears was lacking until recently. Our aim has been to gain a deeper understanding of this behavior by performing comprehensive PIMC simulations. It is worth mentioning that the efficiency of the sampling in PIMC, when the temperature approaches the zero limit, drops progressively by the low acceptance ratio of the sampling movements. In order to overcome, at least in part, these technical issues it is crucial to work with an accurate action, that allows for reducing the number of terms (beads), and a good permutation sampling as the one provided by the worm algorithm.

We have studied the properties of incommensurate solid 4He at finite temperature carrying out PIMC simulations of N=179 4He atoms, interacting through an accurate Aziz pair potential [11], in an almost cubic simulation box matching the periodicity of an hcp lattice made up of N s =180 sites at a density ρ=0.0294 Å−3. As usual, we apply periodic boundary conditions to the simulation box to emulate the infinite dimensions of the bulk system.

Thanks to the accuracy of the Chin approximation for the action, it is possible to reach convergence of the physical observables in the limit ε→0 with a rather large value of the imaginary time step ε, making thus feasible the simulation of the quantum system with a small number of beads, even at low temperature [18]. More precisely, the convergence of the one-body density matrix ρ 1(r) is achieved with a time step ε=0.033 K−1.

PIMC results for ρ 1(r) at different temperatures and at the density quoted above are shown in Fig. 1. We have plotted, in the same figure, the zero-temperature estimation of ρ 1 for the same system and for a perfect hcp crystal, obtained with the Path Integral Ground State method [21]. We notice that the highest temperature at which the system presents a non-zero condensate fraction n 0, indicated by a plateau in the large r behavior of ρ 1(r), is T 0=0.2 K. Our estimation for n 0 at this temperature is n 0=(8.4±0.8)×10−4. At temperatures T>T 0, the plateau disappears and the one-body density matrix presents an exponential decay at large r, which becomes more pronounced as the temperature increases, up to T=0.75 K. Above this temperature, the decay of ρ 1(r) becomes independent of T and it is similar to the large r behavior of ρ 1(r) in commensurate (perfect) crystals.

Fig. 1
figure 1

The one-body density matrix ρ 1(r) for an hcp crystal with vacancy concentration X v =1/180 at density ρ=0.0294 Å−3 and at different temperatures: T=1 K (triangles down), T=0.75 K (triangles up), T=0.5 K (diamonds), T=0.25 K (squares) and T=0.2 K (circles). The dotted and dashed lines represent ρ 1(r) at zero temperature respectively for the commensurate (X v =0) and incommensurate crystal (X v =1/180) at the same density, taken from Ref. [21]

Full size image

A relevant feature of PIMC is the possibility of giving a qualitative microscopic description of atomic positions in 4He crystals by means of its ring-polymer representation; the spreading of beads of each polymer gives an account of the delocalization of the atoms due to their zero-point motion. In Fig. 2, we show snapshots of the typical configurations of the incommensurate crystal at different temperature, plotting two-dimensional projections of the PIMC polymers lying in a basal plane of the hcp lattice.

Fig. 2
figure 2

Two-dimensional projection of basal planes of the incommensurate hcp crystal at different temperatures, represented according to the PIMC isomorphism of the classical polymers. At T=1 K (high-left panel) the vacancy is localized and indicated by the circle. At T=0.5 K (high-right panel), the vacancy begins to delocalize: the ellipse indicates a quantum particle delocalized over two different lattice sites. At T=0.2 K (low-left panel), the vacancy is completely delocalized and cannot be easily detected. Below T=0.2 K (low-right panel), the delocalization of vacancy strongly enhance the exchange between the bosons and allows the appearance of paths presenting a non-zero winding number, like the one represented by the thick line

Full size image

At the highest temperature that we have studied, that is T=1 K, the polymers do not spread on distances larger than the interatomic distance, indicating that the 4He atoms tend to stay localized around their equilibrium positions. In this case, the vacancies are easily detectable inside the lattice. This behavior explains the fact that, at this temperature, the presence of vacancies does not affect noticeably the overall behavior of ρ 1 which, for the incommensurate crystal, is similar to the one of the perfect crystal.

At lower temperatures, the delocalization of 4He atoms increases, allowing polymers to occupy different lattice points. In typical configurations at T=0.5 K, we can detect polymers which spread on distances higher than the interatomic distance. This eventuality, which indicates that the vacancies begin to delocalize, enhances the possibility for the different polymers to superpose and thus to permute. However, at this temperature the polymers spreading on different lattice points are still rare events and the formation of long permutation cycles, which are necessary for BEC, is inhibited.

If we further decrease the temperature, the polymers spreading on different lattice points become more frequent and it is impossible to associate a well defined lattice point to every quantum particle, as in the case at higher temperature. At T=0.2 K, the typical configuration of the incommensurate crystal looks like a commensurate system, indicating that the vacancies at this temperature are completely delocalized and thus undetectable inside the crystal. The frequent occurrence of a same lattice point occupied by beads belonging to different polymers strongly enhances the exchanges between the 4He atoms and allows also the creation of long permutation cycles. In particular, for T≤0.2 K, it is possible to sample configurations presenting a non-zero winding number, as the one shown in the low left panel of Fig. 2. In this picture, we show two following basal planes of the incommensurate hcp lattice and we highlight a path which winds around the boundary conditions of the simulation box. The appearance of non-zero winding number paths in the sampled configurations is a clear signal that the simulated incommensurate crystal supports superfluidity at temperatures below T 0=0.2 K. On the other hand, this onset temperature is observed to be an increasing function of the vacancy concentration [22].

4 Vacancies and the Elastic Constants

We have carried out a computational study of the elastic properties of perfect (e.g. free of defects) and incommensurate solid 4He in the hcp structure based on the diffusion Monte Carlo approach. This zero-temperature study is intended to improve our understanding of the response of solid helium to external strain, and extends the work initiated by Pessoa et al. [23]. In particular, we provide the zero-temperature dependence of C 44 on pressure up to ∼110 bar. This is a significantly higher pressure than previously considered both experimentally and theoretically. Our results are compared to experimental data and other calculations when available and, as it will be shown later on, good agreement is generally found. The computational method that we employ is fully quantum and virtually exact, that is, in principle only affected by statistical uncertainties. In this sense, our study also represents an improvement with respect to previous zero-temperature first-principles work [23] based on variational Monte Carlo calculations (i.e., subject to bias stemming from the choice of the trial wavefunction).

For small strains, the zero-temperature energy of a crystal can be expressed as

$$E = E_{0} + \frac{1}{2} V_{0} \sum^{6}_{i,j = 1} C_{ij} s_{i} s_{j}, $$
(3)

where V 0 and E 0 are the volume and internal energy of the undistorted solid, {C ij } the elastic constants and {s i } the strain components defined such that s 1, s 2 and s 3 are fractional increases in the x, y and z directed axes, and s 4, s 5 and s 6 angular increases of the xy, xz and yz angles [24, 25]. The symmetry of the crystal under consideration defines the number of elastic constants which are non-zero. In hcp crystals, this number reduces to five namely C 11, C 12, C 33, C 13 and C 44, where C 44 is commonly known as the shear modulus. To calculate these elastic constants, is necessary to compute the second derivative of the internal energy of the crystal with respect to the strain tensor σ ij . For this, we express the primitive hcp unit cell in terms of the translational vectors

(4)
(5)
(6)

where a and c are the lattice parameters in the basal plane and along the z axis respectively, and i, j and k correspond to the usual unitary Cartesian vectors, and two-atom basis set \(\mathbf{r}_{1} = \frac{1}{2}\mathbf{a}_{1} + \frac{1}{3}\mathbf{a}_{2}+ \frac{2}{3}\mathbf{a}_{3}\) and r 2=(0,0,0).

In particular, the shear modulus C 44 quantifies the response of the hcp crystal to a heterogeneous strain in which the angle between by the c-axis and basal plane is tilted and the volume of the unit cell kept fixed. Such a shear deformation can be expressed as a transformation between sets of primitive translational vectors, {a 1,a 2,a 3}→{e 1,e 2,e 3}, where [25]

(7)

ε being a dimensionless parameter. It follows that

$$C_{44} = \frac{1}{V_{0}} \biggl( \frac{\partial^{2} E}{\partial\varepsilon^{2}}\biggr)_{V=V_{0}}, $$
(8)

where the equilibrium condition is fulfilled at ε=0.

The simulation box used in our perfect (defected) pure shear calculations contains 200 (199) 4He atoms and was generated by replicating the hcp unit cell 5 times along e 1 and e 2, and 4 times along e 3. In proceeding so, hexagonal symmetry in our supercell calculations is guaranteed by construction. Periodic boundary conditions were imposed along the three directions defined by the edges of the non-orthorhombic simulation box. Prior to our shear modulus calculations, we determined the value of the equilibrium c/a ratio at each volume. We found that regardless of the pressure considered the optimal c/a value was always 1.62(1). In order to express our C 44 (V) results as a function of pressure we employed the equations of state P(V) reported in Ref. [13] (in both perfect and defected cases), which were deduced employing the DMC method and considering accurate finite-size corrections to the total energy [30]. Additional details of our elastic constant calculations can be found in Ref. [15].

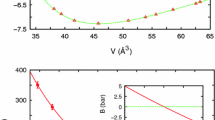
In Fig. 3, we plot the pressure dependence of the shear modulus of perfect and defected solid 4He as obtained in our T=0 calculations. We found that these results can be accurately reproduced with a linear function of the form C 44(P)=a 44+b 44 P. In the perfect crystal, parameters a 44 and b 44 adopt the values 92.2 (1.7) bar and 1.83 (0.04) respectively, whereas in the defected structure these are 93.3 (1.7) bar and 1.72 (0.04). It is observed that the elastic properties of perfect and defected helium are very similar at pressures close to melting (that is ∼25 bar). Also we note that both sets of C 44 data are compatible with experiments performed at low pressures and temperatures [26–29]. A similar agreement is achieved with the other elastic constants that we report at a pressure close to melting in Table 1. At this particular pressure, all the constants of the defected crystal except C 44 are larger than the ones of the perfect solid, with differences of variable size depending on the particular C ij . As compression is increased, the shear modulus of the defected crystal becomes appreciably smaller than that of perfect 4He. In relation to recent shear modulus experiments [29] we must conclude that, based on this preliminary computational study, the increase of C 44 observed at low-T can not be explained in terms of point defects.

Fig. 3
figure 3

Pressure-dependence of the calculated shear modulus of perfect and defected solid 4He at zero temperature. Experimental data are taken from Refs. [26] (Crepeau et al.), [27, 28] (Greywall), and [29] (Syshchenko et al.) Linear fits to our results are also shown

Full size image
Table 1 Elastic constants of the perfect (commensurate) and defected (incommensurate) hcp solid 4He calculated with the DMC method at P=26 bar. Experimental values obtained by Crepeau et al. [26] at a pressure P=25.33 bar. Numbers within parenthesis stand for errors
Full size table

5 Summary and Conclusions

In the present work, we have reported recent results on the microscopic properties of hcp 4He with a tiny fraction of point defects, i.e., vacancies. To make our study as free of approximations as possible we have used state-of-the-art quantum Monte Carlo methods, both at zero and finite temperature. Relying only on the Hamiltonian, we have studied two particular aspects that we think relevant in the present discussion about the possible supersolid 4He phase. First, we have addressed the question of the behavior of vacancies when the temperature decreases, approaching the temperatures where NCRI is observed. Our PIMC results unambiguously show that there is an onset temperature for Bose-Einstein condensation that depends on the vacancy concentration. For the lowest concentrations that we can access with our approach this onset temperature is close to the experimental one. At this same temperature, the vacancies are observed to change their spatial behavior. Our simulations show that for T larger than the onset temperature, vacancies appear as classical entities in the sense that we can always identify where they are, as it happens in a classical crystal. For temperatures smaller than the onset one, the vacancy is completely delocalized and the polymers representing the particles in the PIMC formalism spread over all the sites as if the crystal were perfect.

In a second part, we have studied the elastic behavior of solid 4He in the limit of zero temperature. Technically, this is achieved by calculating energies of the deformed crystal by means of the DMC method. This approach is quite standard in classical simulations but much less worked out in quantum Monte Carlo. We have reported results for all the elastic constants at melting and the pressure dependence of C 44. The presence of vacancies is also studied. Our preliminary results show a globally small effect with the more relevant result being the different slope of the elastic constants with the pressure: the slope for the incommensurate crystal is systematically smaller than the one for the commensurate phase.

The role of vacancies in a supersolid scenario for solid 4He has been frequently excluded due to two arguments: the relatively high energy cost of its formation (above 10 K) and the possibility that vacancies form aggregates and eventually evaporate. It is certainly difficult that vacancies appear at very low temperature by thermal activation but we think that we cannot exclude the appearance of point defects along the growing process. Concerning the possible aggregation of vacancies due to a short-range attraction between them, there are different theoretical predictions with contradictory observations. We are currently exploring this issue as a function of temperature.