Introduction

The WEST tokamak is equipped with a full-tungsten actively cooled divertor and serves as a test bed for ITER-like tungsten monoblocks [1]. Tungsten (W) impurities entering the plasma pose a major risk to plasma core performance by radiative cooling. In principle, the tungsten concentration \(c_\text{W}=n_\text{W}/n_\text{e}\) must be lower than \(10^{-4}\) for fusion-relevant operation [2, 3]. Therefore, it is highly desirable to determine reliable, space-resolved estimates of the tungsten density and avoid tungsten accumulation. Diagnostics measuring the plasma emission, e.g., extreme ultra-violet spectroscopy [4], X-ray spectroscopy [5] and bolometry [6] are often used for this purpose. However, inference of the tungsten concentration from the plasma emission also requires the electron density and temperature obtained by other diagnostics. The various sources of uncertainty and the intrinsic interdependencies of multiple diagnostics greatly increase the difficulty of obtaining reliable results that are consistent with all measurements, as well as credible estimates of the uncertainty on individual parameters of interest. Indeed, when the analysis using data from one diagnostic also depends on physical quantities inferred from other diagnostics, the error propagation can be quite difficult to deal with, especially when the errors are not Gaussian [7]. Instead of treating the data from different diagnostics separately and evaluating the uncertainty through complicated conventional error propagation analysis, one can resolve such challenges with a coherent combination of various measurements using the integrated data analysis (IDA) approach based on Bayesian probability theory [8]. Since a number of years, IDA has seen increased adoption in fusion experimental data analysis, where heterogeneous diagnostics often provide complementary, but also partially redundant information. The method can help resolving data inconsistencies and may reduce the uncertainty on estimates of physical quantities. Typical applications of IDA in the fusion community include the inference of temperature and density profiles [7, 9,10,11,12], the effective ion charge [13,14,15], the magnetic equilibrium [16], etc. In order to improve the reliability of physical parameters and allow uncertainty estimates, we apply IDA approach for the joint analysis of measurements of the soft X-ray emissivity at WEST, combined with density and temperature measurements.

This paper is organized as follows. We first introduce some basic concepts of Bayesian inference in “Bayesian Inference”, followed by the application to tomographic reconstruction of the soft X-ray emissivity at WEST in “Bayesian Soft X-ray Tomography with Gaussian Process”. “Integrated Analysis of Tungsten Concentration” concerns the integrated estimation of tungsten concentration profiles from both synthetic and real data. Finally, in “Preliminary Exploration on Speeding Up the Inference with Surrogate Models” we briefly discuss the possibility of accelerating the inference using neural network surrogate models, with a preliminary application to fast inference of electron density profiles.

Bayesian Inference

Parameter estimation, i.e., to determine values of unobserved parameters of interest \(\vec{H} = [H_1, H_2, \ldots , H_n]\) from experimental data \(\vec{D} = [D_1, D_2, \ldots , D_m]\), is a common data analysis problem. In Bayesian inference, this is done by inferring the conditional probability distribution of the parameters \(\vec{H}\) given the data \(\vec{D}\), i.e., the posterior distribution \(p(\vec{H} | \vec{D})\), which follows from Bayes’ theorem:

$$\begin{aligned} p(\vec{H} | \vec{D}) = \frac{p(\vec{D} | \vec{H}) \, p(\vec{H})}{p(\vec{D})} \propto p(\vec{D} | \vec{H}) \, p(\vec{H}). \end{aligned}$$
(1)

The likelihood \(p(\vec{D} | \vec{H})\) quantifies the mismatch between the data obtained from experiments and the predictions by the forward model for given parameter values \(\vec{H}\). The prior distribution \(p(\vec{H})\) represents the state of knowledge about the parameters before any observations are taken and can be used to implement regularization and physical constraints. The evidence or marginal likelihood \(p(\vec{D}) = \int p(\vec{D} | \vec{H}) p(\vec{H}) \text{d} \vec{H}\) is a normalization constant with no explicit dependence on \(\vec{H}\). It is usually omitted for parameter estimation problems [17].

By maximizing the posterior with respect to \(\vec{H}\), we obtain a single most probable solution, known as the maximum a posteriori (MAP) estimate \(\vec{H}_{\text{MAP}}\). However, the MAP estimate is not always optimal, and more generally one needs to calculate the marginal distribution of the individual parameters \(H_i\), by integrating over the others:

$$\begin{aligned} p(H_i | \vec{D}) = \int p(\vec{H} | \vec{D}) \; \text{d} H_1 \ldots \text{d} H_{i-1} \text{d} H_{i+1} \ldots \text{d} H_n. \end{aligned}$$
(2)

In most cases, the posterior distribution cannot be obtained in an analytical form and therefore the marginalization integral also has no closed-form expression. Exceptions can be found only for some special situations, for instance when both the prior and the likelihood are Gaussian and the forward model is linear, as will be explained in the next section. Numerical methods like Markov chain Monte Carlo (MCMC) are usually required in Bayesian inference to sample from the posterior distribution [17]. The values of \(H_i\) collected from the joint samples \([H_1, H_2, \ldots , H_n]\) of the joint distribution \(p(H_1, H_2, \ldots , H_n | \vec{D})\) are also samples from the marginal distribution \(p(H_i | \vec{D})\) [10].

Bayesian Soft X-ray Tomography with Gaussian Process

Soft X-ray Diagnostic at WEST

A new soft X-ray (SXR) diagnostic with energy discrimination has been developed for WEST [18]. It consists of two gas electron multiplier (GEM) cameras providing vertical and horizontal views, aiming at 2D tomographic reconstruction. However, as currently there is only limited data available from the GEM diagnostics [19], in this work, we use the line-integrated SXR emissivity measured by silicon diodes. This is part of the former SXR diagnostic, DTOMOX, developed for Tore Supra (TS) and still operational on WEST. DTOMOX has 82 lines-of-sight considered, among which 45 are horizontal and 37 are vertical [20]. The viewing geometry is depicted in Fig. 1. However, the vertical camera of DTOMOX has been dismantled for WEST due to the lack of space for plasma observation, as will be explained in the subsection ''Test on Real Data''.

Fig. 1
figure 1

The geometry of the soft X-ray diagnostic system DTOMOX

Full size image

In order to infer the local SXR emissivity in a poloidal cross-section, we first discretize the cross-section in 3600 pixels using a \(60 \times 60\) grid, and then only consider the n pixels inside the last closed flux surface (LCFS) for tomography. The n emissivities are represented by a vector \(\vec {\varepsilon }_{\text{SXR}} = [\varepsilon _{\text{SXR}}(\vec{r}_1), \varepsilon _{\text{SXR}}(\vec{r}_2), \ldots , \varepsilon _{\text{SXR}}(\vec{r}_n))]\), where \(\varepsilon _{\text{SXR}}(\vec{r}_i)\) denotes the emissivity at location \(\vec{r}_i\). Then, based on the line-of-sight approximation [21], the line-integrated emissivity along m viewing chords \(\vec{d}_{\text{SXR}} = [d_{\text{SXR, 1}}, d_{\text{SXR, 2}}, \ldots , d_{\text{SXR, m}}]\) can be calculated using the forward model in a matrix form

$$\begin{aligned} {\vec{d}} _{\text{SXR}} = \bar{{\bar{R}}} \vec{\boldsymbol{\varepsilon}} _{\text{SXR}}. \end{aligned}$$
(3)

Here \(\bar{{\bar{R}}}\) is the response matrix or transfer matrix describing how much each of the n pixels contributes to the signal recorded in each of the m channels.

Gaussian Process Tomography Method

The tomographic reconstruction of the local SXR emissivity at n points from m line integrals is essentially an ill-posed problem, as the number of unknowns n is much larger than m. A unique solution does not exist without additional regularizing assumptions. There are various ways to impose regularization. One of the most commonly used methods is Tikhonov regularization, where a regularization matrix imposes smoothness on the emissivity profiles, for instance by minimizing the Fisher information [22, 23]. In the Bayesian framework, regularization is built into the prior probability distribution, which in our case is a Gaussian process.

Non-stationary Gaussian Process Prior Distribution

Basically, a Gaussian process (GP) is a generalization of multivariate Gaussian distribution to a function space. A Gaussian process \(f(\vec{r})\) describing the SXR emissivity over a poloidal cross-section is completely specified by a mean function \(\mu (\vec{r})\) and a covariance function \(k(\vec{r}, \vec{r}^{\prime })\), evaluated at positions \(\vec{r}\) and \(\vec{r}^{\prime }\) in the cross-section. Any finite number of function values \(f(\vec{r}_i)\), i.e. SXR emissivities at pixel positions \(\{\vec{r}_{i}\}\) jointly follow a multivariate Gaussian distribution [24]. The covariance function determines the correlation between any two points and therefore regularizes the problem of estimating the local emissivities by controlling the smoothness of the emissivity profile. A stationary covariance function (only depends on \(\vec{r} - \vec{r}^{\prime }\)) assumes the same smoothness everywhere, an example of which is the squared exponential covariance function

$$\begin{aligned} k_{\text{SE}}(\vec{r}_i, \vec{r}_j) = \sigma _\text{f}^2 \exp \left( - \frac{\Vert \vec{r}_{i} - \vec{r}_{j}\Vert ^2}{2l^2}\right) . \end{aligned}$$
(4)

Here the amplitude \(\sigma _\text{f}\) controls the level of variability and the characteristic length scale l controls the degree of smoothness, while \(\Vert \vec{r}_{i} - \vec{r}_{j}\Vert \) denotes the Euclidean distance between \(\vec{r}_{i}\) and \(\vec{r}_{j}\). In general, free parameters like \(\sigma _{\text{f}}\) and l that specify the prior distribution are called hyperparameters. In comparison, a nonstationary GP allows varying degrees of smoothness in different locations and is therefore more flexible. Both stationary [25, 26] and nonstationary [27, 28] Gaussian processes have been applied to tomography problems on several fusion devices. The Bayesian tomography method with Gaussian processes is also referred to as Gaussian process tomography [29].

To reconstruct emissivity profiles with spatially varying smoothness, we adopt a nonstationary covariance proposed by Gibbs [30]. Under an isotropic assumption of equal lengths scales in the radial (R) and vertical (z) directions (\(l_R(\vec{r}) = l_z(\vec{r}) = l(\vec{r})\)), the covariance function can be written as

$$\begin{aligned} k_{\text{NS}}(\vec{r}_i, \vec{r}_j) = \sigma _\text{f}^2 \frac{2 l(\vec{r}_i) l(\vec{r}_j)}{l^2(\vec{r}_i) + l^2(\vec{r}_j)} \exp \left( - \frac{\Vert \vec{r}_{i} - \vec{r}_{j}\Vert ^2}{l^2(\vec{r}_i) + l^2(\vec{r}_j)}\right) , \end{aligned}$$
(5)

where \(l(\vec{r}_i)\) and \(l(\vec{r}_j)\) are the length scales employed at spatial positions \(\vec{r}_i\) and \(\vec{r}_j\). In order to incorporate information about the magnetic equilibrium, we assume a flux-dependent length scale. This is quite reasonable considering the dominant impurity transport along the flux surface, causing the emissivity field to be strongly correlated with the magnetic equilibrium [26]. In practice, we find that local length scales with linear dependence on the normalized poloidal flux \(\psi _{N}\) are sufficient to model the emissivity profile:

$$\begin{aligned} l(\psi _{N}) = (1-\psi _{N}) l_\text{c} + \psi _{N} l_\text{e}. \end{aligned}$$
(6)

In this expression, the length scales at the core (\(l_{\text{c}}=l(0)\)) and the edge (\(l_{\text{e}}=l(1)\)) are two hyperparameters. Merging all hyperparameters in a vector \(\vec {\theta }\), the prior distribution of the SXR emissivity profile, which is conditional on the hyperparameters, is given by

$$\begin{aligned} p(\vec {\varepsilon }_{\text{SXR}} | \vec {\theta }) = \frac{1}{(2\pi )^{\frac{n}{2}} |\Sigma _{\text{prior}}|^{\frac{1}{2}}} \times \exp \left[ -\frac{1}{2}\left( \vec {\varepsilon }_{\text{SXR}} - \vec {\mu }_{\text{prior}}\right) ^{\top } \Sigma _{\text{prior}}^{-1} \left( \vec {\varepsilon }_{\text{SXR}} - \vec {\mu }_{\text{prior}}\right) \right] . \end{aligned}$$
(7)

The prior mean vector \(\vec {\mu }_{\text{prior}}\) is usually set to zero and the prior covariance matrix \(\Sigma _{\text{prior}}\) is determined by the covariance function, i.e., \(\Sigma _{\text{prior}}[i, j] = k_{\text{NS}}(\vec{r}_i, \vec{r}_j)\).

Likelihood

The observations from different channels are usually assumed to be affected by independent Gaussian noise. Therefore the likelihood is a multivariate Gaussian distribution:

$$\begin{aligned} p(\vec{d}_{\text{SXR}} | \vec {\varepsilon }_{\text{SXR}}, \vec {\theta }) = \frac{1}{\left( 2\pi \right) ^{\frac{m}{2}} |\Sigma _\text{d}|^{\frac{1}{2}}} \times \exp \left[ -\frac{1}{2} \left( \vec{d}_{\text{SXR}} - \bar{{\bar{R}}}\vec {\varepsilon }_{\text{SXR}}\right) ^{\top } \Sigma _\text{d}^{-1} \left( \vec{d}_{\text{SXR}} - \bar{{\bar{R}}}\vec {\varepsilon }_{\text{SXR}}\right) \right] , \end{aligned}$$
(8)

where the covariance \(\Sigma _{\text{d}}\) is a diagonal matrix given by \(\Sigma _{\text{d}} = \text{diag}[\sigma _1^2, \sigma _2^2, \ldots , \sigma _m^2]\). Here, the standard deviation of each channel \(\sigma _i\) is assumed to depend on the signal level,

$$\begin{aligned} \sigma _i = \alpha \cdot d_{\text{SXR}, i}, \end{aligned}$$
(9)

where \(\alpha \) here is a hyperparameter controlling the noise level.

Posterior Distribution

With a Gaussian process for the prior and a Gaussian likelihood, and the forward model being linear, the posterior \(p(\vec {\varepsilon }_{\text{SXR}} | \vec{d}_{\text{SXR}}, \vec {\theta })\) is also a Gaussian process. The mean vector and covariance matrix corresponding to a set of discrete pixels are therefore available in a closed form [29]:

$$\begin{aligned} \vec {\mu }_{\text{post}}&= \vec {\mu }_{\text{prior}} + (\bar{{\bar{R}}}^{\top } \Sigma _\text{d}^{-1} \bar{{\bar{R}}} + \Sigma _{\text{prior}}^{-1})^{-1} \bar{{\bar{R}}}^{\top } \Sigma _\text{d}^{-1} (\vec{d}_{\text{SXR}} - \bar{{\bar{R}}} \vec {\mu }_{\text{prior}}), \\ \Sigma _{\text{post}}&= (\bar{{\bar{R}}}^{\top } \Sigma _\text{d}^{-1} \bar{{\bar{R}}} + \Sigma _{\text{prior}}^{-1})^{-1}. \end{aligned}$$
(10)

The posterior mean provides an estimate of the emissivity profile and the diagonal elements of the posterior covariance matrix are used to quantify the uncertainty of the inference.

Hyperparameter Optimization

The quality of the reconstructed emissivity profile strongly relies on the choice of hyperparameters \(\vec {\theta } = \left[ \alpha , \sigma _f, l_c, l_e\right] \). In principle, a fully Bayesian analysis also takes into account the uncertainty on the hyperparameters by marginalizing them out. This approach provides reliable estimate of uncertainty but is computationally expensive. As this fully Bayesian approach is computationally demanding, here we use an empirical Bayes approach, determining the hyperparameters from the data [31, 32]. This can be done for instance by maximizing the marginal likelihood

$$\begin{aligned} p(\vec{d}_{\text{SXR}} | \vec {\theta }) = \int p(\vec{d}_{\text{SXR}} | \vec {\varepsilon }_{\text{SXR}}, \vec {\theta }) \, p(\vec {\varepsilon }_{\text{SXR}} | \vec {\theta }) \; \text{d} \vec {\varepsilon }_{\text{SXR}}. \end{aligned}$$
(11)

Again, thanks to the Gaussian prior and likelihood, and the linear forward model, this integration is analytically tractable [24]. The logarithm of the marginal likelihood is

$$\begin{aligned} \ln \left[ p(\vec{d}_{\text{SXR}}|\vec {\theta })\right] =&-\frac{m}{2} \ln (2\pi ) -\frac{1}{2} \ln |\Sigma _\text{d} + \bar{{\bar{R}}} \Sigma _{\text{prior}} \bar{{\bar{R}}}^{\top }|\\&-\frac{1}{2} (\vec{d}_{\text{SXR}} - \bar{{\bar{R}}}\vec {\mu }_{\text{prior}})^{\top }(\Sigma _\text{d} + \bar{{\bar{R}}} \Sigma _{\text{prior}} \bar{{\bar{R}}}^{\top })^{-1} (\vec{d}_{\text{SXR}}-\bar{{\bar{R}}}\vec {\mu }_{\text{prior}}). \end{aligned}$$
(12)

The hyperparameters obtained through maximization of Eq. (12) are then substituted into Eq. (10) to obtain the reconstructed emissivity distribution. This maximization can be done numerically with the help of the optimization algorithms implemented in the python package SciPy [33].

Validation on Synthetic Data

To validate our method, we created three different synthetic SXR emissivity profiles from a known magnetic equilibrium, with characteristic patterns of the Gaussian shape, the hollow shape and the poloidally asymmetric banana shape, as shown in Fig. 2. The phantom models used to generate the emissivity profiles were based on an a priori assumption of strong correlation between emissivity and magnetic flux. Synthetic line-integrated measurements were generated from these artificial emissivity profiles using all 82 lines-of-sight of DTOMOX, with 5% additive Gaussian noise. Then, Gaussian process tomography with the nonstationary covariance function in Eq. (5) was applied to reconstruct the original emissivity profiles from the artificial noisy measurements. Since the noise level of the synthetic data was already known, the covariance matrix of the measurements was simply \(\Sigma _{\text{d}} = \text{diag} \left[ (0.05 d_{\text{SXR}, 1})^2, (0.05 d_{\text{SXR}, 2})^2, \ldots , (0.05 d_{\text{SXR}, m})^2\right] \). After optimizing the hyperparameters, the posterior mean and posterior covariance matrix of the emissivity profiles were immediately available according to Eq. (10). The reconstructions are shown in Fig. 3. Here the reconstruction error is defined as the absolute difference between the true and reconstructed emissivity. The characteristic shapes of all three emissivity profiles were well recovered by our Gaussian process tomography method, including the asymmetric banana shape, which is often challenging for conventional tomographic techniques. For all three reconstructions, the local errors are less than 0.05 arb. unit on most area of the poloidal section and the largest errors are below 0.12 arb. unit. The line integrals calculated from the reconstructed emissivity profiles also show good agreement with the synthetic measurements.

Fig. 2
figure 2

Synthetic SXR emissivity profiles with a Gaussian shape, b hollow shape and c banana shape. The red line represents the last closed flux surface

Full size image
Fig. 3
figure 3

Reconstructions of SXR emissivity profiles from synthetic data with 5% noise level. Left column: reconstructed emissivity \(\varepsilon _{\text{SXR}}^{\text{rec}}\). Middle column: error map defined as the absolute difference between the true and the reconstructed emissivity \(\vert \varepsilon _{\text{SXR}}^{\text{rec}} - \varepsilon _{\text{SXR}}^{\text{true}}\vert \). Right column: measured and calculated line-integrated emissivity. The white lines correspond to the lines-of-sight of the DTOMOX system

Full size image

Further test has also been performed on synthetic data with a higher noise level of 10%. The results are illustrated in Fig. 4. Although the reconstruction error for the hollow and banana shapes gets larger with the increased noises, the overall performance is still quite good in all three cases.

Fig. 4
figure 4

Similar to Fig. 3, except the noise level of the synthetic line integrals is now 10%

Full size image

Test on Real Data

The application on real WEST data turned out to be challenging for several reasons. Due to the installation of an upper divertor, many vertically viewing diodes from DTOMOX are masked on WEST. Therefore, in practice only 45 horizontally viewing lines-of-sight are available [18], which poses difficulties for resolving certain spatial emissivity distributions with horizontal asymmetry (see appendix “Phantom Test with Only Horizontal Lines-of-Sight”). Moreover, the SXR data can also contain outliers caused by saturation or insufficient signal-to-noise ratio. Furthermore, we found that the error model described in Eq. (9) tends to underestimate the measurement uncertainty, especially for low-signal channels. Therefore, a new error model was used, consisting of background noise with variance \(\sigma _{\text{bg}, i}^2\) (estimated without plasma), in addition to a proportional measurement error:

$$\begin{aligned} \sigma _i^2 = \sigma _{\text{bg}, i}^2 + (\alpha \cdot d_{\text{SXR}, i})^2. \end{aligned}$$
(13)

This method has been applied to the SXR data from a real WEST pulse (#55191) with high \(n_{\text{e}}\) and \(T_{\text{e}}\) at the flat-top phase, for example t = 1.40 s. The result is shown in Fig. 5. Compared with the previous error model, the new model fits the measured line integrals better and significantly improves the posterior uncertainty by reducing the largest posterior standard deviation from 66.6 \(\mathrm {W \cdot m^{-3}}\) to 25.0 \(\mathrm {W \cdot m^{-3}}\). Without vertical lines-of-sight, the reconstructed emissivity profile hardly exhibits any horizontal asymmetry. The double-lobed structure in the uncertainty profile Fig. 5 (f) also suggests the limits of having only the horizontal camera. Considering this lack of information, in the remainder we will consider 1D radial profiles \(c_\text{W}(\rho )\), \(n_\text{e}(\rho )\) and \(T_\text{e}(\rho )\) instead of their 2D distributions.

Fig. 5
figure 5

Reconstructed SXR emissivity, line-integrated emissivity and error map (given by the posterior standard deviation) for WEST pulse #55191, \(t = 1.40\) s, without a–c and with d–f background noise considered

Full size image

Integrated Analysis of Tungsten Concentration

SXR Emissivity and Cooling Factors

The measured SXR emissivity from an ion species S in the plasma, \(\varepsilon _\text{S}\) (in \(\mathrm {W \cdot m^{-3}}\)), is usually modelled using the cooling factor (filtered by the spectral response of the detector) \(L_\text{S}\) (in \(\mathrm {W \cdot m^3}\)): \(\varepsilon _{\text{S}} = n_\text{e} \cdot n_\text{S} \cdot L_\text{S}\), with \(n_\text{e}\) the electron density and \(n_{\text{S}}\) the density of S. The cooling factor, defined as the energy loss rate per free electron per ion due to radiative cooling, is also called the radiative cooling rate [34] or the radiation loss parameter [35]. It can be calculated theoretically using atomic physics [2, 36]. In a hydrogenic plasma with dominant tungsten impurities at trace concentration (\(c_\text{W}=n_\text{W}/n_\text{e} \ll 1\)), the detected SXR emissivity is approximately the sum of contributions from the main ion species (denoted here as H) and tungsten:

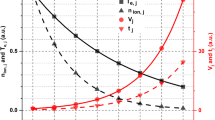
$$\begin{aligned} \varepsilon _{\text{SXR}} = n_\text{e}^2 \left[ L_\text{H}(T_\text{e}) + c_\text{W} \cdot L_\text{W}(T_\text{e})\right] . \end{aligned}$$
(14)

The cooling factors of deuterium and tungsten are calculated using atomic data from the OPEN-ADAS database [37]. They depend primarily on the electron temperature \(T_{\text{e}}\), as shown in Fig. 6. Under the above assumptions, the tungsten concentration can in principle be estimated on the basis of measurements of the SXR emissivity, \(n_{\text{e}}\) and \(T_{\text{e}}\).

Fig. 6
figure 6

\(T_\text{e}\) dependence of W and H cooling factors filtered by the SXR spectral response

Full size image

Integrated Data Analysis for \(c_{\text{W}}\)

With the SXR emissivity profile reconstructed using Gaussian process tomography, the electron density profile measured by interferometry (INT) and the electron temperature profile measured by electron cyclotron emission (ECE), the tungsten concentration can directly be estimated by reformulating Eq. (14):

$$\begin{aligned} c_{\text{W}} = \frac{\varepsilon _{\text{SXR}}}{n_{\text{e}}^2 L_{\text{W}}(T_{\text{e}})} - \frac{L_{\text{H}}(T_{\text{e}})}{L_{\text{W}}(T_{\text{e}})}. \end{aligned}$$
(15)

Such direct estimation of W concentration based on the tomographic reconstruction of plasma emission and the \(T_{\text{e}}\) dependent cooling factors has been applied to several devices, for example JET [38] and HL-2A [6]. However, this calculation does not take into account the sources of uncertainty from individual diagnostics or their interdependencies. In order to treat the data in an integrated way, we follow an integrated data analysis (IDA) approach using Bayesian probability theory [7]. IDA considers the joint posterior distribution of \(\vec{c}_{\text{W}}\), \(\vec{n}_{\text{e}}\) and \(\vec{T}_{\text{e}}\):

$$\begin{aligned}&p(\vec{c}_{\text{W}}, \vec{n}_{\text{e}}, \vec{T}_{\text{e}} \mid \vec{d}_{\text{SXR}}, \vec{d}_{\text{INT}}, \vec{d}_{\text{ECE}}) \\ \propto \;&p(\vec{d}_{\text{SXR}} \mid \vec{c}_{\text{W}}, \vec{n}_{\text{e}}, \vec{T}_{\text{e}}) \, p(\vec{d}_{\text{INT}} \mid \vec{n}_{\text{e}}) \, p(\vec{d}_{\text{ECE}} \mid \vec{T}_{\text{e}}) \, p(\vec{c}_{\text{W}}) \, p(\vec{n}_{\text{e}}) \, p(\vec{T}_{\text{e}}). \end{aligned}$$
(16)

The prior distributions of \(c_\text{W}\), \(n_\text{e}\) and \(T_\text{e}\) are modeled by three stationary Gaussian processes (so far with fixed hyperparameters). An additional constraint of zero gradient at the core \(c_{\text{W}}^{\prime }(0) = 0\) is imposed on the W concentration profile by adding an artificial ‘observation’ [31]. The likelihoods are also assumed to be Gaussian in analogy with the distribution expressed in Eq. (8), with the following corresponding forward models:

$$\begin{aligned} \vec{d}_{\text{SXR}} =&\bar{{\bar{R}}}_{\text{SXR}} \vec {\varepsilon }_{\text{SXR}} \left( \vec{n}_{\text{e}}, \vec{T}_{\text{e}}, \vec{c}_{\text{W}}\right) , \\ \vec{d}_{\text{INT}} =&\bar{{\bar{R}}}_{\text{INT}} \vec{n}_{\text{e}}, \\ \vec{d}_{\text{ECE}} =&\vec{T}_{\text{e}}. \end{aligned}$$
(17)

The interferometry system measures the line-integrated electron density and the geometry of the 10-channel WEST interferometry is illustrated in Fig. 7. Its forward model is linear and can be expressed in a matrix form with the help of a response matrix \(\bar{{\bar{R}}}_{\text{INT}}\). Under the blackbody assumption and considering the plasma being optically thick, the Rayleigh-Jeans approximation tells us that the intensity of the electron cyclotron radiation is proportional to the electron temperature and the forward model of the ECE system should also be linear. However, in the WEST ECE system, empirical corrections are required during data processing in order to yield reliable temperature estimates. This makes it relatively difficult to specify a detailed forward model, which is why we use the (validated) \({T}_{\text{e}}\) measurements from ECE as the raw data \(\vec{d}_{\text{ECE}}\). Nevertheless, due to the nonlinear forward model used in \(p(\vec{d}_{\text{SXR}} \mid \vec{c}_{\text{W}}, \vec{n}_{\text{e}}, \vec{T}_{\text{e}})\), the posterior distribution does not have an analytical expression and needs to be approximated numerically with MCMC sampling methods.

Fig. 7
figure 7

The beam chord trajectories of the WEST interferometry system

Full size image

Validation on Synthetic Data

For validation purposes, we generated synthetic data for ECE, interferometry and SXR diagnostics, starting from an artificial Gaussian-shaped radial tungsten concentration profile with a peak value of \(c_{\text{W}} = 10^{-4}\) at the core, and radial profiles of density and temperature taken from real measurements at WEST. These synthetic diagnostic data were then used as the input for IDA, and samples of \(c_\text{W}\), \(n_\text{e}\) and \(T_\text{e}\) were drawn from the joint posterior distribution in Eq. (16). An example result is shown in Fig. 8. Here, the reconstructed W concentration profile (blue) is estimated by taking the average of posterior samples. It matches the original profile (red) well in the center of the plasma and the re-integrated emissivity is in good agreement with the synthetic measurements. However, further outside the central plasma the uncertainty of the reconstructed \(c_{\text{W}}\) quickly grows, because the measured SXR emissivity is less sensitive to the tungsten concentration at low \(n_\text{e}\) and \(T_\text{e}\). In other words, the SXR measurements provide little information on the edge tungsten concentration.

Fig. 8
figure 8

a W concentration estimated from synthetic data and b re-integrated SXR emissivity

Full size image

Test on Real Data

Despite the difficulties with reconstruction of the W concentration profiles outside the very core plasma, a preliminary test was carried out with the same method using real data from WEST. This yielded a reasonable estimate of the core tungsten concentration (Fig. 9), although further outside the decreasing trend of \(c_{\text{W}}\) is not realistic. As the tungsten impurity at the edge has little impact on the measured SXR emissivity, the reconstructed tungsten concentration profile is quite sensitive to the choices of hyperparameters. In fact, the inferred tungsten concentration profile can have quite a different trend towards the edge under another set of hyperparameters, even if the measured data remain unchanged. An example tungsten concentration profile inferred under a different set of hyperparameters is shown in Fig. 10. In addition, the slight mismatch between the calculated and measured line-integrated SXR emissivity may arise from uncertainty on the magnetic equilibrium, combined with the rather strong assumption of constant W concentration on each flux surface.

Fig. 9
figure 9

a Estimated W concentration for WEST pulse #55191, \(t = 1.40\) s and b re-integrated SXR emissivity, when \(\sigma _{\text{f}, c_{\text{W}}} = 0.56\) and \(l_{c_{\text{W}}} = 0.4\)

Full size image
Fig. 10
figure 10

a Estimated W concentration for WEST pulse #55191, \(t = 1.40\) s and b re-integrated SXR emissivity, when \(\sigma _{\text{f}, c_{\text{W}}} = 0.56\) and \(l_{c_{\text{W}}} = 0.25\)

Full size image

Preliminary Exploration on Speeding Up the Inference with Surrogate Models

A fully Bayesian inference with MCMC sampling is computationally expensive and does not lend itself to a potential real-time implementation. A possible approach for speeding up the inference is using neural network surrogate models trained on synthetic data [39]. As a first step, we investigate the application on a single diagnostic, the interferometry, for the reconstruction of electron density profiles. Preliminary results are obtained with a single-hidden-layer neural network called extreme learning machine [40], based on the implementation by a python package PyRCN [41]. The input-to-hidden layer weights of an extreme learning machine are initialized randomly and left untrained, while the hidden-to-output weights are determined using linear regression, therefore the training is very fast. The model was trained on 165,000 synthetic line-integrated density measurements corresponding to realistic \(n_\text{e}\) profiles sampled from a prior distribution (Fig. 11) and evaluated on real data from interferometry on WEST (Fig. 12). The training took about 2.5 s on a normal laptop with Core i7 CPU and the evaluation time for a single input is shorter than 1 ms. The good agreement of the density profile inferred by the neural network and that calculated by the equilibrium code NICE [42] demonstrates the potential of the surrogate model. However, further validations on a larger scale are still required. Ultimately, this approach will be extended to the joint estimation of impurity concentration, density and temperature profiles.

Fig. 11
figure 11

Training set consisting of (left) density profiles sampled from the prior distribution and (right) synthetic noisy line-integrated measurements

Full size image
Fig. 12
figure 12

Left: density profiles reconstructed by the neural network (red) and by the equilibrium code NICE (black) for WEST pulse #53259 at t = 4 s. Right: comparison of calculated and measured line-integrated densities

Full size image

Summary

In this paper, tomographic reconstruction of SXR emissivity profiles in tokamak plasmas has been demonstrated using nonstationary Gaussian processes in a Bayesian probabilistic approach. The validation on synthetic data generated from emissivity profiles of several different characteristic shapes verifies the robustness of this method for different noise levels. By incorporating information about the magnetic equilibrium, the reconstruction from synthetic data of only horizontal lines-of-sight also gives reliable estimates for emissivity profiles with limited asymmetry. This was supported by an application to real WEST SXR data: using a realistic error model, the reconstruction of SXR emissivity profiles on WEST achieved relatively good performance, with the advantage of reliable uncertainty estimates. Moreover, the IDA approach was followed for joint estimation of tungsten concentrations and kinetic profiles from heterogeneous diagnostics on WEST. This allowed a realistic estimate of the tungsten concentration in the core plasma, but revealed difficulties for reconstructing the full profile based on these measurements alone. Due to the lack of information from low ionization states of tungsten, which primarily radiate outside the observed SXR range, the edge tungsten concentration inferred from SXR is not reliable. As a result, the estimated tungsten concentration profile is quite sensitive to the choice of hyperparameters. Therefore, in a next step we intend to incorporate additional diagnostics, such as bolometry. In addition, we aim to extend neural network surrogate modeling to the full inference process of the tungsten concentration profile and the kinetic profiles.