Intra- and Inter-Specific Competitions of Two Stage-Structured Species in a Patchy Environment

Abstract

With metamorphosis or not, creatures have varying ability in their different life stages to compete for resource, space or mating. Interaction of species with environment and competition between species are key factors in the evolution of ecological population. Taking these concerns into account, we study a model with two life stages, immature and mature, and incorporate both intra- and inter-specific competitions between two species in a two-patch environment. The structure of monotone dynamics in such a model leads us to explore its local and global dynamics. The investigation starts with the single-species model on which we establish the threshold dynamics that either the species eventually goes extinction or exists on both patches, which is determined by the parameters. Then we study the two-species model and formulate the threshold competition strength which monotonously but oppositely depends on the maturation times of two species, and indicates how the competitor invade an environment. Moreover, we demonstrate two mechanisms which give rise to dominance dynamics, under competition-dependent and -independent criteria respectively. Finally, we conduct numerical simulations to show that the proposed model admits multiple positive equilibria due to the consideration of two life stages.

1 Introduction

Creatures may adjust their behaviors to adapt themselves to the habitat and the superior species may win the evolution game in the long run [8]. Due to limited resource in the environment and opportunity to reproduce, individuals compete with each other for different reasons in different stages, for example, immature and mature life stages. The competition may be against self species or different species, according to which life stage the individual stays in. In addition to face-to-face competition, regulating the mechanism of life, for instance, changing the maturation time, is also an approach to win the competition. These two competitions in different life stages determine the evolution outcome collectively. On the other hand, spatial heterogeneity characterizes the main feature of a habitat, which may accommodate dissimilar carrying capacities at different locations. Thus, considering both factors influencing the behaviors of creatures, i.e., competition between species under their life regulation, and the interaction of species with the environment is crucial in understanding the realization of ecological evolution.

Behaviors of a species are mostly stage-structured, which means that the individuals may act according to the physiological features in their variant life stages, for a common example, immature or mature. [1] is one of the pioneer works to explore the two-stage population models. Therein, the optimal value of maturation time was explicitly derived to reach the maximum carrying capacity. A subsequent work [11] further studied a stage-structured consumer with resource dynamics, where rich dynamics such as sustainable oscillations were found, even with only a single-species consumer. Recently, stage-structured models have been employed to study mosquito populations [25], vector-borne diseases [41], insect populations [4], etc. In these studies, the natural death of individuals in the immature stage will reduce the number of new population in the mature stage. Such consideration leads to mathematical models which are represented by delay differential equations with delay-dependent parameters. Successful invasion of an exotic species resulted from the competition between multiple species can convert the ecological system. Competition in the immature stage also diminishes the immature population and subsequently influences the mature population. In the sequel, the studies taking into account intra- and inter-specific competitions in immature stage to explore its effect on the mature population and determine the species survival were reported in [13, 23, 24]. Therein, the competition in mature stage was not considered. Notably, the consideration on inter-specific competition in immature stage, but only against those at the same age, results in a delay differential equation with implicit nonlinearity due to the difficulty in solving the corresponding coupled age-structured larval (immature) equations, even under the assumption of same maturation delay for two species [13]. Regarding the solution after the maturation time to coupled larval equations as a Poicaré map and combining the monotone theory for planar maps, global convergence to equilibria was established in [24]. A further consideration on inter-specific competition against all immature competitors with whatever age can complicate the formulation of mature population. Liu et al. [23] employed a perturbation theory to investigate well-posedness of the model, stability of equilibria and persistence of solutions, when the competition strength is small. Meanwhile, inter-specific competition raises difficulty in explicitly formulating the equation for mature population. In fact, intra- and inter-specific competitions not only occur in immature stage, but also in mature stage, and has become a key component in modeling species evolution, for example, for Drosophila [10, 31] and beetles [2, 9]. We will take this into account to expand the findings from the existing results.

Due to the local habitation of insects and small animals, and some natural/man-made barriers such as rivers, mountains, buildings and highways, a patchy environment is often considered in population models. [21] proposed a two-patch model to explore the spatial heterogeneity of a single species population. In subsequent studies [35, 36] on the model assuming patch-type environment, global convergence dynamics was obtained by constructing Lyapunov functions. The question of how diffusion affects the competition outcome of two competing species on a patchy environment, according to their strategies of spatially distributing the birth rates, was proposed by Gourley and Kuang [12]. The conjectures posed therein were later resolved in [6] and [22]. Competition outcome due to the network topology of patchy environment for advective three-patch models was studied in [17]. Their results on bi-stability and coexistence were jointly determined by drift rates between patches and dispersal rates of individuals. When individuals disperse with distinct rates in different directions between two patches, the problem of convergence dynamics is challenging. A recent study [5] solved this problem by using a graph-theoretic approach and the monotone dynamics theory.

In order to explore the effects from the competition between species, within species, and from the dispersal due to the spatial heterogeneity on the outcome of ecological evolution, we assume the following in this study:

• The environment consists of two patches on which individuals can randomly disperse.

• Each species experiences immature and mature life stages, which is distinguished by an average maturation time.

• There is only intra-specific competition for immature individuals at the same age, because of their weak mobility.

• Mature individuals face with both intra- and inter-specific competitions since their mobility may lead to more face-to-face activity between individuals at different ages.

Under these assumptions, the mathematical model for the mature populations of the two species inhabiting on the two-patch environment is governed by a system of four delay differential equations, with delay-dependent parameters that relate to the maturation time. Although with complicated recruitment function, the proposed model admits the structure of monotone dynamics, which provides us an analytical framework to explore the local and global dynamics. The main goal is to elucidate how the competition between species, dispersal rates among patches, and species features, such as reproduction, mortality and maturation time, jointly influence the invasion (survival) of species. This work aims at attaining such goal and proceeds from a single-species model to a competitive two-species model.

The rest of this work is organized as follows. In Sect. 2, we analyze a single-species model, and derive the threshold dynamics for that either the species eventually goes extinction or exists in both patches with convergent quantity. In Sect. 3, we consider a two-species model and present the basic properties as well as monotone structure under a special cone. We also demonstrate the local stability of trivial and boundary equilibria, and the invasion of species (uniform persistence) by finding a threshold value of competition strength, which monotonously but oppositely depends on the maturation times of two species. In addition, we show the global convergence to the trivial equilibrium and to the two boundary equilibria by applying the theory of asymptotically autonomous systems and the monotone dynamics. In Sect. 4, we conduct numerical simulations to demonstrate the sharpness of the criterion for uniform persistence, dependence of the threshold competition strengths on both maturation times and dispersal rates, and the bifurcation of multiple positive equilibria. Finally, we conclude by summarizing the study, and discussing the feature and possible extensions of the model in Sect. 5. Some technical proofs and quoted theories are collected in the Appendices.

2 Single Species

In this section, we discuss a single-species population on one habitat and on a two-patch environment respectively. Let u(t, a) be the density of individuals at time t of age a. We define here by $\tau$ the maturation time, i.e., the immature individuals are those of age less than the threshold age $\tau$ and mature individuals are those of age exceeding $\tau$. We consider the situation that the competition is only within the species, and there is no competition with other species. Based on the balance law, the evolution of the immature population is governed by

$$\begin{aligned} \frac{\partial u(t,a)}{\partial t} + \frac{\partial u(t,a)}{\partial a} = -\underbrace{\mu _{l}u(t,a)}_{\mathrm{natural~mortality}} - \underbrace{\Gamma _l(u(t,\cdot ))~,}_{\mathrm{competition~at~immature~stage}}~0<a<\tau , \end{aligned}$$

(2.1)

where $\mu _{l}$ is the per-capita natural death rate for immature individuals, and $\Gamma _l(\cdot )$ describes the intra-specific competition in the immature stage. The mature individuals are governed by

$$\begin{aligned} \frac{\partial u(t,a)}{\partial t} + \frac{\partial u(t,a)}{\partial a} = -\underbrace{\mu _{m}u(t,a)}_{\mathrm{natural~mortality}} - \underbrace{\Gamma _m(u(t,\cdot ))~,}_{\mathrm{competition~at~mature~stage}}~a>\tau , \end{aligned}$$

(2.2)

where $\mu _{m}$ is the per-capita natural death rate for mature individuals, and $\Gamma _m(\cdot )$ describes the competition within species in the mature stage. In this study, we consider the species without mobility in the immature stage, so that each immature individual competes with others at the same age, and with mobility in the mature stage, hence each mature individual competes with the whole group in mature stage. For example, the growth of Drosophila involves only the intra-specific competition in the larval stage, which proceeds with population regulation [10]. Let us denote the total number of the mature by

$$\begin{aligned} U(t):=\int ^{\infty }_{\tau }u(t,a)da. \end{aligned}$$

From the law of mass action, we explicitly consider

$$\begin{aligned} \Gamma _l(u(t,\cdot ))= & {} k_{l}[u(t,a)]^2, \end{aligned}$$

(2.3)

$$\begin{aligned} \Gamma _m(u(t,\cdot ))= & {} k_mu(t,a) \cdot U(t), \end{aligned}$$

(2.4)

where $k_l, k_m >0$ stand for the strengths of intra-specific competition in immature and mature stages respectively. The birth rate u(t, 0) depends on the total number of the mature, and hence we assume

$$\begin{aligned} u(t,0)=b(U(t)), \end{aligned}$$

(2.5)

where b is a function with nonnegative values.

Solving the immature equation (2.1) along the characteristics and integrating (2.2) with respect to a, the total mature population U(t) satisfies

$$\begin{aligned} \frac{dU(t)}{d t} =B(U(t-\tau )) -\mu _{m}U(t) - k_m(U(t))^2, \end{aligned}$$

(2.6)

where

$$\begin{aligned} B(\xi ) = \frac{\mu _{l}e^{-\mu _{l}\tau }b(\xi )}{\mu _{l} + k_{l} (1-e^{-\mu _{l}\tau }) b(\xi )}. \end{aligned}$$

(2.7)

Denote the solution semiflow of (2.6) by $\Psi _t$. The detailed derivations of (2.7) for a similar model with general $\Gamma _l(\cdot )$ can be found in [13]. Here, for function b in (2.5), we assume $b \in C^2([0,\infty ))$, and

$$\begin{aligned} b(0)=0,~b'(\xi )\ge 0,~b''(\xi )\le 0,~\textrm{and}~\limsup _{\xi \rightarrow \infty } b(\xi ):=\tilde{b}<\infty . \end{aligned}$$

(2.8)

One classical example is

$$\begin{aligned} b(\xi )= \frac{\beta \xi }{1+\vartheta \xi }. \end{aligned}$$

(2.9)

The delay differential equation (2.6) describes the population of adult members, and it is derived under the assumption that both the larval members and the adult members experience intra-specific competition of quadratic type (2.3) and (2.4), respectively. The formulation with (2.3) had been discussed in [13]. However, inter-specific competition in the mature stage was not considered therein, and so the equations are as (2.1)-(2.2) with $k_m=0$. In this case, equation (2.6) belongs to the well-known population model

$$\begin{aligned} \frac{dU(t)}{dt}=\mathcal {K}(U(t-\tau )) - \mu _m U(t), \end{aligned}$$

(2.10)

where $\mathcal {K}$ is a continuous function. This equation includes the Mackey-Glass equation and the Nicholson’s blowflies equation [20, 26]. While equation (2.10) with a monotonously increasing $\mathcal {K}$ generates a monotone system [32], periodic solutions may exist in some parameter range [19]. However, the delay feedback in (2.6) comes from intra-specific competition in the immature stage and periodic solutions never emerge, as shown in the following result. This is different from the dynamics in equations of the form (2.10), reported in [13].

For $\textbf{x} \in {{\mathbb {R}}}^n$, we denote by $\hat{\textbf{x}}$ the constant function $\hat{\textbf{x}}(\theta ) \equiv \textbf{x}$, for $\theta \in [-\tau , 0]$. Given $\phi ,\psi \in \Pi _{i=1}^nC([-\tau _i,0],{{\mathbb {R}}}_+)$, we denote $\phi \le \psi$ if $\phi _i(\theta )\le \psi _i(\theta )$ for $\theta \in [-\tau _i,0]$, $i=1,2,\ldots ,n$, and $\phi <\psi$ if $\phi \le \psi$ and $\phi \ne \psi$. In addition, $\phi \ll \psi$ indicates $\phi _i(\theta )<\psi _i(\theta )$ for $\theta \in [-\tau _i,0]$, $i=1,2,\ldots ,n$. A solution semiflow $\Phi ^0$ is monotone (resp., strongly monotne) if $\Phi ^0_t(\phi )\le \Phi ^0_t(\psi )$ (resp., $\Phi ^0_t(\phi )\ll \Phi ^0_t(\psi )$) whenever $\phi \le \psi$ and $t\ge 0$. In addition, $\Phi ^0$ is strongly order preserving (SOP), cf. [32], if moreover there exist neighborhoods of any two ordered initial values that are eventually separated in order under the solution flow.

Under clear-cut conditions, we establish the uniqueness of equilibrium in the corresponding regions and the global asymptotical stability for the equilibrium in the following theorem. The result is justified by the property of SOP and the uniform persistence of equation (2.6). We abbreviate “globally asymptotically stable" as GAS, and arrange the proof in Appendix A.I.

Theorem 2.1

Consider equation (2.6) with $b(\cdot )$ satisfying (2.8).

• (i) If $b'(0)e^{-\mu _l\tau }<\mu _m$, then the trivial solution is GAS in $C([-\tau ,0],\mathbb {R}_+)$.

• (ii) If $b'(0)e^{-\mu _l\tau }>\mu _m$, then there is a positive equilibrium which is GAS in $C([-\tau ,0],\mathbb {R}_+)\setminus \{\hat{0}\}$.

Spatial heterogeneity is also an important factor to determine the evolution of a species. One of the scenarios is regarding the habitat fragmentation as connected patches between which individuals can move [3, 6, 22, 28]. Immature and mature individuals may have variant abilities to move between patches. For example, mature Drosophila moves faster compared to the immature ones with low mobility [7, 27]. This feature of immature and mature life stages motivates us to consider the mature population dispersing between two patches, depicted by

$$\begin{aligned} \frac{dU_1(t)}{dt}= & {} B_1(U_1(t-\tau )) - \mu _{m1}U_1(t) -k_{m1}(U_1(t))^2 + DU_2(t) - DU_1(t), \nonumber \\ \frac{dU_2(t)}{dt}= & {} B_2(U_2(t-\tau )) - \mu _{m2}U_2(t) -k_{m2}(U_2(t))^2 + DU_1(t) - DU_2(t), \end{aligned}$$

(2.11)

where

$$\begin{aligned} B_i(\xi ) = \frac{\mu _{li}e^{-\mu _{li}\tau }b_i(\xi )}{\mu _{li} + k_{li} (1-e^{-\mu _{li}\tau }) b_i(\xi )},~i=1,2, \end{aligned}$$

each $b_i$ satisfies (2.8), and $D>0$ represents the dispersal rate of individuals between two patches. The well-posedness of (2.11) will be confirmed in next section, since the single-species model (2.11) can be regarded as a special case of the two-species model. We note that delay differential equation (2.11) is also an eventually strongly monotone system on $C([-\tau ,0],\mathbb {R}_+^2)$, cf. Corollary 5.3.5 [32].

The stationary equation of (2.11) can be expressed as

$$\begin{aligned} U_1 = \frac{1}{D}[(\mu _{m2}+D)U_2 + k_{m2}(U_2)^2 -B_2(U_2) ]=: & {} f_2(U_2), \nonumber \\ U_2 = \frac{1}{D}[(\mu _{m1}+D)U_1 + k_{m1}(U_1)^2 -B_1(U_1) ]=: & {} f_1(U_1). \end{aligned}$$

(2.12)

It is clear that the equilibrium (0, 0) of (2.11) always exists. Analogous to (A.1) and (A.2) in Appendix A.I, we have $B_i'(\xi )>0$, $B_i''(\xi )<0$, for all $\xi \ge 0$, $i=1,2$. Hence each function $B_i(\xi )$ is increasing and concave downward on $[0,+\infty )$ with a saturation as $\xi \rightarrow \infty$. Accordingly, each function $f_i(\xi )$ is concave upward with unlimited derivative as $\xi \rightarrow \infty$. Also note that $f_i(0)=0$ and

$$\begin{aligned} f_i'(0)=(\mu _{mi}+D-e^{-\mu _{li}\tau }b_i'(0))/D, \end{aligned}$$

for $i=1,2$. We thus conclude that (2.12) has a positive solution, denoted by $(\overline{U}_1, \overline{U}_2)$, if and only if $f_1'(0)\le 0$, or $f_2'(0)\le 0$, or $0< f_1'(0)<\frac{1}{f_2'(0)}$, which is equivalent to

$$\begin{aligned} (\mathcal {S}) \left\{ \begin{array}{l} \mu _{m1}+D< e^{-\mu _{l1}\tau }b'_1(0),~\textrm{or} \\ \mu _{m2}+D< e^{-\mu _{l2}\tau }b'_2(0),~\textrm{or} \\ 0 \le \left( \mu _{m1}+D-e^{-\mu _{l1}\tau }b'_1(0) \right) \left( \mu _{m2}+D-e^{-\mu _{l2}\tau }b'_2(0) \right) <D^2, \end{array} \right. \end{aligned}$$

where $e^{-\mu _{li}\tau }b'_i(0)=B'_i(0)$, $i=1, 2$. We note that the cases with either $f_1'(0)=0$ or $f_2'(0)=0$ are included in the last inequality in $(\mathcal {S})$. We summarize:

Theorem 2.2

System (2.11) has a unique positive equilibrium $(\overline{U}_1, \overline{U}_2)$ if and only if ($\mathcal {S}$) holds.

Remark 2.1

Note that when the two patches are identical ($\mu _{li}=\mu _l,\mu _{mi}=\mu _m,k_{li}=k_m,k_{li}=k_m,b_i=b$ for $i=1,2$), and $D=0$, criterion $(\mathcal {S})$ reduces to

$$\begin{aligned} \mu _m < e^{-\mu _l\tau }b'(0), \end{aligned}$$

which agrees with the criterion in Theorem 2.1 for the existence of positive equilibrium in a single-patch model.

For later use, we grasp how the values of $\overline{U}_1, \overline{U}_2$ vary with the parameters in (2.11). First, we regard $B_i$ as a function of these parameters. It is obvious that $\frac{\partial B_i}{\partial k_{li}},~\frac{\partial B_i}{\partial \tau }<0$. Next,

$$\begin{aligned} \frac{\partial B_i}{\partial \mu _{li}}= & {} \frac{1}{[\mu _{li} + k_{li} (1-e^{-\mu _{li}\tau }) b_i(\xi )]^2} \left\{ [e^{-\mu _{li}\tau }b_i(\xi ) - \mu _{li}\tau e^{-\mu _{li}\tau }b_i(\xi )] \right. \\{} & {} \left. \cdot [\mu _{li} + k_{li} (1-e^{-\mu _{li}\tau }) b_i(\xi )] - \mu _{li} e^{-\mu _{li}\tau }b_i(\xi ) [1 + \tau k_{li}e^{-\mu _{li}\tau }b_i(\xi )] \right\} \\= & {} \frac{e^{-\mu _{li}\tau }b_i(\xi )}{[\mu _{li} + k_{li} (1-e^{-\mu _{li}\tau }) b_i(\xi )]^2} [\tilde{h}(\mu _{li}\tau ) k_{li}b_i(\xi ) - \tau \mu _{li}^2 ], \end{aligned}$$

where

$$\begin{aligned} \tilde{h}(\xi ):=1-\xi -e^{-\xi }, \end{aligned}$$

which satisfies $\tilde{h}(0)=0$ and $\tilde{h}(\xi )<0$ for $\xi >0$. Hence, we have $\frac{\partial B_i}{\partial \mu _{li}}<0$. In addition, for the case $b_i(\xi )= \frac{\beta _i \xi }{1+\vartheta _i\xi }$, $i=1,2$, we have

$$\begin{aligned} \frac{\partial B_i}{\partial \vartheta _i}= & {} \frac{\mu _{li}^2e^{-\mu _{li}\tau }\frac{\partial b_i}{\partial \vartheta _i}}{[\mu _{li} + k_{li} (1-e^{-\mu _{li}\tau }) b_i(\xi )]^2} <0, \\ \frac{\partial B_i}{\partial \beta _i}= & {} \frac{\mu _{li}^2e^{-\mu _{li}\tau }\frac{\partial b_i}{\partial \beta _i}}{[\mu _{li} + k_{li} (1-e^{-\mu _{li}\tau }) b_i(\xi )]^2} >0. \end{aligned}$$

Based on these facts, we can derive the relationship between the values of $\overline{U}_i$, $i=1,2$, with each parameter in system (2.11). For example, fixing all parameters except $\mu _{l1}$, we rewrite (2.12) as

$$\begin{aligned} U_1 = f_2(U_2),~~~U_2 = f_1(U_1;\mu _{l1}). \end{aligned}$$

Then $f_1(U_1;\mu ^-_{l1})<f_1(U_1;\mu ^+_{l1})$ for all $U_1>0$ whenever $0<\mu ^-_{l1}<\mu ^+_{l1}$. From the concavity of functions $f_i(\cdot )$, we see that the equilibrium $(\overline{U}_1, \overline{U}_2)=(\overline{U}_1(\mu _{l1}), \overline{U}_2(\mu _{l1}))$ satisfies $\overline{U}_i(\mu ^+_{l1})< \overline{U}_i(\mu ^-_{l1})$, and hence $\frac{\partial \overline{U}_i}{\partial \mu _{l1}}<0$, for $i=1,2$. We summarize these results for later use:

Remark 2.2

Regarding $\overline{U}_i$ as a function of the parameters in system (2.11), then it follows that for $i,j=1,2$

$$\begin{aligned} \frac{\partial \overline{U}_i}{\partial \mu _{mj}},~\frac{\partial \overline{U}_i}{\partial k_{mj}},~\frac{\partial \overline{U}_i}{\partial \mu _{lj}},~\frac{\partial \overline{U}_i}{\partial k_{lj}},~\frac{\partial \overline{U}_i}{\partial \tau }<0,~\frac{\partial \overline{U}_i}{\partial D}>0. \end{aligned}$$

If $b_i(\xi )= \frac{\beta _i \xi }{1+\vartheta _i\xi }$, $i=1,2$, it further holds that

$$\begin{aligned} \frac{\partial \overline{U}_i}{\partial \vartheta _j}<0,~\frac{\partial \overline{U}_i}{\partial \beta _j}>0. \end{aligned}$$

The following property of uniform persistence follows from the theory for the two-species model to be presented in the next section, as system (2.11) will become a special case therein.

Theorem 2.3

Assume that condition $(\mathcal {S})$ holds. The solution of system (2.11) is uniformly persistent in the sense that there is a positive constant $\rho ^*$ such that every solution $(U_1(t),U_2(t))$ of (2.11) starting from $\phi \in C([-\tau ,0],\mathbb {R}_+^2)\setminus \{(\hat{0}, \hat{0})\}$ satisfies

$$\begin{aligned} \liminf _{t\rightarrow \infty }U_i(t)\ge \rho ^*,~\textrm{for}~i=1,2. \end{aligned}$$

Since system (2.11) is cooperative and irreducible, it also generates a SOP dynamics. Hence, Theorem 2.3 leads to the following global dynamics for system (2.11). We arrange the detailed proof in Appendix A.I.

Theorem 2.4

Consider system (2.11).

• (i) If $(\mathcal {S})$ does not hold and $\left( \mu _{m1}+D-e^{-\mu _{l1}\tau }b'_1(0) \right) \left( \mu _{m2}+D-e^{-\mu _{l2}\tau }b'_2(0) \right) \ne D^2$, then the trivial solution is GAS in $C([-\tau ,0],\mathbb {R}_+^2)$.

• (ii) If $(\mathcal {S})$ holds, then the positive equilibrium $(\overline{U}_1, \overline{U}_2)$ is GAS in $C([-\tau ,0],\mathbb {R}_+^2)\setminus \{(\hat{0},\hat{0})\}$.

3 Competition Between Two Species

The studies in Sect. 2 build up a basis for us to explore the competition between two species with different reproduction, mortality and maturation time, and also different competition strengths and dispersal rates. In the rest of this paper, we will study a system of delay differential equations, which models two species in a two-patch environment, under only intra-specific competition in the immature stage, and both intra- and inter-specific competitions in the mature stage.

As in Sect. 2, the model involves delayed recruitment to the mature population because of the process of maturation for each species. By adopting the bilinear reaction to describe the inter-specific competition, we consider

$$\begin{aligned} \frac{dU_1(t)}{dt}= & {} B_{u1}(U_1(t-\tau _u)) - \mu _{mu1}U_1(t) -k_{mu1}(U_1(t))^2 \nonumber \\ {}{} & {} - c_{uv}U_1(t)V_1(t) + D_u[U_2(t) - U_1(t)], \nonumber \\ \frac{dU_2(t)}{dt}= & {} B_{u2}(U_2(t-\tau _u)) - \mu _{mu2}U_2(t) -k_{mu2}(U_2(t))^2 \nonumber \\ {}{} & {} - c_{uv}U_2(t)V_2(t) + D_u[U_1(t) - U_2(t)], \nonumber \\ \frac{dV_1(t)}{dt}= & {} B_{v1}(V_1(t-\tau _v)) - \mu _{mv1}V_1(t) -k_{mv1}(V_1(t))^2 \nonumber \\ {}{} & {} - c_{vu}U_1(t)V_1(t) + D_v[V_2(t) - V_1(t)], \nonumber \\ \frac{dV_2(t)}{dt}= & {} B_{v2}(V_2(t-\tau _v)) - \mu _{mv2}V_2(t) -k_{mv2}(V_2(t))^2 \nonumber \\ {}{} & {} - c_{vu}U_2(t)V_2(t) + D_v[V_1(t) - V_2(t)], \end{aligned}$$

(3.1)

where

$$\begin{aligned} B_{ui}(\xi )= & {} \frac{\mu _{lui}e^{-\mu _{lui}\tau _u}b_{ui}(\xi )}{\mu _{lui} + k_{lui} (1-e^{-\mu _{lui}\tau _u}) b_{ui}(\xi )}, \\ B_{vi}(\xi )= & {} \frac{\mu _{lvi}e^{-\mu _{lvi}\tau _v}b_{vi}(\xi )}{\mu _{lvi} + k_{lvi} (1-e^{-\mu _{lvi}\tau _v}) b_{vi}(\xi )}, ~i=1,2, \end{aligned}$$

and both $b_{ui}(\cdot )$ and $b_{vi}(\cdot )$ belong to the class of functions in (2.8). Here, $c_{uv},c_{vu}>0$ measure the strengths of inter-specific competition between two species in the mature stage, and $D_u,D_v>0$ are respectively the dispersal rates of u- and v-species between patches.

3.1 Preliminaries and Monotone Dynamics

In this subsection, we introduce some preliminary properties for the solutions of (3.1), including well-posedness, non-negativity, boundedness, positively invariant sets, and some basic dynamics. Write system (3.1) as

$$\begin{aligned} \textbf{W}'(t)=\textbf{F}(\textbf{W}_t), \end{aligned}$$

where $\textbf{W}=(U_1, U_2, V_1, V_2)$, $\textbf{W}_t(\theta )=\textbf{W}(t+\theta )$, and $\textbf{F}=(F_1, \ldots , F_4)$. Let $\mathbb {X}:=\mathcal {C}_u \times \mathcal {C}_v$, where $\mathcal {C}_u:=C([-\tau _u,0],\mathbb {R}^2_+)$ and $\mathcal {C}_v:=C([-\tau _v,0],\mathbb {R}^2_+)$.

From the assumption on $b_{ui}$ and $b_{vi}$ in (2.8), we see that function $\textbf{F}$ is Lipschitz on each compact set in $\mathbb {X}$, and the local existence of unique solution to system (3.1) is assured by Theorem 2.3 [14]. In addition, from Theorem 2.2 [14], the solution continuously depends on the initial value. Hence, system (3.1) is well posed. In fact, the solution globally exists due to the following property of boundedness.

Proposition 3.1

The solutions of system (3.1) starting from initial values in $\mathbb {X}$ are nonnegative and eventually uniformly bounded.

Proof

It can be seen that $F_i(\phi )\ge 0$ if $\phi \in \mathbb {X}$ satisfies $\phi \ge 0$, $\phi _i(0)=0$, for $i\in \{1,2,3,4\}$. Thus, non-negativity of the solutions follows from Theorem 5.2.1 [32]. Set $U(t)=U_1(t)+U_2(t)$ and observe that

$$\begin{aligned} \frac{dU(t)}{dt}\le & {} B_{u1}(U_1(t-\tau _u)) + B_{u2}(U_2(t-\tau _u)) - \mu _{mu1}U_1(t) - \mu _{mu2}U_2(t) \\\le & {} \bar{B} - \bar{\mu }_{mu}U(t), \end{aligned}$$

where $\bar{B}:=\limsup _{\xi \rightarrow \infty } (B_{u1}(\xi )+B_{u2}(\xi ))$ and $\bar{\mu }_{mu}:=\min \{\mu _{mu1},\mu _{mu2}\}$. An analog about v-species can also be derived. We thus conclude that the solutions of system (3.1) are eventually uniformly bounded. $\square$

Define

$$\begin{aligned} \mathbb {X}_u:= & {} \{\phi =(\phi _1,\phi _2,\phi _3,\phi _4)\in \mathbb {X}~\textrm{with} ~\phi _i\ne \hat{0}~\textrm{for}~i=1~\textrm{or}~2\}, \\ \mathbb {X}_v:= & {} \{\phi =(\phi _1,\phi _2,\phi _3,\phi _4)\in \mathbb {X}~\textrm{with} ~\phi _i\ne \hat{0}~\textrm{for}~i=3~\textrm{or}~4\}, \end{aligned}$$

and $\mathbb {X}_u^p := \{\phi \in \mathbb {X}~\textrm{with} ~\phi _i\gg \hat{0}~\textrm{for}~i=1~\textrm{and}~2\}$, $\mathbb {X}_v^p := \{\phi \in \mathbb {X}~\textrm{with} ~\phi _i\gg \hat{0}~\textrm{for}~i=3~\textrm{and}~4\}$. For later use, we summarize the solution behavior of (3.1), starting from elements in $\mathbb {X}_u$ or $\mathbb {X}_v$:

Proposition 3.2

(i) The subsets $\mathbb {X}_u$ and $\mathbb {X}_v$ of $\mathbb {X}$, and $\textrm{int}(\mathbb {X})$ are positively invariant under the solution flow of system (3.1). (ii) A solution starting from $\mathbb {X}_u$ (resp., $\mathbb {X}_v$) will enter and stay in $\mathbb {X}_u^p$ (resp., $\mathbb {X}_v^p$) for $t\ge \tau _u$ (resp., $t\ge \tau _v$).

We arrange the proof in Appendix A.I. In fact, system (3.1) is endowed with a monotone structure. Consider the cone $\mathcal {C}_K:=\mathcal {C}_u \times (-\mathcal {C}_v)$. For $\phi ,\psi \in \mathbb {X}$, we define an order $\phi \le _K \psi$ whenever $\phi _i(\theta )\le \psi _i(\theta )$ for $\theta \in [-\tau _u,0]$, $i=1,2$, and $\phi _i(\theta )\ge \psi _i(\theta )$ for $\theta \in [-\tau _v,0]$, $i=3,4$, and a strict order $\phi \ll _K \psi$ whenever these inequalities are strict. From the competition terms in (3.1) and the cone $\mathcal {C}_K$, we have $\textbf{F}_i(\phi )\le \textbf{F}_i(\psi )$ for $i=1,2$, and $\textbf{F}_i(\phi )\ge \textbf{F}_i(\psi )$ for $i=3,4$, for given $\phi ,\psi \in \mathbb {X}$ with $\phi \le _K\psi$ and $\phi _i(0)=\psi _i(0)$. That is, the criterion in Theorem 4.1 [32] is satisfied. Thus, system (3.1) is (quasi)monotone with respect to cone $\mathcal {C}_K$, also cf. Chapter 5 (Smit 1995). Hence, the semiflow $\Phi _t(\phi )$ generated by system (3.1) is type-K monotone. That is, if $\phi ,\psi \in \mathbb {X}$ with $\phi \le _K \psi$, i.e., $\phi _i\le \psi _i$ for $i=1,2$ and $\phi _i\ge \psi _i$ for $i=3,4$, then $\Phi _t(\phi )\le _K \Phi _t(\psi )$ for any $t>0$, i.e., $(\Phi _t(\phi ))_i\le (\Phi _t(\psi ))_i$ for $i=1,2$ and $(\Phi _t(\phi ))_i\ge (\Phi _t(\psi ))_i$ for $i=3,4$, cf. Theorem 5.1.1 (Smit 1995) (see also [15] for a general cone, and [18] for the case of an ordinary differential equation). The concepts of strongly monotone and SOP can be defined under the cone $\mathcal {C}_K$. In summary, we have the following property:

Proposition 3.3

System (3.1) is (quasi)monotone in $\mathbb {X}$, that is, $\Phi _t(\phi )\le _K \Phi _t(\psi )$ whenever $\phi \le _K \psi$.

In fact, system (3.1) admits an even stronger monotone property when time gets larger:

Proposition 3.4

System (3.1) is strongly monotone in $\textrm{int}(\mathbb {X})$ for $t\ge 2\tau _m$, where $\tau _m:=\max \{\tau _u,\tau _v\}$.

Proof

Note that $\textrm{int}(\mathbb {X})$ is positively invariant under the the semiflow $\Phi _t$, see Proposition 3.2(i). Write system (3.1) as $\textbf{W}'(t)=\textbf{G}(\textbf{W}(t),\textbf{W}^u (t),\textbf{W}^v (t))$, where $\textbf{W}^u (t)=\textbf{W}(t-\tau _u)$ and $\textbf{W}^v (t)=\textbf{W}(t-\tau _v)$. Direct calculations give

$$\begin{aligned} D_\textbf{W} \textbf{G}(\phi )= & {} \begin{pmatrix} G_1 &{} D_u &{} -c_{uv}\phi _1(0) &{} 0 \\ D_u &{} G_2 &{} 0 &{} -c_{uv}\phi _2(0) \\ -c_{vu}\phi _3(0) &{} 0 &{} G_3 &{} D_v \\ 0 &{} -c_{vu}\phi _4(0) &{} D_v &{} G_4 \end{pmatrix}, \\ D_{\textbf{W}^u} \textbf{G}(\phi )= & {} \begin{pmatrix} B_{u1}'(\phi _1(-\tau _u)) &{} 0 &{} 0 &{} 0 \\ 0 &{} B_{u2}'(\phi _2(-\tau _u)) &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \end{pmatrix}, \\ D_{\textbf{W}^v} \textbf{G}(\phi )= & {} \begin{pmatrix} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} B_{v1}'(V\phi _3(t-\tau _v)) &{} 0 \\ 0 &{} 0 &{} 0 &{} B_{v2}'(\phi _4(-\tau _v)) \end{pmatrix}, \end{aligned}$$

where, for $i=1,2$,

$$\begin{aligned} G_i= & {} -\mu _{mui}-2k_{mui}\phi _i(0)-c_{uv}\phi _{i+2}(0)-D_u, \\ G_{i+2}= & {} -\mu _{mvi}-2k_{mvi}\phi _{i+2}(0)-c_{vu}\phi _i(0)-D_v. \end{aligned}$$

It can be examined that $D_\textbf{W} \textbf{G}, D_{\textbf{W}^u} \textbf{G}, D_{\textbf{W}^v} \textbf{G}(\phi )$ satisfy the criteria in Corollary 4.9 [32] because of the positive invariance of $\textrm{int}(\mathbb {X})$. We omit the proof to save space. Therefore, the assertion holds, according to Theorem 4.8 and Corollary 4.9 [15]. $\square$

3.2 Equilibria

The trivial equilibrium $E_0=(0,0,0,0)$ always exists. It follows from Theorem 2.2 that a unique boundary equilibrium in the form of $E_u:=(\overline{U}_1,\overline{U}_2,0,0)$ exists, called the u-species dominance equilibrium, if and only if

$$\begin{aligned} (\mathcal {S}_u) \left\{ \begin{array}{l} \mu _{mu1}+D_u< e^{-\mu _{lu1}\tau _u}b'_{u1}(0),~\textrm{or} \\ \mu _{mu2}+D_u< e^{-\mu _{lu2}\tau _u}b'_{u2}(0),~\textrm{or} \\ 0 \le \left( \mu _{mu1}+D_u-e^{-\mu _{lu1}\tau _u}b'_{u1}(0) \right) \left( \mu _{mu2}+D_u-e^{-\mu _{lu2}\tau _u}b'_{u2}(0) \right) <D_u^2. \end{array} \right. \end{aligned}$$

Analogously, there exists a unique boundary equilibrium in the form of $E_v:=(0,0,\overline{V}_1,\overline{V}_2)$, called the v-species dominance equilibrium, if and only if

$$\begin{aligned} (\mathcal {S}_v) \left\{ \begin{array}{l} \mu _{mv1}+D_v< e^{-\mu _{lv1}\tau _v}b'_{v1}(0),~\textrm{or} \\ \mu _{mv2}+D_v< e^{-\mu _{lv2}\tau _v}b'_{v2}(0),~\textrm{or} \\ 0 \le \left( \mu _{mv1}+D_v-e^{-\mu _{lv1}\tau _v}b'_{v1}(0) \right) \left( \mu _{mv2}+D_v-e^{-\mu _{lv2}\tau _v}b'_{v2}(0) \right) <D_v^2. \end{array} \right. \end{aligned}$$

Note that $e^{-\mu _{lui}\tau _u}b'_{ui}(0)=B_{ui}'(0)$ and $e^{-\mu _{lvi}\tau _v}b'_{vi}(0)~=B_{vi}'(0)$, $i=1, 2$. With conditions $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$, we can derive the following eventual upper bounds for the solutions, which will be used later to discuss the non-existence of positive equilibrium in system (3.1), and study the uniform persistence and global convergence.

Proposition 3.5

Consider system (3.1).

• (i) If $(\mathcal {S}_u)$ does not hold, then $\lim _{t\rightarrow \infty }U_i(t)=0$, $i=1,2$; if $(\mathcal {S}_u)$ holds, then $\limsup _{t\rightarrow \infty }U_i(t)\le \overline{U}_i$, $i=1,2$.

• (ii) If $(\mathcal {S}_v)$ does not hold, then $\lim _{t\rightarrow \infty }V_i(t)=0$, $i=1,2$; if $(\mathcal {S}_v)$ holds, then $\limsup _{t\rightarrow \infty }V_i(t)\le \overline{V}_i$, $i=1,2$.

Proof

Let us prove (i). From the non-negativity of the solution, we see that

$$\begin{aligned} \frac{dU_1(t)}{dt}\le & {} B_{u1}(U_1(t-\tau _u)) - \mu _{mu1}U_1(t) -k_{mu1}(U_1(t))^2 + D_uU_2(t) - D_uU_1(t), \nonumber \\ \frac{dU_2(t)}{dt}\le & {} B_{u2}(U_2(t-\tau _u)) - \mu _{mu2}U_2(t) -k_{mu2}(U_2(t))^2 + D_uU_1(t) - D_uU_2(t), \end{aligned}$$

for all $t \ge 0$. Consider the auxiliary system

$$\begin{aligned} \frac{dx_1(t)}{dt}= & {} B_{u1}(x_1(t-\tau _u)) - \mu _{mu1}x_1(t) -k_{mu1}(x_1(t))^2 + D_ux_2(t) - D_ux_1(t), \nonumber \\ \frac{dx_2(t)}{dt}= & {} B_{u2}(x_2(t-\tau _u)) - \mu _{mu2}x_2(t) -k_{mu2}(x_2(t))^2 + D_ux_1(t) - D_ux_2(t), \end{aligned}$$

(3.2)

which is in the form of single-species system (2.11), and satisfies the quasimonotone condition in Chapter 5 [32] due to the monotonicity of $B_{ui}$, $i=1,2$. With the convergence dynamics established in Theorem 2.4 for system (2.11) and the comparison principle in Theorem 5.1.1 [32], we conclude that

$$\begin{aligned} \limsup _{t\rightarrow \infty }U_i(t) \le \limsup _{t\rightarrow \infty }x_i(t) = 0,~i=1,2, \end{aligned}$$

when $(\mathcal {S}_u)$ does not hold, and

$$\begin{aligned} \limsup _{t\rightarrow \infty }U_i(t) \le \limsup _{t\rightarrow \infty }x_i(t) =\overline{U}_i,~i=1,2, \end{aligned}$$

when $(\mathcal {S}_u)$ holds true. The proof for (ii) is similar. $\square$

Next, we examine the nonexistence and existence of positive equilibrium. First, we discuss the nonexistence by arguing for contradiction. A positive equilibrium $(U^*_1,U^*_2,V^*_1,V^*_2)$, if exists, satisfies

$$\begin{aligned} U^*_1 = \frac{1}{D_u} \left[ (\mu _{mu2}+D_u+c_{uv}V^*_2)U^*_2 + k_{mu2}(U^*_2)^2 -B_{u2}(U^*_2) \right]=: & {} g_2^u(U^*_2,V^*_2), \nonumber \\ U^*_2 = \frac{1}{D_u} \left[ (\mu _{mu1}+D_u+c_{uv}V^*_1)U^*_1 + k_{mu1}(U^*_1)^2 -B_{u1}(U^*_1) \right]=: & {} g_1^u(U^*_1,V^*_1), \nonumber \\ V^*_1 = \frac{1}{D_v} \left[ (\mu _{mv2}+D_v+c_{vu}U^*_2)V^*_2 + k_{mv2}(V^*_2)^2 -B_{v2}(V^*_2) \right]=: & {} g_2^v(V^*_2,U^*_2), \nonumber \\ V^*_2 = \frac{1}{D_v} \left[ (\mu _{mv1}+D_v+c_{vu}U^*_1)V^*_1 + k_{mv1}(V^*_1)^2 -B_{v1}(V^*_1) \right]=: & {} g_1^v(V^*_1,U^*_1).\qquad \end{aligned}$$

(3.3)

Proposition 3.6

There exists a positive equilibrium of system (3.1) only if both boundary equilibria $E_u$ and $E_v$ exist.

Proof

Assume that there exists a positive equilibrium, denoted by $(U_1^*,U_2^*,V_1^*,V_2^*)$. Define functions $f_i^u(U_i), f_i^v(V_i)$, $i=1,2$, for u- and v-species respectively as in (2.12). Then

$$\begin{aligned} U_2^*=g_1^u(U^*_1,V^*_1)> f_1^u(U_1^*). \end{aligned}$$

(3.4)

Similarly, we have

$$\begin{aligned} U_1^*> f_2^u(U_2^*),~ V_2^*> f_1^v(V_1^*),~V_1^* > f_2^v(V_2^*). \end{aligned}$$

(3.5)

Now, if the boundary equilibrium $E_u$ does not exist, then the criterion $(\mathcal {S}_u)$ does not hold, or equivalently $0< \frac{1}{(f_2^u)'(0)} \le (f_1^u)'(0)$, as discussed in Sect. 2. Combining this with the concavity of each $f_i^u(\cdot )$, we see that the graphs of $U_2=f_1^u(U_1)$ and $U_2=(f_2^u)^{-1}(U_1)$ (i.e., $U_1=f_2^u(U_2)$) have no intersection in the first quadrant, and the first graph is above the second. Also note that $(f_2^u)^{-1}$ is an increasing function. Hence, from (3.4) and (3.5), the following contradiction arises

$$\begin{aligned} U_2^*> f_1^u(U_1^*)> (f_2^u)^{-1}(U_1^*) > (f_2^u)^{-1}(f_2^u(U_2^*)) = U_2^*. \end{aligned}$$

Thus, the boundary equilibrium $E_u$ exists. Similarly, the boundary equilibrium $E_v$ also exists. This completes the proof. $\square$

Now, let us discuss the non-existence of equilibrium. Consider the solution $(U_1,U_2)$ of

$$\begin{aligned} U_1=g_2^u(U_2,V_2),~~U_2=g_1^u(U_1,V_1), \end{aligned}$$

(3.6)

for given $V_1$ and $V_2$. Similar to Remark 2.2, we see that the value of $U_1$ (resp., $U_2$) decreases as either $c_{uv}$ or $V_2$ (resp., either $c_{uv}$ or $V_1$) increases. Note that when $(\mathcal {S}_u)$ holds, there exists a unique $c_{uv}^*>0$ such that

$$\begin{aligned} \left\{ \begin{array}{l} \mu _{mu1}+D_u+c_{uv}\overline{V}_1 \ge B'_{u1}(0),~\textrm{and} \\ \mu _{mu2}+D_u+c_{uv}\overline{V}_2 \ge B'_{u2}(0),~\textrm{and} \\ ( \mu _{mu1}+D_u+c_{uv}\overline{V}_1-B'_{u1}(0)) ( \mu _{mu2}+D_u+c_{uv}\overline{V}_2-B'_{u2}(0)) \ge D_u^2, \end{array} \right. \end{aligned}$$

(3.7)

if and only if $c_{uv}\ge c_{uv}^*$. This can be seen by regarding $c_{uv}$ as a variable in the function formed by the difference of the two sides for each of the inequalities in $(\mathcal {S}_u)$. Hence, the condition $c_{uv}<c_{uv}^*$ is equivalent to

$$\begin{aligned} \left\{ \begin{array}{l} \mu _{mu1}+D_u+c_{uv}\overline{V}_1< B'_{u1}(0),~\textrm{or} \\ \mu _{mu2}+D_u+c_{uv}\overline{V}_2< B'_{u2}(0),~\textrm{or} \\ 0\le ( \mu _{mu1}+D_u+c_{uv}\overline{V}_1-B'_{u1}(0) ) ( \mu _{mu2}+D_u+c_{uv}\overline{V}_2-B'_{u2}(0)) < D_u^2. \end{array} \right. \end{aligned}$$

(3.8)

Similarly, we can see that when $(\mathcal {S}_v)$ holds, there exists a unique $c_{vu}^*>0$ such that

$$\begin{aligned} \left\{ \begin{array}{l} \mu _{mv1}+D_v+c_{vu}\overline{U}_1 \ge B'_{v1}(0),~\textrm{and} \\ \mu _{mv2}+D_v+c_{vu}\overline{U}_2 \ge B'_{v2}(0),~\textrm{and} \\ ( \mu _{mv1}+D_v+c_{vu}\overline{U}_1-B'_{v1}(0)) ( \mu _{mv2}+D_v+c_{vu}\overline{U}_2-B'_{v2}(0)) \ge D_v^2, \end{array} \right. \end{aligned}$$

(3.9)

if and only if $c_{vu}\ge c_{vu}^*$.

Theorem 3.7

Assume that both $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$ hold in system (3.1). Then for given $c_{uv}<c_{uv}^*$ there exists a $c_{vu}^{\natural }>0$, depending on $c_{uv}$, such that (3.1) admits no positive equilibrium whenever $c_{vu}>c_{vu}^{\natural }$. Analogously, for given $c_{vu}<c_{vu}^*$ there exists a $c_{uv}^{\natural }>0$, depending on $c_{vu}$, such that the same assertion holds whenever $c_{uv}>c_{uv}^{\natural }$.

Proof

We justify the first assertion, and the second one is similar. Suppose there exists a positive equilibrium $(U^*_1,U^*_2,V^*_1,V^*_2)$ in (3.1). From Proposition 3.5, it satisfies $0<U^*_i\le \overline{U}_i$ and $0<V^*_i\le \overline{V}_i$ for $i=1,2$. For a given $c_{uv}<c_{uv}^*$, condition (3.8) is satisfied. Then, similar to previous discussion on (2.12), there exists a unique positive solution $(U_1, U_2)$ to

$$\begin{aligned} U_1 = \frac{1}{D_u} \left[ (\mu _{mu2}+D_u+c_{uv}\overline{V}_2)U_2 + k_{mu2}(U_2)^2 -B_{u2}(U_2) \right] = g_2^u(U_2,\overline{V}_2), \nonumber \\ U_2 = \frac{1}{D_u} \left[ (\mu _{mu1}+D_u+c_{uv}\overline{V}_1)U_1 + k_{mu1}(U_1)^2 -B_{u1}(U_1) \right] = g_1^u(U_1,\overline{V}_1), \end{aligned}$$

denoted by $(\breve{U}_1,\breve{U}_2)$. From the monotone dependence of the solution on $V_1$ and $V_2$ in (3.6), we see that $U_1^*\ge \breve{U}_1$ and $U_2^*\ge \breve{U}_2$. Now, consider

$$\begin{aligned} V_1 = \frac{1}{D_v} \left[ (\mu _{mv2}+D_v+c_{vu}U^*_2)V_2 + k_{mv2}(V_2)^2 -B_{v2}(V_2) \right] = g_2^v(V_2,U^*_2), \nonumber \\ V_2 = \frac{1}{D_v} \left[ (\mu _{mv1}+D_v+c_{vu}U^*_1)V_1 + k_{mv1}(V_1)^2 -B_{v1}(V_1) \right] = g_1^v(V_1,U^*_1). \end{aligned}$$

(3.10)

It admits a positive solution $(V_1^*,V_2^*)$ if there exists a positive equilibrium $(U_1^*,U_2^*,V_1^*,V_2^*)$ in (3.1). By regarding $c_{vu}$ as a variable, we can see that since $(\mathcal {S}_v)$ holds, there exists a unique $c_{vu}^{\natural }>0$ large enough, depending on $\breve{U}_1$ and $\breve{U}_2$ and hence depending on $c_{uv}$, such that

$$\begin{aligned} \left\{ \begin{array}{l} \mu _{mv1}+D_v+c_{vu}\breve{U}_1 \ge B'_{v1}(0),~\textrm{and} \\ \mu _{mv2}+D_v+c_{vu}\breve{U}_2 \ge B'_{v2}(0),~\textrm{and} \\ ( \mu _{mv1}+D_v+c_{vu}\breve{U}_1-B'_{v1}(0) ) ( \mu _{mv2}+D_v+c_{vu}\breve{U}_2-B'_{v2}(0)) \ge D_v^2, \end{array} \right. \end{aligned}$$

if and only if $c_{vu}\ge c_{vu}^{\natural }$. Thus, for all $c_{vu}>c_{vu}^{\natural }$, we have

$$\begin{aligned} \left\{ \begin{array}{l} \mu _{mv1}+D_v+c_{vu}U^*_1> B'_{v1}(0),~\textrm{and} \\ \mu _{mv2}+D_v+c_{vu}U^*_2> B'_{v2}(0),~\textrm{and} \\ ( \mu _{mv1}+D_v+c_{vu}U^*_1-B'_{v1}(0)) ( \mu _{mv2}+D_v+c_{vu}U^*_2-B'_{v2}(0)) > D_v^2. \end{array} \right. \end{aligned}$$

(3.11)

Under this condition, there exists no positive solution to (3.10), by arguments similar to the ones for Theorem 2.2. Therefore, we conclude that there is no positive equilibrium of system (3.1) when $c_{uv}<c_{uv}^*$ and $c_{vu}>c_{vu}^{\natural }$. $\square$

The rest of this subsection is devoted to exploring the existence of positive equilibria when both $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$ hold. Similar to the discussions for (3.8) and (3.9), there exist constants $d_u$, $d_v>0$ such that

$$\begin{aligned} \left\{ \begin{array}{l} \mu _{mu1}+D_u+d< B'_{u1}(0),~\textrm{or} \\ \mu _{mu2}+D_u+d< B'_{u2}(0),~\textrm{or} \\ 0\le ( \mu _{mu1}+D_u+d-B'_{u1}(0)) ( \mu _{mu2}+D_u+d-B'_{u2}(0)) < D_u^2, \end{array} \right. \end{aligned}$$

(3.12)

if and only if $d<d_v$, and

$$\begin{aligned} \left\{ \begin{array}{l} \mu _{mv1}+D_v+d< B'_{v1}(0),~\textrm{or} \\ \mu _{mv2}+D_v+d< B'_{v2}(0),~\textrm{or} \\ 0\le ( \mu _{mv1}+D_v+d-B'_{v1}(0)) ( \mu _{mv2}+D_v+d-B'_{v2}(0)) < D_v^2, \end{array} \right. \end{aligned}$$

(3.13)

if and only if $d<d_u$. With these formulations, we obtain the following existence of positive equilibrium.

Theorem 3.8

When both $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$ hold, there exists at least one positive equilibrium in system (3.1) if $c_{uv}<\frac{d_v}{\max \{\overline{V}_1,\overline{V}_2\}}$ and $c_{vu}<\frac{d_u}{\max \{\overline{U}_1,\overline{U}_2\}}$.

Proof

When $c_{uv}<\frac{d_v}{\max \{\overline{V}_1,\overline{V}_2\}}$ and $c_{vu}<\frac{d_u}{\max \{\overline{U}_1,\overline{U}_2\}}$, we define $\Omega :=[0,\overline{U}_1]\times [0,\overline{U}_2]\times [0,\overline{V}_1]\times [0,\overline{V}_2]$. Given a point $(\tilde{U}_1,\tilde{U}_2,\tilde{V}_1,\tilde{V}_2)\in \Omega$, we solve the following equations

$$\begin{aligned} \left\{ \begin{array}{l} U_1=g_2^u(U_2,\tilde{V}_2), \\ U_2=g_1^u(U_1,\tilde{V}_1), \end{array} \right. ~~\textrm{and}~ \left\{ \begin{array}{l} V_1=g_2^v(V_2,\tilde{U}_2), \\ V_2=g_1^v(V_1,\tilde{U}_1). \end{array} \right. \end{aligned}$$

(3.14)

In fact, for given $y\ge 0$, each function $g_i^{\bullet }(x;y)$ in x, $i=1,2$ and $\bullet =u$ or v, is increasing, concave upward for $i=1$ and concave downward for $i=2$. Also note that

$$\begin{aligned} \begin{array}{l} g_1^u(U_1,0)\le g_1^u(U_1,\tilde{V}_1)\le g_1^u(U_1,\overline{V}_1),~\forall ~U_1\ge 0, \\ g_2^u(U_2,0)\le g_2^u(U_2,\tilde{V}_2)\le g_2^u(U_2,\overline{V}_2),~\forall ~U_2\ge 0, \\ g_1^v(V_1,0)\le g_1^v(V_1,\tilde{U}_1)\le g_1^v(V_1,\overline{U}_1),~\forall ~V_1\ge 0, \\ g_2^v(V_2,0)\le g_2^v(V_2,\tilde{U}_2)\le g_2^v(V_2,\overline{U}_2),~\forall ~V_2\ge 0. \end{array} \end{aligned}$$

Since $c_{uv}\cdot \max \{\overline{V}_1,\overline{V}_2\}<d_v$ and $c_{vu}\cdot \max \{\overline{U}_1,\overline{U}_2\}<d_u$, there exist unique $U^{\diamond }_i\in [0,\overline{U}_i]$ and $V^{\diamond }_i\in [0,\overline{V}_i]$, $i=1,2$, such that

$$\begin{aligned} \left\{ \begin{array}{l} U^{\diamond }_1=g_2^u(U^{\diamond }_2,\tilde{V}_2), \\ U^{\diamond }_2=g_1^u(U^{\diamond }_1,\tilde{V}_1), \end{array} \right. ~~\textrm{and}~ \left\{ \begin{array}{l} V^{\diamond }_1=g_2^v(V^{\diamond }_2,\tilde{U}_2), \\ V^{\diamond }_2=g_1^v(V^{\diamond }_1,\tilde{U}_1). \end{array} \right. \end{aligned}$$

(3.15)

Figure 1 demonstrates the scenario for the first system in (3.15). Accordingly, we define a mapping $\mathcal {P}:\Omega \rightarrow \Omega$, by

$$\begin{aligned} \mathcal {P}(\tilde{U}_1,\tilde{U}_2,\tilde{V}_1,\tilde{V}_2)=(U^{\diamond }_1,U^{\diamond }_2,V^{\diamond }_1,V^{\diamond }_2). \end{aligned}$$

Since each function $g_i^{\bullet }(x;y)$ in x, $i=1,2$, $\bullet =u$ or v, is continuous in x and y, we see that $\mathcal {P}$ is a continuous mapping from the convex compact set $\Omega$ to $\Omega$. By the Brouwer’s fixed point theorem, there exists a fixed point of $\mathcal {P}$ in $\Omega$, which corresponds to an equilibrium of system (3.1), say $(U_1^*,U_2^*,V_1^*,V_2^*)$. It suffices to confirm that the equilibrium $(U_1^*,U_2^*,V_1^*,V_2^*)$ is positive. From $0\le V_i^*\le \overline{V}_i$, for $i=1,2$, and the assumption $c_{uv}\cdot \max \{\overline{V}_1,\overline{V}_2\}<d_v$, we see that the intersection of the graphs of $U_1=g_1^u(U_2,V_1^*),~~U_2=g_2^u(U_1,V_2^*)$, i.e. the point $(U_1^*,U_2^*)$, is component-wise positive. Analogously, we see that $(V_1^*,V_2^*)$ is also component-wise positive. This concludes the assertion. $\square$

Fig. 1

Illustration of the graphs of functions $g_i^u(U_i,\tilde{V}_i)$, $i=1,2$, in (3.14), and their upper/lower boundedness by $g_i^u(U_i,\overline{V}_i)$ and $g_i^u(U_i,0)$

The existence of positive equilibrium in Theorem 3.8 is assured under a sense of (relatively) weak competition between two species. The existence of positive equilibrium under strong competition, i.e., with sufficiently large competition strengths $c_{uv}$ and $c_{vu}$, is challenging, and remains open.

3.3 Stability of Equilibria

In this subsection, we investigate stability for the equilibria of system (3.1). The linearization of system (3.1) at an equilibrium $\tilde{E}=(\tilde{U}_1,\tilde{U}_2,\tilde{V}_1,\tilde{V}_2)$ reads

$$\begin{aligned} \frac{dx_1(t)}{dt}= & {} B_{u1}'(\tilde{U}_1)x_1(t-\tau _u) - \mu _{mu1}x_1(t) - 2k_{mu1}\tilde{U}_1x_1(t) \nonumber \\{} & {} - c_{uv}\tilde{V}_1x_1(t) - c_{uv}\tilde{U}_1y_1(t) + D_ux_2(t) - D_ux_1(t), \nonumber \\ \frac{dx_2(t)}{dt}= & {} B_{u2}'(\tilde{U}_2)x_2(t-\tau _u) - \mu _{mu2}x_2(t) - 2k_{mu2}\tilde{U}_2x_2(t) \nonumber \\{} & {} - c_{uv}\tilde{V}_2x_2(t) - c_{uv}\tilde{U}_2y_2(t)+ D_ux_1(t) - D_ux_2(t), \nonumber \\ \frac{dy_1(t)}{dt}= & {} B_{v1}'(\tilde{V}_1)y_1(t-\tau _v) - \mu _{mv1}y_1(t) - 2k_{mv1}\tilde{V}_1y_1(t) \nonumber \\{} & {} - c_{vu}\tilde{V}_1x_1(t) - c_{vu}\tilde{U}_1y_1(t)+ D_vy_2(t) - D_vy_1(t), \nonumber \\ \frac{dy_2(t)}{dt}= & {} B_{v2}'(\tilde{V}_2)y_2(t-\tau _v) - \mu _{mv2}y_2(t) - 2k_{mv2}\tilde{V}_2y_2(t) \nonumber \\{} & {} - c_{vu}\tilde{V}_2x_2(t) - c_{vu}\tilde{U}_2y_2(t)+ D_vy_1(t) - D_vy_2(t). \end{aligned}$$

(3.16)

First, we define

$$\begin{aligned} \Delta _u= & {} \left[ (B_{u1}'(0)-\mu _{mu1}-D_u)\overline{V}_2 - (B_{u2}'(0)-\mu _{mu2}-D_u)\overline{V}_1 \right] ^2 +4\overline{V}_1\overline{V}_2D_u^2, \\ \Delta _v= & {} \left[ (B_{v1}'(0)-\mu _{mv1}-D_v)\overline{U}_2 - (B_{v2}'(0)-\mu _{mv2}-D_v)\overline{U}_1 \right] ^2 +4\overline{U}_1\overline{U}_2D_v^2, \end{aligned}$$

and

$$\begin{aligned} c_{uv}^+= & {} \frac{(B_{u1}'(0)-\mu _{mu1}-D_u)\overline{V}_2 + (B_{u2}'(0)-\mu _{mu2}-D_u)\overline{V}_1+\sqrt{\Delta _u}}{2\overline{V}_1\overline{V}_2}, \\ c_{vu}^+= & {} \frac{(B_{v1}'(0)-\mu _{mv1}-D_v)\overline{U}_2 + (B_{v2}'(0)-\mu _{mv2}-D_v)\overline{U}_1+\sqrt{\Delta _v}}{2\overline{U}_1\overline{U}_2}. \end{aligned}$$

These terms will be used in the following discussions. Let us first make a preparation.

Lemma 3.9

The condition

$$\begin{aligned} {\left\{ \begin{array}{ll} B_{u1}'(0)-\mu _{mu1}+B_{u2}'(0)-\mu _{mu2}-2D_u >c_{uv} (\overline{V}_1+\overline{V}_2),~\textrm{or} \\ (B_{u1}'(0)-\mu _{mu1}-D_u-c_{uv}\overline{V}_1)(B_{u2}'(0)-\mu _{mu2}-D_u-c_{uv}\overline{V}_2)<D_u^2, \end{array}\right. } \end{aligned}$$

(3.17)

is equivalent to $c_{uv}<c_{uv}^+$, and

$$\begin{aligned} {\left\{ \begin{array}{ll} B_{v1}'(0)-\mu _{mv1}+B_{v2}'(0)-\mu _{mv2}-2D_v >c_{vu} (\overline{U}_1+\overline{U}_2),~\textrm{or} \\ (B_{v1}'(0)-\mu _{mv1}-D_v-c_{vu}\overline{U}_1)(B_{v2}'(0)-\mu _{mv2}-D_v-c_{vu}\overline{U}_2)<D_v^2, \end{array}\right. } \end{aligned}$$

(3.18)

is equivalent to $c_{vu}<c_{vu}^+$.

Lemma 3.9 is confirmed in Appendix A.I. The stability of the equilibria $E_0$, $E_u$ and $E_v$ can be examined from their associated characteristic values for the linearized system (3.16), as indicated by the following theorem, where monotone dynamics plays a crucial role.

Theorem 3.10

Consider system (3.1).

• (i) $E_0$ is stable when neither $(\mathcal {S}_u)$ nor $(\mathcal {S}_v)$ holds, while unstable when either $(\mathcal {S}_u)$ or $(\mathcal {S}_v)$ holds.

• (ii) When $(\mathcal {S}_u)$ holds, $E_u$ is stable if $c_{vu}>c_{vu}^+$, while unstable if $c_{vu}<c_{vu}^+$.

• (iii) When $(\mathcal {S}_v)$ holds, $E_v$ is stable if $c_{uv}>c_{uv}^+$, while unstable if $c_{uv}<c_{uv}^+$.

Proof

• (i) Via a direct computation, the characteristic equation from the linearization at $E_0$ can be expressed as $\Sigma _1(\lambda )\cdot \Sigma _2(\lambda ) =0$, where

  $$\begin{aligned} \Sigma _1(\lambda ):= & {} \left\{ \lambda ^2 + (p_1+p_2)\lambda + (p_1p_2-D_u^2) - (B_{u1}'(0) + B_{u2}'(0)) \lambda e^{-\tau _u\lambda } \right. \\{} & {} \left. - (p_1B_{u2}'(0) + p_2B_{u1}'(0)) e^{-\tau _u\lambda } + B_{u1}'(0)B_{u2}'(0) e^{-2\tau _u\lambda } \right\} , \\ \Sigma _2(\lambda ):= & {} \left\{ \lambda ^2 + (q_1+q_2)\lambda + (q_1q_2-D_v^2) - (B_{v1}'(0) + B_{v2}'(0)) \lambda e^{-\tau _u\lambda } \right. \\{} & {} \left. - (q_1B_{v2}'(0) + q_2B_{v1}'(0)) e^{-\tau _v\lambda } + B_{v1}'(0)B_{v2}'(0), e^{-2\tau _v\lambda } \right\} \end{aligned}$$

  with

  $$\begin{aligned} p_1 := \mu _{mu1} +D_u,{} & {} q_1 := \mu _{mv1} +D_v, \\ p_2 := \mu _{mu2} +D_u,{} & {} q_2 := \mu _{mv2} +D_v. \end{aligned}$$

  Note that $\Sigma _1(\lambda )=0$ is exactly the characteristic equation (A.8), with different symbols. Hence, as in the proof of Theorem 2.4 for (A.8) and by using Corollary 5.5.2 [32], all roots of $\Sigma _1(\lambda )$ have negative real parts when $(\mathcal {S}_u)$ does not hold, and admits a root with positive real part under $(\mathcal {S}_u)$. Similarly, all roots of $\Sigma _2(\lambda )$ have negative real parts when $(\mathcal {S}_v)$ does not hold, and admits a root with positive real part when $(\mathcal {S}_v)$ holds true. The assertion is thus justified.

• (ii) The characteristic equation associated with $E_u$ can be computed as $\tilde{\Sigma }_1(\lambda )\cdot \tilde{\Sigma }_2(\lambda )=0$, where

  $$\begin{aligned} \tilde{\Sigma }_1(\lambda ):= & {} \left\{ \lambda ^2 + (\tilde{p}_1+\tilde{p}_2)\lambda + (\tilde{p}_1\tilde{p}_2-D_u^2) - (B_{u1}'(\overline{U}_1) + B_{u2}'(\overline{U}_2)) \lambda e^{-\tau _u\lambda } \right. \\{} & {} ~~~~~\left. - (\tilde{p}_1B_{u2}'(\overline{U}_2) + \tilde{p}_2B_{u1}'(\overline{U}_1)) e^{-\tau _u\lambda } + B_{u1}'(\overline{U}_1)B_{u2}'(\overline{U}_2) e^{-2\tau _u\lambda } \right\} , \\ \tilde{\Sigma }_2(\lambda ):= & {} \left\{ \lambda ^2 + (\tilde{q}_1+\tilde{q}_2)\lambda + (\tilde{q}_1\tilde{q}_2-D_v^2) - (B_{v1}'(0) + B_{v2}'(0)) \lambda e^{-\tau _u\lambda } \right. \\{} & {} ~~~~~\left. - (\tilde{q}_1B_{v2}'(0) + \tilde{q}_2B_{v1}'(0)) e^{-\tau _v\lambda } + B_{v1}'(0)B_{v2}'(0) e^{-2\tau _v\lambda } \right\} , \end{aligned}$$

  with

  $$\begin{aligned} \tilde{p}_1 := \mu _{mu1} + 2k_{mu1} \overline{U}_1 +D_u,{} & {} \tilde{q}_1 := \mu _{mv1} + c_{vu} \overline{U}_1 +D_v, \\ \tilde{p}_2 := \mu _{mu2} + 2k_{mu2} \overline{U}_2 +D_u,{} & {} \tilde{q}_2 := \mu _{mv2} + c_{vu} \overline{U}_2 +D_v. \end{aligned}$$

As in the proof of Theorem 2.4 for (A.11) and by using Corollary 5.5.2] [32], all roots of $\tilde{\Sigma }_1(\lambda )$ have negative real parts when $(\mathcal {S}_u)$ holds. Thus, the stability of $E_u$ is determined by the roots of $\tilde{\Sigma }_2(\lambda )$. Again, by using Corollary 5.5.2 [32], it suffices to determine the stability modulus of the associated system without delay, i.e.,

$$\begin{aligned} \lambda ^2 + (\tilde{q}_1+\tilde{q}_2-B_{v1}'(0)-B_{v2}'(0))\lambda + (\tilde{q}_1-B_{v1}'(0))(\tilde{q}_2-B_{v2}'(0)) -D_v^2=0.\nonumber \\ \end{aligned}$$

(3.19)

When $(\mathcal {S}_u)$ holds and $c_{vu}>c_{vu}^+$, i.e., both inequalities in (3.18) are invalid, we see that equation (3.19) has negative stability modulus, and thus the equilibrium $E_u$ is stable, thanks to Lemma 3.9. On the other hand, (3.19) has a solution with positive real part, and thus equilibrium $E_u$ is unstable, when $c_{vu}<c_{vu}^+$. A similar argument justifies the assertion for $E_v$ in (iii). $\square$

Remark 3.1

(i) From (3.8) and (3.17), we see that $c_{uv}<c_{uv}^+$ is equivalent to $c_{uv}<c_{uv}^*$, that is $c_{uv}^+=c_{uv}^*$. (ii) From the second assertion in Lemma 3.9, we see that $c_{vu}>c_{vu}^+$ is equivalent to

$$\begin{aligned} {\left\{ \begin{array}{ll} B_{v1}'(0)-\mu _{mv1}+B_{v2}'(0)-\mu _{mv2}-2D_v <c_{vu} (\overline{U}_1+\overline{U}_2),~\textrm{and} \\ (B_{v1}'(0)-\mu _{mv1}-D_v-c_{vu}\overline{U}_1)(B_{v2}'(0)-\mu _{mv2}-D_v-c_{vu}\overline{U}_2)>D_v^2. \end{array}\right. } \end{aligned}$$

(3.20)

In addition, the fact $U^*_i\le \overline{U}_i$, $i=1,2$, together with (3.11) imply

$$\begin{aligned} \left\{ \begin{array}{l} \mu _{mv1}+D_v+c_{vu}\overline{U}_1> B'_{v1}(0),~\textrm{and} \\ \mu _{mv2}+D_v+c_{vu}\overline{U}_2> B'_{v2}(0),~\textrm{and} \\ ( \mu _{mv1}+D_v+c_{vu}\overline{U}_1-B'_{v1}(0)) ( \mu _{mv2}+D_v+c_{vu}\overline{U}_2-B'_{v2}(0)) > D_v^2, \end{array} \right. \end{aligned}$$

(3.21)

when $c_{vu}>c_{vu}^{\natural }$. Hence, from (3.20) and (3.21), it reveals that $c_{vu}>c_{vu}^{\natural }$ implies $c_{vu}>c_{vu}^+$.

3.4 Uniform Persistence

We establish the uniform persistence of the species in system (3.1) by determining the threshold competition strengths. Such results depend on conditions $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$, and the competition strengths of the species. We also discuss how such threshold dynamics depends on the delays $\tau _u$ and $\tau _v$.

Theorem 3.11

Consider system (3.1). Assume that

$$\begin{aligned}{} & {} (\mathcal {S}_u)~\mathrm{holds,~and~in~addition~either}~(\mathcal {S}_v)~\mathrm{does~not~hold,~or}~(\mathcal {S}_v)~\mathrm{holds~and~}c_{uv}<c^+_{uv}, \\{} & {} (resp., (\mathcal {S}_v)~\mathrm{holds,~and~in~addition~either}~(\mathcal {S}_u)~\mathrm{does~not~hold,~or}~(\mathcal {S}_u)~\mathrm{holds~and~}c_{vu}<c^+_{vu}). \end{aligned}$$

Then u-species (resp., v-species) is uniformly persistent in the sense that there is a positive constant $\varrho ^*$ such that every solution $(U_1(t),U_2(t),V_1(t),V_2(t))$ of (3.1) with $\phi \in \mathbb {X} \setminus \{\phi _1=\phi _2=\hat{0}\}$ (resp., $\phi \in \mathbb {X}\setminus \{\phi _3=\phi _4=\hat{0}\}$) satisfies

$$\begin{aligned} \liminf _{t\rightarrow \infty }U_i(t)\ge \varrho ^*~\left( \textrm{resp}., ~ \liminf _{t\rightarrow \infty }V_i(t)\ge \varrho ^* \right) ,~\textrm{for}~i=1,2. \end{aligned}$$

We prove Theorem 3.11 in Appendix A.I, by using the persistence theory in [39].

Remark 3.2

• (i) Both species uniformly persist in system (3.1) if both $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$ hold, and $c_{uv}<c^+_{uv}$ and $c_{vu}<c^+_{vu}$. That is, each species can intrinsically exist in the environment under weak competition.

• (ii) Note that $c_{uv}< c_{uv}^+$ in one of the criteria for u-species to persist in the environment, which is about the competition strength of v-species, but not on that of u-species. However, this criterion certainly relates to the characters of u-species, since the value of $c_{uv}^+$ depends on the intrinsic birth rate, the death rate and the maturation time of u-species.

• (iii) Based on the comparison principle, we used an auxiliary system in the proof of Theorem 3.11 to show the uniform persistence of u-species (resp., v-species) under the condition $c_{uv}<c^+_{uv}$ (resp., $c_{vu}<c^+_{vu}$). A question arises that whether the criteria are necessary to achieve the property of uniform persistence. In fact, the stability of boundary equilibria leads us to confirm the necessary condition. If $c_{uv}>c^+_{uv}$, from Theorem 3.10 (iii), we see that $E_v$ is stable, which means that solutions with initial conditions sufficiently close to $E_v$ will approach it eventually, and then u-species goes extinction. Hence, we see that $c^+_{uv}$ is the threshold value to determine the uniform persistence of u-species. An analog holds true for the threshold value $c^+_{vu}$.

How the values of $c^+_{uv}$ and $c^+_{vu}$ depend on $\tau _v$ and $\tau _u$ is not only mathematically but also biologically interesting. For convenience, we denote

$$\begin{aligned} d_{ui}:=B_{ui}'(0)-\mu _{mui}-D_u \end{aligned}$$

for $i=1,2$. Then direct algebraic calculations show that the following inequalities are equivalent.

Lemma 3.12

The following inequalities are equivalent

• (i) $D_u^2\le (>) d_{u1}d_{u2}$,

• (ii) $|d_{u1}\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 }| \ge (<) |d_{u1}(d_{u2}\overline{V}_1-d_{u1}\overline{V}_2)-2D_u^2\overline{V}_1|$,

• (iii) $|d_{u2}\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 }| \ge (<) |d_{u1}(d_{u1}\overline{V}_2-d_{u2}\overline{V}_1)-2D_u^2\overline{V}_2|$,

• (iv) $\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } \le (>) |d_{u1}\overline{V}_2+d_{u2}\overline{V}_1|$.

In addition, the assertion also holds if replacing u and $\overline{V}_i$ by v and $\overline{U}_i$, respectively.

We use Lemma 3.12 to derive the following dependence of the values of $c^+_{uv}$ and $c^+_{vu}$ on $\tau _v$ and $\tau _u$, respectively. Its proof is arranged in Appendix A.I.

Proposition 3.13

Whenever the values of $c^+_{uv}$ and $c^+_{vu}$ are positive, they satisfy

$$\begin{aligned} \frac{\partial c^+_{uv}}{\partial \tau _u}<0,{} & {} \frac{\partial c^+_{uv}}{\partial \tau _v}>0, \\ \frac{\partial c^+_{vu}}{\partial \tau _u} >0,{} & {} \frac{\partial c^+_{vu}}{\partial \tau _v} <0. \end{aligned}$$

Remark 3.3

• (i) From Theorem 3.11 and Proposition 3.13, we see that shorter maturation time of u-species (smaller value of $\tau _u$) facilitates its persistence since the range for the competition strength $c_{uv}$ is wider. In addition, longer maturation time of the competitor v-species (larger value of $\tau _v$) also benefits u-species to persist in the environment. On the other hand, v-species persists under an analogous criterion.

• (ii) Note that the values of $c_{uv}^+$ and $c_{vu}^+$ also depend on both dispersal rates $D_u$ and $D_v$. The numerical simulations in Sect. 5 will show that such dependence may not be monotone. This indicates that in model (3.1) the dispersal of a species between two patches does not always facilitate or damage the persistence of its competitor.

3.5 Global Dynamics

System (3.1) may admit multiple positive equilibria, as demonstrated in numerical simulations in Sect. 4. It is therefore difficult to establish the global convergence to one positive equilibrium. In this subsection, we shall discuss the global dynamics centered around the trivial and two boundary equilibria. There are two situations to take into account according to essential existence or not for a competitor. They will be treated by applying the theory of asymptotically autonomous systems and the monotone dynamics based on the special cone $\mathcal {C}_K$, respectively.

First, by Proposition 3.5(ii), that the criterion $(\mathcal {S}_v)$ does not hold implies $\lim _{t\rightarrow \infty }V_i(t)=0$, $i=1,2$, i.e., v-species can not essentially survive, and the limiting system of (3.1) becomes (2.11) with parameters in u-species. An analog also follows when $(\mathcal {S}_u)$ does not hold. The theory of asymptotically autonomous systems in [38] provides an approach to confirm the global attractivity of an equilibrium. A detailed demonstration for our delay case is arranged in Appendix A.II and A.III.

Theorem 3.14

Consider system (3.1).

• (i) $E_0$ is GAS in $\mathbb {X}$ when neither $(\mathcal {S}_u)$ nor $(\mathcal {S}_v)$ holds.

• (ii) $E_u$ attracts all solutions in $\mathbb {X}_u$ when $(\mathcal {S}_u)$ holds and $(\mathcal {S}_v)$ does not hold.

• (iii) $E_v$ attracts all solutions in $\mathbb {X}_v$ when $(\mathcal {S}_v)$ holds and $(\mathcal {S}_u)$ does not hold.

Proof

• (i) From Proposition 3.5 and Theorem 3.10(i), $E_0$ is GAS when neither $(\mathcal {S}_u)$ nor $(\mathcal {S}_v)$ holds.

• (ii) Suppose that $(\mathcal {S}_u)$ holds and $(\mathcal {S}_v)$ does not hold. Then $\lim _{t\rightarrow \infty }V_i(t)=0$, $i=1,2$, by Proposition 3.5(ii). Thus, the system

  $$\begin{aligned} \frac{dU_1(t)}{dt}= & {} B_{u1}(U_1(t-\tau _u)) - \mu _{mu1}U_1(t) -k_{mu1}(U_1(t))^2 + DU_2(t) - DU_1(t), \nonumber \\ \frac{dU_2(t)}{dt}= & {} B_{u2}(U_2(t-\tau _u)) - \mu _{mu2}U_2(t) -k_{mu2}(U_2(t))^2 + DU_1(t) - DU_2(t), \nonumber \\ \frac{dV_1(t)}{dt}= & {} -D_vV_1(t),~~\frac{dV_2(t)}{dt} =-D_vV_2(t), \end{aligned}$$

  (3.22)

  acts as a limiting equation of (3.1), see Theorem A.2. Note that $E_u$ is also an equilibrium of (3.22). Obviously, the associated characteristic equation of the linearized system at $E_u$ is $\tilde{\Sigma }_1(\lambda )\cdot (\lambda +D_v)^2=0$. As discussed in the proof of Theorem 3.10, all roots of $\tilde{\Sigma }_1(\lambda )=0$ have negative real parts. Hence, $E_u$ is stable under the solution flow of (3.22). In addition, according to Theorem 2.4(ii), it is GAS in $\mathbb {X}_u$. Back to system (3.1), we see from Proposition 3.1 that each solution orbit in $\mathbb {X}_u$ is pre-compact. Moreover, the $\omega$-limit set under the semiflow of (3.1) is contained in $\mathbb {X}_u$, and hence it intersects $\mathbb {X}_u$ which is the basin of attraction of $E_u$ under the semiflow of (3.22). Thus, the result in Theorem A.1 implies the global convergence dynamics to $E_u$. This completes the proof for (ii). The proof for (iii) is similar. $\square$

As for the case that each species can individually survive when its competitor is absent, the dynamics further depends on the competition ability of each species. In a general setting for competitive systems, a trichotomy of either the global convergence to one of the two boundary equilibria or the existence of a positive equilibrium was reported in [16]. The existence of stable boundary equilibrium is connected to the notion of competitive exclusion in ecology. A further detailed classification of possible asymptotic dynamics was established in [34], which includes the competitive exclusion, the stable coexistence, and the bi-stability (two simultaneously stable boundary equilibria). Such bi-stability occurs when the coexistence state exists and the mono-stable boundary equilibrium is not taking place, see also [33]. When both $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$ hold, system (3.1) satisfies the assumption in [16], and the trichotomy takes place:

Theorem 3.15

Consider system (3.1), and let both $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$ hold. Then the $\omega$-limit set of every orbit is contained in $I:=[\hat{\textbf{0}},\hat{\overline{\textbf{U}}}]\times [\hat{\textbf{0}},\hat{\overline{\textbf{V}}}]$, where $\textbf{0}=(0,0)$, $\overline{\textbf{U}}=(\overline{U}_1,\overline{U}_2)$ and $\overline{\textbf{V}}=(\overline{V}_1,\overline{V}_2)$, and exactly one of the following holds:

• (i) There exists a positive equilibrium of $\Phi _t$ in I.

• (ii) $\Phi _t(\phi )\rightarrow E_u$ for every $\phi =(\tilde{\phi }_1,\tilde{\phi }_2)\in I$ with $\tilde{\phi }_i\ne \hat{\textbf{0}}$, $i=1,2$.

• (iii) $\Phi _t(\phi )\rightarrow E_v$ for every $\phi =(\tilde{\phi }_1,\tilde{\phi }_2)\in I$ with $\tilde{\phi }_i\ne \hat{\textbf{0}}$, $i=1,2$.

Moreover, if (b) or (c) holds, $\phi =(\tilde{\phi }_1,\tilde{\phi }_2)\in \mathbb {X}\setminus I$ and $\tilde{\phi }_i\ne \hat{\textbf{0}}$, $i=1,2$, then either $\Phi _t(\phi )\rightarrow E_u$ or $\Phi _t(\phi )\rightarrow E_v$ as $t\rightarrow \infty$.

Note that the property of strongly monotone in Proposition 3.4 implies that system (3.1) is strictly order-preserving (see the proof of Theorem 3.15 for the definition), which is one of the criteria in [16]. We arrange the proof of Theorem 3.15 in Appendix A.I. Based on the facts in Remark 3.1, applying the results of trichotomy dynamics in Theorem 3.15, and nonexistence of positive equilibrium in Theorem 3.7, we obtain the following global convergence dynamics to the boundary equilibria. Such scenario is called “dominance dynamics". Recall that $c_{uv}^+$ and $c_{vu}^+$ were defined in Sect. 3.3.

Theorem 3.16

Assume that both $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$ hold in system (3.1).

• (i) If, in addition, $c_{uv}<c_{uv}^+$, then there exists a $c_{vu}^{\natural }>0$, depending on $c_{uv}$, such that $E_u$ attracts all solutions in (3.1) whenever $c_{vu}\ge c_{vu}^{\natural }$.

• (ii) If, in addition, $c_{vu}<c_{vu}^+$, then there exists a $c_{uv}^{\natural }>0$, depending on $c_{vu}$, such that $E_v$ attracts all solutions in (3.1) whenever $c_{uv}\ge c_{uv}^{\natural }$.

Proof

We justify the first assertion, and the proof for the second one is similar. Assume that both $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$ hold, and $c_{uv}<c_{uv}^+$. Then u-species unoformly persists by Theorem 3.11. In addition, from Remark 3.1(i), it holds that $c_{uv}<c_{uv}^*$. Theorem 3.7 implies that there exists a $c_{vu}^{\natural }>0$, depending on $c_{uv}$, such that (3.1) admits no positive equilibrium whenever $c_{vu}>c_{vu}^{\natural }$. Therefore, the only possible dynamics of the trichotomy in Theorem 3.15 is the global convergence to $E_u$. $\square$

Remark 3.4

The results in Theorem 3.14 and Theorem 3.16 are both concerned with the dominance dynamics. However, the first one is a competition-independent outcome, which can be determined by the single-species feature under $(\mathcal {S}_u)$ or $(\mathcal {S}_v)$, with whatever competition strengths $c_{uv}$ and $c_{vu}$. In contrast, the second one is a competition-dependent outcome. More precisely, when each species can essentially survive in the environment with the absence of its competitor (both $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$ hold), the species with relatively strong ability to compete wins the competition and dominates the environment. For example, only u-species survives in the environment when $c_{uv}<c_{uv}^+$ and $c_{vu}\ge c_{vu}^{\natural }$, where the value of $c_{vu}^{\natural }$ is sufficiently large and depends on the value of $c_{uv}$.

4 Numerical Illustrations

In this section, we conduct numerical simulations and present the following examples to demonstrate our theoretical results and make further observations. For the birth functions in (2.9), herein we adopt $b_{u i}(\xi )=\frac{\beta _{u i}\xi }{1+\vartheta _{u i}\xi }$, $b_{v i}(\xi )=\frac{\beta _{v i}\xi }{1+\vartheta _{v i}\xi }$ for $i=1,2$.

4.1 Sharp Criterion for Uniform Persistence in Theorem 3.11

The question mentioned in Remark 3.2(iii) is concerned with whether the criterion $c_{uv}<c^+_{uv}$ (resp., $c_{vu}<c^+_{vu}$) is necessary to attain uniform persistence of u-species (resp., v-species). The following example illustrates that the criterion is sharp.

Example 4.1

Here, we set the parameters in system (3.1) by $\mu _{lu1}=0.3$, $\mu _{lu2}=0.2$, $\mu _{lv1}=0.35$, $\mu _{lv2}=0.15$, $k_{lu1}=0.2$, $k_{lu2}=0.3$, $k_{lv1}=0.15$, $k_{lv2}=0.35$, $\mu _{mu1}=0.2$, $\mu _{mu2}=0.2$, $\mu _{mv1}=0.25$, $\mu _{mv2}=0.15$, $k_{mu1}=0.1$, $k_{mu2}=0.1$, $k_{mv1}=0.15$, $k_{mv2}=0.15$, $\vartheta _{u1}=\vartheta _{u2}=\vartheta _{v1}=\vartheta _{v2}=3$, $\beta _{u1}=\beta _{u2}=\beta _{v1}=\beta _{v2}=5$, $D_u=1$, $D_v=1.2$ and $\tau _u=\tau _v=0.5$. It is easy to check that both $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$ hold true and $c^+_{uv}\approx 1.9998$. In the following discussions, we vary the values of $c_{uv}$ and $c_{vu}$, and compute two solutions evolved from constant initial values (6, 1, 0.3, 0.2) and (0.001, 0.009, 3.5, 7) in each case.

• (i) We choose $c_{uv}=1.95<c^+_{uv}$ and take $c_{vu}=0.1$ (relatively weak competition of u-species against v-species) in case (a), and $c_{vu}=10$ (relatively strong competition of u-species against v-species) in case (b). Evolutions of solutions in both cases exhibit the uniform persistence of u-species, see Fig. 2i a, b.

• (ii) We take $c_{uv}=2.05>c^+_{uv}$ and choose $c_{vu}=0.1$ (relatively weak competition) in case (c), and $c_{vu}=10$ (relatively strong competition) in case (d). It reveals that u-species does not uniformly persist in both cases, i.e., with weak and strong competition strength $c_{vu}$ respectively, see Fig. 2ii c, d. Note that although the components of the first solution in case (d) converge to a positive constant, it is not uniformly persistent because the components of the second solution converge to 0. Hence, this example demonstrates the sharpness on the estimation of the threshold value $c^+_{uv}$ which determines the uniform persistence of u-species. Moreover, we see in this example that, in each of $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$, the first two inequalities hold and the third one is invalid. Nevertheless, we have other numerical examples (not presented here) to confirm that such estimate is sharp, where the third inequality in each of $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$ holds and the first two are invalid.

Fig. 2

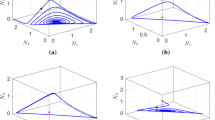
Illustration of the sharpness for the criterion in Theorem 3.11 on the uniform persistence in system (3.1). Components $U_1(t), U_2(t)$ of two solutions to system (3.1) with constant initial values (6, 1, 0.3, 0.2) and (0.001, 0.009, 3.5, 7) in each case, for Example 4.1. u-species uniformly persists in i a $c_{uv}=1.95<c^+_{uv}\approx 2.00$ and $c_{vu}=0.1$ and b $c_{uv}=1.95<c^+_{uv}$ and $c_{vu}=10$. u-species does not uniformly persist, in ii c $c_{uv}=2.05>c^+_{uv}$ and $c_{vu}=0.1$ and d $c_{uv}=2.05>c^+_{uv}$ and $c_{vu}=10$. (The first ones in d approach a positive constant, but it is not a case of uniform persistence since the second ones converge to 0.)

4.2 Effects of Maturation Times and Dispersal Rates

How a species evolves by manipulating the maturation time and the dispersal rate to improve the ability of invasion is an interesting problem. From the result in Theorem 3.11, uniform persistence (successful invasion) of u-species depends on the value of competition strength of v-species against u-species, $c_{uv}$, and larger $c_{uv}^+$ provides wider range of $c_{uv}$ to allow persistence. One way to answer this question is to observe the effect on the value of $c_{uv}^+$ from the maturation time $\tau _u$ for the invader, $\tau _v$ for the indigenous species, and from the dispersal rates of both species, $D_u$ and $D_v$. The result in Proposition 3.13 indicates that the value of $c_{uv}^+$ is decreasing in $\tau _u$ and increasing in $\tau _v$. We shall also explore the influence on the value of $c_{uv}^+$ from $D_u$ and $D_v$, when two species have the same birth function and when their birth functions are different, respectively. That is, $b_{ui}(\xi )=\frac{\beta _{ui}\xi }{1+\vartheta _{ui}\xi }$ may be different from $b_{vi}(\xi )=\frac{\beta _{vi}\xi }{1+\vartheta _{vi}\xi }$, $i=1,2$.

Example 4.2

Here, we observe the effects of maturation times $\tau _u$ and $\tau _v$ on the threshold value $c_{uv}^+$, by setting $\mu _{lui}=\mu _{lvi}=0.2$, $k_{lui}=k_{lvi}=0.2$, $\mu _{mui}=\mu _{mvi}=0.2$, $k_{mui}=k_{mvi}=0.1$, $i=1,2$. In addition, we set $\vartheta _{vi}=3$, $\beta _{vi}=5$, $i=1,2$ in the birth function for v-species, and the dispersal rate $D_v=1$. In the first case, we consider that u-species has the same birth function as v-species, i.e., $\vartheta _{ui}=3$, $\beta _{ui}=5$, $i=1,2$. That is, the resources in two patches are identical for both species u and v. Fig. 3a shows no difference in $c_{uv}^+$ by changing the value of $D_u$ from 0.5, 1 to 2 since the two patches are identical for u-species.

In the second case, we set u-species to have $\vartheta _{u1}=3$, $\beta _{u1}=3$, $\vartheta _{u2}=3$ and $\beta _{u2}=7$, i.e., the resources in two patches are identical for v-species but non-identical for u-species. Under this condition, different values of $D_u$ indeed lead to variant values of $c_{uv}^+$. In Fig. 3b–d, smaller $D_u$ corresponds to larger $c_{uv}^+$, which means that slower movement of u-species between two patches enhances its invasion into a fragmentary habitat when the environment is spatially heterogeneous. In addition, what are indicated in the level curves in Fig. 3 are consistent with the result in Proposition 3.13, i.e., the value of $c_{uv}^+$ is decreasing in $\tau _u$ and increasing in $\tau _v$.

Fig. 3

The contour plot of threshold value of competition strength $c_{uv}^+$ with respect to maturation times $\tau _u$ and $\tau _v$. All subfigures with $\mu _{lui}=\mu _{lvi}=0.2$, $k_{lui}=k_{lvi}=0.2$, $\mu _{mui}=\mu _{mvi}=0.2$, $k_{mui}=k_{mvi}=0.1$ and $\vartheta _{ui}=\vartheta _{vi}=3$, $\beta _{vi}=5$, $i=1,2$, $D_v=1$. In a, $\beta _{ui}=5$, $i=1,2$, and $D_u=0.5,1$ or 2, $c_{uv}^+$ remains the same for $D_u=0.5, 1, 2$. In b–d, $\beta _{u1}=3$, $\beta _{u2}=7$, and b $D_u=0.5$, c $D_u=1$, d $D_u=2$, the value of $c^+_{uv}$ varies with different values of $D_u$ All level curves are consistent with the result in Proposition 3.13, i.e., the value of $c_{uv}^+$ is decreasing in $\tau _u$ and increasing in $\tau _v$

Example 4.3

We further explore how the threshold value $c_{uv}^+$ in Theorem 3.11 is affected by the dispersal rates $D_u$ and $D_v$. We will proceed the discussion under different sets of $\beta _{u1}$, $\beta _{u2}$, $\beta _{v1}$ and $\beta _{v2}$, for the birth functions. Except for this, we set in Fig. 4$\mu _{lu1}=\mu _{lv1}=0.3$, $k_{lu1}=k_{lv1}=0.3$, $\mu _{mu1}=\mu _{mv1}=0.3$, $\mu _{lu2}=\mu _{lv2}=0.1$, $k_{lu2}=k_{lv2}=0.1$, $\mu _{mu2}=\mu _{mv2}=0.1$, $k_{mu1}=k_{mv1}=k_{mu2}=k_{mv2}=0.1$, $\tau _u=\tau _v=0.5$, and $\vartheta _{u i}=\vartheta _{v i}=3$ for $i=1,2$. From Theorem 3.11, larger $c_{uv}^+$ benefits the survival of u-species. In Fig. 4a–c, we see that the value of $c_{uv}^+$ decreases with respect to $D_u$ in all three cases. However, it increases with respect to $D_v$ in (a), decreases with respect to $D_v$ in (b), and even has a non-monotone dependence on $D_v$ in (c). Therefore, this provides us an example to see that (i) u-species can actively facilitate its survival by proceeding a slower dispersal, and (ii) the dispersal of the competitor (v-species) does not always prevent or facilitate the invasion of u-species. Analogues for interchanging u- and v-species are also true by observing the value of $c_{vu}^+$ in Fig. 4d–f.

Fig. 4

From Theorem 3.11, larger $c_{uv}^+$ (resp., $c_{vu}^+$) benefits the survival of u-species (resp., v-species). Contour plots in the subfigures show how the threshold values of competition strengths a–c $c_{uv}^+$ and d-f $c_{vu}^+$ are affected by the dispersal rates $D_u$ and $D_v$. All subfigures with $\mu _{lu1}=\mu _{lv1}=0.3$, $k_{lu1}=k_{lv1}=0.3$, $\mu _{mu1}=\mu _{mv1}=0.3$, $\mu _{lu2}=\mu _{lv2}=0.1$, $k_{lu2}=k_{lv2}=0.1$, $\mu _{mu2}=\mu _{mv2}=0.1$, $k_{mu1}=k_{mv1}=k_{mu2}=k_{mv2}=0.1$ and $\tau _u=\tau _v=0.5$, and $\vartheta _{u i}=\vartheta _{v i}=3$, $i=1,2$. a and b $\beta _{u1}=\beta _{v1}=3$, $\beta _{u2}=\beta _{v2}=7$, b and e $\beta _{u1}=\beta _{v1}=4.8$, $\beta _{u2}=\beta _{v2}=5.2$, c and f $\beta _{u1}=\beta _{v1}=6$, $\beta _{u2}=\beta _{v2}=4$

4.3 Bifurcation of Positive Equilibria and Multi-stability

To explore the complex dynamics in system (3.1), we plot the bifurcation diagram of equilibria by using package MATCONT and setting one competition strength as the bifurcation parameter, and accordingly simulate evolutions of solutions to compare the dynamics. In fact, even considering two intrinsically identical species in the same environment except the competition abilities, it can undergo equilibria bifurcation as increasing one of the competition strength. Specifically, we vary the value of $c_{vu}$ and fix the other parameters in the following example.

Example 4.4

We take the parameter values in system (3.1) as $c_{uv}=1.5$, $\mu _{lu1}=\mu _{lv1}=0.2$, $k_{lu1}=k_{lv1}=0.2$, $\mu _{mu1}=\mu _{mv1}=0.2$, $\mu _{lu2}=\mu _{lv2}=0.2$, $k_{lu2}=k_{lv2}=0.2$, $\mu _{mu2}=\mu _{mv2}=0.2$, $k_{mu1}=k_{mv1}=k_{mu2}=k_{mv2}=0.1$, $\tau _u=\tau _v=0.1$, $\vartheta _{u1}=\vartheta _{v1}=3$, $\vartheta _{u2}=\vartheta _{v2}=3$ and $\beta _{u1}=\beta _{v1}=5$, $\beta _{u2}=\beta _{v2}=5$. In Figs. 5 and 6, as increasing the value of $c_{vu}$ from 1 to 2, the number of positive equilibria varies from 1 to 2, 3, 2, 1 and finally becomes 0 which agrees with the result for the nonexistence of positive equilibrium in Theorem 3.7 for sufficiently large $c_{vu}$. It indeed undergoes limit point (LP) bifurcation (also called tangent bifurcation), which means that two positive equilibria merge and then disappear, and boundary point (BP) bifurcation, which means that one branch of positive equilibrium merges to a boundary equilibrium. Based on this illustration, we conduct further simulations to see how the convergence dynamics changes with respect to the value of $c_{vu}$:

• (i) In Fig. 7, by choosing the competition strength $c_{uv}=1.4$, there exists a unique stable positive equilibrium which attracts all positive solutions.

• (ii) In Fig. 8, with $c_{vu}=1.5$, for two completely identical species (note that $c_{uv}=1.5$), there exist three positive equilibria. Among them, two have their own basins of attraction and the other one is located on the boundary of basins of attraction. The solution in Fig. 8a converges to a stable positive equilibrium; so does the one in Fig. 8b. The solution in Fig. 8c with symmetric initial values converges to an unstable positive equilibrium along its stable manifold.

• (iii) In Fig. 9, with $c_{vu}=1.63$, there are two positive equilibria, and one is stable and the other is unstable. However, the boundary equilibrium $E_u$ becomes stable, and together with the stable positive equilibrium, the bi-stability prevails in system (3.1).

Fig. 5

Bifurcation diagram of $U_1^*$ with respect to $c_{vu}$ ($V_1^*<0$ for $c_{cu}>1.67$ along the upper branch in Fig. 6). As increasing the value of competition strength $c_{vu}$ from 1 to 2, the number of positive equilibria varies from 1 to 2, 3, 2, 1 and finally becomes 0, which agrees with the result for the nonexistence of positive equilibrium in Theorem 3.7 for sufficiently large $c_{vu}$. It undergoes limit point (LP) bifurcation, which means that two positive equilibria merge and then disappear, and boundary point (BP) bifurcation, which means that one branch of positive equilibrium merges with a boundary equilibrium. Parameters: $c_{uv}=1.5$, $\mu _{lu1}=\mu _{lv1}=0.2$, $k_{lu1}=k_{lv1}=0.2$, $\mu _{mu1}=\mu _{mv1}=0.2$, $\mu _{lu2}=\mu _{lv2}=0.2$, $k_{lu2}=k_{lv2}=0.2$, $\mu _{mu2}=\mu _{mv2}=0.2$, $k_{mu1}=k_{mv1}=k_{mu2}=k_{mv2}=0.1$, $\tau _u=\tau _v=0.1$, $\vartheta _{u1}=\vartheta _{v1}=3$, $\vartheta _{u2}=\vartheta _{v2}=3$ and $\beta _{u1}=\beta _{v1}=5$, $\beta _{u2}=\beta _{v2}=5$

Fig. 6

Bifurcation diagram of $V_1^*$ with respect to $c_{vu}$. The same interpretation on the number of positive equilibria and the same parameter values as in Fig. 5

Fig. 7

Figs. 7, 8 and 9 show the change of convergence dynamics when varying the value of $c_{vu}$. This figure shows three solutions converge to the positive equilibrium (0.0941, 0.0941, 2.4121, 2.4121), evolved from constant initial value a (2, 2.2, 0.1, 0.1), b (0.1, 0.1, 4.5, 3), c (0.1, 0.1, 0.1, 0.1), when $c_{vu}=1.4$; other parameter values as in Fig. 5. Herein, the competition strength of u-species against v-species is relatively small, $c_{vu}<c_{uv}$, and the population of u-species tends to an amount relatively less than that of v-species

Fig. 8

When $c_{vu}=1.5$, convergence of solution to positive equilibrium (2.4299, 2.4299, 0.0877, 0.0877), (0.0877, 0.0877, 2.4299, 2.4299) and (0.7753, 0.7753, 0.7753, 0.7753), respectively, evolved from constant initial value a (2, 2.2, 0.1, 0.1), b (0.1, 0.1, 4.5, 3), c (0.1, 0.1, 0.1, 0.1); other parameter values as in Fig. 5. The equilibrium (0.7753, 0.7753, 0.7753, 0.7753) is a saddle point. Biologically, when two species have close competition strengths and $c_{vu}$ is between the first LP point and the BP point in the bifurcation diagrams in Figs. 5 and 6, there are two stable coexistence states, and the final outcome depends on the initial values of two species

Fig. 9

When $c_{vu}=1.63$, which is larger than but close to the boundary bifurcation point, the solution evolved from a (2, 2.2, 0.1, 0.1), and the one from b (0.1, 0.1, 4.5, 3), converge to the boundary equilibrium (2.8991, 2.8991, 0, 0). The solution evolved from c (0.1, 0.1, 0.1, 0.1) converges to the positive equilibrium (0.1318, 0.1318, 2.1774, 2.1774); other parameter values as in Fig. 5. Biologically, when the competition strength of u-species, $c_{vu}$, is larger than but close to the BP point in the bifurcation diagrams in Figs.  5 and 6, there are two coexistence equilibria, stable and unstable respectively, and the boundary equilibrium $E_u$ becomes stable. This reveals another bi-stability in system (3.1), one coexistence equilibrium and one boundary equilibrium, which is different from that in Fig.  8 where two stable states are both coexistent

5 Conclusion and Discussion

In this work, we proposed and analyzed a two-species competition model over a two-patch environment, where immature individuals face with only intra-specific competition against the same generation, and mature individuals live under intra- and inter-specific competitions. The consideration of immature stage incurs a delayed recruitment to the total mature population. Combined with the dispersal behavior between patches, the system may admit multiple positive equilibria, and this increases the complexity to explore the global convergence dynamics. However, the structure of monotone dynamics provided us an analytical approach to investigate the dynamical properties, starting from analyzing the local stability of boundary equilibria to establishing the criterion for the global convergence dynamics. It is complicated to depict all possible convergence dynamics completely, due to the possible existence of multiple positive equilibria. Nevertheless, we have managed to apply the theory of uniform persistence to explore the invasion of species.

In the single-species model, we have shown the following dichotomy dynamics:

• The trivial solution is GAS in $C([-\tau ,0],\mathbb {R}_+^2)$, i.e., the species will die out if condition $(\mathcal {S})$ does not hold. The positive equilibrium is GAS in $C([-\tau ,0],\mathbb {R}_+^2)\setminus \{(\hat{0},\hat{0})\}$, i.e., the population of species will tend toward a positive stationary state, if $(\mathcal {S})$ holds.

In the two-species model, we established criteria $(\mathcal {S}_u)$ (resp., $(\mathcal {S}_v)$) to determine the occurrence of u-species (resp., v-species) dominance equilibrium, and threshold competition strengths $c_{uv}^+$ and $c_{vu}^+$ to determine the uniform persistence for each of the species:

• The trivial equilibrium $E_0$ is GAS, i.e., both species will die out, when neither $(\mathcal {S}_u)$ nor $(\mathcal {S}_u)$ holds. In addition, there are two mechanisms to bring on dominance dynamics in system (3.1), which were stated in Theorem 3.14 and Theorem 3.16 respectively. More precisely, the u-dominance equilibrium $E_u$ can be GAS, i.e., v-species will die out and the population of u-species will tend toward a positive state when it initially exists at least in one patch. The first mechanism acts when $(\mathcal {S}_u)$ holds and $(\mathcal {S}_v)$ does not hold, with whatever competition strengths $c_{uv}$ and $c_{vu}$. The second one depends on the competition strength. More precisely, when each species can essentially survive in the environment when its competitor is absent (i.e., both $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$ hold), the species with a relatively strong competition strength will win the competition and dominate the environment. An analogous scenario takes place for v-dominance equilibrium.

• u-species uniformly persists (successfully invade the environment) when $(\mathcal {S}_u)$ holds, and in addition either $(\mathcal {S}_v)$ does not hold, or $(\mathcal {S}_v)$ holds and $c_{uv}<c_{uv}^+$. From a biological viewpoint, u-species can survive in the environment when either the competitor essentially dies out, or essentially persists but with weak competitiveness. Similarly, v-species uniformly persists due to analogous criteria.

• Dependence of the value $c^+_{uv}$ on two maturation times is monotone. More precisely, shorter maturation time of u-species (smaller value of $\tau _u$) or longer maturation time of the competitor v-species (larger value of $\tau _v$) will facilitate the persistence of u-species in the environment. An analog holds for $c^+_{vu}$ and v-species.

• A species can facilitate its survival by actively proceeding a slower dispersal. However, a species may not prevent the invasion of its competitor by regulating the dispersal of itself. This is illustrated in Example 4.3.

The work [1] considered a single species with intra-competition in the mature stage, and without competition in the immature stage. The evolution of mature population therein is a special case of our (2.6), and it admits the global convergence to the positive equilibrium, which indicates a mono-stable dynamics. On the other hand, when taking the maturation times of both species to approach zero in model (3.1), function $B_{ui}$ (resp., $B_{vi}$) becomes simply $b_{ui}$ (resp., $b_{vi}$), i.e., there is only single life stage for all individuals. Recalling the studies on two competing species over a two-patch environment in [6, 22], with single life stage, the authors showed a switching convergence dynamics between the two single-species dominance equilibria and the coexistence equilibrium when changing the value of the dispersal rate. In other words, such a system also admits the dynamics of mono-stability. As a comparison, we see that two life stages, as studied in this work, is one of the key factors for incurring multi-stability in the model of competing species over patchy environments.

The birth function we considered is monotone and we employed the theory of monotone dynamics to obtain local stability and global convergence in the proposed model. On the other hand, a non-monotone birth function also characterizes certain features, for example, the one of Ricker type: $b(\xi )= \varsigma \xi e^{-\gamma \xi }$, see [26, 30, 37] and the references therein. This function generates the well-known negative feedback and periodic solutions frequently occur in the systems. We expect that there will be multiple periodic solutions if we adopt the Ricker-type birth functions in our model. We will take such consideration as a future research project. In addition, when the resource dynamics is taken into account to combine with the life-staged structure of a population, the dynamics can also become rich, as illustrated in [11], where even only one single-species consumer was considered. Therein, with the predator admitting two life stages, the interaction of predator and prey was explored, and sustainable oscillatory dynamics were found in a certain range of maturation time. This motivates us a future study on the resource-consumer models with considerations of the life-stage structures of populations, intra- and inter-competitions of species, and spatially heterogeneous environments, partially or comprehensively. Since the dynamics of even a basic resource-consumer model like the Lotka–Volterra equation is non-monotone, further methodologies different from the monotone dynamics theory employed in this study will be expected.

Appendices

Appendices

1.1 A.I Proofs of Lemma, Propositions and Theorems

Proof of Theorem 2.1

Equation (2.6) is a cooperative and irreducible delay differential equation, cf. Chapter 5 [32]. In addition, the corresponding semiflow is eventually strongly monotone, and then SOP, see Corollary 5.3.5 and Proposition 1.1.1 [32]. A SOP semiflow possesses an important property of generic convergence to equilibrium, and even the global convergence dynamics to an equilibrium if it is unique, cf. Theorem 2.3.1 [32].

All solutions of (2.6) are uniformly eventually bounded. Indeed, from equation (2.6) with (2.8), we have

$$\begin{aligned} \frac{dU(t)}{d t} \le \tilde{b}_0 -\mu _{m}U(t), \end{aligned}$$

where $\tilde{b}_0:=(\mu _{l}e^{-\mu _{l}\tau }\tilde{b})/[\mu _{l} + k_{l} (1-e^{-\mu _{l}\tau }) \tilde{b}]$, and $\tilde{b}$ is given in (2.8). Thus $\limsup _{t\rightarrow \infty } U(t) \le \tilde{b}_0/\mu _{m}$.

To observe the configuration of $B(\xi )$, we compute

$$\begin{aligned} B'(\xi ) = \frac{\mu _{l}^2e^{-\mu _{l}\tau } b'(\xi )}{[\mu _{l}+k_{l}(1-e^{-\mu _{l}\tau })b(\xi )]^2} >0, \end{aligned}$$

(A.1)

and

$$\begin{aligned} B''(\xi )= & {} [\mu _{l}+k_{l}(1-e^{-\mu _{l}\tau })b(\xi )]^{-4} \cdot \mu _{l}^2e^{-\mu _{l}\tau }[\mu _{l}+k_{li}(1-e^{-\mu _{l}\tau })b(\xi )] \nonumber \\{} & {} \cdot \left\{ b''(\xi )[\mu _{l}+k_{l}(1-e^{-\mu _{l}\tau })b(\xi )] - 2k_{l}(1-e^{-\mu _{l}\tau })(b'(\xi ))^2\right\} \nonumber \\< & {} 0, \end{aligned}$$

(A.2)

due to (2.8). Note that $B'(0)=b'(0)e^{-\mu _l\tau }$. From the configuration of $B(\xi )$, we can see that a unique positive equilibrium $\overline{U}$ exists if and only if $B'(0)>\mu _m$. The intersections for the graphs of functions $B(\xi )$ and $h(\xi ):=\mu _m \xi +k_m\xi ^2$ are located at $\xi =0,~\overline{U}$. From these graphs, we have

$$\begin{aligned} B'(\overline{U})<\mu _m+2k_m\overline{U}. \end{aligned}$$

(A.3)

When $b'(0)e^{-\mu _l\tau }<\mu _m$, the trivial solution $U \equiv \hat{0}$ is the unique equilibrium, and it attracts every element in $C([-\tau ,0],\mathbb {R}_+)$, according to Theorem 2.3.1 [32]. In addition, the corresponding characteristic equation is $\lambda + \mu _m-B'(0)e^{-\lambda \tau }=0$. By Theorem 2.3 [40], we see that the trivial solution is stable (resp., unstable) when $B'(0)<\mu _m$ (resp., $B'(0)>\mu _m$). Hence, assertion (i) is confirmed.

The condition $b'(0)e^{-\mu _l\tau }>\mu _m$, i.e., $B'(0)>\mu _m$, enforces the existence of positive equilibrium $\overline{U}$, and a sufficiently small $\rho ^*>0$ such that

$$\begin{aligned} B'(\rho ^*)-\mu _m-k_m\rho ^*>0. \end{aligned}$$

(A.4)

In order to conclude the global convergence to $\overline{U}$, we first claim the uniform persistence for (2.6) by using the persistence theory in Theorem 4.6 [39]. Define

$$\begin{aligned} \mathcal {X} = C([-\tau ,0],\mathbb {R}_+),~~\mathcal {X}_0 = \left\{ \varphi \in \mathcal {X}~\textrm{with} ~\varphi \ne \hat{0}\right\} . \end{aligned}$$

Then $\partial \mathcal {X}_0:= \mathcal {X}\setminus \mathcal {X}_0 =\{ \hat{0} \}$. As shown in Theorem 5.2.1 [32], a solution starting nonnegative remains nonnegative in future time. That is, $\mathcal {X}$ is positively invariant. In addition, from

$$\begin{aligned} \frac{dU(t)}{d t} \ge B(U(t-\tau )) -\mu _{m}U(t) - k_m \mathcal {U}U(t), \end{aligned}$$

where $\mathcal {U}:=\sup _{t\ge 0}U(t)<\infty$, we have

$$\begin{aligned} U(t) \ge e^{-(\mu _m+k_m \mathcal {U}) t}U(0) + \int ^t_0e^{-(\mu _m+k_m \mathcal {U})(t-\xi )} B(U(\xi -\tau ))d\xi >0, \end{aligned}$$

for $t >0$, whenever $U(0) \in \mathcal {X}_0$. Hence, $\mathcal {X}_0$ is positively invariant. Thus, $\mathcal {M}_{\partial }:=\{ \varphi \in \mathcal {X}~|~\Psi _t(\varphi )\in \partial \mathcal {X}_0,~\forall ~t\ge 0 \}=\{\hat{0}\}$, and note that $\mathcal {X}\setminus \mathcal {X}_0=\{ \hat{0}\}$ is relatively closed in $\mathcal {X}$. Next, we claim that

$$\begin{aligned} \limsup _{t\rightarrow \infty }U(t)>\rho ^*,~\mathrm{for~all}~\varphi \in \mathcal {X}_0. \end{aligned}$$

(A.5)

Suppose, on the contrary, that there exists an initial value $\varphi \in \mathcal {X}_0$ and a $t_1>0$ such that $U(t)\le \rho ^*$ for $t\ge t_1-\tau$. From (2.6) and the concavity of $B(\cdot )$, for $t\ge t_1$,

$$\begin{aligned} \frac{dU(t)}{d t} \ge B'(\rho ^*)U(t-\tau )-(\mu _m+k_m\rho ^*)U(t). \end{aligned}$$

Consider the auxiliary equation

$$\begin{aligned} \frac{dx(t)}{d t} = B'(\rho ^*)x(t-\tau )-(\mu _m+k_m\rho ^*)x(t). \end{aligned}$$

(A.6)

Equation (A.6) is cooperative and irreducible, and generates a semiflow of (A.6) which is eventually strong monotone, with $\hat{0}$ an equilibrium. Under (A.4), Eq. (A.6) admits a positive stability modulus associated with a positive eigenvector $\textbf{z}_0$, according to Theorem 5.5.1 and Corollary 5.5.2] [32]. Denote the solution semiflow of (A.6) by $\tilde{\Psi }_t$. For the initial value $\varphi$ of (2.6), there exist a $t_2>t_1$ and a small $\alpha _0>0$ such that

$$\begin{aligned} \hat{0}\ll \alpha _0\hat{\textbf{z}}_0\ll \Psi _{t_2}(\varphi ). \end{aligned}$$

Hence, we have

$$\begin{aligned} \tilde{\Psi }_t(\alpha _0\hat{\textbf{z}}_0) \le \Psi _t(\alpha _0\hat{\textbf{z}}_0) \ll \Psi _{t+t_2}(\varphi ), \end{aligned}$$

for $t\ge 0$, which is a contradiction to the boundedness of semiflow $\Psi _t$. This contradiction proves (A.5). Obviously, $\{\hat{0}\}$ is an isolated invariant set in $\partial \mathcal {X}_0$, and thus the set $\mathcal {M}_{\partial }$ consists of an acyclic equilibrium point. From (A.5), $W^s(\hat{0})\cap \mathcal {X}_0 = \emptyset$, where $W^s(\hat{0})$ denotes the stable manifold of $\hat{0}$. By the persistence theory in Theorem 4.6 [39], system (2.6) is uniformly persistent with respect to $(\mathcal {X}_0,\partial \mathcal {X}_0)$ under $b'(0)e^{-\mu _l\tau }>\mu _m$, which means that there exists a $\rho ^{**}>0$, with $\rho ^{**}<U^*$, such that $\liminf _{t\rightarrow \infty }U(t)>\rho ^{**}$. Accordingly, it suffices to consider (2.6) in the space $\mathcal {X}^*:=C([-\tau ,0],[\rho ^{**}/2,\infty ))$. In fact, the equilibrium $\overline{U}$ is the unique equilibrium in $\mathcal {X}^*$, and again Theorem 2.3.1 [32] implies its global attractivity. The characteristic equation at $\overline{U}$ is $\lambda + \mu _m+2k_m \overline{U}-B'(\overline{U})e^{-\lambda \tau }=0$. If it has a root with nonnegative real part, then

$$\begin{aligned} \mu _m+2k_m \overline{U} \le |\lambda + \mu _m+2k_m \overline{U}| = |B'(\overline{U})e^{-\lambda \tau }| < B'(\overline{U}) \end{aligned}$$

which contradicts to (A.3) for any $\tau >0$. Thus, it has only roots with negative real parts. Therefore, assertion (ii) is justified. $\square$

Proof of Theorem 2.4

System (2.11) is also cooperative and irreducible. By using a similar argument as in Theorem 2.1, we can show that the solutions of system (2.11) are ultimately bounded. The linearization of system (2.11) at an equilibrium $(\tilde{U}_1, \tilde{U}_2)$ reads

$$\begin{aligned} \frac{dx_1(t)}{dt}= & {} B_1'(\tilde{U}_1)x_1(t-\tau ) - \mu _{m1}x_1(t) - 2k_{m1}\tilde{U}_1x_1(t) + Dx_2(t) - Dx_1(t), \nonumber \\ \frac{dx_2(t)}{dt}= & {} B_2'(\tilde{U}_2)x_2(t-\tau ) - \mu _{m2}x_2(t) - 2k_{m2}\tilde{U}_2x_2(t) + Dx_1(t) - Dx_2(t). \end{aligned}$$

(A.7)

Suppose that $(\mathcal {S})$ does not hold. The trivial solution is the unique nonnegative equilibrium, and hence the property of SOP implies the global convergence dynamics. In addition, by a direct computation we obtain the characteristic equation at the trivial equilibrium

$$\begin{aligned}{} & {} \lambda ^2 + (p_1+p_2)\lambda + (p_1p_2-D^2) - (B_1'(0) + B_2'(0)) \lambda e^{-\tau \lambda } \nonumber \\{} & {} ~~~ - (p_1B_2'(0) + p_2B_1'(0)) e^{-\tau \lambda } + B_1'(0)B_2'(0) e^{-2\tau \lambda } =0, \end{aligned}$$

(A.8)

here

$$\begin{aligned} p_1 := \mu _{m1} +D,~~p_2 := \mu _{m2} +D. \end{aligned}$$

Since (2.11) is a cooperative and irreducible delay differential system, from Corollary 5.5.2 [32], the characteristic equation (A.8) has the stability modulus of the same sign as that of the characteristic equation for the associated ordinary differential equation of (A.7) at the trivial equilibrium, i.e.,

$$\begin{aligned}{} & {} \qquad \qquad \lambda ^2 + m_1 \lambda +m_0 =0, \end{aligned}$$

(A.9)

$$\begin{aligned}{} & {} m_1 := p_1+p_2 - B'_1(0) - B'_2(0), \nonumber \\{} & {} m_0 := (p_1- B'_1(0))(p_2 - B'_2(0)) - D^2. \end{aligned}$$

(A.10)

Obviously, both $m_1$ and $m_0$ are positive. Hence, both roots of (A.9) have negative real parts, and thus we conclude that all roots of (A.8) have negative real parts. Together with the global convergence dynamics from SOP, we conclude that the trivial equilibrium of (2.11) is GAS in $C([-\tau ,0],\mathbb {R}_+^2)$.

Suppose that $(\mathcal {S})$ holds. From Theorem 2.3, we have the uniform persistence for the (2.11). Hence, it suffices to consider the solutions with initial values in the set $C([-\tau ,0],[\rho ^*,\infty )^2)$. It attracts all solutions starting from $C([-\tau ,0],\mathbb {R}_+^2)\setminus \{(\hat{0}, \hat{0})\}$, and contains the unique equilibrium $(\overline{U}_1, \overline{U}_2)$. Together with the eventually uniform boundedness, the SOP property implies the global convergence to $(\overline{U}_1, \overline{U}_2)$. Thus, it remains to show that $(\overline{U}_1, \overline{U}_2)$ is stable. With a direct calculation, we obtain the characteristic equation at $(\overline{U}_1, \overline{U}_2)$

$$\begin{aligned}{} & {} \lambda ^2 + (\tilde{p}_1+\tilde{p}_2)\lambda + (\tilde{p}_1\tilde{p}_2-D^2) - (B_1'(\overline{U}_1) + B_2'(\overline{U}_2)) \lambda e^{-\tau \lambda } \nonumber \\{} & {} ~~~ - (\tilde{p}_1B_2'(\overline{U}_2) + \tilde{p}_2B_1'(\overline{U}_1)) e^{-\tau \lambda } + B_1'(\overline{U}_1)B_2'(\overline{U}_2) e^{-2\tau \lambda } =0, \end{aligned}$$

(A.11)

where

$$\begin{aligned} \tilde{p}_1:= & {} \mu _{m1} + 2k_{m1} \overline{U}_1 +D, \\ \tilde{p}_2:= & {} \mu _{m2} + 2k_{m2} \overline{U}_2 +D. \end{aligned}$$

Again, the characteristic equation (A.11) has stability modulus of the same sign as that of the characteristic equation for the corresponding ordinary differential equation of (A.7) at $(\overline{U}_1, \overline{U}_2)$, i.e.,

$$\begin{aligned}{} & {} \qquad \qquad \qquad \lambda ^2 + \tilde{m}_1 \lambda +\tilde{m}_0 =0,\nonumber \\{} & {} \tilde{m}_1 := \tilde{p}_1+\tilde{p}_2 - B_1'(\overline{U}_1) - B_2'(\overline{U}_2), \nonumber \\{} & {} \tilde{m}_0 := (\tilde{p}_1-B_1'(\overline{U}_1))(\tilde{p}_2-B_2'(\overline{U}_2)) - D^2. \end{aligned}$$

(A.12)

We claim that both roots of (A.12) have negative real parts. The equilibrium $(\overline{U}_1, \overline{U}_2)$ satisfies

$$\begin{aligned} B_1(\overline{U}_1)-\mu _{m1}\overline{U}_1-k_{m1}(\overline{U}_1)^2+D\overline{U}_2-D\overline{U}_1=0. \end{aligned}$$

Since $f_1$ has a positive derivative at $\overline{U}_1$, we see that

$$\begin{aligned} \mu _{m1}+2k_{m1}\overline{U}_1+D-B_1'(\overline{U}_1)>0, \end{aligned}$$

and then

$$\begin{aligned} \tilde{p}_1-B_1'(\overline{U}_1)>0. \end{aligned}$$

Similarly, it holds that $\tilde{p}_2-B_2'(\overline{U}_2)>0$. Thus, $\tilde{m}_1>0$. In addition, since the point $(\overline{U}_1,\overline{U}_2)$ is the intersection of the graphs $U_2=f_1(U_1)$ and $U_1=f_2(U_2)$, we have

$$\begin{aligned} f_1'(\overline{U}_1)= & {} \frac{1}{D}[\mu _{m1}+D + 2k_{m1}\overline{U}_1 -B_1'(\overline{U}_1) ] \\= & {} \frac{\overline{U}_2}{\overline{U}_1} + \frac{1}{D} \left( \frac{B_1(U_1)}{U_1}+ k_{m1}\overline{U}_1 -B_1'(\overline{U}_1) \right) \\> & {} \frac{\overline{U}_2}{\overline{U}_1}, \end{aligned}$$

due to the property of $B_1(\cdot )$ as in (A.1) and (A.2). Similarly, $f_2'(\overline{U}_2)> \frac{\overline{U}_1}{\overline{U}_2}$. Hence, we see that $f'_1(\overline{U}_1)f'_2(\overline{U}_2)>1$, which leads to

$$\begin{aligned} \tilde{m}_0=(\tilde{p}_1-B_1'(\overline{U}_1))(\tilde{p}_2-B_2'(\overline{U}_2)) - D^2 >0. \end{aligned}$$

Accordingly, we conclude that all roots of (A.11) have negative real parts, and therefore the positive equilibrium $(\overline{U}_1, \overline{U}_2)$ is GAS in $C([-\tau ,0],\mathbb {R}_+^2)\setminus \{(\hat{0},\hat{0})\}$, when $(\mathcal {S})$ holds. $\square$

Proof of Proposition 3.2

We only justify the assertion for $\mathbb {X}_u$, as the one for $\mathbb {X}_v$ is similar. (i) Suppose that $t_1>0$ is the first time such that the solution is out of $\mathbb {X}_u$, that is $U_1(t)=U_2(t)=0$ for $t\in [t_1-\tau _u,t_1]$. Then for $0<\epsilon <\tau _u$, there is an $s\in [t_1-\epsilon -\tau _u,t_1-\epsilon ]$ such that $U_{i_0}(s)>0$ for $i_0=$ 1 or 2. In fact, $s\in [t_1-\epsilon -\tau _u,t_1-\tau _u)$, and then $s+\tau _u\in [t_1-\epsilon ,t_1)\subset [t_1-\tau _u,t_1]$. Hence, $U'_{i_0}(s+\tau _u)=0$. However, $U'_{i_0}(s+\tau _u)=B_{ui_0}(U_{i_0}(s))>0$, which is a contradiction. Hence, $\mathbb {X}_u$ is positively invariant under the solution flow of (3.1).

To show the positive invariance of $\textrm{int}(\mathbb {X})$, we consider an initial condition $\phi \in \textrm{int}(\mathbb {X})$, which means that $\phi _i(\theta )>0$, $\theta \in [-\tau _u,0]$ for $i=1,2$, and $\phi _i(\theta )>0$, $\theta \in [-\tau _v,0]$ for $i=3,4$. From Proposition 3.1, we obtain, for $i=1,2$,

$$\begin{aligned} \frac{dU_i(t)}{dt} \ge B_{ui}(U_i(t-\tau _u)) - \tilde{b}U_i(t), \end{aligned}$$

where $\tilde{b}_i=\mu _{mui}+k_{mui}\mathcal {U}_i+c_{uv}\mathcal {V}_i+D_u$, $\mathcal {U}_i=\sup _{t\ge 0}U_i(t)<\infty$, and $\mathcal {V}_i=\sup _{t\ge 0}V_i(t)<\infty$. Hence, for $0<t\le \tau _u$,

$$\begin{aligned} U_i(t) \ge e^{-\tilde{b}t}U_i(0) + \int ^t_0e^{-\tilde{b}(t-\xi )} B_{ui}(\phi _i(\xi -\tau _u))d\xi , \end{aligned}$$

and, for $t>\tau _u$,

$$\begin{aligned} U_i(t) \ge e^{-\tilde{b}t}U_i(0) + \int ^{\tau _u}_0e^{-\tilde{b}(t-\xi )} B_{ui}(\phi _i(\xi -\tau _u))d\xi + \int ^t_{\tau _u}e^{-\tilde{b}(t-\xi )} B_{ui}(U_i(\xi -\tau _u))d\xi . \end{aligned}$$

Thus, $U_i(t)>0$ for $t>0$ because of $U_i(0)>0$. Similarly, $V_i(t)>0$ for $t>0$. We conclude that $\textrm{int}(\mathbb {X})$ is positively invariant.

• (ii) We observe that, for $i,j=1,2$ and $i\ne j$,

  $$\begin{aligned} \frac{dU_i(t)}{dt} \ge B_{ui}(U_i(t-\tau _u))-\tilde{b}_iU_i(t)+D_uU_j(t). \end{aligned}$$

  (A.13)

Now, suppose $\phi _{i_0}\ne \hat{0}$ for some $i_0=1,2$. Then, for $t\in [0,\tau _u]$,

$$\begin{aligned} U_{i_0}(t)\ge e^{-\tilde{b}_{i_0}t}\phi _{i_0}(0) + \int ^t_0 e^{-\tilde{b}_{i_0}(t-\xi )} [B_{ui_0}(\phi _{i_0}(\xi -\tau _u)) + D_uU_{j_0}(\xi )] d\xi . \end{aligned}$$

(A.14)

We first claim that there is an $t_2\in [0,\tau _u)$ such that $U_{i_0}(t_2)>0$. Otherwise, we have $U_{i_0}(t)=0$ for $t\in [0,\tau _u)$, and (A.14) enforces $\phi _{i_0}(0)=0$ and $\phi _{i_0}(\xi -\tau _u)=0$ for $\xi \in [0,\tau _u)$, which contradicts to $\phi _{i_0}\ne \hat{0}$. Next, we claim that $U_1(t)>0$ and $U_2(t)>0$ for $t>t_2$. From (A.13), we see that, for $t_2\le t\le \tau _u$,

$$\begin{aligned} U_{i_0}(t)\ge e^{-\tilde{b}_{i_0}(t-t_2)}U_{i_0}(t_2) + \int ^t_{t_2} e^{-\tilde{b}_{i_0}(t-\xi )} [B_{ui_0}(\phi _{i_0}(\xi -\tau _u)) + D_uU_{j_0}(\xi )] d\xi , \end{aligned}$$

and for $t> \tau _u$,

$$\begin{aligned} U_{i_0}(t)\ge & {} e^{-\tilde{b}_{i_0}(t-t_2)}U_{i_0}(t_2) + \int ^{\tau _u}_{t_2} e^{-\tilde{b}_{i_0}(t-\xi )} [B_{ui_0}(\phi _{i_0}(\xi -\tau _u)) + D_uU_{j_0}(\xi )] d\xi \\{} & {} + \int ^t_{\tau _u} e^{-\tilde{b}_{i_0}(t-\xi )} [B_{ui_0}(U_{i_0}(\xi -\tau _u)) + D_uU_{j_0}(\xi )] d\xi . \end{aligned}$$

Hence, $U_{i_0}(t)>0$ for $t\ge t_2$ since $U_{i_0}(t_2)>0$. From (A.13), we also have, for $t_2\le t\le \tau _u$,

$$\begin{aligned} U_{j_0}(t)\ge e^{-\tilde{b}_{j_0}(t-t_2)}U_{j_0}(t_2) + \int ^t_{t_2} e^{-\tilde{b}_{j_0}(t-\xi )} [B_{uj_0}(\phi _{j_0}(\xi -\tau _u)) + D_uU_{i_0}(\xi )] d\xi , \end{aligned}$$

and for $t> \tau _u$,

$$\begin{aligned} U_{j_0}(t)\ge & {} e^{-\tilde{b}_{j_0}(t-t_2)}U_{j_0}(t_2) + \int ^{\tau _u}_{t_2} e^{-\tilde{b}_{j_0}(t-\xi )} [B_{uj_0}(\phi _{j_0}(\xi -\tau _u)) + D_uU_{i_0}(\xi )] d\xi \\{} & {} + \int ^t_{\tau _u} e^{-\tilde{b}_{j_0}(t-\xi )} [B_{uj_0}(U_{i_0}(\xi -\tau _u)) + D_uU_{i_0}(\xi )] d\xi . \end{aligned}$$

Hence, $U_{j_0}(t)>0$ for $t> t_2$ since $U_{i_0}(t)>0$ for $t\ge t_2$. Finally, we conclude that $U_1(t)>0$ and $U_2(t)>0$ for $t\ge \tau _u(>t_2)$. This completes the proof. $\square$

Proof of Lemma 3.9

Let us justify the first assertion, and the second one is similar. Obviously, the first inequality in (3.17) is equivalent to $c_{uv}<\tilde{c}_{uv}$, where

$$\begin{aligned} \tilde{c}_{uv}:=\frac{B_{u1}'(0)-\mu _{mu1}+B_{u2}'(0)-\mu _{mu2}-2D_u}{\overline{V}_1+\overline{V}_2}. \end{aligned}$$

On the other hand, the second inequality in (3.17) is equivalent to $\mathcal {J}(c_{uv}):=(c_{uv})^2 +Pc_{uv} +Q <0$, where

$$\begin{aligned} P= & {} - \frac{(B_{u1}'(0)-\mu _{mu1}-D_u)\overline{V}_2 + (B_{u2}'(0)-\mu _{mu2}-D_u)\overline{V}_1}{\overline{V}_1\overline{V}_2}, \\ Q= & {} \frac{(B_{u1}'(0)-\mu _{mu1}-D_u)(B_{u2}'(0)-\mu _{mu2}-D_u)-D_u^2}{\overline{V}_1\overline{V}_2}. \end{aligned}$$

Note that the discriminant of the quadratic function $\mathcal {J}$ is $\frac{\Delta _u}{\overline{V}_1^2\overline{V}_2^2}$ which is positive. Hence, the second inequality in (3.17) holds for $c_{uv}^-< c_{uv} < c_{uv}^+$, where

$$\begin{aligned} c_{uv}^{\pm }:=\frac{(B_{u1}'(0)-\mu _{mu1}-D_u)\overline{V}_2 + (B_{u2}'(0)-\mu _{mu2}-D_u)\overline{V}_1 \pm \sqrt{\Delta _u}}{2\overline{V}_1\overline{V}_2}. \end{aligned}$$

A tedious calculation shows that $c_{uv}^-\le \tilde{c}_{uv}<c_{uv}^+$. In summary, the inequalities in (3.17) are equivalent to $c_{uv}<\tilde{c}_{uv}$ and $c_{uv}^-< c_{uv} < c_{uv}^+$, respectively. Thus, condition (3.17) is equivalent to their union, which is $c_{uv}<c_{uv}^+$. $\square$

Proof of Theorem 3.11

We only justify the assertion for u-species and assume that $(\mathcal {S}_u)$ holds. We will discuss the case that both $(\mathcal {S}_v)$ and $c_{uv}<c^+_{uv}$ hold, and the simpler case that $(\mathcal {S}_v)$ does not hold can be treated in a similar way. We will follow the persistence theory in Theorem 4.6 [39] for the justification. Since $c_{uv}<c^+_{uv}$, from the fact that $B_{ui}$, $i=1,2$, are continuously differentiable and Lemma 3.9, there is a sufficiently small $\varrho ^*>0$ such that

$$\begin{aligned}{} & {} B_{u1}'(\varrho ^*)+B_{u2}'(\varrho ^*) > \mu _{mu1}+k_{mu1}\varrho ^*+c_{uv}(\overline{V}_1+\varrho ^*) \nonumber \\{} & {} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad +\,\mu _{mu2}+k_{mu2}\varrho ^*+c_{uv}(\overline{V}_2+\varrho ^*)+2D_u,~\textrm{or} \nonumber \\{} & {} (B_{u1}'(\varrho ^*)-\mu _{mu1}-k_{mu1}\varrho ^*-c_{uv}(\overline{V}_1+\varrho ^*)-D_u)\cdot \nonumber \\{} & {} (B_{u2}'(\varrho ^*)-\mu _{mu2}-k_{mu2}\varrho ^*-c_{uv}(\overline{V}_2+\varrho ^*)-D_u)<D_u^2. \end{aligned}$$

(A.15)

We aim to justify the assertion with this positive $\varrho ^*$. Let us divide our proof into the following four parts:

(I) An auxiliary system: From Proposition 3.5, for this $\varrho ^*>0$, there is a $t_0>0$ such that $U_i(t)<\overline{U}_i+\varrho ^*$ and $V_i(t)<\overline{V}_i+\varrho ^*$ for $t\ge t_0$. From the U-equation, for $t\ge t_0$, we have

$$\begin{aligned} \frac{dU_1(t)}{dt}\ge & {} B_{u1}(U_1(t-\tau _u)) - \mu _{mu1}U_1(t) -k_{mu1}(U_1(t))^2 \nonumber \\{} & {} - c_{uv}(\overline{V}_1+\varrho ^*)U_1(t) + D_uU_2(t) - D_uU_1(t), \nonumber \\ \frac{dU_2(t)}{dt}\ge & {} B_{u2}(U_2(t-\tau _u)) - \mu _{mu2}U_2(t) -k_{mu2}(U_2(t))^2 \nonumber \\{} & {} - c_{uv}(\overline{V}_2+\varrho ^*)U_2(t) + D_uU_1(t) - D_uU_2(t). \nonumber \end{aligned}$$

Shift the time t by $\tilde{t}=t-t_0$ but retain the symbols. Then we need to justify the same assertion. Consider the auxiliary system

$$\begin{aligned} \frac{d\omega _1(t)}{dt}= & {} B_{u1}(\omega _1(t-\tau _u)) - \mu _{mu1}\omega _1(t) -k_{mu1}(\omega _1(t))^2 \nonumber \\{} & {} - c_{uv}(\overline{V}_1+\varrho ^*)\omega _1(t) + D_u\omega _2(t) - D_u\omega _1(t), \nonumber \\ \frac{d\omega _2(t)}{dt}= & {} B_{u2}(\omega _2(t-\tau _u)) - \mu _{mu2}\omega _2(t) -k_{mu2}(\omega _2(t))^2 \nonumber \\{} & {} - c_{uv}(\overline{V}_2+\varrho ^*)\omega _2(t) + D_u\omega _1(t) - D_u\omega _2(t). \end{aligned}$$

(A.16)

By the comparison principle, the solutions of (3.1) and (A.16) starting from the same initial condition satisfy $U_i(t)\ge \omega _i(t)$ for all $t>0$. Thus it suffices to show that system (A.16) is uniformly persistent. Define

$$\begin{aligned} X= & {} \mathcal {C}_u~(=C([-\tau _u,0],\mathbb {R}^2_+)~), \\ X_0= & {} \{ \varphi =(\varphi _1,\varphi _2) \in X~\textrm{with} ~\varphi _i\ne \hat{0}~\textrm{for}~i=1,2\}, \\ \partial X_0= & {} X\setminus X_0 =\{ \varphi \in X : \,\textrm{either}\,\,\varphi _1=\hat{0} \,\,\,\textrm{or}\,\,\,\varphi _2=\hat{0}\,\}. \end{aligned}$$

(II) Dynamics of (A.16) in subsets $X_0$ and $\partial X_0$: System (A.16) is point-dissipative, by arguments similar to those for Proposition 3.1. In addition, both X and $X_0$ are positively invariant under the semiflow of (A.16) and $X\setminus X_0$ is relatively closed in X. In fact, the solution of system (A.16) with initial value $\varphi \in X_0$ satisfies, for $i,j=1,2$, $i\ne j$,

$$\begin{aligned} \frac{d\omega _i(t)}{dt} \ge B_{ui}(\omega _i(t-\tau _u)) - [\mu _{mui}+k_{mui}\mathcal {W}_i+c_{uv}(\overline{V}_i+\varrho ^*)+D_u]\omega _i(t) + D_u\omega _j(t), \end{aligned}$$

where $\mathcal {W}_i=\sup _{t\ge 0}\omega _i(t)$, which is finite. By the comparison principle, we have, for $t\in (0,\tau _u]$,

$$\begin{aligned} \omega _i(t) \ge e^{-\tilde{a}t}\omega _i(0) + \int ^t_0e^{-\tilde{a}(t-\xi )} [B_{ui}(\varphi _i(\xi -\tau _u))+D_u\omega _j(\xi )]d\xi , \end{aligned}$$

(A.17)

where $\tilde{a}:=\mu _{mui}+k_{mui}\mathcal {W}_i+c_{uv}(\overline{V}_i+\varrho ^*)+D_u$. Suppose there is a $t_1\in (0,\tau _u]$ and some $i_0\in \{1,2\}$ such that $(\omega _{i_0})_{t_1}(\cdot )=\hat{0}$. Then $\varphi _{i_0}(\theta )=0$ for $\theta \in [t_1-\tau _u,0]$, and $\omega _{i_0}(t)=0$ for $t\in [0,t_1]$. The latter one together with (A.17) imply that $\varphi _{i_0}(\theta )=0$ for $\theta \in [-\tau _u,t_1-\tau _u]$, and then $\varphi _{i_0}(\cdot )=\hat{0}$. It contradicts to the assumption $\varphi \in X_0$. Hence $\omega _t(\cdot )$ stays in $X_0$ for $t\in (0,\tau _u]$. By proceeding the same arguments for $t\in [k\tau _u,(k+1)\tau _u]$, $k=1,2,3,\ldots$, we see that $X_0$ is positively invariant under (A.16).

(III) The maximal positively invariant subset of (A.16) in the boundary $\partial X_0$: We set

$$\begin{aligned} M_{\partial }=\{ \varphi \in X~|~\check{\Phi }_t(\varphi )\in \partial X_0,~\forall ~t\ge 0 \}, \end{aligned}$$

where $\check{\Phi }_t$ is the semiflow generated by (A.16). Then obviously $M_{\partial } \subset \partial X_0$. We claim that $M_{\partial }=\{ \hat{\textbf{0}} \}$, where $\textbf{0} =(0,0)$. It is clear that $\{\hat{\textbf{0}}\} \subset M_{\partial }$, so it suffices to show $M_{\partial } \subset \{\hat{\textbf{0}} \}$. Assume the opposite, that there is $\varphi =(\varphi _1, \varphi _2) \in M_{\partial }$ and $\varphi \ne \hat{\textbf{0}}$. Without loss of generality, we suppose $\varphi _1\ne \hat{0}$, $\varphi _2=\hat{0}$. Let us discuss three possibilities: (i) If $\varphi _1(0)>0$, we have $\frac{d\omega _2(0)}{dt}>0$, and then there is a small $t_0>0$ such that $\omega _2(t)>0$ for $t\in (0,t_0)$. Since $\varphi _1(0)>0$, the continuity of the solution implies the existence of a $t_1\le t_0$ such that $\omega _1(t)>0$ for $t\in (0,t_1)$. Thus, $\check{\Phi }_t(\varphi )\in X_0$ for $t\in (0,t_1)$, a contradiction to the fact that $\varphi \in M_{\partial }$. (ii) If $\varphi _1(0)=0$ and $\varphi _1(-\tau _u)>0$, we see that

$$\begin{aligned} \frac{d\omega _1(0)}{dt}=B_{u1}(\omega _1(-\tau _u))=B_{u1}(\varphi _1(-\tau _u))>0. \end{aligned}$$

By continuity of the solution to (A.16) and $\varphi \in X$, there is a $t_2>0$ such that

$$\begin{aligned} \frac{d\omega _1(t)}{dt}>B_{u1}(\varphi _1(-\tau _u))/2=:K_1>0, \end{aligned}$$

for $t\in [0,t_2]$. Then $\omega _1(t)\ge K_1t$, for $t\in [0,t_2]$. In addition,

$$\begin{aligned} \frac{d\omega _2(t)}{dt}\ge & {} -\mu _{mu2}\omega _2(t) -k_{mu2}(\omega _2(t))^2 -c_{uv}(\overline{V}_2+\varrho ^*)\omega _2(t) +D_uK_1t-D_u\omega _2(t) \\= & {} -(\mu _{mu2}+k_{mu2}\omega _2(t)+c_{uv}(\overline{V}_2+\varrho ^*)+D_u)\omega _2(t) +D_uK_1t \\\ge & {} -K_2\omega _2(t)+D_uK_1t, \end{aligned}$$

where

$$\begin{aligned} K_2:= \mu _{mu2}+k_{mu2}\mathcal {W}_2+c_{uv}(\overline{V}_2+\varrho ^*)+D_u < \infty . \end{aligned}$$

By the comparison principle,

$$\begin{aligned} \omega _2(t)\ge e^{-K_2t}\omega _2(0)+\int _0^te^{-K_2t}D_uK_1sds>0, \end{aligned}$$

for $t\in (0,t_2]$, also a contradiction to $\varphi \in M_{\partial }$. (iii) If $\varphi _1(0)=0$ and $\varphi _1(-\tau _u)=0$, we set $\tau _u^*=\sup \{ -\theta | \theta \in [-\tau _u,0],~ \varphi _1(\theta )\ne 0 \} \le \tau _u$. Then $\frac{d\omega _1(t)}{dt}=0$ and $\omega _1(t)=0$ for $t\in [0,\tau _u-\tau _u^*]$, allowing $\tau _u-\tau _u^*=0$. From the assumption $\varphi _2=\hat{0}$, it also holds that $\omega _2(t)=0$ for $t\in [0,\tau _u-\tau _u^*]$. Since $\varphi \in C$, there is a small $\epsilon _1>0$ such that $\varphi _1(-\tau _u^*+\epsilon _1)>0$. Define

$$\begin{aligned} \psi (\theta )=\left\{ \begin{array}{ll} \varphi (\theta +\tau _u-\tau _u^*+\epsilon _1), &{} \textrm{if}~\theta \in [-\tau _u,\tau _u^*-\epsilon _1-\tau _u), \\ \omega (\theta +\tau _u-\tau _u^*+\epsilon _1), &{} \textrm{if}~\theta \in [\tau _u^*-\epsilon _1-\tau _u,0], \end{array} \right. \end{aligned}$$

where $\omega =(\omega _1,\omega _2)$. Then $\psi _2(\theta )\ge \hat{0}$ for $\theta \in [-\tau _u,0]$ and

$$\begin{aligned}{} & {} \psi _1(0) = \omega _1(\tau _u-\tau _u^*+\epsilon _1)\ge 0, \\{} & {} \psi _1(-\tau _u) = \varphi _1(-\tau _u^*+\epsilon _1)>0. \end{aligned}$$

By the comparison principle (for $\psi _2\ge \tilde{\psi }_2:=\hat{0}$) and previous result in (ii) (for $\varphi _1=\psi _1$ and $\varphi _2=\tilde{\psi }_2$), it yields that $\psi \notin M_{\partial }$. Note that $\check{\Phi }_t(\psi )=\check{\Phi }_{t+\tau _u-\tau _u^*+\epsilon _1}(\varphi )$. By the positive invariance of the set $M_{\partial }$, it leads to $\varphi \notin M_{\partial }$, a contradiction again. From the contradictions in all three cases (i)-(iii), we conclude that $M_{\partial } \subset \{ \hat{\textbf{0}} \}$, and hence $M_{\partial } = \{ \hat{\textbf{0}} \}$. The claim is thus justified.

(IV) The trivial equilibrium is a weak repeller in system (A.16): We claim that

$$\begin{aligned} \limsup _{t\rightarrow \infty }\max _{i} \{\omega _i(t)\}>\varrho ^*,~\mathrm{for~all}~\varphi \in X_0, \end{aligned}$$

(A.18)

where $\varrho ^*$ is defined in (A.15). Suppose, on the contrary, there exist an initial value $\varphi \in X_0$ and an $t_3>0$ such that $|\omega _i(t)|\le \varrho ^*$, $i=1,2$, for $t\ge t_3-\tau _u$. From (A.16), for $t\ge t_3$,

$$\begin{aligned} \frac{d\omega _1(t)}{dt}&\ge B'_{u1}(\varrho ^*)\omega _1(t-\tau _u)-(\mu _{mu1}+k_{mu1}\varrho ^*+c_{uv}(\overline{V}_1+\varrho ^*)+D_u)\omega _1(t)+D_u\omega _2(t), \\ \frac{d\omega _2(t)}{dt}&\ge B'_{u2}(\varrho ^*)\omega _2(t-\tau _u)-(\mu _{mu2}+k_{mu2}\varrho ^*+c_{uv}(\overline{V}_2+\varrho ^*)+D_u)\omega _2(t)+D_u\omega _1(t). \end{aligned}$$

We consider an auxiliary equation

$$\begin{aligned} \frac{dx_1(t)}{dt}&= B'_{u1}(\varrho ^*)x_1(t-\tau _u)-(\mu _{mu1}+k_{mu1}\varrho ^* +c_{uv}(\overline{V}_1+\varrho ^*)+D_u)x_1(t)+D_ux_2(t), \nonumber \\ \frac{dx_2(t)}{dt}&= B'_{u2}(\varrho ^*)x_2(t-\tau _u)-(\mu _{mu2}+k_{mu2}\varrho ^* +c_{uv}(\overline{V}_2+\varrho ^*)+D_u)x_2(t)+D_ux_1(t).\nonumber \\ \end{aligned}$$

(A.19)

From the comparison theory in Theorem 5.5.1 [32], we have

$$\begin{aligned} \tilde{\Phi }_t(\varphi )\le \check{\Phi }_t(\varphi ),~\textrm{for}~t\ge 0, \end{aligned}$$

where $\tilde{\Phi }_{t}$ is the semiflow of (A.19). Consider the ordinary differential equation associated with (A.19),

$$\begin{aligned} \frac{dy_1(t)}{dt}&= B'_{u1}(\varrho ^*)y_1(t)-(\mu _{mu1}+k_{mu1} \varrho ^*+c_{uv}(\overline{V}_1+\varrho ^*)+D_u)y_1(t)+D_uy_2(t), \nonumber \\ \frac{dy_2(t)}{dt}&= B'_{u2}(\varrho ^*)y_2(t)-(\mu _{mu2}+k_{mu2} \varrho ^*+c_{uv}(\overline{V}_2+\varrho ^*)+D_u)y_2(t)+D_uy_1(t). \nonumber \\ \end{aligned}$$

(A.20)

The characteristic equation at the trivial equilibrium is

$$\begin{aligned} \lambda ^2 -(r_1+r_2) \lambda +r_1r_2-D_u^2=0, \end{aligned}$$

(A.21)

where, for $i=1,2$,

$$\begin{aligned} r_i = B'_{ui}(\varrho ^*)-[\mu _{mui}+k_{mui}\varrho ^* +c_{uv}(\overline{V}_i+\varrho ^*)+D_u]. \end{aligned}$$

Equation (A.21) has a solution with positive real part whenever $r_1+r_2>0$ or $r_1r_2-D_u^2<0$, which are valid because of (A.15). Therefore, the stability modulus of (A.20) is positive. Also note that (A.19) is a cooperative irreducible system. From Theorem 5.5.1 and Corollary 5.5.2 [32], system (A.19) also admits a positive stability modulus associated with a positive eigenvector $\textbf{z}$. Note that the semiflow of (A.16) is eventually strong monotone in $[\hat{\textbf{0}},\hat{\textbf{r}}^*]$, where $\textbf{r}^*=(\rho ^*,\rho ^*)$, see Corollary 5.3.5 [32], and $\hat{\textbf{0}}$ is an equilibrium therein. There exist a $t_4>t_3$ and a small $\alpha >0$ such that

$$\begin{aligned} \hat{\textbf{0}}\ll \alpha \hat{\textbf{z}}\ll \check{\Phi }_{t_4}(\varphi ). \end{aligned}$$

Hence, we have

$$\begin{aligned} \tilde{\Phi }_t(\alpha \hat{\textbf{z}}) \le \check{\Phi }_t(\alpha \hat{\textbf{z}}) \ll \check{\Phi }_{t+t_4}(\varphi ), \end{aligned}$$

for $t\ge 0$, which is a contradiction to boundedness of the semiflow $\check{\Phi }_t$, and this contradiction proves (A.18).

Obviously, $\{\hat{\textbf{0}}\}$ is an isolated invariant set in $\partial X_0$, and the set $M_{\partial }$ consists of an acyclic equilibrium point. From (A.18), $W^s(\hat{\textbf{0}})\cap X_0 = \emptyset$, where $W^s(\hat{\textbf{0}})$ denotes the stable manifold of $\hat{\textbf{0}}$. By the persistence theory in Theorem 4.6 [39], system (A.16) is uniformly persistent with respect to $(X_0,\partial X_0)$ and the assertion is proved.

As for the case when $(\mathcal {S}_v)$ does not hold, we see from $(\mathcal {S}_u)$ that there exists a $\varrho ^{**}>0$ such that

$$\begin{aligned}{} & {} B_{u1}'(\varrho ^{**})>\mu _{mu1}+D_u,~\textrm{or}~~B_{u2}'(\varrho ^{**})>\mu _{mu2}+D_u,~\textrm{or} \nonumber \\{} & {} 0 \le \left( \mu _{mu1}+D_u-B_{u1}'(\varrho ^{**}) \right) \left( \mu _{mu2}+D_u-B_{u1}'(\varrho ^{**}) \right) <D_u^2. \end{aligned}$$

(A.22)

In addition, from Proposition 3.5, there exists a $t_5>0$ such that $V_i(t)<\varrho ^{**}$ for $t\ge t_5$ and $i=1,2$. Therefore, the U-equation in (3.1) is bounded below by the auxiliary system

$$\begin{aligned} \frac{d\tilde{\omega }_1(t)}{dt}= & {} B_{u1}(\tilde{\omega }_1(t-\tau _u)) - \mu _{mu1}\tilde{\omega }_1(t) -k_{mu1}(\tilde{\omega }_1(t))^2 \\{} & {} - c_{uv}\varrho ^{**}\tilde{\omega }_1(t) + D_u\tilde{\omega }_2(t) - D_u\tilde{\omega }_1(t), \\ \frac{d\tilde{\omega }_2(t)}{dt}= & {} B_{u2}(\tilde{\omega }_2(t-\tau _u)) - \mu _{mu2}\tilde{\omega }_2(t) -k_{mu2}(\tilde{\omega }_2(t))^2 \\{} & {} - c_{uv}\varrho ^{**}\tilde{\omega }_2(t) + D_u\tilde{\omega }_1(t) - D_u\tilde{\omega }_2(t), \end{aligned}$$

or $t\ge t_5$. In this case, the uniform persistence of u-species can be established by the same arguments with condition (A.22). This completes the proof. $\square$

Proof of Proposition 3.13

We show the case of $c^+_{uv}$. Note that the value of $\overline{V}_i$ depends on $\tau _v$ but not on $\tau _u$. A direct calculation gives

$$\begin{aligned} \frac{\partial c^+_{uv}}{\partial \tau _u}= & {} \frac{1}{2\overline{V}_1\overline{V}_2} \left\{ -\mu _{lu1}b'_1(0)e^{-\mu _{lu1}\tau _u}\overline{V}_2 -\mu _{lu2}b'_2(0)e^{-\mu _{lu2}\tau _u}\overline{V}_1\right. \\{} & {} \left. +\frac{d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1}{\sqrt{\Delta _u}} (-\mu _{lu1}b'_1(0)e^{-\mu _{lu1}\tau _u}\overline{V}_2 +\mu _{lu2}b'_2(0)e^{-\mu _{lu2}\tau _u}\overline{V}_1) \right\} \\< & {} 0. \end{aligned}$$

The last inequality holds true because of the fact $|(d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1)/\sqrt{\Delta _u}|\le 1$.

Now, we only vary the value of $\tau _v$ in

$$\begin{aligned} c_{uv}^+ = \frac{d_{u1}\overline{V}_2 + d_{u2}\overline{V}_1+\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 }}{2\overline{V}_1\overline{V}_2 }. \end{aligned}$$

Note that in the right hand side, only $\overline{V}_i=\overline{V}_i(\tau _v)$, $i=1,2$, depends on $\tau _v$, and from Remark 2.2, $(\overline{V}_i)':=\frac{\partial \overline{V}_i}{\partial \tau _v}<0$ for $i=1,2$. Thus, we obtain

$$\begin{aligned} \frac{\partial c^+_{uv}}{\partial \tau _v}= & {} \frac{1}{(2\overline{V}_1\overline{V}_2)^2} \Bigg \{ \Bigg [ d_{u1}(\overline{V}_2)'+d_{u2}(\overline{V}_1) \nonumber \\{} & {} +\frac{(d1\overline{V}_1-d_{u2}\overline{V}_1)(d1(\overline{V}_2)'-d_{u2}(\overline{V}_1)') + 2D_u^2((\overline{V}_1)'\overline{V}_2+\overline{V}_1(\overline{V}_2)')}{\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 }}\Bigg ] \cdot 2\overline{V}_1\overline{V}_2 \nonumber \\{} & {} \left. - 2\left[ d_{u1}\overline{V}_2 + d_{u2}\overline{V}_1+\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 }\right] ( (\overline{V}_1)'\overline{V}_2+\overline{V}_1(\overline{V}_2)' ) \right\} \nonumber \\= & {} \frac{1}{(2\overline{V}_1\overline{V}_2)^2\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 }} \cdot \nonumber \\{} & {} \Bigg \{ (\overline{V}_1)' 2\overline{V}_2 \Bigg [ d_{u2}\overline{V}_1\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } - d_{u2}\overline{V}_1(d_{u1}\overline{V}_2-d_{u2}\overline{V}_1) \nonumber \\{} & {} - (d_{u1}\overline{V}_2+d_{u2}\overline{V}_1)\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } \nonumber \\{} & {} - (d_{u1}\overline{V}_2-d_{u2}\overline{V}_1)^2 - 2D_u^2\overline{V}_1\overline{V}_2 \Bigg ] \nonumber \\{} & {} + (\overline{V}_2)' 2\overline{V}_1 \Bigg [ d_{u1}\overline{V}_2\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } + d_{u1}\overline{V}_2(d_{u1}\overline{V}_2-d_{u2}\overline{V}_1) \nonumber \\{} & {} - (d_{u1}\overline{V}_2+d_{u2}\overline{V}_1)\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } \nonumber \\{} & {} - (d_{u1}\overline{V}_2-d_{u2}\overline{V}_1)^2 - 2D_u^2\overline{V}_1\overline{V}_2 \Bigg ] \Bigg \} \nonumber \\= & {} \frac{ (\overline{V}_1)' (\overline{V}_2)^2 \Lambda _1(\tau _v) + (\overline{V}_2)' (\overline{V}_1)^2 \Lambda _2(\tau _v)}{2(\overline{V}_1\overline{V}_2)^2\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 }}, \end{aligned}$$

(A.23)

where

$$\begin{aligned} \Lambda _1(\tau _v)= & {} d_{u1}\left( d_{u2}\overline{V}_1-d_{u1}\overline{V}_2 - \sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } \right) -2 D_u^2\overline{V}_1, \\ \Lambda _2(\tau _v)= & {} d_{u2}\left( d_{u1}\overline{V}_2 -d_{u2}\overline{V}_1 - \sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } \right) -2 D_u^2\overline{V}_2. \end{aligned}$$

Suppose that $D_u^2\le d_{u1}d_{u2}$. There are two cases to discuss. If $d_{u1}>0$ and $d_{u2}>0$, from (A.23) we obtain $\frac{\partial c^+_{uv}}{\partial \tau _v} >0$. If $d_{u1}<0$ and $d_{u2}<0$, from Lemma 3.12, we have $\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } \le |d_{u1}\overline{V}_2+d_{u2}\overline{V}_1|=-d_{u1}\overline{V}_2-d_{u2}\overline{V}_1$, and then $c_{uv}^+\le 0$.

Suppose that $D_u^2> d_{u1}d_{u2}$. From Lemma 3.12, it holds that $\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } >|d_{u1}\overline{V}_2+d_{u2}\overline{V}_1|$. Hence $\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } +d_{u1}\overline{V}_2 +d_{u2}\overline{V}_1>0$ which means that $c_{uv}^+$ is always positive. In addition, from Lemma 3.12 we have

$$\begin{aligned} \left| d_{u1}\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 }\right|< & {} \left| d_{u1}(d_{u2}\overline{V}_1-d_{u1}\overline{V}_2)-2D_u^2\overline{V}_1\right| , \qquad \qquad \end{aligned}$$

(A.24)

$$\begin{aligned} \left| d_{u2}\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 }\right|< & {} \left| d_{u1}(d_{u1}\overline{V}_2-d_{u2}\overline{V}_1)-2D_u^2\overline{V}_2\right| . \qquad \qquad \end{aligned}$$

(A.25)

If $d_{u1}>0$ and $d_{u2}>0$, from (A.23) we obtain $\frac{\partial c^+_{uv}}{\partial \tau _v} >0$. If $d_{u1}\le 0$ and $d_{u2}>0$, (A.24) implies that

$$\begin{aligned} 0\ge d_{u1}\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } > d_{u1}(d_{u2}\overline{V}_1-d_{u1}\overline{V}_2)-2D_u^2\overline{V}_1, \end{aligned}$$

which means that

$$\begin{aligned} \Lambda _1(\tau _v)<0. \end{aligned}$$

In addition, we observe that

$$\begin{aligned} d_{u2}\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 }>0>d_{u2}(d_{u1}\overline{V}_2-d_{u2}\overline{V}_1)-2D_u^2\overline{V}_2, \end{aligned}$$

which means that

$$\begin{aligned} \Lambda _2(\tau _v)<0. \end{aligned}$$

Together with the fact $(\overline{V}_i)'<0$ for $i=1,2$, we see that $\frac{\partial c^+_{uv}}{\partial \tau _v} >0$. If $d_{u1}> 0$ and $d_{u2}\le 0$, a similar argument under (A.25) also leads to $\frac{\partial c^+_{uv}}{\partial \tau _v} >0$. If $d_{u1}\le 0$ and $d_{u2}\le 0$, from (A.24) we obtain

$$\begin{aligned} 0\ge d_{u1}\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } > d_{u1}(d_{u2}\overline{V}_1-d_{u1}\overline{V}_2)-2D_u^2\overline{V}_1, \end{aligned}$$

which implies $\Lambda _1(\tau _v)<0$. From (A.25) we obtain

$$\begin{aligned} 0\ge d_{u2}\sqrt{ ( d_{u1}\overline{V}_2 - d_{u2}\overline{V}_1 )^2 +4\overline{V}_1\overline{V}_2D_u^2 } > d_{u1}(d_{u1}\overline{V}_2-d_{u2}\overline{V}_1)-2D_u^2\overline{V}_2, \end{aligned}$$

which implies $\Lambda _2(\tau _v)<0$. Again, we see that $\frac{\partial c^+_{uv}}{\partial \tau _v} >0$. This completes the proof. $\square$

Proof of Theorem 3.15

We first state conditions (H1)–(H4) in Theorem B [16], with the notations for system (3.1), as follows:

• (H1) The semiflow $\Phi _t$ is strictly order-preserving with respect to the order induced from the cone $\mathcal {C}_K$, that is $\Phi _t(\phi ) <_K \Phi _t(\psi )$ whenever $\phi <_K \psi$. In addition, for each $t>0$, $\Phi _t:\mathbb {X}\rightarrow \mathbb {X}$ is order compact, i.e., for each $(\tilde{\phi }_1,\tilde{\phi }_2)\in \mathbb {X}$, $\Phi _t([\hat{\textbf{0}},\tilde{\phi }_1]\times [\hat{\textbf{0}},\tilde{\phi }_2])$ has compact closure in $\mathbb {X}$.

• (H2) The trivial solution $E_0$ is a repelling equilibrium.

• (H3) $\Phi _t(\mathcal {C}_u\times \{\hat{\textbf{0}}\}) \subset \mathcal {C}_u\times \{\hat{\textbf{0}}\}$ for $t\ge 0$. $E_u$ attracts all solutions in $\mathcal {C}_u\times \{\hat{\textbf{0}}\}$ except the trivial solution. The symmetric conditions hold for $\Phi _t$ on $\{\hat{\textbf{0}}\} \times \mathcal {C}_v$.

• (H4) If $\phi =(\tilde{\phi }_1,\tilde{\phi }_2)\in \mathbb {X}$ and $\tilde{\phi }_i\ne \hat{\textbf{0}}$, $i=1,2$, then $\Phi _t(\phi )\gg \hat{\textbf{0}}$ for $t>\tau _m$. If $\phi ,\psi \in \mathbb {X}$ satisfy $\phi <_K \psi$, and either $\phi$ or $\psi$ belongs to $\textrm{int}(\mathbb {X})$, then $\Phi _t(\phi )\ll _K \Phi _t(\psi )$ for $t\ge 2\tau _m$.

Next, we show that all conditions hold under $(\mathcal {S}_u)$ and $(\mathcal {S}_v)$. For (H1), suppose $\phi <_K \psi$. From Proposition 3.3, it satisfies $\Phi _t(\phi ) \le _K \Phi _t(\psi )$. Hence, it suffices to show that $\Phi _t(\phi ) \ne \Phi _t(\psi )$ for $t>0$. Denote $\Phi _t(\phi )=(U^{\phi }_1(t),U^{\phi }_2(t),V^{\phi }_1(t),V^{\phi }_2(t))$ and $\Phi _t(\psi )=(U^{\psi }_1(t),U^{\psi }_2(t),V^{\psi }_1(t),V^{\psi }_2(t))$ for $t\ge 0$. If $\phi _{i_0}\ne \psi _{i_0}$ for $i_0=1$ or 2 (denote $j_0=2$ or 1, respectively), we claim that $\Phi _t(\phi ) \ne \Phi _t(\psi )$ for $t\in [0,\tau _u]$. Otherwise, there is a $t_1\in [0,\tau _u]$ such that $\Phi _{t_1}(\phi ) = \Phi _{t_1}(\psi )$, which means that

$$\begin{aligned} \phi (\theta )=\psi (\theta )~\textrm{for}~t_1-\tau _u\le \theta \le 0, \end{aligned}$$

(A.26)

and $U^{\phi }(t)=U^{\psi }(t)$ for $0\le t\le t_1$. In addition, from (3.1) we have

$$\begin{aligned} U^{\phi }_{i_0}(t_1)= & {} \int ^{t_1}_0[B_{ui_0}(U^{\phi }_{i_0}(\xi -\tau _u)) -\mu _{mui_0}U^{\phi }_{i_0}(\xi ) -k_{mui_0}(U^{\phi }_{i_0}(\xi ))^2 \\{} & {} ~~~~~~~~~~ -c_{uv} U^{\phi }_{i_0}(\xi )V^{\phi }_{i_0}(\xi ) +D_uU^{\phi }_{j_0}(\xi ) -D_uU^{\phi }_{i_0}(\xi )] d\xi , \\ U^{\psi }_{i_0}(t_1)= & {} \int ^{t_1}_0[B_{ui_0}(U^{\psi }_{i_0}(\xi -\tau _u)) -\mu _{mui_0}U^{\psi }_{i_0}(\xi ) -k_{mui_0}(U^{\psi }_{i_0}(\xi ))^2 \\{} & {} ~~~~~~~~~~ -c_{uv} U^{\psi }_{i_0}(\xi )V^{\psi }_{i_0}(\xi ) +D_uU^{\psi }_{j_0}(\xi ) -D_uU^{\psi }_{i_0}(\xi )] d\xi . \end{aligned}$$

Since $U^{\phi }_{i_0}(\xi -\tau _u)\le U^{\psi }_{i_0}(\xi -\tau _u)$, $U^{\phi }_{i_0}(\xi )= U^{\psi }_{i_0}(\xi )$, $U^{\phi }_{j_0}(\xi )\le U^{\psi }_{j_0}(\xi )$, and $V^{\phi }_{i_0}(\xi )\ge V^{\psi }_{i_0}(\xi )$ for $\xi \in [0,t_1]$, it enforces $U^{\phi }_{i_0}(\xi -\tau _u)= U^{\psi }_{i_0}(\xi -\tau _u)$ for $\xi \in [0,t_1]$, i.e.,

$$\begin{aligned} U^{\phi }_{i_0}(\theta )= U^{\psi }_{i_0}(\theta )~\textrm{for}~\theta \in [-\tau _u,t_1-\tau _u]. \end{aligned}$$

(A.27)

From (A.26) and (A.27), it leads to $\phi _{i_0}=\psi _{i_0}$, which is a contradiction. Hence, $\Phi _t(\phi ) \ne \Phi _t(\psi )$ for $t\in [0,\tau _u]$. Proceeding the arguments successively for $t\in [k\tau _u,(k+1)\tau _u]$, $k=1,2,\cdots$, we derive $\Phi _t(\phi ) \ne \Phi _t(\psi )$ for $t\ge 0$. When $\phi _{i_0}\ne \psi _{i_0}$ for $i_0=3$ or 4, the same result can be shown by the same argument. Therefore, $\Phi _t(\phi ) <_K \Phi _t(\psi )$ for $t\ge 0$. In addition, the second assertion is true because of eventually uniform boundedness shown in Theorem 3.1.

For (H2), when $(\mathcal {S}_u)$ holds, there exists a sufficiently small $\eta ^*>0$ such that

$$\begin{aligned} \left\{ \begin{array}{l} (\mathcal {S}_u^1)~~\mu _{mu1}+k_{mu1}\eta ^*+c_{uv}\eta ^*+D_u< e^{-\mu _{lu1}\tau _u}b'_{u1}(\eta ^*),~\textrm{or} \\ (\mathcal {S}_u^2)~~\mu _{mu2}+k_{mu2}\eta ^*+c_{uv}\eta ^*+D_u< e^{-\mu _{lu2}\tau _u}b'_{u2}(\eta ^*),~\textrm{or} \\ (\mathcal {S}_u^3)~~0 \le \left( \mu _{mu1}+k_{mu1}\eta ^*+c_{uv}\eta ^*+D_u-e^{-\mu _{lu1}\tau _u}b'_{u1}(\eta ^*) \right) \times \\ ~~~~~~~~~~~~~~~~~ \left( \mu _{mu2}+k_{mu2}\eta ^*+c_{uv}\eta ^*+D_u-e^{-\mu _{lu2}\tau _u}b'_{u2}(\eta ^*) \right) <D_u^2, \end{array} \right. \end{aligned}$$

due to the assumption on functions $b_{ui}$ and $b_{vi}$, $i=1,2$. We claim that $E_0$ repels the set $N_{\eta ^*}:=\{\phi \in \mathbb {X} | \hat{0}\le \phi _i\le \hat{\eta }^*,~i=1,2,3,4\}\setminus \{E_0\}$, i.e., for each $\phi \in N_{\eta ^*}$, there exists a $t_2>0$ such that $\Phi _{t_2}(\phi )\notin N_{\eta ^*}$. Suppose, for the sake of contradiction, $\Phi _t(\phi )\in N_{\eta ^*}$ for $t>0$. Then $0\le U_1(t),U_2(t),V_1(t),V_2(t)\le \eta ^*$ for $t>0$. However, from the U-equation of (3.1), we see that

$$\begin{aligned} \frac{dU_1(t)}{dt}\ge & {} B_{u1}'(\eta ^*)U_1(t-\tau _u) - \mu _{mu1}U_1(t) -k_{mu1}\eta ^*U_1(t) - c_{uv}\eta ^*U_1(t) \\ {}{} & {} + D_uU_2(t) - D_uU_1(t), \\ \frac{dU_2(t)}{dt}\ge & {} B_{u2}'(\eta ^*)U_1(t-\tau _u) - \mu _{mu2}U_2(t) -k_{mu2}\eta ^*U_2(t) - c_{uv}\eta ^*U_2(t) \\ {}{} & {} + D_uU_1(t) - D_uU_2(t). \end{aligned}$$

When $(\mathcal {S}_u^1)$ holds, we consider

$$\begin{aligned} \frac{dU_1(t)}{dt} \ge B_{u1}'(\eta ^*)U_1(t-\tau _u) - \mu _{mu1}U_1(t) -k_{mu1}\eta ^*U_1(t) - c_{uv}\eta ^*U_1(t) - D_uU_1(t). \end{aligned}$$

By Theorem 2.3 [40] and a comparison principle, it holds that $\lim _{t\rightarrow \infty } U_1(t)=\infty$, which is a contradiction. A similar contradiction also occurs when $(\mathcal {S}_u^2)$ holds. When $(\mathcal {S}_u^3)$ holds, we consider the auxiliary equation

$$\begin{aligned} \frac{dx_1(t)}{dt}&= B'_{u1}(\eta ^*)x_1(t-\tau _u)-(\mu _{mu1}+k_{mu1}\eta ^*+c_{uv}\eta ^*+D_u)x_1(t)+D_ux_2(t), \nonumber \\ \frac{dx_2(t)}{dt}&= B'_{u2}(\eta ^*)x_2(t-\tau _u)-(\mu _{mu2}+k_{mu2}\eta ^*+c_{uv}\eta ^*+D_u)x_2(t)+D_ux_1(t). \nonumber \\ \end{aligned}$$

(A.28)

Denote $\hat{\Upsilon }_t(\phi )=(U_1(t),U_2(t))$. From the comparison theory in Theorem 5.5.1 [32], we have

$$\begin{aligned} \Upsilon _t(\phi )\le \hat{\Upsilon }_t(\phi ),~\textrm{for}~t\ge 0,~\phi \in \mathcal {C}_u, \end{aligned}$$

where $\Upsilon _t$ is the semiflow of (A.28). Discussing (A.28) under condition $(\mathcal {S}_u^3)$ as in the proof (IV) of Theorem 3.11, a contradiction arises, as there exists a solution of system (3.1) with unbounded $(U_1(t),U_2(t))$. Therefore, $E_0$ repels the set $N_{\eta ^*}$. Note that with only condition $(\mathcal {S}_v)$, it also enforces $E_0$ to be repelling, once we manipulate a similar argument.

For (H3), obviously, the set $\mathcal {C}_u\times \{\hat{\textbf{0}}\}$ is positively invariant under $\Phi _t$ and Theorem 2.4 implies the global attractivity of $E_u$ in $\mathcal {C}_u\times \{\hat{\textbf{0}}\}\setminus \{\hat{\textbf{0}}\times \hat{\textbf{0}}\}$. Similarly, the symmetric case holds true.

For (H4), the first assertion is confirmed by Proposition 3.2(ii). We discuss the second one in two cases. If $\phi <_K \psi$ and $\phi \in \textrm{int}(\mathbb {X})$, Proposition 3.4 implies $\Phi _t(\phi )\ll _K \Phi _t(\psi )$ for $t>2\tau _m$. If $\phi <_K \psi$, $\phi \in \partial \mathbb {X}$ and $\psi \in \textrm{int}(\mathbb {X})$, we denote the non-empty subset $\mathcal {I}\subset \{1,2,3,4\}$ with $\phi _i\ne \psi _i$ for $i\in \mathcal {I}$. Define $\phi ^p$ by $\phi ^p_i=\psi _i$ for $i\notin \mathcal {I}$, and $\phi ^p_i=\frac{1}{2}(\phi _i+\psi _i)$ for $i\in \mathcal {I}$. Then $\hat{\textbf{0}}\ll \phi ^p$, where $\textbf{0}=(0,0,0,0)$, and $\phi<_K\phi ^p <_K\psi$ since $\mathcal {I}$ is non-empty. From Proposition 3.3 and Proposition 3.4, it reveals that

$$\begin{aligned} \Phi _t(\phi ) \le _K \Phi _t(\phi ^p) \ll _K\Phi _t(\psi ), \end{aligned}$$

for $t\ge 2\tau _m$. This completes the proof. $\square$

1.2 A.II Limit Semiflows of (Non-autonomous) Continuous Semiflows

We first define limit autonomous semiflows, and refer to [38] for more details. Let $\Phi _{t+t_0}(t_0,\psi )$ be a continuous semiflow on a metric space $\textbf{X}$, with initial time $t_0$ and initial value $\psi$.

Definition A.1

A (non-autonomous) continuous semiflow $\Phi$ is called asymptotically autonomous, with a limit-semiflow $\Theta$, if $\Phi _{t_j+s_j}(s_j,\psi ^{(j)})\rightarrow \Theta _t(\psi ),~\textrm{as}~j\rightarrow \infty$, for any sequences $t_j\rightarrow t$, $s_j\rightarrow \infty$, $\psi ^{(j)}\rightarrow \psi$ for $j\rightarrow \infty$, with $\psi ^{(j)}$, $\psi \in \textbf{X}$, $0\le t_j,~t<\infty$, and $s_j\ge 0$.

If $\Phi$ is an asymptotically autonomous continuous semiflow and $\Theta$ is its continuous limit-semiflow, the global convergence dynamics of $\Phi$ to an equilibrium can be obtained by checking its asymptotical stability and basin of attraction under the limit semiflow.

Theorem A.1

(Theorem 4.1 [38]) Let e be a locally asymptotically stable equilibrium of $\Theta _t$ and $\mathcal {B}(e)=\{x\in \textbf{X}~:~\Theta _t(x)\rightarrow e,~\textrm{as}~t\rightarrow \infty \}$ its basin of attraction. Then every pre-compact $\Phi$-orbit whose $\omega$-$\Phi$-limit set intersects $\mathcal {B}(e)$ converges to e.

1.3 A.III A Limit Semiflow of (3.1) When $(\mathcal {S}_v)$ Does Not Hold

We discuss the limit semiflow of system (3.1) based on the method in [29], where a scalar case was considered.

Theorem A.2

When $(\mathcal {S}_v)$ does not hold, the solution flow of system (3.22) is a limit semiflow of system (3.1).

Proof

Let $\textbf{W}=(W_1(t),W_2(t),W_3(t),W_4(t))$ and $\textbf{Z}=(Z_1(t),Z_2(t),Z_3(t),Z_4(t))$ be a solution for system (3.1) and system (3.22) respectively, where $W_1=U_1$, $W_2=U_2$, $W_3=V_1$ and $W_4=V_2$, and similarly for $Z_j$, $j=1,\ldots ,4$. With $\textbf{W}_t(\theta ):=\textbf{W}(t+\theta )$ and $\textbf{Z}_t(\theta ):=\textbf{Z}(t+\theta )$, $\textbf{W}(t)$ and $\textbf{Z}(t)$ satisfy

$$\begin{aligned} \textbf{W}'=\mathcal {F}(\textbf{W}_t) + \mathcal {G}(t)~\textrm{and}~\textbf{Z}'=\mathcal {F}(\textbf{Z}_t), \end{aligned}$$

respectively, where $\mathcal {F}=(\mathcal {F}_1,\mathcal {F}_2,\mathcal {F}_3,\mathcal {F}_4)$ with

$$\begin{aligned} \mathcal {F}_1(\textbf{W}_t)= & {} B_{u1}(W_1(t-\tau _u)) -\mu _{mu1}W_1(t) - k_{mu1}(W_1(t))^2 +D_uW_2(t)-D_uW_1(t), \\ \mathcal {F}_2(\textbf{W}_t)= & {} B_{u2}(W_2(t-\tau _u)) -\mu _{mu2}W_2(t) - k_{mu2}(W_2(t))^2 +D_uW_1(t)-D_uW_2(t), \\ \mathcal {F}_3(\textbf{W}_t)= & {} -D_vW_3(t), \\ \mathcal {F}_4(\textbf{W}_t)= & {} -D_vW_4(t), \end{aligned}$$

and $\mathcal {G}(t)=(\mathcal {G}_1,\mathcal {G}_2,\mathcal {G}_3,\mathcal {G}_4)=\mathcal {G}(\textbf{W}_t)$ with

$$\begin{aligned} \mathcal {G}_1(t)= & {} -c_{uv}W_1(t)W_3(t), \\ \mathcal {G}_2(t)= & {} -c_{uv}W_2(t)W_4(t), \\ \mathcal {G}_3(t)= & {} B_{v1}(W_3(t-\tau _v)) -\mu _{mv1}W_3(t) - k_{mv1}(W_3(t))^2 +D_vW_4(t)-c_{uv}W_1(t)W_3(t), \\ \mathcal {G}_4(t)= & {} B_{v2}(W_4(t-\tau _v)) -\mu _{mv2}W_4(t) - k_{mv2}(W_4(t))^2 +D_vW_3(t)-c_{uv}W_2(t)W_4(t). \end{aligned}$$

As in Definition A.1, we denote the semiflow of (3.1) by $\Phi _{t+t_0}(t_0,\psi )$, with initial time $t_0$ and initial value $\psi$, and by $\Theta _t(\psi )$ the semiflow of (3.22), with initial time 0 and initial value $\psi$. Then we may express

$$\begin{aligned} \Phi _{t+t_0}(t_0,\psi )=\textbf{W}_{t+t_0}(t_0,\psi ),~~\Theta _t(\psi )=\textbf{Z}_t(0,\psi ), \end{aligned}$$

which satisfy $\textbf{W}_{t_0}=\psi$ and $\textbf{Z}_0=\psi$. Note that $\textbf{Z}_t(0,\psi )=\textbf{Z}_{t+s}(s,\psi )$ for all $s\ge 0$. Given sequences $t_j\rightarrow t$, $s_j\rightarrow \infty$, $\psi ^{(j)}\rightarrow \psi$ as $j\rightarrow \infty$, with $\psi ^{(j)}$, $\psi \in \mathbb {X}$, and $s_j\ge 0$, we define

$$\begin{aligned} \mathcal {D}_k^{(j)}(\theta )=W_{k,t_j+s_j}\left( s_j,\psi ^{(j)}\right) (\theta ) - Z_{k,t}(0,\psi )(\theta ). \end{aligned}$$

Then

$$\begin{aligned} \mathcal {D}_k^{(j)}(\theta )= & {} W_{k,t_j+s_j}\left( s_j,\psi ^{(j)}\right) (\theta ) - Z_{k,t+s_j}(s_j,\psi )(\theta ) \\= & {} W_k^{(j)}(t_j+s_j+\theta ) - Z_k^{(j)}(t+s_j+\theta ), \end{aligned}$$

where $\textbf{W}_{t+s_j}^{(j)}$ and $\textbf{Z}_{t+s_j}^{(j)}$ are the solutions of (3.1) and (3.22) respectively, both starting from the initial time $s_j$ and respectively from the initial values $\psi ^{(j)}$ and $\psi$. It suffices to show that

$$\begin{aligned} \max _{-\tau _m\le \theta \le 0} \sum _{k=1}^4 \left| \mathcal {D}_k^{(j)}(\theta ) \right| \rightarrow 0,~\textrm{as}~ j\rightarrow \infty . \end{aligned}$$

Since $s_j\rightarrow \infty$ as $j\rightarrow \infty$, we assume, without loss of generality, that $t_j+s_j+\theta >0$ for all j. Define $\mathcal {G}^{(j)}(t)=\mathcal {G}(\textbf{W}_t^{(j)})$, and note that

$$\begin{aligned} W_k^{(j)}(t_j+s_j+\theta )= & {} \psi ^{(j)}_k(0) + \int ^{t_j+s_j+\theta }_{s_j} \left[ \mathcal {F}_k(\textbf{W}_{\xi }^{(j)}) + \mathcal {G}_k^{(j)}(\xi )\right] d\xi , \\ Z_k^{(j)}(t+s_j+\theta )= & {} \psi _k(0) + \int ^{t+s_j+\theta }_{s_j} \mathcal {F}_k\left( \textbf{Z}_{\xi }^{(j)}\right) d\xi . \end{aligned}$$

Thus

$$\begin{aligned} \mathcal {D}_k^{(j)}(\theta )= & {} \psi ^{(j)}_k(0)-\psi _k(0) + \int ^{t_j+s_j+\theta }_{s_j} \mathcal {G}_k^{(j)}(\xi ) d\xi \\{} & {} + \int ^{t_j+s_j+\theta }_{s_j} \mathcal {F}_k\left( \textbf{W}_{\xi }^{(j)}\right) d\xi - \int ^{t+s_j+\theta }_{s_j} \mathcal {F}_k\left( \textbf{Z}_{\xi }^{(j)}\right) d\xi \\= & {} \psi ^{(j)}_k(0)-\psi _k(0) + \int ^{t_j+s_j+\theta }_{s_j} \mathcal {G}_k^{(j)}(\xi ) d\xi \\{} & {} + \int ^{t_j+s_j+\theta }_{s_j} \left[ \mathcal {F}_k\left( \textbf{W}_{\xi }^{(j)}\right) - \mathcal {F}_k\left( \textbf{Z}_{\xi }^{(j)}\right) \right] d\xi - \int ^{t+s_j+\theta }_{t_j+s_j+\theta } \mathcal {F}_k\left( \textbf{Z}_{\xi }^{(j)}\right) d\xi . \end{aligned}$$

In addition, we see that

$$\begin{aligned}{} & {} \int ^{t_j+s_j+\theta }_{s_j} \left[ \mathcal {F}_1\left( \textbf{W}_{\xi }^{(j)}\right) - \mathcal {F}_1\left( \textbf{Z}_{\xi }^{(j)}\right) \right] d\xi \\{} & {} \quad \le L_1 \int ^{t_j+s_j+\theta }_{s_j} \left( \left| W_1^{(j)}(\xi -\tau _u)-Z_1^{(j)}(\xi -\tau _u)\right| +\left| W_1^{(j)}(\xi )-Z_1^{(j)}(\xi )\right| \right. \\{} & {} \quad \quad \left. +\left| W_2^{(j)}(\xi )-Z_2^{(j)}(\xi )\right| \right) d\xi \\{} & {} \quad \le L_1 \int ^{t_j+s_j+\theta }_{s_j-\tau _u} \left( 2\left| W_1^{(j)}(\xi )-Z_1^{(j)}(\xi )\right| +\left| W_2^{(j)}(\xi )-Z_2^{(j)}(\xi )\right| \right) d\xi , \\{} & {} \quad \le L_1 \int ^{\theta }_{-t_j-\tau _u} \left( 2\left| W_1^{(j)}(t_j+s_j+\xi )-Z_1^{(j)}(t_j+s_j+\xi )\right| \right. \\{} & {} \quad \quad \left. +\left| W_2^{(j)}(t_j+s_j+\xi )-Z_2^{(j)}(t_j+s_j+\xi )\right| \right) d\xi , \end{aligned}$$

where $L_1=\max \{B_{u1}'(0),\mu _{mu1}+k_{mu1}(\mathcal {U}_1^W+\mathcal {U}_1^Z)+D_u\}<\infty$, $\mathcal {U}_1^W=\sup _{t\ge 0}U_1(t)<\infty$ for the solution in (3.1), and $\mathcal {U}_1^Z=\sup _{t\ge 0}U_1(t)<\infty$ for the solution in (3.22). Similarly, we have

$$\begin{aligned}{} & {} \int ^{t_j+s_j+\theta }_{s_j} \left[ \mathcal {F}_2\left( \textbf{W}_{\xi }^{(j)}\right) - \mathcal {F}_2\left( \textbf{Z}_{\xi }^{(j)}\right) \right] d\xi \\{} & {} \quad \le L_2 \int ^{\theta }_{-t_j-\tau _u} \left( 2\left| W_2^{(j)}(t_j+s_j+\xi )-Z_2^{(j)}(t_j+s_j+\xi )\right| \right. \\{} & {} \quad \quad +\left. \left| W_1^{(j)}(t_j+s_j+\xi )-Z_1^{(j)}(t_j+s_j+\xi )\right| \right) d\xi , \end{aligned}$$

for some positive consttant $L_2<\infty$. Obviously, denoting $L_k=D_v$ for $k=3,4$, we have

$$\begin{aligned}{} & {} \int ^{t_j+s_j+\theta }_{s_j} \left[ \mathcal {F}_k\left( \textbf{W}_{\xi }^{(j)}\right) - \mathcal {F}_k\left( \textbf{Z}_{\xi }^{(j)}\right) \right] d\xi \\ {}{} & {} \quad \le L_k \int ^{\theta }_{-t_j} \left| W_k^{(j)}(t_j+s_j+\xi )-Z_k^{(j)}(t_j+s_j+\xi )\right| d\xi \\{} & {} \quad \le L_k \int ^{\theta }_{-t_j-\tau _u} \left| W_k^{(j)}(t_j+s_j+\xi )-Z_k^{(j)}(t_j+s_j+\xi )\right| d\xi . \end{aligned}$$

Therefore,

$$\begin{aligned} \sum _{k=1}^4 \left| \mathcal {D}_k^{(j)}(\theta )\right|\le & {} \sum _{k=1}^4 \left\{ \left| \psi ^{(j)}_k(0)-\psi _k(0)\right| + \int ^{t_j+s_j+\theta }_{s_j} \left| \mathcal {G}_k^{(j)}(\xi ))\right| d\xi \right. \\{} & {} \left. + \int ^{t_j+s_j+\theta }_{s_j} \left| \mathcal {F}_k\left( \textbf{W}_{\xi }^{(j)}\right) - \mathcal {F}_k\left( \textbf{Z}_{\xi }^{(j)}\right) \right| d\xi + \int ^{t+s_j+\theta }_{t_j+s_j+\theta } \left| \mathcal {F}_k\left( \textbf{Z}_{\xi }^{(j)}\right) \right| d\xi \right\} \\\le & {} \sum _{k=1}^4 \left\{ \left| \psi ^{(j)}_k(0)-\psi _k(0)\right| + \int ^{t_j+s_j+\theta }_{s_j} \left| \mathcal {G}_k^{(j)}(\xi ))\right| d\xi + \int ^{t+s_j+\theta }_{t_j+s_j+\theta } \left| \mathcal {F}_k\left( \textbf{Z}_{\xi }^{(j)}\right) \right| d\xi \right. \\{} & {} \left. + \tilde{L} \int ^{\theta }_{-t_j-\tau _u} \left| W_k^{(j)}(t_j+s_j+\xi )-Z_k^{(j)}(t_j+s_j+\xi )\right| d\xi \right\} \\= & {} \mathcal {H}(\theta ;j) + \tilde{L} \int ^{\theta }_{-t_j-\tau _u} \sum _{k=1}^4 \left| \mathcal {D}_k^{(j)}(\xi )\right| d\xi , \end{aligned}$$

where $\tilde{L}=\max \{2L_1+L_2,L_1+2L_2,L_3,L_4\}$ and

$$\begin{aligned} \mathcal {H}(\theta ;j) = \sum _{k=1}^4 \left\{ \left| \psi ^{(j)}_k(0)-\psi _k(0)\right| + \int ^{t_j+s_j+\theta }_{s_j} \left| \mathcal {G}_k^{(j)}(\xi ))\right| d\xi + \int ^{t+s_j+\theta }_{t_j+s_j+\theta } \left| \mathcal {F}_k(\textbf{Z}_{\xi }^{(j)})\right| d\xi \right\} . \end{aligned}$$

Using Gronwall’s inequality, it leads to

$$\begin{aligned} \sum _{k=1}^4 \left| \mathcal {D}_k^{(j)}(\theta )\right| \le \mathcal {H}(\theta ;j) + \tilde{L} \int ^{\theta }_{-t_j-\tau _u} \mathcal {H}(\xi ;j) \exp \left( \int ^{\theta }_{\xi }\tilde{L} d\tilde{\xi } \right) d\xi . \end{aligned}$$

Note that each $\mathcal {G}^{(j)}(t)$ exponentially decays in time when $(\mathcal {S}_v)$ does not hold. In fact, $(W_3(t),W_4(t))$ is dominated by the solution of

$$\begin{aligned} \frac{dx_3(t)}{dt}= & {} B_{v1}'(0)x_3(t-\tau ) - \mu _{mv1}x_1(t) + Dx_4(t) - Dx_3(t), \nonumber \\ \frac{dx_4(t)}{dt}= & {} B_{v2}'(0)x_4(t-\tau ) - \mu _{mv2}x_2(t) + Dx_3(t) - Dx_4(t), \end{aligned}$$

(A.29)

which exponentially decays in time due to its negative stability modulus when $(\mathcal {S}_v)$ does not hold, as in the proof in Theorem 2.4. Thus, $\lim _{j\rightarrow \infty }\int ^{t_j+s_j+\theta }_{s_j} |\mathcal {G}_k^{(j)}(\xi ))| d\xi = 0$. In addition, since $\psi ^{(j)}\rightarrow \psi$ as $j\rightarrow \infty$, and each $\mathcal {F}_k$ is continuous, it holds that $\mathcal {H}(\theta ;j)\rightarrow 0$, and then $\sum _{k=1}^4 |\mathcal {D}_k^{(j)}(\theta )|\rightarrow 0$, as $j\rightarrow \infty$. This completes the proof.