Asymptotic Spreading for a Diffusive Chemostat System in Space-Time Periodic Environment

Abstract

This paper presents the dynamics that one microorganism spatially expands with two nutrients in space-time periodic environment. The generalized principal eigenvalue defined by the linear periodic parabolic operator is applied as a threshold to discuss the associated initial value problem. When the generalized principal eigenvalue is nonnegative, the solutions approach to the microorganism-extinction equilibrium uniformly. When the generalized principal eigenvalue is negative, the spreading speeds of the model are established when the initial distribution of microorganism has nonempty compact support, which are determined by a family of periodic parabolic eigenvalue problems. In the homogeneous environment, we show that the solutions locally uniformly converge to the microorganism-existent steady state by constructing upper and lower solutions. Finally, numerical simulations are performed to illustrate that the leftward or rightward spreading speed is approximately a constant under various circumstances.

1 Introduction

In the past decades, various chemostat models have been proposed to understand dynamic behaviors of the microorganisms. There are a large amount of issues to show how the growth of microorganisms is affected by some factors such as limiting nutrients, growth functions and death rates [6, 20, 36]. As we know, Rhodopseudomonas palustris (Rp), one kind of photosynthetic bacteria, can remove microcystin from the water body during algal blooms, which is widely applied in the production of lycopene. In particular, carbon source and nitrogen source are two main nutrients for the growth of Rp [10, 36]. Wang et al. [37] investigated the dynamic behavior of the microorganism Rp by considering the model

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial U(x, t)}{\partial t}=D_{1}\Delta U(x, t)+d_1(x, t)(U^{0}-U(x, t))-\frac{\beta _{1}(x, t)U(x, t)W(x, t)}{1+a_{1}(x, t)U(x, t)+b_{1}(x, t)W(x, t)},\\ \frac{\partial V(x, t)}{\partial t}=D_{2}\Delta V(x, t)+d_2(x, t)(V^{0}-V(x, t))-\frac{\beta _{2}(x, t)V(x, t)W(x, t)}{1+a_{2}(x, t)V(x, t)+b_{2}(x, t)W(x, t)},\\ \frac{\partial W(x, t)}{\partial t}=D_{3}\Delta W(x, t)-d_3(x, t)W(x, t)\\ \qquad \qquad \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\frac{\beta _{1}(x, t)U(x, t)W(x, t)}{1+a_{1}(x, t)U(x, t)+b_{1}(x, t)W(x, t)}+\frac{\beta _{2}(x, t)V(x, t)W(x, t)}{1+a_{2}(x, t)V(x, t)+b_{2}(x, t)W(x, t)},\\ U(x,0)=U_{0}(x),V(x,0)=V_{0}(x),W(x,0)=W_{0}(x),\ x\in \Omega ,\ t>0, \end{array}\right. } \end{aligned}$$

(1.1)

in which $\Omega \subset {\mathbb {R}}^N$ is a domain. All the unknown functions and parameters are similar to that in the next model. When $\Omega$ is bounded and (1.1) is equipped with Neumann boundary condition, a threshold-type result and a bang-bang-type configuration optimization conclusion were obtained. Meanwhile, the existence of time-periodic travelling waves was established in the unbounded domain with time-periodic coefficients. In this study, based on (1.1), we consider a more general model with space-time dependent diffusion coefficients

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial U(x, t)}{\partial t}=D_{1}(x, t)\Delta U(x, t)+d_1(x, t)(U^{0}-U(x, t))-\frac{\beta _{1}(x, t)U(x, t)W(x, t)}{1+a_{1}(x, t)U(x, t)+b_{1}(x, t)W(x, t)},\\ \frac{\partial V(x, t)}{\partial t}=D_{2}(x, t)\Delta V(x, t)+d_2(x, t)(V^{0}-V(x, t))-\frac{\beta _{2}(x, t)V(x, t)W(x, t)}{1+a_{2}(x, t)V(x, t)+b_{2}(x, t)W(x, t)},\\ \frac{\partial W(x, t)}{\partial t}=D_{3}(x, t)\Delta W(x, t)-d_3(x, t)W(x, t)\\ \qquad \qquad \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\frac{\beta _{1}(x, t)U(x, t)W(x, t)}{1+a_{1}(x, t)U(x, t)+b_{1}(x, t)W(x, t)}+\frac{\beta _{2}(x, t)V(x, t)W(x, t)}{1+a_{2}(x, t)V(x, t)+b_{2}(x, t)W(x, t)},\\ U(x,0)=U_{0}(x),V(x,0)=V_{0}(x),W(x,0)=W_{0}(x),\ x\in {{\mathbb {R}}},\ t>0, \end{array}\right. } \end{aligned}$$

(1.2)

where $U_{0}(x),V_{0}(x)$ and $W_{0}(x)$ are bounded, nonnegative and uniformly continuous on ${\mathbb {R}}$. Here, U(x, t), V(x, t) and W(x, t) denote the concentrations of carbon source, nitrogen source, and microorganisms, respectively, at location x and time t, the positive constants $U^{0}$ and $V^{0}$ denote the input concentrations of carbon source and nitrogen source, respectively, $d_1(x, t)$ and $d_2(x,t)$ are the dilution rate of the carbon source and the nitrogen source in chemostat and $d_{3}(x, t)$ is the total loss rate of the microorganisms. The Beddington-DeAngelis functional responses are used to represent the growth of the microorganism. $\beta _{1}(x, t)$ and $\beta _{2}(x, t)$ are the production rates of the microorganism [4, 12]. $D_{1}(x, t),D_{2}(x, t)$ and $D_{3}(x, t)$ stand for the diffusion rates of carbon source, nitrogen source and microorganisms, respectively. In this paper, we use the asymptotic speed of spreading (for short, spreading speed) to describe the spatial propagation dynamics of model (1.2) when the coefficients are periodic in x and t.

Spreading speed is a vital subject for us to understand the propagation dynamics of reaction-diffusion equations. The notion of spreading speed was introduced in the pioneering works [1, 2]. Considerable attention has devoted to studying the spreading speed for reaction-diffusion equations in the heterogeneous environment [39]. For reaction-diffusion equations with space periodic coefficients, Berestycki and Hamel [8] described the speed of propagation for KPP-type problems, see also [9], Weinberger [38] proved that the spreading speed coincides with the minimal wave speed for a recursion defined by an order-preserving operator of monostable type. For a monostable semiflow in one-dimensional periodic environment, Liang and Zhao [22] introduced a topologically conjugate semiflow defined in spatially discrete homogeneous environment and then showed that the spreading speed exists, also see [19, 41]. When the coefficients are time periodic, the propagation thresholds were studied in [3, 18, 21]. In space-time periodic media, we can refer to [27,28,29,30] for general reaction-diffusion equations and see [14] for monotone space-time semiflows situation. Furthermore, in the general space-time heterogeneity media, much attention has been paid to the spreading speed of scalar reaction-diffusion equations too, see [7, 23, 34, 35] and references therein.

In the above studies, the monotonicity of solution semiflows or the cooperative property of systems plays a pivotal role. However, many parabolic systems are non-cooperative, such as some epidemic dynamical models, predator-prey systems and chemostat models. In particular, when the positive solution is concerned, system (1.2) cannot generate monotone semiflows. When a system cannot generate monotone semiflows, its spreading speed cannot be directly determined by the above conclusions, and some different techniques have been utilized to study its propagation dynamics. For example, we may refer to [11, 13, 24, 31] using uniform persistence theory of dynamical systems, auxiliary equations and other recipes.

In what follows, we apply the generalized principal eigenvalue defined by the linearized equation at the microorganism-extinction equilibrium as a threshold to characterize the persistence and extinction about the microorganism. Meanwhile, we give two auxiliary equations to estimate the spreading speeds. Our result shows that when $W_0(x)$ has nonempty compact support, W(x, t) can expand almost at two constant speeds from the left and right. For two special cases, we give the exact formulas of the spreading speeds. Furthermore, we characterize the long time behavior of the solutions between the invasion fronts (leftward and rightward) about model (1.2) in the homogeneous environment. Our main recipe is to construct the proper upper and lower solutions. Finally, we give some numerical examples to illustrate our conclusions and explore the role of inhomogeneous environment. From our numerical simulations, it is possible that the spatial heterogeneity may enhence the spatial expansion ability.

The rest of this paper is organized as follows. In Sect. 2, we present some preliminaries and state our main results. The initial value problem is studied to estimate the upper and lower bounds of spreading speeds in Sect. 3. Meanwhile, we discuss the asymptotic spreading behavior at the head of the propagating front. In Sect. 4, we obtain the convergence result about the microorganism of model (1.2) in the homogeneous environment. Numerical simulations and a brief discussion are given in Sect. 5.

2 Preliminaries and Main Results

In this paper, we use the standard partial ordering in ${\mathbb {R}}^3$. Let $X:=C({\mathbb {R}},{\mathbb {R}})$ be the Banach space of all bounded and uniformly continuous functions with the supremum norm $\parallel \cdot \parallel _{X}$, and $X_{+}:=\{u\in X:u(x)\ge 0, x\in {\mathbb {R}} \}$ be the positive cone of X. Before presenting some lemmas and our main results, we introduce the following hypotheses that will be imposed without further illustrations.

Hypothesis 2.1

We assume that the space-time periodic coefficient $g(x,t):{\mathbb {R}}\times {\mathbb {R}}\rightarrow {\mathbb {R}}_{+}$ is of class $C^{\alpha ,\frac{\alpha }{2}}$, $0<\alpha <1$, and there exist two positive constants $\omega$ and l such that

$$\begin{aligned} g(x+l,t)=g(x,t+\omega )=g(x,t)>0,\ \ x, t\in {\mathbb {R}}, \end{aligned}$$

where $g\in \{ D_{1}, D_{2}, D_{3}, d_1, d_2, d_3, a_{1}, a_{2}, b_{1}, b_{2},\beta _{1},\beta _{2}\}$.

Hypothesis 2.2

We assume that the initial value

$$\begin{aligned} U_{0}(x),V_{0}(x),W_{0}(x)\in X_{+},\,\, U_{0}(x) \le U^0, \,\, V_{0}(x)\le V^0, \,\, x\in {\mathbb {R}}. \end{aligned}$$

In addition, we require that the initial value $W_{0}(x)$ has nonempty compact support.

Definition 2.3

([1]) (Spreading speed) Two constants $c^+_{w}$ and $c^-_{w}$ are called the rightward and leftward spreading speeds of a nonnegative function w(x, t) respectively, provided the following two statements hold:

(i):

$\limsup \limits _{t\rightarrow \infty }\sup \limits _{x> (c^+_{w}+\epsilon )t}w(x,t)=\limsup \limits _{t\rightarrow \infty }\sup \limits _{x< (-c^-_{w}-\epsilon )t}w(x,t)=0$ for $\epsilon >0$.

(ii):

$\liminf \limits _{t\rightarrow \infty } \inf \limits _{(-c_{w}^-+\epsilon )t<x<(c_{w}^+-\epsilon )t}w(x,t)>0$ for any small $\epsilon >0$.

In order to describe the dynamics behavior of model (1.2), we first consider the corresponding linear principal eigenvalue problem. Linearizing the third equation of system (1.2) at the microorganism-extinction equilibrium $(U^0,V^0,0)$, we have

$$\begin{aligned} \frac{\partial W(x,t)}{\partial t}=D_{3}(x,t)\Delta W(x,t) +\left[ \frac{\beta _{1}(x, t)U^0 }{1+a_{1}(x, t)U^0} +\frac{\beta _{2}(x, t)V^0 }{1+a_{2}(x, t)V^0}-d_{3}(x,t)\right] W(x,t) \end{aligned}$$

(2.1)

for all $x\in {\mathbb {R}},\ t>0.$ Define the space-time periodic parabolic operator

$$\begin{aligned} {\mathcal {L}}\varphi =\partial _{t}\varphi -D_{3}(x,t)\Delta \varphi -\bigg [\frac{\beta _{1}(x, t)U^0}{1+a_{1}(x, t)U^0} +\frac{\beta _{2}(x, t)V^0}{1+a_{2}(x, t)V^0}-d_{3}(x,t)\bigg ]\varphi , \end{aligned}$$

(2.2)

and the modified operator

$$\begin{aligned} {\mathcal {L}}_{\alpha }\varphi&=e^{-\alpha \cdot x}{\mathcal {L}} (e^{\alpha \cdot x}\varphi )\\&=\partial _{t}\varphi -D_{3}(x,t)\Delta \varphi -2\alpha D_{3}(x,t) \varphi _{x}-\alpha ^{2}D_{3}(x,t)\varphi \\&\quad -\bigg [\frac{\beta _{1}(x, t)U^0}{1+a_{1}(x, t)U^0} +\frac{\beta _{2}(x, t)V^0}{1+a_{2}(x, t)V^0}-d_{3}(x,t)\bigg ] \varphi \text { with } \alpha \in {\mathbb {R}}. \end{aligned}$$

Here the space-time periodic parabolic operator ${\mathcal {L}}$ may admit two generalized principal eigenvalues $\lambda '_1$ and $\lambda _1$ (for details, we may refer to Nadin [27, Sect. 2]), of which the existence can also be described by a family space-time periodic principal eigenvalue problems, see Definition 2.4, Lemmas 2.5 and 2.6 as follows.

Definition 2.4

([27, Definition 2.6]) A space-time periodic principal eigenfunction of the operator ${\mathcal {L}}_{\alpha }$ is a function $\varphi _\alpha \in C^{2,1}({\mathbb {R}}\times {\mathbb {R}})$ such that there exists a constant $k(\alpha )$ satisfying

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathcal {L}}_{\alpha }\varphi _\alpha =k(\alpha )\varphi _\alpha ~~~~in ~~{\mathbb {R}}\times {\mathbb {R}},\\ \varphi _\alpha >0,\\ \varphi _\alpha (x+l,t)=\varphi _\alpha (x,t+\omega )=\varphi _\alpha (x,t). \end{array}\right. } \end{aligned}$$

(2.3)

Such a $k(\alpha )$ is called a space-time periodic principal eigenvalue of ${\mathcal {L}}_{\alpha }$.

The following lemma regards the existence and the uniqueness of the eigenelements.

Lemma 2.5

([27, Theorem 2.7]) For any $\alpha \in {\mathbb {R}}$, there exists a couple $(k(\alpha ),\varphi _{\alpha })$ that satisfies (2.3). Furthermore, $k(\alpha )$ is unique and $\varphi _\alpha$ is unique up to multiplication by a positive constant.

The family $(k(\alpha ),\varphi _{\alpha })_{\alpha \in {\mathbb {R}}}$ enables us to give the following characterization for the generalized principal eigenvalues $\lambda '_{1}$ and $\lambda _{1}$.

Lemma 2.6

([27, Theorems 2.12 and 2.13]) One has the following characterization

$$\begin{aligned} k(\alpha )=\max \limits _{\begin{array}{c} \varphi>0~\text {in}~(x,t), \\ \varphi ~ \text {is}~\omega -\text {periodic in }t \end{array}}\min \limits _{{\mathbb {R}} \times {\mathbb {R}}}\left( \frac{{\mathcal {L}}_{\alpha }\varphi }{\varphi }\right) =\min \limits _{\begin{array}{c} \varphi >0~\text {in}~(x,t), \\ \varphi ~\text {is}~\omega -\text {periodic in }t \end{array}}\max \limits _{{\mathbb {R}} \times {\mathbb {R}}}\left( \frac{{\mathcal {L}}_{\alpha }\varphi }{\varphi }\right) . \end{aligned}$$

Moreover, $\lambda '_{1}=k(0)$ and $\lambda _{1}=\max \nolimits _{\alpha \in {\mathbb {R}}} k(\alpha )$ are well-defined.

Consider the auxiliary Fisher-KPP equation

$$\begin{aligned} \frac{\partial w(x,t)}{\partial t}&=D_{3}(x,t)\Delta w(x,t)-d_{3}(x,t)w(x,t) +\frac{\beta _{1}(x, t)U^0 w(x,t)}{1+a_{1}(x, t)U^0+b_1(x,t)w(x,t)}\nonumber \\&\quad +\frac{\beta _{2}(x, t)V^0 w(x,t)}{1+a_{2}(x, t)V^0+b_2(x,t)w(x,t)}, ~~x\in {\mathbb {R}},\ t>0, \end{aligned}$$

(2.4)

with the initial value

$$\begin{aligned} w(x,0)=w_{0}(x),\ x\in {\mathbb {R}}. \end{aligned}$$

(2.5)

It is easy to see that ${\mathcal {L}}$ is the linearized operator of Eq. (2.4) in the neighborhood of zero. Using the existence and uniqueness of generalized principal eigenvalue $\lambda '_{1}$, we have the following three lemmas that can be found in [28, 29].

Lemma 2.7

Equation (2.4) admits a unique positive space-time periodic solution $p(x,t)\in C^{2,1}({\mathbb {R}}\times {\mathbb {R}})$ with positive infimum if and only if $\lambda '_{1}<0$. If $\lambda '_{1}\ge 0$, then the only nonnegative bounded entire solution of Eq. (2.4) is zero.

Define

$$\begin{aligned} c^+_*=\min \limits _{\alpha>0}\frac{-k(\alpha )}{\alpha }, \ ~~c^-_*=\min \limits _{\alpha >0}\frac{-k(-\alpha )}{\alpha }, \end{aligned}$$

(2.6)

which are finite if $\lambda '_{1}<0$ from [28, 29]. Then the following two lemmas hold from [28].

Lemma 2.8

If $\lambda '_{1}<0$ and $c=c_*^-$, then Eq. (2.4) has a positive pulsating traveling wave solution $w(x,t)=\phi ^-(x+c_*^-t,x,t)$ such that $\phi ^-(z,x,t)$ is nondecreasing almost everywhere in z and

$$\begin{aligned} \lim \limits _{z\rightarrow -\infty }\phi ^-(z,x,t)=0, ~~\lim \limits _{z\rightarrow \infty }\phi ^-(z,x,t)=p(x,t). \end{aligned}$$

If $\lambda '_{1}<0$ and $c=c_*^+$, then Eq. (2.4) also has a positive pulsating traveling wave solution $w(x,t)=\phi ^+(x-c_*^+t,x,t)$ such that $\phi ^+(z,x,t)$ is nondecreasing almost everywhere in z and

$$\begin{aligned} \lim \limits _{z\rightarrow -\infty }\phi ^+(z,x,t) =p(x,t),~~\lim \limits _{z\rightarrow \infty }\phi ^+(z,x,t)=0. \end{aligned}$$

Lemma 2.9

If $w_0(x)$ admits nonempty compact support in (2.5), then the solution w(x, t) of (2.4)–(2.5) satisfies

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }w(x+c_1t,t) =\limsup \limits _{t\rightarrow \infty }w(x-c_2t,t)=0 \text { for any given } c_1>c_*^{\varepsilon ,+}, c_2 > c_*^{\varepsilon ,-} \end{aligned}$$

locally uniformly in $x\in {\mathbb {R}}$. If $\lambda '_{1}< 0$ and the initial condition w(x, 0) admits nonempty compact support in (2.5), then for all $-c_*^-<c<c_*^+$, w(x, t) defined by (2.4)–(2.5) satisfies

$$\begin{aligned} w(x-ct,t)\rightarrow p(x-ct,t)~~as~~t\rightarrow \infty , \end{aligned}$$

in which the convergence is locally uniform in $x\in {\mathbb {R}}$.

Now we use the generalized principal eigenvalue $\lambda '_{1}$ as a threshold to describe the spatial propagation for model (1.2). Our first result regards the global dynamics of (1.2) when $\lambda '_{1}\ge 0$. In such a situation, the microorganism uniformly dies out and our result is summarized as follows.

Theorem 2.10

Assume that $\lambda '_{1}\ge 0$. Then the solution of model (1.2) satisfies

$$\begin{aligned} \lim _{t\rightarrow \infty }(U(x,t),V(x,t),W(x,t))={(U^{0},V^{0},0)} \end{aligned}$$

uniformly in $x\in {\mathbb {R}}$.

When $\lambda '_{1}<0$, the situation is more delicate. We first give the following results on leftward and rightward spreading speeds.

Theorem 2.11

Assume that $\lambda '_{1}<0$ holds and $c_*^+, c_*^-$ are defined by (2.6). Then the following spreading properties are true.

(i):

For any given $c<c_*^+$ and $c'<c_*^-$, $x\in {\mathbb {R}}$, there holds

$$\begin{aligned}&\liminf \limits _{t\rightarrow \infty }\inf \limits _{-c^{\prime }t<x<ct}U(x,t)> 0,\ \,\liminf \limits _{t\rightarrow \infty }\inf \limits _{-c^{\prime }t<x<ct}V(x,t)>0,\ \,\liminf \limits _{t\rightarrow \infty }\inf \limits _{-c^{\prime }t<x<ct}W(x,t)>0, \\&\limsup \limits _{t\rightarrow \infty }\sup \limits _{-c^{\prime }t<x<ct}U(x,t)< U^{0},\ \,\limsup \limits _{t\rightarrow \infty }\sup \limits _{-c^{\prime }t<x<ct}V(x,t)<V^{0}. \end{aligned}$$

(ii):

For any given $c>c_*^+$ and $c'>c_*^-$, $x\in {\mathbb {R}}$, there holds

$$\begin{aligned}&\limsup \limits _{t\rightarrow \infty } \sup \limits _{x>ct}[W(x,t)+|U(x,t)-U^{0}|+|V(x,t)-V^{0}|] =0, \\&\limsup \limits _{t\rightarrow \infty } \sup \limits _{x<-c^{\prime }t}[W(x,t)+|U(x,t)-U^{0}|+|V(x,t)-V^{0}|] =0. \end{aligned}$$

Remark 1

If $\lambda '_1<0$, then $c_*^+=c_W^+=c_{U^0 -U}^+=c_{V^0 -V}^+, c_*^-=c_W^-=c_{U^0 -U}^-=c_{V^0 -V}^-.$

By Theorem 2.11, we can estimate the spreading speeds by numerical simulations. But from (2.6), it is possible that $c^+_W \ne c_W^-$, since $\lambda '_1\ne \lambda _1$ is possible. For the scalar equations, [14, 28] showed some examples that may have two distinct leftward and rightward spreading speeds. Particularly, in time-periodic and homogeneous environments, we have $\lambda '_1=\lambda _1$ according to [17], which implies the following formulas from [30, Proposition 2.1] directly.

Theorem 2.12

In the time-periodic environment, if $\overline{\kappa }>0$, then $\lambda '_1<0$ and

$$\begin{aligned} c^{**}=2\sqrt{\overline{D_3}\overline{\kappa }}=c_h^+=c_h^-, \quad h\in \{W,U^0 -U, V^0 -V \}, \end{aligned}$$

(2.7)

where

$$\begin{aligned} \overline{D_3}=\frac{1}{\omega }\int _0^\omega D_3(t)dt, \quad \overline{\kappa }=\frac{1}{\omega }\int ^{\omega }_{0} \left[ \frac{\beta _{1}(t)U^0}{1+a_{1}(t)U^0} +\frac{\beta _{2}(t)V^0}{1+a_{2}(t)V^0}-d_{3}(t)\right] dt. \end{aligned}$$

For constant parameters, if $\frac{\beta _{1}U^0}{1+a_{1}U^0} +\frac{\beta _{2}V^0}{1+a_{2}V^0}>d_{3}$, then $\lambda '_1<0$ and

$$\begin{aligned} c^*=2\sqrt{D_3\bigg (\frac{\beta _{1}U^0}{1+a_{1}U^0} +\frac{\beta _{2}V^0}{1+a_{2}V^0}-d_{3}\bigg )} =c_h^+=c_h^-, \quad h\in \{W,U^0 -U, V^0 -V \}. \end{aligned}$$

(2.8)

In particular, when all the parameters are positive constants, model (1.2) becomes

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial U(x, t)}{\partial t}=D_{1}\Delta U(x, t)+d_1(U^{0}-U(x, t))-\frac{\beta _{1}U(x, t)W(x, t)}{1+a_{1}U(x, t)+b_{1}W(x, t)},\\ \frac{\partial V(x, t)}{\partial t}=D_{2}\Delta V(x, t)+d_2(V^{0}-V(x, t))-\frac{\beta _{2}V(x, t)W(x, t)}{1+a_{2}V(x, t)+b_{2}W(x, t)},\\ \frac{\partial W(x, t)}{\partial t}=D_{3}\Delta W(x, t)-d_3W(x, t)\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\frac{\beta _{1}U(x,t)W(x, t)}{1+a_{1}U(x, t)+b_{1}W(x, t)}+\frac{\beta _{2}V(x, t)W(x, t)}{1+a_{2}V(x, t)+b_{2}W(x, t)},\\ U(x,0)=U_{0}(x),V(x,0)=V_{0}(x),W(x,0)=W_{0}(x),\ x\in {{\mathbb {R}}},\ t>0, \end{array}\right. } \end{aligned}$$

(2.9)

in which the initial value satisfies Hypothesis 2.2. To estimate the limit behaviors of U(x, t), V(x, t) and W(x, t), we consider the model (2.9) with

$$\begin{aligned} \inf _{x\in {\mathbb {R}}}U_{0}(x)>0,\ \, \inf _{x\in {\mathbb {R}}} V_{0}(x)>0,\ \, \inf _{x\in {\mathbb {R}}}W_{0}(x)>0. \end{aligned}$$

(2.10)

(C):

Assume that (2.10) holds. Then

$$\begin{aligned} \lim _{t\rightarrow \infty }\sup _{x\in {\mathbb {R}}}[|U(x,t)-U^*| +|V(x,t)-V^*|+|W(x,t)-W^*|]=0, \end{aligned}$$

where $(U^*,V^*,W^*)$ is the unique positive spatially homogeneous steady state of (2.9).

Here the uniqueness of $(U^*,V^*,W^*)$ can be obtained by a monotone argument, which will be discussed at the beginning of the proof of Proposition 2.1.

Proposition 2.1

If $c^*>0,\ b_1>\frac{\beta _1}{d_1}$, $b_2>\frac{\beta _2}{d_2}$ in (2.9), then (C) holds.

For the proof of Proposition 2.1, we put it in Appendix. Finally, we give the limit behavior of U(x, t), V(x, t), W(x, t) for model (2.9) when the initial value satisfies the Hypothesis 2.2.

Theorem 2.13

If $c^* >0,\ (C)$ hold in (2.9), then

$$\begin{aligned} \limsup _{t\rightarrow \infty }\sup _{|x|<ct}[|U(x,t)-U^*|+|V(x,t)-V^*|+|W(x,t)-W^*|]=0 \end{aligned}$$

uniformly for any given $c\in (0,c^*)$.

3 Spreading Speed

In this section, we study the initial value problem (1.2) and prove Theorems 2.10 and 2.11 based on several technical lemmas. Firstly, we introduce the following lemma regarding the well-posedness and uniform boundedness of the bounded classical solution of the initial value problem (1.2).

Lemma 3.1

For any given initial value $(U_{0}(x),V_{0}(x),W_{0}(x))$, model (1.2) has a unique classical solution (U(x, t), V(x, t), W(x, t)) such that

$$\begin{aligned} 0<U(x,t)<U^0,\ \ 0<V(x,t)<V^0,\ \ 0<W(x,t) <\max \{\overline{W}^0,\Vert W_0(x)\Vert _X\}, \ \ x\in {\mathbb {R}}, t>0, \end{aligned}$$

where the constant $\overline{W}^0 >0$ satisfies

$$\begin{aligned} d_3(x, t)\ge \frac{\beta _{1}(x, t)U^0}{1+a_{1}(x, t)U^0 +b_{1}(x, t)\overline{W}^0}+\frac{\beta _{2}(x, t)V^0}{1+a_{2}(x, t) V^0+b_{2}(x, t)\overline{W}^0} \end{aligned}$$

for $x\in {\mathbb {R}}$ and $t>0.$ For any given $t_0 >0,$

$$\begin{aligned} H_t(x,t),H_{x}(x,t),H_{xx}(x,t) \in C^{\alpha ,\frac{\alpha }{2}},\quad H\in \{U,V,W\}, \end{aligned}$$

are uniformly bounded for all $t\ge t_0$ and there exists $\delta >0$ such that

$$\begin{aligned} U(x,t)> \delta ,\ \ V(x,t) > \delta ,\ \, x\in {\mathbb {R}},\ t\ge t_0. \end{aligned}$$

Proof

The existence and uniqueness of classical solution can be obtained by the standard theory of reaction-diffusion systems [40], the regularity may be obtained from Lunardi [26, Chapter 5], which are omitted here. We now check the last assertion. Let S(t) be defined by

$$\begin{aligned} S'(t)=\widetilde{D}_1(U^0-S(t))-\widetilde{\beta }_1S(t),\quad S(0)=0, \end{aligned}$$

where

$$\begin{aligned} \widetilde{D}_1=\inf \limits _{(x,t)\in [0,l]\times [0,\omega ]}D_1(x,t), \quad \widetilde{\beta }_1= \sup \limits _{(x,t)\in [0,l] \times [0,\omega ]}[\beta _1(x,t)/b_{1}(x,t)]. \end{aligned}$$

Then, S(t) is positive and strictly increasing and $U(x,t) \ge S(t_0)>0$ for $x\in {\mathbb {R}}$ and $t\ge t_0.$ By a similar argument, the conclusion on V(x, t) holds too. The proof is complete. $\square$

Proof of Theorem 2.10

From Lemma 3.1, we have

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial W(x, t)}{\partial t}\le D_{3}(x, t)\Delta W(x, t)-d_{3}(x, t)W(x, t)+\frac{\beta _{1}(x, t)U^0W(x, t)}{1+a_{1}(x, t)U^0+b_{1}(x, t)W(x, t)}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\frac{\beta _{2}(x, t)V^0W(x, t)}{1+a_{2}(x, t)V^0+b_{2}(x, t)W(x, t)},\\ W(x,0)=W_{0}(x),~x\in {\mathbb {R}},~t>0. \end{array}\right. } \end{aligned}$$

(3.1)

When $\lambda '_1\ge 0$, from Lemma 2.7 and the comparison principle, we can obtain that $\lim \limits _{t\rightarrow \infty }W(x,t)=0$ uniformly for $x\in {\mathbb {R}}$. Then we can deduce that $\lim \limits _{t\rightarrow \infty }(U(x,t)-U^0)=0$ and $\lim \limits _{t\rightarrow \infty }(V(x,t)-V^0)=0$ uniformly for $x\in {\mathbb {R}}$. The proof is complete. $\square$

To prove Theorem 2.11, we firstly discuss the outer spreading property of model (1.2) and then prove Theorem 2.11 (ii) by applying the following Lemmas 3.2 and 3.3.

Lemma 3.2

Assume that $\lambda '_{1}<0$. Then

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }\sup \limits _{x> ct}W(x,t) =\limsup \limits _{t\rightarrow \infty }\sup \limits _{x< -c't}W(x,t)=0 \end{aligned}$$

for any given $c>c_*^+$ and $c'>c_*^-$.

Proof

From (3.1) and Lemma 2.8, there exists $A>1$ such that

$$\begin{aligned} W_{0}(x)\le \min \{ A\phi ^+(x,x,0),A \phi ^- (x,x,0)\},~x\in {\mathbb {R}}, \end{aligned}$$

in which $\phi ^+(z,x,t)$ and $\phi ^-(z,x,t)$ are given by Lemma 2.8. Then the comparison principle implies that

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }\sup \limits _{x> ct}W(x,t) =\limsup \limits _{t\rightarrow \infty }\sup \limits _{x< -c't}W(x,t)=0 \end{aligned}$$

for any given $c>c_*^+$ and $c'>c_*^-$. The proof is complete. $\square$

Lemma 3.3

Assume that $\lambda '_{1}<0$. Then

$$\begin{aligned}&\limsup \limits _{t\rightarrow \infty }\sup \limits _{x> ct}[\mid U(x,t) -U^0\mid +\mid V(x,t)-V^0\mid ]=0,\\&\limsup \limits _{t\rightarrow \infty }\sup \limits _{x<-c't}[\mid U(x,t) -U^0\mid +\mid V(x,t)-V^0\mid ]=0 \end{aligned}$$

for any given $c>c_*^+$ and $c'>c_*^-$.

Proof

We can assume by contradiction similar to that in [13]. For the rightward side, assume that there exist $\varepsilon >0$, a sequence $\{x_n\}_{n\ge 0}\subset {\mathbb {R}}$ and a sequence $\{t_n\}\subset [1,\infty )$ tending to $\infty$ as $n \rightarrow \infty$ such that

$$\begin{aligned} \mid U(x_n,t_n)-U^0\mid \ge \varepsilon ~for~any~ n\ge 0, \quad x_n > ct_n. \end{aligned}$$

Consider the sequences of maps

$$\begin{aligned} g_n(x,t)=g(x+x_n,t+t_n),g\in \{ D_{1}, D_{2}, D_{3}, d_1, d_2, d_3, a_{1}, a_{2}, b_{1}, b_{2},\beta _{1},\beta _{2}\} , \end{aligned}$$

(3.2)

and

$$\begin{aligned} U_{n}(x,t)=U(x+x_n,t+t_n),\,\, V_{n}(x,t)=V(x+x_n,t+t_n), \,\, W_{n}(x,t)=W(x+x_n,t+t_n). \end{aligned}$$

(3.3)

By the smoothness and periodic property in (3.2), up to a subsequence and still denoted by the current label, there exist $x_0\in [0, l],t_0\in [0,\omega ]$ such that

$$\begin{aligned} g_n(x,t)\rightarrow g(x+x_0,t+t_0),n\rightarrow \infty ,\quad g\in \{ D_{1}, D_{2}, D_{3}, d_1, d_2, d_3, a_{1}, a_{2}, b_{1}, b_{2},\beta _{1},\beta _{2}\} . \end{aligned}$$

In fact, due to the periodic property, it suffices to consider

$$\begin{aligned}&g_n(x,t)=g(x+x_n-l[x_n/l],t+t_n-\omega [t_n/\omega ]),\\&g \in \{ D_{1}, D_{2}, D_{3}, d_1, d_2, d_3, a_{1}, a_{2}, b_{1}, b_{2},\beta _{1},\beta _{2}\} , \end{aligned}$$

Since $x_n-l[x_n/l],t_n-\omega [t_n/\omega ]$ are uniformly bounded for all $n\in {\mathbb {N}},$ then the existence of $x_0,t_0$ are evident.

Further using the parabolic estimate in (3.3), a subsequence of $\{(U_n,V_n,W_n)\}$ locally uniformly converges to some entire solution $(U_\infty ,V_\infty ,W_\infty )$ of the following model

$$\begin{aligned}&\frac{\partial U(x,t)}{\partial t}=D_{1}(x+x_{0},t+t_{0}) \Delta U(x,t) \nonumber \\&\ \ \ \ \ \ \ \ \ +d_{1}(x+x_{0},t+t_{0})(U^{0}-U(x,t)) -\frac{\beta _{1}(x+x_{0},t+t_{0})U(x,t)W(x,t)}{1+a_{1} (x+x_{0},t+t_{0})U(x,t)+b_{1}(x+x_{0},t+t_{0})W(x,t)}, \nonumber \\&\frac{\partial V(x,t)}{\partial t}=D_{2}(x+x_{0},t+t_{0}) \Delta V(x,t) \nonumber \\&\ \ \ \ \ \ \ \ \ +d_{2}(x+x_{0},t+t_{0})(V^{0}-V(x,t)) -\frac{\beta _{2}(x+x_{0},t+t_{0})V(x,t)W(x,t)}{1+a_{2} (x+x_{0},t+t_{0})V(x,t)+b_{2}(x+x_{0},t+t_{0})W(x,t)}, \nonumber \\&\frac{\partial W(x,t)}{\partial t}=D_{3}(x+x_{0},t+t_{0}) \Delta W(x,t)-d_{3}(x+x_{0},t+t_{0})W(x,t) \nonumber \\&\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\frac{\beta _{1}(x+x_{0},t+t_{0}) U(x,t)W(x,t)}{1+a_{1}(x+x_{0},t+t_{0})U(x,t)+b_{1}(x+x_{0},t+t_{0})W(x,t)}\nonumber \\&\qquad +\frac{\beta _{2}(x+x_{0},t+t_{0})V(x,t)W(x,t)}{1+a_{2}(x+x_{0},t +t_{0})V(x,t)+b_{2}(x+x_{0},t+t_{0})W(x,t)},\nonumber \\ \end{aligned}$$

(3.4)

which also satisfies

$$\begin{aligned} \mid U_{\infty }(0,0)-U^0 \mid \ge \varepsilon . \end{aligned}$$

(3.5)

However, due to the convergence of W(x, t) and strong comparison principle, we know that $W_{\infty }(0,0)=0$ and so $W_{\infty }(x,t)\equiv 0$. Hence the function $U_{\infty }$ becomes an entire solution of

$$\begin{aligned} \frac{\partial U(x, t)}{\partial t}=D_{1}(x+x_0, t+t_0)\Delta U(x, t) +d_1(x+x_0, t+t_0)(U^{0}-U(x, t)), \end{aligned}$$

which leads to $U_{\infty }(x,t) \equiv U^0.$ This is a contradiction with (3.5).

In a similar way, we can verify the remainder and finish the proof. $\square$

In order to describe the property of inner spreading or the lower bounds of spreading speed, we consider the following auxiliary Fisher-KPP type equation

$$\begin{aligned} \frac{\partial w^{\varepsilon }(x,t)}{\partial t}&=D_{3}(x,t)\Delta w^{\varepsilon }(x,t)+\bigg [\frac{\beta _{1}(x, t) U^0}{1+a_{1}(x, t)U^0}+\frac{\beta _{2}(x, t)V^0}{1+a_{2}(x, t)V^0} \bigg ]w^{\varepsilon }(x,t) \nonumber \\&\quad -(d_{3}(x,t)+\varepsilon )w^{\varepsilon }(x,t) -M[w^{\varepsilon }(x,t)]^2,\ ~x\in {\mathbb {R}},~t>0, \end{aligned}$$

(3.6)

with the initial value

$$\begin{aligned} w^{\varepsilon }(x,0)=w_{0}^{\varepsilon }(x),\ x\in {\mathbb {R}}, \end{aligned}$$

(3.7)

where $\varepsilon$ and M are positive constants. Consider the corresponding eigenvalue problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \psi _{t}=D_{3}(x,t)\Delta \psi +\bigg [\frac{\beta _{1}(x, t)U^0}{1+a_{1}(x, t)U^0} +\frac{\beta _{2}(x, t)V^0}{1+a_{2}(x, t)V^0}-d_{3}(x,t)-\varepsilon \bigg ]\psi +\lambda \psi ,\\ \psi (x+l,t)=\psi (x,t),~~~\psi (x,t+\omega )=\psi (x,t),~~x\in {\mathbb {R}},\ t>0. \end{array}\right. } \end{aligned}$$

(3.8)

Similar to that in Sect. 2, we can define ${\mathcal {L}}^{\varepsilon }, {\mathcal {L}}^{\varepsilon }_{\alpha }, k^{\varepsilon }(\alpha ), \psi _{\alpha }^{\varepsilon }, \lambda ^{\varepsilon '}_{1}, \lambda _1^{\varepsilon }, p^{\varepsilon }(x,t)$ and

$$\begin{aligned} c^{\varepsilon ,+}_*=\min \limits _{\alpha>0}\frac{-k^{\varepsilon }(\alpha )}{\alpha }, \ ~~c^{\varepsilon ,-}_*=\min \limits _{\alpha >0}\frac{-k^\varepsilon (-\alpha )}{\alpha }. \end{aligned}$$

(3.9)

Then, [28, Propositions 2.9 and 2.10] implies that $\lambda ^{\varepsilon '}_{1}, c^{\varepsilon ,+}_*, c^{\varepsilon ,-}_*$ are well defined and satisfy the following propagation property.

Lemma 3.4

When $w^{\varepsilon }(x,0)$ admits nonempty compact support in (3.7), the solution $w^{\varepsilon }(x,t)$ of (3.6)–(3.7) satisfies

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }w^{\varepsilon }(x+c_1t,t) =\limsup \limits _{t\rightarrow \infty }w^{\varepsilon }(x-c_2t,t) =0 \text { for any given } c_1>c_*^{\varepsilon ,+}, c_2 > c_*^{\varepsilon ,-} \end{aligned}$$

locally uniformly in $x\in {\mathbb {R}}$. If $\lambda ^{\varepsilon '}_{1}< 0$ and the initial condition $w^{\varepsilon }(x,0)$ admits nonempty compact support in (3.7), then for all $-c_*^{\varepsilon ,-}<c<c_*^{\varepsilon ,+}$, we have

$$\begin{aligned} w^{\varepsilon }(x-ct,t)\rightarrow p^{\varepsilon }(x-ct,t)~~as~~t\rightarrow \infty \end{aligned}$$

locally uniformly in $x\in {\mathbb {R}}$.

Lemma 3.5

Assume that $\lambda '_{1}<0$. Then

$$\begin{aligned} \liminf \limits _{t\rightarrow \infty }\inf \limits _{-c't<x< ct}W(x,t)>0 \end{aligned}$$

for any given $c<c_*^+$ and $c'<c_*^-$.

Proof

By Lemma 3.1, there exist $T>1$ and $\widetilde{L}>0$ such that

$$\begin{aligned} \frac{\beta _{1}(x,t)U(x,t)W(x,t)}{1+a_{1}(x,t)U(x,t)+b_{1}(x,t)W(x,t)}\ge & {} \frac{\beta _{1}(x,t)U^0W(x,t)}{1+a_1(x,t)U^0+b_1(x,t)W(x,t)}\\&-\widetilde{L}(U^0-U(x,t))W(x,t), \\ \frac{\beta _{2}(x,t)V(x,t)W(x,t)}{1+a_{2}(x,t)V(x,t)+b_{2}(x,t)W(x,t)}\ge & {} \frac{\beta _{2}(x,t)V^0 W(x,t)}{1+a_2(x,t)U^0+b_2(x,t)W(x,t)}\\&-\widetilde{L}(V^0-V(x,t))W(x,t) \end{aligned}$$

for all $t\ge T$ and $x\in {\mathbb {R}}$.

Set $U'(x,t)=U^0-U(x,t)$, $0\le U'(x,0)=U'_0(x)\le U^0$. We have

$$\begin{aligned} \frac{\partial U^{\prime }(x,t)}{\partial t}= & {} D_{1}(x,t) \Delta U^{\prime }(x,t)-d_1(x,t)U^{\prime }(x,t) \\&+\frac{\beta _{1}(x,t)(U^{0} -U^{\prime }(x,t))W(x,t)}{ 1+a_{1} (x,t)(U^{0}-U^{\prime }(x,t))+b_{1}(x,t)W(x,t)} \\\le & {} D_{1}(x,t)\Delta U^{\prime }(x,t)-d_1(x,t)U^{\prime }(x,t) +\frac{\beta _{1}(x,t)U^{0}}{1+a_{1}(x,t)U^{0}}W(x,t) \\\le & {} D_{1}(x,t)\Delta U^{\prime }(x,t)-d_1(x,t)U^{\prime }(x,t)+aW(x,t) \end{aligned}$$

with $a=\max \limits _{(x,t)\in [0,l]\times [0,\omega ]}\frac{\beta _{1}(x,t) U^0}{1+a_1(x,t)U^0}$.

Similarly, set $V'(x,t)=V^0-V(x,t)$, $0\le V'(x,0)=V'_0(x)\le V^0$. Then

$$\begin{aligned} \frac{\partial V'(x, t)}{\partial t}\le D_{2}(x, t) \Delta V'(x, t)-d_2(x, t)V'(x, t)+ bW(x,t) \end{aligned}$$

with $b=\max \limits _{(x,t)\in [0,l]\times [0,\omega ]} \frac{\beta _{2}(x,t)V^0}{1+a_2(x,t)V^0}$.

Let $\Gamma _{i}(x,t,s)$, $t\ge s$, $x\in {\mathbb {R}}$ be the fundamental function of

$$\begin{aligned} u_{t}=D_{i}(x,t)\Delta u-d_{i}(x,t)u,~~x\in {\mathbb {R}},~t\ge s,~i\in \{1,2,3\}. \end{aligned}$$

(3.10)

We can refer to [33] for the existence and properties of $\Gamma _{i}(x,t,s)$. Define

$$\begin{aligned} \bar{p}_{i}(t):=e^{\int ^{t}_0 \sup _{x\in {\mathbb {R}}}[D_{i}(x,s)\rho _i^2-d_i(x,s)]ds}, \end{aligned}$$

(3.11)

where $\rho _i>0$ is a positive number and small enough such that

$$\begin{aligned} g_i(t)=\int ^{t}_0\sup _{x\in {\mathbb {R}}}[D_{i}(x,s)\rho _i^2-d_i(x,s)]ds<0,\ \ t>0. \end{aligned}$$

Then we can get a pair of upper-lower solutions for the fundamental solution $\Gamma _{i}(x,t,0)$:

$$\begin{aligned} \bar{u}_i(x,t):=e^{-\rho _i|x|}\bar{p}_{i}(t),~~\underline{u}_i(x,t) :=e^{-\rho _i|x|}e^{-\int ^{t}_0[\sup _{x\in {\mathbb {R}}}d_i(x,s)]ds}. \end{aligned}$$

(3.12)

Since

$$\begin{aligned}&-\bar{u}_{i,t}(x,t)+D_{i}(x,t)\Delta \bar{u}_i(x,t)-d_{i}(x,t)\bar{u}_i(x,t)\\&\quad =\bar{u}_i(x,t)\bigg (-\frac{\bar{p}'_{i}(t)}{\bar{p}_{i} (t)}+D_{i}(x,t)\rho ^2_i-d_i(x,t)\bigg )\\&\quad =\bar{u}_i(x,t)\bigg \{D_{i}(x,t)\rho ^2_i-d_i(x,t) -\sup _{x\in {\mathbb {R}}}[D_{i}(x,t)\rho _i^2-d_i(x,t)]\bigg \} \le 0, \end{aligned}$$

and

$$\begin{aligned}&-\underline{u}_{i,t}(x,t)+D_{i}(x,t)\Delta \underline{u}_i(x,t)-d_{i}(x,t)\underline{u}_i(x,t)\\&\quad =\underline{u}_i(x,t)\bigg (\sup _{x\in {\mathbb {R}}}d_i (x,t)+D_{i}(x,t)\rho ^2_i-d_i(x,t)\bigg )\ge 0, \end{aligned}$$

we can obtain the estimation about the decay behavior of the $\Gamma _{i}(x,t,0)$.

Moreover, there exists a positive number $K>0$ such that

$$\begin{aligned} \frac{\partial W(x, t)}{\partial t}&= D_{3}(x, t)\Delta W(x, t)-d_{3}(x, t)W(x, t) +\frac{\beta _{1}(x, t)U(x,t)W(x, t)}{1+a_{1}(x, t)U(x,t)+b_{1}(x, t)W(x, t)}\\&\quad +\frac{\beta _{2}(x, t)V(x,t)W(x, t)}{1+a_{2}(x, t)V(x,t)+b_{2}(x, t)W(x, t)}\\&\ge D_{3}(x, t)\Delta W(x, t)+\bigg [\frac{\beta _{1}(x,t)U^0}{1+a_1(x,t)U^0} +\frac{\beta _{2}(x,t)V^0}{1+a_2(x,t)V^0}-d_{3}(x, t)\bigg ]W(x,t)\\&\quad -\widetilde{L}\bigg [(U^0-U(x,t))+(V^0-V(x,t))\bigg ]W(x,t)-KW^2(x,t),~~t\ge T. \end{aligned}$$

Utilizing the theory of semigroup and the decay estimation about the $\Gamma _{i}(x,t,0)$, for any $\varepsilon >0$ small enough, we can fix $T_1(\varepsilon )>\tau (\varepsilon )>0$ and $N(\varepsilon )>0$ such that

$$\begin{aligned} U^0-U(x,t)&\le a\int ^t_0\int _{{\mathbb {R}}}\Gamma _{1}(y,t-s,0) W(x-y,s)dyds+\int _{{\mathbb {R}}}\Gamma _{1}(y,t,0)U'_0(x-y)dy\\&<\int _{t-T_1}^{t-\tau }\int ^{N}_{-N}\Gamma _{1}(y,t-s,0)W(x-y,s)dyds +\frac{\varepsilon }{4\widetilde{L}}\\&:= A(x,t)+\frac{\varepsilon }{4\widetilde{L}} \end{aligned}$$

and

$$\begin{aligned} V^0-V(x,t)&\le b\int ^t_0\int _{{\mathbb {R}}}\Gamma _{2}(y,t-s,0)W(x-y,s)dyds +\int _{{\mathbb {R}}}\Gamma _{2}(y,t,0)V'_0(x-y)dy\\&<\int _{t-T_1}^{t-\tau }\int ^{N}_{-N}\Gamma _{2} (y,t-s,0)W(x-y,s)dyds+\frac{\varepsilon }{4\widetilde{L}}\\&:= B(x,t)+\frac{\varepsilon }{4\widetilde{L}} \end{aligned}$$

hold for $x\in {\mathbb {R}}$ and $t>T+T_1+1$, in which A(x, t) and B(x, t) only depend on W(y, s), $y\in [x-2N,x+2N]$, and $s\in [t-T-T_1,t-\tau ]$.

If $\widetilde{L}[A(x,t)+B(x,t)]\le \frac{\varepsilon }{2}$, then

$$\begin{aligned} \frac{\partial W(x, t)}{\partial t}&\ge D_{3}(x, t)\Delta W(x, t) +\bigg [\frac{\beta _{1}(x,t)U^0}{1+a_1(x,t)U^0} +\frac{\beta _{2}(x,t)V^0}{1+a_2(x,t)V^0}-d_{3}(x, t)\bigg ]W(x,t)\\&\quad -\varepsilon W(x,t)-KW^2(x,t). \end{aligned}$$

If $\widetilde{L}[A(x,t)+B(x,t)]>\frac{\varepsilon }{2}$, due to the uniform boundedness and uniform continuity of $\Gamma _{i}(x,t,0)$ and W(x, t), there exist $\eta >0$ and $\nu >0$ such that

$$\begin{aligned} W(y,s)>\eta , \end{aligned}$$

(3.13)

where $y\in [x_0-\nu ,x_0+\nu ]$ for some $x_0\in [x-2N,x+2N]$, $s\in [t-T-T_1,t-\tau ]$ and $\eta >0$, $\nu >0$ are independent on x, t.

Consider the following initial value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial \widetilde{W}(x, t)}{\partial t} = D_{3}(x, t)\Delta \widetilde{W}(x, t)+[-d_{3}(x, t)-K\widetilde{W}(x,t)]\widetilde{W}(x, t),\\ \widetilde{W}(x, 0)=\widetilde{w}(x), \end{array}\right. } \end{aligned}$$

where $\widetilde{w}(x)$ is a continuous function satisfying

(1):

$\widetilde{w}(x)=\eta$, $|x|\le \frac{\nu }{2}$,

(2):

$\widetilde{w}(x)=0$, $|x|\ge \nu$,

(3):

$\widetilde{w}(x)$ is decreasing for $x\in [\frac{\nu }{2},\nu ]$ and increasing for $x\in [-\nu ,-\frac{\nu }{2}]$.

Then $\widetilde{W}(x, t)>0$ for $x\in {\mathbb {R}}$ and $t>0$. Define

$$\begin{aligned} \eta '=\min \limits _{|x|\le 2N+1,\ ~t\in [\tau ,T+T_1]}\widetilde{W}(x, t). \end{aligned}$$

Then $\eta '>0$ is well-defined and $\widetilde{L}[A(x,t) +B(x,t)]>\frac{\varepsilon }{2}$ implies that

$$\begin{aligned} W(x,t)>\eta ', \ ~t\ge T+T_1+1. \end{aligned}$$

(3.14)

We now consider (3.6) for any $\varepsilon >0$. There exists an $M>0$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial W(x, t)}{\partial t}= D_{3}(x, t)\Delta W(x, t)-d_{3}(x, t)W(x, t)+\frac{\beta _{1}(x, t)U(x,t)W(x, t)}{1+a_{1}(x, t)U(x,t)+b_{1}(x, t)W(x, t)}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\frac{\beta _{2}(x, t)V(x,t)W(x, t)}{1+a_{2}(x, t)V(x,t)+b_{2}(x, t)W(x, t)}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ge D_{3}(x, t)\Delta W(x, t)+\bigg [\frac{\beta _{1}(x, t)U^0}{1+a_{1}(x, t)U^0}+\frac{\beta _{2}(x, t)V^0}{1+a_{2}(x, t)V^0}-d_{3}(x, t)\bigg ]W(x,t)\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,-\varepsilon W(x,t)-MW^2(x, t),\\ W(x,T')=W'_{0}(x),~x\in {\mathbb {R}},~t\ge T'=T+T_1+1. \end{array}\right. } \end{aligned}$$

(3.15)

In fact, as for a fixed $\varepsilon$, we only need

$$\begin{aligned} \widetilde{L}[A(x,t)+B(x,t)]-\frac{\varepsilon }{2}<(M-K)\eta ' \end{aligned}$$

(3.16)

to be true. From Lemma 3.1 and (3.14), the positive number M is bounded for every $\varepsilon >0$.

Thus, we obtain

$$\begin{aligned} \frac{\partial W(x, t)}{\partial t}&\ge D_{3}(x, t)\Delta W(x, t) +\bigg [\frac{\beta _{1}(x,t)U^0}{1+a_1(x,t)U^0} +\frac{\beta _{2}(x,t)V^0}{1+a_2(x,t)V^0}-d_{3}(x, t)\bigg ]W(x,t)\\&\quad -\varepsilon W(x,t)-MW^2(x,t), \end{aligned}$$

if $t\ge T'=T+T_1+1$.

Then we continue to prove this lemma. Now we need to prove a continuity property that as $\varepsilon \rightarrow 0$, we have $\lambda _1^{\varepsilon '}\rightarrow \lambda '_{1}$. Consider the operator

$$\begin{aligned} \widehat{{\mathcal {L}}}\theta&=({\mathcal {L}}^{\varepsilon } -{\mathcal {L}})\theta =\varepsilon \theta . \end{aligned}$$

Obviously, $\widehat{{\mathcal {L}}}$ is a space-time periodic bounded positive linear operator and the corresponding eigenvalue problem has a unique principal eigenvalue $\hat{k}(\varepsilon )=\varepsilon >0$. Meanwhile, we can see that $\varepsilon \rightarrow \widehat{{\mathcal {L}}}(\varepsilon )$ is a monotone increasing map and $\hat{k}(\varepsilon )\rightarrow 0$ as $\varepsilon \rightarrow 0$.

Then from the definition of the modified operator

$$\begin{aligned} {\mathcal {L}}^{\varepsilon }_{\alpha }\theta =({\mathcal {L}}_{\alpha } +\widehat{{\mathcal {L}}})\theta \end{aligned}$$

such that for $\alpha \in {\mathbb {R}},$ we have

$$\begin{aligned} k^{\varepsilon }(\alpha )=k(\alpha )+\hat{k}(\varepsilon ). \end{aligned}$$

(3.17)

As $\varepsilon \rightarrow 0$, $\mid k^{\varepsilon }(\alpha )-k(\alpha )\mid =\hat{k}(\varepsilon )\rightarrow 0$. We set $\alpha =0$, then

$$\begin{aligned} \lambda _1^{\varepsilon '}=\lambda '_1+\hat{k}(\varepsilon ). \end{aligned}$$

(3.18)

Thus, as $\varepsilon \rightarrow 0$, we have $\lambda _1^{\varepsilon '}\rightarrow \lambda '_{1}$. Moreover, we know that when $\varepsilon$ is small enough, $\lambda '_1<0$ holds and we have $\lambda _1^{\varepsilon '}<0$ from the monotonicity.

Next, we prove that as $\varepsilon \rightarrow 0$, $c^{\varepsilon ,+}_*\rightarrow c_*^{+}$ and $c^{\varepsilon ,-}_*\rightarrow c_*^{-}$ hold. Here we only prove the rightward spreading speed, because the discussion for the other case is similar. From the definitions of $c^+_*$ and $c^{\varepsilon ,+}_*$, we have

$$\begin{aligned} c^{\varepsilon ,+}_*=\min \limits _{\alpha>0}\frac{-k^{\varepsilon }(\alpha )}{\alpha } =\min \limits _{\alpha >0}\frac{-k(\alpha )-\hat{k}(\varepsilon )}{\alpha }. \end{aligned}$$

(3.19)

From Lemma 2.6 and (2.6), we set

$$\begin{aligned} c_*^+=\min \limits _{\alpha >0}\frac{-k(\alpha )}{\alpha }=\frac{-k(\alpha _1)}{\alpha _1}. \end{aligned}$$

(3.20)

Then

$$\begin{aligned} c^{\varepsilon ,+}_*=\min \limits _{\alpha >0}\frac{-k(\alpha )-\hat{k} (\varepsilon )}{\alpha }\le \frac{-k(\alpha _1)-\hat{k}(\varepsilon )}{\alpha _1}, \end{aligned}$$

(3.21)

so $c_*^{+}\ge c^{\varepsilon ,+}_*$. Thus we have

$$\begin{aligned} |c^{\varepsilon ,+}_*-c^+_*|\le \bigg |\frac{-k(\alpha _1) -\varepsilon }{\alpha _1}-\frac{-k(\alpha _{1})}{\alpha _{1}}\bigg | \le \bigg |\frac{-\hat{k}(\varepsilon )}{\alpha _1}\bigg |. \end{aligned}$$

(3.22)

From $-\hat{k}(\varepsilon )\rightarrow 0$ as $\varepsilon \rightarrow 0$, we have $c^{\varepsilon ,+}_*\rightarrow c_*^{+}$ as $\varepsilon \rightarrow 0$.

Therefore, from Lemmas 2.9 and  3.4, we can directly deduce that

$$\begin{aligned} \liminf \limits _{t\rightarrow \infty }\inf \limits _{-c't<x< ct}W(x,t)>0 \end{aligned}$$

for any given $c<c_*^+$ and $c'<c_*^-$. The proof is complete. $\square$

Lemma 3.6

Assume that $\lambda '_{1}<0$. Then

$$\begin{aligned} \limsup \limits _{t\rightarrow \infty }\sup \limits _{-c^{\prime }t<x<ct}U(x,t)< U^{0},\ \,\limsup \limits _{t\rightarrow \infty } \sup \limits _{-c^{\prime }t<x<ct}V(x,t)<V^{0} \end{aligned}$$

for any given $c<c_*^+$ and $c'<c_*^-$.

Proof

We now prove it by contradiction discussion. We first assume that the former conclusion does not hold, then for some $c_1<c_*^+$ and $c_2<c_*^-,$ we can select $\{t_n\}\subset [1,\infty )$ with $\lim _{n\rightarrow \infty }t_n = \infty$ and $\{x_n\}$ with $x_n\in [-c_2t_n, c_1 t_n]$ such that

$$\begin{aligned} \lim _{ n\rightarrow \infty } ( U^{0} -U(x_n,t_n))=0. \end{aligned}$$

Define maps as those in (3.2) and (3.3). Similar to the proof of Lemma 3.3, a subsequence of $\{(U_n,V_n,W_n)\}$ locally uniformly converges to some entire solution $(U_\infty ,V_\infty ,W_\infty )$ of model (3.4) such that

$$\begin{aligned} U_\infty (0,0)= U^{0}, \,\, U_\infty (x,t)\le U^{0}, x,t\in {\mathbb {R}}. \end{aligned}$$

Let $u(x,t)=U^0- U_{\infty }(x,t),$ then it is nonnegative such that

$$\begin{aligned} \frac{\partial u(x, t)}{\partial t}\ge D_{1}(x+x_0, t+t_0) \Delta u(x, t)- d_1(x+x_0, t+t_0)u(x, t),\,\, u(0,0)=0. \end{aligned}$$

Applying the maximal principle, we have $u(x,t)\equiv 0$ and so $U_{\infty }(x,t)=U^0, x,t\in {\mathbb {R}}.$ Moreover, from Lemma 3.5, we see that $\inf _{x,t\in {\mathbb {R}} }W_{\infty }(x,t)>0$ holds. From the strict positivity of $W_{\infty }(x,t),$ there exists $\sigma >0$ such that

$$\begin{aligned} \frac{\partial U_{\infty }(x,t)}{\partial t}\le D_{1}(x+x_0, t+t_0) \Delta U_{\infty }(x,t)+d_{1}(x+x_0, t+t_0)(U^{0}-U_{\infty }(x,t) -\sigma U_{\infty }(x,t)). \end{aligned}$$

Therefore, $U_{\infty }(x,t) \le U^{0} /(1+\sigma ), x,t\in {\mathbb {R}}$ and a contradiction occurs.

Similarly, we can analyze V(x, t) and finish the proof. $\square$

Proof of Theorem 2.11

As we see, the proof of Theorem 2.11 (i) follows from Lemmas 3.5 and 3.6, Theorem 2.11 (ii) follows from Lemmas 3.2–3.3 immediately. The proof is complete. $\square$

4 Convergence Result

In this section, we will prove Theorem 2.13.

Proof of Theorem 2.13

Following [5], we are to prove that for any given $c\in (0,c^*)$, $\epsilon >0$, there exists $T>0$ such that

$$\begin{aligned} \sup \limits _{|x|<ct}(|U(x,t)-U^*|+|V(x,t)-V^*|+|W(x,t)-W^*|)<\epsilon ,~t>T. \end{aligned}$$

(4.1)

By virtue of Theorem 2.11, we know that there exist $\delta >0$, $T_1>0$ such that

$$\begin{aligned} \inf \limits _{|x|<(c+2c^*)t/3}U(x,t)>\delta ,\inf \limits _{|x|<(c+2c^*) t/3}V(x,t)>\delta ,\inf \limits _{|x|<(c+2c^*)t/3}W(x,t)>\delta ,~t>T_1. \end{aligned}$$

Let $\widetilde{U}(x,t),\widetilde{V}(x,t),\widetilde{W}(x,t)$ be the solution of (2.9) with the initial value satisfying

$$\begin{aligned} \inf _{x\in {\mathbb {R}}}U_{0}(x)>\delta ,\ \inf _{x\in {\mathbb {R}}} V_{0}(x)>\delta ,\ \inf _{x\in {\mathbb {R}}}W_{0}(x)>\delta . \end{aligned}$$

Then (C) implies that there exists $T_3>0$ such that

$$\begin{aligned} \sup \limits _{x\in {\mathbb {R}}}(|\widetilde{U}(x,t)-U^*| +|\widetilde{V}(x,t)-V^*|+|\widetilde{W}(x,t)-W^*|)<\frac{\epsilon }{4},~t>T_3. \end{aligned}$$

Then we only need to prove that for any $T_2$ large enough,

$$\begin{aligned} \sup \limits _{|x|<(2c+c^*)(T_3+t+1)/3}(|U(x,t)-U^*|+|V(x,t) -V^*|+|W(x,t)-W^*|)<\epsilon , \end{aligned}$$

(4.2)

where $t\in [T_2,\,T_2+1]$. Since $ct<(2c+c^*)(T_3+t+1)/3$, then (4.2) ensures (4.1).

Let

$$\begin{aligned} u(x,t)= & {} \widetilde{U}(x,t)-U(x,t),v(x,t)=\widetilde{V}(x,t) -V(x,t),w(x,t)\\= & {} \widetilde{W}(x,t)-W(x,t), \\ (T_{i}(t)i(\cdot ,r))(x)= & {} \frac{1}{\sqrt{4\pi D_it}} \int _{{\mathbb {R}}}e^{\frac{-y^2}{4D_it}}i(x-y,r)dy,\ i={1,2,3}. \end{aligned}$$

There exists a constant $L>0$ such that

$$\begin{aligned} |u(x,t)|\le & {} (T_{1}(t-r)|u(\cdot ,r)|)(x) +L\int _{r}^{t}T_{1}(t-s)[|u(\cdot ,s)|+|v(\cdot ,s)|+|w(\cdot ,s)|]ds, \\ |v(x,t)|\le & {} (T_{2}(t-r)|v(\cdot ,r)|)(x) +L\int _{r}^{t}T_{2}(t-s)[|u(\cdot ,s)|+|v(\cdot ,s)|+|w(\cdot ,s)|]ds, \\ |w(x,t)|\le & {} (T_{3}(t-r)|w(\cdot ,r)|)(x) +L\int _{r}^{t}T_{3}(t-s)[|u(\cdot ,s)|+|v(\cdot ,s)|+|w(\cdot ,s)|]ds \end{aligned}$$

for any $r\in [0,t)$. Then $u(x,t),\, v(x,t),\, w(x,t)$ satisfy

$$\begin{aligned} |u(x,t)|\le X(x,t),|v(x,t)|\le Y(x,t),|w(x,t)|\le Z(x,t),~x\in {\mathbb {R}},~t>0, \end{aligned}$$

where

$$\begin{aligned} X(x,t)= & {} (T_{1}(t-r)|X(\cdot ,r)|)(x)+L\int _{r}^{t}T_{1}(t-s)[|X(\cdot ,s)|+|Y(\cdot ,s)|+|Z(\cdot ,s)|]ds, \\ Y(x,t)= & {} (T_{2}(t-r)|Y(\cdot ,r)|)(x)+L\int _{r}^{t}T_{2}(t-s)[|X(\cdot ,s)|+|Y(\cdot ,s)|+|Z(\cdot ,s)|]ds, \\ Z(x,t)= & {} (T_{3}(t-r)|Z(\cdot ,r)|)(x)+L\int _{r}^{t}T_{3}(t-s)[|X(\cdot ,s)|+|Y(\cdot ,s)|+|Z(\cdot ,s)|]ds \end{aligned}$$

with

$$\begin{aligned} X(x,0)=|u(x,0)|,\ Y(x,0)=|v(x,0)|,\ Z(x,0)=|w(x,0)|. \end{aligned}$$

Let $N>0$ be a fixed constant (clarified later) such that

$$\begin{aligned} X(x,0)=Y(x,0)=Z(x,0)=0,\ |x|\le N,\ x\in {\mathbb {R}} \end{aligned}$$

and

$$\begin{aligned} \sup \limits _{x\in {\mathbb {R}}}X(x,0)+\sup \limits _{x\in {\mathbb {R}}}Y(x,0) +\sup \limits _{x\in {\mathbb {R}}}Z(x,0)<Q, \end{aligned}$$

where Q is a positive constant.

Let $C>0$ be large and $\lambda >0$ be small such that

$$\begin{aligned} D_i\lambda ^2-C\lambda +3L\le 0,\ i={1,2,3}. \end{aligned}$$

Define a continuous function as

$$\begin{aligned} \Phi (x,t)=\min \{Q[e^{\lambda (x-N+Ct)}+e^{\lambda (-x-N+Ct)}], \,Qe^{3Lt}\},\ x\in {\mathbb {R}}, \end{aligned}$$

which implies

$$\begin{aligned} \Phi (x,0)\ge X(x,0),\ \Phi (x,0)\ge Y(x,0),\ \Phi (x,0)\ge Z(x,0). \end{aligned}$$

Then we have

$$\begin{aligned} \Phi (x,t)\ge (T_i(t-r)|\Phi (\cdot ,r)|)(x)+L\int _r^tT_i(t-s)[3\Phi (\cdot ,s)]ds \end{aligned}$$

for $0\le r<t<\infty$ and $x\in {\mathbb {R}}$, $i={1,2,3}$. Thus we get

$$\begin{aligned} \Phi (x,t)\ge X(x,t),\ \Phi (x,t)\ge Y(x,t),\ \Phi (x,t)\ge Z(x,t), \ x\in {\mathbb {R}},\ t\ge 0. \end{aligned}$$

By the property, we can fix $N=N(T_3)>0$ such that

$$\begin{aligned} X(0,T_3)\le \frac{\epsilon }{4},\ Y(0,T_3) \le \frac{\epsilon }{4},\ Z(0,T_3)\le \frac{\epsilon }{4}. \end{aligned}$$

Let $T_2>0$ such that

$$\begin{aligned} (2c+c^*)(T_3+t+1)/3+N<(c+2c^*)t/3,\quad t>T_2, \end{aligned}$$

then (4.2) holds. Consequently, we have arrived at (4.1). The proof is complete. $\square$

5 Numerical Simulations and Discussions

In this section, we give three examples to illustrate our main results and explore further propagation dynamics of this system. Denote the level set by

$$\begin{aligned} L^{u}_t(\alpha )=\inf \{ x\in {\mathbb {R}} : u(x,t)=\alpha \}, u\in \{ U, V, W\}. \end{aligned}$$

Moreover, we define a continuous function

$$\begin{aligned} W_0(x)= {\left\{ \begin{array}{ll} \cos x,x\in [-\pi /2,\pi /2],\\ 0,|x|\ge \pi /2. \end{array}\right. } \end{aligned}$$

Example 5.1

Consider the initial value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial U(x, t)}{\partial t}=\Delta U(x, t)+0.1(1-U(x, t))-\frac{0.5U(x, t)W(x, t)}{1+U(x, t)+5W(x, t)},\\ \frac{\partial V(x, t)}{\partial t}=2\Delta V(x, t)+0.1(1-V(x, t))-\frac{3V(x, t)W(x, t)}{1+3V(x, t)+6W(x, t)},\\ \frac{\partial W(x, t)}{\partial t}=\Delta W(x, t)-0.75W(x, t)+\frac{0.5U(x, t)W(x, t)}{1+U(x, t)+5W(x, t)}+\frac{3V(x, t)W(x, t)}{1+3V(x, t)+6W(x, t)},\\ U(x,0)=1,V(x,0)=1,W(x,0)=W_{0}(x),\ x\in {{\mathbb {R}}},\ t>0. \end{array}\right. } \end{aligned}$$

(5.1)

Fig. 1

Spatial-temporal plots of (5.1) when $t\in [0, 150]$

Fig. 2

Spatial plots of model (5.1) at $t=100,150$

Table 1 Approximate level sets in Fig. 2

From Theorem 2.12, we obtain $c^*=1$. We show the spatial-temporal plots of unknown functions as that in Fig. 1, from which we see that W invades the habitat almost in a constant speed. To further estimate the invasion speed, we obverse that the invasion speed $c^*_W\approx 1$ by comparing some level sets in Fig. 2 and Table 1. Moreover, for such a model, the local convergence to the constant steady state is true, since Proposition 2.1 holds from the fact that $b_1=5>\beta _1/d_1=0.5$ and $b_2=6>\beta _2/d_2=1.5$.

Example 5.2

Consider the initial value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial U(x, t)}{\partial t}=0.1\Delta U(x, t)+0.1(1-U(x, t))-\frac{0.5(1+\cos (\frac{\pi t}{5}))U(x, t)W(x, t)}{1+U(x, t)+5W(x, t)},\\ \frac{\partial V(x, t)}{\partial t}=0.2\Delta V(x, t)+0.1(1-V(x, t))-\frac{3(1+\sin (\frac{\pi t}{5}))V(x, t)W(x, t)}{1+3V(x, t)+6W(x, t)},\\ \frac{\partial W(x, t)}{\partial t}=\Delta W(x, t)-0.75W(x, t)+\frac{0.5(1+\cos (\frac{\pi t}{5}))U(x, t)W(x, t)}{1+U(x, t)+5W(x, t)}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\frac{3(1+\sin (\frac{\pi t}{5}))V(x, t)W(x, t)}{1+3V(x, t)+6W(x, t)},\\ U(x,0)=1,V(x,0)=1,W(x,0)=W_{0}(x),\ x\in {{\mathbb {R}}},\ t>0. \end{array}\right. } \end{aligned}$$

(5.2)

Fig. 3

Spatial-temporal plots of (5.2) when $t\in [0, 150]$

Fig. 4

Spatial-temporal plots of (5.2) when $t\in [100, 150]$

From the values of coefficients, we can calculate that $\overline{\kappa }=\frac{1}{4}$ and $c^{**}=1$. We show the spatial-temporal plots of unknown functions as that in Figs. 3 and 4, from which we observe that W invades the habitat almost in a constant speed. In addition, we take $t=100,140$ to plot the spatial distribution of unknown functions and list the movement of level sets in Fig. 5 and Table 2, from which we find that the invasion speed of W is close to $c_W^{**}\approx 1$.

Fig. 5

Spatial plots of model (5.2) at $t=100,140$

Table 2 Approximate level sets in Fig. 5

Example 5.3

We simulate the following initial value problem

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial U(x, t)}{\partial t}=0.1\Delta U(x, t)+0.1(1-U(x, t))-\frac{0.5(1+\cos (\frac{\pi t}{5}))(1+\cos x)U(x, t)W(x, t)}{1+U(x, t)+5W(x, t)},\\ \frac{\partial V(x, t)}{\partial t}=0.2\Delta V(x, t)+0.1(1-V(x, t))-\frac{3(1+\sin (\frac{\pi t}{5}))(1+\sin x)V(x, t)W(x, t)}{1+3V(x, t)+6W(x, t)},\\ \frac{\partial W(x, t)}{\partial t}=\Delta W(x, t)-0.75W(x, t)+\frac{0.5(1+\cos (\frac{\pi t}{5}))(1+\cos x)U(x, t)W(x, t)}{1+U(x, t)+5W(x, t)}\\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,+\frac{3(1+\sin (\frac{\pi t}{5})(1+\sin x)V(x, t)W(x, t)}{1+3V(x, t)+6W(x, t)},\\ U(x,0)=1,V(x,0)=1,W(x,0)=W_{0}(x),\ x\in {{\mathbb {R}}},\ t>0. \end{array}\right. } \end{aligned}$$

(5.3)

Fig. 6

Spatial-temporal plots of model (5.3) when $t\in [100, 150]$

Fig. 7

Spatial plots of W of model (5.3)

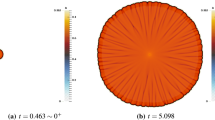
We show the spatial-temporal plots of unknown functions as that in Fig. 6, from which we see that W invades the habitat from the left and right directions, and leftward and rightward invasion speeds are approximately different constants. In addition, we take $t=100, 120, 140$ to plot the spatial distribution of unknown functions and list the movement of level sets in Fig. 7 and Table 3, from which we see the rightward invasion speed $c_*^+$ of W is close to 1.27, and the leftward invasion speed $c_*^-$ of W is close to 1.12.

From our theoretical analysis, we may estimate the spreading speed by numerical results and our numerical examples give us the useful illustration. Let the spatial periodic average of parameters be fixed. Our numerical results show that spreading speed in space-time periodic environment could be faster than the speed in time periodic environment. Does this indicate that the spatial expansion ability benefits from the spatial heterogeneity? When the domain is bounded, the spatial heterogeneity may lead to larger capacity of a species [25]. Moreover, for the propagation speeds of the KPP-type problems in space periodic media, the results about the positive effect of the heterogeneities were stated in [9, 15, 16]. Motivated by our numerical results, for the propagation dynamics in such a non-cooperative system, we conjecture that the heterogeneity may speed up the spreading speed when diffusion coefficients are constants.

Furthermore, in the space-time environment, our results immensely depend on the sign of the generalized principal eigenvalue $\lambda '_1$ that is not larger than another generalized principal eigenvalue $\lambda _1$. In the study of scalar equations, the convergence of solution depends on the sign of the generalized principal eigenvalue $\lambda _1$, see Nadin [29, Theorem 1.6]. Then for the case $\lambda '_1<0$, further applying the property of $\lambda _1,$ can we achieve some convergence results about model (1.2)? In particular, the convergence also depends on the existence and uniqueness of nontrivial positive entire solutions of (1.2). This question deserves our further investigation.

Table 3 Approximate level sets in Fig. 6

Appendix: The verification of Proposition 2.1

In this Appendix, we will prove Proposition 2.1. Our main tool is the method of upper and lower solutions [32]. First of all, we introduce the definition of the upper and lower solutions and comparison principle for system (2.9).

Definition 5.4

Assume that $(\overline{U}(x,t),\overline{V}(x,t),\overline{W}(x,t))$, $(\underline{U}(x,t),\underline{V}(x,t),\underline{W}(x,t))$ are continuous and bounded positive functions for $x\in {\mathbb {R}},\, t\ge 0$. Then they are a pair of upper and lower solutions of (2.9) if

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial {\overline{U}}}{\partial t}\ge D_1\Delta {\overline{U}}+d_1(U^0-{\overline{U}})-\frac{ \beta _1{\overline{U}}\underline{W}}{1+a_1{\overline{U}}+b_1\underline{W}},\\ \frac{\partial {\overline{V}}}{\partial t}\ge D_2\Delta {\overline{V}}+d_2(V^0-{\overline{V}})-\frac{ \beta _2{\overline{V}}\underline{W}}{1+a_2{\overline{V}}+b_2\underline{W}},\\ \frac{\partial {\overline{W}}}{\partial t}\ge D_3\Delta {\overline{W}}-d_3{\overline{W}}+\frac{ \beta _1{\overline{U}}{\overline{W}}}{1+a_1{\overline{U}}+b_1{\overline{W}}}+\frac{ \beta _2{\overline{V}}{\overline{W}}}{1+a_2{\overline{V}}+b_2{\overline{W}}},\\ {\overline{U}}(x,0)\ge U_0(x),\ {\overline{V}}(x,0)\ge V_0(x),\ {\overline{W}}(x,0)\ge W_0(x), \end{array}\right. } \end{aligned}$$

(5.4)

and

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial {\underline{U}}}{\partial t}\le D_1\Delta {\underline{U}}+d_1(U^0-{\underline{U}})-\frac{ \beta _1{\underline{U}}\overline{W}}{1+a_1{\underline{U}}+b_1\overline{W}},\\ \frac{\partial {\underline{V}}}{\partial t}\le D_2\Delta {\underline{V}}+d_2(V^0-{\underline{V}})-\frac{ \beta _2{\underline{V}}\overline{W}}{1+a_2{\underline{V}}+b_2\overline{W}},\\ \frac{\partial {\underline{W}}}{\partial t}\le D_3\Delta {\underline{W}}-d_3{\underline{W}}+\frac{ \beta _1{\underline{U}}{\underline{W}}}{1+a_1{\underline{U}}+b_1{\underline{W}}} +\frac{ \beta _2{\underline{V}}{\underline{W}}}{1+a_2{\underline{V}}+b_2{\underline{W}}},\\ {\underline{U}}(x,0)\le U_0(x),\ {\underline{V}}(x,0)\le V_0(x),\ {\underline{W}}(x,0)\le W_0(x) \end{array}\right. } \end{aligned}$$

(5.5)

for all $x\in {\mathbb {R}},\, t>0 .$

Lemma 5.5

([40]) Assume that $(\overline{U}(x,t),\overline{V}(x,t),\overline{W}(x,t))$ and $(\underline{U}(x,t),\underline{V}(x,t),\underline{W}(x,t))$ are a pair of upper and lower solutions of (2.9). Then (2.9) has a solution such that

$$\begin{aligned} (\underline{U}(x,t),\underline{V}(x,t),\underline{W}(x,t))\le & {} (U(x,t),V(x,t),W(x,t))\\\le & {} (\overline{U}(x,t),\overline{V}(x,t), \overline{W}(x,t)),x\in {\mathbb {R}}, t>0 . \end{aligned}$$

Now we are ready to prove Proposition 2.1.

Proof of Proposition 2.1

By the above Definition 5.4 and Lemma 5.5, we shall divide the proof into the following four steps:

Step 1:

Show the uniqueness of $(U^*,V^*,W^*)$.

Step 2:

Define the potential upper and lower solutions.

Step 3:

Verify the differentiable inequalities.

Step 4:

Consider the initial condition.

Step 1 From the definition of $(U^*,V^*,W^*)$, we have

$$\begin{aligned} d_1(U^0-U^*)=\frac{\beta _{1}U^*W^*}{1+a_{1}U^*+b_{1}W^*}, ~~d_2(V^0-V^*)=\frac{\beta _{2}V^*W^*}{1+a_{2}V^*+b_{2}W^*}, \end{aligned}$$

(5.6)

and

$$\begin{aligned} d_3=\frac{\beta _{1}U^*}{1+a_{1}U^*+b_{1}W^*} +\frac{\beta _{2}V^*}{1+a_{2}V^*+b_{2}W^*}. \end{aligned}$$

(5.7)

In fact, the spatially homogeneous positive steady state is unique. Assume, for the sake of contradiction, that $(\widetilde{U}^*,\widetilde{V}^*,\widetilde{W}^*)$ is another positive spatially homogeneous steady state. Without loss of generality, we assume that $\widetilde{W}^*>W^*$. From (5.6), we have $\widetilde{U}^*<U^*$ and $\widetilde{V}^*<V^*$ based on the monotonicity. Then (5.7) does not hold, so a contradiction occurs. Hence, the spatially homogeneous positive steady state is unique.

Step 2 We now define some continuous functions. Since $b_1>\frac{\beta _1}{d_1}$, we have

$$\begin{aligned} U^0-U^*=\frac{\beta _{1}}{d_1}\frac{U^*W^*}{1+a_{1}U^*+b_{1}W^*}<U^*\frac{b_1W^*}{1+a_{1}U^*+b_{1}W^*}<U^*. \end{aligned}$$

Similarly, we have $V^0-V^*<V^*$. Then we define

$$\begin{aligned} \overline{U}= & {} U^{*}+(U^{0}-U^{*})e^{-\lambda t},~~\underline{U} =U^{*}-(U^{0}-U^{*})e^{-\lambda t}>0, \\ \overline{V}= & {} V^{*}+(V^{0}-V^{*})e^{-\lambda t},~~\underline{V} =V^{*}-(V^{0}-V^{*})e^{-\lambda t}>0, \\ \overline{W}= & {} W^{*}+Ae^{-\lambda t},~~\underline{W}=W^{*}-Ae^{-\lambda t}, \end{aligned}$$

where $\lambda >0$ small enough and $1<\frac{W^*}{A}\le \min \left\{ \frac{d_1b_1}{\beta _1},\frac{d_2b_2}{\beta _2}\right\}$.

Step 3 We verify the differentiable inequalities in (5.4) and (5.5).

• (1) When $0<\lambda \le d_1(1-\frac{A}{W^*})$, we have

  $$\begin{aligned}&-\overline{U}_t+d_1(U^0-\overline{U})-\frac{ \beta _1 \overline{U}\underline{W}}{1+a_1\overline{U}+b_1\underline{W}}\\&\quad =\lambda (U^0-U^*)e^{-\lambda t}+d_1[(U^0-U^*)-(U^0-U^*)e^{-\lambda t}] -\frac{ \beta _1\overline{U}\underline{W}}{1+a_1\overline{U}+b_1\underline{W}}\\&\quad =(\lambda -d_1)(U^0-U^*)e^{-\lambda t}+d_1(U^0-U^*) -\frac{ \beta _1\overline{U}\underline{W}}{1+a_1\overline{U}+b_1\underline{W}}\\&\quad \le (\lambda -d_1)(U^0-U^*)e^{-\lambda t}+d_1(U^0-U^*) -\frac{ \beta _1U^*\underline{W}}{1+a_1U^*+b_1W^*}\\&\quad =(\lambda -d_1)(U^0-U^*)e^{-\lambda t}+d_1(U^0-U^*)\\&\qquad -\frac{ \beta _1U^*W^*}{1+a_1U^*+b_1W^*} +A\frac{ \beta _1U^*}{1+a_1U^*+b_1W^*}e^{-\lambda t}\\&\quad =(\lambda -d_1)(U^0-U^*)e^{-\lambda t} +A\frac{ d_1(U^0-U^*)}{W^*}e^{-\lambda t}\\&\quad =(\lambda -d_1+A\frac{d_1}{W^*})(U^0-U^*)e^{-\lambda t}\le 0. \end{aligned}$$

• (2) When $0<\lambda \le d_2(1-\frac{A}{W^*})$, we have

  $$\begin{aligned}&-\overline{V}_t+d_2(V^0-\overline{V})-\frac{ \beta _2 \overline{V}\underline{W}}{1+a_2\overline{V}+b_2\underline{W}}\\&\quad =\lambda (V^0-V^*)e^{-\lambda t}+d_2[(V^0-V^*)-(V^0-V^*)e^{-\lambda t}] -\frac{ \beta _2\overline{V}\underline{W}}{1+a_2\overline{V}+b_2\underline{W}}\\&\quad =(\lambda -d_2)(V^0-V^*)e^{-\lambda t}+d_2(V^0-V^*) -\frac{ \beta _2\overline{V}\underline{W}}{1+a_2\overline{V}+b_2\underline{W}}\\&\quad \le (\lambda -d_2)(V^0-V^*)e^{-\lambda t}+d_2(V^0-V^*) -\frac{\beta _2V^*\underline{W}}{1+a_2V^*+b_2W^*}\\&\quad =(\lambda -d_2)(V^0-V^*)e^{-\lambda t}+d_2(V^0-V^*)\\&\qquad -\frac{\beta _2V^*W^*}{1+a_2V^*+b_2W^*}+A \frac{\beta _2V^*}{1+a_2V^*+b_2W^*}e^{-\lambda t}\\&\quad =(\lambda -d_2)(V^0-V^*)e^{-\lambda t} +A\frac{d_2(V^0-V^*)}{W^*}e^{-\lambda t}\\&\quad =(\lambda -d_2+A\frac{d_2}{W^*})(V^0-V^*)e^{-\lambda t}\le 0. \end{aligned}$$

• (3) Since $\overline{W} > W^*,$ we only consider

  $$\begin{aligned}&\frac{\beta _{1}\overline{U}}{1+a_{1}\overline{U}+b_{1}\overline{W}} +\frac{\beta _{2}\overline{V}}{1+a_{2}\overline{V}+b_{2}\overline{W}}-d_{3} \\&\quad =\frac{\beta _{1}\overline{U}}{1+a_{1}\overline{U}+b_{1}\overline{W}} -\frac{\beta _{1}U^{*}}{1+a_{1}U^{*}+b_{1}W^{*}} +\frac{\beta _{2}\overline{V}}{1+a_{2}\overline{V}+b_{2}\overline{W}} -\frac{\beta _{2}V^{*}}{1+a_{2}V^{*}+b_{2}W^{*}}. \end{aligned}$$

  Note that

  $$\begin{aligned}&\overline{U}[1+a_{1}U^{*}+b_{1}W^{*}] -U^{*}[1+a_{1}\overline{U} +b_{1}\overline{W}]\\&\quad = (U^0-U^*)e^{-\lambda t}[1+a_{1}U^{*}+b_{1} W^{*}]-U^{*}[a_1(U^0-U^*)e^{-\lambda t}+b_1Ae^{-\lambda t}]\\&\quad =\bigg [(U^0-U^*)(1+b_1W^*)-AU^*b_1\bigg ]e^{-\lambda t}\\&\quad = \bigg [\frac{\beta _1}{d_1}\frac{U^*W^*(1+b_1W^*)}{1+a_{1} U^*+b_{1}W^*}-AU^*b_1\bigg ]e^{-\lambda t}\\&\quad \le \bigg [\frac{Ab_1}{W^*}\frac{U^*W^*(1+b_1W^*)}{1+a_{1} U^*+b_{1}W^*}-AU^*b_1\bigg ]e^{-\lambda t}\\&\quad = -\frac{Ab_1U^*a_{1}U^*}{1+a_{1}U^*+b_{1}W^*}e^{-\lambda t}<0, \end{aligned}$$

  and

  $$\begin{aligned}&\overline{V}[1+a_{2}V^{*}+b_{2}W^{*}] -V^{*}[1+a_{2}\overline{V}+b_{2}\overline{W}]\\&\quad = (V^0-V^*)e^{-\lambda t}[1+a_{2}V^{*} +b_{2}W^{*}]-V^{*}[a_2(V^0-V^*)e^{-\lambda t}+b_2Ae^{-\lambda t}]\\&\quad =\bigg [(V^0-V^*)(1+b_2W^*)-AV^*b_2\bigg ]e^{-\lambda t}\\&\quad = \bigg [\frac{\beta _2}{d_2}\frac{V^*W^*(1+b_2W^*)}{1+a_{2} V^*+b_{2}W^*}-AV^*b_2\bigg ]e^{-\lambda t}\\&\quad \le \bigg [\frac{Ab_2}{W^*}\frac{V^*W^*(1+b_2W^*)}{1+a_{2} V^*+b_{2}W^*}-AV^*b_2\bigg ]e^{-\lambda t}\\&\quad = -\frac{Ab_2V^*a_{2}V^*}{1+a_{2}V^*+b_{2}W^*}e^{-\lambda t}<0, \end{aligned}$$

  we can choose $\lambda >0$ small enough such that the third inequality of (5.4) holds.

• (4) When $0<\lambda \le d_1(1-\frac{A}{W^*})$, we have

  $$\begin{aligned}&-\underline{U}_t+d_1(U^0-\underline{U})-\frac{ \beta _1{\underline{U}} \overline{W}}{1+a_1{\underline{U}}+b_1\overline{W}}\\&\quad =-\lambda (U^0-U^*)e^{-\lambda t}+d_1[(U^0-U^*)+(U^0-U^*) e^{-\lambda t}]-\frac{ \beta _1{\underline{U}} \overline{W}}{1+a_1{\underline{U}}+b_1\overline{W}}\\&\quad =(d_1-\lambda )(U^0-U^*)e^{-\lambda t}+d_1(U^0-U^*) -\frac{ \beta _1{\underline{U}}\overline{W}}{1+a_1{\underline{U}}+b_1\overline{W}}\\&\quad \ge (d_1-\lambda )(U^0-U^*)e^{-\lambda t}+d_1(U^0-U^*) -\frac{\beta _1{U^*}\overline{W}}{1+a_1{U^*}+b_1W^*}\\&\quad = (d_1-\lambda )(U^0-U^*)e^{-\lambda t}+d_1(U^0-U^*)\\&\qquad -\frac{\beta _1{U^*}W^*}{1+a_1{U^*}+b_1W^*} -\frac{A \beta _1{U^*}}{1+a_1{U^*}+b_1W^*}e^{-\lambda t}\\&\quad = (d_1-\lambda )(U^0-U^*)e^{-\lambda t} -\frac{A \beta _1{U^*}}{1+a_1{U^*}+b_1W^*}e^{-\lambda t}\\&\quad = (d_1-\lambda -d_1\frac{ A}{W^*})(U^0-U^*)e^{-\lambda t}\ge 0. \end{aligned}$$

• (5) When $0<\lambda \le d_2(1-\frac{A}{W^*})$, we have

  $$\begin{aligned}&-\underline{V}_t+d_2(V^0-\underline{V})-\frac{\beta _2{\underline{V}} \overline{W}}{1+a_2{\underline{V}}+b_2\overline{W}}\\&\quad =-\lambda (V^0-V^*)e^{-\lambda t}+d_2[(V^0-V^*)+(V^0-V^*) e^{-\lambda t}]-\frac{ \beta _2{\underline{V}}\overline{W}}{1+a_2{\underline{V}} +b_2\overline{W}}\\&\quad = (d_2-\lambda )(V^0-V^*)e^{-\lambda t}+d_2(V^0-V^*) -\frac{\beta _2{\underline{V}}\overline{W}}{1+a_2{\underline{V}}+b_2\overline{W}}\\&\quad \ge (d_2-\lambda )(V^0-V^*)e^{-\lambda t}+d_2(V^0-V^*) -\frac{ \beta _2{V^*}\overline{W}}{1+a_2{V^*}+b_2W^*}\\&\quad = (d_2-\lambda )(V^0-V^*)e^{-\lambda t}+d_2(V^0-V^*)\\&\qquad -\frac{\beta _2{V^*}W^*}{1+a_2{V^*}+b_2W^*}-\frac{ A\beta _2{V^*}}{1+a_2{V^*} +b_2W^*}e^{-\lambda t}\\&\quad =(d_2-\lambda )(V^0-V^*)e^{-\lambda t} -\frac{A\beta _2{V^*}}{1+a_2{V^*}+b_2W^*}e^{-\lambda t}\\&\quad =(d_2-\lambda -d_2\frac{ A}{W^*})(V^0-V^*)e^{-\lambda t}\ge 0. \end{aligned}$$

• (6) Similar to that in (3), we consider

  $$\begin{aligned}&\frac{\beta _1\underline{U}}{1+a_1\underline{U} +b_1\underline{W}}+\frac{\beta _2\underline{V}}{1+a_2\underline{V} +b_2\underline{W}}-d_3\\&\quad =\frac{\beta _1\underline{U}}{1+a_1\underline{U}+b_1\underline{W}} -\frac{\beta _{1}U^*}{1+a_{1}U^*+b_{1}W^*}+\frac{\beta _2 \underline{V}}{1+a_2\underline{V}+b_2\underline{W}} -\frac{\beta _{2}V^*}{1+a_{2}V^*+b_{2}W^*}. \end{aligned}$$

  Note that

  $$\begin{aligned}&\underline{U}(1+a_{1}U^*+b_{1}W^*)-U^*(1+a_1\underline{U}+b_1\underline{W})\\&\quad =U^{*}[a_1(U^0-U^*)e^{-\lambda t}+b_1Ae^{-\lambda t}]-(U^0-U^*) e^{-\lambda t}[1+a_{1}U^{*}+b_{1}W^{*}]\\&\quad =\bigg [AU^*b_1-(U^0-U^*)(1+b_1W^*)\bigg ]e^{-\lambda t}\\&\quad =\bigg [AU^*b_1-\frac{\beta _1}{d_1} \frac{U^*W^*(1+b_1W^*)}{1+a_{1}U^*+b_{1}W^*}\bigg ]e^{-\lambda t}\\&\quad \ge \bigg [AU^*b_1-\frac{Ab_1}{W^*}\frac{U^*W^*(1+b_1W^*)}{1+a_{1}U^* +b_{1}W^*}\bigg ]e^{-\lambda t}\\&\quad =\frac{Ab_1U^*a_{1}U^*}{1+a_{1}U^*+b_{1}W^*}e^{-\lambda t}>0, \end{aligned}$$

  and

  $$\begin{aligned}&\underline{V}[1+a_{2}V^{*}+b_{2}W^{*}]-V^{*}[1+a_{2} \underline{V} +b_{2}\underline{W}]\\&\quad =V^{*}[a_2(V^0-V^*)e^{-\lambda t}+b_2Ae^{-\lambda t}] -(V^0-V^*)e^{-\lambda t}[1+a_{2}V^{*}+b_{2}W^{*}]\\&\quad =\bigg [AU^*b_2-(V^0-V^*)(1+b_2W^*)\bigg ]e^{-\lambda t}\\&\quad = \bigg [AV^*b_2-\frac{\beta _2}{d_2}\frac{V^*W^*(1+b_2W^*)}{1+a_{2} V^*+b_{2}W^*}\bigg ]e^{-\lambda t}\\&\quad \ge \bigg [AV^*b_2-\frac{Ab_2}{W^*}\frac{V^*W^*(1+b_2W^*)}{1+a_{2} V^*+b_{2}W^*}\bigg ]e^{-\lambda t}\\&\quad =\frac{Ab_2V^*a_{2}V^*}{1+a_{2}V^*+b_{2}W^*}e^{-\lambda t}>0, \end{aligned}$$

  we can choose $\lambda >0$ small enough such that the third inequality of (5.5) is true. Hence, we can obtain a properly small constant $\lambda >0$ such that (5.4) and (5.5) hold.

Step 4 We show that there exists a constant $T'_*>0$ such that

$$\begin{aligned} U(x,T'_*)>2U^*-U^0,V(x,T'_*)>2V^*-V^0,W^*-A<W(x,T'_*)<W^*+A \end{aligned}$$

(5.8)

for $A>0$ with $1<\frac{W^*}{A}\le \min \left\{ \frac{d_1b_1}{\beta _1},\frac{d_2b_2}{\beta _2}\right\}$.

From Lemma 3.1, we know $U(x,t)<U^0$, $V(x,t)<V^0$. Note that

$$\begin{aligned} \frac{\partial W(x,t)}{\partial t}\le & {} D_{3}\Delta W(x,t)-d_{3}W(x,t) \\&+\frac{\beta _{1}U^{0}W(x,t)}{1+a_{1}U^{0}+b_{1}W(x,t)} +\frac{\beta _{2}V^{0}W(x,t)}{1+a_{2}V^{0}+b_{2}W(x,t)} \end{aligned}$$

and

$$\begin{aligned} \frac{\beta _{1}U^{0}}{1+a_{1}U^{0}+b_{1}W^{0}} +\frac{\beta _{2}V^{0}}{1+a_{2}V^{0}+b_{2}W^{0}}=d_{3}, \end{aligned}$$

we see that

$$\begin{aligned} \limsup _{t\rightarrow \infty }\sup _{x\in {\mathbb {R}}}W(x,t)\le W^{0}, \end{aligned}$$

which indicates that there exists $T_1' >0$ such that $W(x,t)\le W^0$ for all $t\ge T_1'$. If $W^0<W^*+A$, then there exists a constant $T'_1>0$ such that $W(x,t)<W^*+A$ for all $t \ge T'_1$. Let

$$\begin{aligned} H(w)=\frac{\beta _1U^0}{1+a_1U^0+b_1w}+\frac{\beta _2V^0}{1+a_2V^0+b_2w}-d_3. \end{aligned}$$

We only need to verify $H(W^*+A) <0.$ From

$$\begin{aligned}&U^*(1+b_1W^*+b_1A)-U^0(1+b_1W^*)\\&\quad =U^*+b_1U^*W^*+b_1U^*A-\left( U^*+\frac{\beta _{1}}{d_1} \frac{U^*W^*}{1+a_{1}U^*+b_{1}W^*}\right) (1+b_1W^*)\\&\quad =b_1U^*A-\frac{\beta _{1}}{d_1}U^*W^*\frac{1+b_1W^*}{1+a_{1}U^*+b_{1}W^*}\\&\quad \ge U^*\left( \frac{\beta _{1}}{d_1}W^*-\frac{\beta _{1}}{d_1}W^* \frac{1+b_1W^*}{1+a_{1}U^*+b_{1}W^*}\right) \\&\quad =\frac{\beta _{1}}{d_1}\frac{a_{1}U^*}{1+a_{1}U^*+b_{1}W^*}U^*W^*>0, \end{aligned}$$

one has

$$\begin{aligned}&\frac{\beta _1U^0}{1+a_1U^0+b_1(W^*+A)}-\frac{\beta _{1}U^*}{1+a_{1}U^*+b_{1}W^*}\\&\quad =\frac{\beta _1U^0U^*}{U^*\left[ 1+a_1U^0+b_1(W^*+A)\right] } -\frac{\beta _{1}U^*U^0}{U^0\left[ 1+a_{1}U^*+b_{1}W^*\right] }\\&\quad =\frac{\beta _1U^0U^*}{a_1U^0U^*+U^*(1+b_1W^*+b_1A)} -\frac{\beta _{1}U^*U^0}{a_1U^0U^*+U^0(1+b_1W^*)}\\&\quad <0. \end{aligned}$$

Similarly, we have

$$\begin{aligned} \frac{\beta _2V^0}{1+a_2V^0+b_2(W^*+A)} <\frac{\beta _{2}V^*}{1+a_{2}V^*+b_{2}W^*}. \end{aligned}$$

Hence we obtain

$$\begin{aligned}&H(W^*+A)\\&\quad =\frac{\beta _1U^0}{1+a_1U^0+b_1(W^*+A)} +\frac{\beta _2V^0}{1+a_2V^0+b_2(W^*+A)}-d_3\\&\quad =\frac{\beta _1U^0}{1+a_1U^0+b_1(W^*+A)} -\frac{\beta _{1}U^*}{1+a_{1}U^*+b_{1}W^*}\\&\qquad +\frac{\beta _2V^0}{1+a_2V^0+b_2(W^*+A)} -\frac{\beta _{2}V^*}{1+a_{2}V^*+b_{2}W^*}\\&\quad <0, \end{aligned}$$

which implies that $W^0<W^*+A$.

Next we use the same idea to discuss U(x, t) and V(x, t). For U,  it suffices to verify that $P(2U^*-U^0) <0,$ where

$$\begin{aligned} P(u)=\frac{\beta _1W^0u}{1+a_1u+b_1W^0}+d_1(u-U^0). \end{aligned}$$

Since P(u) has a unique zero point $U_1>0$, it suffices to verify that $U_1>2U^*-U^0$ or $P(2U^*-U^0)<0$ from the monotonicity. Note that

$$\begin{aligned}&P(2U^*-U^0)\\&\quad =\frac{\beta _1(2U^*-U^0)W^0}{1+a_1(2U^*-U^0)+b_1W^0}+d_1(2U^*-U^0-U^0)\\&\quad<\frac{\beta _1(2U^*-U^0)(W^*+A)}{1+a_1\left( U^*-\frac{\beta _{1}}{d_1} \frac{U^*W^*}{1+a_{1}U^*+b_{1}W^*}\right) +b_1(W^*+A)} -\frac{2\beta _{1}U^*W^*}{1+a_{1}U^*+b_{1}W^*}\\&\quad =\frac{2\beta _1U^*W^*+2\beta _1U^*A-\beta _1U^0(W^*+A)}{1+a_{1}U^*+b_{1} W^*+b_1A-\frac{\beta _{1}}{d_1}\frac{a_1U^*W^*}{1+a_{1}U^*+b_{1}W^*}} -\frac{2\beta _{1}U^*W^*}{1+a_{1}U^*+b_{1}W^*}\\&\quad<\frac{2\beta _1U^*W^*+\beta _1U^0(W^*+A)-\beta _1U^0(W^*+A)}{1+a_{1} U^*+b_{1}W^*+\frac{\beta _{1}}{d_1}W^*-\frac{\beta _{1}}{d_1} \frac{a_1U^*W^*}{1+a_{1}U^*+b_{1}W^*}}-\frac{2\beta _{1}U^*W^*}{1+a_{1}U^*+b_{1}W^*}\\&\quad =\frac{2\beta _1U^*W^*}{1+a_{1}U^*+b_{1}W^*+\frac{\beta _{1}}{d_1} W^*\frac{1+b_{1}W^*}{1+a_{1}U^*+b_{1}W^*}} -\frac{2\beta _{1}U^*W^*}{1+a_{1}U^*+b_{1}W^*}\\&\quad <0, \end{aligned}$$

there exists a $T'_2>0$ such that $U(x,t)>U_1>2U^*-U^0$ for all $t\ge T'_2$. Similarly, there exists a $T'_3>0$ such that $V(x,t)>V_1>2V^*-V^0$ for all $t\ge T'_3$.

Finally, from

$$\begin{aligned} \frac{\partial W(x,t)}{\partial t}\ge & {} D_{3}\Delta W(x,t)-d_{3}W(x,t) \\&+\frac{\beta _{1}(2U^{*}-U^{0})W(x,t)}{1+a_{1}(2U^{*} -U^{0})+b_{1}W(x,t)}+\frac{\beta _{2}(2V^{*}-V^{0})W(x,t)}{ 1+a_{2}(2V^{*}-V^{0})+b_{2}W(x,t)}, \end{aligned}$$

it suffices to prove that

$$\begin{aligned} G(w)=\frac{\beta _{1}(2U^{*}-U^{0})}{1+a_{1}(2U^{*}-U^{0})+b_{1}w} +\frac{\beta _{2}(2V^{*}-V^{0})}{1+a_{2}(2V^{*}-V^{0})+b_{2}w}-d_{3} \end{aligned}$$

has a unique positive root $W_1> W^*-A.$ Let

$$\begin{aligned} G_{1}(w)= & {} \frac{\beta _{1}(2U^{*}-U^{0})}{1+a_{1}(2U^{*}-U^{0})+b_1w} -\frac{\beta _{1}U^{*}}{1+a_{1}U^{*}+b_{1}W^{*}}, \\ G_{2}(w)= & {} \frac{\beta _{2}(2V^{*}-V^{0})}{1+a_{2}(2V^{*}-V^{0})+b_2w} -\frac{\beta _{2}V^{*}}{1+a_{2}V^{*}+b_{2}W^{*}}. \end{aligned}$$

Then, $G(w)=G_1(w)+G_2(w)$. Note that

$$\begin{aligned} G_{1}(W^{*}-A)=\frac{\beta _{1}(2U^{*}-U^{0})}{1+a_{1}(2U^{*} -U^{0})+b_{1}(W^{*}-A)}-\frac{\beta _{1}U^{*}}{1+a_{1}U^{*} +b_{1}W^{*}} \end{aligned}$$

and

$$\begin{aligned}&(2U^{*}-U^{0})(1+a_{1}U^{*}+b_{1}W^{*})-U^{*} \left[ 1+a_{1}(2U^{*}-U^{0})+b_{1}(W^{*}-A)\right] \\= & {} \left( U^{*}-\frac{\beta _{1}}{d_{1}}\frac{U^{*} W^{*}}{1+a_{1}U^{*}+b_{1}W^{*}}\right) (1+a_{1}U^{*}+b_{1}W^{*}) \\&-\left[ U^{*}+a_{1}U^{*}\left( U^{*}-\frac{\beta _{1}}{d_{1}} \frac{U^{*}W^{*}}{1+a_{1}U^{*}+b_{1}W^{*}}\right) +b_{1}U^{*}(W^{*}-A)\right] \\= & {} b_{1}U^{*}A-\frac{\beta _{1}}{d_{1}}U^{*}W^{*} \frac{1+b_{1}W^{*}}{1+a_{1}U^{*}+b_{1}W^{*}} \\\ge & {} \frac{\beta _{1}}{d_{1}}U^{*}W^{*}-\frac{\beta _{1}}{d_{1}} U^{*}W^{*}\frac{1+b_{1}W^{*}}{1+a_{1}U^{*}+b_{1}W^{*}} \\= & {} a_{1}U^{*}(U^{0}-U^{*})>0, \end{aligned}$$

we obtain $G_{1}(W^{*}-A)>0.$ Similarly, we can obtain $G_2(W^*-A)>0$, and so $G(W^*-A)>0$. From the monotonicity of G(w), we obtain $W_1>W^*-A>0$. Thus, there exists a $T'_4>0$ such that $W(x,t)>W_1>W^*-A$ for all $t\ge T'_4$.

Choose $T'_*=T'_1+T'_2+T'_3+T'_4>0$. Consequently, (5.8) holds. The proof is complete. $\square$