1 Introduction

The slow oscillation of slow-wave sleep typically takes the form of an approximately 1-Hz rhythmic rising and falling of membrane potential across cortical neurons [1]. In the depolarized “up” state, neurons fire rapidly; in the hyperpolarized “down” state, there is usually no firing. The presence of the oscillation has been linked strongly to memory consolidation [2, 3]. It is likely that the oscillation is linked with bistability in networks of cortical neurons, or within thalamic neurons, or attributable to the interplay between these two brain regions, but the details are not clear. For example, the nature of the cortical and thalamic roles has been investigated recently by Destexhe in a model of thalamic, cortical, and thalamocortical networks [4]. All three situations could produce up and down states in certain circumstances.

In terms of cortical modelling, Compte et al. [5] showed that a simple one-dimensional collection of neurons can support a prototypical slow oscillation. Hill and Tononi [6] have carried out simulations with a more comprehensive thalamocortical network that show the importance of cortical–cortical interactions in establishing and maintaining the oscillation. Experimental work on the cortical nature of the slow oscillation includes that of Steriade et al. [7], who demonstrated that the slow oscillation is maintained in cat cortex following lesioning of the thalamus. Additionally, the difficulty of obtaining a slow oscillation in a thin brain slice (e.g., the investigations of slices of cat cortex by Timofeev et al. [8]) points to the importance of connectivity in establishing this oscillation.

However, there is also evidence pointing to the key role of the thalamus. Blethyn et al. have demonstrated that a thalamic slice can produce slow oscillations, and that the individual thalamic neurons are intrinsically bistable [9]. Additionally, a bistability in reticular neurons in the thalamus has been investigated experimentally by Fuentealba et al. [10]. These studies may point to a thalamic origin of the slow oscillation. However, one should not also discount the possibility of significant interplay between these two brain regions during the presence of the oscillation.

In previous work [11], we have followed Compte et al. [5] and have interpreted the slow oscillation as a form of phase transition. The depolarized “up” and hyperpolarized “down” states are viewed as stable solutions for the mean membrane potential, with the down-to-up transitions being driven possibly by spontaneous neurotransmitter release [12] or random summation of EPSPs [13], and the up-to-down transition driven possibly by voltage-gated ionic (e.g., K + ) currents [5, 6, 14], or changes in synaptic weight [6, 15]. Molaee–Ardekani et al., using a broadly similar model, have taken a different view of the phenomenon, interpreting the small slow waves seen in light anaesthesia as small, unstable excursions away from the equilibrium state, and the large slow waves of deep anaesthesia as limit cycles of the bulk behavior of the cortex [16]. Other possible explanations could include individual cortical neurons being slaves to an oscillation elsewhere in the brain, or a hybrid of collective and individual neuron modes. For example, Robinson et al. have modelled the bursting of neocortical neurons using a model based on two coupled oscillators [17]. One oscillator describes the spiking dynamics of a neuron; the second generates a slow modulation from biophysical conductance-based equations.

In [18], we presented evidence for the phase-transition view; namely, that the fluctuations in membrane potential grow as the transition between the down to the up state approaches, and simultaneously the power shifts towards lower frequencies. These phenomena are in agreement with a first-order phase transition model, in which fluctuations are predicted to grow and slow on the approach to the transition [19, 20].

In this paper, we consider the transition between down and up states itself. Specifically, we use data of membrane potential from the slow oscillation in rats anaesthetized with urethane and analyze the trajectory of the transition, including the difference in membrane potential between the down and up states, and compare this with predictions from phase transition theory. We follow a similar analysis to Cossart et al., who have studied the activation of long-lived up states of activity of neural assemblies during cognitive states [21]. They suggested that the movement in membrane potential could be described by an exponential approach to an equilibrium (i.e., up state) value. However, this work with a conscious brain may not relate directly to an analysis of slow-wave sleep.

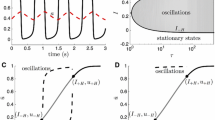
Figure 1 shows a stylized model of a first-order phase transition [19]. The solution to a set of equations describing the system is shown by the solid line; it is characterized by having a region of parameter space with multiple (in this case, three) solutions. If the lower solution is chosen, and the driving parameter is increased far enough (from a to b), the solution will undergo a “step” jump from its lower to upper state. In such transitions, the jump is characterized by a build-up in amplitude of small, random fluctuations about the solution. The size of these fluctuations is inversely related to the stability of the solution, as described for a mean-field cortical model by Steyn-Ross et al. [19].

Fig. 1
figure 1

A stylized depiction of first-order phase transitions. Three curves are shown, corresponding to three different values of a control parameter. In the central region, there are three possible firing rates for the value of the driving parameter. If one considers the driving parameter (shown on the x axis) to increase when the firing rate (y axis) is low, but to decrease when the firing rate is high, we would expect to see orbits, such as that denoted by the trajectory abcd. If the region of multiple firing-rates decreases (trajectory ABCD), the size of the jump will be reduced to BC as compared to bc

Full size image

If the driving parameter is driven downwards when the membrane potential is high (depolarized), and upwards when the membrane potential is low (hyperpolarized), a loop results with the system continually moving between the upper and lower states. The transition between the lower and upper states, once established, is likely to be fairly fast (see, e.g., Wilson et al. [11] and Wilson et al. [22], where numerical simulations of this situation have been performed for a cortical model). This is because, when the random fluctuations or driving currents are great enough for the system to overcome the attractor of the lower branch, the system will be subjected to the strong attractor of the upper branch, which will pull it quickly into the new equilibrium state.

However, one might expect the early onset of the transition away from the lower branch to be slow. This is because of critical slowing in a system close to a saddle-node bifurcation (i.e., close to point b of Fig. 1) [20]. At the limit of the lower attractor, fluctuations occur infinitely slowly. Since the dynamics of the transition grows out of the dynamics of the fluctuation, this could be expected to be a slow process. This may be true even when the system is driven beyond point b by driving currents; although no lower branch equilibrium exists, the dynamics of the onset of the transition will still be slow as the system moves away from the “ghost” of its stable state [23]. In this article, we analyze the dynamics of this transition and compare it with the predictions of the first-order phase transition hypothesis.

2 Materials and methods

All experiments were approved by the University of Otago Animal Ethics Committee (AEC approval number 93/04 and 18/06).

2.1 Surgery

Male Wistar rats (280–390 g) were anaesthetized with an intraperitoneal (ip) injection of urethane (1.6–2.0 g/kg body weight; Sigma-Aldrich, St Louis, MO, USA). The local anaesthetic bupivacaine (up to 2 mg/kg; Astra-Zeneca, North Ryde, Australia) was applied intramuscularly to all incisions and pressure points. Surgical anaesthesia was verified by the absence of the withdrawal reflex following administration of a toe pinch.

For intracellular recording, a craniotomy was performed over the left motor cortex (in relation to bregma: AP, −1.0 to +4.0 mm, ML, +1.0 to +3.0 mm), and for EEG recording, a burr hole was drilled in the skull for placement of a silver wire electrode against the dura. The synchrony of the EEG waveform was used as an indication of depth of anaesthesia. Supplementary urethane (approximately 0.15 g/kg ip every 2 h) was administered on detecting EEG desynchronization. Dental acrylic was used to cement the EEG electrode in place and build a well around the craniotomy. During recording, the well was filled with paraffin wax to increase recording stability, and the cisterna magna was punctured to reduce brain pulsations.

2.2 Intracellular recording

Recording electrodes were sharp micropipettes (60–110 MΩ resistance) pulled from 3-mm glass capillaries, filled with 1 M potassium acetate. These were lowered through the motor cortex in 1-μm steps using a Burleigh Inchworm micromanipulator (New York, NY, USA) until a neuron was impaled or the maximum depth of 1.8 mm was reached. Recordings were made using an Axoclamp-900A amplifier digitized at 10 kHz with a Digidata 1322A and recorded using pClamp 10 software (Axon Instruments, Union City, CA, USA).

The membrane potential activity of the recorded neuron was monitored continuously throughout the experiment. Neurons were included in the study if they exhibited: (1) rhythmic membrane fluctuations between a relatively depolarized up state and a relatively hyperpolarized down state, with a down state membrane potential more negative than −60 mV; (2) a stable average membrane potential for the up and down states; and (3) action potentials that overshot 0 mV, with an amplitude greater than 50 mV. During the analysis of the results, a further criterion was applied, namely that the sequence had to exhibit at least ten identifiable down-to-up transitions—this quantification of requirement 1 is required so that there is a reasonable number of transitions over which to construct an “average” transition trajectory for each neuron. A total of 35 sequences, each from a different rat, were selected in this way. Sequences were of at least 90 s in duration. Stable recording was continued for each neuron for at least 30 s after the end of the analyzed sequence, in most cases for at least several minutes following.

2.3 Neuronal classification

Most neurons were identified electrophysiologically as regular spiking pyramidal neurons, due to the characteristic rapid firing of action potentials elicited in response to intracellular current injection [24, 25]. The neurons not tested with current injection were similar in other respects electrophysiologically to the remainder of the sample. The depth of each neuron in the cortex was estimated by the travel of the pipette distance below the surface of the pia, as displayed on the Burleigh micromanipulator. Using an estimate for the interface between layers 3 and 5 in this region of approximately 600 μm [26, 27], the sample comprises neurons in layer 3 and layer 5. Neurons in each of these subgroups did not differ significantly in their cellular properties. In some experiments, 3% biocytin (Sigma) was included in the solution in the micropipette and the tissue processed after the experiment using established means [28], to identify the neuron. A representative example of a pyramidal neuron recorded during the series of experiments which yielded the sample is shown in Fig. 2.

Fig. 2
figure 2

Electrophysiological and morphological characteristics of a pyramidal neuron in the motor cortex recorded intracellularly in this study. a The spontaneous membrane potential (Vm) activity recorded from the neuron is synchronized with the electroencephalogram recording (EEG, lower trace). Cardiovascular artifact is identified by the arrow. b The membrane potential recorded from the same neuron responds non-linearly to negative current pulses (Im) injected into the soma and fires a single action potential to a just-threshold positive current pulse. c The recovered biocytin-filled neuron recorded in a and b shows distinct morphological features: a pyramidal-shaped soma (S), a prominent apical dendrite (triple arrowhead), basal dendrites (double arrowhead), and axon projecting to the white matter (single arrowhead). Inset shows spines on a basal dendrite

Full size image

3 Analysis

3.1 Data records

For the k-th sequence (k = 1,...,M) where M(=35) is the number of sequences analyzed, we obtained a series of data points for membrane potential y k(j ), where j = 1, ..., N k, with N k being the total number of data points in the sequence. The “time” t j for each index j is equivalent to j/f s , where f s is the sample frequency (104 Hz).

3.2 Location of transitions

First, we use an automated method to identify the positions of transitions between the down and up states. A transition is deemed to occur when the second-derivative with respect to time of the membrane potential exceeds a particular threshold, thus selecting for areas of high upward curvature. (Action potentials are readily identifiable by their highly depolarized membrane potentials and so can be eliminated from this selection criterion.) The method is discussed in detail in [18], and a portion of a sequence showing identified transition points is shown in Fig. 3.

Fig. 3
figure 3

a An example of the membrane potential against time for one of the neurons used in this study. Transition points identified by the numerical algorithm are shown with a plus symbol. b An expanded view of the membrane potential for one of the transitions

Full size image

Specifically, we define the first and second derivatives d (1)k(j ) and d (2)k(j ), respectively, at the point j as:

$$ d^{(1)k}({j\,}) = \frac{f_{\, s}}{51} \left( \frac{1}{50} \sum_{l=1}^{50} y^{\,k}(j+l) - \frac{1}{50} \sum_{l=1}^{50} y^{\,k}(j-l) \right), \label{eq:deriv_calc} $$
(1)
$$ d^{(2)k}({j\,}) = \frac{f_{\, s}}{101} \left( \frac{1}{100} \sum_{l=1}^{100} d^{(1)k}(j+l) - \frac{1}{100} \sum_{l=1}^{100} d^{(1)k}(j-l) \right) . \label{eq:second_deriv} $$
(2)

In effect, we smooth over 50 time points on either side of the point j for the first derivative, and 100 time points for the second. The resulting second derivative is then thresholded at 12,500 mV s − 2, and the points where d (2)k increases through the threshold are selected as transition points \(T^{\,k}_{j}\). For each sequence k, the transition points occur at the indices \(j = T^{\,k}_{i}\), where i = 1, ...P k, with P k being the number of transitions in the kth sequence. In this study, P k ranged from 17 to 78, with a mean value of 52. The exact form of (1) and (2), along with the choice of threshold, was set after an optimization of the curvature method of finding a down-to-up transition. The basis was to find a method that maximized the number of identified transitions but with the constraint that the rate of mis-identification was extremely low.

3.3 Shape of transitions

The shape of a transition, that is, the trajectory by which the membrane potential moves from the down to the up state, can be complicated by the presence of action potentials in the up state. These were removed by identifying spikes through applying a threshold to the sequences at − 30 mV, and removing a short region of data on either side of where the sequence crosses this threshold. Specifically, the region before the upward crossing of the threshold where d (1)k > 500 mV s − 1 was removed, and the region after the downward crossing where d (1)k < − 200 mV s − 1 was removed. A linear interpolation was then applied across the regions of missing data. Although crude, this approach does not affect the results, since we only present averaged values for the membrane potential in the up states.

For each sequence k, the transitions were time-aligned, and the average membrane potential \(\bar{y}^{\,k}({j\,})\) was taken over the 0.25-s period (i.e., 2,500 data points) preceding and the 0.5-s period (i.e., 5,000 data points) following the transition point to produce a mean transition shape. That is, we evaluated:

$$ \bar{y}^{\, k} ({j\,}) = \frac{1}{P^{\, k}} \sum_{i=1}^{P^{\, k}} \tilde{y}^{\, ki}({j\,}) , \label{eq:average_y} $$
(3)

where the sequence \(\tilde{y}^{\, ki}({j\,})\) is given by:

$$ \tilde{y}^{\, ki}({j\,}) = y^{\, k}(T^{k}_i - {\rm 2,\!500} + j\,) \; \; \; j=1, \dots {\rm 7,\!500}. $$
(4)

Figure 4 shows examples for three different sequences (neurons). Also plotted are the standard deviations in \(\tilde{y}^{\, ki}({j\,})\) across the transitions i, to indicate the variability between transitions within one sequence. In the figures in this paper, we have shown time ranging from 0.25 s before transition through to 0.5 s after, i.e., a total time space of 0.75 s. We start the graphs at time = 0 s (i.e., j = 0) so that time = 0.25 s corresponds to the transition.

Fig. 4
figure 4

a–c The average transition shape, averaged over all identified transitions from three different neurons. The central solid line represents the mean membrane potential; the upper and lower dashed lines indicate the spread in the data by showing one standard deviation higher and lower than this value. The 0.75 s segments of data have been time-aligned so that the identified transition points, where the down state finishes, occur at 0.25 s

Full size image

The size and shape of the mean transition across different sequences is somewhat variable from sequence to sequence, but reasonably constant within a sequence. This may be a consequence of differing levels of slow-wave sleep being experienced by the animals in the different experiments. In Fig. 5, we show the mean transition shape \(\bar{y}^{\, k}\), and its first derivative d (1)k, for k = 1, ⋯ 35, i.e., all neurons of this study. We also identify the position of each action potential with respect to the transition point, and in Fig. 6, we present a histogram of the number of action potentials over all the identified up–down transitions in all the neuron sequences, recorded against time. The distribution of action potentials across the up state (Fig. 6) has also been examined by Kerr et al. [29]. In that study, action potentials were found to be uniformly distributed across the up state. Our results are in broad agreement; for the large majority of the up state, this is true; however, we are able to resolve the rapid initial rise in the probability of an action potential as the state commences.

Fig. 5
figure 5

Color online. a The mean membrane potential and b the mean gradient in the membrane potential for all the 35 neurons of this study. Each of the 35 thin lines represents the average over all transitions of a single neuron; the dark, think line represents the mean of these over all these 35 neurons

Full size image
Fig. 6
figure 6

The number of spikes recorded for a given time past the point of transition, summed over all identified transitions in all neuron sequences. The points of transition have been time-aligned to 0.25 s

Full size image

Figure 5 shows that, after the averaging over all sequences, there appears a clear oscillation at frequency 50 Hz, particularly on the lower, gradient graph (b). This is attributed to an artifact of the method used to find the first and second derivatives; such a scheme, involving forward and backward averaging over a number of points, emphasizes any 50-Hz component that is present in the signal. We do not consider this oscillation to be of significance. To test for sensitivity of our results to changes in processing method, we made small changes to the parameters of our analysis; the results were not significantly changed.

We now focus on the shape of the transition. Figure 5 clearly indicates a sharp rise in membrane potential in the early stages of the transition—as the membrane potential rises, its gradient reduces. Figure 6 demonstrates a corresponding increase in frequency of action potentials. This effect has been quantified by looking at the time-difference between the maximum gradient in membrane potential and the “halfway” point of the transition. Specifically, for each transition i in each sequence k, the time of the peak of the first derivative, \(t_{{\rm max},i}^{\,k}\), and the time-centroid of the plot of gradient against time, \(t_{c,i}^{\,k}\), were identified. The difference between the two is a measure of how early in the course of the transition the peak gradient occurs—i.e., how sudden is the transition’s onset? That is, we constructed the quantities:

$$ \Delta t_i^{\,k} = t_{{\rm max},i}^{\,k} - t_{c,i}^{\,k} , $$
(5)

where

$$ t_{c,i}^{\,k} = \frac{\sum_{j\,=T_{i}^{\,k} - R}^{T_i^{\,k} + R} d^{(1)k}({j\,}) t_j } {\sum_{j\,=T_{i}^{\,k} - R}^{T_i^{\,k} + R} d^{(1)k}({j\,})}, $$
(6)

and \(t_{{\rm max},i}^{\,k}\) is the time at which the maximum value of d (1)k occurs for the ith transition of the kth sequence, with R = 2,500 (= f s ×0.25 s) denoting 0.25 s on either side of the transition and t j the time index of the jth data point (= j/f s ). The timing of the peak of the first derivative d (1)k is denoted by \(t^{\,k}_{\rm{max},j}\).

A histogram of the values of \(\Delta t_i^{k}\) for all transitions in all sequences is shown in Fig. 7. It is clear from the figure that the maximum derivative usually occurs before the “halfway point” of the transition, indicating that the movement of membrane potential away from the down state is more sudden than its arrival in the up state.

Fig. 7
figure 7

A histogram of the difference between time of maximum gradient in membrane potential and centroid of the plots of the gradient against time (i.e., the difference between the peak and the time-centroid of the plots of gradient of membrane potential against time). The distribution is skewed towards negative values, indicating that the maximum gradient occurs early in the transition

Full size image

Although there is variation in transition shape, most of the curves of Fig. 5 show an exponential approach to the up state following the transition point. By fitting an exponential function of form \(\bar{y}^{\, k}(s) = A^{\, k} - B^{\, k} {\rm exp}(-s / t^{*k})\) to the region where time s > 0, where A k and B k are constants and t *k are time constants, we can obtain a distribution of time constant t *k for the neurons. This distribution is shown in Fig. 8; the range of time constants is broadly 50 to 150 ms. Although not directly comparable, the analysis of Cossart et al. [21] for the down to up transition involved with cognition obtained a mean value of 58 ms with standard deviation 5 ms, which is of similar magnitude to our results. There can be many time scales that contribute towards the dynamics of the membrane potential; however, it is reasonable to compare this scale with time scales used in the modelling of membrane potential in brain dynamics studies. Indeed, our range of time constants is typical of that used in neural modelling. For example, Bojak and Liley allowed the somatic time constants to range from 5 to 150 ms [30] and Steyn-Ross et al. have used 50 ms [31]. We find that the time constants are correlated with the membrane potential of the down state (R = − 0.47, with a probability of obtaining such a correlation assuming uncorrelated variables as p = 0.0047), presumably because of changes in potassium channel conductance in the down state. Figure 9 shows that the neurons with the most hyperpolarized down states are the ones with the largest time constants—i.e., ones that respond most slowly. It is interesting to note that these time scales are rather longer than those found by Fuentealba et al. for thalamic reticular neurons (48 ms) [10], suggesting that the thalamus would respond more quickly to a depolarizing event.

Fig. 8
figure 8

A histogram of neuron time constants obtained by fitting an exponential response to the membrane potential following the point of transition from a down to up state

Full size image
Fig. 9
figure 9

A plot of neuron time constant against the mean membrane potential of the down state at the point of transition, for each neuron of this study. The line denotes a least squares linear fit to the data. There is a clear negative correlation; neurons with the more hyperpolarized down states have the largest time constants

Full size image

4 Discussion

Although individual down-to-up transitions are fairly variable in shape, the mean transition shape for each neuron shows similar features. Specifically, the membrane potential slowly rises on the approach to the transition, and then undergoes a sudden increase in gradient, driving it towards a more depolarized state. As the membrane depolarizes, the gradient reduces, until it settles into a roughly constant up state, where action potentials may form depending upon the extent of the depolarization.

The trajectory takes on a broadly exponential form. The fast movement of the membrane potential away from the down state is not what would be expected as a result of critical slowing on the approach to a first-order phase transition. Rather, we would expect a slow initial movement away from the ghost of the down state [23]. The exponential trajectory is equivalent to, for example, the response of the potential difference over the capacitor of a resistor–capacitor (RC) circuit to a step-change in input voltage. Such a response suggests that the up and down states experienced by the neurons of this study are merely a passive response to a step-like switch in synaptic (or other) input, possibly from the thalamus. Fuentealba et al. indicate a switching time of order 50 ms for the natural switching of the bistability in reticular cells of the thalamus [10]; this is faster that the response of most of the cortical cells of this study. This indicates that the thalamic input to the cortical cells might be broadly considered step-like on the time scale of the cortical cells. The observation of Wilson et al. [18] that the power spectrum of fluctuations in membrane potential on the approach to a transition decays approximately as 1/f 2, where f is frequency, is also consistent with the hypothesis of the cortical neuron acting like an RC circuit; an input of a broad spectral nature (e.g., as a result of an approximately white noise source) to an RC circuit, or indeed to any linear system [32], would be expected to give rise to a spectrum that decays as 1/f 2.

The correlation between the time constant and the membrane potential of the down state (Fig. 9) is consistent with the fact that membrane input resistances in the up state (approximately 9 MΩ) are much lower compared with those of the down state (approximately 40 MΩ), by around a factor of four [33, 34]. In terms of the RC circuit model, where the time constant is given by RC, this would mean that a hyperpolarized neuron has four times the time constant compared to when it is depolarized. If we assume that the input resistance varies approximately smoothly between the extremes, we may expect a greater time constant for the most hyperpolarized neurons. The range that we see in Fig. 9, namely, about a threefold reduction in time constant for a − 60-mV down state as opposed to a − 90-mV down state, is broadly consistent with the measurements of input resistance. The power surge and slowing of fluctuations that are demonstrated in the neurons studied in [18] could then be considered purely as a response of these neurons to a power surge and critical slowing in a system feeding these cortical neurons.

These results therefore suggest that, while a first-order phase transition may be an underlying driver of the cortical slow oscillation, the phase transition is not entirely located in the cortical neurons themselves. This is in contrast with the result of Sanchez-Vives and McCormick, who found that the slow oscillation in vitro in ferret neocortex appeared first in layer 5 [14]. (Note that layer 5 neurons were included in our study.) Given the relatively short time scales for onset of depolarization in reticular thalamic neurons [10], which can be viewed as quick compared with the cortical neurons, one could speculate that the initiation of the up state in the cortex is merely a response to a fast change in the thalamus. Alternatively, given evidence that there is a cortical component to the slow oscillation [7], one could speculate that the dynamics may be more complicated than a simple picture can represent: the slow oscillation is neither a collective mode of the cortex (as the phase transition model would predict), nor a response in individual cortical neurons to an underlying oscillation elsewhere in the brain. A hybrid mode, combining the two extremes, may be more appropriate. Such a picture would be consistent with the results of Kerr et al. [29], who have determined, through the use of voltage-sensitive dyes, that the active population of neurons is constantly changing, that is, “pacemaker” ensembles might be dynamic in the cortex and thalamus. For example, initiation might be in layer 5 [14], but only in a small subset of neurons. From this study, it is not possible to make a definitive statement on the origin of the slow oscillation, other than to remark that it did not appear to be entirely located within the neurons studied. There are many possibilities that remain. It is therefore plausible that a similar experimental analysis of membrane potential fluctuations in thalamic cells, either in vivo or in vitro, might shed light on the origin and maintenance of the slow oscillation.

Analysis of the data is complicated by the need to define where a transition takes place. In essence, by using a method based on curvature of the membrane potential, we have implicitly assumed that transitions are sudden, and that may bias our results. In fact, merely assuming that a “transition” occurs might be biasing results in favor of a sudden initial jump. However, an examination by eye suggests that one can define a transition point at least loosely, and the analysis is robust to small changes in parameters. Moreover, we have selected the neurons for this study on the grounds that they gave clearly distinguishable down and up states. This itself may introduce bias into the study—e.g., emphasize the suddenness of a transition between the states. If that were the case, however, one would still expect the conclusions to hold for those particular neurons, which are a significant subset of those recorded.

Finally, we must remark that the data have been recorded from animals under urethane anaesthesia, not from naturally sleeping animals. The mechanisms by which the up and down states are generated during anaesthesia may not be identical to that of natural sleep. The electroencephalograms of naturally sleeping and urethane-anaesthetized rats have been compared by Clement et al. who found no major differences between the two and concluded that urethane anaesthesia is a good model of sleep in rats [35]. Additionally, Sceniak and MacIver found that the mechanism of urethane action on rat visual cortical neurons in vitro was activation of a K +  leak current, as opposed to modulation of synaptic transmission; this is similar to natural sleep [36]. However, one should not make the general conclusion that urethane anaesthesia and natural slow-wave sleep are the same state; for example, the down states in anaesthetized cats [1] are longer than those in naturally sleeping animals [37].

5 Conclusion

In this paper, we have looked at the dynamics in the membrane potential of the transition between the down and the up states of the cortical slow oscillation. The transition shows characteristics broadly similar to that of a simple RC circuit. This is not consistent with the hypothesis that the transition is a result of a phase transition within single cortical neurons, or large assemblies of cortical neurons. Rather, results are suggestive of the cortical neurons that were measured being driven by step-like changes in input. It is still possible, or even likely, given the evidence from the changes in power spectrum at the transition point [18], that there exists an underlying phase transition, either in the thalamus, or in a small subset of cortical cells, or some combination of the cortex and thalamus. Alternatively, the brain dynamics causing and maintaining the oscillation may be more complicated still, for example, a hybrid of collective and individual neural modes.