Introduction

As an intelligent material with a millisecond-level reversible rheological response controlled by an external magnetic field, magnetorheological fluids (MRFs) have increased use in various fields [1,2,3]. High-precision modeling of MRFs plays a critical role in controlling and designing magnetorheological devices [4,5,6,7,8]. However, MRFs rapidly convert energy into heat during operation, which inevitably leads to changes in their temperature [8,9,10]. Studies have shown that the rheological properties of MRFs are markedly affected by temperature, so temperature effects must be considered in high-precision modeling [9,10,11,12,13,14].

MRFs usually consist of micron-sized magnetic particles, base carrier fluids, and thixotropic agents [2, 15]. Research shows that the magnetic properties of magnetic particles are approximately constant in the normal working temperature range; thus, the change in the magnetically induced yield stress of MRFs with temperature can be ignored [9, 12, 16]. Temperature mainly affects the plastic viscosity of MRFs by changing the viscosity of the base carrier fluid following the same law under different applied magnetic fields [7, 9, 12, 14]. Therefore, temperature effect modeling should focus on the viscosity-temperature behavior of MRFs and their base carrier fluids.

Previous studies have mainly used the Arrhenius equation (Eq. 1) and the Reynolds equation (Eq. 2) to describe the viscosity-temperature behavior of MRFs [7, 9, 10, 13, 14, 16,17,18,19,20,21]. Although these equations and the linear equation can describe the viscosity-temperature behavior of MRFs over a small temperature range [5], research shows that these equations are usually only suitable for describing the viscosity of some pure fluids in a small temperature range [22,23,24]. Therefore, this study proposes to use the universal Doolittle viscosity-temperature equation (Eq. 3) to describe the viscosity-temperature behavior of MRFs over a wide temperature range [24,25,26].

$$\eta ={\eta }_{0}\mathrm{exp}(a/T)$$
(1)
$$\eta ={\eta }_{0}\mathrm{exp}(aT)$$
(2)
$$\eta ={\eta }_{0}\mathrm{exp}\left[a/(T+b)\right]$$
(3)

Limited by the heat generation of the magnetic field generator and the available temperature range of the bath liquid, neither Anton Paar nor TA Instruments’ existing magnetorheological test platforms can cover the working temperature of automotive-grade devices (− 40  to 125 °C). In addition, testing MRFs and magnetorheological devices at extreme temperatures consumes considerable time and energy. Therefore, this study proposes to use the Doolittle equation to identify the viscosity-temperature characteristics of the fluid based on viscosity-temperature data over a narrow temperature range; and then predict the viscosity-temperature behavior over a wide temperature range.

The previous optimization of MRFs usually only considers the operating temperature range but does not pay enough attention to the effect of temperature on its operational characteristics. This study proposes a corresponding MRF quality factor based on the Doolittle equation. In addition, the Doolittle equation with strong expandability can be used to establish a prospective multiphysics model to systematize MRFs' optimization further.

Materials and methods

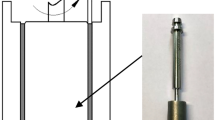
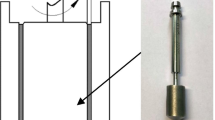
The experimental setup was the Anton Paar MCR-702 rheometer and its magnetorheological and Peltier test accessories. The viscosity-temperature test measured the apparent viscosity of the sample at 100 s−1 over -30–100 °C with a change rate of 1 °C min−1. Low-viscosity fluids were measured with the CP50-1 rotor, while MRFs were measured with the PP25 rotor with a gap of 0.5 mm. The shear rate range of the rheological curve test was 0.1 ~ 1000 s−1 with the rotor of PP20/MRD/TI (Fig. 1).

Figure 1
figure 1

Experimental setup

Full size image

In this paper, each model was obtained by fitting the data using the curve fitting app of MATLAB (no weighting if not declared). More specifically, the app determined parameters by minimizing the mean square error between the model and the data, and the sign of parameters can be constrained to avoid the local optimum. Both the Arrhenius (Eq. 1) and Reynolds (Eq. 2) equations have only two parameters (\({\eta }_{0}\) and a), while the Doolittle formula (Eq. 3) has three parameters (\({\eta }_{0}\), a and b).

Table 1 presents the basic information of the carbonyl iron powder (D50 3.9–5.0 μm, > 99.5% Fe, < 0.05% C, < 0.22% O) and pure base oils, including hydrocarbon oils, silicone oils, and esters (analytical reagent, AR).

Table 1 Basic information on the used materials
Full size table

The tested MRFs were commercial 132-DG and homemade MRF1 and MRF2. More specifically, Lord 132-DG is a hydrocarbon-based medium-density MRF with a solid concentration of about 31.4 vol%. MRF1 and MRF2 are low-density MRFs with the same solid concentration of about 25.4 vol% and are hydrocarbon-based and silicon-based, respectively (see Table 2 for details). To study the correlation of viscosity-temperature characteristics between the magnetorheological fluids and their base carrier fluids, the supernatant of 132-DG (132Base) was also tested.

Table 2 Formulations of the homemade MRFs
Full size table

The preparation process of the homemade MRFs was as follows: in a water bath at 50 °C, the base oil was stirred at 600 rpm, and then organic bentonite (thixotropic agent to improve settling stability), propylene carbonate (activator to improve the strength of the thixotropic network), and T154A (surfactant to avoid agglomeration of solid particles) were sequentially added and stirred for 20 min, 10 min, and 5 min, respectively. Finally, CIP-SQ was added and stirred at 1500 rpm for one hour.

The Doolittle equation

Doolittle found that liquid viscosity \(\eta \) can be expressed as a function of the free volume fraction (\(f={v}_{\mathrm{f}}/{v}_{0}=\left(v-{v}_{0}\right)/{v}_{0}\)):

$$\mathrm{ln}\eta =\mathrm{ln}A+B/f$$
(4)

where A and B are material constants, \({v}_{\mathrm{f}}\) is the volume of free space, \({v}_{0}\) is the volume of liquid extrapolated to absolute zero without phase change, and \(v\) is the total volume.

Turnbull and Cohen [27] related the free volume fraction and diffusion coefficient through theoretical modeling and derived the Doolittle equation by combining the Stokes–Einstein equation linking the diffusion coefficient and viscosity, which provided a theoretical basis for the Doolittle equation.

Assuming that the free volume and the free volume change are relatively small, the free volume fraction can be derived from the definition of the thermal expansion coefficient \({\alpha }_{\mathrm{T}}\):

$$f={f}_{\mathrm{r}}+{\alpha }_{\mathrm{T}}(T-{T}_{\mathrm{r}})$$
(5)

where \({f}_{\mathrm{r}}\) is the free volume fraction of the liquid at the reference temperature \({T}_{\mathrm{r}}\).

Substituting Eq. 5 into Eq. 4:

$$\eta =[{\eta }_{\mathrm{r}}\mathrm{exp}\left(-B/{f}_{\mathrm{r}}\right)]\mathrm{exp}\left[\frac{B/{\alpha }_{\mathrm{T}}}{T+({f}_{\mathrm{r}}/{\alpha }_{\mathrm{T}}-{T}_{\mathrm{r}})}\right]$$
(6)

where \({\eta }_{\mathrm{r}}\) is the viscosity at the reference temperature \({T}_{\mathrm{r}}\).

Thus, the Doolittle viscosity-temperature equation is a three-parameter model (Eq. 3). In Eq. 3, \({\eta }_{0}\) is \({\eta }_{\mathrm{r}}\mathrm{exp}\left(-B/{f}_{\mathrm{r}}\right)\); \(a\) is \(B/{\alpha }_{\mathrm{T}}\); \(b\) is \(({f}_{\mathrm{r}}/{\alpha }_{\mathrm{T}}-{T}_{\mathrm{r}})\).

Results and discussion

Comparison of the Doolittle equation with existing equations

Although the off-state MRFs are usually approximated as Newtonian fluids, they have off-state yield stress that varies with temperature (fitted with the Bingham model: \(\tau =\eta \dot{\gamma }+{\tau }_{0}\)). When the temperature is below zero, the off-state yield stress of the commercial MRF 132-DG rapidly increases by order of magnitude with decreasing temperature (Fig. 2a), so the effect of off-state yield stress cannot be ignored at low temperatures. Since the off-state yield stress of MRFs is affected by many factors such as the thixotropic agent network and the surface friction of solid particles, the mechanism and modeling of its temperature behavior are complicated; thus, this paper mainly studies the plastic viscosity behavior of MRFs over a wide temperature range (Fig. 2b). Therefore, this study first compares the Doolittle equation with the existing viscosity-temperature equations using viscosity-temperature data obtained over a wide temperature range with several Newtonian fluid base oils.

Figure 2
figure 2

Temperature effects of 132-DG over a wide temperature range: a Off-state yield stress; b Off-state plastic viscosity

Full size image

The root-mean-square errors (RMSE) of fitting results (Table 3) indicate that the ordering of the ability of these formulas to describe the liquid viscosity-temperature behavior is Doolittle > Arrhenius > Reynolds. Specifically, compared with Reynolds and Arrhenius equations, the Doolittle equation achieves approximately 17 times and eight times improvement in fitting accuracy, respectively. The comparison of the viscosity-temperature data for three typical fluids with the models fitted using these equations (Fig. 3) shows that the predictions of the Arrhenius and Reynolds equations deviate markedly from the data at extreme temperatures. Thus, when modeling MRFs over a wide temperature range, the existing Reynolds and Arrhenius equations must be replaced by the Doolittle equation.

Table 3 RMSE of different equations for base oil viscosity-temperature data
Full size table
Figure 3
figure 3

Fitting of the three equations to the viscosity-temperature data of typical base oils: a PAO162; b DM20; c PC

Full size image

Correlation of temperature effects between MRFs and their base oils

As mentioned above, at low temperatures, the effect of off-state yield stress on the viscosity of MRFs cannot be ignored. Therefore, this study identifies \({\eta }_{0}\) and the viscosity-temperature characteristic parameters (\(a\) and \(b\) in Eq. 3) of MRFs based on the viscosity-temperature data over 0–100 °C (273.15–373.15 K). PAO162, DM10, and 132Base are the base oils of MRF1, MRF2, and 132-DG, respectively. The high similarity between the viscosity-temperature characteristic parameters of MRFs and their base oils, for example, the deviation is less than 2.5% for 132-DG (Table 4), indicates that the viscosity-temperature characteristics of MRFs are mainly determined by their base oils.

Table 4 Doolittle equation parameters of MRFs and their base oils
Full size table

A comparison of the model identified from the viscosity-temperature data over the mid-high temperature with the overall viscosity-temperature data of the MRFs (Fig. 4) implies that although the off-state yield stress makes the viscosity no longer conform to the Doolittle equation at low temperatures, the relative deviations are still acceptable. Thus, the Doolittle equation can be used to predict the viscosity of MRFs at untested temperatures. For MRF2, using DM20 with good low-temperature fluidity as the base oil, the Doolittle equation can well describe its viscosity-temperature behavior at low temperatures (as shown in Fig. 4), indicating that the thixotropic network of MRF2 does not curdle at low temperatures and that the base oil determines the low-temperature fluidity of thixotropic systems.

Fig. 4
figure 4

Viscosity-temperature data of MRFs with their Doolittle models

Full size image

Applications of the Doolittle equation

The Doolittle equation is a semi-theoretical equation based on the free volume theory and provides a good description of the viscosity-temperature curves of various fluids. Thus, the Doolittle equation has the following applications in the field of MRFs:

Temperature-dependent constitutive equations of MRFs. The constitutive equations of MRFs usually only consider two independent variables: shear rate and magnetic field strength. However, this paper and many studies have found that the plastic viscosity of MRFs changes up to approximately an order of magnitude with the influence of temperature [14]. Simultaneously, the inevitable temperature change of MRFs, caused by the external environment and the heat generated in work, affects the operational characteristics of the corresponding magnetorheological devices. Thus, it is critical to consider the temperature effect in the constitutive equation of MRFs. Taking the Bingham model as an example, the form is:

$$\tau \left(H,\dot{\gamma },T\right)={\tau }_{0}\left(H\right)+\dot{\gamma }\times \eta \times \mathrm{exp}\left[a/(T+b)-a/({T}_{\mathrm{r}}+b)\right]$$
(7)

where \({\tau }_{0}(B)\) is the postyield stress of the MRF when the magnetic field strength is \(H\); \(\eta \) is the infinite plastic viscosity of the MRF when the temperature is \({T}_{\mathrm{r}}\).

Design and optimization of the formulation. Based on the correlation between the viscosity-temperature characteristics of the base carrier fluid and the MRF, the viscosity-temperature curve of the MRF can be directly predicted based on the viscosity-temperature characteristics of the base carrier fluid. Taking the commercial MRF 132-DG as an example, we predict its overall viscosity-temperature curve based on the viscosity-temperature characteristics of its supernatant 132Base and its viscosity at the reference temperature \({T}_{\mathrm{r}}=40\mathrm{^\circ{\rm C} }\) (Fig. 5). The high coincidence of the prediction model with the viscosity-temperature data of 132-DG (Fig. 5) indicates that it is feasible to predict the viscosity-temperature behavior of MRFs based on the viscosity-temperature data of the base carrier fluid.

Figure 5
figure 5

Prediction of 132-DG viscosity-temperature behavior based on the base oil

Full size image

Assuming that the viscosity-temperature characteristics of MRFs and their base carrier fluids are highly similar (as shown in Fig. 5), the Doolittle equation can be used to design the formulation of MRFs. Ideally, according to the empirical equations, the volume fraction \(\phi \) of magnetic particles can be used to estimate the maximum adjustable yield stress of MRFs (\(g(\phi )={\tau }_{0,\mathrm{ max}}-{\tau }_{0,\mathrm{ off}}\approx {\tau }_{0,\mathrm{ max}}\)) and the ratio between the off-state viscosities of the MRF and its base oil (\(f\left(\phi \right)={\eta }_{\mathrm{MRF}}/{\eta }_{\mathrm{Base}}\)) [28,29,30]. Combining \(f\left(\phi \right)={\eta }_{\mathrm{MRF}}/{\eta }_{\mathrm{Base}}\) with Eq. 4 yields Eq. 8, so the addition of solid particles only changes the material constant A (\({A}_{\mathrm{MRF}}=f\left(\phi \right){A}_{\mathrm{Base}}\)), and does not change the free volume fraction of the system (\({f}_{\mathrm{MRF}}={f}_{\mathrm{Base}}\)). Then, we can carry out a formulation optimization that considers temperature.

$$\mathrm{ln}{\eta }_{\mathrm{MRF}}=\mathrm{ln}\left(f\left(\phi \right){A}_{\mathrm{Base}}\right)+{B}_{\mathrm{Base}}/{f}_{\mathrm{Base}}$$
(8)

The smaller the change in the off-state viscosity of the MRF with temperature, the better. Thus, this study proposes to take the reciprocal of the relative viscosity change rate at the reference temperature \({T}_{\mathrm{r}}\) with the Doolittle viscosity-temperature equation \({({T}_{\mathrm{r}}+b)}^{2}/a\) as the quality factor. The viscosity-temperature quality factors of typical base oils at the reference temperature \({T}_{\mathrm{r}}=273.15 \mathrm{K}\) (Table 5) indicate the following: 1. The viscosity-temperature quality factor of the base oil decreases with increasing average molecular weight; 2. The viscosity-temperature quality factor of DOS is between PAO162 and PAO164; 3. The viscosity-temperature quality factor of PDMS is markedly higher than that of PAO.

Table 5 Viscosity-temperature quality factors of base oils
Full size table

Prediction of viscosity-temperature behavior. To overcome the limitation of the temperature control range of the test device or to save test costs, this study proposes to use the Doolittle equation to predict the viscosity-temperature behavior of fluids. Specifically, this study identifies the viscosity-temperature characteristics of the fluid using the Doolittle equation based on viscosity-temperature data over a narrow temperature range and then predicts its viscosity-temperature behavior over a wide temperature range. The Doolittle equation is fitted with the sample viscosities at − 10, 0, 20, and 40 °C (using the inverse of the squared viscosity as the weight), and this fitting is then compared with the sample viscosity-temperature data from − 30 to 100 °C.

The high coincidence between the viscosity-temperature data of the four typical base oils and their prediction models (shown in Fig. 6) indicates that the Doolittle equation can well predict fluid viscosity at untested temperatures based on a small amount of data obtained over a narrow temperature range. Compared with the model obtained by fitting the overall data (Fig. 3c), the deviation between the PC prediction model and its viscosity-temperature data in the high-temperature range increases markedly (Fig. 6), which is because the data do not fully reflect the viscosity-temperature behavior of this fluid. Thus, for predicting the fluid viscosity-temperature behavior using the Doolittle equation, the distribution range of data is far more critical than the amount of data.

Figure 6
figure 6

Prediction of the viscosity-temperature behavior of typical base oils

Full size image

The relative RMSE (calculated by Eq. 9) of the prediction models for the viscosity-temperature data of the base oils does not exceed 5% (Table 6) and demonstrates the excellent predictability of the Doolittle equation. The RMSE of the prediction model for each fluid (Table 6) is approximately an order of magnitude higher than the corresponding RMSE in Table 3, which implies that the accuracy of the prediction model is still expected to be markedly improved. In addition, the application of this method on the viscosity-temperature data of 132DG from – 30 to 130 °C also shows good performance, i.e., Relative RMSE = 12.47% and the relative error at 130 °C is about 20%. In summary, the Doolittle equation can predict the viscosity-temperature behavior of fluids well based on a small amount of data over a narrow temperature range.

$$\mathrm{Relative RMSE}=\sqrt{(1/N)\sum_{i=1}^{N}{(1-f({x}_{i})/{y}_{i})}^{2}}$$
(9)

where \(N\) is the number of data points; \(f({x}_{i})/{y}_{i}\) is the ratio between the predicted viscosity and the experimental value when the temperature is \({x}_{i}\).

Table 6 Overall biases of the prediction models
Full size table

Prediction of pressure effects. Although fluids are usually assumed to be incompressible materials, many studies have considered the compressibility of MRFs to improve the modeling accuracy [2, 31]. In addition, the most widely used magnetorheological single-cylinder dampers are designed with an air chamber, which is usually filled with high-pressure nitrogen, to balance the volume change caused by the movement of the piston rod [2]. Therefore, it is also critical for the design of magnetorheological devices to establish the constitutive equation of MRFs considering the pressure effect. Based on the free volume theory [32], we can also correlate the free volume fraction with the pressure referring to Eq. 5 [33], and then substitute this into the Doolittle equation (Eq. 4) to describe the viscosity-pressure behavior of the liquid:

$$f={f}_{\mathrm{r}}+{\alpha }_{\mathrm{P}}(P-{P}_{\mathrm{r}})$$
(10)

where \({f}_{\mathrm{r}}\) is the free volume fraction under the reference pressure \({P}_{\mathrm{r}}\); \({\alpha }_{\mathrm{P}}\) is the isothermal compressibility coefficient.

The free volume theory implies that the free volume fraction has a positive correlation with the compressibility of the liquid [34]. Combining the thermal expansion coefficient \({\alpha }_{\mathrm{T}}\) and the fitted viscosity-temperature characteristic parameters, this study further obtained the free volume fraction \({f}_{\mathrm{r}}\) at the reference temperature \({T}_{\mathrm{r}}\) for PAO and PDMS base oils (Table 7). The larger free volume fraction of PDMS base oils compared to PAO base oils implies that the compressibility of PDMS base oils is greater than that of PAO base oils, which is consistent with reality.

Table 7 Free volume parameters of the base oils
Full size table

Moreover, the free volume theory provides insight into the effects of temperature and pressure on liquids. For instance, although the thermal expansion coefficients of PDMS base oils are larger than those of PAO base oils, the temperature effect of PDMS base oils is still much smaller than that of PAO base oils (Fig. 6) due to their larger free volume fraction at the reference temperature (as shown in Table 7). It is reasonable to speculate that the viscosity-pressure effect of DM base oils would be weaker than PAO base oils and lead to worse durability [33, 35], which is also consistent with reality.

Conclusions

This paper proposes the Doolittle equation based on free volume theory to study the temperature effects of MRFs over a wide temperature range and obtains the following conclusions: (1) When the temperature is higher than 0 °C, the effect of off-state yield stress on the temperature effect of MRFs can be ignored; thus, the modeling only needs to consider the viscosity-temperature effect; (2) Compared with the existing Reynolds and Arrhenius equations, the Doolittle equation achieves an accuracy improvement up to 17 times and eight times, respectively; (3) The viscosity-temperature characteristics of MRFs and their base oils have high coincidence (the deviation of commercial MRF 132-DG is less than 2.5%), which can be used for the formulation design; (4) Based on four data points that take over a narrow temperature range, the Doolittle equation predicts the overall viscosity-temperature behavior of liquids with a relative RMSE of no more than 5%; (5) The prediction of the liquid pressure effects based on the free volume theory is consistent with reality.