Introduction

Fiber reinforced composites are multiphase materials whose mechanical properties are closely related to microstructures and constituents [1,2,3]. However, the microscopic void defects generated during the curing process will lead to the degradation of material properties more or less. As a typical microscopic defect, voids have been proven to exist in composites, and different methods were used to measure their contents. For example, Kergariou et al. [4] measured the porosity of fiber reinforced composites by six methods, computed tomography scanning, gravimetry in ethanol and water, scanning electron microscopy, optical microscope measurement, and inverse identification from tests. The porosity of composites ranged from 3.8% ± 2.9% to 21.1% ± 0.7%. Bhat et al. [5] tested the porosity of carbon fiber reinforced polymers (CFRPs) composites through ultrasonic imaging and X-ray imaging methods. The subsequent mechanical test showed that the interlaminar shear strength was reduced by about 46% at a porosity of 5.4%. Microvoids can also affect bending [6,7,8] and tensile and compression properties [9,10,11].

Micromechanics motivated continuum damage mechanics models have been proposed to establish the relationship between void contents and macroscopic properties. For example, the Gurson model [12], Gurson–Tvergaard–Needleman (GTN) model [13], and the modified GTN model [14, 15], these models can be used to describe the influence of microvoids on the macroscopic mechanical behaviors of materials. However, the parameter of void shapes in them is neglected. Moreover, Madsen et al. [16] defined a new rule-of-mixtures (ROM) by fitting the obtained experimental data, which could only be used with supplemented parameters of composites void contents, and the experimental data-based ROM ignores the influence of void shapes.

Nevertheless, theoretical models and the experimental methods mentioned above cannot explain the failure process caused by microvoids from a microscopic perspective. Recently, the finite element model based on the representative volume elements (RVEs) containing voids has been established to investigate the influences of microvoids on the macroscopic mechanical properties. Carrera [17] used the RVE model to investigate the influence of voids distributed in the matrix on the properties of composites and found that the void arrangement can influence the distribution of stress fields. Tan et al. [18] found that the tensile strength of composites was reduced by approximately 17% in the presence of a 10% void volume fraction. Other similar RVE-based simulation researches [19, 20] were also carried out to study the effect of microvoids on the properties of composites. All of them focus on the microvoids in the matrix and ignore the large numbers of microvoids in interfiber which have been experimentally proved to exist widely [21, 22]. Hence, Danial [23, 24] and Hyde [9] studied the effect of interfiber voids on mechanical properties. The void types in their work are square interfiber voids among four fibers and triangular interfiber voids among three fibers. Hyde also studied the pentagonal interfiber voids among five fibers and found that the pentagonal interfiber void reduces the tensile strength more than triangular or square voids. The void orientation has minor consequences on compression strength. However, the actual composites should contain various void shapes simultaneously, and the damage evolution, failure mechanism, and coupling effect of various voids are unclear.

The present work aims to visualize the damage evolution of fiber reinforced composites with various voids, explain the failure mechanisms and the coupling effects between voids, and provide a simplified strength prediction model with known porosity. It should be noted that it is difficult to determine the thickness and material parameters of the interface between the fiber and the matrix. Although many authors have analyzed the influence of the interface, the interface parameters are all based on assumptions, without experimental verification. This paper analyzes the coupling effect of different void types and their influence on failure mechanism; the interface will not be considered. The organization of this paper is as follows: First, a computational model is introduced and compared with empirical prediction formulas in Sect. 2.2. Then the failure behavior and coupling effect of unidirectional CFRPs are investigated under typical loading conditions in Sect. 2.4. Next, the influence of void type and volume fraction on the strength of CFRPs is investigated in Sects. 3.1 and 3.2. The coupling effect of void type on strength is analyzed in Sect. 3.3. Finally, the failure envelopes are provided in \({\tau }_{13}-{\sigma }_{22}\) stress space which is verified by comparing with Hashin–Rotem and Puck failure criteria in Sect. 3.4. The conclusion is given in Sect. 4.

Computational model

The computational model includes the RVE with various randomly distributed voids and the micromechanics model of damage evolution and failure. The boundary condition of RVE is periodic, and the computational model is validated by comparing it with empirical prediction formulas.

RVE model of CFRPs with various voids

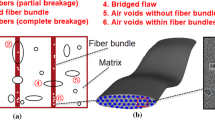
During the manufacturing process of composites, voids are formed unavoidably (Fig. 1 [25]). According to the distribution location, they are usually divided into two types, matrix voids and interfiber voids. Interfiber voids can also be divided into the pentagonal, square, and triangular interfiber voids. The three-dimensional (3D) RVE model with fibers, matrix voids, and interfiber voids is established, where fibers and matrix voids are circular, distributed periodically and randomly, and interfiber voids are distributed randomly between fibers. The modeling flowchart is shown in Fig. 2. The RVE modeling procedure is:

Figure 1
figure 1

Cross-sectional optical images of voids with different shape in composites [25]

Full size image
Figure 2
figure 2

RVE modeling flowchart

Full size image

Step (1): Create fibers in a plate and name them set-fiber. The randomly distributed points are created in the plate, and the distance between two points d is calculated to judge whether it is greater than two times of fiber radius \(2{r}_{f}\). If so, the point is kept and outputs its coordinates. Otherwise, create another point.

Step (2): Create matrix voids in a plate and name them set-vmat. Ensure that \({d}_{\mathrm{vmat}}>{2r}_{\mathrm{vmat}}\), and \({d}_{\mathrm{vmat}}>{r}_{\mathrm{vmat}}+2{r}_{f}\), where \({d}_{\mathrm{vmat}}\) is the distance between two matrix voids, \({2r}_{\mathrm{vmat}}\) is two times of matrix voids diameter to guarantee the voids are only distributed on the matrix. If so, create matrix voids. Otherwise, create new points of matrix voids.

Step (3): Create interfiber voids and name them set-vint. After creating fibers and matrix voids, calculate the distance \({d}_{i}\) between point A and B based on the outputted coordinates. Judge whether the distance is less than \(2{r}_{f}+{r}_{f}/2\). If so, calculate the distance \({d}_{i+1}\) between point B and C, until a closed loop is formed. The total distance \({d}_{n}=\sum_{1}^{n}{d}_{i}\) (n = 3,4,5) in a closed loop can be obtained if \({d}_{n}\) is less than n(\(2{r}_{f}+\frac{{r}_{f}}{2}\)), mark and link the coordinates of points, and choose distance \({d}_{n}\) from small to large until the volume fraction of interfiber voids meets the requirement.

The fiber volume fraction \({V}_{f}={N}_{f}\pi {r}_{f}^{2}/{l}^{2}\) is set as 55% in this study, \({N}_{f}\) is the number of fibers, \({r}_{f}\) is the radius of fibers, and l is the length and width of RVEs. The total voids volume fraction \({V}_{v}\) is the sum of matrix voids volume fraction \({V}_{v-\mathrm{mat}}\) and interfiber voids volume fraction \({V}_{v-\mathrm{int}}\), the ratio of these two voids volume is set as \(\frac{{V}_{v-\mathrm{mat}}}{{V}_{v-\mathrm{int}}}=1\). Matrix voids volume fraction \({{V}_{v-\mathrm{mat}}=N}_{v}\pi {r}_{v}^{2}/{l}^{2}\), \({N}_{v}\) is the number of matrix voids, \({r}_{v}\) is the radius of matrix voids, \({r}_{v}\)= 0.3 \({r}_{f}\). The thickness T for all 3D RVEs is 0.5 \({r}_{f}\), microscopic RVEs with voids are established using PYTHON script language. Two RVE samples with and without voids established using the above method are shown in Fig. 3. The volume fraction of fibers and voids can be changed to acquire the required model in the following sections of the paper.

Figure 3
figure 3

RVE models a with different void types and b without voids

Full size image

Micromechanics model

Due to the different properties of fiber and matrix, different failure criteria for these two materials are considered in this paper. The computational model is implemented by a user-defined material subroutine.

(a) Fiber failure criterion.

Fibers are anisotropic linear elastic materials whose properties are given in Table 1. The maximum stress failure criterion is used to predict fiber failure.

$${f}_{t}=\frac{{\sigma }_{\mathrm{ij}}}{{F}_{\mathrm{it}}}$$
(1)
$${f}_{c}=\frac{{\sigma }_{i}}{{F}_{\mathrm{ic}}}$$
(2)

where \({f}_{t}\) and \({f}_{c}\) are the fiber tensile and compressive failure index, \({F}_{\mathrm{it}}\) and \({F}_{\mathrm{ic}}\) (i = 1,2,3) are the fiber tensile and compressive strength, and \({\sigma }_{\mathrm{ij}}\) (i, j = 1, 2, 3) are stress components in ij direction.

Table 1 Material parameters of fiber and matrix [27, 28]
Full size table

(b) Matrix failure criterion.

The matrix behavior corresponds to an isotropic epoxy resin with different tensile and compressive strengths. The Von Mises or Tresca criteria that do not depend on the hydrostatic stress components for isotropic materials do not apply to the prediction of matrix failure [26]. Therefore, the Stassi criterion, modified from the Von Mises criterion, is used to predict matrix failure.

$${f}_{m}=\frac{{\sigma }_{\mathrm{mises}}^{2}}{{C}_{m}{T}_{m}}+{I}_{1}\left(\frac{1}{{T}_{m}}-\frac{1}{{C}_{m}}\right)$$
(3)
$${I}_{1}={\sigma }_{11}+{\sigma }_{22}+{\sigma }_{33}$$
(4)
$${\sigma }_{\mathrm{mises}}=\sqrt{\frac{1}{2}({\left({\sigma }_{11}-{\sigma }_{22}\right)}^{2}+{\left({\sigma }_{11}-{\sigma }_{33}\right)}^{2}+{\left({\sigma }_{22}-{\sigma }_{33}\right)}^{2}+6({\sigma }_{12}^{2}+{\sigma }_{13}^{2}+{\sigma }_{23}^{2}))}$$
(5)

where \({f}_{m}\) is the matrix failure index, \({\sigma }_{\mathrm{ij}}\) (i, j = 1, 2, 3) is the stress component,\({\sigma }_{\mathrm{mises}}\) is the Von Mises equivalent stress,\( {I}_{1}\) is the first invariant, and \({T}_{m}\) and \({C}_{m}\) are the tensile strength and compressive strength of matrix.

(c) Damage evolution model.

After the material meets the failure criterion, the stiffness will be reduced to low the bearing capacity of the material. The stiffness degradation model is classified into three main types [26]: loading invariant model, progressive unloading model, and instantaneous unloading model, as is shown in Fig. 4. In the microscale damage of unidirectional fiber reinforced composite, both the matrix and fiber are brittle materials, the initial failure response of matrix and fiber is characterized by linear-elasticity [29]. Any kind of damage mode will cause it completely loses its carrying capacity. Therefore, the instantaneous unloading model is chosen in this analysis. A solution-dependent state variable is 1 when the material satisfies the failure criterion.

Figure 4
figure 4

Stiffness degradation model

Full size image

The periodic boundary condition of RVE model

According to the RVE model established in this paper, the boundary of two adjacent unit cells under external loading must satisfy the continuity of displacement and stress, the periodic boundary condition (PBC) proposed by Xia et al. [30], based on the hypothesis of small deformation, is applied to the unit cell.

$${u}_{i}^{j+}=\overline{{\varepsilon }_{ik}}{x}_{k}^{j+}+{u}_{i}^{*}$$
(6)
$${u}_{i}^{j-}=\overline{{\varepsilon }_{\mathrm{ik}}}{x}_{k}^{j-}+{u}_{i}^{*}$$
(7)
$${{u}_{i}^{j+}-u}_{i}^{j-}=\overline{{\varepsilon }_{\mathrm{ik}}}{({x}_{k}^{j+}-x}_{k}^{j-})=\overline{{\varepsilon }_{\mathrm{ik}}}{\Delta x}_{k}^{j}$$
(8)

where \({u}_{i}^{j+}\) and \({x}_{i}^{j+}\) are the displacement and coordinate of the node of unit cell, the superscript \(j+ \)and \(j-\)represent the positive and negative direction along the axis, \(\overline{{\varepsilon }_{\mathrm{ik}}}\) is the average strain of unit cell, and \({u}_{i}^{*}\) is the displacement correction. The displacement load s is applied on the point (Fig. 5) according to different loading conditions, the PBC is implemented by running PYTHON scripting language.

Figure 5
figure 5

Schematic diagram of boundary constraints

Full size image
  1. (a)

    Longitudinal tension and compression. \({U}_{A1}={U}_{A2}={U}_{A3}=0\)\({U}_{B2}={U}_{B3}=0\), \({U}_{C1}={U}_{C3}=0\), \({U}_{D1}={U}_{D2}=0\), \({U}_{B1}=s\)

  2. (b)

    Transverse tension and compression.\({U}_{A1}={U}_{A2}={U}_{A3}=0\), \({U}_{B2}={U}_{B3}=0\), \({U}_{C1}={U}_{C3}=0\), \({U}_{D1}={U}_{D2}=0\), \({U}_{C2}=s\)

  3. (c)

    Longitudinal shear. \({U}_{A1}={U}_{A2}={U}_{A3}=0\), \({U}_{B1}={U}_{B2}={U}_{B3}=0\), \({U}_{C1}={{U}_{C2}=U}_{C3}=0\), \({U}_{D2}={U}_{D3}=0\), \({U}_{D1}=s\)

  4. (d)

    Transverse shear. \({U}_{A1}={U}_{A2}={U}_{A3}=0\), \({U}_{B1}={U}_{B2}={U}_{B3}=0\), \({U}_{C1}={U}_{C2}=0\), \({U}_{D1}={U}_{D2}={U}_{D3}=0\), \({U}_{C3}=s\)

where 1, 2, and 3 are three directions of the coordinate system, \({U}_{\Delta i}\) (\(\Delta \)=A, B, C, D; i = 1,2,3) is the displacement loading.

Validation of the computational model

Figure 6A shows the finite element RVE model without void (\({V}_{v}\)= 0%) with 60,705 solid elements. The fiber volume fraction is 55%, and the PBC and micromechanics model mentioned above is applied to the RVE model. Figure 6b shows its stress–strain curves under different loads. The ultimate strength in the following analysis is the peak stress on the curves. To confirm the validity of the computational model, the empirical prediction formulas [31, 32] that do not consider the void content are used to validate the predicted results. The prediction formulas are shown in Eq. (9–13).

$${E}_{22}=\frac{{E}_{m}}{1-\sqrt{{V}_{f}}(1-{E}_{m}/{E}_{f22})}$$
(9)
$${G}_{12}=\frac{{G}_{m}}{1-\sqrt{{V}_{f}}(1-{G}_{m}/{G}_{f12})}$$
(10)
$${G}_{23}=\frac{{G}_{m}}{1-\sqrt{{V}_{f}}(1-{G}_{m}/{G}_{f23})}$$
(11)
$${Y}_{t}=\left[1-(\sqrt{{V}_{f}}-{V}_{f})(1-{E}_{m}/{E}_{f22})\right]{T}_{m}$$
(12)
$${Y}_{c}=\left[1-(\sqrt{{V}_{f}}-{V}_{f})(1-{E}_{m}/{E}_{f22})\right]{T}_{c}$$
(13)

where \({E}_{\mathrm{ij}}\), \({G}_{\mathrm{fij}}\), and \({v}_{\mathrm{fij}}\) are the elastic modulus, shear modulus, and Poisson’s ratio of composites, respectively; \({Y}_{t}\) and \({Y}_{c}\) are the tensile strength and compressive strength of composites.

Figure 6
figure 6

Validation of computational model with a finite element model and b numerical stress–strain curves at different loads

Full size image

In this study, the transverse tensile, compressive, and shear properties of the model are considered, and the predicted results obtained from Fig. 6 are presented in Table 2. The numerical results are in good agreement with the results obtained by empirical prediction formulas; the computational model is validated. Therefore, it can be considered that the results obtained by the computational model in the following sections, such as the effect of voids on CFRPs strength and the visualization of the damage evolution process, are effective and reliable.

Table 2 Comparisons of predicted results and empirical prediction formulas
Full size table

Results and discussion

Effects of volume fraction on strength

The RVEs model with and without void established using the method in Sect. 2.1 are shown in Fig. 7a-d, corresponding to void volume fraction 0–3%, respectively. The effect of different void volume fractions on transverse tensile and longitudinal shear is analyzed by adopting the micromechanics model in Sect. 2.2. The overall stress–strain curves of different RVEs are plotted in Fig. 7e and f. The void reduces the strength in the two different loads because the increasing void volume fraction brings about less bearing area of the matrix phase. Besides, the existence of voids leads to the stress concentration in the matrix and the strength reduction. The void volume fraction increases from 1% to 3%, the tensile strength decreases by 27.65%–35.29%, and the shear strength decreases by 22.76%–29.14%. The influence of voids on tensile strength is more significant than that of shear strength. The void significantly reduces the tensile and shear strength at a void volume fraction of 1%, while the magnitude of strength reduction is small for the void volume fraction from 1% to 3%. The reason behind this phenomenon is that voids are easy to cause damage. After the structure is damaged, the stress concentration drives the void-induced damage to expand rapidly inside the structure.

Figure 7
figure 7

RVEs model a without void, with b \({V}_{v}\)= 1%, c \({V}_{v}\)= 2%, and d \({V}_{v}\)= 3%. The overall stress–strain curves of RVE under e transverse tensile load and f longitudinal shear load

Full size image

Effects of void type on strength

Voids are formed unavoidably in composites. The microscopic model does not include voids defect may overestimate the properties of composite materials, and it is unknown whether the influence of varying void types properties is different. Three different void types, including matrix voids (Fig. 8b), interfiber voids (Fig. 8c), and mixed voids (Fig. 8d,\( {V}_{v-\mathrm{mat}}:{V}_{v-\mathrm{int}}\)= 1) are established, and their effects on transverse tensile strength are studied. An RVE without voids is used as a reference for comparison, as shown in Fig. 8a.

Figure 8
figure 8

a RVEs without voids, RVEs (\({V}_{v}\)= 1%) with b matrix voids, c interfiber voids, and d mixed voids

Full size image

Figure 9 shows the ultimate transverse tensile strength of RVEs at various void volume fractions with different void types. From Fig. 9, the presence of voids leads to the strength reduction of composites more or less. Among them, take \({V}_{v}\)= 1% as an example, the reduction of matrix voids, mixed voids, and interfiber voids is 19.5%, 27.65%, and 33.55%, respectively, compared with RVE without voids, which means interfiber voids have a more significant negative influence on strength than matrix voids and mixed voids. The strength of RVE with mixed voids is lower than the average strength of interfiber voids and matrix voids (dashed purple line), which is caused by the coupling effect between interfiber voids and matrix voids, which will be discussed in the next section. In addition, the strength decreases with the increase of void volume fractions for each void type.

Figure 9
figure 9

Ultimate tensile strength of different RVEs at different volume fractions

Full size image

Coupling effect of void type

Figure 10 shows the damage distribution of different RVEs with variable void volume fractions (1%, 2%, and 3%), which corresponds to the ultimate transverse tensile strength in Fig. 9. The red regions are failed elements of RVE. It can be seen from Fig. 10a that the damage mainly emanates from the matrix phase between adjacent fibers for the structure with matrix voids. Keep \({V}_{f}\) and \({r}_{v}\) constant, when the volume fraction of matrix voids increases from 1% to 3%, the damage is greater in the matrix phase. Because with the increasing volume fraction of matrix voids, the number of matrix voids is on the increase, the bearing area of the matrix is reduced, which leads to higher stress concentration in the adjacent fibers, and higher stress concentration causes damage more likely to occur. For interfiber voids (Fig. 10b), the damage is mainly induced by interfiber voids. With the increasing voids volume fraction, interfiber voids cause more local geometry within composites, such as sharp angles. More local geometry causes higher stress concentration, leading to the damage more easily starting from interfiber voids, less from matrix phase, which means interfiber voids are more likely to cause stress concentration than matrix phase.

Figure 10
figure 10

Damage distributions at ultimate strength of RVEs with a matrix voids, b interfiber voids and c mixed voids

Full size image

Unlike matrix voids or interfiber voids, the reason for damage to mixed voids (Fig. 10c) is more complicated, which is determined by the coupling effect between matrix voids and interfiber voids, that is, the competition of stress concentration in different damage regions. There are three regions where stress concentration may occur: interfiber voids, matrix voids, and the matrix phase. As mentioned above, the increased volume fractions of matrix voids make the stress concentration more easily originate from the matrix phase, while less emanates from the matrix phase for interfiber voids. The opposite phenomenon defines the variation of damaged regions of composites with mixed voids together. As can be seen from Fig. 10c, damage regions distributed in the matrix phase decrease as the volume fraction of mixed voids increases, suggesting that interfiber voids-induced stress concentration plays a dominant role in the coupling effect. This finding corresponds to the macroscopic tensile strength in Fig. 9. If matrix voids RVE evenly determines the strength between matrix voids and interfiber voids, the average strength should be equal to that of mixed voids. However, the numerical results are lower than average strength, verifying the dominance of interfiber voids in terms of reducing strength. According to the findings found from the analysis above, we can conclude that the interfiber voids are more likely to cause stress concentration than the matrix phase, the matrix phase is more likely to lead to stress concentration than matrix voids.

Taking RVE with mixed voids of \({V}_{v}\)= 2% as an example, as is shown in Fig. 11, the initial damage of structure mainly originates from interfiber voids. With the increase of displacement load, damage begins to propagate in the matrix phase, and the matrix voids-induced damage occurs at the last stage. This rule has also certificated the conclusion obtained in Fig. 10. The damage starts from interfiber voids or matrix phase, extends to the matrix along the edge of fibers, then connects with the other damaged elements as the constant load, the bearing capacity of composites is declined. As the further increased load, damage intersects the whole structure, composites are failed. Furthermore, the coupling effect leads to the change of damage evolution path (dashed yellow line) of mixed voids. The mixed voids (Fig. 11d) are the combination of matrix voids (Fig. 11e) and interfiber voids (Fig. 11f). The damage path of RVE with mixed voids is distinct from that of matrix voids but more similar to interfiber voids. The added matrix voids partly bring the change of path direction, as shown by the ellipse in Fig. 11d. This finding also proves that the interfiber voids-induced stress concentration is dominant in the coupling effect. The path is approximately perpendicular to the loading direction, and the fibers are not damaged during the loading process.

Figure 11
figure 11

Damage evolution process of structure of a damage initiation from interfiber voids, and b damage evolution in matrix phase, c damage occurs in matrix voids. The damage path of RVE with c mixed voids, d interfiber voids and e matrix voids. The void volume fraction in d is the sum of the void volume fraction in e and f

Full size image

Failure envelopes of CFRPs with various void volume fractions

Former researchers [7, 23] indicate that composite structures are not acceptable when the void volume fraction is greater than 5% in most industries. Thus, the upper bounds of the void volume fraction are set as 5% in this work. Four RVEs (Fig. 12a-c) with void volume fractions of 0%, 1%, 3%, and 5% are employed to explore the failure envelopes of CFRPs.

Figure 12
figure 12

Different RVEs with a \({V}_{v}\)= 0% b \({V}_{v}\)= 1%, c \({V}_{v}\)= 3%, d \({V}_{v}\)= 5% and e schematic of biaxial loading

Full size image

Additionally, the stress space is studied and verified by Hashin–Rotem [33] and Puck [34] failure criteria. These two criteria have been validated to accurately predict the envelope of different RVE void models [21, 22, 35]. Hashin–Rotem failure criteria consider that the composite has two failure modes: fiber failure and matrix failure. Matrix failure is caused by the combined action of transverse stress and longitudinal shear stress, expressed as

$${\left(\frac{{\tau }_{13}}{{S}_{13}}\right)}^{2}+{\left(\frac{{\sigma }_{22}}{{Y}_{t}}\right)}^{2}=1$$
(14)

where \({S}_{13}\) and \({Y}_{t}\) are longitudinal shear strength and transverse tensile strength, respectively. \({\tau }_{13}\) is longitudinal shear stress, and \({\sigma }_{22}\) is transverse tensile stress.

Puck established failure criteria to distinguish fiber and interfiber fractures. Matrix fracture is split into three modes: mode-A, mode-B, and mode-C. In mode-A, composites are subjected to transverse tensile and longitudinal shear load, which leads to the fracture plane perpendicular to tensile load, and the fracture angle is \({\theta }_{\mathrm{fp}}\)= 0\(^\circ \). Similar to mode-A, mode-B is defined as the longitudinal shear with transverse compressive load, and mode-C is determined as the transverse compressive with the longitudinal shear load. In this study, only mode-A is discussed, and the failure criteria are [36]

$$\sqrt{{\left(\frac{{\tau }_{13}}{{S}_{13}}\right)}^{2}+{\left(1-{P}_{\perp \parallel }^{(+)}\frac{{Y}_{t}}{{S}_{13}}\right)}^{2}{\left(\frac{{\sigma }_{22}}{{Y}_{t}}\right)}^{2}}+{P}_{\perp \parallel }^{(+)}\frac{{\sigma }_{22}}{{S}_{13}}=1$$
(15)

where \({P}_{\perp \parallel }^{(+)}\) is the slope of the failure envelope in \({\tau }_{13}-{\sigma }_{22}\) plane, \({P}_{\perp \parallel }^{(+)}\)= 0.2 [37], the transverse tensile and longitudinal shear strength calculated by the computational model of different void volume fractions is listed in Table 3. The schematic of biaxial loading of \({\tau }_{13}\) and \({\sigma }_{22}\) is shown in Fig. 12e.

Table 3 Strengths of composites with void volume fractions
Full size table

The \({\tau }_{13}-{\sigma }_{22}\) curves under biaxial loading with different displacement ratios of \({\Delta }_{13}/{\Delta }_{22}\) (from 1 to 12) for different void volume fractions are shown in Fig. 13a-d. \({\Delta }_{13}\) and \({\Delta }_{22}\) are the shear and tensile displacements, respectively. The results show that the slope of curves increases with the increase of displacement ratios. The failure envelopes of composites can be acquired by linking the failure points, and they become smaller with the increase of the void volume fractions. The change of tensile strength under different void volume fractions is more significant than that of shear strength, indicating that the void affects the tensile strength more significantly than the shear strength of composites under the combined loads. The damage contour plots are shown in Fig. 14, which are the failure under mode-A. From the figure, the damage regions in different displacement ratios are different. With the increasing ratios of \({\Delta }_{13}/{\Delta }_{22}\), the damage path changes gradually, from perpendicular to horizontal. The damage path is perpendicular to the loading direction at pure tension or shear.

Figure 13
figure 13

Tensile–shear stress curves under biaxial loading with different displacement ratios of RVE with a \({V}_{v}\)= 0%, b \({V}_{v}\)= 1%, c \({V}_{v}\)= 3%, and d \({V}_{v}\)= 5%

Full size image
Figure 14
figure 14

a The applied load, damage contour plots of RVE (\({V}_{v}\)= 3%) subjected to b pure tension, c combined load of \({\Delta }_{13}/{\Delta }_{22}\)=1, d combined load of \({\Delta }_{13}/{\Delta }_{22}\)=3, e combined load of \({\Delta }_{13}/{\Delta }_{22}\)=6, f combined load of \({\Delta }_{13}/{\Delta }_{22}\)=9, g combined load of \({\Delta }_{13}/{\Delta }_{22}\)=12, and h pure shear

Full size image

The comparison of \({\tau }_{13}-{\sigma }_{22}\) stress space obtained by the computational model and failure criteria at different void volume fractions under different displacements ratios are plotted in Fig. 15. The computational model agrees well with the failure criteria. However, the failure envelopes calculated by the computational model are larger than the failure criteria under biaxial loading because the influence of the interface between fiber and matrix on the overall properties of materials is not considered in this paper. Research [23, 24, 37] reveals that the failure mechanism in mode-A is related to interfacial debonding, and the interfacial strength is generally lower than the tensile strength of the matrix. Thus the existence of interface will reduce the properties of composites. Besides, if the interface and voids exist simultaneously, voids will lead to interfacial debonding occurring under lower stress, and the properties of composites will be further decreased. However, the property parameter and the thickness of the interface are difficult to determine, thus the interface is not considered in this paper.

Figure 15
figure 15

Comparison of failure envelopes by computational model and failure criteria at a \({V}_{v}\)= 0%, b \({V}_{v}\)= 1%, c \({V}_{v}\)= 3% and d \({V}_{v}\)= 5%

Full size image

In addition, the failure envelopes predicted by the Hashin–Rotem criteria are more significant than the Puck criteria in this calculation. The Puck failure mechanism is dominated by the matrix yielding in shear in mode-A [35]. In contrast, the Hashin–Rotem failure mechanism is determined by tensile and shear stress, quadratic interaction between tensile stress and shear stress may improve the strength of the composite under biaxial loading partly.

From Fig. 15, the presence of voids can affect the failure envelopes of composites. The failure envelopes decreased significantly from 1% to 5% of void volume fractions. The transverse tensile strength is reduced by 39.99% at \({V}_{v}\)= 5%, the former research is 38% with 60% fiber volume fraction [22]. The longitudinal shear strength decreased by 44.12% at \({V}_{v}\)= 5%, this value is about 35% in reference [24]. The difference in the results can be controlled by the size and shape of the voids, and the volume fraction and radius of the fibers. Moreover, it is difficult to measure the shear strength \({S}_{13}\) experimentally; thus, this work is effective in the prediction of shear strength.

For other problems of structural composite failure, such as mechanical response with rate-dependent nonlinearity [38], voids size problem [39], buckling problem [40, 41], and the multi-scale problem [29, 42], the RVE model and computational framework established in this paper can be easily further developed for application by changing the failure model or RVE parameters.

Conclusions

In this paper, the microstructure models are established to investigate the void type and volume fraction on the strength of fiber reinforced composites. The failure mechanisms and coupling effect between matrix voids and interfiber voids are explained at the microscale. The failure envelopes of composites with different void volume fractions calculated by the computational model are provided and compared with two eminent failure criteria. The main conclusions obtained from numerical analysis are as follows:

  1. (1)

    The modeling procedure is developed to generate different RVE void models. The RVE-based computational model is verified by comparing the numerical results with the empirical prediction formulas. The difference between them is within 10%. The validated computational model could be used in the visualization study of damage mechanisms and evolution process, as well as the investigation of the effect of voids on strength.

  2. (2)

    The existence of various voids reduces the tensile and shear strength more or less, but the influence degree depends on the voids type. Even if only 1% void volume fraction exists, the interfiber voids, mixed voids, and matrix voids will reduce the tensile strength of CFRPs by 33.55%, 27.65%, and 19.5%, respectively, compared with RVE without voids. The effect of voids should not be ignored in strength prediction. The interfiber voids negatively influence tensile strength, bringing higher stress concentration; the circular voids in the matrix have a relatively weak influence.

  3. (3)

    The failure mechanisms caused by increasing volume fraction of different void types differ. The increased volume fraction of matrix voids makes the matrix phase between adjacent fibers thinner, causing stress concentration easier to distribute in them. The increased interfiber voids bring more sharp angles, also leading to more stress concentration around voids.

  4. (4)

    The coupling effect is the competition of voids-induced stress concentration in different damaged regions. The interfiber voids-induced stress concentration plays a dominant role in the coupling effect. Additionally, the areas prone to damage are interfiber voids, matrix phases between adjacent fibers, and matrix voids. This conclusion indicates that fibers should be distributed evenly to avoid the accumulation of fibers and the resulting interfiber voids.

  5. (5)

    In the \({\tau }_{13}-{\sigma }_{22}\) stress space, the failure envelopes calculated by the computational model have good agreements with both Hashin–Rotem and Puck failure criteria. This computational model provides a convenient failure prediction method, which is also suitable for studying other microstructural features, such as cracks and impurities.

The effect of the matrix voids size on the properties of composites is not discussed in this paper, which will be analyzed in future work. The RVE modeling procedure still needs to be improved because it is time-consuming.