Introduction

High-temperature polymer matrix composites (PMCs) are widely used in high-speed transport airframe structures and aircraft engine components due to their high strength, high stiffness, high temperature tolerance, and high light weight properties. In many applications, these materials must withstand from room temperature (RT) to high temperature while maintaining structural integrity. Due to the viscoelastic behavior of the polymer matrix, the physical properties of polymer and its composite can change drastically over relatively small changes in temperature [1]. In other words, understanding the relationship between temperature and mechanical properties from RT to high temperature is not only important but also interesting.

Many researchers have investigated the relationship between temperature and dynamic storage modulus [2–14]. Havriliak and Negami [2] modeled the dynamic mechanical properties of polymers. Szabo and Keough [3] studied the dynamic mechanical thermal analysis data by Havriliak–Negami model. Setua et al. [4] studied the dynamic mechanical properties of engineering thermoplastics using Havriliak–Negami model. Bai et al. [5, 6] modeled the temperature-dependent modulus by the Arrhenius-type equations. The model was similar to the nth-order cure kinetic of matrix which has three independent parameters. Mahieux and Reifsnider [7, 8] modeled the stiffness variation with respect to temperature by Weibull distribution which included three independent parameters. Gibson et al. [9] presented a semi-empirical model based on the hyperbolic tanhx function to describe the properties from glass state to rubber state. Their model was derived from phenomenological observations (curve fitting), and the physical meaning for parameters was not mentioned. Kandare et al. [10, 11] developed a coupled thermo-mechanical model which was used to predict the residual flexural stiffness of polymer composites with and without flame-retardant additives following exposure to one-sided radiant heating. Their model was also based on the form of a tanhx function. Nam [12] studied the storage modulus of phenolic resin/carbon fiber composite system by DMA under nine different frequencies (from 0.01 to 5 Hz). Guo et al. [13, 14] proposed a new simple temperature-dependent model to describe dynamic storage modulus and static flexural modulus. Recently, Feng and Guo [14] improved their model [13] to study the dynamic mechanical properties of epoxy resin. Among these models, some are able to predict the dynamic storage modulus with complicated expressions. Some models which have simple forms show excellent agreement with experimental data in glass transition region and rubber state.

Some researchers also studied the changes of loss modulus of a polymer with temperatures [3, 15–17]. The semi-empirical model developed by Fuoss and Kirkwood [15] is also used to describe the dynamic mechanical properties of polymers [16, 17]. Nevertheless, neither Havriliak–Negami model nor Fuoss and Kirkwood model can describe the high-temperature and low-temperature properties of the polymers.

In this paper, new models were developed to describe the storage modulus and loss modulus changes of epoxy resin and glass/epoxy composites from RT to elevated temperatures. Theoretical results were compared with corresponding experimental results which were obtained by dynamic mechanical analysis (DMA). Combined with the Arrhenius equation, the new models can be extended to describe the temperature–frequency-dependent dynamic modulus over the whole temperature range.

Experimental

Materials and specimen description

The glass/epoxy composite laminates (unidirectional [0] and cross-ply [0–90] symmetric laminate) were manufactured by Shanghai FRP Research Institute Co., Ltd. The specimens were cut using a low-speed precision diamond blade saw. Specimens of nominal dimensions 60 × 14.5 × 3.5 mm (length × width × thickness) were prepared for all experiments.

Dynamic mechanical properties

Q-800 dynamic mechanical analyzer (TA Instruments, New Castle, DE, USA) was utilized to conduct the experiments. The storage modulus (\( E^{\prime} \)), loss modulus (\( E^{\prime\prime} \)), loss factor (\( \tan \delta \)), and glass transition temperature (T g) were determined by single cantilever (SC) and double cantilever (DC) loading mode at frequencies 1, 5, 10, 40, 50, 100, and 160 Hz. The specimens were tested with a heating rate of 3 K/min in the range from RT to 400 K. Three tests for each condition were conducted and averaged.

Methods of determining T g

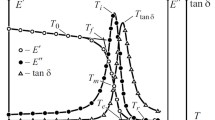
The T g shown in Fig. 1 can be determined by measuring the peak value on the loss modulus curves, the peak value of the loss factor curves (T g \( \left( {\tan \delta } \right)_{\hbox{max} } \)), or the first inflection point for the storage modulus curve (T mg) [18–20]. The latter is the most conservative, and T g \( \left( {\tan \delta } \right)_{\hbox{max} } \) is the least conservative.

Fig. 1
figure 1

Various methods of determining the glass transition temperature

Full size image

Result and discussion

Dynamic mechanical properties at a frequency of 1 Hz under DC loading mode

Figure 2 shows the curves of the storage modulus (\( E^{\prime} \)), loss modulus (\( E^{\prime\prime} \)), and loss factor (\( \tan \delta \)) for epoxy resin and its composites versus temperature at a frequency of 1 Hz under DC loading mode. It can be seen that all samples are in the glassy state below 340 K and rubbery state above 360 K. The glass transition region is from about 340 to 360 K. It can be found that the dynamic mechanical properties of epoxy resin and its composites change dramatically in the glass transition region.

Fig. 2
figure 2

Dynamic mechanical properties of epoxy resin and its composites at 1 Hz frequency under DC loading mode (Color figure online)

Full size image

From Fig. 2a, it can be seen that \( E^{\prime} \) for all samples is quite large in the glassy state, while it changes slightly and remains very small in the rubbery state. The difference in the storage modulus of neat resin and the composites is small at high temperature showing that fiber incorporation does not contribute to stiffness of the material at high temperature. The composites exhibit much higher storage modulus when compared with the neat resin, and this clearly shows the fiber effect.

In Fig. 2b, although the values of \( E^{\prime\prime} \) for all samples are small and not changed in the glass state and rubber state compared with the maximum value in the glass transition region, but the values in glass state are larger than the ones in the rubber state.

From Fig. 2c, it can be seen that the neat resin exhibited the highest \( \tan \delta \) maximum. According to the definition, \( \tan \delta \) is related to the degree of molecular mobility in the material. The fibers restricted the mobility of polymer molecules and reduced the viscoelastic lag between the stress and strain, and hence the \( \tan \delta \) peak values are decreased in the composites. This is also due to the fact that there is less matrix by volume to dissipate the vibration energy. This may be taken as an effect of interaction between fiber and polymer matrix.

Dynamic mechanical properties at different frequencies under different loading modes

The viscoelastic properties of a material are dependent on temperature and time (frequency). Hence, it is interesting to study the influence of frequency on the dynamic properties of polymer matrix and its composites. Figures 3 and 4 show the viscoelastic properties (\( E^{\prime} \), \( E^{\prime\prime}, \) and \( \tan \delta \)) of [0] laminate, [0–90] symmetric laminate, and epoxy resin at different loading frequencies and under two different loading modes (SC and DC).

Fig. 3
figure 3

Dynamic mechanical behaviors of epoxy resin and its composites at different loading frequencies under SC loading mode (Color figure online)

Full size image
Fig. 4
figure 4

Dynamic mechanical behaviors of epoxy resin and its composites at different loading frequencies under DC loading mode (Color figure online)

Full size image

Figures 3a and 4a show that the \( E^{\prime} \) decreases with increasing temperature and increases with increasing frequency. This is attributed to the lesser mobility of polymeric chains at high frequency. As shown in Figs. 3b and 4b, the temperature at \( E^{\prime\prime}_{\hbox{max} } \) shifts toward higher temperature region when the loading frequency goes up. Figures  3c and 4c show that the peak of \( \tan \delta \) shifts to higher temperature with the increasing frequency. In other words, the damping shows its highest value at 1 Hz and decreases as frequency is increased. This can be attributed to better fiber/matrix adhesion. The phenomena are similar to other results of different polymers or composites [12, 14, 21–23]. From Figs. 3c and 4c, it can also be found that the width of the \( \tan \delta \) peak becomes wider with increasing frequency.

Figure 5 shows the relationship between T g s and loading frequencies under different loading modes. The T g s are shifted to higher temperature as the frequency is increased for all different loading modes. The T g s of the neat resin are also found to be increased with increasing frequency [14]. The onset for \( E^{\prime} \), maxima for \( E^{\prime\prime}, \) and \( \tan \delta \) peaks appear at the beginning, at the middle, and at the end, respectively, of the glass transition region which becomes wider when frequency increases. These are indications of high degree of reinforcement.

Fig. 5
figure 5

Glass transition temperatures (T g) of epoxy at different loading frequencies (Color figure online)

Full size image

The glass transition temperature may be expressed in the form of Arrhenius-type equation with frequency, which was widely used not only in DMA [14, 21, 22], but also in fatigue strength prediction [24] and water diffusion [25]:

$$ \ln (f) = \ln (A) - \left( {{{\Delta E} \mathord{\left/ {\vphantom {{\Delta E} R}} \right. \kern-0pt} R}} \right) \cdot \left( {{1 \mathord{\left/ {\vphantom {1 {T_{\text{g}} }}} \right. \kern-0pt} {T_{\text{g}} }}} \right), $$
(1)

where \( \Delta E \) is the activation energy, R is the gas constant, and A is a constant. Figure 6 shows the relationship between T g s and loading frequencies under two different loading modes. It can be seen that \( \ln (f) \) and \( {1 \mathord{\left/ {\vphantom {1 {T_{\text{g}} }}} \right. \kern-0pt} {T_{\text{g}} }} \) have a very good linear relationship. In other words, the relationship between T g and frequency can be expressed by Arrhenius equation very well. The values of the activation energies determined by four definitions of glass transition temperatures, T eig, T mg, T g (\( E^{\prime\prime}_{\hbox{max} } \)), and T g (\( \left( {\tan \delta } \right)_{\hbox{max} } \)), are summarized in Table 1. It can be seen that the activation energies determined under SC mode are quite larger than those determined under DC mode. The activation energies determined by T eig have a large difference because it is difficult to apply tangents, especially with nonlinear curves to determine T g using storage modulus onset.

Fig. 6
figure 6

Arrhenius relationships between T g s and loading frequencies (Color figure online)

Full size image
Table 1 Activation energy \( \Delta E \) determined at different T gs
Full size table

Models of dynamic modulus

Temperature-dependent storage modulus model

The degree of glass transition, \( a_{\text{gt}} \), which was used in many studies [5, 9, 14], is defined in Eq. (2):

$$ a_{\text{gt}} = \frac{{E^{\prime}_{\text{g}} - E^{\prime}}}{{E^{\prime}_{\text{g}} - E^{\prime}_{\text{r}} }}, $$
(2)

where \( E^{\prime}_{\text{g}} \) is the storage modulus in the glassy state, \( E^{\prime}_{\text{r}} \) is the storage modulus in the rubbery state, and \( E^{\prime} \) is the instantaneous storage modulus. The relationship between \( a_{\text{gt}} \) and temperature was reported in our previous paper [9, 14], which is expressed by Eq. (3):

$$ {{da_{\text{gt}} } \mathord{\left/ {\vphantom {{da_{\text{gt}} } {dT}}} \right. \kern-0pt} {dT}} = k \cdot (1 - a_{\text{gt}} ) \cdot a_{\text{gt}}, $$
(3)

where k is the intrinsic growth rate of the number of rubber-state molecules per unit temperature. A new parameter m which controls the symmetry of glass transition region is introduced to consider the asymmetry of glass transition region. The modified model is expressed by Eq. (4):

$$ {{da_{\text{gt}} } \mathord{\left/ {\vphantom {{da_{\text{gt}} } {dT}}} \right. \kern-0pt} {dT}} = k \cdot (1 - a_{\text{gt}}^{m} ) \cdot a_{\text{gt}}. $$
(4)

When the temperature approaches T mg, \( a_{\text{gt}} \) attains the value of 1/2. Thus, the solution of differential Eq. (4) is

$$ a_{\text{gt}} (T) = \frac{1}{{[(2^{m} - 1) \cdot e^{{mk \cdot (T_{\text{mg}} - T)}} + 1]^{{\left( {1/m} \right)}} }}. $$
(5)

Substituting Eq. (5) in Eq. (2), the temperature-dependent storage modulus could be determined by Eq. (6):

$$ E^{\prime}(T) = E^{\prime}_{\text{g}} - \frac{{E^{\prime}_{\text{g}} - E^{\prime}_{\text{r}} }}{{[(2^{m} - 1) \cdot e^{{mk \cdot (T_{\text{mg}} - T)}} + 1]^{{\left( {{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0pt} m}} \right)}} }}. $$
(6)

The influence of parameter m on storage modulus is shown in Fig. 7. When m = 1, the model can be degenerated to our previous model [9]. The storage modulus is central symmetry regarding the point \( \left( {T_{\text{mg}} ,{{E^{\prime}_{\text{g}} + E^{\prime}_{\text{r}} } \mathord{\left/ {\vphantom {{E^{\prime}_{\text{g}} + E^{\prime}_{\text{r}} } 2}} \right. \kern-0pt} 2}} \right) \) in the glass transition region; when m > 1, it drops slowly before T mg and fast after T mg, and on the contrary when 0 < m < 1, it drops fast before T mg and slowly after T mg. Figure 2a, b also shows the model prediction. It can be seen that the predictions of \( E^{\prime} \) are in good agreement with experimental data in the entire region. The values of parameters k, m, and T mg are summarized in Table 2. It can be concluded that the parameter k of composites is larger than that of epoxy resin [14]. That is to say, the glass transition regions of glass/epoxy composites are narrower than those of epoxy resin. Another phenomenon is that the parameter m is smaller than that of epoxy resin matrix when the storage modulus of composites drops more slowly before T mg. The reason may be that the chain segment motions of epoxy resin are blocked after the glass fibers are incorporated with matrix. It makes the glass transition region become narrow and T mg shifts to high temperature.

Fig. 7
figure 7

The influence of parameter m on storage modulus \( E^{\prime} \) (Color figure online)

Full size image
Table 2 The parameters k and m of epoxy resin and its composites under DC loading mode
Full size table

Temperature-dependent loss modulus model

A very interesting result can be found from the DMA data of glass/epoxy composites. The temperature of the maxima in loss modulus and \( {{dE^{\prime}} \mathord{\left/ {\vphantom {{dE^{\prime}} {dT}}} \right. \kern-0pt} {dT}} \)(\( {{da_{\text{gt}} } \mathord{\left/ {\vphantom {{da_{\text{gt}} } {dT}}} \right. \kern-0pt} {dT}} \)) coincide, and the variation tendencies of loss modulus and \( {{da_{\text{gt}} } \mathord{\left/ {\vphantom {{da_{\text{gt}} } {dT}}} \right. \kern-0pt} {dT}} \) are very similar. The similar observation was also reported by other researchers [14, 20, 26]. The expression of \( {{da_{\text{gt}} } \mathord{\left/ {\vphantom {{da_{\text{gt}} } {dT}}} \right. \kern-0pt} {dT}} \) is

$$ \frac{{da_{\text{gt}} }}{dT} = \frac{{k \cdot (2^{m} - 1) \cdot e^{{mk(T_{\text{mg}} - T)}} }}{{\left[ {(2^{m} - 1) \cdot e^{{mk(T_{\text{mg}} - T)}} + 1} \right]^{{\frac{1}{m} + 1}} }} $$
(7)

When \( T = T_{\text{mg}} - {{\ln \left( {\frac{m}{{2^{m} - 1}}} \right)} \mathord{\left/ {\vphantom {{\ln \left( {\frac{m}{{2^{m} - 1}}} \right)} {mk}}} \right. \kern-0pt} {mk}} \), \( \frac{{da_{\text{gt}} }}{dT} \) reaches the maximum:

$$ \frac{{da_{\text{gt}} }}{dT}|_{\hbox{max} } = \frac{k \cdot m}{{(m + 1)^{1 + (1/m)} }}. $$
(8)

If we suppose that loss modulus is linearly related to \( {{da_{\text{gt}} } \mathord{\left/ {\vphantom {{da_{\text{gt}} } {dT}}} \right. \kern-0pt} {dT}} \), the model of loss modulus can be written as

$$ E^{\prime\prime}(T)\; = \;C \cdot \frac{{k \cdot (2^{m} - 1) \cdot e^{{mk(T_{\text{mg}} - T)}} }}{{[(2^{m} - 1) \cdot e^{{mk(T_{\text{mg}} - T)}} + 1]^{1 + (1/m)} }}, $$
(9)

where \( C\; = \;E^{\prime\prime}_{\hbox{max} } /\left( {k \cdot m/(m + 1)^{(1 + (1/m))} } \right) \) is the proportional coefficient.

Analyzing Eq. (9), it can be found that when the temperature is in the glass state (\( T > > T_{\text{mg}} \)) or in the rubber state (\( T < < T_{\text{mg}} \)), \( E^{\prime\prime} \) will be almost close to zero. We know that the model predictions are in excellent agreement with experimental data in glass transition region and rubber state from Fig. 2b. But in the glass state, the discrepancy gradually increases when the temperature descends. It means that loss moduli of [0] laminate, [0–90] symmetric laminate, and epoxy resin are not close to zero in the glass state, whereas these remain very small in rubber state. The reason for this discrepancy may be related with the influence of β transition. As demonstrated in Fig. 8, the epoxy resin and its composites have α and β transitions in the temperature region from 170 to 390 K. However, in the glass state, these two transitions overlap each other and as a result the loss modulus cannot decrease to zero in the temperature region from 250 to 330 K. Consequently, the loss modulus model predictions have little discrepancies with the experimental data in the glass state.

Fig. 8
figure 8

The overlap of α and β transitions of epoxy resin

Full size image

From Eq. (9), it can be found that when \( T^{*} = T_{\text{mg}} - {{\ln \left( {\frac{m}{{2^{m} - 1}}} \right)} \mathord{\left/ {\vphantom {{\ln \left( {\frac{m}{{2^{m} - 1}}} \right)} {mk}}} \right. \kern-0pt} {mk}} \), loss modulus will reach the maximum value. Thus the model predication of \( T_{\text{g}} (E^{\prime\prime}_{\hbox{max} } ) \) will be equal to \( T^{*} \). The values of \( T_{\text{g}} (E^{\prime\prime}_{\hbox{max} } ) \) experimental data and model predictions at different loading frequencies under two loading modes are shown in Fig. 9. It is very interesting that the model predictions are very close to the experimental results.

Fig. 9
figure 9

Comparisons of \( T_{\text{g}} (E^{\prime\prime}_{\hbox{max} } ) \) experimental data and model predications (Color figure online)

Full size image

Temperature–frequency-dependent dynamic modulus

As discussed in “Dynamic mechanical properties at different frequencies under different loading modes” section, when frequency changes, the glass transition temperature and width of glass transition region will also change. Therefore, the parameters k and m in Eq. (6) which controlled the width and shape of glass transition region are no longer constants but functions of frequency. Loading frequency has greatly altered the shape of storage modulus versus temperature relationship of epoxy resin: the higher loading frequency, the wider the glass transition region which is shown in Fig. 3, corresponding to the decreasing values of k and m.

It is very interesting that the 1/k and 1/m values of epoxy resin and its composites under two loading modes increase linearly with increasing ln(f) as clearly shown in Fig. 10. Thus, the parameters k and m are supposed to be expressed by the similar Arrhenius-type equation as

Fig. 10
figure 10

Relationships between the parameters k and m and frequency of epoxy resin and its composites (Color figure online)

Full size image

\( \ln (f) = A_{1} + B_{1} \cdot \left( {{1 \mathord{\left/ {\vphantom {1 k}} \right. \kern-0pt} k}} \right) \) and

$$ \ln (f) = A_{2} + B_{2} \cdot \left( {{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0pt} m}} \right), $$
(10)

where A 1, B 1, A 2, and B 2 are constants which are summarized in Table 3. Combined with Eqs. (1), (6), and (9), the temperature–frequency-dependent dynamic modulus models can be expressed as

Table 3 The constants A 1, B 1, A 2, and B 2 of epoxy resin and its composites
Full size table
$$ E^{\prime}(T) = E^{\prime}_{\text{g}} - \frac{{E^{\prime}_{\text{g}} - E^{\prime}_{\text{r}} }}{{[(2^{m(f)} - 1) \cdot e^{{m(f) \cdot k(f) \cdot (T_{\text{mg}} (f) - T)}} + 1]^{1/m(f)} }} $$
(11)
$$ E^{\prime\prime}(T){ = }\frac{{E^{\prime\prime}_{\hbox{max} } \cdot (2^{m(f)} - 1) \cdot e^{{m(f) \cdot k(f) \cdot (T_{\text{mg}} (f) - T)}} \cdot (m(f) + 1)^{1 + (1/m(f))} }}{{m(f) \cdot \left[ {(2^{m(f)} - 1) \cdot e^{{m(f) \cdot k(f) \cdot (T_{\text{mg}} (f) - T)}} + 1} \right]^{1 + (1/m(f))} }}, $$
(12)

where \( k(f) \), \( m(f), \) and \( T_{\text{mg}} (f) \) are the functions of frequency. Figure 11 shows the typical comparison of model predictions and experimental results at frequencies of 1 and 100 Hz under DC loading mode. It can be seen that the measured storage modulus of epoxy resin and its composite at different frequencies (1 and 100 Hz) can be well modeled by the extended model (Eq. 11). Meanwhile, in glass transition region and rubber state, the model prediction and experimental data of loss modulus match very well although in glass state the overlap of α and β transitions results in a little discrepancy. The similar results which were not demonstrated here can be obtained at all the frequencies and under both SC and DC loading modes.

Fig. 11
figure 11

Dynamic mechanical properties of experimental data and model predictions of epoxy resin and its composites at different loading frequencies (1 and 100 Hz) under DC loading mode (Color figure online)

Full size image

It should be pointed out that the temperature-dependent storage and loss modulus models can also be extended to describe multiple transitions. For example, the epoxy resin passes through three transitions in the test region: α transition, β transition, and γ transition. The Eqs. (6) and (9) of storage and loss modulus models can be extended to give

$$ E^{\prime}(T) = E^{\prime}_{u} |_{\gamma } - \frac{{E^{\prime}_{u} \text{|}_{\gamma } - E^{\prime}_{r} \text{|}_{\gamma } }}{{[(2^{{m_{\gamma } }} + 1) \cdot e^{{ - m_{\gamma } k_{\gamma } \cdot (T - T_{\text{mg}} |_{\gamma } )}} + 1]^{{1/m_{\gamma } }} }} - \frac{{E^{\prime}_{u} \text{|}_{\beta } - E^{\prime}_{r} \text{|}_{\beta } }}{{[(2^{{m_{\beta } }} + 1) \cdot^{{ - m_{\beta } k_{\beta } \cdot (T - T_{\text{mg}} \text{|}_{\beta } )}} + 1]^{{1/m_{\beta } }} }} = - \frac{{E^{\prime}_{u} \text{|}_{\alpha } - E^{\prime}_{r} \text{|}_{\alpha } }}{{[(2^{{m_{\alpha } }} + 1) \cdot e^{{ - m_{\alpha } k_{\alpha } \cdot (T - T_{\text{mg}} |_{\alpha } )}} + 1]^{{1/m_{\alpha } }} }} $$
(13)
$$ E^{\prime\prime}(T) = \frac{{E^{\prime\prime}_{\hbox{max} } \text{|}_{\alpha } \cdot (2^{{m_{\alpha } }} - 1) \cdot e^{{m_{\alpha } k_{\alpha } (T_{mg} \text{|}_{\alpha } - T)}} \cdot (m_{\alpha } + 1)^{{1 + (1/m_{\alpha } )}} }}{{m_{\alpha } \cdot \left[ {(2^{{m_{\alpha } }} - 1) \cdot e^{{m_{\alpha } k_{\alpha } (T_{mg} \text{|}_{\alpha } - T)}} + 1} \right]^{{1 + (1/m_{\alpha } )}} }} + \frac{{E^{\prime\prime}_{\hbox{max} } \text{|}_{\beta } \cdot (2^{{m_{\beta } }} - 1) \cdot e^{{m_{\beta } k_{\beta } (T_{\text{mg}} \text{|}_{\beta } - T)}} \cdot (m_{\beta } + 1)^{{1 + (1/m_{\beta } }} }}{{m_{\beta } \cdot \left[ {(2^{{m_{\beta } }} - 1) \cdot e^{{m_{\beta } k_{\beta } (T_{\text{mg}} \text{|}_{\beta } - T)}} + 1} \right]^{{1 + (1/m_{\beta } )}} }} = + \frac{{E^{\prime\prime}_{\hbox{max} } \text{|}_{\gamma } \cdot (2^{{m_{\gamma } }} - 1) \cdot e^{{m_{\gamma } k_{\gamma } (T_{\text{mg}} \text{|}_{\gamma } - T)}} \cdot (m_{\gamma } + 1)^{{1 + (1/m_{\gamma } )}} }}{{m_{\gamma } \cdot \left[ {(2^{{m_{\gamma } }} - 1) \cdot e^{{m_{\gamma } k_{\gamma } (T_{\text{mg}} \text{|}_{\gamma } - T)}} + 1} \right]^{{1 + (1/m_{\gamma } )}} }}, $$
(14)

where \( E^{\prime}_{u} |_{\alpha } \) or \( E^{\prime}_{r} |_{\alpha } \), \( E^{\prime}_{u} |_{\beta } \) or \( E^{\prime}_{r} |_{\beta } \), and \( E^{\prime}_{u} |_{\gamma } \) or \( E^{\prime}_{r} |_{\gamma } \) are the unrelaxed or relaxed modulus before or after α transition, β transition, and γ transition, respectively. \( T_{\text{mg}} |_{\alpha } \), \( T_{\text{mg}} |_{\beta }, \) and \( T_{\text{mg}} |_{\gamma } \) are the glass transition temperatures determined by the middle of storage modulus in every transition. \( k_{i} \) and \( m_{i} \) (\( i = \alpha ,\beta ,\gamma \)) are the intrinsic growth rates and the different growth parameters for the α transition, β transition, and γ transition, respectively. Further experimental work will have to be done on temperature–frequency-dependent storage and loss modulus in multi-transition region.

Conclusion

New models have been developed to calculate the temperature–frequency-dependent dynamic mechanical properties of glass/epoxy composites. The following conclusions can be obtained:

  1. (1)

    An improved temperature-dependent storage modulus model which could describe the properties in the full temperature region was established. The model parameters k and m have specific physical meaning.

  2. (2)

    A new temperature-dependent loss modulus model was also developed. The model prediction agreed well with the experimental data in glass transition region and rubber state. The values of \( T_{\text{g}} (E^{\prime\prime}_{\hbox{max} } ) \) were also predicted very well.

  3. (3)

    The temperature–frequency-dependent storage and loss modulus models were established by combining the relationship between T g and loading frequency. Model predictions and experimental data agreed very well.