First-principles calculation of grain boundary energy and grain boundary excess free volume in aluminum: role of grain boundary elastic energy

Abstract

We examined the grain boundary energy (GBE) and grain boundary excess free volume (BFV) by applying the first-principles calculation for six [110] symmetric tilt grain boundaries in aluminum to clarify the origin of GBE. The GBE increased linearly as BFV increased. The elastic energy associated with BFV, namely the grain boundary elastic energy, was estimated as a function of BFV and the shear modulus. The grain boundary elastic energies were close in value to the GBEs. The charge density distributions indicated that the bonding in the grain boundary region is significantly different from the bonding in the bulk. The grain boundary elastic energies were 15–32% higher than the GBEs. This overestimation of the grain boundary elastic energy is caused by the characteristics of the electronic bonding at the grain boundary, which is different from bonding in the bulk. We have concluded that GBE results mainly from the grain boundary elastic energy.

Introduction

A grain boundary is the interface between two differently oriented crystallites of the same phase in a crystalline solid. In order to accommodate the lattice mismatch, both crystallites must expand locally at the grain boundary. This expansion of the local region where two grains meet is referred to as the grain boundary excess free volume (BFV). Several authors have considered the BFV concept previously. Merkle et al. [1] measured BFV by high-resolution transmission electron microscopy (HRTEM), observing changes of the lattice parameter in the vicinity of the grain boundary in gold. Shvindlerman et al. [2] obtained the BFV from the experimental pressure dependence of grain boundary surface tension in aluminum. Shem et al. [3] derived BFVs from linear fits of the relationship between the change in lattice volume and the reciprocal of grain size for nanocrystalline semiconductors, metals, alloys, and oxides.

Wolf [4, 5] demonstrated using molecular dynamics calculation by the embedded atom model (EAM) and Lennard-Jones potentials to show that BFV is proportional to the grain boundary energy (GBE) in gold and copper. Wolf [4, 5] revealed that the proportionality coefficient of the relationship between GBE and BFV can be different depending on the specific variety of metals. However, the physical meaning of the proportionality coefficient of the relationship between GBE and BFV has been unclear. Similar EAM results of the proportionality relationship between GBE and BFV were obtained in silver [6] and copper [7]. The EAM calculations have been successful in reproducing and explaining the atomic structure and energy of grain boundary in various metals [4–10]. The EAM potentials do not, in principle, represent the self-consistent distribution of electron density; therefore, inaccurate estimations may be given with respect to interatomic interaction, especially for the irregular atomic structures observed around various defects such as grain boundaries. On the other hand, first-principles calculation yields self-consistent electron states and can, in principle, be applied to any material. So, recently the first-principles calculations have been preformed for studying various defects including grain boundaries [11–18].

Several authors have reported the first-principles results of GBE [13–18]. Wright and Atlas [13] studied the GBEs for $\Upsigma 11(1\bar{1}3)[110]$ and $\Upsigma 3(1\bar{1}2)[110]$ tilt grain boundaries in aluminum using the first-principles calculation, basing their calculations on the local density approximation (LDA). Lu and Kioussis [14] reported LDA results of the GBE and BFV for $\Upsigma 5(210)[001]$ tilt grain boundary in aluminum. Usually, generalized gradient approximation (GGA) calculations improve LDA results such as the lattice constants and elastic constants [19]. Wang et al. [15] also reported GGA results of the GBE and BFV for tilt $\Upsigma 9(2\bar{2}1)[110]$ and twist $\Upsigma 5(001)$ grain boundaries in aluminum and copper [15]. However, to the best of our knowledge, no study has used the first-principles calculation to verify the proportional relationship between GBE and BFV.

In this article, six [110] symmetric tilt grain boundaries in aluminum are investigated using the first-principles calculation. The relationship between GBE and BFV is examined to understand the role of elastic energy associated with BFV.

Calculation procedure

The first-principles calculations in this study were performed using the Cambridge Serial Total-Energy Package (CASTEP) [20]. The CASTEP is an ab initio pseudopotential method code for solving the electronic ground state of periodic systems with the wave functions expanded in a plane-wave basis set using a technique based on the density functional theory (DFT) [21, 22]. The electronic exchange–correlation energy was given by the GGA proposed by Perdew et al. [23] (PW91) in the DFT. The LDA was also used in the calculations of the $\Upsigma 11(1\bar{1}3)[110]$ and $\Upsigma 3(1\bar{1}2)[110]$ grain boundaries for comparison with previous results reported by Wright and Atlas [13]. The ultra-soft pseudopotential [24] implemented in the CASTEP was used for aluminum. A cut-off energy of 280 eV for the plane-wave basis was used in all calculations, which gave a good converged value of the GBE within 3 mJ/m².

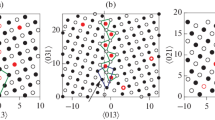
The calculated tilt grain boundaries were constructed using the coincidence site lattice (CSL) model. In CSL construction, one imagines that the two crystals on either side of the grain boundary interpenetrate. In this situation, there will be lattice sites that are common to both crystals, and this lattice of the common sites forms the CSL. The CSL is usually characterized by the Σ value, which is defined as the reciprocal of the density of the coincident sites. In this study, six <110> tilt CSL boundaries: $\Upsigma 3(1\bar{1}1)[110]$, $\Upsigma 11(1\bar{1}3)[110]$, $\Upsigma 3(1\bar{1}2)[110]$, $\Upsigma 9(1\bar{1}4)[110]$, $\Upsigma 27(1\bar{1}5)[110]$, and $\Upsigma 19(1\bar{1}6)[110]$ were examined in aluminum. The structures of these CSL boundaries are modeled in orthorhombic supercells containing 24, 44, 46, 72, 104, and 152 for $\Upsigma 3(1\bar{1}1)$, $\Upsigma 11(1\bar{1}3)$, $\Upsigma 3(1\bar{1}2)$, $\Upsigma 9(1\bar{1}4)$, $\Upsigma 27(1\bar{1}5)$, and $\Upsigma 19(1\bar{1}6)$, respectively, as shown in Fig. 1. The $\Upsigma 3(1\bar{1}1)$, $\Upsigma 11(1\bar{1}3)$, $\Upsigma 3(1\bar{1}2)$, $\Upsigma 9(1\bar{1}4)$, $\Upsigma 27(1\bar{1}5)$, and $\Upsigma 19(1\bar{1}6)$ tilt grain boundaries were formed by rotating the grain by 70.53°, 129.52°, 109.47°, 141.06°, 148.41°, and 153.47°, respectively, along the [110] axis. The initial atomic configurations in these supercells before the atomic relaxation were referenced by EAM results reported by Rittner and Seidman [8]. The $\Upsigma 3(1\bar{1}1)$, $\Upsigma 11(1\bar{1}3)$, $\Upsigma 9(1\bar{1}4)$, $\Upsigma 27(1\bar{1}5)$, and $\Upsigma 19(1\bar{1}6)$ structures have a simple mirror symmetry while the $\Upsigma 3(1\bar{1}2)$ structure has mirror/glide-plane symmetry. In these supercells, two symmetric grain boundaries are introduced in the y direction to create the three dimensional periodicity.

Fig. 1

Schematics of supercells modeling the [110] tilt grain boundaries of a $\Upsigma 3(1\bar{1}1)$, b $\Upsigma 11(1\bar{1}3)$, c $\Upsigma 3(1\bar{1}2)$, d $\Upsigma 9(1\bar{1}4)[110]$, f $\Upsigma 27(1\bar{1}5)$, and e $\Upsigma 19(1\bar{1}6)$. The white and black circles represent aluminum atoms in (110) and (220) atomic layers, which have been projected in a plane normal to the [110] direction. The solid lines indicate the boundaries of the supercells

The GBE is determined from the difference in energy between the supercell containing the grain boundary and another supercell of a single crystal, divided by the area of the grain boundary. The area of the grain boundary per supercell is equal to the cross-section area on the zx plane in the supercell. Therefore, the GBE, γ, is given by

$$ \gamma = {\frac{{E_{\text{g}} - E_{\text{s}} }}{2S}}, $$

(1)

where E _g is the total energy of the supercell containing the grain boundary, E _s is the total energy of the single crystal supercell containing an equal number of atoms, and S is the cross-section area on the zx plane in the supercell. In Eq. 1, we introduced a factor of 1/2 since the supercell contains two grain boundary planes. Similar to the GBE, the BFV, Ω, is given by

$$ \Omega = {\frac{{V_{\text{g}} - V_{\text{s}} }}{2S}} , $$

(2)

where V _g is the total volume of the supercell containing the grain boundary, and V _s is the total volume of the single crystal supercell containing an equal number of atoms.

The formation of a grain boundary leads to an increase of lattice strain and supercell volume. Hence, after optimization of both atomic configurations (atomic relaxation) and lattice constants (volume relaxation), E _g and V _g are obtained. The stable atomic configurations are obtained through relaxation according to the Hellmann–Feynman forces calculated from first principles. The lattice constants at zero pressure are also optimized using a Broyden–Fletcher–Goldfarb–Shanno (BFGS) [25] minimization algorithm with the stress calculated from first principles.

It is noted that E _s and V _s are calculated using an orthorhombic supercell that is of similar size and geometry to the supercell containing the grain boundary to cancel out any finite sampling error in the eigenvalue sum. The finite sampling error remains because of few k-points. The energy integration over the Brillouin zone is carried out using the Monkhorst and Pack [26] k-point grids. It is well known that many k-points sampled in the Brillouin zone are required to obtain converged values of the formation energy of various defects such as a vacancy, stacking fault, and twin boundary in a metallic system, especially in aluminum [27–29]. The numbers of k-points required are dependent on the cell size, and a trade-off exists between the cell size and the number of k-points. The effective total number of atoms in the crystal N _tot is useful, and is defined by

$$ N_{\text{tot}} = N_{\text{a}} N_{k} $$

(3)

where N _a is the number of atoms per supercell and N _k is the number of k-points sampled in the whole Brillouin zone [27]. For example, at least N _tot = ~16000 is necessary to obtain well converged values for the vacancy formation energy [27]. The convergence tests were performed preliminarily. Figure 2 shows the convergence tests for the k-points sampling, showing the GBEs of $\Upsigma 11(1\bar{1}3)$ and $\Upsigma 3(1\bar{1}2)$ boundaries with respect to N _tot. At least N _tot = 9504 and N _tot = 11040 are necessary to obtain good converged values of GBEs within 5 mJ/m² for $\Upsigma 11(1\bar{1}3)$ and $\Upsigma 3(1\bar{1}2)$ boundaries, respectively. Convergence tests were performed for the other grain boundaries as well as $\Upsigma 11(1\bar{1}3)$ and $\Upsigma 3(1\bar{1}2)$ grain boundaries. Finally, the k-point meshes of the Brillouin zone sampling were 12 × 2 × 16 (N _tot = 9216), 6 × 2 × 18 (N _tot = 9504), 8 × 2 × 18 (N _tot = 13248), 4 × 2 × 18 (N _tot = 10368), 3 × 2 × 16 (N _tot = 9984), and 3 × 2 × 16 (N _tot = 14592), for $\Upsigma 3(1\bar{1}1)$, $\Upsigma 11(1\bar{1}3)$, $\Upsigma 3(1\bar{1}2)$, $\Upsigma 9(1\bar{1}4)$, $\Upsigma 27(1\bar{1}5)$, and $\Upsigma 19(1\bar{1}6)$, respectively.

Fig. 2

Convergence tests for k-points sampling; GBEs of $\Upsigma 11(1\bar{1}3)$ and $\Upsigma 3(1\bar{1}2)$ grain boundaries with respect to the effective total number of atoms

Results and discussion

The values of GBEs examined in this study using the first-principles calculation were 44, 179, 379, 402, 448, and 471 mJ/m² for $\Upsigma 3(1\bar{1}1)$, $\Upsigma 11(1\bar{1}3)$, $\Upsigma 3(1\bar{1}2)$, $\Upsigma 9(1\bar{1}4)$, $\Upsigma 27(1\bar{1}5)$, and $\Upsigma 19(1\bar{1}6)$ grain boundaries, respectively. Figure 3 shows the GBEs of the <110> tilt grain boundaries as a function of the misorientation angle together with the experimental values [30] and calculated values using an EAM potential [9]. Two large cusps of GBEs are found at $\Upsigma 3(1\bar{1}1)$ (70.53°) and $\Upsigma 11(1\bar{1}3)$ (129.52°) grain boundaries. The $\Upsigma 3(1\bar{1}1)$ grain boundary is identical to the twin boundary. The same two deep cusps of grain boundary energies were found in <110> symmetric tilt boundaries for several fcc metals [5, 8].

Fig. 3

GBEs of the <110> tilt grain boundaries as a function of the misorientation angle together with the experimental values [30] and calculated values using an EAM potential [9]

Wright and Atlas [13] have already studied the GBEs for $\Upsigma 11(1\bar{1}3)$ and $\Upsigma 3(1\bar{1}2)$ grain boundaries in aluminum using the first-principles calculation, basing their calculations on the LDA. In this study, the GBEs for $\Upsigma 11(1\bar{1}3)$ and $\Upsigma 3(1\bar{1}2)$ grain boundaries were calculated not only within the GGA, but also the LDA. Table 1 presents the GGA and LDA values along with the previous LDA values by Wright and Atlas [13]. Our LDA results are in good agreement with previous LDA results by Wright and Atlas. The GGA values of GBE are ~8% lower than the LDA values. This is consistent with a tendency of the LDA; LDA values tend to overestimate the defect formation energies such as a vacancy formation energy and surface energy compared to GGA [23, 31, 32].

Table 1 Comparisons between GGA and LDA values of the GBE for $\Upsigma 11(1\bar{1}3)[110]$ and $\Upsigma 3(1\bar{1}2)[110]$ grain boundaries

After the optimization of both atomic configurations and lattice constants, the supercells were expanded normal to the grain boundary plane (y direction in Fig. 1). The changes of the lattice constants normal to the grain boundary plane from the single crystal supercell to the supercell containing grain boundary were 0.006, 0.051, 0.077, 0.075, 0.094, and 0.083 nm for $\Upsigma 3(1\bar{1}1)$, $\Upsigma 11(1\bar{1}3)$, $\Upsigma 3(1\bar{1}2)$, $\Upsigma 9(1\bar{1}4)$, $\Upsigma 27(1\bar{1}5)$, and $\Upsigma 19(1\bar{1}6)$ grain boundaries, respectively. The supercells shrunk in grain boundary plane (xz plane in Fig. 1) slightly. The changes of the lattice constants in x direction were −0.001, −0.008, −0.004, −0.009, −0.009, and −0.009 nm for $\Upsigma 3(1\bar{1}1)$, $\Upsigma 11(1\bar{1}3)$, $\Upsigma 3(1\bar{1}2)$, $\Upsigma 9(1\bar{1}4)$, $\Upsigma 27(1\bar{1}5)$, and $\Upsigma 19(1\bar{1}6)$ grain boundaries, respectively. The changes of the lattice constants in z direction were negligibly small (<0.001 nm) for all grain boundaries. The values of BFVs examined in this study using the first-principles calculation were 0.0033, 0.0133, 0.0266, 0.0262, 0.0323, and 0.0323 nm for $\Upsigma 3(1\bar{1}1)$, $\Upsigma 11(1\bar{1}3)$, $\Upsigma 3(1\bar{1}2)$, $\Upsigma 9(1\bar{1}4)$, $\Upsigma 27(1\bar{1}5)$, and $\Upsigma 19(1\bar{1}6)$ grain boundaries, respectively. Figure 4 shows the relationship between the GBE and BFV calculated from the first principles. GBE increases linearly as BFV increases. Wolf has already demonstrated that BFV is proportional to GBE by using molecular dynamics calculation by EAM and Lennard-Jones potentials [4, 5]. However, to the best of our knowledge, this is the first study using the first-principles calculation to verify the proportional relationship between GBE and BFV.

Fig. 4

GBEs as a function of BFV calculated from the first principles in aluminum. The dotted line indicates the grain boundary elastic energy, (2/3)G _m Ω

Figure 5 shows the interlayer strain (percentage) normal to the grain boundary plane as a function of the distance from the grain boundary plane for the six tilt grain boundaries. The interlayer strain is the relative strain of the interlayer spacing. The interlayer spacing of the nth atomic layer normal to the grain boundary plane, d _n , is determined by d _n  = (l _n+1 − l _n−1)/2, where l _n+1 is the length between the (n + 1)th and nth atomic layers and l _n−1 is the length between the (n − 1)th and nth atomic layers. The interlayer strain, ε, is given by

$$ \varepsilon = (d_{n} { - }d_{0} ) /d_{0} $$

(4)

where d ₀ is the interlayer spacing of a middle layer of the grain, which is sufficiently distant from the grain boundary. We can see an oscillatory strain profile that has a maximum positive value at the grain boundary plane and decays into the bulk. The interlayer strain is localized in a narrow region at the grain boundary, which is less than ~0.5 nm wide. The positive value of the interlayer strain indicates local volume expansion, which corresponds to the BFV. And the GBE increases linearly as BFV increases, as described above. So, the grain boundary with a higher GBE exhibits a higher value of the interlayer strain. This higher interlayer strain causes higher elastic energy, which appears to be one of the origins of the GBE.

Fig. 5

The interlayer strain (percentage) normal to the grain boundary planes as a function of the distance from the grain boundary plane for the six tilt grain boundaries in aluminum

The elastic energy associated with the BFV can be estimated in the framework of a classical elasticity theory. The simplest model of all the approaches to the lattice distortion around a defect is a sphere-in-hole model, which is based on the isotropic elasticity theory developed by Eshelby and Friedel [33, 34]. In this model, a hole with volume V _m in the matrix of a metal is partly filled by a sphere of another metal inclusion with volume V _i. The crystal lattice is distorted by the difference in size of the two constituent metals. The remaining volume, V _m − V _i, will disappear by an elastic deformation of the matrix and inclusion. The elastic energy is given by

$$ \Updelta E_{\text{s}} = {\frac{{B_{\text{i}} (\Updelta V_{\text{i}} )^{2} }}{{2V_{\text{i}} }}} + {\frac{{2G_{\text{m}} (\Updelta V_{\text{m}} )^{2} }}{{3V_{\text{m}} }}} $$

(5)

where ΔV _i and ΔV _m are the volume changes of sphere and hole due to the internal stress. B _i is the bulk modulus of the inclusion, and G _m is the shear modulus of the matrix. The pressures are adjusted such that they continue across the interface between matrix and inclusion; which leads to a rewritten expression for the elastic energy:

$$ \Updelta E_{\text{s}} = {\frac{{2B_{\text{i}} G_{\text{m}} (V_{\text{m}} - V_{\text{i}} )^{2} }}{{3B_{\text{i}} V_{\text{m}} + 4G_{\text{m}} V_{\text{i}} }}}. $$

(6)

In the case of vacancy, the deformation of inclusion contributes not at all to elastic energy. The volume of hole for vacancy is equal to the atomic volume of one atom, V ₀. So, the elastic energy for vacancy, ΔE _vac, can be rewritten from Eq. 5 by

$$ \Updelta E_{\text{vac}} = {\frac{{2G_{\text{m}} V_{0} }}{3}}\left( {{\frac{{\Updelta V_{0} }}{{V_{0} }}}} \right)^{2} . $$

(7)

This expression is exactly the same as the elastic energy for solute atom [35]. The atomic volume of aluminum is 0.0166 nm³ [36], and the shear modulus of aluminum is 26.5 GPa [37]. ΔV ₀/V ₀ of vacancy in aluminum is −0.31, which has been investigated from the first-principles calculation [28]. So, the elastic energy for vacancy in aluminum was 0.18 eV derived by Eq. 7. This value is smaller than the vacancy formation energy of 0.67 eV in aluminum [38].

In the case of the grain boundaries, there is no inclusion. Hence, the volume of the inclusion, V _i, is equal to zero. The volume of the hole disappears by the elastic deformation of the only matrix. This elastic deformation of the matrix is observed as the expanding volume of the matrix. Hence, we can obtain the relationship $V_{\text{m}} /S = \Omega$, where Ω is the BFV and S is an area of the grain boundary. The elastic deformation of the matrix associated with BFV causes the elastic energy per an area of the grain boundary, which is defined as a grain boundary elastic energy in this study. This grain boundary elastic energy, γ _s, is given by $\gamma_{\text{s}} = \Updelta E_{\text{s}} /S$. From the relationships, $V_{\text{i}} = 0$ and $V_{\text{m}} /S = \Omega$, the grain boundary elastic energy can be given by

$$ \gamma_{\text{s}} = \frac{2}{3}G_{\text{m}} \Omega . $$

(8)

This equation indicates that the grain boundary elastic energy increases linearly as the BFV increases, similar to the relationship between the GBE and BFV. Figure 4 also shows the relationship between the grain boundary elastic energy and BFV as a dotted line. The grain boundary elastic energy is calculated by using G _m = 26.5 GPa, which is the experimental value of the shear modulus of aluminum [37] and close to the first-principles value. The grain boundary elastic energy is close in value to the GBE. This agreement between the grain boundary elastic energy and GBE indicates that the GBE results mainly from the elastic energy. The grain boundary elastic energies are 15–32% higher than the GBEs. This overestimation of the grain boundary elastic energy would be caused by the characteristics of the electronic bonding at the grain boundary, which is different from the bonding in the bulk as described below.

Figure 6 shows the charge density distributions. These charge density distributions indicate that the bonding in the boundary region is significantly different from bonding in the bulk. The charge density is decreased significantly at the grain boundary as shown in the green area of Fig. 6, which indicates a relatively low charge density. This is consistent with the intuitive notion that the strength in the grain boundary region is weaker than that in the bulk region. This would mean that the shear modulus locally would be decreased in the grain boundary region. This, in turn, causes decreases in the grain boundary elastic energy derived from Eq. 8. We also can see charge accumulations at the local open regions formed by less coordinated atoms. This feature is remarkable in $\Upsigma 27(1\bar{1}5)$ and $\Upsigma 19(1\bar{1}6)$ grain boundaries. Wang et al. [15] previously reported the feature of charge accumulations for local regions formed by less coordinated atoms at tilt $\Upsigma 9(2\bar{2}1)[110]$ and twist $\Upsigma 5(001)$grain boundaries in aluminum. In general, in defective or distorted configurations of aluminum atoms such as grain boundaries, surfaces, and vacancies, the covalent behavior of valence electrons of aluminum has been observed, including charge accumulations or directional-bond formation at less coordinated atoms [15, 28, 31, 39]. Wang et al. [15] explained that the covalent nature of aluminum causes a smaller GBE than that of copper, which exhibits simple metallic bonding at the grain boundaries. There is no doubt that the electronic bonding at the grain boundary affects supplementary GBE and that GBE results mainly from the elastic energy.

Fig. 6

Charge density distributions in (110) plane for the [110] tilt grain boundaries of a $\Upsigma 3(1\bar{1}1)$, b $\Upsigma 11(1\bar{1}3)$, c $\Upsigma 3(1\bar{1}2)$, d $\Upsigma 9(1\bar{1}4)[110]$, f $\Upsigma 27(1\bar{1}5)$, and e $\Upsigma 19(1\bar{1}6)$. The white and pink balls represent aluminum atoms in (110) and (220) atomic layers, respectively. The solid lines indicate the boundaries of the supercells (Color figure online)

Summary

GBEs and BFVs were examined from the first-principles calculation for six [110] symmetric tilt grain boundaries in aluminum. The GGA values of GBE were ~8% lower than the LDA values for $\Upsigma 11(1\bar{1}3)$ and $\Upsigma 3(1\bar{1}2)$ grain boundaries. This is consistent with a tendency of LDA; LDA values tend to overestimate the defect formation energies such as vacancy formation energy and surface energy compared to GGA. GBE increased linearly as BFV increased. The elastic energy associated with BFV, namely the grain boundary elastic energy, was estimated in the framework of a classical elasticity theory. The grain boundary elastic energy was expressed as a function of BFV and the shear modulus. It was found that the grain boundary elastic energies were close in value to the GBEs. The charge density distributions indicated that the bonding in the grain boundary region is significantly different from the bonding in the bulk. We conclude that GBE results mainly from the elastic energy. The characteristic of the electronic bonding at the grain boundary, which is different from bonding in the bulk, affects supplementary GBE.