Introduction

The life assessment and potential for failure of “in-service” components is a critical issue in the safety and reliability of operating power stations which are approaching the end of their design lives. New policies relating to environmental protection and safety at work, together with major advances in analytical techniques for life assessment—which suggest the initial safety factors of these plants were unduly high—have made it more profitable to invest in the modernisation of existing plants rather than in building new ones. However, such modernisation only makes economic sense if existing plants have sufficient residual life and so reducing the uncertainty in evaluating remaining plant life is of primary importance to the power generating industry.

However, traditional tests, such as the uniaxial creep test, are not well suited to this problem. This is because of insufficient material to sample and because the size of the required sample could undermine the structural integrity of the in-service component. The small punch test is an innovative technique based on miniaturised specimens and is a promising solution to this problem. The small punch test was developed at MIT for radiation embrittlement and first reported in 1981 [1]. It was then extensively developed in Japan, particularly at Tohoku University [2]. The first collaborative efforts in small punch test standardisation were reported by the Japanese Atomic Energy Research Institute (JAERI) in 1988 [3]. In the United States, further work by Electric Power Research Institute (EPRI) and Failure Analysis Associates (now Exponent) since the late 1980s [4] led to the introduction of the technique into Europe from 1992 by Swansea University [5] and Electric Research Association (ERA) in the UK and Centro Elettroecnico Sperimentale Italiano (CISE) in Italy (now CESI) [6, 7].

The small punch test (SP) is a semi-destructive technique because it uses a very limited amount of material, with the specimens being discs of around 0.5 mm thick and around 8–10 mm in diameter. Such small samples taken from components in service not only leave the structural integrity of thick components intact or at least repairable, but allow also for the possibility of focusing on the critical locations of the component (those areas that are more highly stressed and damaged).

Despite these advantages, the power generating industry has been slow to accept the use of this technique. This in part reflects concerns that the reproducibility of the results from such a test is highly dependent upon the geometry of the specimen and the test apparatus. This concern can only be overcome through the development and imposition of a strong code of practice covering both testing and analysis. The other major concern with the technique is that associated with converting the small punch test data into the required uniaxial equivalents. Solutions to these two problems can be sought either through detailed experimentation or through the computer modelling of the small punch creep test.

On the experimental front and in Europe an important push towards such standardisation has come from two main sources. First, between 1994 and 1997 the Copernicus SP project [8] developed a creep small punch test configuration but no code of practice was agreed. Second, between 2000 and 2003, and inside the European Pressure Equipment Research Council (EPERC]), a collaborative project was set up among a few interested parties (CESI in Italy, Joint Research Centre Institute for Energy of the European Community (JRC) in the Netherlands and the University of Swansea in the UK) that consisted of a creep round robin exercise [9]. As a result of that exercise a step towards a real code of practice was made. Over a more recent time span the CEN (one of three European Standardisation organisations recognised by the EC) has been working to produce a code of practice for the small punch creep test. In 2006 they published, as a Workshop Agreement, a CEN code of practice [10]. With regard to test specimen geometry they concluded that test specimens should measure 8 mm in diameter with a thickness of 0.5 mm and these should be tested in an inert argon environment.

A major concern with this experimental approach is that the large scatter known to be present in small punch creep test data would make the identification of a suitable code of practice problematic and inconclusive. To avoid this issue of experimental scatter and so compliment the experimental approach, Evans et al. [11, 12] developed an elastic–viscoplastic finite element model of the punch creep test, written in Salford Fortran, which produces as an output the displacement time curve up to the point of fracture. The model uses the realistic creep deformation law of Evans [13], which includes strain hardening, thermal softening and damage accumulation. Unlike other finite element models of the small punch creep test (e.g. Hankin et al. [14]), these laws enable the model to be run for any amount of preexisting continuum damage. In the model, the displacement time curve is made a function of the following variables which form the inputs into the model: The hole diameter (x 1), the disc diameter (x 2), the disc thickness (x 3), the punch head radius (x 4), the coefficient of friction (x 5), the preexisting damage present in the disc (x 6) and the punch load (x 7). The model is stochastic in nature in that it has built into it experimentally measured creep variability, so that confidence intervals for the models predictions are also obtainable.

Evans and Wang [15] have made use of the finite element model of the small punch test, together with a response surface methodology, to determine whether there is indeed a specific geometry (and hence a code of practice for testing) that makes the test most useful. That is, maximises the sensitivity of the test to preexisting damage and minimises the sensitivity of the test to the geometry of the specimen and test apparatus. They found that the failure time was most sensitive to disc thickness, hole diameter, initial damage and the punch head radius but least sensitive to disc diameter and load (see Fig. 1 for explanation of the above variables). Under clamping, the optimum specimen geometry was found to be one with a disc diameter of 9.2 mm and a disc thickness of 0.65 mm—both slightly higher than that recommended by CEN. To be acceptable as recommendations, the numerical model used above requires detailed verification.

Fig. 1
figure 1

Schematic of axi-symmetric small punch test (punch hole diameter = x 1, disc diameter = x 2, disc thickness = x 3, punch head radius = x 4, axial load (F) = x 7. ABCDEFG are points on the discs surface. z and r are disc point coordinates

Full size image

This article addresses this verification issue and also the second issues raised above concerning the conversion of small punch test data into the required uniaxial equivalents. Measurements of minimum displacement rates from the small punch creep test when plotted against time to failure (t f) frequently show the same type of dependency of t f on applied stress as observed in uniaxial creep tests, but with a shift along the t f axis. This shift is different for different materials and different test geometries. The main objective of this article is to develop a better understanding of this shift, its dependence on test parameters and whether it is always parallel in nature. The experimental approach to this problem has proved to be rather inconclusive with some studies (e.g. Stratford et. al. [16]) showing minimum displacement rates (from the punch test) and minimum creep rates (from uniaxial tests) sitting on parallel lines when plotted against t f on a log–log scale, while other studies have shown them to sit on nonparallel lines (e.g. National Physical Laboratory [17]). This article therefore takes the alternative approach of using the results from a finite element model of the small punch creep test to help resolve this issue.

To meet this objective the article is structured as follows. The next section briefly discusses the materials tested for this article. The following section provides a quick overview of the small punch creep test model. This is followed by a results section that is split into two parts. The first part verifies the punch test model using both virgin 0.5Cr–0.5Mo–0.25V steel and pre-damaged 1.25Cr–0.5Mo steel. The second part shows the Monkman–Grant type results obtained from the model for 0.5Cr–0.5Mo–0.25V steel and compares these to some uniaxial experimental data. The final section concludes with recommendations for future work.

The materials

The uniaxial creep testing on 0.5Cr–0.5Mo–0.25V was carried out in the creep laboratories at the Interdisciplinary Research Centre (Swansea) as part of a research programme financed by the Engineering & Physical Science Research Council and the Central Electricity Generating Board in 1983. This was short-term accelerated constant stress creep testing. All the tests were carried out in an air atmosphere. The 0.5Cr–0.5Mo–0.25V material, supplied by CEGB, consisted of fabricated header pipe and its chemical composition (in wt.%) is shown in Table 1. Following the standard heat treatment (10 h at 1,238 K, 15 h 973 K and 15 h at 933 K) for this material, it had a yield stress of 263 MPa at 808 K and a yield stress of 191 MPa at 868 K. This data has appeared extensively in the literature since it was first published by Evans et al. [18].

Table 1 Chemical analysis of test material in wt.%
Full size table

Twenty-two test pieces, with gauge lengths of 28 mm and diameters of 5 mm, were tested in tension over a range of stresses at 808, 838, 868 and 913 K using high-precision constant-stress machines. At 808 K, five specimens were placed on test over the stress range 250–350 MPa, at 838 K eight specimens were placed on test over the stress range 175–310 MPa, at 868 K six specimens were tested over the stress range 160–250 MPa and at 913 K three specimens were tested over the stress range 128–200 MPa. The longest recorded failure time was 1,471 h. Up to 400 creep strain/time readings were taken during each of these tests and normal creep curves were observed under all these test conditions.

The 1.25Cr–0.5Mo material was supplied by Ontario Hydro, Canada, and was taken from new thick wall seamless pipe and its chemical composition (in wt.%) is shown in Table 1. This data was first published by Stratford [16].

Experimental creep punch tests were conducted on both 0.5Cr–0.5Mo–0.25V and 1.25Cr–0.5Mo steel in a argon environment. The 0.5Cr–0.5Mo–0.25V discs were cut from the same virgin material described above. In total, 15 discs with 9.0 mm diameter and a thickness of 0.5 mm were then cut from the virgin material. (Note this disc thickness is as recommended by CEN, but the diameter is closer to that recommended by the analysis of the numerical modelling results.) These discs were then tested at a single temperature of 848 K but over a load range of 170–420 N. The 1.25Cr–0.5Mo steel material described above was first uniaxially tested at 848 K and at a constant load of 135 MPa. Under these conditions the material has a life of around 536 h, but the specimen was removed from test after 300 h (approximately three times the minimum creep rate). Ten discs with 9.0 mm diameter and a thickness of 0.5 mm were then cut from the tested specimen. This pre-damaged steel was then punch tested at temperatures of 848 and 903 K and over a load range of 170–300 N. The experimental rig (see Fig. 1 for details) used a disc diameter of 9.0 mm and a disc thickness of 0.5 mm. It had a punch radius of 1.0 mm and a punch hole radius of 4.0 mm. No attempt was made to lubricate specimens and the disc edges were rigidly clamped.

During all small punch creep tests described above, measurements were made of punch displacement (in millimetre) through time (in seconds) so that complete displacement–time curves were derived. Displacement rates (in millimetre/second) were then found by numerically differentiating this displacement–time data and minimum displacement rates found by smoothing through these displacement rates.

Finite element modelling of the small punch test

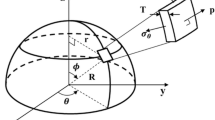
Figure 1 shows the punch test at some point where the punch has been displaced a distance d. The initial disc had a diameter x 2 and thickness x 3, the hemispherical punch has a radius x 4 and the punch hole a diameter x 1. An axial load F(= x 7) is applied to the rear of the punch and this results in deformation of the specimen disc (ABCDEFG are points on the disc surface). Deformation is assumed to be visco-plastic and at constant volume with deformation rates being governed by the creep properties of the material. The driving force for deformation is F but the disc sees this through the interface AB(area = ΩAB). There are frictional forces along ΩAB and therefore the distribution of normal and shear tractions are not known a priori. Frictional forces will be described by the constant shear rule,

$$ k=x_5 \frac{\bar{\tau}}{\sqrt{3}} $$
(1)

where 0 ≤ x 5 ≤ 1 and \(\bar{\tau} \) is the local Von Mises flow stress. The disc surface area CDEF is either clamped to prevent any relative movement or unclamped. Clamped is taken to mean that points on the disc surface adjacent to CD and FE are restrained from movement in both the r and z direction. Unclamped means that the same surface points are restrained only in the direction of z. Figure 1 represents the test at one instant and changes in the geometry occur with time as punch penetration proceeds. Measured outputs from the test are the displacement of the punch, d, as a function of time, the time to rupture and the displacement to rupture. From this minimum displacement rates are easily calculated.

At any disc configuration and neglecting body forces the equilibrium equations are

$$ \tau_{ij,j} =0 $$
(2)

where τij is the Cauchy stress tensor. For any arbitrary perturbation of the velocity field u i

$$ \int_V {\tau_{ij,j} \delta u_i\, \hbox{d}V=0} $$
(3)

and from the divergence theorem, the symmetry of the stress tensor and imposing δu i = 0 on essential boundary conditions,

$$ \int_V {\tau_{ij} \delta \dot {\xi}_{ij}\, \hbox{d} V-\int_{\Upomega^{\rm AB}} {F_i \delta u_i\, \hbox{d}\Upomega^{\rm AB}-\int_{\Upomega^{\rm CF}} {F_i \delta u_i\, \hbox{d}\Upomega^{\rm CF}=0}}} $$
(4)

F i are the local surface tractions at u i and \(\dot{\xi}_{ij}\) is the strain rate tensor. For incompressible deformation

$$ \int_V{{\tau}_{ij}^{\prime} \delta \dot {\xi}_{ij}\, \hbox{d}V+\int_V {\tau_m \delta \dot {\xi}_{ii}\, \hbox{d}V}} -\int_{\Upomega^{\rm AB}} {F_i \delta u_i\, \hbox{d}\Upomega^{\rm AB}-\int_{\Upomega^{\rm CF}} {F_i \delta u_i\, d\Upomega^{\rm CF}=0} } $$
(5)

where \({\tau}_{ij}^{\prime} \) is the deviatoric stress and τm the mean stress, subject to the constraint

$$ \int_V {\dot {\varepsilon}_{ii}\, \hbox{d}V=0} $$
(6)

For the quasi-static situation of Fig. 1, Eq. 5 has been solved by finite element methods and full details have been given elsewhere [11] together with examples of the meshes used and typical graphical outputs from the programme. The equation has been discretised with eight nodded iso-parametric quadrilateral elements with the constraint of Eq. 6 applied by a penalty function procedure. Equation 5 and its discretised form are non-linear so that the solution for the admissible velocity field must be approached iteratively. Furthermore, the values of F i are not known so that further iteration is required to ensure that the total punch load is equal to F. The iterative algorithm is given in [11]. The whole problem is also geometrically non-linear and after each stable iteration nodal coordinates are updated by a one-step Euler algorithm. The updating also keeps account of punch displacement as a function of time and of the current values of the internal variables in the constitutive equation including the accumulation of creep damage.

The high temperature creep properties used in the model have been derived from extensive uniaxial and biaxial creep testing of 0.5Cr–0.5Mo–0.25V and 1.25Cr–0.5Mo steels at 565 °C [19, 20]. These multi-axial stress tests have confirmed that the material behaves as a Von–Mises solid (i.e. the Levy–Mises flow rule is obeyed). The general constitutive relationship relating strain rate to current material conditions has been derived as a phenomenological internal variable model [13]. The basic rate equation includes work hardening, thermal softening and creep damage as internal variables and includes subsidiary equations which govern the growth of these variables in the creep situation [11]. In particular, the growth of creep damage during the punch test can be followed.

While, for virgin material, the internal variables are initially set to zero, this is not a necessary condition so that the model can be run with any preexisting continuum damage. Thus damage can be regarded as an independent variable when running the model and simulations for materials with preexisting damage are possible. Damage has been assigned the variable x 6. The creep experiments have shown that fracture occurs when the accumulated damage reaches a critical value [13, 20]. This value has been shown to be a function of the current stress tensor and this forms the basis of a fracture criterion which has been incorporated in the punch test model. More specifically, at a given load and temperature, the accumulated damage at failure is given by

$$ W_{\rm crit} =\frac{1}{\theta_3} \left[ {\varepsilon_{\rm f} -\theta_1 \left({1-\hbox{e}^{-\theta_2 t_{\rm f}}} \right)} \right] $$
(7a)

where t f is the time at failure, ɛf is elongation at failure and θ1 to θ3 are the theta values used to describe the creep curve for 0.5Cr–0.5Mo–0.25V and 1.25Cr–0.5Mo steels at such a given load and temperature

$$ \varepsilon_t =\theta_1 \left({1-\hbox{e}^{-\theta_2 t}} \right)+\theta_3 (\hbox{e}^{\theta_{4,} t}+1) $$
(7b)

where ɛt is the strain at time t. To calculate a value for Wcrit, the punch test model obtains θj (j = 1, 4) and ɛf values at any stress or temperature using the following empirical relations

$$ \hbox{ln}\, \theta_j =a_{j,0} +b_{j,0} \sigma +c_{j,0} T+d_{j,0} \sigma T\quad j = 1, 4 $$
(8a)
$$ \hbox{ln}\, \varepsilon_{\rm f} =a+b\sigma +cT +d\sigma T $$
(8b)

where T is temperature and σ is stress. The failure time t f (defined as the time to reach the failure strain) is obtained by numerically solving

$$ \varepsilon_{\rm f} =\theta_1 \left({1-\hbox{e}^{-\theta_2 t_{\rm f}}} \right)+\theta_3 \left({\hbox{e}^{\theta_i t_{\rm f}} +1} \right) $$
(8c)

These theta values, and the parameters in Eqs. 8, have been published extensively and can be found, for example, in Evans and Wilshire [21]. The value for x 6 in the punch test model can therefore be given a quantity between 0 (corresponding to no preexisting damage) and just below W crit (corresponding to preexisting damage that exists just before failure).

This punch test model can be made stochastic by taking into account the variability in the estimated θj values as measured by their variance, γj. Consequently, the parameters of Eq. 7b and W crit in Eq. 7a are also subject to uncertainty. The above deterministic model is made stochastic as follows:

  1. 1.

    From a series of multiaxial tests produce estimates of θj using the nonlinear optimisation procedure put forward by Evans [22]. Then using the estimated theta values produce estimates for the parameters a j,0, b j,0, c j,0, d j,0 of Eq. 8a, and a, b, c, and d of Eq. 8b using the weighted least squares procedure put forward by Evans [22]. This makes Eqs. 8a, b operational. This equation should be interpreted as determining the mean value for \(\Uptheta_{j,}\bar{\Uptheta}_j. \) That is,

    $$ \bar{\Uptheta}_j =a_{j,0} +b_{j,0} \sigma +c_{j,0} T+d_{j,0} \sigma_i T $$
    (9a)

    where ln(θj) = Θj.

    However, there is no reason to suppose that the variance of each Θj will also depend on the test conditions. The natural log of each θj is therefore assumed to have the same variance given by the average, over all test conditions, of the individually estimated variances. Call this ρj.

  2. 2.

    In the absence of any prior knowledge on theta distributions, each θj is assumed to follow a log normal distribution, implying that the ln(θj) = Θj, are normally distributed. Thus, ln(θj) is taken to be normally distributed with a mean and variance of

    $$ \hbox{ln} (\theta_j)\sim N(\bar{\Uptheta}_j,\rho_j) $$

    Values for Θj can be drawn from this distribution using

    $$ \hat{\Uptheta}_j =\bar{\Uptheta}_j +\sqrt{\rho_j }\left[ {\Upphi (U)^{-1}} \right] $$
    (9b)

    where U is a randomly drawn number between 0 and 1 and Φ(U) is the cumulative normal density function, i.e. Φ(U)−1 is a standard normal variate. By drawing random values between 0 and 1 for U (four at each of the test conditions), Eq. 9b can be used to obtain simulated values for each Θj at each test condition, and therefore \(\hat{\theta}_j = \hbox{exp}(\hat{\Uptheta}_j).\)

  3. 3.

    Using these simulated values for \(\hat{\theta}_j\) the following regressions can be carried out

    $$ \hat{\Uptheta}_{j,k} =a_{j,k} +b_{j,k} \sigma +c_{j,k} T+d_{j,k} \sigma_i T $$
    (9c)

    The parameters are again estimated using weighted least squares. k = 1 in Eq. 9c.

  4. 4.

    For each of the stresses and temperatures that make-up the test matrix of step 1, the punch test model obtains interpolated values for θj, and ɛf by using Eqs. 9c and 8b. t f is then obtained by solving Eq. 8c using these θj and ɛf values. All these are then substituted into Eq. 7a to obtain the simulated value of W crit at each test condition.

  5. 5.

    The empirical relationship between ln(W crit) and σ and T can then be established through use of a simple linear regression. Linear least squares is applied to

    $$ \hbox{ln}\, W_{{\rm crit},k} =m_k +f_k\, \hbox{ln}\, \sigma^\ast $$
    (9d)

    so as to obtain estimates for m k and f k, (k = 1) where

    $$ \sigma^\ast =\frac{\sigma} {163309+127.1T-0.1419T^{2}} $$
    (9e)
  6. 6.

    Select a variety of stress and temperature combinations within the range of conditions defined by the experimental test matrix in step 1. The punch test model is then run at each of these test conditions, using the W crit values obtained from Eqs. 9d and 9e until a failure time is observed (i.e. until W = W crit). This produced a complete time–displacement graph for each of the selected test conditions (including the eventual failure time of the disc). From these time–displacement curves minimum displacement rates can be easily calculated.

  7. 7.

    Repeated the above steps k = 1 to M times so that M failure time predictions and time–displacement curves are obtained at each of the test conditions selected in step 6. In this article M = 15.

Results

Estimated values for θj, a j,0, b j,0, c j,0, d j,0 a, b, c, d, m and f have been tabulated in a previous paper by Evans and Wang [23] and readers are referred to that paper for further details. All the predictions from the punch test model shown in this article are derived using a friction factor of 0.35 (x 5 = 0.35).

Verification results

0.5Cr–0.5M0–0.25V steel was selected for verifying the model under undamaged conditions. Corresponding to step 6 in the above section, Table 2 contains the stresses chosen to run the punch model. At all these stresses the temperature selected was 848 K. Substituting these test conditions into Eqs. 9e and 9d yields predictions for critical damage at these test conditions. The second column of Table 2 contains these predicted W crit. The punch test model was then run using the W crit values shown in Table 2 until failure times were observed (i.e. until W = W Crit,i). These predicted failure times are shown in the final column of Table 2.

Table 2 Disc modelled failure times as determined by the damage parameters given by Eq. 9d for a temperature of 848 K
Full size table

The above steps were repeated another 14 times to yield k = 15 failure time predictions at all the stresses shown in Table 2. All these predictions, in seconds, are shown in Table 3. At the bottom of Table 3 are the averages and standard deviations of the 15 predictions at each test condition. Figure 2 plots these 15 predictions at each stress together with the average predictions at each load. As can be seen, the scatter present in the 15 predictions also appears to increase with decreasing stress. Figure 3 plots the average predictions of Fig. 2 together with bars that depict the range given by these averages plus and minus three of their standard deviations. The experimental punch test results described in the section "The materials" are also superimposed on this graph. It appears that the punch test model is replicating the experimental data very well. All the data appears to be within these approximate 99% confidence intervals and the scatter present in the experimental data match the magnitude of these error bars.

Table 3 Disc modelled failure times associated with 15 runs of the stochastic model
Full size table
Fig. 2
figure 2

The k = 15 disc modelled failure times at 848 K using virgin 0.5Cr–0.5Mo–0.25V steel

Full size image
Fig. 3
figure 3

Failure times from experimental punch tests together with the modelled predictions at 848 K for virgin 0.5Cr–0.5Mo–0.25V steel

Full size image

1.25Cr–0.5Mo steel was selected for verification of the model under damaged conditions. Figure 4a plots the experimental punch test results described in the section "The materials". At each temperature the experimental results suggest that time to failure for these pre-damaged discs varies with stress in a power law fashion. Also superimposed onto the figure are a few punch test results done on undamaged 1.25Cr–0.5Mo steel and the effect of preexisting damage on failure time is easily observed. Figure 4b plots the average predictions made by the punch test model for the load conditions shown in Fig. 4a and at 848 K together with bars that depict the range given by these averages plus and minus three of their standard deviations. All the data appears to be within these approximate 99% confidence intervals.

Fig. 4
figure 4

(a) Failure times from experimental punch tests for damaged and virgin 1.25Cr–0.5Mo steel. (b) Failure times from experimental punch tests together with the modelled predictions at 848 K for damaged 1.25Cr–0.5Mo steel

Full size image

The predictions made for both damaged and undamaged materials appear to fully validate the finite element model of the punch test in that nearly all the experimental data falls within the 99% confidence intervals for the models predictions of the experimental data. The model is therefore a realistic description of the small punch creep test when using virgin and damaged material.

Minimum displacement and creep rates

Plots of minimum displacement rate against failure time for the small punch test frequently show the same type of dependency as observed in uniaxial creep tests, but with a shift along the time to failure axis. Figure 5a shows the experimental data obtained on minimum displacement rates (for the small punch test) and minimum creep rates (from preexisting uniaxial tests held at the IRC Swansea) for 0.5Cr–0.5Mo–0.25V steel. The minimum displacement rates are those associated with the experimental failure times in Fig. 3. The source reference for the uniaxial data is [11] and corresponds to the 0.5Cr–0.5Mo–0.25V data set described in the section "The materials". As can be seen, the results do not sit on parallel lines as some other studies have suggested [17]. It is debatable therefore as to whether this similarity or not of the Monkman–Grant type relation is an intrinsic property of the small punch test or is due to the expected scatter in both uniaxial and more especially small punch test results.

Fig. 5
figure 5

(a) Monkman–Grant type relations in uniaxial and small punch testing of 0.5Cr–0.5Mo–0.25V steel. (b) Slope parameter of the Monkman–Grant type relation from experimentation and computer modelling of virgin 0.5Cr–0.5Mo–0.25V steel

Full size image

An important objective of this article was to develop a better understanding of this shift, its dependence on test conditions and whether it is always parallel in nature. The punch test model was therefore run 15 times over a wide range of loads with a disc diameter of 9.0 mm, disc thickness of 0.5 mm, punch radius of 1.0 mm and a punch hole radius of 4.0 mm. The resulting 15 slope estimates of the Monkman–Grant type relation are shown in Fig. 5b, together with their average and the models prediction of the 95% confidence interval for this slope. Also shown is the slope estimated from the uniaxial experimental data in Fig. 5a together with its 95% interval.

Having taken into account creep variability, the results from the punch test model suggest that the slope of the Monkman–Grant type relation is the same in uniaxial as it is in small punch test data—as revealed by the overlapping intervals. The model therefore predicts identical slopes within the intrinsic variability, so that there is not a statistically significant difference between the two slopes at the 5% significance level. This parallel nature suggests that it will be possible, from the outcomes of future research, to convert small punch test data into uniaxial data using simple analytical expressions.

A number of possible avenues suggest themselves. By comparing the model’s failure time predictions for varies loads at the optimal test and specimen geometries identified by Evans and Wang [12] with the experimental uniaxial failure times at varies accelerated stresses (both at a given temperature), it should be possible to derive an equation giving the stress corresponding to a particular punch load—F = f(σ). (As a lot of short-term uniaxial data is already available, so this presents no additional experimentation). Using this relation the model can be run at the load corresponding to operating stresses and the time to failure recorded. Alternatively, a disc can be cut from an in-service component and put on test at a load corresponding to the operating stress until the minimum creep rate is observed (the test can then be discontinued). This rate can then be inserted into the Monkman–Grant relation implied by the small punch test model to predict when the disc will fail. This procedure will work because, as shown by Evans and Wang [23], the Monkman–Grant relation predicted by the model is the same at all levels of preexisting damage. Then a parallel adjustment to this failure time will give a prediction of the components remaining life.

Conclusions

The small punch test is an innovative technique based on miniaturised specimens and is a promising solution to the problem of undermining the structural integrity of operating components through the extraction of large test samples. It was found that this model was capable of producing accurate predictions of disc life for disc samples cut from virgin 0.5Cr–0.5Mo–0.25V and damaged 1.25Cr–0.5Mo steel. For both materials it was found that the average predictions from the model at each test condition were in broad agreement with the experimental data and that all the data appeared to be within the approximate 95% confidence intervals for these predictions. Having taken into account creep variability in this verified model, displacement rate results from the punch test model suggest that the slope of the Monkman–Grant type relation is the same in uniaxial as it is in small punch test data. The next step is to use the numerical model to identify precisely the nature of the small punch—uniaxial test correlation.