Introduction

Friction stir welding (FSW) has been widely applied in the modern industries such as aerospace, ship manufacture, and automobile industry since it was invented by the Welding Institute (TWI) in 1991. The basic concept of FSW is [1]: In FSW, a non-consumable tool with a designed pin and shoulder, which is rotated by a certain angular velocity, is inserted into the abutting edges of sheets or plates to be joined, and then traversed with a constant speed, which is called welding speed or translational velocity along the welding line. It is very important to learn the mechanism of FSW, and even to study the effect of the process parameters on the quality of the friction stir welds. Liu et al. [2] investigated the effect of zigzag line on the mechanical properties of the friction stir welds. The experiments performed by Sutton et al. [3] show that the segmented, banded microstructure consisting of alternating hard particle rich and hard particle poor regions is developed in FSW. Salem et al. [4] compared the superplastic behavior of the welded sections with the one of base metal, which shows that the high welding rates increase the density of dislocations and develop microstructures consisting of tangled dislocation structures and subgrains with small misorientations. Peel et al. [5] reported the results of microstructure, mechanical properties, and residual stresses of four aluminum AA5083 friction stir welds produced under varying conditions, which demonstrate that the controlling of the energy input can dominate the welds properties. Boz and Kurt [6] studied the influence of the stirrer geometry on bonding and mechanical properties in friction stir welding process. Reynolds et al. [7] investigated the properties and residual stress, and show that the region of the large tensile residual stress becomes wider with the increase in the angular velocity of the pin. Park et al. [8] found that the sigma formation in friction stir welds can be accelerated by the emergence of delta-ferrite at high temperature and subsequent decomposition of the ferrite under the high strain, and recrystallization induced by friction stirring. Ericsson and Sandström [9] compared the fatigue of friction stir welds with the welds from MIG and TIG, and studied the influence of the welding speed on the fatigue. The effect of the rotating speed on the formation of the friction stir processing zone is investigated by Elangovan and Balasubramanian [10]. Both the welding speed and the rotating speed can affect the mechanical properties of the friction stir welds [5, 11, 12]. So, it is necessary to further study the mechanism on how the welding parameters affect the properties of friction stir welds. Numerical method is the right tool for this study.

To help the understanding of the mechanism of FSW, the material flow patterns and the spatial velocity field around the special pin were studied by Deng and Xu [13] by using two different tool–material interface models. The material flows in FSW were divided into two modes by Muthukumaran and Mukherjee [14]: the material flow caused by the shoulder and by the pin. Steel shot tracer technique was used by Colligan [15] to visualize the material flow behavior in FSW of aluminum. The material flow patterns were also studied by Guerra et al. [16] and Zhang et al. [17, 18], which show that the material flow at the advancing side and the one at the retreating side are different.

But in fact, the temperature caused by the movement of the rotating tool can usually reach 80–90% of the melting temperature of welding material. So, more reasonable formulations to simulate the FSW process are the rate-dependent constitutive equations. Although rate-dependent models of FSW have been established by Santiago et al. [19] and Ulysse [20], the welding quality has not been considered. Moreover, the computation of a fully coupled thermo-mechanical analysis by using rate-dependent constitutive model is still time consuming. To further reduce the computational costs, a semi coupled thermo-mechanical FEM code developed by the authors is combined with the general finite element code—ABAQUS as a user subroutine. Loading speeds are also increased to accelerate the computational convergence.

Model description

Mesh and boundary conditions

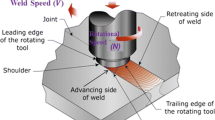
This article deals with a butt weld, which joins two identical plates made of 1018CR steel. The radii of the pin and the shoulder are 5 and 22.7 mm respectively. The rake angle of the rotating tool is taken as zero in the current research. The dimensions of the two plates are 100 mm in length, 40 mm in width, and 8 mm in thickness. Z = 0 mm represents the bottom surface of the friction stir welds and Z = 8 mm corresponds to the top surface. The tool pin rotates with a certain angular velocity, and the translational velocity is applied on the boundaries of the plates in numerical modeling. According to the rotational direction of the pin, an advancing side and a retreating side can be defined, as shown in Fig. 1.

Fig. 1
figure 1

Geometry model and the boundary conditions

Full size image

The plates are divided into 8464 eight-node hexahedron elements and consist of 10972 nodes. The rotational tool is treated as a rigid body, which is meshed into 3038 four-node 3D bilinear rigid quadrilateral elements which consist of 3040 nodes. The meshes of the welding tool and the welding plate are shown in Fig. 2. Reduced integration with hourglass control is used to avoid mesh-locking problems associated with incompressible plastic deformation. The material near the rotational tool undergoes large plastic deformation. In order to model the contacting surfaces and handle mesh distortions, arbitrary Lagrangian-Eulerian (ALE) mesh and adaptive remeshing technique are employed in this study.

Fig. 2
figure 2

Meshes of rotating tool and welding plate

Full size image

Temperature field

A semi coupled thermo-mechanical analysis of the FSW process is devised by using a general finite element code due to the limitation of the PC computation power. To compensate for the lack of the temperature field in the FSW process, the measured temperature values [21] from an actual test are used to construct an approximate temperature field in the numerical model. This temperature field is input into the solid finite element model before moving the pin and the plates. During the FSW process, the temperature field is kept as constant. The temperature values in the test are measured in the mid-plane, which is 3.18 mm from the surfaces. The drilling holes are inserted into the plates and are aligned along the line normal to the welding line to obtain the temperature history values at various distances from the welding line, as shown in Fig. 3. On the basis of these values, an approximate temperature field can be constructed.

Fig. 3
figure 3

Fitted temperature field in friction stir welding [21]

Full size image

The material flows under different process parameters including the translational speeds and the rotational speeds, are modeled to obtain a more general conclusion. When the process parameters are changed, the temperature field may be changed simultaneously. But variations by the temperature values are limited by the melting point of welding material and the maximum temperature ranges from 80% to 90% [22, 23]. It implies that the variation in process parameters does not affect the temperature field significantly, although there exists a relation between the temperature field and process parameters. Moreover, the material flow patterns in numerical models under different welding parameters in Ref. [17] have been proved to be fitted well with experimental tests. This is why the same approximate temperature field under different process parameters is used in this study.

Material properties

The welding plates are made of 1018CR steel, as a rate dependent elastic–plastic material. The Young’s modulus and yield stress are the functions of temperature. The properties of the material at different temperatures are shown in Fig. 4 [24].

Fig. 4
figure 4

Material properties used in the FSW modeling [24]

Full size image

The generalization of the classic von Mises model of the rate dependent material is [25],

$$ f=\bar{\sigma}-\sigma_{0} (T)-\eta (\bar{\varepsilon}^{p})^{n}(\dot{\bar{\varepsilon}}^{p})^{m}=0 $$
(1)

where σ0(T) is the current yield stress which can be the function of temperature, m is the viscosity exponent, n is the strain hardening exponent, and η is the viscosity coefficient.

The equation can be transformed to the idealized elastic–plastic model when η = 0. If n = 0, the strain rate hardening/softening model can be obtained as follows,

$$ f=\bar{\sigma}-\sigma_{0} (T)-\eta (\dot{\bar{\varepsilon}}^{p})^{m}=0 $$
(2)

where η > 0 represents the state of strain rate hardening, and η < 0, strain softening.

In contrast to the case of rate-independent plasticity, the effective stress is no longer constrained to remain less than or equal to the yield stress. The loading function based on von Mises condition can be defined as,

$$ g(\sigma)=\bar{\sigma}-\sigma_{0} (T) $$
(3)

where \(\bar{\sigma}=\sqrt{(3/2)\sigma^{\prime}:\sigma^{\prime}}\) is the equivalent stress and σ′ is the deviatonic stress.

For Perzyna model, the flow law is given by,

$$ \dot{\varepsilon}^{\rm vp}=\gamma \frac{\partial g(\sigma)}{\partial \sigma} $$
(4)

where γ is the slip rate and,

$$ \gamma =\left\langle g(\sigma)\right\rangle /\eta $$
(5)

where 〈〉 denotes MacAuley brackets which are defined by 〈x 〉 = 1/2(x + | x |).

Considering thermal strain, the stress can be expressed as,

$$ {\rm d} \sigma_{ij} =C_{ijkl} \left({\rm d}\varepsilon_{kl} -{\rm d}\varepsilon_{kl}^p -{\rm d}\varepsilon_{kl}^T -\frac{{\rm d}C^{-1}_{ijkl}}{{\rm d}T}\sigma_{kl}\right){\rm d}T $$
(6)

where C ijkl is a material elastic constant tensor, for heat transfer problems in high temperature, C ijkl = C ijkl (T), and \(\rm {d}\varepsilon_{ij}^T\) is the thermal strain.

Return mapping algorithm

The numerical algorithm for integrating the rate constitutive equations is called a constitutive integration algorithm or stress update algorithm [26]. Constitutive integration algorithms are presented for rate-independent and rate-dependent material. For a rate-dependent case, in the state of plastic loading,

$$ \Updelta \gamma =\gamma \Updelta t > 0 $$
(7)

The plastic flow residual can be defined as:

$$ \user2{R}_{n+1} =-\varvec{\varepsilon}_{n+1}^{\rm p} + \varvec{\varepsilon}_n^{\rm p} +\Updelta \gamma \nabla f $$
(8)

where

$$ f_{n+1} =f(\sigma_{n+1}) $$
(9)

Since the total strain is fixed during the return mapping stage, it follows that

$$ \Updelta \varvec{\varepsilon}_{n+1}^{{\rm p}^{\rm (k)}} =- \user2{C}^{-1}:\Updelta \varvec{\sigma}_{n+1}^{(k)} $$
(10)

Linearization of Eqs. 8 and 9 gives,

$$ \frac{\partial \user2{R}_{n+1}}{\partial \varvec{\sigma}_{n+1}}=\left[ \user2{C}^{-1}+\Updelta \gamma_{n+1} \nabla^{2}f_{n+1} \right]+\Updelta t/\eta \left[ \nabla f_{n+1} \otimes \nabla f_{n+1} \right] $$
(11)
$$ f_{n+1}^{(k)} +\nabla f_{n+1}^{(k)} :\Updelta \sigma_{n+1}^{(k)} =0 $$
(12)

Hessian matrix can be given by:

$$ \left[ \Upxi_{n+1}^{(k)} \right]^{-1}=C^{-1}+\Updelta \gamma_{n+1}^{(k)} \nabla^{2}f(\sigma_{n+1}^{(k)}) $$
(13)

Solving the linearized problem to obtain the increment of the viscoplastic strain,

$$ \Updelta \varvec{\varepsilon}_{n+1}^{{\rm vp}^{\rm (k)}}= \user2{C}^{-1}:\left[ \left[ \varvec{\Upxi}_{n+1}^{\rm vp} \right]^{-1}+\Updelta t/\eta \nabla f_{n+1}^{\rm vp} \otimes \nabla f_{n+1}^{\rm vp} \right]^{-1}:\user2{R}_{n+1}^{\rm vp} $$
(14)

So the plastic strain ɛvp can be updated until the residual is less than a specific value.

Computational costs

The estimate of the critical time increment can be defined as [27],

$$ \Updelta t=\frac{L_{\rm min}}{c_{\rm d}} $$
(15)

where L min is the smallest element dimension, c d is the wave speed,

$$ c_{\rm d} =\sqrt\frac{\lambda +2\mu }{\rho} $$
(16)

where λ and μ are Lame constants, and ρ is the density.

So the iteration number of the solving process can be approximately obtained as,

$$ n=\frac{t}{\Updelta t}=\frac{t}{L_{\rm min}}\sqrt\frac{\lambda +2\mu}{\rho} $$
(17)

where t is the natural time.

In the present semi-coupled thermal stress calculation, the estimate of the time increment Δt is only approximate, and in most cases is not conservative. So a safe factor, which ranges from \(1/\sqrt{3}\) to 1 is introduced for the current three-dimensional case. From the above Eq. 17, some methods can be used to reduce the computational costs, such as increasing the loading speeds to speed up the simulation process or artificially increasing the material density, which is called mass scaling. When the inertia forces dominate the solution in a rate dependent problem, mass scaling cannot be used. Even the other method to increase the loading speeds needs to be carefully cautioned. According to Eq. 1, the viscosity coefficient η must be changed to keep the results obtained, unaffected when the loading speeds are changed. When the viscosity exponent m = 1 and the strain hardening exponent n = 0, a linear relation occurs between the loading speeds and the viscosity coefficient. If the simulation speed is increased too much, the increased inertia forces will change the predicted response (in an extreme case the problem will exhibit wave propagation response). The only way to avoid this error is to choose a speed-up that is not too large.

Interaction properties

Although slipping interface model can provide a possible connection between the material flow in solid state and the fluid dynamics, the frictional contact model is believed to be more realistic to model friction stir welding process because the friction force on the pin–plate interface cannot be increased without any limit. So the interface may experience frictional contact described by a modified Coulomb friction law, as shown in Fig. 5. The Coulomb friction law is modified so that there exists a maximum critical frictional stress, above which the frictional stress stays constant and is no longer equal to the product of friction coefficient and the contact pressure. In this article, a reasonable upper bound \(\tau_{\rm max} =\sigma_{\rm s}/\sqrt{3}\) is used, where σs means the current yield strength of the material.

Fig. 5
figure 5

Modified Coulomb law

Full size image

Benchmark tests

Example 1: The dimensions of the beam used here are 1 m  ×  1 m  ×  5 m. The beam is meshed into 2  ×  2  ×  10 eight node hexahedral elements. The freedoms are fixed on the respective three surfaces of the beam, as shown in Fig. 6. The pressure acting on the surface is 520 MPa. The elastic modulus is 210 GPa. The yield stress is 400 MPa and the Poisson’s ratio is 0.3. The viscosity coefficient is 100 MPa for 1018 steel.

Fig. 6
figure 6

Boundary conditions of the beam in the Benchmark tests

Full size image

The results are calculated in ANSYS and the code developed in this research are shown in Fig. 7. It can be found that the results calculated by using the codes developed agree well with those obtained by ANSYS both in the elastic and in the viscoplastic domain. Due to the effect of the rate of the plastic strain, the material is enhanced after the elastic stage. At the current example, the stress can be increased to 520 MPa when the strain is increased to 0.27.

Fig. 7
figure 7

Stress–strain relationship obtained by ANSYS and ABAQUS/VUMAT

Full size image

Example 2: The dimensions of the beam used here are 1 m  ×  1 m  × 5 m. The beam is meshed into 2 × 2 × 10 eight node hexahedral elements. The freedoms are fixed on the respective three surfaces of the beam. The displacement acting on the surface is 0.05 m, as shown in Fig. 6. The viscosity coefficient is 100 MPa for 1018 steel.

Table 1 shows the results in the two cases when the natural time t is different. t Represents the natural time of the event being simulated. One case is that the dynamic solving process is not accelerated. The other case is that the loading speed is accelerated by ten times, but it is noted that the viscosity coefficient is decreased by ten times to eliminate the influence of the rate of plastic strain on the history of stress and strain at the same time. The results at different times are given to compare the history results in the two cases. It is shown that the error in plastic stage is smaller than that in the elastic stage. The error is lower than 0.4% in the plastic stage. So it can be concluded that in a large deformation problem, the error caused by speeding up the solving process is small enough to keep the accuracy of the computation.

Table 1 Calculating results under different loading speeds
Full size table

Results and discussions

The results obtained under different process parameters are shown as follows:

It can be seen from Fig. 8 that the shoulder, especially the border of the shoulder, can affect the material flow near the shoulder–plate interface. The deformation of the material in the nugget zone is severer than that outside the stirring zone. So the grains in the nugget zone are destroyed and recrystallized as smaller ones.

Fig. 8
figure 8

Distribution of the equivalent plastic strain in the cross section perpendicular to the welding line (v = 2.363 mm/s, ω = 240 r/min)

Full size image

Figure 9 shows the distributions of the equivalent plastic strain in the section perpendicular to the welding line under different angular velocities. The variations in the angular velocity can affect the mechanical deformations of the material in the weld region. The deformation of the material, which is slightly away from the welding line can be increased with the increase in the angular velocity. This means that the influence region of the pin can be increased with the augment of the angular velocity. Moreover, the deformation of the material in lower half of the nugget zone can become more uniform when the angular velocity is increased. That is, the gradient of the material’s deformation in x direction becomes smaller with the increase in the angular velocity of the pin.

Fig. 9
figure 9

Distributions of the equivalent plastic strain in the section perpendicular to the welding line under different angular velocities

Full size image

The distributions of the equivalent plastic strain in section perpendicular to the welding line under different translational velocities are shown in Fig. 10. It can be seen that the equivalent plastic strain outside the nugget zone is decreased with the increase in translational velocity of the pin, which means that the influence region of the pin is decreased with the increase in translational velocity. The gradient of the equivalent plastic strain in lower half of the friction stir weld becomes smaller when the translational velocity is decreased.

Fig. 10
figure 10

Distributions of the equivalent plastic strain in section perpendicular to the welding line under different translational velocities

Full size image

From the above discussions, it can be concluded that the material in lower half of the friction stir weld can be fully mixed with the increase in the angular velocity or the decrease in the translational velocity. So the deformation in lower half of the friction stir weld can become more uniform in x direction when the angular velocity is increased or the translational velocity is decreased. But it should be noted that the gradient of the equivalent plastic strain in the direction of thickness becomes larger when the angular velocity is increased or the translational velocity is decreased, which means that the mixture of the material in the direction of thickness becomes poorer. Then flaws may occur when the angular velocity is very high or the translational velocity is very small. It means that it is very important to select an appropriate value of v/ω in FSW.

When the rotating tool is moving, a steady state material flow can be quickly formed around the welding tool. Figure 11 shows the radial material flow on the circle path, which is 0.2 mm away from the tool–plate interface on the bottom surface of welded plate at different times, when v = 2.363 mm/s and ω = 240 r/min. It can be seen that the distribution of the radial velocity is very similar to that obtained by using a rate independent constitutive model [18, 28]. The variation in time does not have an apparent effect on the radial material flow. The corresponding tangent velocity distributions are shown in Fig. 12. Although the values of the tangent velocity are affected by the variation in time, the distribution rule of tangent material flow has not been changed significantly. So in the following discussions, the material flows at the instant when a length of 11.815 mm weld is formed on the circle path, which is 1 mm away from the interface are analyzed for the investigations on the effect of the welding parameters.

Fig. 11
figure 11

Radial velocity distributions at different times

Full size image
Fig. 12
figure 12

Tangent velocity distributions at different times

Full size image

Figure 13 shows the velocity vector plotted around the rotating tool. It can be seen that the material flow near the top surface is faster than that near the bottom surface. Compared with the material flow on the advancing side, the material flow on the retreating side is relatively faster.

Fig. 13
figure 13

Velocity vector plot around the pin

Full size image

The effect of variation in the angular velocity on the radial flow around the pin is shown in Fig. 14. The radial material flow fluctuates around zero near the tool–plate interface. This means that some material particles move away from the interface due to the rotation and the translation of the welding tool, but some other material particles move toward the interface to fulfill the vacant place caused by leaving of the material particles from the interface. This material movement is the cause for formation of the hydrostatic pressure near the welding tool.

Fig. 14
figure 14

Radial velocity around the pin under different angular velocities

Full size image

Compared with the radial velocity, the tangent velocity is much larger, as shown in Fig. 15. It should be noted that there exists a region near θ = 0° in which the tangent velocity is negative. It means that there may exist swirls in the tangent material flow during FSW. With the increase in the angular velocity, the negative maximum of the tangent velocity is also increased. That is, swirl or vortex may be easier to be observed with the increase in the angular velocity of the pin.

Fig. 15
figure 15

Tangent velocity around the pin under different angular velocities

Full size image

Figure 16 shows the material flow in the direction of thickness, i.e., the vertical velocity, under different angular velocities. When the angular velocity applied on the pin is small, i.e., ω = 240 r/min, it can seen that the vertical velocity in front of the pin (θ = 0∼ 180°) is mostly positive, but negative behind the pin (θ = 180∼ 360°). When the angular velocity is increased, the vertical velocity approximately occurs in the region of θ = 90∼ 270°, as shown in Fig. 16(b, c). The positive vertical velocity means that the material moves upwards. This is caused by the extrusion of the pin. The extruded material is limited by the shoulder and then has to move downwards in the wake. From Fig. 16(a–c), it can be seen that the movement of the material in the vertical direction can be affected by variation in the angular velocity.

Fig. 16
figure 16

Vertical velocity around the pin under different angular velocities

Full size image

The effect of the welding speed on the radial velocity distributions around the pin is shown in Fig. 17. The effect of the welding speeds on the radial velocity distributions is not very clear. But it can be seen that the negative radial material flow is faster near θ = 270°. This place is located near the welding line. Compared with Fig. 14, it can be found that the radial material flow can be easily observed when the angular velocity is relatively high.

Fig. 17
figure 17

Radial velocity around the pin under different welding speeds

Full size image

The variation in the welding speed does not affect the maximum tangent velocity significantly, as shown in Fig. 18. It can be seen that the rotation of the shoulder can increase the tangent material flow apparently, especially when the welding speed is lower. When the welding speed is higher, the material flows in different depths become similar.

Fig. 18
figure 18

Tangent velocity around the pin under different welding speeds

Full size image

The vertical velocity is fluctuating around zero, as shown in Fig. 19. When the welding speed is increased to 3.316 mm/s, the vertical velocity in front of the pin is mostly positive, but negative behind the pin. This means that the role of the extrusion of pin on the transport of material in FSW becomes very important. It is the real cause to push the material in front of the pin upwards. And then the upward material is limited by the shoulder, and has to rotate with the rotating tool. Behind the pin, the upward material deposits in the wake. But when the welding speed is lower, i.e., v = 1.279 mm/s, this phenomenon is difficult to be revealed.

Fig. 19
figure 19

Vertical velocity around the pin under different welding speeds

Full size image

Compared with the fully coupled thermo-mechanical model developed by Schmidt et al. [27], the computational time can be decreased from nearly 2 weeks to 260 min for v = 2.363 mm/s, ω = 240 r/min, 259 min for v = 2.363 mm/s, ω = 290 r/min, 258 min for v = 2.363 mm/s, ω = 340 r/min, 454 min for v = 1.279 mm/s, ω = 390 r/min, 261 min for v = 2.363 mm/s, ω = 390 r/min, and 188 min for v = 3.316 mm/s, ω = 390 r/min in the current semi-coupled thermo-mechanical numerical model of FSW.

Conclusions

Rate dependent constitutive model with return mapping algorithm is used to simulate the material behaviors around the pin. The acquired results are summarized as follows:

  1. (1)

    The border of the shoulder can affect the material flow near the shoulder–plate interface.

  2. (2)

    The mixture of the material in the lower half of the friction stir weld can benefit from the increase in the angular velocity or the decrease in the welding speed. But flaws may occur when the angular velocity is very high or the translational velocity is very small.

  3. (3)

    When the angular velocity applied on the pin is small or the welding speed is high, the role of the extrusion of pin on the transport of material in FSW becomes very important.

  4. (4)

    Swirl or vortex may be easier to be observed with the increase in the angular velocity of the pin.