Fast Exact Hyper-graph Matching with Dynamic Programming for Spatio-temporal Data

Abstract

Graphs and hyper-graphs are frequently used to recognize complex and often non-rigid patterns in computer vision, either through graph matching or point-set matching with graphs. Most formulations resort to the minimization of a difficult energy function containing geometric or structural terms, frequently coupled with data attached terms involving appearance information. Traditional methods solve the minimization problem approximately, for instance resorting to spectral techniques. In this paper, we deal with the spatio-temporal data, for a concrete example, human actions in video sequences. In this context, we first make three realistic assumptions: (i) causality of human movements; (ii) sequential nature of human movements; and (iii) one-to-one mapping of time instants. We show that, under these assumptions, the correspondence problem can be decomposed into a set of subproblems such that each subproblem can be solved recursively in terms of the others, and hence an efficient exact minimization algorithm can be derived using dynamic programming approach. Secondly, we propose a special graphical structure which is elongated in time. We argue that, instead of approximately solving the original problem, a solution can be obtained by exactly solving an approximated problem. An exact minimization algorithm is derived for this structure and successfully applied to action recognition in two settings: video data and Kinect coordinate data.

1 Introduction

Many computer vision problems can be formulated as graphs and their associated algorithms, since graphs provide a structured, flexible and powerful representation for visual data. Graph representation has been successfully used in problems such as tracking [51, 60], object recognition [1, 4, 52], object categorization [15], and shape matching [30, 46]. In this paper, we propose a novel method for point-set matching via hyper-graphs embedded in space–time coordinates, where the point sets correspond to interest points of the model and scene videos, respectively. We focus on applications of object or event recognition [29]; in particular, in localizing and recognizing human actions in video sequences.

The action recognition problem is solved via graph matching, which is conceived as a search problem for the best correspondence between two point-sets, i.e., the one belonging to the model structured into a graph—a model graph—and the other one belonging to the scene—a scene point set. In this context, an action is represented by a model graph consisting of a set of nodes with associated geometric and appearance features, and of a set of edges that represent relationships between nodes. Action recognition itself becomes then a graph matching problem, which can be formalized as a generic energy-minimization problem [52]. The graph matching energy is a scalar quantity which is lower for likely assignments respecting certain invariances and geometric transformations from model to scene, whereas it results in higher values for unrealistic and unlikely assignments.

The energy function, more explicitly, is composed of two terms, i.e., an appearance term and a geometric term. The appearance term takes into consideration the difference between intrinsic properties of points between the model and the scene. Popular examples of appearance information are SIFT [35], histograms of gradient and optical flow [25], shape contexts [3] etc. The geometric term, on the other hand, takes into consideration the structural deformation between model and scene point assignments. The geometric term is conceived to provide certain invariance properties, such as the rate of action realization. In this work, we utilize hyper-graphs, which are a generalization of graphs and allow edges (hyper-edges, strictly speaking) to connect any number of vertices, typically more than two. Similar to other formulations in object recognition, our hyper-edges connect triplets of nodes, which allow verifying geometric invariances that are invariant to scale-changes, as opposed to pairwise terms that are restricted to distances [14, 48, 59]. Unlike [14, 48, 59], our geometric terms are split into spatial terms and temporal terms, which is better suited to the spatio-temporal data.

Our graphs are built on space–time interest points, as in [48], similar to spatial formulations for object recognition as in [11, 14, 59] and others. This allows us stay independent of preceding segmentation steps, as in [10], or on parts models, where an object or an action is decomposed into a set of parts [5, 17]. Parts based formulations like [5] are able to achieve good results with graphs which are smaller than our graphs, but they depend on very strong unary terms constructed from machine learning.

Inference is the most challenging task in graph matching, as useful formulations are known to be NP-hard problems [52]. While the graph isomorphism problem is conjectured to be solvable in polynomial time, it is known that subgraph isomorphism—exact subgraph matching—is NP-complete [19]. Practical solutions for graph matching therefore must rely on approximations or heuristics.

We propose an efficient hyper-graph matching method for spatio-temporal data based on three realistic assumptions: (i) causality of human movements; (ii) sequential nature of human movements and limited warping; and (iii) one-to-one mapping of model-to-scene time instants. We present a theoretical result stating that, under these assumptions, the correspondence problem can be decomposed into a set of subproblems such that each subproblem can be solved recursively in terms of the others, and hence derive an exact minimization algorithm. A constructive proof shows that the minimization problem can be solved efficiently using dynamic programming.

The approximated model enables us to achieve performance faster than real-time. This work thus falls into the category of methods calculating the exact solution for an approximated model, unlike methods calculating an approximate solution, for instance [5, 14, 30, 48, 52, 58, 59] or methods which perform exact structure preserving matching like [29]. In this sense, it can be compared to [11], where the original graph of a 2D object is replaced by a k-tree allowing exact minimization by the junction tree algorithm. Our solution is different in that the graphical structure is not created randomly but is derived from the temporal dimensions of video data. We propose three different approximated graphical structures, all characterized by a reduction in the number of interest points, which allows faster than real-time performance on mid-level GPUs.

1.1 Related Work: Graph Matching

There is a plethora of literature on optimization and practical solutions of graph matching algorithms. This extensive research on practical solutions to graph matching can be analyzed under different perspectives. One common classification is:

• 1. Exact matching: A strictly structure-preserving correspondence between the two graphs (e.g., graph isomorphism) or at least between parts (e.g., subgraph isomorphism) is searched.

• 2. Inexact matching: Compromises in the correspondence are allowed in principle by admitting structural deformations up to some extent. Matching proceeds by minimizing an objective (energy) function.

In the computer vision context, most recent papers on graph matching are based on inexact matching of valued graphs, i.e., graphs with additional geometric and/or appearance information associated with nodes and/or edges. Practical formulations of this problem are known to be NP-hard [52], which requires approximations of the model or the matching procedure. Two different strategies are frequently used:

• 1. Calculation of an approximate solution of the minimization problem;

• 2. Calculation of the exact solution, most frequently of an approximated model.

1.2 Approximate Solution

A well known family of methods solves a continuous relaxation of the original combinatorial problem. Zass and Shashua [59] presented a soft hyper-graph matching method between sets of features that proceeds through an iterative successive projection algorithm in a probabilistic setting. They extended the Sinkhorn algorithm [23], which is used for soft assignment in combinatorial problems, to obtain a global optimum in the special case when the two graphs have the same number of vertices and an exact matching is desired. They also presented a sampling scheme to handle the combinatorial explosion due to the degree of hyper-graphs. Zaslavskiy et al. [58] employed a convex–concave programming approach to solve the least-squares problem over the permutation matrices. More explicitly, they proposed two relaxations to the quadratic assignment problem over the set of permutation matrices which results in one quadratic convex and one quadratic concave optimization problem. They obtained an approximate solution of the matching problem through a path following algorithm that tracks a path of local minimum by linearly interpolating convex and concave formulations.

A specific form of relaxation is done by spectral methods, which study the similarities between the eigen-structures of the adjacency or Laplacian matrices of the graphs or of the assignment matrices corresponding to the minimization problem formulated in matrix form. In particular, Duchenne et al. [14] generalized the spectral matching method from the pairwise graphs presented in [30] to hyper-graphs by using a tensor-based algorithm to represent affinity between feature tuples, which is then solved as an eigen-problem on the assignment matrix. More explicitly, they solved the relaxed problem by using a multi-dimensional power iteration method, and obtained a sparse output by taking into account $l_1$-norm constraints instead of the classical $l_2$-norm. Leordeanu et al. [31] made an improvement on the solution to the integer quadratic programming problem in [14] by introducing a semi-supervised learning approach. Lee et al. [28] solved the relaxed problem by a random walk algorithm on the association graph of the matching problem, where each node corresponds to a possible matching between the two hyper graphs. The algorithm jumps from one node (matching) to another one with given probabilities.

Another approach is to decompose the original discrete matching problem into subproblems, which are then solved with different optimization tools. A case in point, Torresani et al. [52] solved the subproblems through graph-cuts, Hungarian algorithm and local search. Lin et al. [33] first determined a number of subproblems where each one is characterized by local assignment candidates, i.e., by plausible matches between model and scene local structures. For example, in action recognition domain, these local structures can correspond to human body parts. Then, they built a candidacy graph representation by taking into account these candidates on a layered (hierarchical) structure and formulated the matching problem as a multiple coloring problem. Finally, Duchenne et al. [15] extended one dimensional multi-label graph cuts minimization algorithm to images for optimizing the Markov Random Fields (MRFs).

1.3 Approximate Graphical Structure

Many optimization problems in vision are NP-hard. The computation of exact solutions is often unaffordable, e.g., in real-time video processing. A common approach is to approximate the data model, for instance the graphical structure, as opposed to applying an approximate matching algorithm to the complete data model. One way is to simplify the graph by filtering out the unfruitful portion of the data before matching. For example, a method for object recognition has been proposed by Caetano et al. [11], which approximates the model graph by building a k-tree randomly from the spatial interest points of the object. Then, matching was calculated using the classical junction tree algorithm [27] known for solving the inference problem in Bayesian Networks.

A special case is the work by Bergthold et al. [5], who perform object recognition using fully connected graphs of small size (between 5 and 15 nodes). The graphs can be small because the nodes correspond to semantically meaningful parts in an object, for instance landmarks in a face or body parts in human detection. A spanning tree is calculated on the graph, and from this tree a graph is constructed describing the complete state space. The $A^{*}$ algorithm then searches the shortest path in this graph using a search heuristic. The method is approximative in principle, as hypotheses are discarded due to memory requirements. However, for some of the smaller graphs used in certain applications, the exact solution can be calculated. Matching is typically done between 1 and 5 s per graph, but the worst case is reported to take several minutes.

1.4 Related Work: Action Recognition

While the methods described in Sect. 1.1 focus on object recognition in still images or in 3D as practical applications, we here present a brief review on the most relevant methods that apply graph matching to human action recognition problem in video sequences. Graph-based methods frequently exploit sparse local features extracted from the neighborhood of spatio-temporal interest points (STIPs). A spatio-temporal interest point can be defined as a point exhibiting saliency in the space and time domains, i.e., high gradient or local maxima of the spatio-temporal filter responses. The most frequently used detectors are periodic (1D Gabor filters) [13], 3D Harris corner detector [25], extension of Scale-invariant Feature Transform (SIFT) to time domain [45] etc. It is typical to describe the local neighborhood of an interest point by concatenation of gradient values [13], of optical flow values [13], or of spatial-temporal jets [44], histogram of gradient and optical flow values (HoG and HoF) [25] or 3D Scale-invariant Feature Transform (SIFT) [45].

Ta et al. [48] have built hyper-graphs from proximity information by thresholding distances between spatio-temporal interest points [13]. Given a model and a scene graph, matching is conducted by the algorithm of Duchenne et al. in [14]. Similarly, Gaur et al. [20] modeled the relationship of STIPs [25] in a local neighborhood, i.e., they have built local feature graphs from small temporal segments instead of the whole video. These temporally ordered local feature graphs composed the so-called String of Feature Graphs (SFGs). Dynamic Time Warping (DTW) was utilized to measure the similarity between a model and a scene SFG, where matching of two graphs was implemented using the method proposed in [30]. In particular, these two methods in [48] and [20] resorted to off-the-shelf spectral methods. In a different vein, Brendel and Todorovic [10] formulated the graph matching problem as a weighted least squares problem on the set permutation matrices. They built directed graphs from adjacency and hierarchical relationships of spatio-temporal regions and learned the representative nodes and edges in the weighted least squares sense from a set of training graphs.

Graph embedding has been used in several studies [34, 57]. For example, Liu et al. [34] have used graphs to model the relationship between different components. While the nodes can be spatio-temporal descriptors, spin images or action classes, edges represent the strength of the relationship between these components, i.e., feature-feature, action-feature or action-action similarities. The graph is then embedded into a k-dimensional Euclidean space; hence correspondence is solved by spectral technique.

Graphs also used to model different types of data: still images [41, 55] and MoCap data [56]. Inspired from pictorial structures [17], Raja et al. [41] jointly estimate the pose and action using a pose-action graph where the nodes correspond to the five body parts, e.g., head, hands, feet, and the energy function is formulated based on both detected body parts and possible relative positioning of parts given the action class. In [55], Yao and Fei-Fei structure salient points on the human body, namely skeletal joints, into a graph. Body joints are detected again by pictorial structures [17]; however, the main difference is that they use the method in [50] to recover depth information, and then attribute the 3D position information of the joints as well as appearance features to the nodes and 3D pose features to the edges. Similary, in [56], graphs model the relationship of skeletal joints from MoCap Data.

Causality with respect to time has motivated sparse graphical models [7, 36] in which inference can be carried out by means of dynamic programming. An extension of sequential models are trees, which offer an alternative structured representation to graphs. Mikolajczyk and Uemura [38] built a vocabulary from appearance-motion features and exploited randomized kd-trees to match a query feature to the vocabulary. Jiang et al. [22] used trees for assigning each frame to a shape-motion prototype, and aligned the two sequences of prototypes by DTW.

2 Problem Formulation

In this paper, we formulate the problem as a particular case of the general correspondence problem between two point sets. The objective is to assign points from the model set to points in the scene set, such that some geometrical invariance is satisfied. We solve this problem through a global energy minimization procedure, which operates on a hyper-graph constructed from the model point set. The $M$ points of the model are organized as a hyper-graph ${{\mathcal {G}}}=\{{\fancyscript{V}},{\fancyscript{E}}\}$, where ${\fancyscript{V}}$ is the set of hyper-nodes (corresponding to the points) and ${\fancyscript{E}}$ is the set of hyper-edges. The edges ${\fancyscript{E}}$ in our hyper-graph connect sets of three nodes, thus triangles. From now on we will abusively call hyper-graphs “graphs” and hyper-edges “edges”.

The matching problem under consideration is an optimization problem over maps from the model nodes ${\fancyscript{V}}$ to scene interest points ${\fancyscript{V}}^{\prime }$ plus an additional interest point $\epsilon$ which is interpreted as a missing detection, i.e., $z: {\fancyscript{V}} \rightarrow {\mathcal {V}}^{\prime } \cup \{\epsilon \}$. The temporal coordinates of each point are explicitly denoted by the maps $t: {\fancyscript{V}} \rightarrow \mathbb {N}$ and $t^{\prime }: {\fancyscript{V}}^{\prime } \rightarrow \mathbb {N}^{\prime }$ from nodes to frames. Note that edges need not be such that all their nodes belong to the same frame.

2.1 Objective Function

Each node (point) $i$ in the two sets (model and scene) is assigned a space–time position and a feature vector that describes the appearance in a local space–time neighbourhood around this point. Discrete variable $z_i,\ i=1\dots M$ represents the mapping from the ith model node to some scene node, and which can take values from $\{1\dots S\}$, where $S$ is the number of scene nodes. We use the shorthand notation $z$ to denote the whole set of map variables $\{z_i\}_{i=1:M}$. A solution of the matching problem is given through the values of the $z_i$, that is, through the optimization of the set $z$, where $z_i = j$, $i=1\dots M$, is interpreted as model node $i$ being assigned to scene node $j=1\dots S$. To handle cases where no reliable match can be found, such as occlusions, an additional dummy value $\epsilon$ is admitted, which semantically means that no assignment has been found for the given variable ($z_i=\epsilon$).

Each combination of assignments $z$ evaluates to a figure of merit in terms of an energy function $E(z)$, which will be given below. In principle, the energy should be lower for assignments that correspond to a realistic transformation from the model image to the scene image, and it should be high otherwise. We search for the assignments that minimize this energy.

We illustrate the matching problem in Fig. 1. Our proposed energy function is as follows:

$$\begin{aligned} E(z) = \lambda _1 \sum _{i=1}^{M} U(z_i) + \lambda _2 \sum _{(i,j,k)\in {\fancyscript{E}}} D(z_i,z_j,z_k), \end{aligned}$$

(1)

where $U(\cdot )$ is a data-attached term taking into account feature distances, $D(\cdot )$ is the geometric distortion between two space–time triangles, and $\lambda _1$ and $\lambda _2$ are weighting parameters. More explicitly, while $U(\cdot )$ is simply defined as the Euclidean distance between the appearance features of model nodes and of their assigned points, $D(\cdot )$ is measured in terms of time warping and shape deformation based on angles. For simplicity, in Eq. (1), we have omitted all variables over which we do not optimize. These terms are explained in detail in Appendix 1.

Fig. 1

Model nodes are structured into a graph, while those of the scene nodes are not. The numbering of the nodes in the figure is arbitrary

2.2 Matching Constraints

Since our data structure is defined in the spatio-temporal domain, we consider the following constraints related to the temporal domain:

Assumption 1

Causality—Each point in the two sets (i.e., model and scene) lies in a spatio-temporal space. In a feasible matching, the temporal order of the model points and the temporal order of their possibly assigned scene points should be retained, which can be formalized as follows:

$$\begin{aligned} \forall \ (i,j) \in {\fancyscript{V}}: \ t(i) < t(j) \Leftrightarrow t^{\prime }(z_i) < t^{\prime }(z_j), \end{aligned}$$

(2)

where $t(i)$ stands for the temporal coordinate (a discrete frame number) of model point $i$, and $t^{\prime }(z_i)$ stands for the temporal coordinate of scene point $z_i$.

Assumption 2

Temporal closeness—Two points which are close in time must be close in both the model set and the scene set. In other words, the extent of time warping between model and scene time axes must be limited to eliminate implausible matching candidates and hence to reduce the search space. This can be handled by thresholding time distances when constructing the hyper-edges as follows:

$$\begin{aligned} \forall \ (i,j,k)&\in {\fancyscript{E}}: |t^{\prime }(z_i) - t^{\prime }(z_j)| < T \ \wedge |t^{\prime }(z_j) - t^{\prime }(z_k)| \nonumber \\&\quad < T \wedge |t^{\prime }(z_i) - t^{\prime }(z_k)| < T, \end{aligned}$$

(3)

where $T$ bounds the node differences in time.

3 Proposed Method

In this section, we introduce two solutions to the exact minimization of the matching problem. First, we reformulate the problem taking into consideration the inherent nature of the action data. This results into a feasible form without having compromised the optimality of the solution, given that the NP-hard problem becomes of polynomial complexity. Second, we introduce approximations to the graphical structure to substantially reduce the computational complexity and explore three such alternatives.

Assumption 3

One-to-One Mapping of Time Instants—We assume that time instants cannot be split or merged. In other words, all points of a model frame should be matched to points of one and only one scene frame, and vice versa.

$$\begin{aligned} \begin{array}{cccc} \forall (i,j) \in {\fancyscript{V}}:&(t(i) = t(j))&\Leftrightarrow (t^{\prime }(z_i) = t^{\prime }(z_j)) \end{array} \end{aligned}$$

(4)

While the assumptions of causality and temporal closeness are realistic assumptions deduced from the inherent properties of the action data, Assumption 3 of one-to-one mapping of time instants is actually a requirement of the recursive solution method we opt for. The correspondence problem can now be decomposed into a set of subproblems such that each subproblem can be solved recursively in terms of the others. Consequently, we can formulate an exact minimization algorithm, and this minimization problem can be efficiently solved by using a dynamic programming technique. We will start with the following definition:

Definition 1

Consider a general hyper-graph ${\mathcal {G}}=\{{\fancyscript{V}},{\fancyscript{E}}\}$ with no specific restrictions on the graphical structure. The temporal span of the graph is defined as the maximum number of nodes associated with an interval $[a,b]$ of frames, where the interval $[a,b]$ is covered by one of the hyper-edges $e \in {\fancyscript{E}}_a^b$ of the graph: $a$ is the lowest temporal coordinate in $e$ and $b$ is the highest temporal coordinate in $e$.

Theorem 1

Consider a general hyper-graph ${\mathcal {G}}=\{{\fancyscript{V}},{\fancyscript{E}}\}$ with no specific restrictions on the graphical structure. Consider Assumptions 1, 2 and 3. Then, the energy function given in Eq. (1) can be solved by a computational complexity which is exponential in the temporal span of the graph.

The temporal span is generally low if the graph is built from proximity information. A constructive proof of this theorem, the minimization via dynamic programming and the computational complexity bounds are all given in Appendix 2. However, although now feasible, the complexity remains still too high for practical usage. It becomes than necessary to further reduce the computational complexity by introducing the notion of sparse graphs. In this case, the reduced graphical structures represent an approximation, but otherwise the graph matching is solved exactly. In the subsequent section, we proposed three different graphical approximation structures, all characterized by a reduction in the number of interest points. Each one assumes very few interest points, i.e., from 1 to 3 points per frame.

3.1 Graphical Structure

The graphical structure is approximated in two steps. First, the graphical structure (the set ${\fancyscript{E}}$ of edges) is restricted by constraints on the combinations of temporal coordinates. The triplets of temporal coordinates $(t(i),t(j),t(k))$ allowed in a hyper-edge are restricted to triplets of consecutive frames: $(t(i),t(j),t(k)) = (t(i),t(i)+1,t(i)+2)$. Depending on the visual content of a video, there may be frames which do not contain any STIPs, and therefore no nodes in the model graph. These empty frames are not taken into account when triplets of consecutive frame numbers are considered.

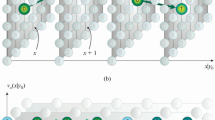
This structure can be visualized by a meta graph, which contains a single node for each (non empty) frame and a hyper-edge connecting the triplets of consecutive frames, as seen in Fig. 2a. The meta graph¹ is planar with triangular structure. Figure 2b, c show model graphs which satisfy the restrictions described above. Note that each triangle in the meta graph (Fig. 2a) corresponds to a set of triangles in the model graphs (Fig. 2b, c).

Fig. 2

a A special graphical structure designed for very low computational complexity: a second order chain. This meta-graph describes the restrictions on the temporal coordinates of model graphs; b a sample model graph satisfying the restrictions in (a); c a sample model graph limited to a single point per frame (the single-point/single-chain model)

Given these restrictions, we propose three different model graphs and three different associated matching algorithms. They differ in the number of model nodes per frame and the way they are linked.

3.1.1 Single-Chain–Single-Point Model

In this model, we keep only a single node per model frame by choosing the most salient one, e.g., the one with the highest confidence. The scene frames may contain an arbitrary number of points, we do not impose any restrictions or pruning upon them. In this case, the graphical structure of the meta graph is identical to the graphical structure of the model graph, and the node indexes $(i,j,k)$ are one-to-one related to the temporal coordinates $t(i),t(j),t(k)$. An example of this model graph is given in Fig. 2c. In particular, each model point $i$ is connected to its two immediate frame-wise predecessors $i-1$ and $i-2$ as well as to its two immediate successors $i+1$ and $i+2$.

The neighborhood system of this simplified graph can be described in a very simple way using the index of the nodes of the graph, similar to the dependency graph of a second order Markov chain:

$$\begin{aligned} E(z) = \sum _{i=1}^{M} U(z_i) + \sum _{i=3}^{M} D(z_i,z_{i-1},z_{i-2}). \end{aligned}$$

(5)

For ease of notation we also drop the parameters $\lambda _1$ and $\lambda _2$ which can be absorbed into the potentials $U$ and $D$. A factor graph for this energy function is given in Fig. 3. Round nodes are variables, square nodes are terms in the energy function. Shaded nodes are constant (observed) data (locations and features).

Fig. 3

A factor graph for the single chain model with $M$ nodes and $M-2$ hyper-edges as given in Eq. (5). Shaded round nodes correspond to data: interest point locations and appearance features, which have been omitted in the notation

Given this special graphical structure, we can now derive the following recursive formula to efficiently find the set of assignments $\widehat{z}$ that minimizes energy in Eq. (5):

$$\begin{aligned} \alpha _i(z_{i-1},z_{i-2})&= \displaystyle {\min _{z_i} } \bigg [ U(z_i) + D(z_{i},z_{i-1},z_{i-2}) \nonumber \\&\qquad \quad + \ \alpha _{i+1}(z_i,z_{i-1}) \ \bigg ], \end{aligned}$$

(6)

with the initialization

$$\begin{aligned} \alpha _{M}(z_{{M}-1},z_{{M}-2}) = \min _{z_{M}} \left[ U(z_{M}) + D(z_{M},z_{{M}-1},z_{{M}-2}) \right] \!.\nonumber \\ \end{aligned}$$

(7)

During the calculation of the trellis, the arguments of the minima in Eq. (6) are stored in a table $\beta _i(z_{i-1},z_{i-2})$. Once the trellis is completed, the optimal assignment can be calculated through classical backtracking:

$$\begin{aligned} \widehat{z_i} = \beta _{i}(z_{i-1},z_{i-2}), \end{aligned}$$

(8)

starting from an initial search for $z_1$ and $z_2$:

$$\begin{aligned} (\widehat{z_1},\widehat{z_2}) = \arg \min _{z_1,z_2} [U(z_1) + U(z_2) + \alpha _3(z_1,z_2)]. \end{aligned}$$

(9)

The algorithm as given above is of complexity $O(M{\cdot }S^3)$. Recall that the total number of model and scene points are denoted by $M$ and $S$, a trellis is calculated in an $M\times S \times S$ matrix, where each cell corresponds to a possible value of a given variable. The calculation of each cell requires to iterate over all $S$ possible combinations of $z_i$.

Exploiting the assumptions on the spatio-temporal data introduced in Sect. 3, the complexity can be decreased further:

• Assumption 1. Taking causality constraints into account, we can prune many combinations from the trellis of the optimization algorithm. In particular, if we consider all possibilities in the trellis given a certain assignment for a given variable $z_i$, its predecessors $z_{i-1}$ and $z_{i-2}$ must necessarily come before $z_i$, i.e., must have lower values.

• Assumption 2. For any assignment $z_i$, its successors are expected to be close in time, thus we allow a maximum number of $T$ frames between the successor pairs $(z_i, z_{i+1})$ and $(z_{i+1}, z_{i+2})$.

Thus, the expression in Eq. (6) is only calculated for values $(z_{i-1},z_{i-2})$ satisfying the following constraints:

$$\begin{aligned} \begin{array}{cccl} |t^{\prime }(z_{i}) - t^{\prime }(z_{i-1})|< T &{} \wedge &{} |t^{\prime }(z_{i-1}) - t^{\prime }(z_{i-2})|< T &{}\\ t^{\prime }(z_{i}) > t^{\prime }(z_{i-1}) &{} \wedge &{} t^{\prime }(z_{i-1}) > t^{\prime }(z_{i-2}). \end{array} \end{aligned}$$

(10)

These pruning measures decrease the complexity to $O(M{\cdot }S{\cdot }{T}^2)$, where $T$ is a small constant measured in the number of frames (we set $T=10$ in our experiments).

Note that our formulation does not require or assume any probabilistic modeling. At a first glimpse it could be suspected that the single-point-per-frame approach could be too limited to adequately capture the essence of an action sequence. Experiments have shown, however, that the single chain performs surprisingly well.

3.1.2 Single-Chain–Multiple-Points Model

Keeping multiple points per model frame and solving the exact minimization problem given in Eq. (1) is of polynomial complexity (see Appendix 2). However, the complexity is still too high even under the restrictions imposed by the meta-graph structure given in Fig. 2a. In this case, we approximate the matching algorithm by separating the set of discrete variables into two subsets and by solving for each subset independently.

We therefore propose the following (partially) greedy algorithm. Using Assumption 3, we first reformulate the energy function in Eq. (1) by splitting each node assignment variable $z_i$ into two subsumed variables $x_i$ and $y_{i,l}$, which are interpreted as follows: $x_i$, a frame variable, denotes the index of the scene frame that is matched to $i^{th}$ model frame, $i=1\dots \overline{M}$. Each model frame $i$ also possesses a number $M_i$ of node variables $\{y_{i,1},\ldots ,y_{i,M_i}\}$ where $y_{i,l}$ denotes the index of scene node that is assigned to $l^{th}$ node at frame $i$ in the model graph. Note that the number of possible values for variable $y_{i,l}$ depends on the value of $x_i$, since different model frames may contain different number of nodes. We can now separate frame assignments and node assignments into two consecutive steps:

• For each possible frame assignment $x_i$, we solve the node assignment variables $y_{i,l}$ with local geometric and appearance information extracted from the given frames.

• We calculate the solution for the frame assignment variables $x_i$ by minimizing the energy function. In this step, the node assignment variables $y_{i,l}$ are considered constant.

The node assignments in the first step can be done by minimizing appearance information alone, i.e., for each model node we select a scene node having minimal feature difference. To make this assignment more robust, we add deformation costs on in-frame triangles, which requires taking the decision jointly for all nodes of each model frame.

The second step, which optimally aligns the frames given the pre-calculated node assignments, is equivalent to the matching algorithm of the single point model described in Sect. 3.1.1. However, the graphical structure on which the algorithm operates is now the meta-graph (given in Fig. 2a) and not the model graph (given in Fig. 2b). In the multiple point case these two graphs are not identical. For this reason, the terms $U(\cdot )$ and $D(\cdot )$, originally defined on edges in the model graph, i.e., on triangles in space–time are now defined on edges in the meta graph, i.e., on sets of triangles in space–time, and the energy function is reformulated as follows:

$$\begin{aligned} E(x) = \sum _{i=1}^{\overline{M}} U^{*}(x_i) + \sum _{i=3}^{\overline{M}} D^{*}(x_i,x_{i-1},x_{i-2}). \end{aligned}$$

(11)

$U^{*}(\cdot )$ and $D^{*}(\cdot )$ can be set as sums over the respective model graph nodes/triangles corresponding to a given node/triangle in the meta graph:

$$\begin{aligned} \begin{array}{cccc} U^{*}(x_i)&{}=&{} \displaystyle { \sum ^{M_i}_{l=1}} &{} U(x_i,y_{i,l}) \\ D^{*}(x_i,x_{i-1},x_{i-2})&{}=&{} \displaystyle { \sum _{c\in (i,i-1,i-2)}} &{} D(x_c,y_c). \end{array} \end{aligned}$$

(12)

Here the expressions $U(\cdot )$ and $D(\cdot )$ are defined in Sect. 2 and in Appendix 1. The notation $x_c$ and $y_c$ is a slight abuse of notation and denotes the variables corresponding to the triangles linked to meta/frame triangle $(x_i,x_{i-1},x_{i-2})$.

The computational complexity of the global frame alignment step is identical to the single point model, apart from the sums over the nodes and triangles in Eq. (12). If the triangles of meta-triangle are defined as all possible combinations of the nodes of the three respective frames, complexity is increased by an additional factor of $R^3$ (see Table 3).

3.1.3 Multiple-Chains Model

An alternative way to approximate the model is by separating the full graph into a set of independent model graphs, each one featuring a single point per frame, i.e., similar to the type shown in Fig. 2c. As in Sect. 3.1.1, the exact global solution of each individual chain is computed.

In this case, the definitions for $U(z_i)$ and $D(z_i,z_{i-1},z_{i-2})$ are identical to the single-point model. The energy function to be minimized is a sum over the energy functions corresponding to the individual graphs (chains) as follows:

$$\begin{aligned} E^{*}(z) = \frac{1}{N} \sum _{k=1}^N E_k(z), \end{aligned}$$

(13)

where $N$ is the number of single chain models and $E_k(\cdot )$ is the kth single-chain–single-point energy function which is formulated in Eq. (5). In other words, we match each single-chain-single-point model to a scene sequence and average the resulting $N$ energies to reach a final decision. Notice that the computational complexity increases linearly with $N$ as compared to the single-chain model where $N$ is typically a small number (we set $N=2$ in our experiments).

3.2 Model Prototype Selection

In action recognition, intra-class variability can be large enough to impede good discrimination among different classes. For this reason, we decided to learn a reduced set of representative model graphs, called prototypes, for each action type, using Sequential Floating Forward Search (SFFS) method [40]. Thus irrelevant or outlier model graphs are removed from the training set. Briefly, we start with a full dictionary (all models) and proceed to remove conditionally the least significant models from the set, one at a time, while checking the performance variations on a validation set. Deletions that improve the performance are first accepted in this greedy search. After a number of removal steps, however, we reintroduce one or more of the removed models provided they improve the performance at that stage. We report the performance results of this scheme in Sect. 4.1.3.

4 Experimental Results

In this section, we demonstrate the viability of the proposed algorithm in two specific tasks: action recognition from video sequences and action recognition from sequences of articulated poses.

4.1 Action Recognition from Video Sequences

Given the training set of model action graphs, for a scene sequence to be tested, our strategy is to calculate the matching energy of each one of the model graphs with the set of interest points in the scene sequence, and infer the action class by the nearest neighbour classification rule.

4.1.1 Experimental Setup

We used two different methods to extract spatio-temporal interest points: 3D Harris detector [26] and 2D Gabor filters [9]. The detected interest points constitute the nodes of the graphs.

The well-known Harris interest point detector [21] was extended into the spatio-temporal domain by Laptev et al. [26]. The detector is based on the spatio-temporal second moment matrix of the Gaussian smoothed video volume [26]. To detect interest points, we search for the locations where second moment matrix contains three large eigenvalues, namely, strong intensity variation along three orthogonal spatio-temporal directions. In our experiments, we used the off-the-shelf code in [26].

As a second method, we use 2D Gabor filters as proposed by Bregonzio et al. in [9]. To detect interest points, we take the difference between the consecutive frames and convolve the resulting image with a bank of 2D Gabor filters having different orientation and scale parameters pairs. The responses are calculated for different parameter pairs and then summed up. Spatio-temporal interest points are located at local maxima of the resulting function. In our experiments, we used the publicly available code from [9].

For appearance features, we used the well known histogram of gradient and optical flows (HoG+HoF) extracted with the publicly available code from [26]. The local neighborhood of a detected point is divided into a grid with $M\times M\times N$ (i.e., $3\times 3\times 2$) spatio-temporal blocks. For each block, 4-bin gradient and 5-bin optical flow histograms are computed and concatenated into a 162-length feature vector.

The proposed matching algorithms have been evaluated on the widely used public KTH database [44]. This database contains $25$ subjects performing $6$ actions (walking, jogging, running, handwaving, handclapping and boxing) recorded in four different scenarios including indoor/outdoor scenes and different camera viewpoints, totally $599$ video sequences. Each video sequence is also composed of three or four action subsequences, resulting in 2391 subsequences in total. The subdivision of the sequences we used is the same as the one provided on the official dataset website [24]. In our experiments, we have used these subsequences to construct the model graphs. Each subsequence consists of 20–30 frames, and we made sure that each frame contains at least one or more salient interest points.

All experiments use the leave-one-subject-out (LOSO) strategy. Action classes on the unseen subjects are recognized with a nearest neighbor classifier. The distance between scene and model prototypes is based on the matching energy given in Eq. (1). However, experiments have shown that the best performance is obtained if only the appearance terms $U(\cdot )$ are used for distance calculation instead of the full energy in Eq. (1). This results in the following two step procedure:

• 1. Node correspondences: The correspondence problem is solved using the total energy in Eq. (1), that is the sum of $U(\cdot )$ and $D(\cdot )$ terms. This step provides a solution for the hidden variables $z$, that is, frame and node assignments.

• 2. Decision for action class: The distance between model and scene graphs is calculated using only the $U(\cdot )$ term evaluated on the assignments calculated in the first step, i.e., on solutions for variables $z$.

Results have been analyzed in terms of three criteria: (i) performance of the various graphical structures with different number of interest points per frame; (ii) impact of prototype selection; and (iii) computational efficiency. These will be detailed in the following sections.

4.1.2 Choice of Graphical Structure

The three graphical structures introduced in Sect. 3.1 have been evaluated on the dataset:

• Single-chain-single-point model: The interest points are detected by the 3D Harris detector [26]. Each frame of a model sequence is represented by its single most salient point. There are no such restrictions on the scene sequences.

• Single-chain-multiple-points model: The 3D Harris detector results in very few interest points, i.e., the number of points varies between $1$ and $4$ per frame on average. It constitutes a good choice, if our only goal is to select a single point per frame. However, in the case of multiple-points model, it is not appropriate. We therefore used 2D Gabor filters [9] and extracted at least $20$ points per frame. To eliminate irrelevant points, we fitted a bounding box on the human body and applied Canny edge detector to choose the points that are on or closer to the human silhouette. Finally, out of all available scene points, $N=3$ points per frame are selected to be used in the model sequence. To better capture the global property of the human body, these three points are selected so as to constitute the biggest possible triangle. There are no restrictions on the scene sequences, only the points outside the bounding box are eliminated.

• Multiple-chains model: We again used 2D Gabor filters [9] to extract interest points. N single-chain-single-point models are matched, separately, against the set of scene nodes, and a final decision is obtained by averaging the matching energies over the chains. We have chosen $N=2$.

In Table 1, the results for different graphical structures are given without the prototype selection method. The best recognition performance of the proposed scheme is found to be $89.2~\%$ under the single-chain model. Looking at the confusion matrices in Table 1, it can be observed that major part of the errors is due to confusion between the jogging and running classes, which are indeed quite similar.

Table 1 Confusion matrices before prototype selection

At first sight, it might come as a surprise that the single-point model performs slightly better than the two alternative models using multiple points per frame. One explanation why the two multiple point models do not perform any better than the single point method lies in the choice of interest points, that is, the Gabor set in lieu of the Harris set. In fact, when the single-point-single-chain method is tested with the Gabor features, the performance stalls at $85.6$ %, while it achieves $89.2$ % with Harris features. Furthermore, the single-chain-multiple-point model does not fully exploit the rich space–time geometry of the problem. In fact, we force this model to choose the triple of interest points per frame (that will constitute one of the nodes of its hyper-graph) all from the same model frame and the same scene frame. Even though the subsequent hyper-graph matching uses the space–time geometry, it cannot make-up for the lost flexibility in the in-frame triple point correspondence stage.

The multiple-chain model, on the other hand, is similar in nature to the single-chain model as it consists of chains successively established with mutually exclusive model nodes (scene nodes can be re-used). Individual performance of chains are $85.6$ and $84.6$ %, respectively. The additional information content gathered by the second chain seems to translate into slightly better performance, which increases to $86.6$ % when we do score fusion (average the energies). A plausible explanation is that two models, single-chain and multiple-chain, basically differ in their interest point detection methods used, 3D Harris detector [26] and 2D Gabor filters [9], respectively, which is noisy for multiple-chains model. However, this gap is compensated by the prototype selection algorithm as shown in the following section.

4.1.3 Prototype Selection

We conjectured that the discrimination power can be improved by judicious selection of prototypes, in effect removing the noisy prototypes. We learned a set of discriminative models by the prototype selection method. We used the same data partition protocol $(8/8/9)$ given in [44]: Model graph prototypes are created from the training subjects and the prototype selection is optimized over the validation set. We have determined the optimal set of prototypes by a grid search where the increments were in groups of $5$ graphs. In Table 2, we have presented our results after prototype selection. For example, for single-chain-single-point model, SFFS yielded $50$ models out of the initial $750$ ones as the best subset of model graph prototypes. Learning prototypes increased the test performance by $2$ % points, up to $91$ %. As expected, handwaving-handclapping and jogging-running sequences benefit the most from dictionary learning (see Table 2). Similar observations can be made for single-chain-multiple-points and multiple-chains model, where the number of model graph prototypes are reduced to $250$ and $50$ from $750$, respectively.

Table 2 Confusion matrices after prototype selection

Sample matched model and scene sequences are illustrated in Fig. 4 where in each sub-figure the left image is from the model sequence and the corresponding matched scene frame is given on its right. One can observe that the proposed method is also successful at localizing a model action sequence in a much longer scene sequence. We illustrate in Fig. 4a–c successfully recognized actions handwaving, handclapping, walking, and in Fig. 4d a misclassification case, where running was recognized as jogging.

Fig. 4

Examples for matched sequences. a Model: Handclap (first column), Scene: Handclap (second column); b Model: Handwave, Scene: Handwave; c Model: Walk, Scene: Walk; d Model: Jog, Scene: Run. Here, a, b, c show a case of correct recognition, while b is a case of misclassification

4.1.4 Discussions and Comparison with State-of-the-Art

Table 3 summarizes our experimental results and compares run times of each graphical structures. Each model allows performing exact minimization with complexity that grows only linearly in the number of model frames and the number of scene frames, and grows exponentially in the temporal search range and the number of interest-points per scene frame. Note that the complexity of the proposed approaches is very much lower than the complexity of the brute force approach (given by $O(M {\cdot } S^M {\cdot } |{\fancyscript{E}}|)$). The run times given in Table 3 do not include interest point detection and feature extraction, but these are negligible compared to the matching requirements.

Table 3 Summary of the experimental results

We would like to point out that although many research results have been published on the KTH database, most of these results cannot be directly compared due to their differing evaluation protocols, as has been indicated in the detailed report on the KTH database [18]. Nevertheless, for completeness we give our performance results along with those of some of the state-of-the-art methods as reported in the respective original papers. Details of these methods were discussed in Sect. 1.4. In Table 4, we report average action recognition performance and computation time of the compared methods. Although methods to calculate run times and protocols employed differ between the papers, this table is intended to give an overall idea. We claim that our method has significantly lower complexity compared to the state of the art, the difference being several orders of magnitude, with performances which are almost comparable. In particular, we can process a single frame in 3.5 ms (0.0035 s). For example, the method proposed by Ta et al. [48] is the closest approach to our method. They also used graph matching but based on spectral methods, so that they do approximate matching of the exact problem. Recall that ours was the exact minimization of the approximated graph problem. As can be seen, our approach shows a competitive performance but with the advantage of much lower computational time.

Table 4 Comparison with the state-of-the-art methods on the KTH database (LOOCV = Leave-one-out-cross validation)

4.1.5 A Real-Time GPU Implementation

A GPU implementation enables real-time performance on standard medium end GPUs, e.g., a Nvidia GeForce GTS450. Table 5 compares single-chain-single-point model run times of the CPU implementation in Matlab/C and the GPU implementation running on different GPUs with different characteristics, especially the number of calculation units. The run times are given for matching a single model graph with 30 nodes against blocks of scene video of different lengths. If the scene video is segmented into smaller blocks of 60 frames, which is necessary for continuous video processing, real time performance can be achieved even on the low end GPU model. With these smaller chunks of scene data, matching all 50 graph models to a block of 60 frames (roughly 2 s of video) takes about $3$ ms per frame regardless of the GPU model.

Considering scene video in smaller groups of frames is necessary for continuous video processing. Thus, for example, if we take chunks of $60$ scene frames (roughly $2$ s of video), matching all $50$ graph models to them takes about $3$ ms per frame. Thus real-time performance can be achieved even on the low-end GPU model. The processing time of $3$ ms per frame is much lower than the requirement for real time processing, which is $40$ ms for video acquired at $25$ frames per second. With the additional processing required to treat overlapping blocks, the runtime actually increases to $6$ ms per frame. Note that some of the best methods for KTH require order of seconds of processing per frame.

Table 5 Run-times in milliseconds for two different GPUs and for two different scene block sizes

4.2 Action Recognition from Articulated Pose

In this section, we present results from a different problem, that is, action recognition from articulated poses. We use depth sequences recorded with a Kinect camera [37], which yields the coordinates of the tracked skeleton joints [47].

4.2.1 Experimental Setup

We adapt the single-chain-multiple-points-model in Sect. 3.1.2 for aligning the tracked skeleton sequences [12]. In this context, each action sequence is structured into a single chain graph where the frame variables $x_i$ coincide with the frames (skeletons) and each $x_i$ assumes a number of node variables $y_{i,l}$, namely skeleton joints. As illustrated in Fig. 5, in this case, the graphical structure models the temporal relationship of three consecutive skeleton joints, all of the same type. Since the Kinect system provides the positions of the skeleton joints, the problem of assigning the node variables has already been solved. However, the problem of which model frame to match with which scene frame remains still very challenging in nature due to noisy, missing or occluded joints. Graph matching offers a robust and flexible solution to the sequence alignment problem in the presence of these disturbances.

Fig. 5

Each triangle models the spatial relationship between three consecutive skeletons in the triangular structure graph

In our experiments, we consider $15$ joints and ignore the joints related to hand and foot, since these are more prone to errors and occlusions. Prior to any feature extraction, we applied a preprocessing stage to render each skeleton independent from position and body size, and also to mitigate possible coordinate outliers. Following the preprocessing stage, we extract two types of pose descriptors. The first descriptor considers the angle subtended by that joint and the orientation angle of the plane formed by the three joints. To that effect, for each joint, we consider its two adjacent joints, and calculate azimuth and elevation angles. The second descriptor consists of the Euclidean distance between joint position pairs, that is $15\times (15-1)/2 = 95$ measurements. The body pose descriptor, in the ith frame, is the concatenation of the angle-based and distance-based pose descriptor vectors.

The proposed framework was tested on MSR Action 3D dataset [32] and WorkoutSu-10 Gesture dataset [39]. In MSR Action 3D dataset [32], there are 20 actions performed by 10 subjects. Each subject performs each action 2 or 3 times, resulting in 567 recordings in total. However, we have used 557 recordings in our experiments as in [54]. Each recording contains a depth map sequence with a resolution of $640\times 480$ and the corresponding coordinates of the $20$ skeleton joints. Actions are selected in the context of interacting with game consoles, for example, arm wave, forward kick, tennis serve etc. The second dataset, that is Workout SU-10 Gesture dataset [39] has the same recording format as the MSR Action 3D dataset. However, the context is physical exercises performed for therapeutic purposes. Lateral stepping, hip adductor stretch, freestanding squats, oblique stretch etc. can be given as examples of exercises (actions). There are 15 subjects and 10 different exercises. Each subject repeats an exercise 10 times, resulting in 1500 action sequences in total. In our experiments, we used 600 sequences for training and tested our algorithm on the unseen part of the dataset (we ignored one subject, and tested on 800 sequences).

4.2.2 Experimental Results

We used nearest neighbour classifier where the distance measure was the matching energy and the prototype selection approach in [12]. We obtained $72.9$ % performance on the more challenging and noisier MSR Action 3D dataset and $99.5$ % performance on Workout on the SU-10 Gesture datasets. These results are given in Table 6.

Table 6 Recognition performances (%) on MSR: MSR Action 3D Dataset and WSU: WorkoutSU Gesture datasets

4.2.3 Comparison with State-of-the-Art Methods

For the sake of completeness, we compared our algorithm with the state-of-the-art methods [32, 39, 53]. While Li et al. [32] proposed a method in the spirit of Bag of 3D points to characterize the salient poses, Negin et al. [39] and Venkataraman et al. [53] proposed a correlation-based method. However, the main drawback of the correlation approach is that it does not incorporate time warping.

In Table 7, we tabulated our results on MSR Action 3D Dataset [32]. The performance is computed using a cross-subject test setting where half of the subjects were used for training, and testing was conducted on the unseen portion of the subjects. Li et al. [32] proposed to divide the dataset into three subsets in order to reduce the computational complexity during training. Each action set (AS) consists of eight action classes similar in context. We repeated the same experimental setup $100$ times where, each time, we randomly selected five subjects for training and used the rest for testing. Finally, we reported the average recognition rate over all repetitions in Table 7. As seen in Table 7, the proposed method performs better in AS1 and AS2, and has a competitive performance in AS3. Our proposed method is more successful in overall performance, especially in discriminating actions with similar movements.

Table 7 Recognition performances (%) for MSR Action 3D Dataset [32] in cross-subject test setting

We also compared our results on Workout SU-10 Gesture dataset with the method proposed in [39]. For a fair comparison, we used the same experimental setup, namely, cross-subject test setting where we used the same six subjects for training and the same remaining six subjects for testing as in [39]. Our recognition performance is found to be $96.1$ and $99.6$ % before and after prototype selection, respectively. Our method with graph mining scheme performs better than Negin et al. [39], who obtained $98$ % performance.

5 Discussions and Conclusions

We have first addressed the graph matching problem, which is known to be NP-complete, and showed that, if one takes into consideration the characteristics of spatio-temporal data generated from action sequences, the point set matching problem with hyper-graphs can be solved exactly with bounded complexity. However, the complexity is still exponential in nature, albeit with a small exponent, nevertheless it is still not practical. Second, we have considered an approximation to the graph search by limiting model nodes and/or scene node correspondences, and this special graphical structure allows performing exact matching with complexity that grows only linearly in the number of model nodes and the number of scene nodes.

There is a relationship of the proposed energy function to the energy functions of graphical models, in particular MRFs or CRFs. The junction tree algorithm [27] can in principle calculate the exact solution for any Maximum a Posteriori (MAP) problem on MRFs through message passing, with a computational complexity which is exponential on the number of nodes in the largest clique of the graph after triangulation. It can, in principle, also be applied to the situation described in this paper. However, our proposed solution has two important advantages. First, the junction tree algorithm takes into account the conditional independence relationships between the random variables of the problem (which are coded in the topology of the graph) to derive an efficient inference algorithm. Exploiting Assumption 3, however, allows us to impose restrictions on the domains of random variables by restricting the specific admissible combinations of random variables. The junction tree algorithm does not prune these combinations and is therefore of sub-optimal complexity. Secondly, the junction tree algorithm requires a preceding triangulation of the graph, which takes as input the hyper-graph converted into a graph, each hyper-edge being converted into a clique of size 3. The triangulation step will create a chordal graph from the original graph, which can add edges to the graph. This can increase the number of nodes in the maximal clique, and therefore the complexity of the algorithm. Recall that optimal graph triangulation is an open problem for which no exact solution exists.

As a proof of concept of our graph matching algorithm, we applied it to human action recognition problem in two different settings. The proposed algorithm has shown competitive performance vis-à-vis the state-of-the-art in the literature; more importantly, it has the advantage of very low execution time, several orders of magnitude less than its nearest competitor (see Table 4).

We should remark that, for cluttered motion scenes, the graph-based action recognition strategy is more dependent upon scene segmentation as compared to methods like Bag of Visual Words (BoW). It will be of interest to explore the coupling of the object segmentation with graph building for robustness of the method.

In this work, we have used STIPs for matching two action sequences. However, our graphical structure enables to replace the interest points by high-level features such as the joints of the human skeleton [47]. Hence, a potential research direction will be to investigate the use of pairwise spatio-temporal features as in [6, 49] or human body parts [8, 16].

Appendices

Appendix 1: A Objective Function

The graph energy function

$$\begin{aligned} E(z) = \lambda _1 \sum _{i=1}^{M} U(z_i) + \lambda _2 \sum _{(i,j,k)\in {\fancyscript{E}}} D(z_i,z_j,z_k) \end{aligned}$$

as defined in Eq. (1) consists of two terms. The $U(\cdot )$ term is defined as the Euclidean distance between the appearance features of assigned points in the case of a candidate match, and it takes a penalty value $W^d$ for dummy assignments in order to handle situations where a model point cannot be found in the scene:

$$\begin{aligned} U(z_i)=\left\{ \begin{array}{ll} W^d&{} \mathrm {if} z_i=\epsilon ,\\ ||f_i - f^{\prime }_{z_i}||&{} \mathrm {else}, \\ \end{array}\right. \end{aligned}$$

(14)

$f_i$ and $f^{\prime }_{z_i}$ being respectively the feature vector of model point $i$ and the feature vector of scene point $z_i$.

The $D$ term penalizes geometric shape discrepancy between triangles of node triples, and hence it is based on angles. Since our data is embedded in space–time, angles include a temporal component not related to scale changes induced by zooming. We therefore split the geometry term $D$ into a temporal distortion term $D^t$ and a spatial geometric distortion term $D^g$:

$$\begin{aligned} D(z_i,z_j,z_k) = D^t(z_i,z_j,z_k) + \lambda _3 D^g(z_i,z_j,z_k) \end{aligned}$$

(15)

where the temporal distortion $D^t$ is defined as truncated time differences over two pairs of nodes of the triangle:

$$\begin{aligned} D^t(z_i,z_j,z_k)&= \left\{ \begin{array}{lll} W^t &{} \mathrm {if} &{} \Delta (i,j) > T \ \vee \\ &{}&{} \Delta (j,k) > T, \nonumber \\ \Delta (i,j) + \Delta (j,k) &{} \mathrm{else } \\ \end{array}\right. \end{aligned}$$

(16)

$$\begin{aligned} \Delta (i,j)&= |(t(i)-t(j)) - (t^{\prime }(z_i)-t^{\prime }(z_j))|. \end{aligned}$$

(17)

Here, $\Delta (i,j)$ is the time distortion due to the assignment of model node pair $(i,j)$ to scene node pair $({z_i},{z_j})$, and $T$ bounds the node pair differences in time, e.g., in frame number. The search interval of extent $T$ enables inherently dynamic time warping during graph matching. The model node pairs should not be too close while scene nodes are far apart, and vice versa, they should not be too far apart while scene nodes are close by. Finally, $D^g$ is defined over differences of angles:

$$\begin{aligned} D^g(z_i,z_j,z_k) =\left| \left| \begin{array}{l} a(i,j,k)-a^{\prime }(z_i,z_j,z_k) \\ a(j,i,k)-a^{\prime }(z_j,z_i,z_k) \\ \end{array}\right| \right| . \end{aligned}$$

(18)

Here, $a(i,j,k)$ and $a^{\prime }(i,j,k)$ denote the angles subtended at point $j$ for, respectively, model and scene triangles indexed by $(i,j,k)$. Note that, for an exact notation, one has to denote $U(\cdot )$ and $D(\cdot )$ as $U_i(\cdot )$ and $D_{ijk}(\cdot )$ since these terms also depend on the appearance features and angles. However, for ease of notation, we absorbed these variables into $z$ variables.

In our experiments, parameters have been fixed or estimated as follows. The penalty parameter $W^d$ should theoretically be higher than the average energy of correctly matched triangles and lower than the average energy of incompatible triangles. We define $W^d$ as the mean value of all, compatible or incompatible, triangle matching energies. The weighting parameters are set so that each distortion measure has the same range of values: $\lambda _1=0.6$, $\lambda _2=0.2$, $\lambda _3=5$, $T=10$, and $W^t=20$.

Appendix 2: Matching in Space–Time with General Graphs

Assumption 3 implies that a correct sequence match is an injective map, that is, it consists of a collection of single model-frame-to-scene-frame matches. We therefore first reformulate the energy function in Eq. (1) by splitting each variable $z_i$ into two subsumed variables $x_i$ and $y_{i,l}$, which are interpreted as follows: $x_i$, a frame variable, denotes the index of the scene frame that is matched to $i$th model frame. The number of model frames and scene frames are denoted as $\overline{M}$ and $\overline{S}$, respectively. Each model frame $i$ also possesses a number $M_i$ of node variables $y_{i,1},\dots ,y_{i,M_i}$, where $y_{i,l}$ denotes the index of scene node that is assigned to lth node at frame $i$ in the model graph. Note that the number of possible values for variable $y_{i,l}$ depends on the value of $x_i$, since different frames may contain different number of nodes.

The objective remains to calculate the globally optimal assignment of all nodes of the graph, i.e., the optimal values for all variables $x_i$ and $y_{i,l}, \forall i \ \forall l$. In other terms, a node of a given frame $i$ is not necessarily matched to the (locally only) best fitting node in the frame-to-frame sense. This will be detailed in the rest of this section.

For convenience, we will also simplify the notation by representing a hyper-edge (the corresponding frame indices and node indices) as $c$ and the corresponding variables as $(z_c, y_c)$. In other words, $(z_c)$ implies a triple assignment of model frames (say, $i,j,k$), to scene frames, and $(y_c)$ implies the connection of the three model nodes to the three frames $(z_c)$. For ease of notation, we also drop the parameters $\lambda _1$ and $\lambda _2$ which can be absorbed into the potentials $U$ and $D$.

The reformulated energy function is now given as:

$$\begin{aligned} E(x,y)= \displaystyle { \sum _{(i,l)\in \overline{M} \times M_i}} U(x_i,y_{i,l}) + \displaystyle { \sum _{c\in {\fancyscript{E}}}} D(x_c, y_c). \end{aligned}$$

(19)

We now introduce a decomposition of the set of hyper-edges ${\fancyscript{E}}$ into disjoint subsets ${\fancyscript{E}}^{i}$, where ${\fancyscript{E}}^{i}$ is the set of all hyper-edges which contain at least one node with temporal coordinate equal to $i$ and no node has a higher (later) temporal coordinate. It is clear that the set of all possible sets ${\fancyscript{E}}^{i}$ forms a complete partition of ${\fancyscript{E}}$, i.e. ${\fancyscript{E}} = \bigcup _{i=1}^{\overline{M}} {\fancyscript{E}}^{i}$. We can now exchange sums and minima according to this partitioning:

$$\begin{aligned} \begin{array}{ll} \displaystyle {\min _{x,y} E(x,y) }&{}\\ =\displaystyle {\min _{x_1;y_{1,1},\dots ,y_{1,M_1}}}&{}\Bigg [\displaystyle { \sum _{l=1}^{M_1} U(x_1,y_{1,l}) } + \displaystyle { \sum _{c\in {\fancyscript{E}}^1} D(x_c, y_c) + }\\ \displaystyle {\min _{x_2;x_{2,1},\dots ,y_{2,M_2}}} &{}\Bigg [\displaystyle {\sum _{l=1}^{M_2}U(x_2,y_{2,l}) + \sum _{c\in {\fancyscript{E}}^2} D(x_c, y_c) +}\\ &{} \vdots \end{array} \end{aligned}$$

$$\begin{aligned} \begin{array}{ll} \displaystyle {\min _{x_{M};y_{M,1},\dots ,y_{M,M_{\overline{M}}}}}&\Bigg [\displaystyle {\sum _{l=1}^{M_{\overline{M}}} U(z_{M},y_{M,l}) + \sum _{c\in {\fancyscript{E}}^{{\overline{M}}}} D(z_c, y_c)} \Bigg ]\dots \Bigg ] \end{array}\nonumber \\ \end{aligned}$$

(20)

Hyper-edges have variable temporal spans, which makes it impossible to define a recursion scheme with regular structure. We therefore define the concept of the reach $\mathcal {R}^i$ of frame $i$, which consists of the set of edges which reach into the past of frame $i$ and which are also part of $i$ or of its future:

$$\begin{aligned} {\mathcal {R}}^{i} = \left\{ c \in {\fancyscript{E}} : [ \mathrm {min} ^{\langle t\rangle }(c) < i ] \wedge [ \mathrm {max} ^{\langle t\rangle }(c) \ge i ] \right\} \end{aligned}$$

(21)

where $\mathrm {min} ^{\langle t\rangle }(c)$ and $\mathrm {max} ^{\langle t\rangle }(c)$ are, respectively, the minimum and the maximum temporal coordinate of the nodes of edge $c$. Note that, by definition ${\fancyscript{E}}^i \subseteq \mathcal {R}^i$.

We also introduce the expression ${\mathcal {X}}^i$ for the set of all variables $x_k$ or $y_{k,l}$ involved in the reach $\mathcal {R}^i$:

$$\begin{aligned} {\mathcal {X}}^i =\begin{array}{ll} \left\{ (x_k,y_{k,l}): [\exists q,r: (k,q,r) \in c] \wedge [c \in \mathcal {R}^{i} ] \right\} . \end{array} \end{aligned}$$

(22)

Finally, the set of variables ${\mathcal {X}}^i$ that belongs to the frames before $i$ is denoted as ${\mathcal {X}}_-^{i}$

$$\begin{aligned} {\mathcal {X}}_-^{i} = \ \{ (z_k,y_{k,l}) \in {\mathcal {X}}^{i} : k < i\}. \end{aligned}$$

(23)

Now, a general recursive calculation scheme for Eq. (20) can be devised by defining a recursive variable $\alpha _i$ which minimizes the variables of a given frame as a function of the reach variables before it as follows:

$$\begin{aligned} \alpha _i ({\mathcal {X}}_-^{i})&= \displaystyle { \min _{x_i;y_{i,1},\dots ,y_{i,M_i}} } \Bigg [ \displaystyle { \sum _{l=1}^{M_i} U(x_i,y_{i,l})} + \displaystyle { \sum _{c\in {\fancyscript{E}}^{i}} D(x_c, y_c) }\nonumber \\&\qquad \qquad \qquad \quad + \alpha _{i+1} ({\mathcal {X}}_-^{(i+1)})\Bigg ]. \end{aligned}$$

(24)

It is easy to see that Eq. (24) is valid, if the following lemma holds:

Lemma 1

Consider a general hyper-graph ${\mathcal {G}}=\{{\fancyscript{V}},{\fancyscript{E}}\}$ with no specific restrictions on the graphical structure. Consider the sets of discrete variables ${\mathcal {X}}_-^{i}$, each set being associated to a frame $i$. Then, the following relation holds:

$$\begin{aligned} {\mathcal {X}}_-^{i+1} \subseteq \ \bigg ( \ {\mathcal {X}}_-^{i} \cup \{x_i;y_{i,1},\dots ,y_{i,M_i}\} \ \bigg ) \end{aligned}$$

(25)

Proof

The left hand side and the right hand side of Eq. (25) involve edges from the two sets $\mathcal {R}^{i+1}$ and $\mathcal {R}^{i}$. From Eq. (21), we can see that the only triangles which are part of $\mathcal {R}^{i+1}$ and which are not part of $\mathcal {R}^{i}$ are the ones whose lowest temporal coordinate is $i$. The question is whether any variables of these triangles may be in ${\mathcal {X}}_-^{i+1}$ but not in $( {\mathcal {X}}_-^{i} \cup \{x_i;y_{i,1},\dots ,y_{i,M_i}\} )$. From Eq. (23), since we get that no variables from frames later than $i$ are part of ${\mathcal {X}}_-^{i}$, this concerns only variables from frame $i$ itself, which are explicitly included in the right hand side of Eq. (25). $\square$

Illustrative example of the recursion scheme. Figure 6 is a simple example illustrating how the recursion scheme works. The vertical blue bars correspond to the frame instances. Our model graph assumes five frame variables $x_{i}$, each associated with one or more node variables $y_{i,l}$. The recursion starts from the last frame $i=5$ where we define the respective reach variable and the assignment variable sets as $\mathcal {R}^5=\{(x_3,x_4,x_5)\}$, ${\mathcal {X}}^5=\{(x_3,y_{3,1}),(x_4,y_{4,1}),(x_5,y_{5,1}) \}$ and ${\mathcal {X}}_-^5=\{(x_3,y_{3,1}),(x_4,y_{4,1}) \}$. Thus, we obtain

$$\begin{aligned} \alpha _5({\mathcal {X}}_-^5){=}\displaystyle { \min _{x_5,y_{5,1}}} \Bigg [\!U(x_5,y_{5,1}) {+} D(x_3,y_{3,1},x_4,y_{4,1},x_5,y_{5,1})\!\Bigg ]. \end{aligned}$$

And the recursion continues as follows: For $i=4$, we can set $\mathcal {R}^4{=}\{(x_2,x_3,x_4),(x_3,x_4,x_5)\}$, ${\mathcal {X}}^4{=}\{(x_2,y_{2,1}),(x_3,y_{3,1}), (x_4,y_{4,1}),(x_5,y_{5,1})\}$ and ${\mathcal {X}}_-^4=\{(x_2,y_{2,1}),(x_3,y_{3,1}) \}$, the recursion iterates by calculating $\alpha _4$ from $\alpha _5$ as below

$$\begin{aligned} \begin{array}{ll} \alpha _4({\mathcal {X}}_-^4)&{}=\displaystyle { \min _{x_4,y_{4,1}}} \Bigg [U(x_4,y_{4,1}) \\ &{} \qquad \qquad + \ D(x_2,y_{2,1},x_3,y_{3,1},x_4,y_{4,1}) {+} \alpha _5({\mathcal {X}}_-^5)\! \Bigg ]. \end{array} \end{aligned}$$

Finally, for $i=3$, we obtain

$$\begin{aligned} \begin{array}{ll} \alpha _3({\mathcal {X}}_-^3){=}\displaystyle { \min _{x_3,y_{3,1}}} &{} \Bigg [U(x_3,y_{3,1}) {+} D(x_1,y_{1,1},x_2,y_{2,1},x_3,y_{3,1}) \\ &{}\; {+} \ D(x_2,y_{2,2},x_2,y_{2,3},x_3,y_{3,1}) {+} \alpha _4({\mathcal {X}}_-^4) \Bigg ], \end{array} \end{aligned}$$

where $\mathcal {R}^3=\{(x_1,x_2,x_3),(x_2,x_3,x_4),(x_3,x_4,x_5)\}$, ${\mathcal {X}}^3=\{(x_1,y_{1,1}),(x_2,y_{2,1:3}),..,(x_5,y_{5,1}) \}$ and ${\mathcal {X}}_-^3=\{(x_1,y_{1,1}), (x_2,y_{2,1:3}) \}$. Note that we can write these relations because Eq. (25) is always satisfied.

Fig. 6

An example hyper-graph. Vertical blue bars correspond to the frames. The recursion starts from the last frame $i=5$ and iterates by calculating $\alpha _i$ from $\alpha _{i+1}$ where the evolution of the iteration is illustrated with solid lines. For simplicity, node variables $y_{i,l}$ are absorbed into the frame variables $x_i$. At each step, a minimum is calculated over all variables of frame $i$ for all possible values of the variables in ${\mathcal {X}}_-^{i}$

1.1 Computational Complexity

The recursion starts at the last frame $i=\overline{M}$ and iterates by calculating $\alpha _i$ from $\alpha _{i+1}$. At each step, a minimum is calculated over all variables of frame $i$ for all possible values of the variables in ${\mathcal {X}}_-^{i}$. The computational complexity can thus be bounded by the maximum number of variables $x$ and $y$ in $( \ {\mathcal {X}}_-^{i} \cup \{x_i;y_{i,1},\dots ,y_{i,M_i}\} \ )$, which are denoted by $|{\mathcal {X}}^{i^{*}}_x|$,$|{\mathcal {X}}^{i^{*}}_y|$ in the following expression:

$$\begin{aligned} O \left( {\overline{M}} {\cdot } {\overline{S}}^{|{\mathcal {X}}^{i^{*}}_x|} {\cdot } {R}^{|{\mathcal {X}}^{i^{*}}_y|} \right) \end{aligned}$$

(26)

where $\overline{M}$ and $\overline{S}$ are the number of model and scene frames, $R$ is the maximum number of nodes per frame in the scene sequence. The complexity is thus very much lower than the complexity of the brute force approach, which is given by $O(M S^M |{\fancyscript{E}}|)$. Let us recall that $S$ is the total number of nodes in the scene and $M$ is the total number of nodes in the model, i.e. $S \gg \overline{S}$ and $S \gg R$. Furthermore, both $|{\mathcal {X}}^i_x|$ and $|{\mathcal {X}}^i_y|$ are bounded and in fact quite small when the graph is constructed from proximity constraints. This concludes the proof of Theorem 1. However, for general graphs, it is still too high for practical usage. In Sect. 3.1, we therefore introduce an approximation to the graphical structure which further decreases complexity.