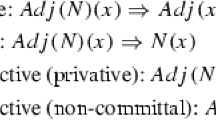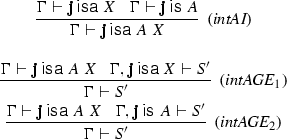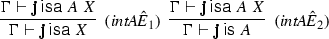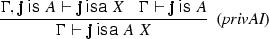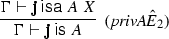A Proof-Theoretic Semantics for Adjectival Modification

Abstract

The paper introduces a proof-theoretic semantics (PTS) for adjectival modification (adjective–noun combination) as an alternative to the traditional model-theoretic semantics basing meaning on truth-conditions. The paper considers the proof-theoretic meaning of modification by means of the three traditional adjective classes: intersective, subsective and privative. It does so by introducing a meaning-conferring natural-deduction proof system for such modification. The PTS theory of meaning is not polluted by ontological commitments, for example, a scale for beauty and a yardstick for being beautiful. It only uses syntactic artefacts of the proof language. The paper also defines, by suitable rules, iterated modification, shedding light on the relationship between iteration and adjectival classes. Modification via coordinated adjectives is covered too. An appendix delineates briefly the main ingredients of PTS.

1 Introduction

The purpose of this paper is to provide a proof-theoretic semantics (PTS) for adjectival modification by means of (a subclass of the) adjectives in natural language (NL, here, English). PTS is a theory of meaning [see its exposition in Francez (2015d)] conceived as an alternative to the traditional, Montague-style, model theoretic semantics (MTS) based on meaning as truth-conditions in arbitrary models. I will not attempt here either to motivate or to defend PTS against MTS, tasks taken over in Francez (2015d), Francez and Dyckhoff (2010a). Here I just extend its scope of applicability to adjectival modification, and all considerations involve the latter only. This application of PTS for defining the meaning of adjectival modification is an innovation of this paper.

I would like to stress that I am dealing with the meaning of adjectival modification (adjective–noun combination), and not with the actual meanings of the adjectives themselves. In the literature, often there is no sharp distinction between the meaning of the adjective–noun combination and the meanings of the adjectives themselves. The main linguistics resource I rely on for a typology (in an idealised form) is Morzycki (2015), a comprehensive recent account on modification in NL, within the more standard MTS. The principles of PTS (in particular as applied to NL) can be found in Francez (2015d), as well as in Francez and Dyckhoff (2010a), Francez and Ben-Avi (2015e) (Introduction sections), and are delineated in “Appendix” to this paper. The language fragment used as a basis for this study is delineated in Sect. 2.

The induced PTS for adjectives themselves is partial only, capturing just those aspects of adjectival meaning arising from the way adjectives combine with nouns and with themselves. In particular, no specific lexical meaning or world knowledge will be considered except for the determination of the class of adjectives to which a given adjective belongs. For example, the fact that being red ¹ (all over) and being blue (all over) are mutually exclusive is not accounted for, as this fact depends on the actual meaning of color adjectives and world knowledge about colors. Also, the fact that alleged has a modal character is not accounted for either. Similarly, selectional restrictions are not incorporated, and a clever chair is not excluded. Finally, no contextual meaning variation is considered here. See Francez and Wieckowski (2014), Francez (2014b) for examples of proof-theoretic semantic for two other contextual meaning variations.

The main logical tool to be applied in the analysis of the combination of adjectives and their modified nouns is a representation of this combination as a family of products (of which the “usual” conjunction is a special case), the definition of which relies on sub-structurality in the logic used. In a companion paper Francez (2015b), two new products (called semi-fusions), not discussed in the logic literature, are identified and defined for the task at hand. Another mathematical view of adjective–noun combination, presenting the (extensional) adjective meaning as an operator acting on the noun meaning, can be found in Bankston (2003).

2 A Small NL Fragment

The NL fragment I consider is a kind of a minimal fragment that suffices to accommodate the discussion of adjective–noun modification and its meanings. It is a simplification of the fragment in Francez and Dyckhoff (2010a). The fragment contains (singular, count) nouns, ranged over by X, both simple (lexical) and compound (modified), intransitive verbs, ranged over by P, and the two determiners every and some, forming determiner phrases ($\textit{dps}$) when combined with nouns. Adjectives are ranged over by A. The omission of transitive verbs allows ignoring the quantifier-scope ambiguity, orthogonal to the current concerns. In addition, there are two copulas, isa and is.

Typical sentences, ranged over by S, have the forms

$$\begin{aligned}&\mathsf{\cdots \ isa\ girl} \end{aligned}$$

(2.1)

$$\begin{aligned}&\cdots \ \mathsf{is\ beautiful} \end{aligned}$$

(2.2)

$$\begin{aligned}&\mathsf{every/some\ beautiful\ girl\ smiles} \end{aligned}$$

(2.3)

The PTS is based on a dedicated meaning-conferring natural-deduction proof system, a simplification of the systems in Francez and Dyckhoff (2010a), Francez and Ben-Avi (2015e), Francez (2015d), and is presented in Fig. 1. The rules for adjectival modification are added below.

The proof-system is formulated over a language slightly extending the NL fragment, incorporating $\mathcal{P}$, a denumerable set of (individual) parameters, artefacts of the proof-system (not used to make assertions), ranged over by boldface lower-case j, k. Syntactically, a parameter is also regarded as a $\textit{dp}$. Individual parameters, introduced into proof-theory by Gentzen, are a common devise. Unlike constants, they are not interpreted as having a denotation, a reference to an object in a domain. On the other hand, unlike free variables, they are not subject to value assignments via assignments function. Their role is to serve as arguments of predicates with a “life“ spanning the proof (derivation) in which they occur. Their use formalises what in informal proof is expressed by, for example, ‘let n be any integer’, or ‘let ABC’ be any triangle’.

See Francez (2015d) for more details about individual parameters and Francez and Dyckhoff (2010a) for the reason for avoiding the use of proper names.

If a parameter occurs in S in some position (here—subject only, for simplicity), I refer to S as a (ground) pseudo-sentence. The ground pseudo-sentences play the role of atomic sentences, and their meaning is assumed given, externally to the $\textit{ND}$ proof-system. The latter defines sentential meanings of sentences in the fragment relative to the given meanings of ground pseudo-sentences. We get additional types of pseudo-sentences:

$$\begin{aligned} \mathbf{j}\ \mathsf{isa}\ X,\ \ \ \ \ \mathbf{j}\ \mathsf{is}\ A,\ \ \ \ \ \mathbf{j}\ P \end{aligned}$$

(2.4)

For example,

$$\begin{aligned} \mathbf{j}\ \mathsf{isa\ girl},\ \ \ \ \ \mathbf{j}\ \mathsf{is\ beautiful},\ \ \ \ \mathbf{j}\ \mathsf{smiles} \end{aligned}$$

(2.5)

Yet another extension with coordinated-adjectives modification is presented in Sect. 5.

The role of the basic I/E rules is to introduce/eliminate a $\textit{dp}$ into/from the subject² position of a sentence. In Example 2.1 (see below), the transitive verb has two positions of introduction of $\textit{dps}$: both its subject position and its object position. An introduction of a quantified $\textit{dp}$ into any of those position, by the corresponding I-rule, depends on the prior presence (in the derivation) of a pseudo-sentence with a parameter at that position. In the rule names, $e,\ s$ abbreviate every, some, respectively. I indicates an introduction rule and E—an elimination rule. For any $\textit{dp}$-expression D having a quantifier, S[D] refers to a sentence having D as a subject.

For example, $S[\mathsf{every}\ X]$ refers to a sentence S with an occurrence of $\mathsf{every}\ X$ in its subject. I use the conventions that within a rule, both $S[D_{1}], S[D_{2}]$ refer to the same designated position in S.

Rules are defined over sequents of the form $\Gamma \vdash S$, where $\Gamma$ is a context ³—a finite collection⁴ of sentences. I use $\Gamma ,S$ for the context extending $\Gamma$ with sentence S. The usual notion of (tree-shaped) derivation is assumed. I use $\mathcal{D}$ 9 possibly subscripted) to range over derivations.

Fig. 1

Some (simplified) I/E-rules for the fragment

The following is a convenient derived E-rule, that will be used to shorten derivations.

(2.6)

For example, an instance of this rule is (omitting $\Gamma$s)

(2.7)

Example 2.1

(An exemplary derivation) Below is an example⁵ derivation establishing

$$\begin{aligned}&\mathsf{some}\ U\ \mathsf{isa}\ X,\ (\mathsf{every}\ X)_{2}\ R\ (\mathsf{some}\ Y)_{1},\ \mathsf{every}\ Y\ \mathsf{isa}\ Z\ \\&\quad \vdash \ (\mathsf{some}\ U)_{1}\ R\ (\mathsf{some}\ Z)_{2} \end{aligned}$$

To aid the intuition, assume the predicate names abbreviate the following:

• U: Italian

• X: man

• R: loves

• Y: actress

• Z: woman

Thus, the conclusion is some Italian loves some woman.

The derivation is

The interested reader may consult Francez and Dyckhoff (2010a) to see how the more general formulation of those rules copes with quantifier-scope ambiguity in sentences with transitive verbs. Since this issue is orthogonal to the current concerns, the simplified rules in Fig. 1 ignore it.

3 A Simplified Typology of Adjectives

First, there is a basic distinction between two forms of use of adjectives.

• Attributive This is the form according to which an adjective A combines (syntactically) with a noun X, semantically modifying that noun. The syntactic convention prevailing in English, where an adjective precedes the noun, is adopted here. The only basic nouns considered here are singular count nouns. For example,

  $$\begin{aligned} \mathsf{grey\ elephant} \end{aligned}$$

  (3.1)

  as in

  $$\begin{aligned} \mathsf{every\ grey\ elephant\ trumpets} \end{aligned}$$

  (3.2)

  The combination of an adjective A with a noun X forms a compound noun $A\ X$, which itself can be further adjectively modified.

• Predicative This is a form according to which an adjective combines with a determiner-phrase ($\textit{dp}$) using the is copula to form a sentence, semantically expressing predication and/or quantification. As arguments of non-quantificational predication I use individual parameters. The resulting sentence has the form $\mathbf{j}\ \mathsf{is}\ A$. For example, (3.3) is a non-quantified ground pseudo-sentence with predicative adjectival modification, while (3.4) is a quantified sentence with a predicative use of an adjective.

  $$\begin{aligned}&\mathbf{j}\ \mathsf{is\ grey}\end{aligned}$$

  (3.3)
  $$\begin{aligned}&\mathsf{every\ elephant\ is\ grey} \end{aligned}$$

  (3.4)

Not every adjective can take a predicative position, and this ability is supposed to be lexically given from outside the proof-system. For some adjectives, this ability is conditional, depending on some overt modified noun, sometimes assumed contextually salient. For example, j is small is appropriate in case, say, it is the case that j isa mouse is given too, and the modification sentence alludes to $\mathbf{j}\ \mathsf{isa\ small\ mouse}$. As mentioned in the introduction, I do not deal here with contextual meaning variation.

I will consider the following main classes of adjectives, using the terminology of Morzycki (2015).

It is important to note that the class to which some specific adjective belongs is given from outside the proof-system. Therefore, the appropriateness of an application of a rule pertaining to modification by an adjective, determined by this class, is not a premise of the rule!.

The classification is certainly not exhaustive. For each class, a characteristic entailment is presented, to be discussed more later on. I use ‘$\Vdash$’ to indicate entailment, defined proof-theoretically (see “Appendix”).

• Intersective adjectives ($int\!A$) Intersective adjectives combine with their modified nouns in a way resembling a implicit conjunction, hence their name. Intersective adjectives have two characteristic entailments.

  $$\begin{aligned}&(\textit{intA}_{1})\ \ \mathbf{j}\ \mathsf{isa\ grey\ elephant} \Vdash \mathbf{j}\ \mathsf{is\ grey} \end{aligned}$$

  (3.5)
  $$\begin{aligned}&(\textit{intA}_{2})\ \ \mathbf{j}\ \mathsf{isa\ grey\ elephant} \Vdash \mathbf{j}\ \mathsf{isa\ elephant} \end{aligned}$$

  (3.6)

  This class was already considered (in a sketchy way) in the PTS in Francez and Dyckhoff (2010a). The following entailment, arising from extensionality, is also characteristic of intersectivity.

  $$\begin{aligned} (\textit{intA}_{3})\ \ \mathbf{j}\ \mathsf{isa\ Italian\ women},\mathbf{j}\ \mathsf{isa\ musician} \Vdash \mathbf{j}\ \mathsf{isa\ Italian\ musician} \end{aligned}$$

  (3.7)

• Subsective adjectives ($sub\!A$) Those adjectives behave according to a different product to be described below. Examples of subsective (non-intersective⁶) adjectives are Morzycki (2015) small, skillful, lousy, experienced, typical. Subsective adjectives have only one characteristic entailment.

  $$\begin{aligned} (\textit{subA})\ \ \mathbf{j}\ \mathsf{isa\ small\ elephant} \Vdash \mathbf{j}\ \mathsf{isa\ elephant} \end{aligned}$$

  (3.8)

  In particular,

  

  (3.9)

  Here ‘small’ can be informally understood as ‘small as/for an elephant’, being actually a fairly large animal, for example. Or, in the terminology of Paoli (1999), ‘small [given being an elephant]’. Similarly, ‘skillful’ in ‘skillful surgeon’ can be understood as ‘skillful as/for a surgeon’, where one could be a skillful surgeon but a very lousy pianist. In a sense, the adjectives in this class are multiply ambiguous, their modification depending on the modified noun.

• Privative adjectives ($priv\!A$) Those adjectives behave according to a yet another product to be described below. Examples include (cf. Morzycki 2015) fake, pretend, fictitious, artificial. Privative adjectives also have one characteristic entailment.

  $$\begin{aligned} (\textit{privA})\ \ \mathbf{j}\ \mathsf{isa\ fake\ gun} \Vdash \mathbf{j}\ \mathsf{is\ fake} \end{aligned}$$

  (3.10)

  In particular,

  

  (3.11)

  Actually, in the literature there is another entailment for privative adjectives, namely

  $$\begin{aligned} \mathbf{j}\ \mathsf{isa\ fake\ gun} \Vdash \mathbf{j}\ \mathsf{is\ not\ a\ gun} \end{aligned}$$

  (3.12)

  which I will not consider here, in order not to have to drag negation, controversial⁷ in itself, into the proof-theory.

• Non-subsective adjectives ($nsub\!A$) Modification by means of those adjectives seems not to behave as a product. Examples include (cf. Morzycki 2015) alleged, probable, potential. They have no characteristic entailments. In particular,

  

  (3.13)

  (the latter ill-formed in English).

  

  (3.14)

  Those adjective have a modal character in their lexical meaning, and their proof-theoretic treatment calls for other means, the study of which I defer to another occasion.

4 Proof-Theory for Adjectival Modification

The rules proposed below are modelled after the various logical products [described in a logical setting in a companion paper Francez (2015b)], but with several differences originating from the object language being (a fragment of) a natural language. The differences are listed below.

• Diversification In the object language of logic, having only one type of formulas, every formula can serve as a left sub-formula or as a a right sub-formula of any (binary) product. Therefore, as observed by Paoli (1999), the products corresponding to the current object language, when embedded in a in logic have to be non-commutative. On the other hand, the premises of the adjectival modification rules are of different types: an adjectival type and a nominal type. They can serve, respectively, as the left and right sub-formula of an adjective–noun combination. As one consequence, a product of a formula with itself, well-defined in logic, is ill-defined in the proof system for adjective modification (considering adjectives and nouns disjoint classes).

• Implicitness All products are implicit ⁸, and the applicability of a rule is determined by the adjective class of the adjective in question, assumed given from outside the proof-system.

The mathematical view of the adjectival modification as products is not essential for understanding the rules, and can be ignored by readers not familiar with more standard logical products.

4.1 The I/E-Rules for Adjectival Modification

A common property of all the adjective–noun combinations, for which I/E-rules are provided, is that they relate to compound nouns only. In order to derive a sentence with a $\textit{dp}$, a determiner needed to be added, and then one of the $\textit{dp}$ I/E-rules (Fig. 1) used. For example, to deduce some beautiful girl smiles (from some $\Gamma$), the adjectival modification rules will be used to derive the compound noun meaning j is beautiful girl (according to the class to which beautiful belongs), and then the rule (sI), introducing some beautiful girl into the subject position of —smiles is used.

• Intersective adjectives The rules are modelled after the additive conjunction (the classical/intuitionistic conjunction).

  

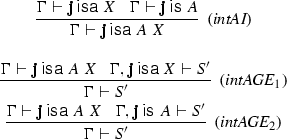  (4.1)

  The $\textit{intAGE}$-rules, having the form of general elimination rules, are equivalent [under the assumption of weakening present for the additive conjunction—see Francez (2015b)] to the following two simpler $int\hat{E}$-rules.

  

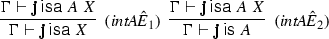  (4.2)

  Since grey is assumed (lexically) intersective, the characteristic inferences (3.5) and (3.6) are instances of the rules (4.2) with A being grey and X being elephant (and $\Gamma$ empty).

• Subsective adjectives As mentioned above, the meaning of the modification by means of adjectives in this class depends on the meaning of the modified noun. To reflect this dependence, the I-rule uses the meaning of the noun as a discharged assumption. The discharged assumption is “recorded” in the conclusion in the modified noun.

  

  (4.3)

  Thus, for $X=\mathsf{elephant}$ and $A=\mathsf{small}$, the conclusion $\mathbf{j}\ \mathsf{isa\ small\ elephant }$ is obtained from a derivation of $\mathbf{j}\ \mathsf{is\ small}$ provided $\mathbf{j}\ \mathsf{isa\ elephant}$ is assumed (and then discharged). Similarly, for $X = \mathsf{mouse}$ and $A = \mathsf{small}$, the conclusion $\mathbf{j}\ \mathsf{isa\ small\ mouse}$ is obtained from a derivation of $\mathbf{j}\ \mathsf{is\ small}$ provided $\mathbf{j}\ \mathsf{isa\ mouse}$ is assumed (and then discharged). The general elimination rules are:

  

  (4.4)

  Again, there is a simplified $\hat{E}$-rule equivalent (since weakening is present in the case of an additive I-rule) to the second GE-rule.

  

  (4.5)

  but not to the first, which is multiplicative and excludes weakening!

Thus, there are two ways of drawing a conclusion from $\mathbf{j}\ \mathsf{isa}\ A\ X$ for a subsective A:

• 1. $\mathbf{j}\ \mathsf{is}\ A$ can be used as a discharged assumption only jointly with $\mathbf{j}\ \mathsf{isa}\ X$ to derive $S^{\prime }$.

• 2. The conclusion $S^{\prime }$ is based only on $\mathbf{j}\ \mathsf{isa}\ X$, including $S^{\prime }$ being $\mathbf{j}\ \mathsf{isa}\ X$ itself.

However, if A is subsective, then on its own.

For example, the two ways of drawing a conclusion from $\mathbf{j}\ \mathsf{isa\ small\ elephant}$ are:

• 1. $\mathbf{j}\ \mathsf{is\ small}$ can be used only jointly with $\mathbf{j}\ \mathsf{isa\ elephant}$ to derive an arbitrary $S^{\prime }$.

• 2. The conclusion $S^{\prime }$ is based only on $\mathbf{j}\ \mathsf{isa\ elephant}$, including $\mathbf{j}\ \mathsf{isa\ elephant}$ itself.

Since small is assumed (lexically) subsective, the characteristic inference (3.8) is an instance of the rule (4.5) with A being small and X being elephant (and $\Gamma$ empty).

• Privative adjectives Here we meet a dual dependence: the meaning of the modification depends on the meaning of the (privative) adjective. A fake gun is a gun only under the assumption of being fake. This is ensured by having the adjective as a discharged assumption in the derivation of the combination.

  

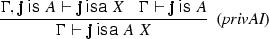  (4.6)
  

  (4.7)

  With the equivalent simplified rule :

  

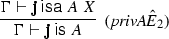  (4.8)

  Thus, there are again two ways of drawing a conclusion from $\mathbf{j}\ \mathsf{isa}\ A\ X$ for a privative A:

• 1. $\mathbf{j}\ \mathsf{isa}\ X$ can be used only jointly with $\mathbf{j}\ \mathsf{is}\ A$ to derive $S^{\prime }$.

• 2. The conclusion $S^{\prime }$ is based only on $\mathbf{j}\ \mathsf{is}\ A$, including $S^{\prime }$ being $\mathbf{j}\ \mathsf{is}\ A$ itself.

However, if A is privative, then on its own.

The two ways of drawing a conclusion from $\mathbf{j}\ \mathsf{isa\ fake\ gun}$ are:

• 1. $\mathbf{j}\ \mathsf{isa\ gun}$ can be used only jointly with $\mathbf{j}\ \mathsf{is\ fake}$ to derive an arbitrary $S^{\prime }$.

• 2. The conclusion $S^{\prime }$ is based only on $\mathbf{j}\ \mathsf{is\ fake}$, including $\mathbf{j}\ \mathsf{is\ fake}$ itself.

Since fake is assumed (lexically) privative, the characteristic inference (3.10) is an instance of the rule (4.8) with A being fake and X being gun (and $\Gamma$ empty).

The following inferences are valid, where red is intersective, small is subsective and fake—privative.

(4.9)

But, the following are invalid inferences.

(4.10)

However, the following are valid inferences.

(4.11)

To complete the picture, the following additional $\hat{E}_{3}$-rules hold too, but they are not interesting in terms of adjectival modification in NL. One way of interpreting those rules is the generation of presupposition.

(4.12)

For example:

(4.13)

To summarise:

• Intersective adjectival modification projects each component (i.e., the adjective and the noun) unconditionally, on its own.

• Subsective adjectival modification projects unconditionally either both components jointly, or the second component (the noun) on its own, and projects the adjective conditionally.

• Privative adjectival modification project both components jointly unconditionally, projects the adjective unconditionally on its own and projects the noun conditionally.

4.2 Are Subsective Adjectives Intersective After All?

Within MTS, there is a common analysis of subsective adjectives that does facilitate viewing them as intersective, by “unfolding” the dependency of their mode of modification meaning on the meaning of the noun by means an additional, implicit argument. See Morzycki (2015) for further references to the adventures of this idea. The implicit argument is best known as a comparison class, to which the explicit argument is compared. For example, $\mathsf{small}_{C}\ \mathsf{elephant}$ combines small with elephant within the comparison class C. This analysis is accompanied by lexical semantics of those adjectives, augmenting the comparison class with a scale (typically, linearly ordered) and a standard of comparison, a yardstick. Much of the literature is concerned with C and its accompanying scale and yardstick being contextually salient. As I do not treat contextual meaning variation here, I will stick to the more obvious choice that C is just determined by the modified noun itself (its extension, in the model-theoretic view). Thus, a small elephant means small (under some standard measure of size) in comparison to elephants, a skillful surgeon means a surgeon skilled (under some standard measure of skill) in comparison to surgeons, and so for every other modified noun.

We thus get the following inferences for subsective adjectives, akin to the intersective case.

$$\begin{aligned} \begin{array}{l} \mathbf{j}\ \mathsf{isa}\ X, \mathbf{j}\ \mathsf{is}\ A_{X} \Vdash {\mathbf{j}\ \mathsf{isa}\ A\ X}\\ {\mathbf{j}\ \mathsf{isa}\ A\ X}\ \Vdash \mathbf{j}\ \mathsf{is}\ A_{X}\\ \mathrm{and,\ as\ before}\\ {\mathbf{j}\ \mathsf{isa}\ A\ X}\ \Vdash \mathbf{j}\ \mathsf{isa}\ X \end{array} \end{aligned}$$

(4.14)

For example,

$$\begin{aligned} \begin{array}{c} \mathbf{j}\ \mathsf{isa\ elephant}, \mathbf{j}\ \mathsf{is\ small_{elephant}} \Vdash \mathbf{j}\ \mathsf{isa\ small\ elephant}\\ \mathbf{j}\ \mathsf{isa\ small\ elephant}\ \Vdash \mathbf{j}\ \mathsf{is\ small_{elephant}}\\ \mathbf{j}\ \mathsf{isa\ small\ elephant}\ \Vdash \mathbf{j}\ \mathsf{isa\ elephant} \end{array} \end{aligned}$$

(4.15)

This approach involves the usual ontological commitments coming with MTS. What exactly are scales? What is a scale for skill? For beauty? And how exactly are those additional ingredients accommodated in models? The literature is very vague on those formal matters.

According to the proof-theoretic approach put forward in this paper, there is no need to assume any ontological commitment. The unfolding of the adjectives can be seen as a purely formal devise to parameterize a subsective adjective: $A_{X}$ is just a family of adjectives originating from A and parameterized⁹ by nouns X. The entailments in (4.14) are the basis for the revised I/E-rules for subsective adjectives. Note the additivity of the revised GE-rules, assimilating them to the GE-rules for intersective adjectival modification.

(4.16)

The $\textit{subAGE}$-rules are equivalent to the following two simpler $\textit{subA}\!\hat{E}$-rules.

(4.17)

The explicit parameterization replaces the dependency in the original rules. I believe that this formal parameterisation sheds new light on the nature of subjectivity of adjectives and its relationship to intersectivity.

4.3 Iterated Modification

Iterated modification takes place when an adjective modifies a compound noun, already having within itself adjectival modification. I distinguish between iterating modification by means of adjectives of the same class and modification via adjective of different classes.

4.4 Same-Class Iteration

Iterating intersective adjectives The main property of iterating modification by means of intersective adjectives is that it commutes. Suppose $A_{1}$ and $A_{2}$ are two different intersective adjectives, and X a noun.

Proposition 4.1

(commuting intersective modifications)

$$\begin{aligned} \mathbf{j}\ \mathsf{isa}\ A_{2}\ A_{1}\ X \Vdash \mathbf{j}\ \mathsf{isa}\ A_{1}\ A_{2}\ X \end{aligned}$$

(4.18)

The derivation is

(4.19)

For example, $\mathbf{j}\ \mathsf{isa\ brown\ round\ cake}\ \Vdash \ \mathbf{j}\ \mathsf{isa\ round\ brown\ cake}$.

Proposition 4.2

$$\begin{aligned} \begin{array}{c} \mathbf{j}\ \mathsf{isa}\ A_{2}\ A_{1}\ X \Vdash \mathbf{j}\ \mathsf{is}\ A_{1}\\ \mathbf{j}\ \mathsf{isa}\ A_{2}\ A_{1}\ X \Vdash \mathbf{j}\ \mathsf{is}\ A_{2}\\ \mathbf{j}\ \mathsf{isa}\ A_{2}\ A_{1}\ X \Vdash \mathbf{j}\ \mathsf{isa}\ X \end{array} \end{aligned}$$

(4.20)

Corollary 1

$$\begin{aligned} \begin{array}{c} \mathbf{j}\ \mathsf{isa}\ A_{2}\ A_{1}\ X \Vdash \mathbf{j}\ \mathsf{is}\ A_{1}\ X\\ \mathbf{j}\ \mathsf{isa}\ A_{2}\ A_{1}\ X \Vdash \mathbf{j}\ \mathsf{is}\ A_{2}\ X\\ \end{array} \end{aligned}$$

(4.21)

Continuing the above example,

$$\begin{aligned} \begin{array}{c} \mathbf{j}\ \mathsf{isa}\ \mathsf{brown\ round\ cake}\ \Vdash \mathbf{j}\ \mathsf{is}\ \mathsf{brown}\\ \mathbf{j}\ \mathsf{isa}\ \mathsf{brown\ round\ cake}\ \Vdash \mathbf{j}\ \mathsf{is}\ \mathsf{round}\\ \mathbf{j}\ \mathsf{isa}\ \mathsf{brown\ round\ cake}\ \Vdash \mathbf{j}\ \mathsf{isa}\ \mathsf{cake} \end{array} \end{aligned}$$

(4.22)

and

$$\begin{aligned} \begin{array}{c} \mathbf{j}\ \mathsf{isa}\ \mathsf{brown\ round\ cake}\ \Vdash \mathbf{j}\ \mathsf{isa}\ \mathsf{brown\ cake}\\ \mathbf{j}\ \mathsf{isa}\ \mathsf{brown\ round\ cake}\ \Vdash \mathbf{j}\ \mathsf{isa}\ \mathsf{round\ cake}\\ \end{array} \end{aligned}$$

(4.23)

What about the special case where $A_{1}=A_{2}=A$, i.e., iterating the same intersective adjective A? This iteration is idempotent¹⁰ in the following sense.

Proposition 4.3

For A an intersective adjective:

$$\begin{aligned} \mathbf{j}\ \mathsf{isa}\ A\ A\ X \Vdash \mathbf{j}\ \mathsf{isa}\ A\ X\ \ \ \mathrm{and} \ \ \mathbf{j}\ \mathsf{isa}\ A\ X \Vdash \mathbf{j}\ \mathsf{isa}\ A\ A\ X \end{aligned}$$

(4.25)

Proof

The omission of an A is just by an application of ($iA\!\hat{E}_{1}$) to the assumption. The introduction of a second A is by repeated use of $\mathbf{j}\ \mathsf{is}\ A$, obtained from the assumption by an application of ($iA\!\hat{E}_{2}$). The respective derivations are shown below.

(4.26)

$\square$

Thus being a grey grey elephant coincides with being a grey elephant.

Iterating subsective adjectives In contrast to intersective adjectives, subsective ones do not commute when iterated. Suppose $A_{1}$ and $A_{2}$ are two different subsective adjectives, and X a noun. Then, from $\mathbf{j}\ \mathsf{isa}\ A_{1}\ A_{2}\ X$ we can only obtain $\mathbf{j}\ \mathsf{isa}\ X$, but the premises needed in order to reintroduce $A_{1}$ and then $A_{2}$ are not obtainable from the iterated modification sentence via E-rules. Thus,

Proposition 4.4

For $A_{1},A_{2}$ subsective adjectives,

(4.27)

For example, from $\mathbf{j}\ \mathsf{isa\ experienced\ skillful\ teacher}$ we only can get $\mathbf{j}\ \mathsf{isa\ teacher}$ and $\mathbf{j}\ \mathsf{isa\ skillful\ teacher}$.

In contrast to intersective adjectives, iterating the same subsective adjective A is not idempotent in the above sense. Omitting one A is derivable, but adding an A is not.

Proposition 4.5

For A a subsective adjective:

(4.28)

Proof

The omission of an A is again just by an application of ($\textit{subA}\!\hat{E}_{2}$) to the assumption. For the introduction of a second A, a derivation of $\mathbf{j}\ \mathsf{is}\ A$ from $\mathbf{j}\ \mathsf{isa}\ A\ X$ is needed, unobtainable from the assumption.

Thus, being a small small elephant implies being a small elephant (as is implied also, given lexical meanings, from being a big small elephant). However, being a small elephant does not imply being a small small elephant, as being a big small elephant is not excluded.

Note that in case of iteration of subsective adjectives, the comparison class of the outermost adjective is the whole compound modified noun. For example, small small elephant is small in comparison to small elephants, not elephants in general.

Iterating privative adjectives Similarly, privative adjectives do not commute when iterated. Suppose $A_{1}$ and $A_{2}$ are two different privative adjectives, and X a noun. Then, from $\mathbf{j}\ \mathsf{isa}\ A_{1}\ A_{2}\ X$ we can only obtain $\mathbf{j}\ \mathsf{is}\ A_{1}$, but the premise $\mathbf{j}\ \mathsf{isa}\ X$ needed in order to reintroduce $A_{1}$ and then $A_{2}$ is not obtainable from the iterated modification sentence via E-rules. Thus,

Proposition 4.6

For $A_{1},A_{2}$ privative adjectives,

(4.29)

For example, from $\mathbf{j}\ \mathsf{isa\ fake\ artificial\ gun}$ we only can get $\mathbf{j}\ \mathsf{is\ fake}$.

Just like subrsective adjectives, iterating the same privative adjective A is not idempotent in the above sense. Omitting one A is not derivable, but adding an A is not.

Proposition 4.7

For A a privative adjective:

(4.30)

The obvious proof is omitted.

Iterating non-subsective adjectives A fortiori, iterated non-subsective adjectives do not commute and, actually yield no immediate direct consequence whatsoever. From $\mathbf{j}\ \mathsf{isa\ alleged\ probable\ murderer}$ we get none of $\mathbf{j}\ \mathsf{is\ alleged/probable}$ and $\mathbf{j}\ \mathsf{isa\ murderer}$.

4.5 Different-Class Iteration

Proposition 4.8

No different-class adjectives commute.

Proof

Suppose that $\mathbf{j}\ A_{1}\ A_{2}\ X$, where $A_{1}$ and $A_{2}$ belong to different classes. In this case, at most one of $A_{1}, A_{2}$ is intersective, so one premise will miss in order to reintroduce the inverse ordering. $\square$

Proposition 4.9

Suppose $A_{2}$ is intersective and $A_{1}$ subsective. Then,

(4.31)

and

(4.32)

Similarly,

Proposition 4.10

Suppose $A_{2}$ is intersective and $A_{1}$ privative. Then,

(4.33)

and

(4.34)

Proposition 4.11

Suppose $A_{2}$ is subsective and $A_{1}$ privative. Then,

(4.35)

and

(4.36)

Digression: compound parameterization

In view of iterated adjectival modification, it is important to note the possibility¹¹ of compound parameters, corresponding to compound nouns. Consider, for $A_{1}, A_{2}$ subsective,

$$\begin{aligned} \mathbf{j}\ \mathsf{isa}\ A_{1}\ A_{2}\ X \end{aligned}$$

(4.37)

Then, a parameterisation of $A_{1}$ has the form $A_{1, A_{2}\ X}$. For example, for

$$\begin{aligned} \mathbf{j}\ \mathsf{isa\ small\ old\ elephant} \end{aligned}$$

(4.38)

small is parameterized as $\mathsf{small_{old\ elephant}}$, while old is parameterized as $\mathsf{old_{elephant}}$. This is a way to predict and explain the non-commutativity of iteration of subsective adjectives discussed above.

5 Coordinated-Adjectives Modification

In this section, I extend the language fragment to include coordinated adjectives, forming compound adjectives. For $A_{1},\ A_{2}$ adjectives, $A_{1}\ \mathsf{and/or}\ A_{2}$ is a (compound) adjectives. We thus have additional pseudo-sentence forms:

$$\begin{aligned} \mathbf{j}\ \mathsf{is}\ A_{1}\ \mathsf{and/or}\ A_{2},\ \ \ \mathsf{every/some}\ X\ \mathsf{is}\ A_{1}\ \mathsf{and/or}\ A_{2} \end{aligned}$$

(5.1)

To simplify matters, let us idealise and assume that every two adjectives can be coordinated. Also, I present only conjunction; disjunction can be added in a similar way. Once again, sub-structurality plays a role here. The immediate I/E rules for additive conjunctive-adjective modification are the expected ones.

(5.2)

The elimination rules simplify to

(5.3)

In view of the standard rule for sentential coordination

(5.4)

this treatment of conjunction is what became to be known conjunction reduction. For example,

$$\begin{aligned} \mathbf{j}\ \mathsf{isa\ brown\ and\ round\ table} \end{aligned}$$

(5.5)

is equivalent to

$$\begin{aligned} \mathbf{j}\ \mathsf{isa\ brown\ table\ and\ \mathbf{j}\ isa\ round\ table} \end{aligned}$$

(5.6)

There is, however, another reading of conjunctive adjectival modification, arising from a different lexical meaning of and. This is akin to np-coordination with non-distributed predication, like in

$$\begin{aligned} \mathsf{John\ and\ Mary\ kissed}\ (each\ other) \end{aligned}$$

(5.7)

Under this reading,

$$\begin{aligned} \mathsf{The\ French\ flag\ is\ red,\ white\ and\ blue} \end{aligned}$$

(5.8)

is not equivalent to

$$\begin{aligned} \mathsf{The\ French\ flag\ is\ red\ and\ the\ French\ flag\ is\ white\ and\ the\ French\ flag\ is\ blue} \end{aligned}$$

(5.9)

This meaning involves multiplicative conjunction elimination rules. Since the meaning of and is not the topic here, I skip further details.

Conjunctive adjectival modification gives rise to another reading of iterated modification, the latter understood as conjunctive. That is, $\mathbf{j}\ \mathsf{isa}\ A_{1}\ A_{2}\ X$ is taken to mean $\mathbf{j}\ \mathsf{isa}\ A_{1}\ \mathsf{and}\ A_{2}\ X$. In the subsective case, both $A_{1}$ and $A_{2}$ get the same parameterisation, namely $A_{1 X}$ and $A_{2 X}$.

Returning to example (4.38), we get a reading equivalent to

$$\begin{aligned} \mathbf{j}\ \mathsf{isa\ small\ and\ old\ elephant} \end{aligned}$$

(5.10)

that is, both small and old are parameterized as $\mathsf{small_{elephant}}$ and $\mathsf{old_{elephant}}$. In MTS terms, that would mean using the same comparison class (elephants) for both adjectives, presumably with different yardsticks for size and age.

6 Conclusions

In this paper, I have extended PTS to cover to a larger fragment of NL (here—English) that includes adjectival modification (of nouns). As emphasized both in the Introduction section and in the “Appendix” (see below), the proof-system presented is taken to be meaning-conferring. Thus, the rules define the meaning of adjectival modification. In doing so, in contrast to MTS, it does not appeal to any models and escapes any ontological commitments to entities like scales (of comparison) or yardsticks, that need to populate MTS models.

Of particular interest is the way subjectivity is captured by means of formal parameterization, revealing in a more transparent way the relationship between subsective and intersective adjectives.

The PTS presented captures the pre-theoretic understanding of adjectival modification, based on a standard typology of adjectives. It supports the pre-theoretic entailment relation among sentences exhibiting adjectival modification. Besides simple modifications, rules are presented also for defining iterated modification, shedding light on the connection between iterated modification and the various adjective classes.

Appendix

In this appendix, I repeat for self-containment of the paper some of the technicalities involved in PTS in general. A detailed presentation of PTS as a theory of meaning is presented in Francez (2015d), with the second part of that book devoted to the application of PTS to NL. Further references are provided in that book. Motivation and justification for PTS can be found also in Francez and Dyckhoff (2010a), Francez and Ben-Avi (2015e).

According to the PTS programme, meaning is determined by a meaning-conferring natural-deduction proof system. Such a system has two kinds of rules:

• Introduction rules (I -rules) Those rules have as their conclusion an expression (formula, sentence) governed by an operator said to be introduced by the rule. Such rules establish the way the expression can be deduced from the premises of the rule. Such an inference is considered the most direct way to infer the conclusion. In the natural language fragment considered in this paper, I-rules introduce a $\textit{dp}$ as a subject of an intransitive verb, and introduce implicit operators combining adjectives and nouns.

• Elimination rules (E -rules) Those rule have as their major premise an expression (formula, sentence) governed by an operator said to be eliminated by the rule. Such rules establish the way a conclusion may be drawn from that expression. Such an inference is considered the most direct way to infer from the major premise. In the natural language fragment considered in this paper, an E-rules eliminate a $\textit{dp}$ from the subject position of an intransitive verb, as well as the implicit operator combining adjectives and verbs.

Both kind of rules may discharge assumptions when applied, rendering the conclusion independent of some temporarily assumed assumptions.

Example 6.1

The simplest example of I/E-rules are those introducing and eliminating a (sentential) conjunction in logic, shown below.

(6.1)

Note that there are two E-rules here. No discharge of assumption is involved in those rules.

The claim of PTS is, that those rules determine the full meaning of conjunction, independently of the model-theoretic definition using truth-tables.

Example 6.2

A simple example involving a discharge of an assumption is the I-rule of the implication.

(6.2)

The rule ($\rightarrow I$) says that in order to derive an implication, temporary assume the antecedent $\varphi$, putting around it square brackets to indicate discharge, indexed i for connecting with a discharging application of the rule indexed by the same index, and derive the consequent $\psi$, potentially using the assumption of the antecedent. Once the consequent has been derived, the assumption of the antecedent is discharged. The E-rule is the familiar modus-ponens.

Once again, according to PTS, those rules tell “the whole story” needed for the meaning of implication.

Officially¹², the I/E-rules are formulated using sequents of the form $\Gamma \vdash \psi$, where $\Gamma$ is a finite collection (most often, a set) of object-language formulas, the undischarged assumptions, and $\psi$ is also a formula. In this presentation, the dependence of a conclusion on assumption is made explicit. However, to avoid notational cluttering, The assumptions $\Gamma$ are left implicit. A derivation $\mathcal{D}$ (of $\psi$ from $\Gamma$) is defined recursively by iterating rule applications starting from assumptions $\Gamma$ and reaching a conclusion $\psi$. The derivability (i.e., existence of a derivation) of $\varphi$ from $\Gamma$ in $\mathcal{N}$ is denoted $\vdash _{\mathcal{N}} \Gamma : \varphi$ (where the subscript on ‘$\vdash$’ is often omitted). A variable is called fresh if it does not occur in any assumption of which a conclusion of a rule depends.

In the PTS literature, meaning is conceived as implicitly defined by the I-rules, not appealing to any proof-theoretic semantic value as an explicit definition. But what exactly can be taken as an explicitly defined proof-theoretic semantic value within PTS as the result of the determination of meaning via the meaning-conferring I-rules?

In Francez and Ben-Avi (September 2011), and subsequently in Francez (2014c), such a proof-theoretic semantic value is proposed as an explicit definition of meaning. I recapitulate this proposal below.

An important concept in PTS, on which the definition of explicit meaning definition is based, is that of a canonical derivation in $\mathcal{N}$. Following Francez (2014a, 2015c), I suggest the following definition, generalizing the standard canonical proof (from no assumptions). Its justification is discussed in detail in Francez (2015c).

Definition 6.1

(canonical derivation from open assumptions). A $\mathcal{N}$-derivation $\mathcal{D}$ for $\Gamma \vdash \psi$ (for a compound $\psi$) is canonical iff it satisfies one of the following two conditions.

• The last rule applied in $\mathcal{D}$ is an I-rule (for the main operator of $\psi$).

• The last rule applied in $\mathcal{D}$ is an assumption-discharging E-rule, the major premise of which is some $\varphi$ in $\Gamma$, and its encompassed sub-derivations $\mathcal{D}_{1},\ldots ,\mathcal{D}_{n}$ are all canonical derivations of $\psi$.

Denote by $\vdash _{\mathcal{N}}^{c}$ canonical derivability in $\mathcal{N}$, and by $\mathbf{[}\! [\varphi \mathbf{] \! ]}^{c}_{\Gamma }$ the (possibly empty) collection of canonical derivations of $\varphi$ from $\Gamma$.

For $\Gamma$ empty, the definition reduces to that of a canonical proof. Note the recursion involved in this definition. The important observation regarding this recursion is that it always terminates via the first clause, namely by an application of an I-rule. I refer to this application of an I-rule as the essential application, the outcome of which is propagated throughout the canonical derivation.

There are no canonical derivations for an atomic sentence, which by definition has no introducible operators. Traditionally, the PTS programme views the meaning of an atomic sentence to be given, possibly from outside the meaning-conferring proof system. To overcome this non-specificity, I take¹³ the rule of assumption $\vdash \Gamma , p : p$ to constitute the canonical way an atomic sentence is introduced into a derivation.

To realize the role of canonicity in the forthcoming definition of reified proof-theoretic meanings, consider the following example derivation in, say, intuitionistic propositional logic.

(6.3)

This is a derivation of a conjunction—but not a canonical one, as it does not end with an application of $(\wedge I)$, nor does it have an essential application of it. Thus, the conjunction here was not derived according to its meaning! As far as this derivation is concerned, it could mean anything, e.g., disjunction. On the other hand, the following example derivation is according to the conjunction’s meaning, being canonical.

(6.4)

I now turn to the definition of what I take to be the reified proof-theoretic meaning determined by a meaning-conferring $\textit{ND}$-system (see Francez (2014c) for a more detailed discussion).

I take the sentential meanings of compound sentences in L to originate from canonical $\mathcal{N}$-derivations. I emphasize once again, that it is sentential meanings that are directly explicitly defined by the $\textit{ND}$-system, whereas meanings of connectives are extracted from compound sentential meanings as shown in Francez et al. (2010b). I refer to functions from contexts to collections of $\textit{ND}$-derivations as contextualized functions.

Definition 6.2

(meaning—sentential semantic values). For $\varphi \in L$, its meaning $\mathbf{[}\! [\varphi \mathbf{] \! ]}$, is given as follows.

$$\begin{aligned} \mathbf{[}\! [\varphi \mathbf{] \! ]}= \lambda \Gamma . \mathbf{[}\! [\varphi \mathbf{] \! ]}_{\Gamma }^{c} \end{aligned}$$

(6.5)

Note that the reified meaning of $\varphi$ is a proof-theoretic object, a contextualized function from contexts to the collection of canonical derivations of $\varphi$ from that context, not to be confused with model-theoretic denotations (of truth-values, in the propositional logic case).

The definition of proof-theoretic consequence (pt-consequence) rests on the notion of grounds for assertion for $\varphi$, closely related to $\mathbf{[}\! [\varphi \mathbf{] \! ]}$, the reified meaning of $\varphi$.

Definition 6.3

(grounds for assertion).

$$\begin{aligned} GA\mathbf{[}\! [\varphi \mathbf{] \! ]}= \{ \Gamma \ |\ \vdash ^{c} \Gamma : \varphi \} \end{aligned}$$

(6.6)

Thus, any $\Gamma$ that canonically derives $\varphi$ serves as grounds for assertion of $\varphi$.

Based on the definitions of grounds for assertion, I define proof-theoretic consequence (pt-consequence).

Definition 6.4

(proof-theoretic consequences). Let $\Gamma ,\psi \in L$. $\psi$ is a proof-theoretic consequence of $\Gamma$ ($\Gamma \Vdash \psi$) iff $GA \mathbf{[}\! [\Gamma \mathbf{] \! ]}\subseteq GA \mathbf{[}\! [\psi \mathbf{] \! ]}$.

Thus, pt-consequences is based on grounds propagation: every grounds for asserting $\psi$ (that derives canonically $\psi$), are already collective grounds for collectively asserting all of $\Gamma$ [depending on the mode of combination of grounds employed, see Francez (2015a)].

By this definition, $\psi$ is a pt-consequence of $\Gamma$ according to $\psi$’s meaning as pt-consequence involves canonical derivability.

I want to stress that according to the PTS programme, the rules proposed are meaning-conferring. That is, they are a definitional tool. They should not be judged against any external yard-stick, in particular not one used in MTS. Completeness proofs as traditionally sought in logic are not a goal here, in spite of being an interesting topic on its own. The rules need, though, meet some proof-theoretic criteria to qualify as meaning-conferring. In Francez and Dyckhoff (2010a), the rules for the extensional fragment are shown to meet the harmony criterion, one central such criterion.