Determining the contributions of divisive and subtractive feedback in the Hodgkin-Huxley model

Abstract

The Hodgkin-Huxley (HH) model is the basis for numerous neural models. There are two negative feedback processes in the HH model that regulate rhythmic spiking. The first is an outward current with an activation variable n that has an opposite influence to the excitatory inward current and therefore provides subtractive negative feedback. The other is the inactivation of an inward current with an inactivation variable h that reduces the amount of positive feedback and therefore provides divisive feedback. Rhythmic spiking can be obtained with either negative feedback process, so we ask what is gained by having two feedback processes. We also ask how the different negative feedback processes contribute to spiking. We show that having two negative feedback processes makes the HH model more robust to changes in applied currents and conductance densities than models that possess only one negative feedback variable. We also show that the contributions made by the subtractive and divisive feedback variables are not static, but depend on time scales and conductance values. In particular, they contribute differently to the dynamics in Type I versus Type II neurons.

1 Introduction

The Hodgkin-Huxley (HH) model revolutionized neuroscience with its description of the action potential using four dynamic variables (Hodgkin and Huxley 1952). In the next decade simpler descriptions of an impulse were developed independently by FitzHugh (Fitzhugh 1961) and Nagumo (Nagumo et al. 1962) that are now known as the FitzHugh-Nagumo model. This model consists of only two dynamic variables, which greatly simplifies analysis at the expense of biophysical detail. Other planar models for membrane excitability were later developed, most notably the Morris-Lecar model that is expressed in terms of ionic currents (Morris and Lecar 1981). In this article, we examine how reductions in dimensionality affect impulse generation in the Hodgkin-Huxley model.

One apparent redundancy of the HH model is the presence of two negative feedback variables. One, the activation of a ${\mathrm{K}}^{+}$ current (n), subtracts from the positive feedback responsible for the upstroke of the impulse. The other, inactivation of the positive feedback ${\mathrm{Na}}^{+}$current (h), divides the current. It is known that models with only one negative feedback variable, such as the Morris-Lecar model, can also produce rhythmic spiking. The Morris-Lecar model uses subtractive feedback, eliminating the redundancy of the HH model by replacing inactivating ${\mathrm{Na}}^{+}$current with non-inactivating Ca²⁺ current, and divisive feedback but no subtractive feedback can also be used in excitable cell models (Wang and Rinzel 1992). Can we detect an advantage to having both subtractive and divisive negative feedback? In the HH model that possesses both types of negative feedback processes, what are the respective contributions of each to rhythmic spiking?

To answer these questions, we use three numerically computed metrics to contrast properties of the full HH model with those of several lower-dimensional reduced models that are related to the FitzHugh-Nagumo and Morris-Lecar models. The first measures the width of a parameter regime within which tonic spiking is a unique and stable limit cycle oscillation. The second metric, contribution analysis, measures how changes in the variables’ time scale parameters affect the durations of the “active phase” (AP) during the action potential and the inter-spike interval “silent phase” (SP) of a tonically spiking model (Tabak et al. 2011). The third metric, dominant scale analysis, measures a sensitivity of the voltage dynamics to each of the ionic currents to rank their influence (Clewley et al. 2005, 2009; Clewley 2011, 2012). Each of these approaches highlights different, but related, properties of action potential dynamics and yields different kinds of insights.

2 Methods

2.1 Models

We use the HH model (Hodgkin and Huxley 1952) of the action potential. It involves a fast sodium current (${I}_{Na}$, with activation variable m and inactivation h), a delayed rectifying potassium current (${I}_K,$with activation variable n), and a leak current (${I}_L$). The differential equations are:

$$ C\frac{dV}{dt}={I}_{app}-{I}_{Na}-{I}_K-{I}_L $$

(1)

$$ \frac{dm}{dt}=\frac{\left({m}_{\infty}\left(\mathrm{V}\right)- m\right)}{\tau_m\left(\mathrm{V}\right)} $$

(2)

$$ \frac{dn}{dt}=\frac{\left({n}_{\infty}\left(\mathrm{V}\right)- n\right)}{\tau_n\left(\mathrm{V}\right)} $$

(3)

$$ \frac{dh}{dt}=\frac{\left({h}_{\infty}\left(\mathrm{V}\right)- h\right)}{\tau_h\left(\mathrm{V}\right)} $$

(4)

$\frac{dm}{dt}$ where I _app is the applied current. The currents used above are:

$$ {I}_{Na}\left|=\right.\kern0.15em {g}_{Na}{m}^3 h\left( V-{V}_{Na}\right) $$

(5)

$$ {I}_K={g}_K{n}^4\left( V-{V}_K\right) $$

(6)

$$ {I}_L\left|={g}_L\left( V-{V}_L\right)\right. $$

(7)

where g _Na, g _K, g _L are the maximal conductances and V _Na, V _K, V _L are the reversal potentials associated with the currents. The steady state activation and inactivation functions are:

$$ {\chi}_{\infty }(V)=\frac{\alpha_{\chi}(V)}{\alpha_{\chi}(V)+{\beta}_{\chi}(V)} $$

(8)

$$ {\tau}_{\chi}(V)=\frac{\lambda_{\chi}}{\alpha_{\chi}(V)+{\beta}_{\chi}(V)} $$

(9)

For χ = m, n, h. The transition rates α _χ andβ _χ for χ = m, n, h are given in Table 1. λ _χ is a parameter that we use to vary the time constant τ _χ and the default is λ _χ  = 1.

Table 1 Transition rates and parameter values for the Type I and Type II HH models. The Type I parameter set is taken from Kopell et al. (2000) and the Type II parameter set is from the standard HH-Model (Hodgkin and Huxley 1952)

Hodgkin (Hodgkin 1948) introduced two types of neurons: Type I neurons have a continuous relationship between firing frequency and applied current, and can fire at arbitrarily low frequencies (Kopell et al. 2000; Ermentrout 1996; Izhikevich 1999). Type II neurons have a nonzero minimum firing frequency, and thus a step discontinuity between firing frequency and applied current (Izhikevich 2000; Hodgkin and Huxley 1952). We examine both types, which correspond to the different sets of parameters given in Table 1.

In addition to analyzing the full HH model (which we refer to as model A), we also examine 3-dimensional and 2-dimensional reductions (Table 2). Model B is a standard 3D reduction of the HH model that takes advantage of the fast dynamics of m relative to the other gating variables. In this case, and in all subsequent models, m = m _∞(V) (Fitzhugh 1960; Rinzel 1985). Model C is similar to model B, but the recovery variables n and h are slowed down by a factor of 50 so that impulses are relaxation oscillations.

Table 2 The full model and its reductions

The 2-dimensional reductions of the HH Model are achieved by freezing one of the two negative feedback variables. In the h-model (Model D), we freeze the gating Variable n by setting n = 1. In the n-model (Model E), we freeze the gating variable h by setting h = 1.

2.2 Contribution analysis

We wish to know the relative contributions of each negative feedback process to spike termination and initiation. If the negative feedback process contributes to impulse termination, then slowing down the feedback variable by increasing its time constant will increase impulse duration. Similarly, if the process contributes to impulse initiation, then slowing down the process by increasing its time constant will significantly delay impulse initiation.

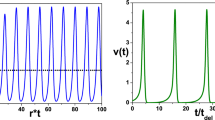
We find the contribution of n to impulse termination and initiation by perturbing its time constant τ _n , and calculating the fractional change in AP and SP durations. This is illustrated in Fig. 1, where the model is in a tonic spiking regime. To measure the contribution of n to the AP, at the start of the action potential τ _n is increased by δτ _n . This slows down the rise in n during that action potential, with a resulting increase in the AP duration of δAP. Therefore, the contribution of $n$ to impulse termination is ${\mathrm{C}}_{\mathrm{AP}}^{\mathrm{n}}=\frac{\updelta \mathrm{AP}}{\mathrm{AP}}\frac{\uptau_{\mathrm{n}}}{{\updelta \uptau}_{\mathrm{n}}}$. Similarly, the contribution of $n$ to impulse initiation is measured by perturbing τ _n at the beginning of the SP, giving ${\mathrm{C}}_{\mathrm{SP}}^{\mathrm{n}}=\frac{\updelta \mathrm{SP}}{\mathrm{SP}}\frac{\uptau_{\mathrm{n}}}{{\updelta \uptau}_{\mathrm{n}}}$ Similar definitions apply for the $h$ variable (Tabak et al. 2011). The AP and SP durations were determined using a simple voltage threshold of -40 mV to detect the start and end of the AP. These measurements were repeated while varying a parameter such as τ _h over a wide range in which spiking solutions occurred. The contribution of variable X was calculated using a δτ _X that perturbed τ _X by 4 %, which we chose so that the perturbation is just large enough to calculate the effects accurately. Numerical simulations for this part of the analysis were performed with XPP (Ermentrout 2002) using the 4th order Runge–Kutta algorithm (dt = 0.01 ms) and independently verified with PyDSTool (Clewley 2012) using the adaptive time-step Radau algorithm (Hairer and Wanner 1999) and after allowing the system to relax to a limit cycle before measuring the change in the AP and SP durations. In the PyDSTool version of this analysis, the AP and SP durations were also defined in terms of regime changes that were detected by dominant scale analysis (see below) rather than simple V thresholds, but the trends in the contribution measures remained the same as those shown in Figs. 7, 9, 10, and 13 (data not shown).

Fig. 1

Increasing ${\uptau}_{\mathrm{n}}$ by ${\updelta \uptau}_{\mathrm{n}}$ at the beginning of an impulse slows down n slightly (red trace), so the active phase is lengthened by $\updelta \mathrm{AP}$ (black trace). V = -40 is used as a threshold to define the onset and the termination of the active phase (AP)

2.3 Dominant scale analysis

This is an alternate approach that determines which variables are dominant during different portions of a trajectory. A portion of a trajectory where one subset of variables is dominant is called a regime. The technique is described in detail in several previous works (Clewley 2004; Clewley et al. 2005, 2009; Clewley 2011). The determination of dominance is based on the asymptotic membrane potential (V _∞) which is derived by rewriting the ODE for V as $\frac{dV}{dt}=\frac{\left({V}_{\infty}\left( m, n, h\right)- V\right)}{\tau_V\left( m, n, h\right)}$. Then, one computes ${D}^s=\left|\frac{d{ V}_{\infty }}{ d s}\right|$ for s = m, n, h, a, and l, where a and l are “dummy” static gating variables for I _app and I _leak , respectively. These sensitivity quantities are ranked at each point in time along a trajectory, and the largest at time t is called “dominant.” Roughly speaking, we define “regime change” as the times when the most dominant variable changes. In the AP, there is a regime dominated by n followed by one that is dominated by h.

We measure the fraction of the AP duration occupied by the n-dominated regime as the effective contribution of n to the AP duration and denote it D ⁿ_AP . As we do not find any AP regime dominated by m in the Type I dynamics, we set D ^m_AP  = 0. Similarly, there is no SP regime dominated by h, so D ^h_SP  = 0.

Numerical simulations for this part of the analysis were performed with PyDSTool (Clewley 2012) using the Radau stiff integrator with variable step size (maximum dt = 0.05 ms for models A and B, $5$ms for model C).

The source code containing the model definitions and the simulation and analysis scripts are available at http://www.math.fsu.edu/~bertram/software/neuron and on modelDB (https://senselab.med.yale.edu/ModelDB). The code is also included as supplementary material.

3 Results

3.1 Robustness of models with one or two negative feedback variables

Here we ask whether there is an advantage of having two negative feedback processes by comparing the HH model with models that have only one negative feedback process: the h-model and the n-model. The measure of robustness that we use is the extent of the parameter range within which tonic spiking is the unique stable limit cycle solution. We use Type II parameter values here but obtained similar results with the Type I parameter set.

While I _app acts as an input to the system, g _Na measures the gain of the positive feedback and g _K measures the amount of subtractive feedback. Figure 2 shows the effects of changing I _app on voltage traces (panels a, b and c) and the durations of the AP and SP (d) for the h-model, the n-model and the HH model (model B). The AP and SP durations are plotted over the full range of I _app for which the model cell exhibits tonic spiking. While AP durations (solid lines) change slightly with I _app , SP durations (dashed lines) drop dramatically with increasing I _app and it is this decrease that is primarily responsible for the increase in spike frequency as I _app is increased in Fig. 2a–c. In the n-model, the decrease in SP is compensated by an increase in AP duration at larger I _app . Also, for the h-model, the range of I _app values that support spiking is comparatively limited.

Fig. 2

The effects of changing applied current on AP and SP durations. Tonic spiking in the (a) h-model (g _k  = 3.6) (b) n-model (g _Na  = 12) and (c) HH model (model B) increases in frequency when I _app is increased from 65μA/cm² to 95μA/cm². (d) Durations of the AP (solid line) and the SP (dashed line) for the h-model, the n-model and the HH model

The SP duration of the h-model is restricted and more sensitive to changes in I _app than the n-model (Fig. 2d). These differences in response to variations in I _app can be explained by phase plane analysis. In Fig. 3, V-nullclines (S shaped for the h-model and Z shaped for the n-model) with different  I _app values are presented along with the h-nullcline for the h-model (left) and the n-nullcline for n-model (left). Fig. 3a shows that changing I _app affects the low knee much more than the high knee for the h-model. This is mostly because h multiplies m ³_∞ (V) in the voltage equation and at low voltages m ³_∞ (V) is almost zero. When I _app is changed, there is a large compensatory change in the value of h needed to bring V to threshold. On the other hand, when the value of V is high, the value of m ³_∞ (V) is near 1, so variations in I _app do not necessitate a large compensatory change in the value of h at the high knee. Therefore, in most models with divisive feedback, as long as m _∞ is small at negative values of V, the low knee will be more sensitive to I _app than the high knee. This is discussed in more detail in (Meng et al. 2012; Tabak et al. 2006). Since the trajectory follows the bottom branch of the V-nullcline during the SP, the sensitivity of the low knee to I _app means that the SP duration will also be sensitive to I _app , as demonstrated in Fig. 2. For I _app sufficiently small, the spiking stops altogether as the system passes through a Hopf bifurcation. The entire dynamic range of the model is covered by the I _app interval from 68 μA/cm² to 100 μA/cm².

Fig. 3

Nullclines for the h-model (a) and n-model (b) for three values of I _app Parameter values are as in Fig. 2

In the n-model, changing I _app also primarily affects the low knee (Fig. 3b), but less so than in the h-model. Therefore, the model is more robust to changes in I _app . On the other hand, for the n-model there is a sensitivity of the high knee to g _Na that is similar to the sensitivity of the low knee to I _app for the h-model (not shown). This is why the range of g _Na values that produce oscillations is small for the n-model (Fig. 5).

Figure 4 shows the changes in AP and SP durations as g _Na and g _K are varied. When the activity is regulated by the Na⁺ current inactivation, as in the h-model, increasing g _Na speeds up the spiking activity by decreasing the SP duration (Fig. 4a, blue dashed line). If the activity is regulated by the K⁺ current activation, as in the n-model, then increasing g _Na slows the activity by increasing the AP duration (Fig. 4a, red solid line). Thus, the two models respond very differently to changes in g _Na . On the other hand, the HH model combines a modest increase of AP duration (as with the n-model) with a modest decrease in SP duration (as with the h-model) when g _Na is increased (Fig. 4a, green solid/dashed lines). Note also that the HH model oscillates over a much larger range of values of g _Na than either the n- or h-model. Finally, Fig. 4b shows that increasing g _K slows the spiking activity by increasing the SP in all models. It also decreases AP duration for the n- and HH-models.

Fig. 4

Effects of changing g _Na and g _K on AP and SP durations. (a) Effects of changing g _Na on AP duration (solid line) and SP duration (dashed line) for the HH model, the h-model and the n-model. (b) Effect of changing g _K on the AP duration (solid line) and the SP duration (dashed line) for the HH model, the h-model and the n-model. Parameter values are as in Fig. 2

The parameter interval for oscillations is delimited by Hopf or saddle-node of periodics (SNP) bifurcations. That is, as a parameter is varied, a model begins to oscillate according to one of these bifurcations. In our models, when an SNP exists, it is very close to a subcritical Hopf bifurcation. For simplicity, we use the Hopf bifurcation as the boundary. If we vary two parameters, the curves of Hopf bifurcations form the approximate boundary between oscillatory and non-oscillatory behavior. We show these in Figs. 5 and 6, varying the pairs of parameters (I _app , g _Na ) and (I _app , g _K ).

Fig. 5

Oscillatory regions for the h-model and the n-model. (a) Oscillatory region for g _Na vs. I _app using the h-model. (b) Oscillatory region for g _Na vs. I _app using the n-model. (c), (d) Oscillatory regions for g _K vs. I _app

Fig. 6

Oscillatory regions for the HH model (Model B) with oscillatory regions for the h model (g _K  = 36mS/cm ²) and the n-model (g _Na  = 120mS/cm ²) superimposed. (a) In the I _app  − g _Na plane, the region is slightly smaller in size for the HH model than the h-model and larger in size for the HH model than the n-model. (b) In the I _app  − g _K plane, the region for the HH model is much larger than for the h-model. The bounding curves are curves of Hopf bifurcations (see text for details)

The size of the oscillatory region for the h-model varies greatly with the frozen conductance, g _K . To illustrate, we show the oscillatory region for several values of g _K (Fig. 5a). The region shifts rightward as g _K is increased since more applied current is required to drive oscillations. In addition, more Na⁺ conductance is required for the action potential upstroke so the oscillatory region grows in the g _K direction. The size of the oscillatory region also grows with larger values of g _K . By comparison, the oscillatory region is much smaller for the n-model (with h frozen) with the same value g _K  = 36mS/cm². For this model, the oscillatory region is severely restricted in the g _Na direction (Fig. 5b, note change in scale), since with h frozen there is no compensation mechanism in the Na⁺ current for an increase in g _Na . Similar behavior is observed when one views the oscillatory region in the I _app  − g _K plane with the n-model. As g _Na is increased the oscillatory region grows and moves upward and to the right (Fig. 5d). However, at the largest g _Na value, where the region is very large in the n-model, the region is very restricted in the g _K direction with the h-model (Fig. 5c, note change in scale). Thus, for each model with a frozen conductance, the oscillatory region is greatly restricted with respect to that conductance.

This limitation is overcome in the full HH model, since now both n and h are free to adapt to changes in g _K and g _Na . This is illustrated in Fig. 6, where the oscillatory regions for the HH model, the h-model (with g _K  = 36mS/cm², from Fig. 5a,c) and the n-model (with g _Na  = 120mS/cm ², from Fig. 5b,d) are shown together. In the I _app  − g _Na plane the h-model has an oscillatory region with similar size to that of the HH model but it is right-shifted. However, in the I _app  − g _k plane the oscillatory region for the HH model is much larger since n can adapt to increases in ${g}_K$ while n is frozen and can’t adapt in the h-model. The n-model behaves similarly, with a larger oscillatory region in the I _app  − g _K plane, but a substantially smaller region in the I _app  − g _Na plane where the variable is frozen. Thus, the HH model provides a good compromise between the two models with a single source of negative feedback.

3.2 Slow variable contributions in the relaxation limit

Our goal in this section is to begin the investigation of the roles played by n and h in the termination of the active phase and the silent phase of the spike pattern (Fig. 1). We employ the two methods for evaluating variable contributions that were described in Methods (sections 2.2, 2.3). First we consider the relaxation limit, which we approximate in our simulations by multiplying the time constants of n and h by 50. In addition, we set m = m _∞(V), so that we have a 3D system with one fast (V) and two slow variables (n − h). For a range of values of n and h the fast voltage equation is bistable, and as n and h slowly vary the voltage moves from one stable point to the other in a relaxation oscillation. In this case, the extreme separation of time scales between slow and fast variables should make the results of the contribution analysis unambiguous. Because the results for Type I and Type II are very similar, we only show results for Type II dynamics in Model C of Table 2.

Intuitively, the faster the rate of change a negative feedback variable is relative to the other, the more it will vary and therefore it should contribute to ending the active and silent phase, so we vary the relative time scales of n and h by varying λ _n /λ _h (see Eq. (9)). Increasing this ratio slows the rate of change of n relative to h.

In Fig. 7a, the contribution of n to the active phase (C ⁿ_AP ) decreases with the ratio λ _n /λ _h so that n contributes less when it is slower relative to h. Panel b shows that the variations of C ^h_AP are complementary to those of C ⁿ_AP ; as the contribution of n to AP duration declines with λ _n /λ _h , the contribution of $h$ increases. As expected, making a variable faster relative to the other increases its contribution. In contrast, $n$ is almost entirely responsible for setting the interspike interval, regardless of λ _n /λ _h (Fig. 7a) and h contributes little (Fig. 7b). Again C ⁿ_SP and C ^h_SP are complementary, but this time they are not much affected by the relative speeds of n and h. These results show that $n$ and $h$ contribute similarly to AP duration, with a dependence on the relative speed of the variable, while only n contributes significantly to setting the SP duration. That is, a spike can occur only when n has decreased to a certain level. For both SP and AP, the sum of the contributions of n and h is nearly equal to 1, indicating that this approach accounts for all contributions to active and silent phase durations (Tabak et al. 2011).

Fig. 7

Contributions of n and h in the relaxation limit (Model C) with Type II dynamics. The relative time scales of n and h are varied by changing λ_n/λ_h, with λ _n  = 1. (a) Contributions of n to episode termination (C ⁿ_AP ) and initiation (C ⁿ_SP ). (b) Contributions of h to episode termination (C ^h_AP ) and initiation (C ^h_SP ). (c) First panel shows the time courses of the variables n, h and m _∞. Second and third panels are the absolute values of the Na⁺ and K⁺ currents for the AP (left) and the SP (right)

Figure 7c shows the time courses of n, h and m _∞ (upper panel) and the absolute values of the Na⁺ and K⁺ currents (lower panels) for λ _n /λ _h =1. During the AP, n rises and h falls, while the opposite occurs during the SP. It is not evident from these time courses why n controls the duration of the SP. Yet, these variables affect the membrane potential through the I _Na and I _K currents. During the SP, the conductance of the Na⁺ current, ${\overline{g}}_{Na}{m}_{\infty}^3 h$, is nearly 0 since m _∞ ≈ 0. Hence h has a little impact on V during the SP, which n controls instead. In contrast, Na⁺ and K⁺ current levels are similar during the AP, which explains why n and h contribute together to the active phase.

3.2.1 Comparison with dominant scale analysis

We employ dominant scale analysis here to determine which fraction of the AP is controlled by n, using D ⁿ_AP , and which fraction is controlled by h, using D ^h_AP . Similar fractions (D ⁿ_SP , D ^h_SP ) are computed for the SP.

Figure 8 shows that n is dominant during the entire SP, regardless of the time scale ratio. This is consistent with the results from contribution analysis (Fig. 7). The n variable is also dominant during much of the AP, when λ _n /λ _h is small (n faster). This dominance is transferred to h as λ _n /λ _h is increased, increasing the speed of h relative to n. Again, there is qualitative agreement with the contribution analysis (Fig. 7).

Fig. 8

Dominant scale analysis in the relaxation limit (Model C) with Type II dynamics. Influence of (a) n and (b) h on AP and SP durations with the ratio λ _n /λ _h

3.3 Contributions away from the relaxation limit

Next, we return the time constants to their default values λ _n  = 1 and λ _h  = 1 for model B of Table 2. The oscillations produced are now recognizable action potentials rather than relaxation oscillations. Figure 9 shows the results of the contribution analysis for n and h for the Type I and Type II parameter sets. The variables contribute to the AP and SP in a similar manner to the relaxation case when Type II excitability parameters are used (Fig. 9a2–c2). This suggests a spiking mechanism similar to spiking at the relaxation limit.

Fig. 9

Away from the relaxation limit, n and h contribute differently with Type I and Type II dynamics. (a1-c1) Contributions with Type I dynamics. (a2-c2) Contributions with Type II dynamics

Figure 9 a1 and b1 shows that the contributions of n and h to the AP duration have similar values with Type II and relaxation cases. Surprisingly, though, for Type I parameter values, neither variable contributes much to the SP duration. This can also be seen in Fig. 9c1, where the sum of the n and h contributions is far below one for the SP. This is in stark contrast to the relaxation oscillation case. What is responsible for terminating the SP away from the relaxation limit? We examine this in Fig. 10. To do so, we increased the membrane capacitance C for the duration of one AP or SP, thereby increasing the time constant of V during that phase. For the Type II parameter set, this shows that V dynamics have a small influence on AP and SP durations (Fig. 10b). For Type I parameters, V dynamics are primarily responsible for the SP duration (Fig. 10a). The contributions of n, h and V sum to 1 for both AP and SP (Fig. 10c), as expected.

Fig. 10

V is responsible for the episode initiation when the Type I parameter set is used. (a) Contribution of V to episode termination and initiation for the Type I parameter set and (b) Type II parameter set. (c) The sums of the contributions of the n, h and V to the AP and to the SP for Type I excitability are close to 1. Similar results are observed for Type II excitability

Figure 11 shows the time courses of n, h and m _∞ (row a), the absolute value of the Na⁺ and K⁺ currents (row b), and the absolute value of the sum of the leak current and applied current (row c) for Type I and Type II parameters. During the AP, Na⁺ and K⁺ current are similar and their values are much higher than I _leak  + I _app . This confirms that n and h are controlling the AP. During the SP, I _K and I _Na are almost 0 for the Type I model, while the net current I _app  − I _leak > 0 slowly depolarizes the membrane towards spike threshold. However, for the Type II model, I_K is larger than the other currents during the silent phase because it deactivates much more slowly during the SP, helping to gate the effects of the depolarizing forces. Thus, we can interpret n to be responsible for spike initiation for the Type II model but not for the Type I model, where I _app and I _leak are the main factors bringing V back from the hyperpolarized levels of the SP.

Fig. 11

Difference between Type I (left) and Type II (right) excitability away from the relaxation limit in terms of the system variables and currents. (Row a) Time courses of the system variables. (Row b) Absolute value of the Na⁺ and K⁺ currents for both the active phase (left sub-plot) and the silent phase (right sub-plot). (Row c) Absolute value of the sum of the applied and the leak currents for both the active phase (left sub-plot) and the silent phase (right sub-plot)

3.3.1 Dominant scale analysis explains the “contribution of V”

In Fig. 9, we observed that none of the negative feedback variable contributes much to SP for Type I. We found a significant contribution of V (Fig. 10), meaning that changing the V time constant affected SP duration. But what does this mean? To understand how V dynamics influence the SP, we can use dominant scale analysis.

Figure 12 shows the dominant scale analysis for model B. For the Type II parameter set, both n and h contribute to the AP with n contributing more when it is faster than h, and vice versa. As was seen with contribution analysis, n is dominant at all times during the SP. With the Type I parameter set the results are again consistent with contribution analysis. In particular, n plays only a partial role and h no role at all in the SP. Instead, the leak and applied currents are important, as is m (Fig. 12c1). As the K⁺ current deactivates (decline in n) it is the leak and applied depolarizing currents that bring the voltage back to spike threshold. As the voltage depolarizes the Na⁺ current begins to activate (m), complementing the effects of I _leak and I _app . In model B, m = m _∞(V) so Na⁺ current activation is instantaneous with V. Thus, the “V contribution” indicated in our contribution analysis (Fig. 10) is mediated by two factors that depend only on V (I _leak and activation of I _Na ) and a constant applied current.

Fig. 12

Dominant scale analysis for Type I (top) and Type II (bottom) excitability away from the relaxation limit (Model B). Influence of (a) n, (b) h and (c) I _leak , I _app and m which is instantaneous (m = m _∞)

3.4 Contributions of the variables in the full HH model

We began our analysis with the relaxation limit as the simplest case, and then we removed the relaxation assumption and found that in this case there was a difference between Type I and Type II dynamics for the HH model. We now remove the rapid equilibrium assumption m = m _∞(V) and analyze the full HH Model (model A of Table 2). This does not significantly affect the relative contributions of n and h (not shown). Fig. 13 shows the m contribution for a range of λ _n /λ _h . Contributions of m are always small and, as expected, are independent of the ratio λ _n /λ _h . A similar result is obtained with dominant scale analysis (not shown). Thus, adding independent dynamics of m has little effect on its contribution to the action potential, confirming that the often-used quasi-equilibrium approximation (m = m _∞(V)) has little qualitative impact on the spike dynamics in these HH models.

Fig. 13

Validating the m = m _∞ assumption used in model B by measuring the contributions of m to the AP and SP in the full model A. (a) Contributions of m to episode termination (C ^m_AP ) and initiation (C ^m_SP ) for the Type I parameter set. (b) Contributions of m to episode termination (C ^m_AP ) and initiation (C ^m_SP ) for the Type II parameter set. When m is not instantaneous it has a weak contribution to both AP and SP (c) Sums of the contributions of all variables including m to the AP (C ⁿ_AP  + C ^h_AP  + C ^m_AP  + C ^V_AP ) and to the SP (C ⁿ_SP  + C ^h_SP  + C ^m_SP  + C ^V_SP )) for the Type I parameter set. Similar results are observed for the Type II parameters

4 Discussion

Biological systems rarely take the simplest approach to achieving a function. Instead, there are often complex pathways where simpler ones would be sufficient and redundancies where none seem needed. We have explored the roles played by two apparently redundant elements of a classic model for neuronal electrical activity, as well as the advantage of having redundancy in this model. Although the results of the analysis are specific to the Hodgkin-Huxley model, the two analysis techniques that we employed could be used for any neuronal model. For example, one could use the techniques to analyze the contribution that inactivation of an A-type K⁺ current or T-type Ca²⁺ current make to spike initiation or termination, or one could analyze the contribution that n and h make in a model with these additional types of ionic currents. In the latter case, the results would likely differ quantitatively, and perhaps qualitatively, from what we show here. Indeed, we have demonstrated that even with a single model the contributions made by n and h are different with Type 1 and Type 2 dynamics, and differ at the relaxation limit versus away from that limit. In other words, the contributions vary with the set of parameter values used. Therefore, the main messages that we wish to convey are (1) divisive and subtractive feedback can contribute very differently to different phases of the impulse and are model- and parameter-dependent, (2) contribution analysis and dominant scale analysis are two complementary techniques that can be used to determine these contributions, and (3) having both variable K⁺ and Na⁺ conductance in the Hodgkin-Huxley model increases the robustness of the oscillations to parameter changes.

4.1 Robustness of rhythmic spiking: two feedback variables are better than one

We first focused on whether there is an advantage to having a model with two negative feedback variables instead of one by analyzing reduced models in which n or h were held constant. One observation from the oscillatory regions of the single negative feedback variable models in Fig. 5 is that the regions are highly sensitive to the conductance associated with the frozen variable. Having an activation variable like n allows the system to compensate for increases in g _K (or I _app ) by simply reducing the values covered by n during spiking. Thus there is a large range of values where oscillations occur. When n is frozen, a change in g _K or I _app may also be compensated by a change in the values covered by h during spiking, but because the V-nullcline is so sensitive to g _K or I _app in that case, the necessary change in values may be too large to support spiking (cf. Fig 3a). Similarly, the n-model shows little compensatory ability to a change in g _Na because its V-nullcline is sensitive to changes in this parameter. On the other hand, if we unfreeze h, then a change in g _Na can be compensated by an opposite change in the range of values covered by h. Since the Hodgkin-Huxley model has compensation in both the Na⁺ and K⁺ currents it can compensate for a wide range of variations in all three parameters I _app , g _K and g _Na (Fig. 6).

Nevertheless, we saw in Figs. 5 and 6 that the h-model could support oscillations in a wide area of the I _app - g _Na   plane, and that the n-model could support oscillations in a wide area of the I _app - g _K plane. Depending on the values of the other parameter, these areas could even be larger than the area supporting oscillations in the HH model. However, these areas, for instance the area shown with g _K  = 18 in Fig. 5a (h-model), comprise parameter values that are much larger than in the HH model. In other words, it would be more costly for a cell to operate in these ranges, because this would require more inputs and more channels on the cell surface. Finally, we note from Figs. 2 and 4 that the HH model typically has a shorter active phase than the n- and h-model, with little variation in AP with parameters. This ensures a short and constant spike duration in many situations.

Thus, adding one extra negative feedback variable to the n- or h-model allows for a robust spiking behavior. It is not surprising that allowing a parameter to “unfreeze” would lead to more flexible behavior. There are indeed many examples in computational biology where the robustness to input or parameter values, or the range of possible behaviors, are increased by adding dynamic variables (Tomaiuolo et al. 2008; Tsai et al. 2008; Howell et al. 2012).

4.2 The contributions of the negative feedback variables are parameter dependent

An interesting finding is that the divisive feedback variable contributes very little to the SP duration in the relaxation limit. This raises the question of whether the h-model can produce impulses in this limit. It does, but only over a restricted range of applied currents, due to sensitivity of the lower knee of the V-nullcline to changes in I _app (Fig. 3). This sensitivity also explains why h does not contribute significantly to the silent phase. Thus, the high sensitivity of the h-model to I _app and the negligible contribution to the SP of h dynamics in the HH model occur for the same reason. Namely, during the silent phase m _∞(V) is close to 0 so h dynamics have little effect. Thus, as long as this holds (m _∞(V) ≈ 0 during the SP), we expect little or no contribution of h to the SP. In models for which m _∞(V) is not close to 0 during the silent phase, recovery from inactivation might contribute to terminating the SP. That is, the negligible contribution of h dynamics to the SP depends on the parameters describing I _Na activation.

Another interesting finding from the contribution analysis arose from examining variable contributions for parameter sets yielding Type I or Type II dynamics. In the relaxation limit, the contributions of n and h with the Type I parameter set are similar to those with the Type II parameter set. This is not the case away from the relaxation limit (Fig. 8). Indeed, for the Type I case, spike initiation relies heavily on elements other than n and h . This was brought to light using contribution analysis (Fig. 10), and then fully explored with dominant scale analysis (Fig. 12). Again, this shows that the results of the contribution analysis depend on the parameters describing channel kinetics.

We also analyzed how the parameters that change excitability, such as the Na⁺ conductance g _Na and the applied current I _app , affect the contributions of n and h to the initiation and termination of the active phase and silent phase (not shown). We observed that the relative contributions of n and h are not sensitive to g _Na or I _app , except in the following way: h contributes a little more to active phase termination when the Na⁺ conductance is higher, while it decreases slightly with I _app for both Type I and Type II cases so that h contributes less when applied current is high. On the other hand, increasing I _app for the Type I model brings back the contribution of n to the SP observed in Type II. This is because at high magnitudes of applied current, V becomes strongly depolarized, driving n _∞ away from zero. Finally, the relative contributions of n and h are also largely unaffected by changes in K⁺ and leak conductances.

4.3 Analysis of the contributions of variables and inputs: two tools are better than one

The combined use of our two forms of analysis brings deeper insights into the action potential mechanism than either method alone. For instance, although there are measures of the contribution of V with C^V, there is no corresponding dominant scale measure D^V. This is because the latter technique measures the effects of distinct input currents on V _∞. In the other direction, the measures of ${\mathrm{D}}^{{\mathrm{I}}_{app}}$ and D^leak do not have a corresponding ${\mathrm{C}}^{{\mathrm{I}}_{app}}$ and C^leak because those inputs do not have intrinsic dynamics involving time constants that can be perturbed.

The m variable is different from n and h in having such a small time constant in all the models. Changing τ _m mostly affects the time during the jumps between active and silent phases. Thus, it may not be surprising that perturbing τ _m has a small effect on the durations of the active phase and silent phase (i.e., a small C^m was measured (Fig. 13)). For instance, at the relaxation limit, there is a folded nullsurface in the (V, n, h) state space, and it is solely the slow dynamics of n and h that controls the flow on each sheet, bringing the system to a fold where it jumps between the two different phases. m (or I _app /I _leak has no contribution to flow on a sheet and both analyses agree in this respect. However, m _∞(V) helps to shape the folded surface, which is the set of points where the V derivative is 0 and m = m _∞(V), and therefore affects the precise position of the transition points between the lower sheet (silent phase) and upper sheet (active phase). Away from the relaxation limit, m, I _app and I _leak depolarize V during the silent phase and therefore they have an effect with the time constant τ _V ,so C^V is positive. This is confirmed by the dominance of m, I _app and I _leak in Fig. 12.

As one would expect, the m activation variable is only dominant towards the end of the silent phase and initiates the action potential upswing in both Type I and Type II excitability regimes (Fig. 11). After the upswing, K⁺ activation dominates the dynamics until Na⁺ inactivation assists in the repolarization of the spike’s downswing. When I _Na once again becomes small, the action potential ends and K⁺ dynamics drive the membrane through the refractory period at the beginning of a new silent phase. The dominant scale analysis showed that m, I _app and I _leak have similar contributions to episode initiation (Fig. 12) so that m controls the transition from silent phase to active phase, while I _app brings V up to the point where m and V can enter a positive feedback loop.

4.4 Concluding remarks

Although the results of the contribution analysis depend on channel kinetic parameters, some of the results shown here for the Hodgkin-Huxley model may apply more generally to oscillators controlled by negative feedback processes. For instance, in excitatory neural networks that produce relaxation oscillations, divisive feedback may be mediated by synaptic depression, while subtractive feedback may be mediated by spike frequency adaptation. Having both types of negative feedback processes in these network models provides a larger parameter space over which the network produces spontaneous episodic activity than in network models that incorporate only one type of negative feedback (Tabak et al. 2006). Also, in these network models both the divisive and subtractive feedback control the duration of the active phase, but the dynamics of the divisive feedback have no effect on the duration of the silent phase (Tabak et al. 2011). This lack of influence of the divisive feedback process in the excitatory networks is also due to the fact that during the silent phase the positive feedback process is not engaged, so recovery from divisive feedback has little effect. Given that biological oscillators generally involve fast positive feedback and one or more slower negative feedback processes (Friesen and Block 1984; Ermentrout and Chow 2002; Tsai et al 2008), the results obtained here with repetitive firing in the Hodgkin-Huxley model, and previously with spontaneously active network models, may be observed in a large class of biological oscillators.