Bouncing Cosmology with 4D-EGB Gravity

Abstract

Not long ago, a novel gravitational scheme i.e, $4D-EGB$ (Einstein-Gauss-Bonnet) gravity have been proposed by Glavan and Lin 2020. They rescaled the coupling factor $\alpha$ with $\frac{\alpha }{D-4}$ and developed the field equations. The purpose of this paper is to workout the cosmic bounce with a cubic form of scale factor and workout the bouncing scenario under these assumptions. The flat FLRW metric is used along with the perfect fluid to study the energy conditions. The conditions are scrutinized by using different coupling factors $\alpha$ and cosmological constant $\Lambda$ values. The stability of the assumed scale factor model is in evidence of universal expansion and allows the universal bounce by developing the validations of energy conditions.

1 Introduction

The beginning of the universe can be studied differently by the bouncing idea referred as Bouncing Cosmology. Scientists believed that there will be a chance in time that universe will shrink and return into its small and unified form [2,3,4,5]. The theory of general relativity tells the space time bending and dynamic nature of the universe. Also, Edwin Hubble proposed and evidently proved the accelerated universal expansion [6, 7]. Since then GR has helped us to understand different universal phenomenons and has passed many tests including Solar System test, provided the galactic black hole evidence and gravitational waves phenomenon coming from compact objects and many other cosmological events. However, some other open questions are still in discussion like big bang singularity, dark energy (DE) and dark matter (DM) problems. The Friedmann-Lemaître-Robertson-Walker (FLRW) frameworks are of great interest while studying the singularities form by the big bang under the effect of $\Lambda$ parameter because of their avoidable singularity nature. Also, the Einstein field equations can be made more realistic by $\Lambda$ and a class of exact solutions can be made by changing $\Lambda$ in a specific manner [8].

The modifications of GR in recent years could lead to provided a chance to resolve different modern issues, some by providing more efficient explaining of GR theory and others by making the gravitational interaction with the energy momentum terms [9,10,11,12,13]. Also, the inclusion of quantum effects in the gravity theory generates higher-order non linear curvature terms. However, different dimensional analysis can be involved to study gravity theory and hence provided some prevailing results. The compact integral for the 4D dimensional parametrization [14,15,16,17,18,19,20,21,22,23] provided the following Euler action $\chi (\aleph _4)$ as

$$\begin{aligned} \chi (\aleph _4)=\int _{\aleph _4}\frac{\sqrt{-g}}{\sqrt{1024\pi ^4}}\mathcal {G}d^{4}x, \end{aligned}$$

(1)

The Gauss-Bonnet invariance term $\mathcal {G}$ is $\mathcal {G}=R^{\alpha \beta \gamma \delta }R_{\alpha \beta \gamma \delta }-4R^{\alpha \beta } R_{\alpha \beta }+R^{2}$. This action is topological invariant under metric variation for the boundary limits produced by $\aleph _4$. Also, a vanishing property in the Einsteins field equations can be understood for the higher dimensional space time with a vanishing factor of $D-4$. The two dimensional gravity theory can be made non trivial by generally applying the dimension D at first and hence after formulating the field equations, a rescaling of $D\rightarrow 2$ can be applied and hence the coupling constant $\alpha$ can be replaced by $\frac{1}{D-2}$. A similar approach was utilized by Glavan and Lin [1] to provide the $4D-EGB$ gravity form. They locally produced finite contributions in the equations for 4D space time with non general symmetries. They extracted the local dynamics by making $\alpha$ to $\frac{\alpha }{D-4}$ within the action. However, a more generalized $2n-D$ form of the action provided in (1), was observed by Ai [24], by making the lagrangian $\mathcal {L}_{(n)}$ to some specific Euler densities $R_{(n)}$. The $2n-D$ form of the integral (1) took the form

$$\begin{aligned} \chi (\aleph _{2n})=\int _{\aleph _{2n}}\frac{R_{(2n)}}{4^{n}\pi ^{n}n!}\sqrt{-g}d^{2n}x. \end{aligned}$$

(2)

There is no such contribution of the topological lagrangian $L_{n}$ in the local dynamics for $2n-D$ space time. However, for $D>2n$ dimension, it provides the explanation to the local dynamics.

The FLRW universe models are considered as the background for the modern cosmology. Different cosmological evolutionary eras and respective data regarding cosmic background radiations, anisotropies of the matter, dynamical formations of galactic structures and relations of the redshift luminosities and nucleosythesis have been covered under the scheme of FLRW space time [25,26,27,28,29,30]. Hence, it covers most of the aspects of the modern cosmology. The dimensional parameterizations of the FLRW metric provides the regular field equations. The $2n-D$ spatially flat form of FLRW space time can be considered as provided

$$\begin{aligned} ds^{2}=-dt^{2}+(a^{2}(t)dx^{2}_{1}+a^{2}(t)dx^{2}_{2}+a^{2}(t)dx^{2}_{3}+... +a^{2}(t)dx^{2}_{2D-1}). \end{aligned}$$

(3)

The universal expansion and contraction phenomenon studied by the scale factor a(t).

A big challenge for the cosmologists and researchers is to define the beginning of the universe. In this regard, bouncing universe is considered one of the most appealing model, that not only describes the universal beginning but also depicts what was before the beginning. This model provides a cyclic behavior of the universe for which the universe contracts due to high gravity effects on the particle level and then expands to form a new universe. This cyclic phenomenon is quite similar to the ekpyrotic phenomenon [31,32,33,34,35,36]. A radiated and matter dominated period is included in the expanded phase whereas the contracting phase includes the gravity dominated period. Ijjas and Steinhardt [37,38,39] worked on the classical bounce model that involved a unique representation of the expanded phase, named as wedge diagram. They resulted that a classical bounce can be achieved by demonstrating high fluctuating densities from the contracting phase, moving into the expansion phase. However, it was also provided that decreasing behavior of a(t) confirms contraction and increasing a(t) determines expanding phase. The a(t) becomes critically zero at the bounce point. In recent years, Cai et al. and Brandenberger et al. carried out remarkable results for the non singular universal bounce [32, 40,41,42,43,44]. Different phenomenological features of the bounce have been studied by them e.g. non singular solutions of the homogenous and isotropic solutions using the Lee-Wick field cosmology, anisotropy free solutions for the matter bounce phenomenon, universal contraction for the cold dark matter era with positive $\Lambda$, dark energy and dark matter role for the non singular bounce, relations of different phases using the Planck and BICEP2 data, universal cyclic bounce as an alternative to the inflation using the recent observational data and the instabilities at different stages during the bounce [35, 45,46,47,48,49,50].

Also, the 4D-EGB theory have been used to study many observational cosmic phenomenons including the charged and uncharged black holes and relativistic, isotropic and anisotropic stars descriptions, gravitational lensing in the presence and absence of different matter forms etc. Konoplya and Zinhailo [51] used 4D-dimensional approach to avoid Ostrogradsky instability and formulated a way for Lovelocks theorem. They used ($3+1$) dimensional scheme to produce the radius of the symmetrically flat blackholes. Mansoori [52] proposed a new formalism for the investigation of transitional phases of AdS black holes. They evaluated the Q-zero hypersurface curvatures for 4D-Gauss Bonnet black holes. Bonifacio et al. [53] studied the interaction of the Lovelock and higher order-dimensional Gauss Bonnet geometries. They investigated that the scattering amplitudes of Gauss Bonnet theory are different from the amplitudes produced in general relativity. They also presented the similarity behavior of these scattering amplitudes with the scalar tensor theories.

Ghosh and Kumar [54] proposed the coincidence of the spherically symmetric solutions produced in EGB gravity. They worked on the black hole solutions with spherically symmetric type II fluid compositions. Wei and Liu [55] studied the thermodynamics structure in the EGB gravity. They constructed the Ruppeiner geometry and resulted the interactional effects of the black holes with the high temperature scheme. Zubair and Farooq [56] considered $4D-EGB$ gravity to analyze the oscillatory behavior of the symmetric and matter bounce. They produced the non singular models to explain the late time acceleration and worked out the energy conditions. They also checked the validity of their results by using cosmographic methods. Donevaa and Yazadjiev [17] studied the relativistic stars structures using EGB gravity. They used different equation of state forms for producing the mass radius relation and provided the exacts solutions for stellar structures. Easson et al. [57] employed the dimensional regularization to the EGB gravity and produced the marching behavior of the EGB gravity with the Horndeski gravity theory. They have also utilized the higher curvature Lovelock theories to generate the cosmic solutions.

This article is our attempt to present bouncing cosmology under the 4D-Gauss Bonnet theory. We suggested a new mechanism of the flat FLRW metric for the dimensional analysis. Different model parameters are involved while defining the scale factor development, that leads to the singularity free accelerated universal model. However, the physical results have also been addressed. The layout of this article is: Section(II) includes a brief review of the dimensional analysis for the 4D-Gauss Bonnet gravity. Section(III), provides the scale factor has been presented as a bounce solution to the modified equations of motion. The deceleration, state equation parameter and stability analysis of the bouncing model has been presented by different energy conditions in Sect.(IV). The graphical analysis has also been presented here. The results and conclusions are given in the last section.

2 Dimensional Analysis and the Field Equations

The GaussBonnet invariant terms in EinsteinHilbert gravitational action resulted in EinsteinGaussBonnet gravity. The succeeding order corrections behavior that was predicted by string theories, are completely narrated by the higher curvature and scalar terms for the gravitational action. Let us consider a general form of the action originally produced for the Lovelock gravity [58,59,60]

$$\begin{aligned} \mathcal {I}=\int \sqrt{-g}\bigg [\sum _{i=0}^{n}\alpha _{i}L_{i}(R,R^{\alpha \beta } ,R^{\alpha \beta \gamma \delta }) +L_{m}\bigg ]d^{D}x, \end{aligned}$$

(4)

where $L_{i}$ and $L_{m}$ show the Lovelock lagrangian and matter contributions in the above action respectively. Also, n gives order of $L_{i}$ and $\alpha _{i}$ are coupling constants. The formulation of $L_{i}$, including curvature tensors and scalars are

$$\begin{aligned} L_{i}= \frac{1}{2^{i}}\delta ^{\zeta _{1}\eta _{1}...\zeta _{i} \eta _{i}}_{\lambda _{1}\xi _{1}...\lambda _{i}\xi _{i}}\prod _{s=1}^{i}R_{\alpha _{s}\beta _{s}} R^{\alpha _{s}\beta _{s}}. \end{aligned}$$

(5)

The term $\delta ^{\zeta _{1}\eta _{1}...\zeta _{i} \eta _{i}}_{\lambda _{1}\xi _{1}...\lambda _{i}\xi _{i}}$ symbolizes the generalized kronecker delta. By varying the index i for $L_{i}$, we get

$$\begin{aligned} L_{0} = 1 , \end{aligned}$$

(6)

$$\begin{aligned} L_{1} = R , \end{aligned}$$

(7)

$$\begin{aligned} L_{3} \equiv \mathcal {G}=R^{\alpha \beta \gamma \delta }R_{\alpha \beta \gamma \delta }-4R^{\alpha \beta } R_{\alpha \beta }+R^{2} , \end{aligned}$$

(8)

Here for $n=0$ we get simple cosmological constant, for $n=1$ it will give Einstein-Hilbert form, for $n=2$ Gauss Bonnet form case will arrived. The variation of the action (4) with respect to $g_{\alpha \beta }$ gives the field equations as

$$\begin{aligned} \sum _{i=0}^{n}\alpha _{i}G^{(i)}_{\alpha \beta }= T_{\alpha \beta }. \end{aligned}$$

(9)

Here $T_{\alpha \beta }$ represents the energy-momentum term in the action (4), and is defined as

$$\begin{aligned} T_{\alpha \beta }=\frac{g^{\alpha \beta }\delta [\sqrt{-g} L_{i}]}{\sqrt{-g}\delta [g^{\alpha \beta }]}. \end{aligned}$$

(10)

For $D=2i$, Eq.(10) vanishes, because of the Kronecker delta antisymmetric definition. To evaluate the bouncing evolution, let us consider the 2D form of Eq. (4) under the effect of $\alpha$ parametrization as

$$\begin{aligned} \mathcal {I}=\int \bigg [\frac{\alpha }{D-2} R-\Lambda + L_{m}\bigg ]\sqrt{-g}d^{D}x, \end{aligned}$$

(11)

and taking the variation for $g_{\alpha \beta }$, the corresponding field equations are as

$$\begin{aligned} \frac{2\alpha R_{\alpha \beta }}{D-2}-\frac{\alpha R g_{\alpha \beta }}{D-2}+\Lambda g_{\alpha \beta }=T_{\alpha \beta }. \end{aligned}$$

(12)

The limit $D\rightarrow 2$ can be taken for making a continual scheme in the above field equations. However if we take the trace of this equation, we get

$$\begin{aligned} -R \alpha +\Lambda D=T \end{aligned}$$

(13)

This equation holds for $D>2$, however if we take $D=2$, (13) becomes $T=- \alpha R+2\Lambda$ and nontrivial solutions can be produced without any issue. Also, the vacuum case gives $R=\frac{2\Lambda }{\alpha }$. If we put $D=3$, the trace (13) becomes $T=-\alpha R+3\Lambda ^{(3)}$. The relation of $\Lambda ^{(3)}$ turns out to be $\Lambda =\frac{3\Lambda ^{(3)}}{2}$. Different values of the D gives different dimensional cosmological constant $\Lambda ^{(D)}$ and the effective $\Lambda$. Let us now considering the flat FLRW universe with the perfect fluid composition for the configuration of the bouncing evolution as

$$\begin{aligned} ds^{2}=-dt^{2}+(a^{2}(t)dx^{2}_{1}+a^{2}(t)dx^{2}_{2}+a^{2}(t)dx^{2}_{3}+... +a^{2}(t)dx^{2}_{2D-1}). \end{aligned}$$

(14)

$$\begin{aligned} T_{\alpha \beta }=(\rho +P)V_{\alpha }V_{\beta }-Pg_{\alpha \beta }. \end{aligned}$$

(15)

Here $\rho (t)$ and P(t) implies the energy density and matter pressure terms respectively. However, the $V_{\alpha }$ implies the four velocity vector and is defined as $V_{\alpha }=(1, 0, 0, 0)$. This velocity obeys the relations, $V^{\alpha }V_{\alpha }=1$ and $V^{\alpha }\nabla V_{\alpha }=0$ for the co-moving system. Also, we take $L_{m}=-p$ to make the description, restricted only for the perfect matter composition. Now by using (12), (14) and (15), the non vanishing gravitational field equations observed as

$$\begin{aligned} \bigg (\frac{\dot{a}}{a}\bigg )^{2}=\frac{\rho +\Lambda }{\alpha (D-1)}, \end{aligned}$$

(16)

$$\begin{aligned} \bigg (\frac{\dot{a}}{a}\bigg )^{2}+\frac{2}{\alpha (D-3)} \bigg (\frac{\ddot{a}}{a}\bigg )=\frac{\Lambda -P}{\alpha (D-3)}, \end{aligned}$$

(17)

and the continuity equation becomes

$$\begin{aligned} \bigg (\frac{\dot{a}}{a}\bigg )=-\frac{\dot{\rho }}{3(D-1)}. \end{aligned}$$

(18)

The D in these equations represents the dimensional parameter and $D=2$ can be opted for the formulation of the Friedman field equations.

3 Ansatz Solution and the Bouncing Conditions

Bouncing cosmology has gained much reputation in recent years because of its enrich properties in describing the beginning of the universe [61]. This cosmological model works on the oscillatory idea for which the universal collapse results in the expansion of the new universe. The contracting universe undergoes into a high density state first and then expands. This expansion is so subsequent that it gives a chance for the removal of singularity in the big bang idea. The successful bounce can be achieved by observing the violated NEC for a certain cosmic time period. Also,the state equation parameter $\omega (t)$ undergoes the transition phase to overcome the contraction and entering into the expansion [40, 62,63,64,65]. One of the dark energy model, i.e, quintom model has been provided in the literature that fully defines these transition phases of $\omega (t)<-1$ to $\omega (t)>-1$. This quintom model helps to obtain the bounce situation in the FLRW cosmic regime. However, the energy conditions [66,67,68,69,70,71,72] also work for the validity of the cosmic bounce. In standard cosmology, following are the major conditions for the observation of the perfect bouncing universe :

• As the expansion and contraction rates of the universe studied through a(t), so for the contraction phase, a(t) becomes negative in magnitude, however it becomes positive for the expansion phase i.e, $a(t)<0$ for the contraction and $a(t)>0$ for the expansion.

• For the bounce, the scale factor attains a critically zero form, that turns the negative ($<0$) value into the positive value ($>0$). This bouncing behavior of the scale factor naturally avoid the chance of the singularity at this bounce point, the critical situation becomes i.e, $\dot{a}(t)=0$.

• A successful model of bounce for the Einstein’s gravity becomes

  $$\begin{aligned} H(t)=4\rho (t) \pi G(1+\omega (t))>0, \end{aligned}$$

  (19)

  which is equal to the NEC violation in the same context. However, $\omega (t)<-1$ can be seen satisfied form (20).

Hence, by the above description of the bounce as the model independent study, we apply the power series form of a(t). This will help us to define the bouncing condition for the field (16) and (17).

$$\begin{aligned} a(t)=a_{0}+a_{1}t^{2}+a_{2}t^{3}+a_{3}t^{4}+.... \end{aligned}$$

(20)

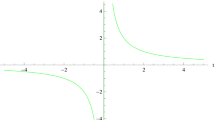
The values of the coefficients are taken as $a_{0}= 0.1, a_{1}= 0.2, a_{2}= 0.3,...$ [73,74,75]. Here, we have an increasing behavior of the scale factor ($a(t)>0$) for $t>0$ in the expanding phase and in the contracting phase decreasing scale factor ($a(t)<0$) for $t<0$. However, at $t=0$ the scale factor a(t) never get zero and implies the null value situation of the Hubble parameter. The functional forms of the Hubble and deceleration parameters are produced as

$$\begin{aligned} H(t)=\frac{ 2 a_{1}t+3 a_{2} t^{2}+...}{a_{0}+t^2 (a_{1}+a_{2} t+...)}, \end{aligned}$$

(21)

$$\begin{aligned} q(t)=-\frac{2 (a_{1}+3 a_{2} t+...) \left( a_{0}+t^2 (a_{1}+a_{2} t+...)\right) }{t^2 (2 a_{1}+3 a_{2} t+...)^2}. \end{aligned}$$

(22)

The evolutional dynamics of the universe can be estimated by the deceleration parameter. The contracting and expanding can be seen in the plot of a(t) provided in Fig. 1. Also, the behavior of the Hubble and deceleration parameter are provided in Fig. 2. The model universe can be seen expanding at an accelerated rate.

Fig. 1

The profile of scale factor a(t)

Fig. 2

The profile of Hubble H(t) and declaration q(t) parameters

Fig. 3

The energy density(left) and matter pressure (right) plots

To develop the necessary condition for the bouncing model, the cosmic energy density and matter pressure forms from (16) and (17), are given as

$$\begin{aligned} \rho (t)=\alpha (D-1) \left( \frac{\dot{a}}{a}\right) ^2-\Lambda . \end{aligned}$$

(23)

$$\begin{aligned} p(t)=-2\alpha \bigg (\frac{\ddot{a}}{a}\bigg )-\alpha (D-3)\bigg (\frac{\dot{a}}{a}\bigg )^{2}+\Lambda \end{aligned}$$

(24)

The state equation takes the form

$$\begin{aligned} \omega (t)=\frac{\rho (t)}{p(t)}=\frac{\alpha (D-1) \left( \frac{\dot{a}}{a}\right) ^2-\Lambda }{-2\alpha \bigg (\frac{\ddot{a}}{a}\bigg )-\alpha (D-3)\bigg (\frac{\dot{a}}{a}\bigg )^{2}+\Lambda } \end{aligned}$$

(25)

The simplified versions of these dynamical quantities under the action of a(t) are given in the Appendix A. Now, for the validation of the above bouncing model, different energy conditions that can be studied and checked. These energy conditions include

• Trace energy condition (TEC) $\Leftrightarrow$ $\rho (t)+3p(t)\ge 0$,

• Weak energy condition (WEC)$\Leftrightarrow$ $\rho (t)\ge 0$, $\rho (t)+p(t)\ge 0$,

• Dominant energy condition (DEC) $\Leftrightarrow$ $\rho (t)\ge 0$, $\rho (t)\pm p(t)\ge 0$,

• Strong energy condition (SEC)$\Leftrightarrow$ $\rho (t)+3p(t)\ge 0$, $\rho (t)+p(t)\ge 0$,

• Null energy condition (NEC)$\Leftrightarrow$ $\rho (t)+p(t)\ge 0$.

The rescaling parameter $\alpha$ and cosmological constant $\Lambda$ served as free parameters. We developed these energy conditions under the role of these parameters. Literature include different values of the $\Lambda$ for the study of the cosmological bounce. In this study, we restricted $\alpha$ to a positive value and measure the validation of these energy conditions for $\Lambda$. Following are the results produced on the energy conditions.

The positive energy density and negative pressure can be observed from Fig. 3. This shows the validation of four energy conditions thereby confirming the accelerated universal expansion. The violated NEC is also justified and can be seen in the left plot of Fig. 4. However, the violation SEC and WEC can be observed from Fig. 4. One can determine the effective role of $\Lambda$ in the accelerating universal expansion from these graphs. Furthermore, the left and right plots of Fig. 5 show that DEC and TEC are satisfied and that was expected for the realistic cosmographic scenario. Lastly, the negative development of the EoS parameter ensures the evolution of the toy model into the quintom model and confirms the bounce.

Fig. 4

The NEC (left) and SEC (right) plots

Fig. 5

The DEC (left) and TEC (right) plots

Fig. 6

The equation of state parameter plot

Fig. 7

The Energy density $\rho (t)$ (left) and matter pressure p(t) (right) plots

Fig. 8

The NEC (left) and SEC (right) plots

Fig. 9

The DEC (left) and TEC (right) plots

However, to understand the role of $\alpha$, we fixed $\Lambda$ and produced the energy conditions. These energy conditions get satisfied for the positive values of the rescaling factor but remain unsatisfied for the negative $\alpha$. A detailed graphical analysis is given in the Appendix B.

4 Conclusion

Newly proposed 4D Einstein-Gauss-Bonnet gravity helped many discussions to carry out fruitful results. This theory presented that the Gauss Bonnet invariant term G produced local dynamical porphyries. A rescaling technique have been presented for the couple parameter $\alpha$ to $\frac{\alpha }{D-4}$ that is in connection with the topological term G. In this study, we first developed the background idea of the dimensional analysis for the $4D-EGB$ gravity and then produced field equations. A flat FLRW space time is taken along with the perfect fluid universal composition for the study of the bounce. A special series form of the scale factor have been applied on the field equations to check the behavior of the dynamical quantities. However the Hubble and deceleration parameter has been discussed to describe the bounce. A detailed graphical analysis has been done under the role of $\alpha$ and $\Lambda$ parameters for the energy conditions in order to verify the bounce model. The concluding remarks are stated as

• For the study of the natural bounce, the $2n-D$ scheme have been set and the general field equations are produced for the perfect fluid composition. The field equations are then checked by the assumption of the series form scale factor i.e, $a(t)=a_{0}+a_{1}t^{2}+a_{2}t^{3}+a_{3}t^{4}+...$. This scale factor shows a radical increase and decrease in the expansion and contraction phase respectively. However, the scale factor allows the Hubble para,meter to get a zero value at the bouncing point i.e, $H(t)=\frac{ 2 a_{1}t+3 a_{2} t^{2}+...}{a_{0}+t^2 (a_{1}+a_{2} t+...)}$. This variational behavior of these two parameters are given in the Figs. 1 and 2 (left plot). These parameters in the Figs.1 and 2 are set accordingly to get a bounce. The deceleration parameter q(t) produced in this study shows the negative value and confirms the accelerated expansion during the phase of expansion.

• To provide the validation of the bounce, we studied different conditions by the formulation of the energy density and matter pressure. Different energy conditions are then produced by the same scheme using $\rho (t)$ and p(t). However, we include the effects of $\alpha$ and $\Lambda$ parameters [76,77,78,79]. All the energy conditions are fulfilled for the positive rescaling parameter $\alpha$ with the different values of cosmological parameter $\Lambda$, and in accordance with the results produced in [56, 80] whereas the energy conditions violated for the negative $\alpha 's$. Figs. 3, 4, 5, 6, 7, 8 and 9 shows these results.

  Energy Conditions	$\Lambda =1$, $-1\le \alpha \le 0$	$\Lambda =1$, $0\ge \alpha \le 1$	$\alpha =1$ and $-1\le \Lambda \le 1$
  $\rho (t)$	$\times$	$\checkmark$	$\checkmark$
  p(t)	$\times$	$\checkmark$	$\checkmark$
  $\rho (t)$+p(t)	$\times$	$\checkmark$	$\checkmark$
  $\rho (t)$-p(t)	$\times$	$\checkmark$	$\checkmark$
  $\rho (t)$+3p(t)	$\times$	$\checkmark$	$\checkmark$
  $\rho (t)$-3p(t)	$\times$	$\checkmark$	$\checkmark$
  $\omega (t)=\rho (t)/p(t)$	$\omega (t)\rightarrow 1$	$\omega (t)\rightarrow -1$	$\omega (t)\rightarrow -1$

• The state equation parameter $\omega (t)$ in (25) shows a similar pattern with as that of the quintal model that is a major condition for a bouncing model to show the non singular bounce [41, 81,82,83]. Therefore, we can conclude that the $4D-EGB$ can be used to obtain a non singular bounce model.

Appendices

Appendix A

For the flat FLRW metric (3), the non vanishing Christoffel symbols for this study are obtained as

$$\begin{aligned} \Gamma ^{0}_{ij}=\dot{a}(t)a(t)\delta _{ij}, \Gamma ^{i}_{0j}=\dot{a}(t)a(t)\delta ^{i}_{j}. \end{aligned}$$

(26)

here, $\delta$ shows the Kronecker symbol. The non vanishing Ricci tensor components are

$$\begin{aligned} R_{00}=-\ddot{a}(t)/a(t)(D-1), R_{jj}=\ddot{a}(t)a(t)+\dot{a}^{2}(t) (D-2). \end{aligned}$$

(27)

The Ricci scalar turns out to be

$$\begin{aligned} R=2\ddot{a}(t)/a(t)(D-1)+(\dot{a}(t)/a(t))(D-1)(D-2). \end{aligned}$$

(28)

Hence the Einstein tensor becomes

$$\begin{aligned} G_{00}=\frac{1}{2}(\dot{a}(t)/a(t))^{2}(D-1)(D-2), \end{aligned}$$

(29)

$$\begin{aligned} G_{jj}=-\ddot{a}(t)a(t)(D-2)-\frac{1}{2}\dot{a}(t)^{2}(D-3)(D-2). \end{aligned}$$

(30)

Here, $i,j=1,2,3,...,D-1$. The mathematical forms of are as follows

$$\begin{aligned} \rho (t)=\frac{\alpha (D-1) t^2 (2 a_{1}+3 a_{2} t+...)^2}{\left( a_{0}+t^2 (a_{1}+a_{2} t)+...\right) ^2}-\Lambda \end{aligned}$$

(31)

$$\begin{aligned} p(t)=-\frac{\alpha (D-3) t^2 (2 a_{1}+3 a_{2} t+...)^2}{\left( a_{0}+t^2 (a_{1}+a_{2} t)+...\right) ^2}-\frac{4 \alpha (a_{1}+3 a_{2} t+...)}{a_{0}+t^2 (a_{1}+a_{2} t+...)}+\Lambda . \end{aligned}$$

(32)

$$\begin{aligned} \nonumber \rho (t)\pm p(t)= & {} \frac{\alpha (D-1) t^2 (2 a_{1}+3 a_{2} t+...)^2}{\left( a_{0}+t^2 (a_{1}+a_{2} t)+...\right) ^2} \pm \frac{-\alpha (D-3) t^2 (2 a_{1}+3 a_{2} t+...)^2}{\left( a_{0}+t^2 (a_{1}+a_{2} t)+...\right) ^2}\\+ & {} \frac{-4 \alpha (a_{1}+3 a_{2} t+...)}{a_{0}+t^2 (a_{1}+a_{2} t+...)}. \end{aligned}$$

(33)

$$\begin{aligned} \nonumber \rho (t)\pm 3p(t)= & {} \frac{\alpha (D-1) t^2 (2 a_{1}+3 a_{2} t+...)^2}{\left( a_{0}+t^2 (a_{1}+a_{2} t)+...\right) ^2} \pm \frac{-3\alpha (D-3) t^2 (2 a_{1}+3 a_{2} t+...)^2}{\left( a_{0}+t^2 (a_{1}+a_{2} t)+...\right) ^2}\\+ & {} \frac{-12 \alpha (a_{1}+3 a_{2} t+...)}{a_{0}+t^2 (a_{1}+a_{2} t+...)}. \end{aligned}$$

(34)

Appendix B

The energy conditions plots.