1 Introduction

For many years, the dynamic properties of disordered systems have always been a hot spot of research. People’s interest in this topic can trace back to a groundbreaking paper published by Anderson in 1958. He pointed out that the localization of non-interacting particles occurs under sufficiently strong quenched disorder conditions to prevent transport in the thermodynamic limit [3]. Anderson localization is one of the fundamental quantum phenomena in nature. The localization of electronic Bloch waves is due to the disordered interference in the system, which is the transmission mechanism behind the metal-insulator phase transition in the solid. Although this mechanism was proposed more than 50 years ago, direct observation of Anderson’s localization has always been a well-known difficulty due to the reliable control of disorder in solid-state systems. But in a diffuse Bose-Einstein condensate in a one-dimensional (1D) waveguide with disordered laser speckle potential, Billy et al. observed Anderson localization [4]. Advances in manipulating ultra-cold atoms provide a useful tool for directly observing this fundamental quantum phenomenon. Roati observed 1D Aubry-André localization (a phase transition closely related to Anderson localization [5]) in cold atoms in asymmetric quasi-periodic potentials [6]. Interestingly, Anderson’s localization can occur in the ground and (high) excited states.

Due to the possibility of localization in interacting systems, many-body localization (MBL) in interacting disordered systems has received extensive attention in recent years. For weak interactions, the perturbation argument supports the existence of localized phases [7,8,9,10], for solid interactions, numerical studies have found the characteristics of many-body localization [11,12,13,14,15,16]. Experiments with ultracold atoms and ions have also been used to explore the properties of MBL transitions [17, 18]. The existence of metal-insulator transition has been confirmed in some projects [11, 12, 19], for example, Basko, Aleiner, and Altshuler proved the possibility of a metal-insulator transition in a disordered and interacting system at a finite temperature [7]. This also describes the ergodic destruction of the MBL state. Recent developments in management experimental technology first proved the presence of localized phases [18, 20,21,22], this result has facilitated extensive research on many-body localization (MBL). The phase transition divides the ergodic phase and the localized phase (which will never reach thermal equilibrium) [12, 23,24,25], the ergodic phase has a non-zero energy level repulsive force, the entanglement entropy obeys the law of volume, and it obeys the eigenstate thermalization hypothesis(ETH) [26,27,28]. In the localized phase, there is no eigenstate of energy level repulsionis which means the Poisson level statistic [13], the entanglement entropy of the eigenstate of the highly excited state obeys the law of area instead of the law of volume [29], which violates ETH. The MBL system has a wide range of emerging integrable operators [30, 31] and protects quantum sequences of excited states [32,33,34].

Recently, the localized phase has existed in the quasi-periodic model of the interaction [35], and characteristics of this phase have been experimentally observed [18]. The MBL transition in the quasi-periodic potential Heisenberg chain is the class of Berezinskii-Kosterlitz-Thouless (BKT) transition [36]. When the weakly interacting bosons in the one-dimensional quasi-periodic potential (Aubry-Azbel-Harper model) are localized in all single-particle states, the interparticle interaction may lead to many-body delocalization, within a wide range of parameters, as the temperature increases, delocalization requires stronger interaction coupling [37]. The quasi-periodic field [3] has a period that is not commensurate with the lattice constant, it destroys translation invariance and introduces disorder with a more controllable method different from the random disorder field. The physical properties of the localized phase in the quasi-periodic potential system have not been explored to a large extent, but they have begun to receive considerable (and necessary) attention because the cold atom system provides precise control of the quasi-periodic potential [18, 22, 38, 39]. However, because many methods rely on coupled random distributions, such as real-space strongly disordered RG, there is a lack of analysis tools for studying quasi-periodic potential transitions. Motivated by those results, in this paper, we study properties of the many-body localization (MBL) in the quasi-disordered one-dimensional spin-1/2 chains, investigate the behaviors of the spin-1/2 chains with distinctive nearest neighbor interaction and quasi-disordered external field. And then explore the many-body localization characteristics of the system through the phase transformation in the model.

2 Model Used for Numerics

We study a classic spin model, namely one-dimensional Heisenberg spin-1/2 chain with quasi-disordered fields along the z-direction, the Hamiltonian reads as follows

$$ H = \sum\limits_{i = 1}^{L - 1} ({J_{x}}{S_{i}^{x}} \cdot S_{i + 1}^{x} + {J_{y}}{S_{i}^{y}} \cdot S_{i + 1}^{y} + {J_{z}}{S_{i}^{z}} \cdot S_{i + 1}^{z}) + \sum\limits_{i = 1}^{L} {{h_{i}}} {S_{i}^{z}} $$
(1)

where the \({S_{i}^{a}}\) (α = x, y, z ) are the spin-1/2 oprators and hi donate the on-site disorder. Here we consider the disorder realization of on-site disorder hi are given as

$$ {h_{i}} = h\cos ({\alpha_{i}}) $$
(2)

we equally divide L points in the range \(\left [ { - \pi ,\pi } \right ]\), and then we choose these points as αi, but each time the disorder is realized, the initial value of αi is different, the quasi-disordered field of the many-body system is realized. Here h is the disorder strength of the quasi-disordered external field. We only consider the nearest-neighbor coupling interaction of the quasi-disordered spin-1/2 chain and Jx, Jy, Jz are the coupling coefficient of the spin on the XYZ axis, we will study the properties of systems given in (1) by exact diagonalization to explore whether the MBL transition can occur in this model and then explore some characteristics of ergodic phase and localized phase. We study the behavior of system for five coupling coefficient ratios of Jx, Jy, Jz, when coupling coefficient ratio is 1:1:1, it is the Heisenberg XXX model; when coupling coefficient ratio are 1:1:3 and 1:1:5, they are the Heisenberg XXY model; when coupling coefficient ratio is 1:2:3, it is the Heisenberg XYZ model; when coupling coefficient ratio is 0:0:1, it is the Ising model. Considering open boundary conditions, the length of the chain is L. We add a quasi-disordered external field controlled by a trigonometric function in an interactive closed system. In a one-dimensional spin-1/2 chain with different coupling coefficient ratios, we explore whether the interplay between disorder and interaction constitutes the driving mechanism of the MBL transition.

Since fidelity can be used to describe the many-body localized phase transition in a closed system [1], fidelity is an important concept in quantum information theory. Particularly, the fidelity minimum near the critical point is studied in several models [40,41,42,43]. Fidelity plays a unique role in distinguishing between the ergodic phase and the localized phase in many-body systems. Following ref. [44] the fidelity of the n-th excited state ψn(λ) is defined as the overlap between \(\left | {\left . {{\psi _{n}}}(\lambda ) \right \rangle } \right .\) and \(\left | {\left . {{\psi _{n}}(\lambda + \delta \lambda )} \right \rangle } \right .\), here δλ is a small shift of this field.

$$ F_{n}(\lambda, \lambda+\delta \lambda)=\left|\left\langle\psi_{n}(\lambda) \mid \psi_{n}(\lambda+\delta \lambda)\right\rangle\right| $$
(3)

The fidelity changes in the observability of the quantum phase transition, which is reflected in the minimum fidelity of the critical point (or the divergence point in the thermodynamic limit). In the studies of QPTs, even if there is no order parameter or symmetry is broken, fidelity also can be used to analyze QPTs from the perspective of geometric [45,46,47,48]. Characterization based on the particularity of fidelity in quantum critical phenomena, in this paper, we calculate the fidelity Fn for excited state and average over all chosen excited states and disordered realizations to obtain the averaged fidelity E[F]. The standard libraries for exact matrix diagonalization was used for numerical analysis.

3 Results and Discussion

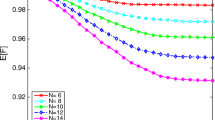
The parallel programming techniques were employed to make computations feasible. Our results reveal that quasi-disorder can cause the occurrence of a transition in a closed system from ergodic phase to localized phase, which agrees with the recent studies [2]. In Fig. 1, we plot averaged fidelity as a function of the disorder strength h for system sizes from 8 to 14 with five different coupling coefficient ratios.

Fig. 1
figure 1

The averaged fidelity as a function of the disorder strength h for system sizes from 8 to 14 with five different coupling coefficient ratios, the coupling coefficient ratios are indicated in the legend. At smaller h (the ergodic phase), the averaged fidelity E[F] generally decays dynamically with the increase of h until it approaches the critical disorder strength hc, then at higher h (the localized phase), E[F] eventually reach saturation at a nearly stable value

Full size image

According to the obvious data changes shown in Fig. 1(a), we can see that when the system size L = 8, in the ergodic phase (smaller h), E[F] generally decays dynamically with the increase of h until it approaches the critical disorder strength hc, in the localized phase (higher h), E[F] eventually reach saturation at a nearly stable value, which means ETH is violated, this also implys to the breakdown of egodic phase. Some insight into the localized phase behaves like integrable systems characterized by many local conservation laws. To intensively study the properties of the ergodic phase and localized phase, we mainly focus on different coupling coefficient ratios highlighting an inherent interaction. We further calculated the values of E[F] for different system, respectively, as the pronounced data change shown in Fig. 1(b), (c) and (d), with the increase of disorder strength we can see a breakdown of egodic phase emerge. Still, comparing results from curves with different coupling coefficients, other models’ localized phase transition characteristics have been found. There are many distinctions between different coupling coefficient ratios. We analyze the behaviors of phase transition, requiring special attention to phase transition trend and the critical point in the spin-1/2 chain model. The critical disorder strength hc in Ising model is the smallest; the XYZ model is corresponding to the coencient ratio 1:2:3, one can see the critical disorder strength hc is the largest; comparing two coupling coencients of the XXZ model, when the proportional coencients of the X and Y terms are equivalent, the more stronger the coupling interaction which associated with the Jz between the two particles, the more diffcult it is for the transition from ergodic phase to localized phase, the larger the critical disorder strength hc required for the phase transition to happen. This implies that the interaction also plays an important role in the many-body localized phase transition. Numerical simulations further demonstrate the established conclusion that the interplay between disorder and interaction constitutes the driving mechanism of the MBL transition [42]. Interactions do enhance the delocalized properties of the system, the more complex the interaction between the two particles, the more difficult it is to lead to many-body localization.

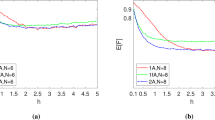
It is highly desired to compare the properties of MBL transition by investigating systems with sufficiently large sizes to solve essential problems reliably, such as whether MBL transitions in quasi-disordered fields and random disordered fields need the exact value of disorder perturbation. Our results are shown in Fig. 2, where we choose the system size L = 8, the averaged fidelity characteristics of the excited state for the Heisenberg XXX model in disordered and quasi-disordered many-body systems have been compared, according to the change of fidelity with h, showing that under the same conditions, the MBL transition of quasi-disordered system requires smaller disorder. This may provide some reference to understand the difference between two disordered systems.

Fig. 2
figure 2

The averaged fidelity as a function of the disorder strength h for a system of size 8, the blue curve represents the random disordered field, and the purple curve represents the quasi disordered field. The MBL transition of the quasi-disordered system requires smaller disorder

Full size image

We study the localization properties of many-body systems at the finite system size, in order to further explore the effect of system size on properties of MBL. The behavior of the averaged fidelity E[F] in the delocalized and localized regimes is observed in Fig. 3, as shown in Fig. 3, for different disorder strength h, at smaller h, the system is in the ergodic phase, at higher h, the system is in the MBL phase, and the drop becomes sharper as the system size L increases. We analyzed one-dimensional spin-1/2 chains for different coupling coefficient ratios, in Fig. 3, we find similar behavioral characteristics for different coupling coefficient ratios. Moreover, we might expect the critical regime to be susceptible to the system size, there is an evident difference of the E[F] and hc for different system sizes. System sizes effects are still an important future issue in MBL. This is also the direction of our future efforts.

Fig. 3
figure 3

(a) The averaged fidelity as a function of the disorder strength h for system sizes from 8 to 14 with the coupling coefficient ratio 001, the system sizes are indicated in the legend. (b) The averaged fidelity as a function of the disorder strength h for system sizes from 8 to 14 with the coupling coefficient ratio 111. (c) The averaged fidelity as a function of the disorder strength h for system sizes from 8 to 14 with the coupling coefficient ratio 113. (d) The averaged fidelity as a function of the disorder strength h for system sizes from 8 to 14 with the coupling coefficient ratio 115

Full size image

4 Summary

Localization due to the intensity of off-diagonal matrix elements is detuned locally, whether in random disorder or quasi-disordered system. This work investigates the properties of MBL in nearest-neighbor interaction models with quasi-disordered onsite modulation. We test the fidelity for high-energy many-body eigenstates, namely, the excited-state fidelity between two excited states related by a small parameter perturbation to investigate properties of MBL. Numerical analysis shows that the quasi-disordered potential can drive the transition from ergodic phase to localized phase. In the ergodic phase (smaller h), the E[F] generally decays dynamically with the increase of h until it approaches the critical disorder strength hc, in the localized phase (higher h), E[F] eventually reach saturation at a nearly stable value which means ETH is violated. It is worth to note that the interplay between disorder and interaction constitutes the driving mechanism of the MBL transition, and the more complex the interaction of the system, the larger the critical disorder strength hc is needed for the phase transition to happen. Besides, these results demonstrate that the MBL phase transition of a quasi-disordered system under the same conditions requires smaller disorder. Our results illustrate the importance of the quasi-disordered fields. Moreover, the critical regime is susceptible to the system size, a complete explanation of this effect requires further interpretation, a more extensive system sizes, and more precise and complex numerical analysis. We hope that the present work can provide a meaningful tool for gaining a better understanding of the MBL transition.