1 Introduction

The digital signature is a vital technique in the informational world realizing the identification of the original information and confirmation of the disavowal. In the quantum information processing and computation, quantum cryptography can provide unconditionally secure communication based on the laws of physics, especially with the no-cloning theorem that Eve cannot duplicate unknown quantum state. These properties make the quantum channel more secure than that of classical channel.

Compared with the classical signature protocol, many quantum signature schemes have been proposed. In 2001, Gottesman and Chuang proposed the first quantum signature protocol in Ref. [1]. Then Buhrman et al. [2] and Barnum et al. [3] made some significant attempts to quantum signature, respectively. In 2002, a pioneering signature protocol named arbitrated quantum signature (AQS) was given by Zeng and Keitel (ZK protocol) [4]. Here a trusted arbitrator is introduced to help the receiver to verify the signature and judges who tells a lie if a disputation happens. Since then, many quantum signature protocols have been studied. In 2009, Li et al. presented a Bell-states-based AQS protocol, which simplified ZK protocol by replacing Greenberger-Horne-Zeilinger (GHZ) states with Bell ones as the carrier [5]. Then, Zou et al. further simplified this protocol by achieving AQS without entangled states [6]. However, Gao et al. pointed out there exist some security loopholes in the previous AQS protocols [7]. They showed that the receiver can make Pauli forgery of the signature, and the signer can successfully disavow the signature. Later, Choi et al. provided an improved idea to prevent the receiver’s Pauli forgery attack with the example of ZK protocol [8]. Recently, Hwang et al. [9] also discussed the security of Zou et al.’s AQS protocol under the denial-of-service attack [10, 11] and Trojan horse attack [12, 13]. Recently, Zhang et al. further analyze the security of AQS [14, 15] and propose some improved ideas [16].

Meanwhile, some special quantum signature protocols have been presented based on the merits of AQS. From 2008, Yang et al. successively proposed some multiparty quantum signature protocols [17–19]. In 2011, they also gave an arbitrated quantum signature protocol against collective amplitude damping noise [20]. At the same time, Wang et al. presented some contributions to the practical quantum signature protocols. In 2010, Wang et al. proposed a fair quantum blind signature protocol based on the fundamental properties of quantum mechanics [21]. A one-time proxy signature with decoherence-free states was also presented to prevent the collective noise in 2012 [22].

A secure quantum signature requires the following conditions: 1) Any two of Trent, message owner and signer will not conspiracy. 2) The scheme will be done strictly by three parties, in the signature process.

In this paper, we will pay attentions to quantum blind signature. In a common digital signature, the original information is visible to signers, which does not match the request of the anonymity of the information holder. To protect the privacy of the information holders, such as electric cash, electric voting and electric auction etc, blind signature makes the related information invisible to signers. The original information is made ”blinded” by the holder before it is delivered to signers. Quantum blind signature is a new research topic combining with classic blind signature and quantum techniques. Similarly with classical blind signature, a secure quantum blind signature also requires the following conditions:

  1. 1)

    Unforgeability. Nobody can generate a valid blind signature except for the legal signer.

  2. 2)

    Undeniability. Once the signer issues a blind signature, he (she) cannot deny it.

  3. 3)

    Blindness. The signer cannot know the content of the message that he has signed.

  4. 4)

    Verifiability. Anyone can verify the validity of blind signatures.

  5. 5)

    Traceability. Once some disagreement emerges, the signer and the receiver can trace the message owner with the help of a trusted entity.

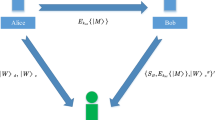
In this paper, we focus on a practical economical situation. When an electric transaction is made in a bank, the consumer needs anonymity and convenience, the shop requests reliability, and the bank requires that no digital cash is reused and that the electric transmitter is not illegally forged. The concrete process is as follows (See Fig. 1)

  1. (1)

    The consumer sets up an account for electric transactions in a bank. Both the bank and the consumer agree on saving a sum of digital cash in a local computer or digital card.

  2. (2)

    The consumer purchases goods or service from the shop using the digital cash.

  3. (3)

    The shop verifies the digital money received from the consumer through the verification centre in the bank. After the money is proved to be true, it sends to the bank to get paid.

  4. (4)

    The bank receives and verifies the request of the payment, then makes the payment to the shop. In this process there is some consumer information that is to be given to the bank secretly, such as consumer personal information. So the consumer must blind the messages before sending to bank to sign.

Fig. 1
figure 1

An electric transaction. In the economical situation, blind signature can be applied

Full size image

In order to describe the quantum version of blind signature protocol which can be applied in the above situation, the rest of this paper is organized as follows. In Section 2, we will review the quantum relations of four-particle GHZ states. The corresponding results will be further used in the protocol design. In Section 3, our quantum blind signature protocol is proposed. Furthermore, its security analysis is presented in Section 4. It can be seen the security requirements can be achieved in this protocol. At last, a conclusion is given in Section 5.

2 Basic Theory

In this section, we will describe the correlation of four-particle GHZ states. Without loss of generality, the X-basis and Y-basis are described as

$$\begin{array}{@{}rcl@{}} |+X\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle); |-X\rangle=\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle); \end{array} $$
(1)
$$\begin{array}{@{}rcl@{}} |+Y\rangle=\frac{1}{\sqrt{2}}(|0\rangle+i|1\rangle); |-Y\rangle=\frac{1}{\sqrt{2}}(|0\rangle-i|1\rangle). \end{array} $$
(2)

In order to show the correlation, we consider the following situations:

  1. (1)

    All the participants measure the four-particle GHZ state with X-basis.

    $$\begin{array}{@{}rcl@{}} |\psi\rangle&=&\frac{1}{\sqrt{2}}(|0000\rangle+|1111\rangle)\\ &=&\frac{1}{2\sqrt{2}}(|+X+X+X+X\rangle+|-X-X-X-X\rangle+|+X+X-X-X\rangle\\ &+&|-X-X+X+X\rangle+|+X-X+X-X\rangle+|-X+X-X+X\rangle\\ &+&|+X-X-X+X\rangle+|-X+X+X-X\rangle) \end{array} $$
    (3)
  2. (2)

    All the participants measure the four-particle GHZ state with Y-basis.

    $$\begin{array}{@{}rcl@{}} |\psi\rangle&=&\frac{1}{\sqrt{2}}(|0000\rangle+|1111\rangle)\\ &=&\frac{1}{2\sqrt{2}}(|+Y+Y+Y+Y\rangle+|-Y-Y-Y-Y\rangle+|+Y+Y-Y-Y\rangle\\ &+&|-Y-Y+Y+Y\rangle+|+Y-Y+Y-Y\rangle+|-Y+Y-Y+Y\rangle\\ &+&|+Y-Y-Y+Y\rangle+|-Y+Y+Y-Y\rangle) \end{array} $$
    (4)
  3. (3)

    Any two of them use X-basis and the other two use Y-basis to measure their particles.

    $$\begin{array}{@{}rcl@{}} |\psi\rangle&=&\frac{1}{\sqrt{2}}(|0000\rangle+|1111\rangle)\\ &=&\frac{1}{2\sqrt{2}}(|-X-X+Y-Y\rangle+|-X-X-Y+Y\rangle+|+X-X-Y-Y\rangle\\ &+&|-X+X-Y-Y\rangle+|+X+X+Y-Y\rangle+|+X+X-Y+Y\rangle\\ &+&|-X+X+Y+Y\rangle+|+X-X+Y-Y\rangle) \end{array} $$
    (5)
  4. (4)

    Any three of them use X-basis (Y-basis) and the other one measures with Y-basis (X-basis) to measure their particles. Without loss of generality, we just discuss the following case.

    $$\begin{array}{@{}rcl@{}} |\psi\rangle&=&\frac{1}{\sqrt{2}}(|0000\rangle+|1111\rangle)\nonumber\\ &=&\frac{1}{4}[(1-i)|+X+X+X+Y\rangle+(1+i)|+X+X+X-Y\rangle\nonumber\\ &+&(1+i)|+X+X-X+Y\rangle+(1-i)|+X+X-X-Y\rangle+(1+i)|+X-X+X+Y\rangle\nonumber\\ &+&(1-i)|+X-X+X-Y\rangle+(1-i)|+X-X-X+Y\rangle+(1+i)|+X-X-X-Y\rangle\nonumber\\ &+&(1+i)|-X+X+X+Y\rangle+(1-i)|-X+X+X-Y\rangle+(1-i)|-X+X-X+Y\rangle\nonumber\\ &+&(1+i)|-X+X-X-Y\rangle+(1-i)|-X-X+X+Y\rangle+(1+i)|-X-X+X-Y\rangle\nonumber\\ &+&(1+i)|-X-X-X+Y\rangle+(1-i)|-X-X-X-Y\rangle] \end{array} $$
    (6)

Here we discuss the relative phases of the measurement states. From the case (1) and (2), it can be seen the number of ”+” and ”-” is even. From the case (3), the number of ”+” and ”-” is odd. From the case (4), there exists no correlation about the relative phases. Furthermore, except for the case (4), three participants’ measurement results will determine the other one’s measurement sate.

3 The Proposed Scheme

In this scheme, four participants are involved: Alice, Bob, Charlie and Trent. Alice is the owner of the message, Bob is the signer, Charlie is the verifier and Trent is the third trusted entity. Specially, Charlie and Alice can be one person in the practice application. The detailed procedure can be seen as follows.

3.1 Initializing Phase

In this phase, Alice, Bob, Charlie and TR share a secret quantum key, and share the GHZ particles for each other.

  1. (I1)

    Quantum key distribution.

    Trent shares secret key K T B with Bob, K T C with Charlie. In addition, Alice shares secret key K A B with Bob, K A C with Charlie. These distribution tasks can be achieved by using some practical quantum key distribution (QKD) techniques [23–27].

  2. (I2)

    Shared GHZ states.

    Trent prepares m GHZ states \(|G\rangle _{ABCT}=\{|g\rangle _{ABCT}^{1},|g\rangle _{ABCT}^{2},\cdots ,|g\rangle _{ABCT}^{m}\}\). We denote the ordered M four-qubit GHZ states with

    $$ [({g_{A}^{1}}, {g_{B}^{1}}, {g_{C}^{1}}, {g_{T}^{1}}), ({g_{A}^{2}}, {g_{B}^{2}}, {g_{C}^{2}}, {g_{T}^{2}}), \cdots ,({g_{A}^{m}}, {g_{B}^{m}}, {g_{C}^{m}}, {g_{T}^{m}})] $$

where \(|g\rangle _{ABCT}^{i}=(|0000\rangle +|1111\rangle )/\sqrt {2}\). The superscript represents the order of each four-qubit GHZ state in the sequence, and the subscripts A, B, C, and T indicate the four photons of each GHZ state.Trent sends the particle |G〉 A to Alice, |G〉 B to Bob, |G〉 C to Charlie and keeps the last one |G〉 T .

In the paper, All subscripts A, B, C and T denote Alice, Bob, Charlie and Trent, respectively. All superscript 1, 2,⋯, i denote marshalling sequence.

3.2 Blinding Messages

  1. (B1)

    Alice generates the message P and transform it into H=|h(P)〉 by quantum fingerprinting [2].

  2. (B2)

    Alice randomly selects X-basis or Y-basis to measure her qubits \(|G\rangle _{A}=\{|g{\rangle _{A}^{1}},|g{\rangle _{A}^{2}},\cdots ,|g{\rangle _{A}^{m}}\}\) and notes the measurement basis she randomly chosen as |B〉={|b〉1,|b〉2,⋯ ,|b〉m}. If Alice uses X-basis to measure her qubit \(|g{\rangle _{A}^{i}}\), she notes |b〉i=0. Otherwise if Alice uses Y-basis to measure the qubit, |b〉i=1.

  3. (B3)

    Alice encodes the measured states according to the following rules: if Alice gets |−X〉 or |−Y〉, let \({t_{A}^{i}}=1\), otherwise she gets |+X〉 or |+Y〉, let \({t_{A}^{i}}=0\). Then the measured state sequence is denoted as \(T_{A}=\{{t_{A}^{1}},\cdots ,{t_{A}^{m}}\}\).

  4. (B4)

    Alice generates |M〉={|m 1〉,⋯ ,|m m〉} , here \(|m^{i}\rangle =|h^{i}\oplus {t_{A}^{i}}\rangle \) and ⊕ means adding mod2.

3.2.1 Signing Phase

  1. (S1)

    Alice sends \(E_{K_{AB}}\{|M\rangle ,|B\rangle \}\) to Bob by use of the quantum encryption algorithm [28] with the key K A B .

  2. (S2)

    After receiving Alice’s notification, he obtains (|M〉,|B〉). According to the measurement basis |B〉, he measures his participle |G〉 B . Similarly, if Bob gets |−X〉 or |−Y〉, let \({t_{B}^{i}}=1\), otherwise she gets |+X〉 or |+Y〉, let \({t_{B}^{i}}=0\). Then the measured state sequence is denoted as \(T_{B}=\{{t_{B}^{1}},\cdots ,{t_{B}^{m}}\}\).

  3. (S3)

    Bob encrypts |V〉=E r (T B ) with his chosen random number r. Then Bob gets \(|M_{B}\rangle =\{|{m_{B}^{1}}\rangle ,\cdots ,|{m_{B}^{m}}\rangle \}\), here \(|{m_{B}^{i}}\rangle =|m^{i}\oplus {t_{B}^{i}}\rangle \). Finally, he generates the signature \(|S\rangle =E_{K_{BT}}\{|M_{B}\rangle ,|V\rangle \}\) and sends it to Alice.

3.2.2 Verifying Phase

  1. (V1)

    Alice receives |S〉, then encrypts \(|Y\rangle =E_{K_{AC}}\{|S\rangle ,|H\rangle ,|B\rangle ,E_{K_{AT}}(T_{a})\}\) and sends |Y〉 to Charlie.

  2. (V2)

    Charlie decrypts |Y〉 and measures his participle |G〉 C with the basis |B〉. The same as Alice and Bob’s performance, Charlie obtains the sequence \(T^{C}=\{{t_{C}^{1}},\cdots ,{t_{C}^{m}}\}\).

  3. (V3)

    Charlie encrypts \(|Y_{CT}\rangle =E_{K_{CT}}\{|S\rangle ,|H\rangle ,|B\rangle ,E_{K_{AT}}(T_{A}),T_{C}\}\) and sends it to Trent.

  4. (V4)

    Trent decrypts |Y C T 〉. Similarly, Trent gets the measurement result \(T^{T}=\{{t_{T}^{1}},\cdots ,{t_{T}^{m}}\}\).

  5. (V5)

    Trent recovers |M B 〉 and generates |H ′〉={h ′1,⋯ ,h ′m}, here \(|h^{\prime i}\rangle =|{m^{i}_{B}}\rangle \oplus |{t^{i}_{C}}\rangle \oplus |{t_{T}^{i}}\rangle \oplus |{t_{A}^{i}}\rangle \ \). Trent compares |H〉 and |H ′〉. If |H ′〉=|H〉, he will accept the signature, and continue the next step, otherwise, he drops the signature.

  6. (V6)

    If Bob raised an objection to the signature, he also can verify the signature. Trent generates |T〉 such that \(|t^{i}\rangle =|{t_{A}^{i}}\rangle \oplus |{t_{C}^{i}}\rangle \oplus |{t_{T}^{i}}\rangle \). Then he encrypts (|T〉,|V〉) to \(|Y_{BT}\rangle =E_{K_{BT}}\{|T\rangle ,|V\rangle \}\) and sends it to Bob.

  7. (V7)

    Bob decrypts |Y B T 〉 to get |V〉. Furthermore, he can get |T B 〉 and |T〉. When the testing condition \(t^{i}\oplus {t_{B}^{i}}=|0\rangle \) is satisfied, Bob accepts the signature.

    Here, all the participants measure the four-particle GHZ state with the same basis lead to \(t^{i}\oplus {t_{B}^{i}}= {t_{A}^{i}}\oplus {t_{B}^{i}}\oplus {t_{C}^{i}} \oplus {t_{T}^{i}}= 0\)

    In step V3 and V4, if the owner of the message and verifier are one person, who is named Alice. Alice computes T C ⊕T A and directly sends \(|Y_{CT}\rangle =E_{K_{CT}}\{|S\rangle ,|H\rangle ,|B\rangle ,T_{A}\oplus T_{C}\}\) to Trent.

4 Security Analysis and Discussion

With the development of quantum cryptography, some feasible attack strategies have been proposed such as intercept-resend attacks [29], entanglement-swapping attacks [30, 31], teleportation attacks [32], dense-coding attacks [33, 34], channel-loss attacks [35, 36], denial-of-service attacks [10, 11], correlation-extractability attacks [37–39], Trojan horse attacks [12, 13], participant attacks [31, 34] and so on. Furthermore, some cryptanalysis of quantum signature have been presented [7–9, 14–16]. Here we analyze the quantum blind signature from the exist ideas. The detailed security analysis can be seen as follows.

4.1 Unforgeability

If the malicious message owner Alice attempts to counterfeit the signatory Bob’s signature |S〉 to her own benefit, she has to know K A B ,r and the state |T B 〉 of Bob. However, this is impossible due to the unconditionally secure quantum key distribution. In the worst situation, for instance, in which the secret keys are exposed to Alice, Alice still cannot forge the signature, since he cannot create appropriate |T B 〉 related to the new message. So Alice’s forgery can be avoided.

Similarly, suppose Alice repudiates the receipt of the signature. Then Trent also can confirm that Alice has received the signature |S〉, since she needs the assistance of the Trent to verify the signature.

If the attacker Eve tries to forge Bob’s signature |S〉 for his own sake, he also should know Bob’s secret key K A B ,r and the state |T B 〉. In the step (V7), Bob can find his forgery. The public information that he can obtain betrays nothing. So the forgery for Eve is also impossible.

4.2 Undeniability

If Bob wants to disavow his signature, Alice, Charlie and Trent can expose him. Alice, Charlie and Trent can lead to recovery \(|h^{\prime i}\rangle =|{m_{B}^{i}}\oplus {t_{A}^{i}}\oplus {t_{C}^{i}}\oplus {t_{T}^{i}}\rangle =|h^{i}\rangle \) without the help of Bob, If |H ′〉=|H〉, they will accept the signature.

4.3 Blindness

In our scheme, Bob is kept blind from the message content. In all above steps, Bob the first and foremost only contacts his own qubit and \(|m^{i}\rangle =|h^{i}\oplus {t_{A}^{i}}\rangle \), which not help him to know |H〉. There is one more point, H=|h(P)〉 is transformed by quantum fingerprinting.

In fact, Bob is not necessary to know the Alice’s transaction content, but he could sign the message |M〉 for Alice. And Charlie could verify and accept the payment message |M〉 signed by the Bob.

4.4 Traceability

In case of any dispute about Bob, Trent submits |V〉 to Bob, Bob can make sure his private key r and believe it is its own signature. Once some disagreement emerges with Alice, according to {K B C ,|M〉,|B〉} and the measuring results of particles, the referee can trace the message owner and judge whether the process is valid or not.

5 Conclusion

In this paper, we present a blind signature scheme based on the correlation of four-particle GHZ states. In our scheme, the signatory is kept blind from the signed message content. However, he could still be able to trace the message owner if some disagreement emerges. Specially, the singer also cannot trail his signature, but he can make sure whether it is his own signature or not. The security of our scheme is guaranteed by the one-time pad and quantum key distribution.