1 Introduction

Nonclassical field state has been a great interesting topic in quantum optics and quantum information [1]. In recent years, both experimentalists and theoreticians have proposed non-Gaussian operations such as photon-addition and photon-subtraction to obtain some nonclassical states [2–11]. These states exhibit numerous nonclassical properties and provide access to a complete engineering of quantum states and fundamental quantum phenomena [12–18]. For example, the superposition operation ta+ra † was studied with possible applications to quantum-state engineering [19] and entanglement (nonlocality) concentration [20]. Some other nonlocal coherent operations, such as a+b [8], a 2+b 2 [21]and a †+b † [22], were also investigated. In addition, an experimental scheme to implement a second-order nonlocal superposition operation was proposed [23]. Several years ago, Agarwal and Tara have introduced a single-mode photon added thermal state [24]. They also construct two-mode photon added thermal state by making the phase-insensitive amplification of N00N states [25]. Moreover, these states have been studied experimentally [4, 6].

On the other hand, many interesting theoretical works were focused on the non-local effects of entangled states [26–31]. Followed by the seminal contribution of Bell [32], the meaning of quantum reality and quantum nonlocality has become a central issue of the modern interpretation and understanding of quantum phenomena [33, 34]. If two subsystem are in an entangled state, the Bell’s inequality may be violated [35]. Non-Gaussian transformation can be useful for implementing nonlocality test [36] and enhancing nonlocality [37, 38].

Enlighten by these ideas, we shall study the superposition of high-order (N) photon addition (a †N+b †N) to two-mode thermal state (SPA-TMTS) and discuss the nonlocality of the nonclassical state in this paper. The paper is organized as follows. In Sect. 2, we introduce SPA-TMTS and obtain its normal ordering form. In Sect. 3, we derive quasi-probability distribution such as Q function and Wigner function (WF) in phase space. By drawing three-dimensional graphics of Q function and WF (whose negativity indicate the nonclassicality), we analyze the nonclassicality of the SPA-TMTS. In Sect. 4, constructing a Clauser-Horrne (CH) Bell inequality from Q function and a Clauser-Horne-Shimony-Holt (CHSH) Bell inequality from Wigner function, we study the quantum nonlocality of the SPA-TMTS.

2 High-Order Superposition Photon Addition Two-Mode Thermal State (SPA-TMTS)

Here we introduce a new kind of quantum state, which can be generated by the superposition of high-order (N) photon addition to two-mode thermal state (SPA-TMTS), i.e. repeatedly operating a † and b † for N times on a two mode thermal state, respectively. Its density operator is given as

$$ \rho=C_{N} \bigl( a^{\dag N}+b^{\dag N} \bigr) \rho_{_{th1}}\rho_{_{th2}} \bigl( a^{N}+b^{N} \bigr), $$
(1)

where N⩾1 is the added photon number in each mode, and C N is the normalization coefficient to be determined by trρ=1. As special case, when N=0, C N =1/4, SPA-TMTS ρ will be two-mode thermal state \(\rho_{_{th1}}\rho_{_{th2}}\). Here \(\rho_{_{th1,2}}\) is a density operator of single-mode thermal state,

$$ \rho_{_{thj}}=\sum_{n=0}^{\infty} \frac{\bar{n}_{j}^{n}}{ ( \bar{n}_{j}+1 ) ^{n+1}}\vert n \rangle \langle n\vert , $$
(2)

where \(\bar{n}_{j}\) is the average photon number of thermal state \(\rho_{_{thj}}\) (j=1,2). For simplicity, we assume the average photon number of \(\rho_{_{th1}}\) and \(\rho_{_{th2}}\) to be identical, i.e. \(\bar{n}_{1}=\bar{n}_{2}=\bar{n}\). It is obvious to see that when \(\bar{n}=0\), SPA-TMTS ρ can be reduced to N00N states (a maximally path-entangled number state), which have important applications to quantum imaging, metrology, and sensing [39].

In addition the P-representation of density operator \(\rho_{_{thj}}\) can be expanded as [40]

$$ \rho_{_{thj}}=\frac{1}{\bar{n}}\int \frac{d^{2}\alpha_{j}}{\pi}e^{-\frac {1}{\bar{n}}\vert \alpha_{j}\vert ^{2}} \vert \alpha _{j} \rangle \langle \alpha_{j}\vert , $$
(3)

which is useful for later calculation and here |α j 〉 (j=1,2) are the coherent states. Therefore, we can re-write \(\rho_{_{th1}}\rho_{_{th2}}\) as

$$ \rho_{_{th1}}\rho_{_{th2}}=\int\!\!\! \int \frac{d^{2}\alpha_{1}d^{2}\alpha_{2}}{ \pi^{2}}P ( \alpha_{1},\alpha_{2} ) \vert \alpha_{1},\alpha_{2} \rangle \langle \alpha_{1},\alpha_{2}\vert , $$
(4)

with the P-representation of two mode thermal state (TMTS)

$$ P ( \alpha_{1},\alpha_{2} ) =\frac{1}{\bar{n}^{2}}\exp \biggl( -\frac{1}{\bar{n}}\vert \alpha_{1}\vert ^{2}- \frac{1}{\bar{n}}\vert \alpha_{2}\vert ^{2} \biggr) $$
(5)

and |α 1,α 2〉=|α 1〉⊗|α 2〉. Using the vacuum projector |0,0〉〈0,0|=:exp(−a † a−b † b): as well as the IWOP technique, we obtain the normal ordering form of \(\rho_{_{th1}}\rho_{_{th2}}\) as follow

$$ \rho_{_{th1}}\rho_{_{th2}}=\kappa^{2}\mathopen{:} \exp \bigl( - \kappa a^{\dag }a-\kappa b^{\dag}b \bigr) \mathclose{:}, $$
(6)

where we have set κ=1 \((\bar{n}+1)\) and used the following integral formula,

$$ \int \frac{d^{2}z}{\pi}\exp \bigl( \zeta \vert z\vert ^{2}+\xi z+ \eta z^{\ast} \bigr) =-\frac{1}{\zeta}\exp \biggl( -\frac{\xi \eta}{\zeta} \biggr) ,\quad \mathrm{Re} ( \zeta ) <0. $$
(7)

Thus the normally ordering form of the SPA-TMTS can also be given as

$$ \rho=C_{N}\kappa^{2}\mathopen{:} \bigl( a^{\dag N}+b^{\dag N} \bigr) \exp \bigl( -\kappa a^{\dag}a-\kappa b^{\dag}b \bigr) \bigl( a^{N}+b^{N} \bigr) \mathclose{:}, $$
(8)

which is important to calculate the normalization coefficient, Q function and Wigner function.

To fully describe a quantum state, we must normalize the SPA-TMTS. Inserting the completeness relation of coherent state \(\int \frac{d^{2}z_{1}d^{2}z_{2}}{\pi^{2}}\vert z_{1},z_{2} \rangle \langle z_{1},z_{2}\vert =1\) into \(\operatorname{tr}\rho=1\) and using Eq. (8), we easily obtain the normalization coefficient

$$ C_{N}^{-1}=2N! ( \bar{n}+1 ) ^{N}=2N!/ \kappa^{N}, $$
(9)

3 Quasi-probability Distribution Function

In order to investigate the quantum nonlocality of the SPA-TMTS, Banaszek established a direct relationship between the quantum nonlocality and the positive phase-space Q function, as well as the nonpositive Wigner function [41]. In this section, we derive the analytical expressions of Q function and Wigner function for the SPA-TMTS.

3.1 Q Function

The Q function [42] for two-mode quantum state ρ is defined as

$$ Q_{ab}(\alpha;\beta)=\frac{1}{\pi^{2}} \langle \alpha,\beta \vert \rho \vert \alpha,\beta \rangle , $$
(10)

where |α,β〉=|α〉 a |β〉 b is the two-mode coherent and \(\alpha=\frac{x_{1}+iy_{1}}{\sqrt{2}},\beta=\frac{x_{2}+iy_{2}}{\sqrt{2}}\). Obviously the Q function is just the expectation value of the density operator in coherent state, so it is always positive. Substituting the density operator of SPA-TMTS state in Eq. (8) into Eq. (10), we have

$$ Q_{ab}(\alpha;\beta)=\frac{\kappa^{N+2}}{2\pi^{2}N!}e^{-\kappa \vert \alpha \vert ^{2}-\kappa \vert \beta \vert ^{2}}\bigl \vert \alpha^{N}+\beta^{N}\bigr \vert ^{2}, $$
(11)

This function is always positive in all space, but it lost the Gaussian charter and exhibit the characteristic of entanglement due to the existence of the intercross term β N α ∗N+α N β ∗N.

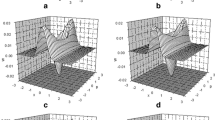
Using Eq. (11), the Q function Q ab (α;β) of the SPA-TMTS are depicted in Fig. 1 in phase space (x 1,0;x 2,0) for several different values N=1,2,3 (from top to bottom) and \(\bar{n}=0,0.2,0.6\) (from left to right). It is easy to see that the Q function exhibits two peaks in phase space for N=1, while N>2, the Q function exhibits four peaks in phase space. The Q function for N=2 have higher symmetrical distribution than other cases. In addition, for a given values N, the distribution of WF becomes wider as the average photon number \(\bar{n}\) increase. From Eq. (11), we also find that the phase space center α=β=0 always has the form Q(0;0)=0 for any \(N,\bar{n}\), which can be seen clearly from Fig. 1.

Fig. 1
figure 1

The Q function Q ab (α;β) in phase space (x 1,0;x 2,0) for several different SPA-TMTS with the following cases N=1,2,3 (from top to bottom) \(\bar{n}=0,0.2,0.6\) (from left to right) (Color figure online)

Full size image

3.2 Wigner Function

The Wigner function (WF) is a quasiprobability distribution, which fully describes the state of a quantum system in phase space. The partial negativity of the WF is indeed a good indication of the highly nonclassical character of the state [43]. Next we derive the analytical expression of Wigner function for the SPA-TMTS for further investigating the nonclassicality.

The WF of a two-mode system ρ in the coherent state representation is given by

$$ W(\alpha;\beta)=\frac{4e^{2\vert \alpha \vert ^{2}+2\vert \beta \vert ^{2}}}{\pi^{2}}\int \frac{d^{2}z_{1}d^{2}z_{2}}{\pi^{2}} \langle -z_{1},-z_{2}\vert \rho \vert z_{1},z_{2} \rangle e^{-2 ( z_{1}\alpha^{\ast}-z_{1}^{\ast}\alpha ) }e^{-2 ( z_{2}\beta^{\ast}-z_{2}^{\ast}\beta ) }, $$
(12)

where |z 1,z 2〉=|z 1〉 a |z 2〉 b is the two-mode coherent state and \(\alpha=\frac{x_{1}+iy_{1}}{\sqrt{2}},\beta=\frac{x_{2}+iy_{2}}{\sqrt{2}}\). Substituting the density operator in Eq. (8) into Eq. (12), we obtain the WF of SPA-TMTS as follow

(13)

where we have set \(\varkappa=1/ ( 2\bar{n}+1 )\), \(\varsigma= ( \bar{n}+1 ) / ( 2\bar{n}+1 ) \) and L N (x) is the N-order Laguerre polynomial. Equation (13) is just the analytical expression of the WF for the SPA-TMTS. It is obvious that the WF lost its Gaussian property in phase space due to the presence of a function of two Laguerre polynomials and an interference term.

Next we would like to discuss the changes in the WF W(α;β) of the SPA-TMTS as we vary the parameters N and \(\bar{n}\). Using Eq. (13), the WFs of the SPA-TMTS are depicted in Fig. 2 in phase space (x 1,0;x 2,0) for several different values N=1,2,3 (from top to bottom) and \(\bar{n}=0,0.2,0.6\) (from left to right). It is easy to see that the WF of the SPA-TMTS exhibits the nonclassicality due to the presence of partial negativity in phase space, which is evidently different from Fig. 1 (in Fig. 1 the Q function has no negative region). For a given values N, the distribution of WF becomes wider as the average photon number \(\bar{n}\) increase; while for the same values \(\bar{n}\), there are more wave valleys and peaks as N increasing. We also find from Eq. (13) that

$$ W(0;0)=\frac{4 ( -1 ) ^{N}}{\pi^{2} ( 2\bar{n}+1 ) ^{N+2}}=\frac{4 ( -1 ) ^{N}\varkappa^{N+2}}{\pi^{2}}, $$
(14)

at the phase space center, which can be seen clearly from Fig. 3. In particular, for the case N=1, L 1(x)=1−x, Eq. (13) reduces to

$$ W_{N=1}(\alpha;\beta)=\frac{4\varkappa^{3}}{\pi^{2}}\exp \bigl( -2\varkappa \vert \alpha \vert ^{2}-2\varkappa \vert \beta \vert ^{2} \bigr) \bigl( 2\varsigma \vert \alpha+\beta \vert ^{2}-1 \bigr) , $$
(15)

which implies that the WF always has its negative region at the phase space region \(\vert \alpha+\beta \vert ^{2}< ( 2\bar{n}+1 ) / ( 2\bar{n}+2 )\) (see Fig. 2(a)–(c)).

Fig. 2
figure 2

The Wigner function W(α;β) in phase space (x 1,0;x 2,0) for several different SPA-TMTS with the following cases N=1,2,3, (from top to bottom) \(\bar{n}=0,0.2,0.6\) (from left to right) (Color figure online)

Full size image
Fig. 3
figure 3

Three-dimensional region \((J,\varphi,\bar{n})\) for CH<−1 with (a) N=1. (b) N=2 (c) N=3 (d) N=4 (Color figure online)

Full size image

4 Violation of Bell Inequalities for the SPA-TMTS

In this section, we turn our attention to the nonlocal properties [44] of the SPA-TMTS in terms of the Bell’s inequality and demonstrate how nonlocality of the SPA-TMTS is revealed by the Q function and the Wigner function. Here we construct Clauser-Horne (CH) inequality from Q function and CHSH inequality from Wigner function.

4.1 CH Inequality

The Q function contains direct information on nonlocal quantum correlations. In order to link the quantum nonlocality with the phase space quasidistribution, we redefine \(\bar{Q}_{ab}(\alpha;\beta)=\pi^{2}Q_{ab}(\alpha;\beta)\) for two mode and \(\bar{Q}_{a}(\alpha)=\pi Q_{a}(\alpha)\) (\(\bar{Q}_{b}(\beta)=\pi Q_{b}(\beta)\)) for one mode. The one-mode Q functions in two-mode quantum state are given by

$$ Q_{a}\bigl(\alpha,\alpha^{\ast}\bigr)=\frac{1}{\pi} \langle \alpha \vert \operatorname{tr}_{b}\rho \vert \alpha \rangle ,\qquad Q_{b}\bigl(\beta ,\beta^{\ast}\bigr)= \frac{1}{\pi} \langle \beta \vert \operatorname{tr}_{a}\rho \vert \beta \rangle . $$
(16)

For the SPA-TMTS, using Eq. (8), we obtain

(17)
(18)

From the resulting three different functions we construct the CH combination

$$ \mathrm{CH}=\bar{Q}_{ab}(0;0)+\bar{Q}_{ab}(\alpha;0)+ \bar{Q}_{ab}(0;\beta)-\bar{Q}_{ab}(\alpha;\beta)- \bar{Q}_{a}(0)-\bar{Q}_{b}(0), $$
(19)

which for local theories satisfies the inequality −1≤CH≤0. If the CH combination given in Eq. (19) violate the inequality −1≤CH≤0, this immediately certifies the nonlocal properties of the quantum state. Substituting Eqs. (11), (17) and (18) into (19), we have the analytical expression of CH inequality for the SPA-TMTS as follow

$$ \mathrm{CH}=\frac{\kappa^{N+2}}{2N!}\vert \alpha \vert ^{2N}e^{-\kappa \vert \alpha \vert ^{2}}+ \frac{\kappa^{N+2}}{2N!}\vert \beta \vert ^{2N}e^{-\kappa \vert \beta \vert ^{2}}- \frac {\kappa^{N+2}}{2N!}\bigl \vert \alpha^{N}+\beta^{N}\bigr \vert ^{2}e^{-\kappa \vert \alpha \vert ^{2}-\kappa \vert \beta \vert ^{2}}-\kappa. $$
(20)

Thus we can say that the SPA-TMTS is quantum mechanically nonlocal as CH<−1, and the nonlocality is stronger with the increase of |CH|. Here we will take equal magnitudes of the coherent displacement |α|2=|β|2=J and a certain phase difference between them β=e 2iφ α, then

$$ \mathrm{CH}=\frac{\kappa^{N+2}}{N!}J^{N}e^{-\kappa J}-\frac{\kappa^{N+2}}{N!}J^{N}e^{-2\kappa J}\cos^{2}N\varphi-\kappa, $$
(21)

From Eq. (21) one can see that the degree of nonlocality not only depends on the coherent amplitude J, on the phases Ω, but also on the parameter \(N,\bar{n}\). In Fig. 3 we make a plot showing the three-dimensional region \((J,\varphi,\bar{n})\) in which CH<−1 is true for different N=1,2,3,4. It is found that the region of violation decrease as N increasing. Moreover, only for small \(\bar{n}\) and some N, there is the violation. In Table 1, we enumerate the minimum of CH value at the position \((J,\varphi,\bar{n})\) for different N. When N>5, the minimum limit to −1 showing no violation.

Table 1 The minimum CH values for several different SPA-TMTS
Full size table

In particular, when \(\bar{n}=0\), Eq. (21) just reduces to

$$ \mathrm{CH}=\frac{e^{-J}}{N!}J^{N}-\frac{J^{N}e^{-2J}}{N!}\cos^{2}N \varphi -1. $$
(22)

which correspond to the CH inequality of N00N state. As a special case, when \(\bar{n}=0\) and N=1, Eq. (22) reduces to

$$ \mathrm{CH}_{N=1}=Je^{-J}-2Je^{-2J}\cos^{2} \varphi-1. $$
(23)

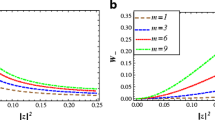
In order to show the violation, we plot CH as the function of J and φ for different N00N states in Fig. 4. It is easy to see that the cases N=1 have some region under the lower bound CH<−1. As depicted in Fig. 4(a), we find that the strongest violation is obtained for φ=0, i.e. when the coherent displacement have same phases. When φ=0, there is some region imposed CH<−1 in the interval J∈[0,ln2] for N=1,2. This result violates the lower bound imposed by local theories (see Fig. 4(a)) when φ=π/2, the weak violation only happen for N=2 (see Fig. 4(b)).

Fig. 4
figure 4

The plot of the CH inequality defined in Eq. (22) as a function of the intensity of coherent displacements J=|α|2=|β|2, for different N00N state. The CH=−1 indicates the lower bound imposed by local theories (Color figure online)

Full size image

4.2 CHSH Inequality

Using correlations between parity measurements, we consider the combination by building the CHSH inequality defined by

$$ B=\frac{\pi^{2}}{4} \bigl( W(0;0)+W(\alpha;0)+W(0;\beta)-W(\alpha ;\beta) \bigr) , $$
(24)

for which local theories impose the bound −2≤B≤2. If the CHSH combination given in Eq. (24) violate the inequality −2≤B≤2, this immediately certifies the nonlocal properties of the quantum state. Next we shall determine how the CHSH inequality of the SPA-TMTS is violated as a function of \(N,\bar{n}\).

Substituting Eq. (13) into Eq. (24), we have

(25)

Again we will take equal magnitudes of the coherent displacement |α|2=|β|2=J and a certain phase difference between them β=e 2iφ α. Thus the CHSH inequality takes the following form

$$ B=\kappa^{N}\varkappa^{2} ( -\varsigma ) ^{N} \biggl[ 1+e^{-2\varkappa J} \bigl( L_{N} ( 4\varsigma J ) +1 \bigr) -e^{-4\varkappa J} \biggl( L_{N} ( 4\varsigma J ) +\frac{ ( -4\varsigma ) ^{N}J^{N}}{N!} \cos2N\varphi \biggr) \biggr] . $$
(26)

Thus we can say that the SPA-TMTS is quantum mechanically nonlocal as |B|>2, and the nonlocality is stronger with the increase of |B|. From Eq. (26) one can see that the degree of nonlocality not only depends on the coherent amplitude J, on the phase φ, but also on the parameter \(N,\bar{n}\). In Fig. 5 we make a plot showing the small three-dimensional region \((J,\varphi,\bar{n})\) in which B<−2 is true for N=1. Moreover, we find the minimum value is −2.1759 at \(\{ \bar{n}=2.3016\times10^{-8},J=0.100148,\varphi=0.0008134\}\) for N=1; while for any N>1 and any \(\bar{n}\), there are no chance to find violation.

Fig. 5
figure 5

(a) Three-dimensional region \((J,\varphi,\bar{n})\) for B<−2 with N=1 and section of violation of (a). (b) φ=0.0008134, N=1, (c) J=0.100148, N=1, (d) \(\bar{n}=2.3016\times10^{-8}\), N=1 (Color figure online)

Full size image

In particular, when \(\bar{n}=0\), Eq. (26) just reduces to

$$ B= ( -1 ) ^{N}+e^{-2J} ( -1 ) ^{N} \bigl( L_{N} ( 4J ) +1 \bigr) -e^{-4J}\biggl[ ( -1 ) ^{N}L_{N} ( 4J ) +\frac{4^{N}J^{N}}{N!}\cos2N\varphi\biggr], $$
(27)

which correspond to the CHSH inequality of N00N state. In order to show the violation, we plot CHSH for different N00N states as the function of J for different N when φ=0,π/2 according to Eq. (27) in Fig. 6. As a special case, when \(\bar{n}=0\) and N=1, Eq. (27) reduces to

$$ B_{N=1}=-1+ ( 4J-2 ) e^{-2J}- \bigl( 8J \cos^{2}\varphi-1 \bigr) e^{-4J}. $$
(28)

It is easy to see that only the cases N=1 have some region under the lower bound B=−2, which indicates the violation of CHSH inequality for 1001 state. As before, the strongest violation is obtained for φ=0, i.e. when the coherent displacements have same phases.

Fig. 6
figure 6

The plot of the CHSH inequality defined in Eq. (27) as a function of the intensity of coherent displacements J=|α|2=|β|2, for different N00N state. The B=−2 indicates the lower bound imposed by local theories (Color figure online)

Full size image

5 Conclusion

In this paper, we have demonstrated that phase-space quasidistribution functions, the Q function and the WF, carry explicit information on nonlocality of the entangled SPA-TMTS. By using the P-representation of thermal state, we obtain the normal ordering form of the SPA-TMTS. Then we derive the normalization coefficient, the Q-function and the WF. It is shown that the WF of the SPA-TMTS with N=1 can possess negative region when the condition \(\vert \alpha+\beta \vert ^{2}< ( 2\bar{n}+1 ) / ( 2\bar{n}+2 ) \) is hold. In addition, the nonlocality of the SPA-TMTS is discussed from CH and CHSH inequalities. It is found that for a given small mean thermal photon number \(\bar{n}\), the CH inequality is violated for some small N and the violation decrease with the increasing N. Therefore the SPA-TMTSs show EPR correlation for any finite N. While the CHSH inequality is violated only for N=1, which show that the test of the different Bell-type inequalities leads to a different result.