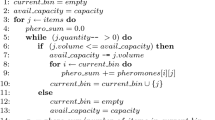1 Introduction

In order to fully exploit the computational capacity of high performance computers, programmers need in-depth knowledge of low-level parallel programming models and have to combine them in a non-trivial way. These are for example OpenMP [1] for shared memory or MPI [2] for distributed memory architectures. Additionally, in the recent decade, accelerators such as Graphics Processing Unit (GPUs) or the Intel Xeon Phi, emerged to further increase the possible performance. They require an additional framework such as CUDA [3] or OpenCL [4] to be used. Low-level parallel programming is error-prone, since the application programmer has to deal with tasks such as communication, synchronization, and data transfer from main memory to GPU memory and vice versa, and it requires a lot of effort. High-level parallel programming models such as algorithmic skeletons [5] shield the application programmer from these low-level aspects and provide a structured way of parallel programming. Thus, they reduce the effort required to develop parallel programs and also the amount of training required to be able to develop parallel programs. Algorithmic skeletons comprise well-known data- and task-parallel building blocks such as map, fold, and zip or farm, branch-and-bound, and divide-and-conquer. In this work, we strive for applying algorithmic skeletons to the domain of metaheuristics.

Metaheuristics are used when computing optimal solutions for optimization problems is intractable. In these cases, metaheuristics are able to find “good” solutions in a feasible time [6]. Swarm Intelligence (SI) algorithms are part of the population-based metaheuristics family. In this family, individuals move through the search space in order to find a good solution. The algorithms use nature-inspired methods that determine the way the individuals move and cooperate with each other [7].

In the SI family, Fish School Search (FSS) [8] is inspired by the behavior of a fish school looking for food. One of the main features of FSS is the ability to change its behavior along the search process, alternating between exploration and exploitation (expanding or contracting the whole fish school). Studies have shown that FSS is a good candidate for solving hard optimization problems [9].

However, for some problems even metaheuristics need a large amount of time to solve them. This is particularly true for problems with a large number of dimensions or with a very complex fitness function. In such cases, parallelism can help. In particular, clusters of multi-core computers provide the necessary computational power, which can be exploited.

The main contribution of this paper is a case study in the domain of SI metaheuristics comparing the implementation effort and performance of a low-level implementation based on frameworks such as MPI and OpenMP to a high-level implementation based on data-parallel algorithmic skeletons. Moreover, we demonstrate the importance of a parallel implementation of FSS to solve complex problems in a reasonable amount of time.

This paper is structured as follows. In Sect. 2, we explain the details of FSS. Section 3 justifies its parallelization. In Sect. 4, the implementations are explained for both approaches explored in this research, low- and high-level. Both approaches are compared in Sect. 5 regarding the implementation effort and the performance of the resulting implementations. Related work is discussed in Sect. 6. Finally in Sect. 7, we conclude and and point out future work.

2 Fish School Search

Mimicking the collective movements of a fish school, FSS has as its main characteristic the ability to switch between exploration and exploitation automatically during the search process [8]. FSS also includes the concept of weight such that a fish gets heavier or lighter according to the success of its last movement. As it gets heavier, it has more influence on the behavior of the whole school, attracting other fish.

During the search process, each fish (a candidate solution) has three movement components, namely individual movement, instinctive movement, and volitive movement. The individual movement is random (Eq. 1). In the case of an improvement, the fish stays in that position. Otherwise it returns to its previous position.

$$\begin{aligned} n_{i,j}(t)=x_{i,j}(t) + rand(-1,1) * step_{ind} \end{aligned}$$
(1)

where \(x_{i,j}(t)\) is the position of fish i in iteration t (where \(1\le i\le N\)) in dimension j (where \(1\le j\le d\)), \(n_{i,j}(t)\) is the candidate position for the same dimension and \(step_{ind}\) is the step size for the individual movement previously set.

The position of the fish is updated just in the case that it has improved. The fitness variation must then be updated according to Eq. 2 and the displacement variation according to Eq. 3.

(2)
(3)

If the candidate solution has a lower fitness than the current position of the fish, the movement is discarded and both, fitness variation and displacement variation, are equal to zero.

After the individual movement, the feeding operator is applied and all fish have their weight updated. The weight \(W_i\) of fish i is updated using Eq. 4. In order to control the growth of all weights, the new factor is a percentage of the maximum fitness variation in that iteration, represented by \(max(\varDelta f (t))\).

$$\begin{aligned} W_{i}(t+1)=W_{i}(t) + \frac{\varDelta f_i (t)}{max_{k=1}^N(\varDelta f_k(t))} \end{aligned}$$
(4)

The second movement component is the instinctive movement. During this phase, the fish are attracted to the successful areas regarding the last movement. Only fish that improved during the individual movement influence the resulting direction of the school on this movement component. The direction is calculated using Eq. 5 and then all fish update their positions according to Eq. 6.

(5)
(6)

The volitive component is responsible for switching between exploration and exploitation. In order to perform this step, it is necessary to calculate the total weight and the barycenter (Eq. 7) of the fish school, and each fish must calculate the Euclidean distance between its current position and the barycenter of the school. If the fish school has a higher weight than in the last iteration, which means that it has improved, the fish school contracts in order to exploit an area. Thus each fish moves towards the barycenter. On the other hand, if the fish school did not improve, it needs to explore other areas. In this case, each fish moves away from the barycenter and the whole fish school expands (Eq. 8).

(7)
(8)

where distance() calculates the Euclidean distance between the position of the fish and the barycenter of the school. \(step_{vol}\) is pre-determined and controls the displacement of the fish.

The vanilla version of FSS follows the steps in Algorithm 1:

figure a

3 Motivation for Parallel Implementation of FSS

An obvious approach for a parallel implementation of FSS is to process the fish in parallel. FSS differs slightly from other parallel computing problems in the sense that it is not the goal to process a given amount of work in the shortest possible time or with the highest possible speedup. Instead, the goal is to find a good (ideally the optimal) solution as quickly as possible. Considering larger fish schools and hence investing more parallelism might help, but it may also happen that a small fish school suffices.

There are four main factors that influence the computational complexity of FSS and should be considered when designing a parallel implementation:

  • the number of fish,

  • the complexity of the fitness function,

  • the number of dimensions of the search space, and

  • the number of iterations.

If the fitness function is complex, the importance of the communication overhead (e.g. for computing the barycenter) is reduced, enabling good speedups for given numbers of fish, dimensions, and iterations. The fitness function and the number of dimensions depend on the given optimization problem and cannot be influenced by the developer. The number of dimensions and the shape of the search space are important for the number of fish, which can effectively be employed. For a simple search space, a small number of fish finds a good solution almost as quickly as a large one.

We found that the question, whether a larger number of fish leads more quickly to better results, is highly dependent on the given problem. Figure 1 shows the fitness of the best found solution for the Rastrigin function with 512 dimensions and 5000 iterations. The results are based on the average of 30 runs. The test has been designed as a minimization problem. Thus a lower fitness value is better. The results show that a high number of fish can certainly lead to improved results for this problem.

Fig. 1
figure 1

Results for Rastrigin function with 512 dimensions and 5000 iterations

Full size image

In the diagram in Fig. 1 there is a step between 8192 and 16,384 fish. As described above, FSS has the ability to switch between exploration and exploitation of the search space, which happens in the collective movement operators. For the collective movement to work effectively a certain threshold of fish is necessary. The same pattern can be observed for other benchmark functions. For example for the less complex Schwefel function, the step from 256 to 512 fish leads to an improvement for the fitness of 9.93%, while the next step to 1024 fish improved the fitness by 30.1%. A swarm needs to have a certain size in order to reach another promising “valley” of the fitness function. If it finds it, the improvement can be arbitrarily large. Another related observation is that increasing the population size typically leads to an improved fitness.

In addition to classic benchmarks as the mentioned ones, we have also considered a practically relevant large supply chain network planning problem. In this scenario, the overall costs of a supply chain network are minimized by optimizing the production, inventory, and transportation quantities. The corresponding fitness function is defined in [10]. The results are presented in Fig. 2. Here with up to 131,072 fish, better solutions can be found than with less fish. However, good solutions can already be reached with 8192 fish. Summing up, the optimal number of fish highly depends on the given problem.

Fig. 2
figure 2

Results for the supply chain planning scenario with 512 dimensions and 5000 iterations

Full size image

Another point to mention is the number of iterations. In FSS each iteration depends on the results of the previous iteration. Thus, there is no potential for parallelization here. However, one could launch several fish schools (i.e. searches) in parallel. Making sure that different fish schools explore different regions of the search space would then be a non-trivial implementation problem. In the present paper, we focus on a single fish school. Nevertheless, a higher number of fish might reduce the required number of iterations to find an equivalent solution.

Figure 3 shows the results for the supply chain network planning scenario with a varying number of iterations and fish. The results are also listed in Table 1. They show that in fact there is a trade-off between the number of fish and the number of iterations. For example, the fitness for \(2^{11}\) fish and 5000 iterations is 2,114,722. For \(2^{15}\) fish and only 3000 iterations, a better fitness can be achieved. Consequently, if the execution time is a major concern and the hardware is available, it is possible to increase the number of fish, which can be processed in parallel, in order to decrease the number of sequential iterations.

Fig. 3
figure 3

Results for the supply chain planning scenario with a varying population size and number of iterations

Full size image
Table 1 Fitness for supply chain planning scenario with varying number of fish and iterations
Full size table

4 Parallel Implementation of FSS

In the following subsections, we outline the parallel implementations of FSS. We have considered a low-level implementation based on MPI and OpenMP and a high-level implementation based on Muesli.

4.1 Low-Level Parallel Implementation with OpenMP and MPI

As already mentioned, the low-level implementation is written in C++ directly based on OpenMP and MPI. The implementation is rather straightforward in the sense that only well-known pragmas are used, such as

figure b

without further parameters such as

figure c

, i.e. GCC’s default settings with dynamic scheduling and a chunk size of 1 are used. Consequently, it is optimized to a degree that is expectable from an average application programmer who is not experienced in parallel programming. This matches the typical target group for high-level parallel programming approaches.

The implementation uses conventional vectors to store fish objects. Each of these objects comprises all the information related to one fish, such as the current position, weight, and the fitness. Moreover, a global state object is used to keep track of information, such as the current iteration and the step size.

figure d

The implementation including the used OpenMP and MPI constructs is outlined in Algorithm 2. The individual movement operator basically consists of two nested for-loops, with the outer loop iterating over the fish and the inner loop iterating over the dimensions. Consequently, we used a parallel for-loop for the outer loop (

figure e

) and a SIMD instruction for the inner loop (

figure f

).

The collective movement components require reductions. This is for example the case for the calculation of the fitness variation sum in the instinctive movement component and for the calculation of the total weight of the fish school in order to calculate the barycenter in the volitive movement. All reductions are handled by an OpenMP reduction, e.g.

figure g

followed by

figure h

.

figure i

Listing 1 illustrates the implementation of the feeding operator. Since the fish are distributed among the processes, in the lines 3–6 the global maximal fitness variation is calculated using the

figure j

routine. The corresponding data structures are hidden in the global

figure k

object. In lines 8–22 the weights are updated. This can be done in parallel, since it is done for each fish separately.

4.2 High-Level Parallel Implementation with Muesli

In addition to the mentioned low-level implementation, we have also developed a high-level implementation of FSS based on the Muenster Skeleton Library (Muesli) [11,12,13,14]. Muesli is a C++ library for parallel programming based on typical patterns for parallel programming, so-called algorithmic skeletons [5]. Programmers can make use of the provided data structures and algorithmic skeletons. They can focus on the given application problem and ignore low-level details of the parallel implementation. For example, in the low-level implementation of the feeding operator in Listing 1, it becomes apparent that the programmer has to use multiple programming models, i.e. MPI in line 6 and OpenMP in line 9. Consequently, the programmer does not only need to know different programming APIs for shared- and distributed-memory architectures, but also during the implementation the location of data has to be considered etc. In contrast as shown in the following, for the high-level implementation there are just skeleton calls on the distributed data structures to be considered. Moreover, from the same code base, different binaries for different hardware architectures can be generated, e.g. a CPU with or without attached GPUs or for whole clusters of such computing nodes. Internally, Muesli makes use of a combination of OpenMP for shared-memory architectures, CUDA for Nvidia GPUs, and MPI for distributed-memory architectures.

As the two main data structures, Muesli provides distributed arrays (DA) and distributed matrices (DM). These data structures are automatically distributed among the started processes by using MPI. To the programmers, it seems as if the data was locally stored on one node. Both data structures offer a set of data-parallel communication and computation skeletons as member functions, which can be used to manipulate the data. Communication skeletons are for example broadcast or permutePartition. Computation skeletons include for example map, fold (also known as reduce), and zip. In addition to the vanilla versions of these skeletons, there are also some variants. For instance, mapIndex expects an argument function, which has the index of the considered DA element as additional argument. mapInPlace does not generate a new DA, but replaces the elements of the considered data structure by the generated results. mapIndexInplace combines both features. Custom user-functions can be provided as C++ functors, i.e. classes that overload the function call operator. These functors are passed as arguments to the skeleton and are applied accordingly. For example, for the map skeleton, the functor is applied to each element of the data structure. The skeletons are automatically executed in parallel by making use of MPI, OpenMP, and CUDA. Moreover, it is possible to reference distributed arrays and matrices as arguments of the custom user functors.

As pointed out above, parallel programs written with Muesli are based on distributed data structures. For the high-level FSS implementation, we use the same parallelization approach as described above. A DA represents the population of the fish swarm. Each process works on the same number of its elements. Moreover, we use several more data structures to store additional data such as fitness or variation of the position.

As described in Sect. 2, FSS has four components: 1. individual movement, 2. feeding, 3. collective instinctive movement, and 4. collective volitive movement.

The individual movement component can be implemented by using the

figure l

skeleton. However, the position of each Fish cannot be directly updated in the population DA. Since fish only move, if their fitness increases, it is necessary to compute an intermediary DA with possible positions and to calculate the corresponding fitness values. If the fitness of a fish has increased, its position in the population DA can be updated. This has been implemented with a

figure m

skeleton and a functor that takes the current fitness and the candidate fitness as arguments so that the values can be compared.

As the FSS formulas for the collective movement components show, it is necessary to calculate the sum of fitness variations over the whole population. This can be done by fold, which in Muesli delivers the result to every process. Similarly, the other operations described in Sect. 2 can be expressed by sequences of

figure n

and

figure o

skeletons. Table 2 summarizes the used skeletons for the FSS implementation.

Table 2 Summary of the skeletons used in the high-level FSS implementation
Full size table
figure p
figure q

Listings 2 and 3 show the implementation of the feeding operator with Muesli so that it can be compared to the low-level implementation in Listing 1. The listings demonstrate the structured implementation process that is used when programming with Muesli.

First, the functors are implemented as shown in Listing 2. The functor for the feeding (lines 1–32) is used to update the array that stores the weight of each fish. The required parameters can already be set in the constructor. Only the maximum fitness variation has to be updated in each iteration. Therefore, there is an additional setter (lines 9–12). Moreover, the functor contains a pointer to the

figure r

data structure (line 30) so that the value can be used in the calculation of the new weight (line 19).

Second, the data structures are created as shown in Listing 3 in lines 3–5. Both arrays have the size of the number of fish used by the algorithm and are initialized with 0 and the lower bound of the weight, respectively. The argument

figure s

determines that a data structure is distributed among the used processes.

Finally, the functors are instantiated (Listing 3, lines 7–9) and applied to the data structures (lines 14–17). The maximum fitness variation of the current iteration is calculated by applying the fold skeleton with the

figure t

functor, which returns the higher value of two arguments, to the fitness variation data structure (line 15). Afterwards, the feeding functor has to be updated (line 15) and the weights are calculated by using the

figure u

skeleton with the feeding functor (line 17), which has been described above.

5 Evaluation

In the following subsections, we will evaluate the implementations both in terms of performance and required effort.

5.1 Effort

We use two metrics to measure the implementation effort for the low-level and high-level implementation of FSS: first, lines of code and second, cyclomatic complexity. We are aware of the fact that these code metrics do not really reflect the implementation effort, but they are widely adopted and there are no real alternatives, which can be measured with acceptable effort [15].

Fig. 4
figure 4

Code metrics for low-level and high-level implementation of FSS. a Lines of code, b cyclomatic complexity

Full size image

As Fig. 4 shows that the implementation effort can be reduced by using a high-level framework such as Muesli. The number of lines of code decreases by 26 lines from 710 to 684. We want to point that we have always used functors in the high-level implementation, even though sometimes it would have been possible to use lambda expressions instead. Additionally, the total cyclomatic complexity is only 77 for the high-level implementation compared to 123 for the low-level implementation. In fact, the cyclomatic complexity reflects the perceived implementation effort better, since it takes into account that in Muesli, there is no need to think about synchronisation and other low-level parallel programming aspects. Muesli provides predefined terms in which the programmer can think to structure the algorithm. Therefore, the implementation can be performed much faster and in a more structured way.

5.2 Performance

In order to compare the efficiency of both implementations, they have been executed on an HPC cluster. Each node of the cluster has a pair of Intel Xeon E5-2680 v3 CPUs, 12 cores each. In our experiments, up to 16 nodes have been used and the source code has been compiled with g++ 7.1.0. The execution times presented below correspond to the whole execution time of FSS in the SCP scenario in Table 1, including instantiation of data structures, data transfer, etc. We have used a fixed number of 5000 iterations, 512 dimensions, and 2048 fish. As you can see in Fig. 3, this is a configuration, which already leads to a very good solution. Here, we were mainly interested in the speedups, which can be obtained by increasing the number of nodes and cores.

For each set up, 30 runs have been executed and the results presented below show the arithmetic mean of these runs. Table 3 shows the pleasing execution times and speedups of the implementations. The speedups are calculated based on the current hardware configuration in relation to the sequential execution time, i.e. a hardware configuration with one node and one core. In addition, Figs. 5 and 6 depict the execution times graphically.

The speedups for the low-level and high-level implementations follow a similar pattern. In particular, increasing the number of nodes leads to a super-linear speedups for both implementations, which can be attributed to the cache effect, i.e. less data has to be handled by each node and therefore, data can be kept in the faster CPU cache and the number of cache misses can be reduced. By increasing the number of cores, slightly worse speedups can be achieved, e.g. due to increasing memory congestions because of cores sharing the main memory and parts of the cache.

Table 3 Execution times, speedups, and overhead for the low-level and high-level implementations
Full size table
Fig. 5
figure 5

Performance of the low-level implementation

Full size image
Fig. 6
figure 6

Performance of the high-level implementation

Full size image

Also in Table 3, the overhead between the low- and high-level implementations is shown. It ranges between 0.64 and 85.93%. It is caused by the fact that skeletons are higher-oder functions, which require the call of an argument function for every element of a distributed data structure. Since these argument functions are typically simple, the overhead for the additional calls is considerable. It could be avoided or at least substantially reduced by massive inlining of these argument functions. A corresponding program transformation is still in progress and hence has not been applied here. The challenging task is to map the high-level skeletons to low-level representations, especially when distributed-memory architectures and additional accelerators have to be considered. Moreover, it might be preferred to rewrite certain expressions to obtain an even better performance.

Moreover, there is an implicit synchronization after each skeleton call. The analysis of the execution times shows that the high-level implementation has slightly higher spin times and overhead times related to the organization of threads. Depending on the hardware configuration, these additional operations add up to overheads of about 3s to 8s for most configurations, which leads to significant percentual overhead for configurations with short execution times.

To some extent, the lower performance of the Muesli implementation of FSS is compensated by the gain in development time. Moreover, the Muesli code is ready to run also on other parallel hardware architectures such as in a multi-node/multi-GPU environment, which, for the low-level approach, requires a re-implementation from scratch.

To demonstrate this, we use FSS and the Rastrigin function with 512 dimensions and 5000 iterations, since the implementation of the fitness function for the supply chain planning scenario makes use of libraries, which cannot be easily ported to GPUs. However, this example is not particularly well suited to run on GPUs, since the computation effort for the Rastrigin function is rather low and therefore, the expensive data transfer from the main memory to the GPUs and vice versa as well as the management of the GPUs can outweigh the potential speedup for parallel computations offered by the GPUs.

For example, with 2048 fish the execution time is 43.93s on one node with 24 cores. On one node with one GPU the execution time is 35.96s, so only a rather small advantage, and for two GPUs the execution time even goes up to 43.38s. Only with a higher workload the advantage of GPUs becomes apparent. Therefore, we increased the number of fish to 32,768. Now the execution time on one node with one GPUs is 290.70s, which can be reduced to 125.34s by using four GPUs. In contrast, on a node with 24 CPU cores, the execution time increases significantly to 748.75s. To sum up, a quite substantial speedup can be achieved by utilizing GPUs, if the parallel workload is high, i.e. with a complex fitness function, a high number of dimensions, and a high number of fish, and by using high-level approaches such as Muesli, there is no need for a re-implementation.

6 Related Work

A parallel version of FSS was presented first by Lins et al. in 2012 [9]. Their implemenation is based on CUDA’s basic functions. In this implementation, each fish is handled by one thread to perform the steps of the algorithm. They analyze the performance of three parallel FSS variants on GPUs. The first version is a synchronous one, where all the threads respect barriers set after all steps. These barriers are used to prevent race conditions. The two other versions work asynchronously, one with less barriers and one without any barriers inside the iterations. The results enable a comparison (of fitness and speedup) between parallel and sequential versions of FSS using traditional benchmark functions, namely Griewank, Rosenbrock and Rastrigin. Regarding the obtained fitness, there is no big difference between the versions but regarding the speedup, the asynchronous versions are clearly superior.

In 2014, Lacerda et al. [16] introduced a multithreaded version of FSS, so called MTFSS. In this approach, every fish has its own thread and two barriers are present inside each iteration, one after the individual movement and one other after the feeding process. The experiments were executed using 5 traditional benchmark functions (namely Rastrigin, Rosembrock, Griewank, Ackley and Schwefel) with 30 dimensions, 30 fish, and 5000 iterations. The results show that speedups only occur when the problem gets more complex.

These two works present similar parallelization strategies having one thread per fish. In our approach, we treat not only the different fish in parallel but also the different dimensions of their properties. This approach is propitious for problems with many dimensions and when running the algorithm in environments that can take a big computational load, such as clusters of multicore processors.

To the best of our knowledge, there is no implementation of FSS using a high-level approach. However the MALLBA library [17] provides skeletons for optimization methods such as tabu search and genetic algorithms. In 2002, Garcia-Nieto used a parallel implementation of Particle Swarm Optimization (PSO) provided by MALLBA to tackle the gene selection problem [18]. Later on, another work from Alba et al. [19] presents some metaheuristics implemented using MALLBA, namely Ant Colony Optimization (ACO), Particle Swarm Optimization (PSO), and Scatter Search. In contrast to Muesli, MALLBA is just based on MPI and does not support GPUs and multi-cores. Also, Muesli offers generic skeletons that enable the implementation of any parallel version of a metaheuristic, while MALLBA encapsulates a whole metaheuristic as a skeleton. Thus, the user is limited to choosing the parameters it offers. Consequently, both approaches pursue a different purpose and target different users. While MALLBA targets users who just want to use a certain metaheuristic, Muesli does not choose to provide such an even higher level of abstraction, but stays at a level of abstraction that shields the programmer from low-level programming models, yet still provides the possibility to implement any application in parallel.

The parallelization of metaheuristics has been explored by other researches for quite some time already and many approaches have been presented. For example, in 2009, a parallel version of Particle Swarm Optimization (PSO) has been presented by Zhou et al. [20].

There are many case studies comparing the performance of low- and high-level parallel implementations. E.g. in [11], this has been done for matrix multiplication, all-pairs shortest path, Gaussian elimination, FFT, and samplesort. To the best of our knowledge, our case study is the first such comparison for SI algorithms.

7 Conclusions and Future Work

In this work, we have presented a high-level parallel version of FSS based on the skeleton library Muesli. We have compared it to a low-level implementation based on OpenMP, CUDA, and MPI. The comparison was performed in terms of development effort and runtime efficiency. The complexity of the implementation was measured in terms of two debatable but frequently used performance indicators, namely lines of code and cyclomatic complexity. It turned out that the low-level code was about 4% longer and 60% more complex, where the cyclomatic complexity reflects the perceived effort clearly better. The skeleton-based approach relieves the developer from considering synchronization and communication problems. The reduced implementation effort had to be paid by a performance penalty ranging between 0.64 and 85.93% on a 16-node cluster of 12-core Intel Xeon processors. Both implementations of FSS, low-level and high level, show good execution times and speedups.

In the continuity of this research, other SI algorithms will be implemented in Muesli, namely PSO and ACO. These implementations will be tested not only on classical benchmark functions, but also on complex practical application problems with high computational costs. Moreover, we will work on the platform-specific optimization of the skeletons in the spirit of an approach by Steuwer et al. [21].