Abstract
Bulk Synchronous Parallel (BSP) is a model for parallel computing with predictable scalability. BSP has a cost model: programs can be assigned a cost which describes their resource usage on any parallel machine. However, the programmer has to manually derive this cost. This paper describes an automatic method for the derivation of BSP program costs, based on classic cost analysis and approximation of polyhedral integer volumes. Our method requires and analyzes programs with textually aligned synchronization and textually aligned, polyhedral communication. We have implemented the analysis and our prototype obtains cost formulas that are parametric in the input parameters of the program and the parameters of the BSP computer and thus bound the cost of running the program with any input on any number of cores. We evaluate the cost formulas and find that they are indeed upper bounds, and tight for data-oblivious programs. Additionally, we evaluate their capacity to predict concrete run times in two parallel settings: a multi-core computer and a cluster. We find that when exact upper bounds can be found, they accurately predict run-times. In networks with full bisection bandwidth, as the BSP model supposes, results are promising with errors < 50%.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Limits of sequential computing have led to an explosion of parallel architectures, which are now present in systems ranging from small embedded devices to supercomputers. Parallel programs must be scalable: ideally their performance should grow linearly with the number of cores. We also want the performance of a given program on any architecture to be predictable. Manual performance analysis quickly becomes tedious and even intractable as the size of programs grows. Furthermore, use cases such as on-line scheduling, algorithm prototyping and evaluation motivate automatic performance prediction of programs as another desirable quality of any parallel model.
Bulk Synchronous Parallelism [20] is a parallel model which gives the programmer a high-level view of parallel computers and programs. Like PRAM it offers a high degree of abstraction. Furthermore it has a simple but realistic cost model, giving BSP programs predictable scalability. BSPlib [12] is an API standard for imperative BSP programming with many implementations. However, to our knowledge, there are no methods for automatic cost analysis of imperative BSP programs: the BSPlib programmer is charged with manually deriving the cost of his or her program.
Contributions This paper presents a method for automatic parametric cost analysis of BSPlib programs. Specifically, our contributions are:
-
An adaptation of cost analysis for sequential programs [3, 24] to imperative Bulk Synchronous Parallel programs by sequentialization.
-
The application of the polyhedral model to the estimation of communication costs of imperative BSP programs.
-
A prototype implementation combining these two ideas into a tool for static cost analysis of imperative BSP programs.
-
Two evaluations, one symbolic and one concrete, of the implementation on 8 benchmarks.
The obtained cost formulas are parameterized by the input variables of the analyzed program. These variables can represent things such as the size of input arrays and other arguments, but can also include the special variable \({\texttt {nprocs}}\), which contains the number of processors executing the program. Thus the obtained cost formula bound the cost of running the program on any number of processors with any input.
The limitation of our work is that we require that analyzed programs are structured, and thus that they have a reducible control flow graph. Furthermore, we require that they have textually aligned barriers. In our previous work [14], we argue that imperative BSP programs of good quality have textually aligned barriers and describe a static analysis verifying that a program has this property.
We obtain a tight bound on communication cost when the input program has textually aligned, polyhedral communications. When this is not the case, we still obtain safe upper bounds. However, progress in the applicability of the polyhedral model [4] leads us to believe that the communication of most real-world BSP programs can be represented in this model.
Processes in BSPlib communicate by generating requests which are executed when processes synchronize. The BSPlib interface specification [12] defines the effect of processes reading the same memory area from the same target process. However, the effect of two processes writing to the same memory area on the same target process (i.e. concurrent writes) is not defined and the result is implementation specific. To cover any BSPlib implementation, we parameterize our BSPlib formalization by a communication relation as detailed in Sect. 3.2.
The article proceeds as follows. In Sect. 2 we present BSP and its cost model. In Sect. 3 we present the sequential language of our formalization and the sequential cost analysis, as well as the extensions for BSP programming. In Sect. 4, we present the main contribution: the cost analysis for parallel programs. In Sect. 5, we describe the implementation and its evaluation. In Sect. 6 we present related work before concluding in Sect. 7.
2 The BSP Model and Its Cost Model
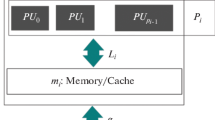
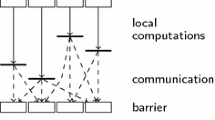
Bulk Synchronous Parallel is a model for parallel computing. It provides an abstract view of both parallel computers and algorithms and, notably, it provides a cost model. BSP computations are performed by a fixed number of p processor–memory pairs. The computation is divided into supersteps. Each superstep consists of three phases: (1) local, isolated computation in each process (2) communication, and (3) global synchronization. Figure 1b graphically depicts a BSP computation.
A parallel prefix calculation in an imperative BSP language, program text and execution. a The program \(s_{\mathrm{scan}}\) implementing parallel prefix calculation. The syntax and the semantics of the language is given in Sect. 3. More details on this program and, in particular, the work annotation\(\{ 1\ \mathbf w \}\) at label 7 are given in Example 3 in the same section. b Graphic representation of the execution of \(s_{\mathrm{scan}}\) with 4 processes in three supersteps. Local computation is drawn as thick horizontal bars, which are annotated with the sequential cost. The communication of one word is drawn as an arrow, and synchronization barriers as vertical thick bars. The first superstep has no local computation. The last has no communication
BSPlib is an API standard and an implementation thereof for imperative BSP programming in C. It follows the Single Program, Multiple Data (SPMD) paradigm. Formally, an SPMD computation can be seen as \(P(0) \Vert P(1) \Vert \ldots \Vert P(p - 1)\) where P is a program taking the process identifier as argument, p is the number of processes, and \(\Vert \) is parallel composition. Communication in BSPlib is enabled by either Direct Remote Memory Access (using the bsp_put and bsp_get functions) or message passing. We focus on DRMA in this article since the two modes are interchangeable in terms of cost in the BSP model. The use of bsp_put and bsp_get generates communication requests: these are logically deferred until the communication phase of the superstep that occurs when all processes call the bsp_sync function.
BSP Cost model The cost model is one of the distinguishing features of BSP. It allows algorithm developers to gauge the performance of their algorithms on different types of parallel computers, and conversely, for hardware developers to understand how different algorithms will perform on their machine.
In addition to p, a BSP computer is specified by the three parameters \(r\), \(g\), and \(l\), which denote the cost of one step of local computation, the cost of communicating one word, and the cost of one barrier synchronization, respectively. The cost of the execution of a BSP algorithm is expressed by the summation
where W is the total number of computation steps on the critical path, H is the total communication volume, and S is the number of supersteps. Precisely, W and H are given by
where \(w_{i,k}\) is the cost of the local computation performed by process i at superstep k while \(H^{+}_{i,k}\) and \(H^{-}_{i,k}\) are the number of words sent, respectively received, by process i at superstep k. The cost of a BSP algorithm is typically given as a function of input parameters and the number of processes.
Example 1
The BSP cost of the execution in Fig. 1b is
since the longest running computation of the three supersteps is 0, 1, and 1 respectively. The first two supersteps contain communication with the cost 1, while the last has no communication.
3 Sequential Language and Parallel Extensions
We first define a sequential language. Its semantics is instrumented to return the information needed to compute the sequential cost of each execution: the cost is a measure on what abstract computational resources are needed to complete that execution. Units are used as arbitrary labels for different kinds of resources (arithmetic operations, floating point operations, I/O, etc.). We assume that the instructions of the input program are annotated with their individual cost and unit. Such annotations can also be added by an automatic pre-analysis. This scheme abstracts away from the specificities of different computer architectures and allows for the segmentation of costs.
We assume the existence of a Sequential Cost Analysis, which is a static analysis giving a safe upper bound on the cost of any execution (as determined by the annotation of each evaluated instruction in that execution) of a given program. The computed worst-case cost is parameterized by the input variables of the program. The description of such analyses can be found in literature [3, 24].
We extend the sequential language with parallel primitives which enable Bulk Synchronous Parallel-programming and give the semantics of this new language. The parallel semantics is also instrumented to return the information needed to obtain the parallel cost of each execution.
3.1 Sequential Language
The sequential language seq with annotations is defined by the following grammar:

where \(\mathbb {X}\) is the set of variables, \(x \in \mathbb {X}\), n is a numeral denoting a natural number, \(\mathbb {L}\) is a set of labels and \(\ell \in \mathbb {L}\). We write \(\bar{e}\) and \(\bar{b}\) to denote sequences of expressions. The function symbols \(f_A\), \(f_R\) and \(f_B\) denote members of a predefined set of arithmetic, relational, and Boolean functions which take sequences of expressions as arguments.
The statements include the no-op, regular assignments, non-deterministic updates, non-deterministic updates constrained to a range, conditional statements, loops, sequences of two statements and work-annotated statements.
Work annotations \(\{ e\ u \}\) can be added to any statement, and consists of an arithmetic expression e and a cost unit \(u\in \mathbb {U}= \{ \mathbf a , \mathbf b , ... \}\). The expression gives the cost of the annotated statement and the unit the group of costs in which it should be counted. For instance, let \(\mathbf a \in \mathbb {U}\) denote the cost of arithmetic operations. Then the annotated assignment \(\{ 1\ \mathbf a \}\ [x {:=} x + 1]^{}\) signifies that the cost of the assignment is 1 and that when executed this cost should be added to the total cost of arithmetic operations. Statements can have multiple annotations, thereby enabling modeling of statements with costs in different units. The cost of a program is given solely by these annotations: statements without annotations do not contribute to the cost of an execution.
In addition to arithmetic expressions, variables can be assigned non-deterministic values (\({\texttt {any}}\)), optionally constrained to a range given by two arithmetic expressions (\([e_l\ldots e_u]\)). Non-deterministic updates are used in Sect. 4 to sequentialize parallel programs.
The semantics of arithmetic and Boolean expressions in \(\textsc {aexp}\) and \(\textsc {bexp}\) is standard [26] and given by the functions \(\mathcal {A}{{\llbracket {\cdot }\rrbracket }} : \textsc {aexp}\times {\varSigma }\rightarrow \mathbb {N}\), and \({\mathcal {B}{{\llbracket {\cdot }\rrbracket }} : \textsc {bexp}\times {\varSigma }\rightarrow \{{\texttt {tt}}, {\texttt {ff}}\}}\) respectively.
The semantics of seq operates on environments \(\sigma \in {\varSigma }= \mathbb {X}\rightarrow \mathbb {N}\), which are mappings from variables to numerical values, and is instrumented to collect work traces. A work trace \(w\in \mathbb {W}= (\mathbb {N}\times \mathbb {U})^{*}\) is a sequence that contains the value and cost unit of each evaluated work annotation in an execution. The empty sequence is denoted \(\epsilon \).
The operational big-step semantics of seq is given by the relation \(\rightarrow \):
The rules defining this relation are given in Fig. 2. The rule (s–work) defines how the evaluation of a work annotation adds an element to the work trace, by evaluating the expression of the annotation and adding it to the trace with the unit of the annotation. The effects of multiple annotations to the same underlying statement are accumulated. A sequence of statements (s–sequence) simply concatenates the traces from the execution of each subprogram. Here  is concatenation of sequences. The semantics of non-deterministic assignments is given by the rules (s–havoc) and (s–havocr) and assigns a non-deterministic value (from a restricted range for the latter) to the variable on the left-hand side, i.e. havocking it. This renders the language non-deterministic. The rules for conditional statements (s–ift and s–iff) and loops (s–whf and s–wht) are standard.
is concatenation of sequences. The semantics of non-deterministic assignments is given by the rules (s–havoc) and (s–havocr) and assigns a non-deterministic value (from a restricted range for the latter) to the variable on the left-hand side, i.e. havocking it. This renders the language non-deterministic. The rules for conditional statements (s–ift and s–iff) and loops (s–whf and s–wht) are standard.
Our semantics does not assign meaning to nonterminating programs. We restrict our focus to terminating programs, as typical BSP programs are algorithms that are intended to finish in finite time. Indeed, the BSP model does not assign cost for programs that do not finish. Some programs, such as reactive programs, repeat infinitely a finite calculation. These can be treated by identifying manually and analyzing separately their finite part, typically the body of an event loop.
Sequential cost Given the work trace of an execution, we can obtain its cost. The cost is a mapping from units to numerical values:
Sequential cost analysis There are sound static analyses automatically deriving conservative upper bounds on the cost of executing sequential, imperative programs [3]. We let \(\textsc {sca}\) denote a sound sequential cost analysis for \(\textsc {seq}\). Given a program it returns an upper bound on the cost of executing that program. The bound is given as a cost expression from \(\textsc {cexp}\) that is parametric in the program’s input-parameters. Cost expressions \(\textsc {cexp}\) are arithmetic expressions extended with the symbol \(\omega \) denoting unbounded cost.

The semantics of cost expressions is given by the function \(\mathcal {C}{{\llbracket {\cdot }\rrbracket }} : \textsc {cexp}\times {\varSigma }\rightarrow \mathbb {N}_\omega \) which is a natural extension of \(\mathcal {A}{{\llbracket {\cdot }\rrbracket }}\) with \(\mathbb {N}_\omega = \mathbb {N}\cup \{ \omega \}\).
Since the halting problem is undecidable in general, \(\textsc {sca}\) returns conservative upper bounds. Consequently, it might return \(\omega \) for a program that actually terminates with any initial environment. However, since \(\textsc {sca}\) is sound, we have the following for any unit \(u\) and program c:
-
If c terminates in any initial environment and the cost of its execution in unit \(u\) is at most n, then \(n \le \textsc {sca}(c)(u)\).
-
If c is nonterminating in some initial environment, then \(\textsc {sca}(c)(u) = \omega \).
Example 2
The sequential program \(c_{\mathrm{fact}}\) in Fig. 3 computes the factorial of the parameter n and stores it in the variable f. For the sake of providing a non-trivial example, assume that n is of arbitrary precision so that multiplication by n consists of \(\log {n}\) additions, and that we are interested in the number of such additions performed in any execution. We add a work annotation to the assignment at label 3 of value \(\log {n}\) with unit \(\mathbf a \) (for addition). With our implementation of \(\textsc {sca}\), based on [3], we have
This is an upper bound on the cost of executing \(c_{\mathrm{fact}}\), parameterized by the input variable n, expressing that it performs at most \(n\log {n}\) additions when calculating the factorial of n.
3.2 Parallel Language
We now extend the sequential language with primitives for Bulk Synchronous Parallel computation, modeling BSPlib. A BSP computation is divided into \(S{} > 0\) supersteps and consists of a fixed number \(p > 0\) of processes executing in parallel. The set of process identifiers is \(\mathbb {P}= \{0,\ldots ,p - 1\}\). We add the sync, put and get primitives which are used for synchronization and buffered communication between processes. The parallel language \(\textsc {par}\) is defined by the following grammar:

where \(e \in \textsc {aexp}\), \(b \in \textsc {bexp}\)\(x, y \in \mathbb {X}\) and \(u\in \mathbb {U}\). We also reserve the variables \({\texttt {pid}}\) and \({\texttt {nprocs}}\).
The operational semantics for par programs is defined by local and global rules operating on environment vectors. The local rules extend the semantics of seq. Intuitively, they compute the new state of one component in the environment vector, corresponding to one process.
The global rules compute the superstep sequence of the BSP computation. They compute the new state of a complete environment vector by applying the local rules to each component, then handle communication and synchronization between processes as detailed below. The global rules are instrumented to compute \(p \times S{}\) matrices of work traces and communication traces that are used to obtain the parallel cost of the execution.
The semantics of local computation is given by the relation \(\Downarrow \) (Fig. 4):

where \(\mathbb {T}\) is the set of termination states, with \({\textit{Ok}}\) denoting end of computation and \({\textit{Wait}}(s)\) a remaining computation to execute in the following superstep. Work traces have the same meaning as in the sequential language. Communication requests are generated by the \({\texttt {put}}\) and \({\texttt {get}}\) primitives. The rule (p–put) appends the form \(\langle n@i \overset{\mathrm {put}}{\longrightarrow } x@i' \rangle \) to the communication request trace, signifying process i requesting that the value n be put into variable x at process \(i'\). The rule (p–get) appends the form \(\langle x@i' \overset{\mathrm {get}}{\longleftarrow } y@i \rangle \) to the communication request trace, signifying process \(i'\) requesting that the value the contents of variable y at process i be retrieved into its variable x. In both forms, we say that the source is i and the destination is \(i'\). Communication request traces are used both to perform communication at the end of supersteps in the global rules and in the calculation of communication costs.
The global level of the operational semantics of par programs is given by the relation \(\Downarrow ^{S{}}\) which is indexed by the number \(S{} \ge 1\) of supersteps in the derivation:
where \(A^p\) denotes a column vector of height p and \(A^{p \times S{}}\) denotes a \(p \times S{}\) matrix. This relation is defined by the rules of Fig. 5. In the rule (p–glb–all–wait), all processes request synchronization: they all calculate a continuation, a new environment, a work trace, and a communication request trace, forming p-vectors of each. After synchronization, global computation continues with the vector of continuations, and the trace vectors of the first superstep are concatenated to the trace matrices computed by executing the remaining supersteps. Concatenation of vectors to matrices is given by the operator \({(:) : A^p \times A^{p \times S{}} \rightarrow A^{p \times (S{}+1)}}\). The \({{\textit{Comm}}: {\varSigma }^p \times \mathbb {R}\times {\varSigma }^p}\) relation defines communication by executing the communication request traces in an implementation specific manner. For instance, \({\textit{Comm}}\) can handle concurrent writes, occurring when the trace contains two put requests to the same variable on the same process, by taking either value of the requests non-deterministically or deterministically by imposing a priority on origin processes, by combining the values, or disabling such writes completely. Thus, different BSPlib implementations can be modeled precisely by varying \({\textit{Comm}}\).
In the rule (p–glb–all–ok), all processes terminate. If neither of the global rules are applicable, as when the termination states of two processes differ, then computation is stuck and the program has no meaning in the semantics.
\(\textsc {par}\) programs are executed in SPMD-fashion: one initial program \(s\) is replicated over all processes. Furthermore, we require that the initial environment is the same on all processes in the first superstep, except for the reserved pid variable, which contains the process identifier of each process. We also give processes access to the total number of processes p with the nprocs variable. We let \({\sigma ^{i,p}}\) denote the local process environment defined by \(\sigma [{\texttt {pid}}\leftarrow i, {\texttt {nprocs}}\leftarrow p]\). The semantics of a par program s with the initial environment \(\sigma \) is thus
Parallel cost The parallel cost of a par program follows the BSP model, and so is given in terms of local computation, communication and synchronization. The units \({\texttt {g}}, {\texttt {l}}\in \mathbb {U}\), assumed not to appear in user-provided work annotations, denote communication and synchronization costs respectively. Remaining units denote local computation and are normalized by the function \(w\).
The BSP cost of an execution is normally given as a sum of computation, communication and synchronization costs, but we shall give it in the form of a function \(f : \mathbb {U}\rightarrow \mathbb {N}\). The classic BSP cost expressed by f is given by \(\sum _{u\not \in \{{\texttt {g}}, {\texttt {l}}\}}f(u)w(u)r+ f({\texttt {g}})g+ f({\texttt {l}})l\).
To define the cost of local computation we use the concept of global work traces. A global work trace is a vector of traces corresponding to the selection of one trace from each column of the work trace matrix of one execution. The set of global work traces of a work trace matrix is defined:
The cost of communication is defined in terms of H-relations. The H-relation of a superstep is defined as the maximum fan-in or fan-out of any process in that superstep, and can be calculated from the communication traces of all processes in that superstep.
We define the \(\mathcal {H}^{+}_i, \mathcal {H}^{-}_i : \mathbb {R}\rightarrow \mathbb {N}\) functions, for \(i \in \mathbb {P}\), giving the fan-out respectively fan-in of process i resulting from the execution of a communication request trace. Using these, we define \(\mathcal {H}: \mathbb {R}\rightarrow \mathbb {N}\) to give the maximum fan-out or fan-in of any process for a given request trace.
The communication relation \({\textit{Comm}}\) that parameterizes the global semantics affects expressibility. Given a problem, different choices of \({\textit{Comm}}\) may permit solutions of different costs, but the program text of each solution would be different. The analysis (Sect. 4), being defined on the program text, would reflect the new cost. A program might generate a request whose effect is not defined by some choice of \({\textit{Comm}}\). However, our analysis returns an upper bound on the communication cost under the assumption that all communication requests are executed, and is therefore independent of \({\textit{Comm}}\).
Using the \(\mathcal {H}\)-function and the concept of global traces, we define the parallel cost of an execution from the generated work trace matrix and communication request trace matrix:

where  gives the concatenation of each trace in a vector and \(R[*,k]\) is the kth column of R. The parallel cost of local computation for some unit \(u\not \in \{ {\texttt {g}}, {\texttt {l}}\}\) is equal to the cost of the global work trace with the highest sequential cost in that unit. The cost of communication (\(u= {\texttt {g}}\)) is the sum of the H-relation of each column in the communication trace matrix. The cost of synchronization (\(u= {\texttt {l}}\)) is equal to the number of supersteps \(S{}\) in the execution.
gives the concatenation of each trace in a vector and \(R[*,k]\) is the kth column of R. The parallel cost of local computation for some unit \(u\not \in \{ {\texttt {g}}, {\texttt {l}}\}\) is equal to the cost of the global work trace with the highest sequential cost in that unit. The cost of communication (\(u= {\texttt {g}}\)) is the sum of the H-relation of each column in the communication trace matrix. The cost of synchronization (\(u= {\texttt {l}}\)) is equal to the number of supersteps \(S{}\) in the execution.
Example 3
The program \(s_{\mathrm{scan}}\) (adopted from [19]) for calculating prefix sum is given in Fig. 1a. The input of the program is a p-vector, where the ith component is stored in the variable x at process i. The assignment at label 7 is annotated with a work annotation 1 of unit \({\texttt {w}}\).
The execution of this program over 4 processes consists of 3 supersteps, and is illustrated in Fig. 6. We write \(\sigma ^{i,p,y}\) to denote \(\sigma ^{i,p}[x \leftarrow y]\). In this example, the initial value of x in all processes is 1. The values of the other variables are omitted for brevity. The cost of this execution is
where the local computation cost is given by the global work trace  and communication cost is given by the fact that the H-relation is 1 in each superstep but the last.
and communication cost is given by the fact that the H-relation is 1 in each superstep but the last.
The cost of \(s_{\mathrm{scan}}\) as a function of the number of processes can be obtained manually by rewriting the program as a recurrence relation. This relation is then solved to obtain a closed-form cost. When executed with p processes, the loop is executed \(\lceil \log _2{p} \rceil \) times, resulting in \(\lceil \log _2{p} \rceil + 1\) supersteps. The largest local computation is performed by the process \(p-1\), which performs the work \(1\ {\texttt {w}}\) at the jth iteration of the loop. The H-relation of each superstep but the last (which has no communication) is 1, since each process receives at most one value and sends at most one value. Thus, the cost of \(s_{\mathrm{scan}}\) is given by the function
which is parametric in the number of processes. The next section describes how to obtain such bounds automatically.
4 Cost Analysis
This section describes our main contribution: a method for transforming a parallel program to a sequential program amenable to the pre-existing sequential cost analysis. The transformation ensures that the worst-case parallel cost of the original program is retained. The transformation consists of 3 steps:
-
1.
First, we verify that the input program s is textually aligned [14]. Intuitively, this ensures that processes always make the same choice at each control flow branch which affect whether they synchronize or not. Consequently, if they synchronize, they are all at the same source code location and in the same iteration of each loop. This property allows us to sequentialize s into the “sequential simulator” \(S^{{\texttt {w}}}(s)\).
-
2.
Knowing the communication distribution of the program is key to obtaining precise bounds on communication costs. The second step analyzes each communication primitive and surrounding control structures in the polyhedral model [9]. This allows us to obtain a precise bound on communication costs that are inserted as work annotations into the sequential simulator, obtaining \(S^{{\texttt {g}}}(s)\).
-
3.
In the third step we insert annotations for counting the number of synchronizations into the sequential simulator, obtaining \(S^{{\texttt {l}}}(s)\).
Finally, the sequential cost analysis analyzes the resulting sequential program \(S^{{\texttt {l}}}(s)\) and returns the parametric parallel cost. This analysis pipeline is summarized by Fig. 7.
4.1 Sequential Simulator
This section describes the transformation of a parallel program with textually aligned synchronization \(s \in \textsc {par}\) into a “sequential simulator” \(S^{{\texttt {w}}}(s) \in \textsc {seq}\) of s, such that all global work traces of s can be produced by \(S^{{\texttt {w}}}(s)\). To do this, we replace parallel primitives with skip and assign non-deterministic values to all variables affected by the parallelism. This will allow us to use the sequential cost analysis to get an upper bound on the local computation cost on the parallel program.
Sequentialization The sequentialization transforms the parallel program so that it non-deterministically chooses the identity and state of one local process before the execution of each superstep. The underlying cost analysis will return the cost of the worst-case choice, coinciding with the definition of the local computation cost of one superstep.
This relies on all processes starting execution at the same source code location in the beginning of each superstep. If they also synchronize at the same source code location at the end of the superstep, then we can do the same non-deterministic identity change for the next superstep, and so on. Parallel programs that synchronize in this way have textually aligned synchronization.
A statement is textually aligned if for all control flow branches that affect whether the statement is executed, all processes choose the same branch. This ensure that either all processes execute the statement, or none of them. By extension, textually aligned statements are executed the same number of times by all processes in any execution. The program has textually aligned synchronization when all synchronization primitives of the program are textually aligned.
The non-deterministic identity switch may switch to an identity that does not correspond to any feasible state of a local process. To restrict the non-determinism, we also identify variables whose value is the same in all processes at the end of the superstep. These variables, called pid-independent, are unaffected by the identity switch.
Textual alignment analysis In the first step, we statically under approximate the set of pid-independent variables. These are then used to obtain the set of textually aligned statements and to verify that synchronization is textually aligned.
Since the pid variable is the one thing that is not replicated in the initial configuration of a par-execution, a sound underapproximation of the set of pid-independent variables can be obtained by tracking data and control dependencies on pid. Communication may introduce additional local variations in the state for the destination variables. The analysis conservatively excludes all destination variables from the set of pid-independent variables.
The set of statements that are textually aligned are now those that are control dependent only on control flow branches that exclusively contain pid-independent variables.
In our previous work [14], we have designed such an analysis for imperative BSP programs. We shall refer to this analysis as rs, of the following functionality:
If a program s can be statically verified to have textually aligned synchronization then \({\textsc {rs}}(s) = (\tau , \pi )\) where \(\tau \) and \(\pi \) are under approximations of textually aligned statements and the set of pid-independent variables at each statement, respectively.
Variables that are pid-independent go through the same series of values on each process at the textually aligned statements where they are pid-independent. Consider any fixed execution and process, let x be a pid-independent variable at some textually aligned statement and let \(n_j\) be the value of x at the jth execution of this statement. Then this series of values will be the same for each process in this execution.
If the program does not have textually aligned synchronization, then \(RS(s) = \top \). In this case, the parallel cost analysis cannot move forward and returns \(\lambda u.\omega \). In the rest of this article we assume that programs have textually aligned synchronization.
Example 4
Consider the program \(s_{\mathrm{scan}}\) in Fig. 1a. The textual alignment analysis gives:
The program has textually aligned synchronization, since all statements in this program are textually aligned except the statements labeled 4 and 7, corresponding to the body of the conditionals in the loop. The body of these conditionals will not be executed by all processes and this is statically detected since the value of the guard conditions depends on the pid variable. The variables assigned at these statements and the variables affected by communication, namely x and \(x_{in}\), will not be pid-independent at any statement reachable by these assignments and communications. However, i has no dependency on pid and so is pid-independent throughout the program.
Sequential simulator The sequential simulator \(S^{{\texttt {w}}}(s)\) of a parallel program s with textually aligned synchronization is obtained by assigning a non-deterministic value to all variables that are not pid-independent after each sync-primitive, and then replacing all parallel primitives (sync, get and put) by a skip with the same label.
We first define the function \(havoc\) that creates a program that assigns a non-deterministic value to each variable given as argument:

where  gives a sequential composition of a set of statements and \(\ell '\) is a fresh label for each assignment.
gives a sequential composition of a set of statements and \(\ell '\) is a fresh label for each assignment.
Now assume \(RS(s) = (\tau , \pi )\), that \(\mathbb {X}_s\) contains the set of variables used in s and again let \(\ell '\) be a fresh label. Then \(S^{{\texttt {w}}}(s)\) is defined:

Intuitively, the sequential simulator will act as any process of the parallel program and will have the same series of values for pid-independent variables. For variables that are not pid-independent, it switches to any value after each synchronization using a non-deterministic assignment. In this way, the sequential simulator can assume the identity of any process at the beginning of each superstep and produce any global trace. This is formalized by the following conjecture:
Conjecture 1
For any \(s \in \textsc {par}\) such that \({\textsc {rs}}(s) = (\tau , \pi )\), and \(\sigma \in {\varSigma }\), if \(\langle [s]_{i \in \mathbb {P}}, [\sigma ^{i,p}]_{i \in \mathbb {P}} \rangle \Downarrow ^{S{}} \langle E, W, R \rangle \) then for all  , \(\exists \sigma ', \langle S^{{\texttt {w}}}(s), \sigma \rangle \rightarrow \langle \sigma ', w\rangle \).
, \(\exists \sigma ', \langle S^{{\texttt {w}}}(s), \sigma \rangle \rightarrow \langle \sigma ', w\rangle \).
Note that the parallel program and its sequential simulator execute the same sequence of textually aligned statements. That is, when executed with the same initial environment, the sequences of executed labels of both programs will coincide after removing all labels that are not in \(\tau \).
Obtaining the local computation cost As an immediate consequence of the previous conjecture the simulator also produces the maximum global work trace. Thus, we can now obtain an upper bound on the parallel cost of the computation of a program s by applying sca to its sequential simulator:
Conjecture 2
For any \(s \in \textsc {par}\) such that \({\textsc {rs}}(s) = (\tau , \pi )\), and \(\sigma \in {\varSigma }\), if \(\langle [s]_{i \in \mathbb {P}}, [\sigma ^{i,p}]_{i \in \mathbb {P}} \rangle \Downarrow ^{S{}} \langle E, W, R \rangle \) then for all \(u\in \mathbb {U}\) we have \(Cost_{\textsc {par}}(W, R)(u) \le \mathcal {C}{{\llbracket {\textsc {sca}(S^{{\texttt {w}}}(s))(u)}\rrbracket }}\ \sigma [p \leftarrow {\texttt {nprocs}}]\).
The non-determinism introduced by the sequential simulator has the potential to render the obtained upper bound imprecise. However, we conjecture that the variables that have most influence on cost, namely those affecting control flow, are also those that are pid-independent and thus this imprecision should have limited influence on the upper bound. Indeed, this is true for data-oblivious programs as our evaluation in Sect. 5 shows.
Example 5
See Fig. 8 for the sequential simulator \(S^{{\texttt {w}}}(s_{\mathrm{scan}})\). Note the non-deterministic assignments to pid, x and \(x_{in}\) after the former synchronization at label 5, and how the sync and get at labels 4 and 5 have been replaced by skip. The effect of the former get is simulated by the non-deterministic update of \(x_{in}\) after the former sync at label 5.
4.2 Analyzing Communication Costs
The second transformation inserts an annotation \(\{ e\ {\texttt {g}} \}\) for each communication primitive s in the simulator. This makes the underlying sequential cost analysis account for communication cost. The expression e must be an upper bound on the addition to the total communication cost of any processes executing s. Without further semantic analysis of the parallel control flow, we must assume that all processes execute the primitive, even if only a subset of them actually do so, and without knowing the exact value in all processes of the first (destination) expression of the put or get, we must also assume that the communication is unbalanced, and thus more costly.
For instance, see the communication primitive at line 4 in the program \(s_{\mathrm{scan}}\) guarded by the conditional at line 3. Without any semantic knowledge about the destination expression \({\texttt {pid}}- i\) and the guarding condition \({\texttt {pid}}\ge i\), one must assume the worst-case addition of \(p\ {\texttt {g}}\) to the programs total communication cost, obtained when all processes execute the get with the same destination (for instance, when \(i = {\texttt {pid}}\)). However, by knowing that i has the same value on all processes in each execution of this \({{\texttt {get}}}\), one can deduce that the destination expression refers to one distinct process for each process executing the get, and thus a tighter bound of \(1\ {\texttt {g}}\) can be obtained.
Polyhedral communicating sections This reasoning is automated by representing the communication primitive and surrounding code, called the communicating section, in the polyhedral model [4]. In this model, each execution of a statement that is nested in a set of loops and conditionals is represented as an integer point in a k-polyhedron, where k is the number of loops. A k-polyhedron is a set of points in \(\mathbb {Z}^{k}\) vector space that is bounded by affine inequalities:
The vector \(\mathbf {x}\) corresponds to the loop iterators. Thus each point in the polyhedron corresponds to one valuation of the loop iterators. A is a constant matrix. The constant vector \(\mathbf {a}\) can contain program variables not in \(\mathbf {x}\) that are constant in the section, called parameters. This model requires that all loop bounds, iterator updates as well as conditionals in the section can be represented as affine combinations of loop iterators and parameters.
For the communication section, the analysis adds two additional variables s and t to \(\mathbf {x}\), corresponding to the pid of the source and destination process. The analysis requires that the entry point of the section is textually aligned, that all parameters are pid-independent, that the destination expression is an affine combination of loop iterators and that the section does not contain a sync.
Finding the polyhedral representation for a section is the subject of “polyhedral extraction” [22], a subject which is outside the scope of this work. In our prototype, simple pattern matching is used to find the largest communication section around each communication primitive, but the method used is orthogonal to our contribution and should not be seen as a limitation.
Interaction sets From a polyhedral communicating section the analysis obtains the exact set of communication requests generated when it is executed by all processes, called the interaction set [9].
From a communication primitive \({{\texttt {put}}}^{\ell }(e_1, e_2, x)\), whose communication section consists of k loops with the loop iterators \(x_0, \ldots , x_{k-1}\), each with lower and upper bounds \(l_0, \ldots , l_{k-1}\) and \(u_0, \ldots , u_{k-1}\), and a set of guard expressions \(C \subseteq \textsc {bexp}\) from the conditionals, the analysis constructs the interaction set:
For \({{\texttt {get}}}^{\ell }(e_1, y, x)\) with the same surrounding code the analysis constructs the interaction set:
In both cases, \([s, t, i_0, \ldots , i_{k-1}] \in \mathcal {D}\) means that process \(s\) will send data to \(t\) at the end of the superstep and that the loop iterators \(x_0, \ldots , x_{k-1}\) have the values \(i_0, \ldots , i_{k-1}\) when the communication primitive is executed.
The constraints here are given as a conjunction, the transformation to the matrix inequalities representation is standard [4].
Example 6
The analysis automatically extracts the polyhedron \(\mathcal {D}_S\) representing the interaction set generated by the communicating section from lines 3-5 of \(s_{\mathrm{scan}}\) (see Fig. 1a). The boundaries of \(\mathcal {D}_S\) are shown first as inequalities, then as the equivalent Boolean formula.

The two variables \(s\) and \(t\) of \(\mathcal {D}_S\) respectively correspond to the identifier of the source and destination process of each request. This set is parameterized by the variable \(i\) that is constant in the section and the BSP parameter p. The constraints are given by the destination expression (\(t = s - i\)), the domain of the pid variable (\(s \ge 0\) and \(p - 1 \ge s\)), and the condition on line 3 (\(s \ge i\)).
Example 7
Figure 9 contains some common communication patterns and the interaction sets obtained by the analysis.
H-relations from Interaction Sets From the interaction set, the analysis extracts a tighter bound on the section’s addition to the total communication cost of the execution, which is inserted as an annotation at the section’s entry. This is done by creating two relations from the interaction set \(\mathcal {D}{}\): from \({\texttt {pid}}\) to the set of outbound (\(\mathcal {D}^{+}{}\)) respectively inbound (\(\mathcal {D}^{-}{}\)) communication requests. The H-relation of this section is the largest of the upper bounds on the cardinality of the image of these relations. This is expressed by \(\mathcal {H}\), where \(\#\) gives the cardinality of a set:
Implementation of communication analysis The analysis uses isl [21] to explicitly create the interaction set \(\mathcal {D}{}\) as described earlier and the two relations \(\mathcal {D}^{+}{}\) and \(\mathcal {D}^{-}{}\) using isl’s operations for creating relations and sets. It then asks isl to compute the expression corresponding to \(\mathcal {H}\), which it does using integer volume counting techniques [23].
Example 8
For the interaction set \(\mathcal {D}_{S}\) from the example \(s_{\mathrm{scan}}\), this technique obtains the H-relation 1. The analysis inserts this bound before the \({{\texttt {if}}}\) statement at line 5 in the sequential simulator of \(s_{\mathrm{scan}}\) (see Fig. 10). Figure 9 contains common communication patterns and upper bounds extracted from their interaction sets using isl.
Discussion This method requires no pattern matching, except for the polyhedral extraction, and automatically extracts a precise upper bound on the communication cost of any communication section that can be represented in polyhedral model. When this is not the case, we fall back on the conservative but sound upper bound cost of \(p\ {\texttt {g}}\), which is added as an annotation in the simulator to the communication primitive.
Soundness The following conjecture states that the simulator with communication bounds soundly upper bounds the cost of the parallel program:
Conjecture 3
Let \(s \in \textsc {par}\) be a program such that \({\textsc {rs}}(s) = (\tau , \pi )\) with polyhedral communications, any environment \(\sigma \in {\varSigma }\) and \(\langle [s]_{i \in \mathbb {P}}, [\sigma ^{i,p}]_{i \in \mathbb {P}} \rangle \Downarrow ^{S{}} \langle E, W, R \rangle \) then
4.3 Analyzing Synchronization Costs
Since we require that synchronization primitives be textually aligned in s, it suffices to annotate each instruction which was sync in the original program with \(\{1\ {\texttt {l}}\}\) in the sequential simulator \(S^{{\texttt {g}}}(s)\) to obtain \(S^{{\texttt {l}}}(s)\). We also add an annotated dummy skip instruction to the end of the program to account for the implicit synchronization barrier at the end of all executions.
Any execution of the parallel program evaluates the same sequence of textually aligned statements as the sequential simulator does on the same initial environment. Thus, the simulator will evaluate exactly as many annotations of unit \({\texttt {l}}\) as there are synchronizations in the execution of the parallel program. This intuition is formalized by the following conjecture:
Conjecture 4
Let \(s \in \textsc {par}\) be a program such that \({\textsc {rs}}(s) = (\tau , \pi )\), \(\sigma \in {\varSigma }\) any environment, and \(\langle [s]_{i \in \mathbb {P}}, [\sigma ^{i,p}]_{i \in \mathbb {P}} \rangle \Downarrow ^{S{}} \langle E, W, R \rangle \). Then
Example 9
The sequential simulator \(S^{{\texttt {l}}}(s_{\mathrm{scan}})\) in Fig. 10 is obtained by adding the communication bounds found in Sect. 4.2 to the conditional at label 3, and annotating the sync at label 5, as well as adding the dummy skip at label 13 to account for the synchronization barrier terminating the execution.
We can now submit the simulator \(S^{{\texttt {l}}}(s_{\mathrm{scan}})\) to the sequential cost analyzer. We use the solver PUBS [2]. The obtained cost is exactly the one obtained earlier by manual analysis, i.e.:
4.4 Time Complexity of Analysis
We treat the time for sequentialization and communication analysis (\(T_{seq}\)) separately from the final sequential cost analysis (\(T_{\textsc {sca}}\)):
Here, e is the number of edges of the program’s control flow graph (which is proportional to its size) and v the number of distinct variables of the program.
Sequentialization is done in linear time but uses the result of a data-flow analysis that is computed in time bounded by \(O(e\cdot {}v)\) [18]. The analysis time of each communication primitive is polynomial in the size of the polytope representing it [23], which in turn is bounded by the maximum nesting level of the program. The latter is often assumed to be bounded by some constant for realistic programs. Hence, \(T_{seq}\) is bounded by some polynomial.
The time of analyzing the sequentialized program, \(T_{\textsc {sca}}\), depends on the details of the implementation of \(\textsc {sca}\). Our implementation translates the input program into “cost relations” [2]. This step involves a data-flow analysis bounded by \(O(e\cdot {}v)\) and an abstract interpretation in the domain of convex polyhedra that is linear in e but exponential in the maximum number of variables in any scope [8].
Finally, the cost relations are solved into a closed form upper bound by PUBS [2] that is done in a time exponential in their bit size (Genaim, personal communication, 2017).
In summary, \(T_{analysis}\) grows exponentially with the size of the program. This is due to our specific implementation of \(\textsc {sca}\) that uses PUBS: another sound \(\textsc {sca}\) with lower complexity could be used. Note that the analysis complexity only depends on the size of the analyzed program and is independent on run-time parameters such as the number of processors executing the program.
5 Implementation and Evaluation
A prototype of the analysis has been implemented in 3 KLOCs of Haskell. The underlying sequential cost analysis is implemented as described in [3] and uses APRON [15] for abstract interpretation, PUBS [2] for solving cost equations, and isl [21] for polyhedral analysis.
We have performed two evaluations of the static upper bounds of the parallel cost given by the implementation on 8 benchmarks. The first evaluates that they are indeed upper bounds and by what margin. The second evaluates the quality of their power to predict actual run times in seconds. While finding exact Worst-Case Execution Times [25] is not our goal, we demonstrate how BSP costs relate to concrete run times.
Benchmarks Table 1 summarizes the benchmarks, their static bounds and analysis running times. The second column indicates whether the program’s control flow is independent of the contents of the input arrays. We call such programs “data-oblivious”, and when it is not the case, “data-dependent”. Note that no attempt has been made to optimize the running time of the prototype. The benchmarks are written in a variant of par (Sect. 3.2), extended with arrays. Array contents are treated as non-deterministic values by the implementation. The benchmarks are inner product (BspIp); parallel prefix in logarithmic and constant number of supersteps (Scan2 and ScanCst2); parallel reduction (BspFold); array compression (Compress); broadcast in one and logarithmic number of supersteps (Bcast1) and (BcastLog); and 2-phase broadcast (Bcast2ph).
Local computation is defined by work annotations added to costly array operations in loops. For simplicity, we only use the unit \({\texttt {w}}\) and thus omit the normalization function w. The static bounds on local computation, communication and synchronization are given in the columns \(W^{\sharp }\), \(H^{\sharp }\), and \(S^{\sharp }\) of Table 1 respectively. Benchmarks and static bounds are parameterized by BSP parameters and input sizes N.
Symbolic evaluation We test that the static bounds are indeed bounds, and evaluate their precision by executing each benchmark in an interpreter simulating \(p=16{}\). The interpreter is instrumented to return the parallel cost (as defined in Sect. 3.2) of each execution.
We found that the static bound is equal to the cost of each execution, except for the communication cost of the program Compress, which is overestimated by a factor of p. As a consequence of its data-dependent control flow, the communication distribution of Compress depends on the values in the input array. The implementation treats these as non-deterministic values, and thus returns the pessimistic static bound \(N{\texttt {g}}\) on communication instead of the tighter bound \(N/p{\texttt {g}}\) which can be found by analyzing the program manually.
Concrete evaluation To evaluate the quality of the static bounds’ capacity to predict actual run times in seconds, we translate the benchmarks to C, compile them, and compare their running times on two different parallel environments with those predicted by the static bounds in the BSP model.
Making such predictions is inherently difficult, especially when several translations are involved. For instance, our model supposes that the execution of one individual operation takes a fixed amount of time. In reality, the time taken may depend on the state of caches, pipelines, and other hardware features. It also depends on optimizations applied by the compiler. Another issue in the model is the network. BSP assumes that the communication bottleneck will be at the end points and, thus, that the time to deliver an h-relation will scale linearly. However, this is not true for current multi-core architectures, which usually have tree-based network topologies, where bottlenecks can occur near the root. All considering, we can hope at best to obtain predictions on the running time that are not too far from the actual run time, but they may still be several factors off.
The first evaluation environment is a desktop computer with an 8-core, 3.20 GHz, Intel Xeon CPU E5-1660 processor, 32GB RAM, and running Ubuntu 16.04. We use gcc 5.4.0. The second environment is an 8-node Intel Sandy Bridge cluster connected by FDR InfiniBand network cards. Each node has 2 Intel E5-2650 2GHz CPUs with 8 cores each, 384 GB RAM and is running CentOS 7.2. Here we use gcc 6.1.0. We use a Huawei-internal BSPlib implementation in both environments.
The same method is used to obtain the BSP parameters of both environments. We modify bspbench to measure r as memory speed, which is the bottleneck in all the benchmarks. To obtain g and l we measure the minimum time taken to deliver all-to-all h-relations of size p, 2p, and \(h_{max}*p\) over a large set of samples, where \(h_{max}\) is the size of the largest h-relation performed in the benchmarks. Then the y-intercept of the line passing through the first two data-points is taken as l, and the slope of the line passing through the last two is taken as g. Example BSP parameters are given above Figs. 11, 12 and 13.
We find that the running times of all benchmarks grow linearly with the input size as predicted by the static bounds. See e.g. Fig. 11. However, the static bounds do not always accurately predict the running times. See e.g. Fig. 13.
We calculate the error in prediction using the formula \(\mid T_{measured} - T_{predicted} \mid / \min (T_{measured}, T_{predicted})\). In this formulation, an overestimation of running time by a factor 2 as well as an underestimation by a factor 2 will correspond to an error of 100% [16]. The largest error factors for each environment-benchmark combination are summarized in Table 2. The large errors in predictions for Compress are explained by the inaccuracy of its statically found bound. For the remaining benchmarks, error factors range from 4.46% for BspFold on the desktop with 4 processes to 372.5% for Bcast1 on the cluster with 128 processes.
Indeed, Bcast1 has the worst predictions. This shows that in the considered environments, the communication pattern of this benchmark (one-to-all) is faster than the one used to estimate g (all-to-all). The discrepancy is even greater in the cluster with \(p=128\) as a consequence of the cluster’s hierarchical topology. The 128 processes correspond to 8 cluster nodes with 16 cores each, but the InfiniBand network is not 16 times faster than the internal node communication. Thus when only one process communicates with all other processes, it has much more bandwidth at its disposal then when all processes communicate outside the node. The former case corresponds to the communication pattern of Bcast1, and the latter to how the parameter g (which is an estimation of the full bisection bandwidth) is measured, explaining the difference between measured and predicted running time. The discrepancy of the other broadcast benchmarks, BcastLog and Bcast2ph, can also be explained by considering the topology of the network and the communication patterns involved.
Conclusion of evaluation We find that (1) the static bounds of the implementation are indeed upper bounds of the parallel cost of all evaluated executions; (2) they are exact for data-oblivious benchmarks, but pessimistic for the one benchmark considered with data-dependent communication distribution; (3) the static bounds predict asymptotic behavior, and when tight static bounds are found, they accurately predict actual run times: the error is < 50% for networks with full bisection bandwidth and for the others the error is never more than the ratio between the fastest link and the bisection bandwidth.
6 Related Work
To the best of our knowledge, no previous work exists on the automatic cost analysis of imperative BSP programs. Consequently, this survey will focus on cost analysis for other forms of BSP programming and other forms of parallel programming. We then treat sequential cost analysis and conclude with notes on the usage of the polyhedral model in the context of communication analysis.
Closest to our work is Hayashi’s [10] cost analysis for shapely skeletal BSP programs. Shapely programs are written so that the size of data structures is always known statically. Skeletons are ready-made parallel constructs which the programmer uses as building blocks for their program. The cost function of each skeleton and the input data size are a priori known and so the matter of computing the cost function for a program is obtained by composing the cost functions of each skeleton, which is done statically.
For other parallel paradigms, we mention Resource Aware ML [13], which implements a type-based approach to amortized cost analysis for ML with parallel extensions. Albert et al. have extended classic cost analysis to handle concurrent and distributed programs with dynamic task spawning [1]. Their work is preceded by that of Zimmermann [27], which uses classic cost analysis for treating functional programs with parallelism restricted to divide-and-conquer algorithms.
A large body of work exists around Cost Analysis of sequential programs. Broadly, it can be divided into Cost Analysis and Worst-Case Execution Time [25] analysis, but the overlap is considerable. The former aims to find asymptotic bounds in a more abstract setting, while the latter has a more concrete view of hardware, taking into account architecture-specific features such as caches and pipelines.
As we take a more algorithmic view on programs, we position ourselves in the vein of Cost Analysis. Cost analysis is pioneered by Wegbreit [24], who translated functional programs into recursive cost-relations, which can be treated by off-the-shelf solvers. This method has been used successfully for the analysis of Java bytecode [3].
The polyhedral model has seen widespread usage in areas such as automatic parallelization [17] verification [6] and communication analysis [5, 7, 11]. Chatarasi et al. [6] uses an extension of this model to represent OpenMP sections and uses SMT solvers to detect data races. Our work is in the same vein as Clauss’ [7], who uses polyhedra to model load distribution in communicating parallel programs. The polyhedral model has also been used for automatically evaluating the data volumes produced by loops and evaluating their different transformations by this measure [5].
7 Conclusion
The cost model is one of the key advantages of the Bulk Synchronous Parallel model. In this model, parallel computers are simplified to four abstract parameters and the cost of algorithms is expressed as a function of these parameters. By knowing the parameters of a specific computer, the implementer can choose the algorithm whose cost function best suits it.
This article presents a method for automatic cost analysis of imperative BSP programs. The method relies on rewriting parallel programs to sequential programs and inserting annotations to handle book-keeping of communication and synchronization. Communicating sections are represented in the polyhedral model to obtain tight bounds on H-relations. The rewritten programs can then be treated by existing methods for cost analysis, obtaining the BSP cost of the original program.
Our evaluation shows that the analysis obtains tight bounds on the cost of data-oblivious BSP programs that accurately predicts their actual run time in two different parallel environments. One possibility opened up by this development is on-line task scheduling in a system with evolving BSP parameters. Parallel straight-line programs present another promising use case of the analysis in its current form. Such programs are common in signal processing and are characterized by simple control flow. However, they can scale to large sizes for which manual analysis is intractable.
The next step of our research includes the full implementation of the proposed method and evaluation on larger programs. Our method puts specific requirements on the parallel control flow of the analyzed program, namely that all barriers are textually aligned. One axis of future development is relaxing these constraints as well as treating a larger fragment of C with BSPlib. Our analysis gives imprecise costs for programs with data-dependent control flow. Treating such programs is an interesting venue of future research. Lastly, we would like to treat other measures on BSP costs (lower bound, average case, etc.) as well as treating costs of resources outside the BSP cost model, such as memory usage.
Abbreviations
- \(n \in \mathbb {N}\) :
-
Non-negative integer
- \(S{} \in \mathbb {N}\) :
-
Number of supersteps
- \(\textsc {aexp}\) :
-
Syntactic group of arithmetic expressions
- \(\textsc {bexp}\) :
-
Syntactic group of Boolean expressions
- \(\textsc {cexp}\) :
-
Syntactic group of cost expressions
- \(\textsc {seq}\) :
-
Syntactic group of sequential programs
- \(\textsc {par}\) :
-
Syntactic group of parallel programs
- \(\mathcal {A}{{\llbracket {\cdot }\rrbracket }} : \textsc {aexp}\times {\varSigma }\rightarrow \mathbb {N}\) :
-
Semantics of arithmetic expressions
- \(\mathcal {B}{{\llbracket {\cdot }\rrbracket }} : \textsc {bexp}\times {\varSigma }\rightarrow \{{\texttt {tt}}, {\texttt {ff}}\}\) :
-
Semantics of Boolean expressions
- \(\mathcal {C}{{\llbracket {\cdot }\rrbracket }} : \textsc {cexp}\times {\varSigma }\rightarrow \mathbb {N}_\omega \) :
-
Semantics of cost expressions
- \(\mathbb {T}\) :
-
Termination states
- \(u\in \mathbb {U}= \{ \mathbf a , \mathbf b , ... \}\) :
-
Cost unit
- \(w\in \mathbb {W}= (\mathbb {N}\times \mathbb {U})^{*}\) :
-
Work trace
- \(\epsilon \) :
-
Empty sequence
- \(\mathbb {R}\) :
-
Communication requests
- \(Cost_{\textsc {seq}}: \mathbb {W}\rightarrow (\mathbb {U}\rightarrow \mathbb {N})\) :
-
The cost of a sequential execution
- \(Cost_{\textsc {par}}: \mathbb {W}^{p \times S{}} \times \mathbb {R}^{p \times S{}} \rightarrow (\mathbb {U}\rightarrow \mathbb {N})\) :
-
The cost of a parallel execution
- \(\textsc {sca}: \textsc {seq}\rightarrow (\mathbb {U}\rightarrow \textsc {cexp})\) :
-
Sequential cost analysis
- \(\omega \) :
-
The expression of unbounded cost
-
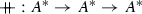 :
: -
Concatenation of sequences
- \((:) : A^p \times A^{p \times S{}} \rightarrow A^{p \times (S{}+1)}\) :
-
Left concatenation of vector to matrix
- \({\textit{Comm}}: {\varSigma }^p \times \mathbb {R}\times {\varSigma }^p\) :
-
Implementation specific communication relation
- \(\sigma \in {\varSigma }= \mathbb {X}\rightarrow \mathbb {N}\) :
-
Environment
- \(\sigma ^{i,p} \in {\varSigma }\) :
-
Process local environment
-
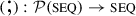 :
: -
Sequential composition of a set of statements
References
Albert, E., Arenas, P., Correas, J., Genaim, S., Gómez-Zamalloa, M., Martin-Martin, E., Puebla, G., Román-Díez, G.: Resource analysis: from sequential to concurrent and distributed programs. In: Proceedings on FM 2015: Formal Methods: 20th International Symposium, Oslo, Norway, 24–26 June 2015, pp. 3–17. Springer (2015). https://doi.org/10.1007/978-3-319-19249-9_1
Albert, E., Arenas, P., Genaim, S., Puebla, G.: Closed-form upper bounds in static cost analysis. J. Autom. Reason. 46(2), 161–203 (2011)
Albert, E., Arenas, P., Genaim, S., Puebla, G., Zanardini, D.: Cost analysis of Java bytecode. In: European Symposium on Programming, pp. 157–172. Springer (2007)
Benabderrahmane, M.W., Pouchet, L.N., Cohen, A., Bastoul, C.: The polyhedral model is more widely applicable than you think. In: International Conference on Compiler Construction, pp. 283–303. Springer (2010)
Boulet, P., Redon, X.: Communication pre-evaluation in HPF. In: Proceedings of the 4th International Euro-Par Conference on Parallel Processing, Euro-Par ’98, pp. 263–272. Springer, London (1998)
Chatarasi, P., Shirako, J., Kong, M., Sarkar, V.: An extended polyhedral model for SPMD programs and its use in static data race detection. In: Ding, C., Criswell, J., Wu, P. (eds.) Languages and Compilers for Parallel Computing, pp. 106–120. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-52709-3_10
Clauss, P.: Counting solutions to linear and nonlinear constraints through Ehrhart polynomials: applications to analyze and transform scientific programs. In: Proceedings of the 10th International Conference on Supercomputing, ICS ’96, pp. 278–285. ACM, New York (1996). https://doi.org/10.1145/237578.237617
Cousot, P., Halbwachs, N.: Automatic discovery of linear restraints among variables of a program. In: Proceedings of the 5th ACM SIGACT-SIGPLAN Symposium on Principles of Programming Languages, pp. 84–96. ACM (1978)
Di Martino, B., Mazzeo, A., Mazzocca, N., Villano, U.: Parallel program analysis and restructuring by detection of point-to-point interaction patterns and their transformation into collective communication constructs. Sci. Comput. Program. 40(2–3), 235–263 (2001). https://doi.org/10.1016/S0167-6423(01)00017-X
Hayashi, Y., Cole, M.: Static performance prediction of skeletal parallel programs. Parallel Algorithms Appl. 17(1), 59–84 (2002)
Heine, F., Slowik, A.: Volume driven data distribution for NUMA-machines. In: Euro-Par 2000 Parallel Processing, pp. 415–424. Springer, Berlin (2000). https://doi.org/10.1007/3-540-44520-X_53
Hill, J.M.D., McColl, B., Stefanescu, D.C., Goudreau, M.W., Lang, K., Rao, S.B., Suel, T., Tsantilas, T., Bisseling, R.H.: BSPlib: the BSP programming library. Parallel Comput. 24(14), 1947–1980 (1998). https://doi.org/10.1016/S0167-8191(98)00093-3
Hoffmann, J., Shao, Z.: Automatic static cost analysis for parallel programs. In: European Symposium on Programming Languages and Systems, pp. 132–157. Springer (2015)
Jakobsson, A., Dabrowski, F., Bousdira, W., Loulergue, F., Hains, G.: Replicated synchronization for imperative BSP programs. In: International Conference on Computational Science (ICCS), Procedia Computer Science. Elsevier., Zürich (2017)
Jeannet, B., Miné, A.: Apron: a library of numerical abstract domains for static analysis. In: International Conference on Computer Aided Verification, pp. 661–667. Springer (2009)
Juurlink, B.H.H., Wijshoff, H.A.G.: A quantitative comparison of parallel computation models. In: Proceedings of the Eighth Annual ACM Symposium on Parallel Algorithms and Architectures, SPAA ’96, pp. 13–24. ACM, New York (1996). https://doi.org/10.1145/237502.241604
Lengauer, C.: Loop parallelization in the polytope model. In: International Conference on Concurrency Theory, pp. 398–416. Springer (1993)
Nielson, F., Nielson, H.R., Hankin, C.: Principles of Program Analysis. Springer, Berlin (2004)
Tesson, J., Loulergue, F.: Formal semantics of DRMA-style programming in BSPlib. In: Wyrzykowski, R., Dongarra, J., Karczewski, K., Wasniewski, J. (eds.) Parallel Processing and Applied Mathematics, vol. 4967, pp. 1122–1129. Springer, Berlin (2008)
Valiant, L.G.: A bridging model for parallel computation. Commun. ACM 33(8), 103–111 (1990). https://doi.org/10.1145/79173.79181
Verdoolaege, S.: isl: An integer set library for the polyhedral model. In: International Congress on Mathematical Software, pp. 299–302. Springer (2010)
Verdoolaege, S., Grosser, T.: Polyhedral extraction tool. In: Second International Workshop on Polyhedral Compilation Techniques (IMPACT’12), Paris (2012)
Verdoolaege, S., Seghir, R., Beyls, K., Loechner, V., Bruynooghe, M.: Counting integer points in parametric polytopes using Barvinok’s rational functions. Algorithmica 48(1), 37–66 (2007)
Wegbreit, B.: Mechanical program analysis. Commun. ACM 18(9), 528–539 (1975). https://doi.org/10.1145/361002.361016
Wilhelm, R., Engblom, J., Ermedahl, A., Holsti, N., Thesing, S., Whalley, D., Bernat, G., Ferdinand, C., Heckmann, R., Mitra, T., et al.: The worst-case execution-time problem—overview of methods and survey of tools. ACM Trans. Embedded Comput. Syst. (TECS) 7(3), 36 (2008)
Winskel, G.: The Formal Semantics of Programming Languages: An Introduction. MIT Press, Cambridge (1993)
Zimmermann, W.: Automatic Worst Case Complexity Analysis of Parallel Programs. International Computer Science Institute, California (1990)
Acknowledgements
I thank Wijnand Suijlen for his help with the evaluation and his comments on the article, as well as Frédéric Loulergue for his insightful comments that greatly improved this article. I also thank the anonymous reviewers for their remarks on earlier drafts.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Jakobsson, A. Automatic Cost Analysis for Imperative BSP Programs. Int J Parallel Prog 47, 184–212 (2019). https://doi.org/10.1007/s10766-018-0562-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10766-018-0562-1
















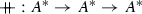 :
: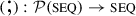 :
: