1 Introduction

Fourier transform infrared photoacoustic spectroscopy (FTIR-PAS) is now widely used for the detection and analysis of various materials in solid and liquid phases due to the possibility of depth profiling [1–4]. The advantages of FTIR-PAS with gas samples are low sample volume, short absorption path length, and direct absorption measurement, which allow sensitive and selective measurements in the presence of large amounts of interfering substances and residual absorptions, e.g., due to optical windows. There is an increasing interest in step-scan FTIR interferometers because of the beneficial application to dynamic spectroscopy [5].

In this paper, a step-scan FTIR-PAS method based on a commercial FTIR spectrometer is developed for air contamination monitoring. A T-cell was used as the resonator because the resonant frequency is independent of absorption cylinder geometry and is determined by the resonance cylinder perpendicular to the optical path [6]. This design provides a possible approach for low- frequency amplitude modulation despite the small-volume sample compartments of today’s FTIR spectrometers.

2 Theory

Although there are numerous publications on FTIR-PAS of solid and liquid samples, few of them on FTIR-PAS theory for gas samples have been published [7]. Furthermore, as T-cell is a kind of novel resonant photoacoustic cell that is being applied in PAS fields [8–13], its full theory on photoacoustic signal analysis has not been well developed comprehensively [12]. To explore the step-scan FTIR-PAS signal theoretically, it is valuable to consider the FTIR-PAS theory for regular cylindrical PA cell as the resonance principles of both kinds of cell are similar [12]. This work can form the basis for predicting the resonant mode of T-cell.

2.1 FTIR-PAS Theory for Cylindrical Cells

The complete record of optical intensity \(I(\delta )\) and the optical spectral intensity of wavenumber \(B(\sigma )\) are Fourier transform pairs of each other for a multiplex wavenumber interferometer. \(\delta \) and \(\sigma \) refer to optical path difference (OPD) and wavenumber. Because of the symmetry of interferograms about the point of zero OPD, \(B(\sigma )\) can be written as [14]

$$\begin{aligned} B\left( \sigma \right) =2\int \limits _0^\infty {I\left( \delta \right) \cos \left( {2\pi \delta \sigma } \right) \mathrm{d}\delta }. \end{aligned}$$
(1)

In a step-scan interferometer, the moving mirror is moved in discrete steps and halts at each retardation at which the interferograms are sampled. The OPD is then changed according to the desired spectral resolution. Assuming that there are N points in one interferogram, and the data are collected (digitized) L times, then averaged at each position, \(I(\delta _{j})\) is the signal the FTIR detector obtains at position \(\delta _{j}\). The averaged value of the signal is

$$\begin{aligned} \bar{I} \left( {\delta _j } \right) =\frac{1}{L}\sum _1^L {I_l \left( {\delta _j } \right) } \qquad l: 1,2,3, \ldots ,L,\quad j:1,2,3, \ldots ,N-1. \end{aligned}$$
(2)

To perform the Fourier transform, we multiply each point by the corresponding point of an analyzing cosine wave of unit amplitude and add the resulting values. Assuming that the interferograms are digitized at equal intervals h, then \(\delta _{j}=jh\). The spectrum signal for any wavenumber \(\sigma _{k}\) can be given as the discrete version of Eq. 1:

$$\begin{aligned} B\left( {\sigma _k } \right) = \bar{I}(0)+2\sum _{j=1}^{N-1} {\bar{I}} \left( {jh} \right) \cos \left( {2\pi \sigma _k jh} \right)&\quad j :1, 2, 3,\ldots ,N-1, \nonumber \\&\quad k:1, 2, 3,\ldots , K. \end{aligned}$$
(3)

The summation in Eq. 3 is performed over all wavenumbers K of interest in the spectrum. Wavenumber interval is determined by phase resolution and wavenumber range is determined by the broadband FTIR excitation source in each case.

The theory of eigenmodes in a regular cylindrical cell has long been described by several authors [15, 16], and is summarized here in combination with step-scan FTIR theory. The heat H(r, t) produced by the absorption and non-radiative conversion of the interference beam \(I(r,\omega )\) modulated by a chopper in the sample (gas) chamber of an FTIR spectrometer acts as a source for the generation of sound in a regular cylindrical cell. The acoustic eigenmodes can be described by the inhomogeneous wave equation [17]:

$$\begin{aligned} \left( {\nabla ^{2}+\omega ^{2}/c^{2}} \right) p\left( {r,\omega } \right) =-\left[ {\left( {\gamma -1} \right) /c^{2}} \right] i\omega \hat{{H}} ( {r,\omega }), \end{aligned}$$
(4)

where \(\gamma \) is the ratio of the specific heat of the gas in the spectrometer chamber at constant pressure \(C_{p}\) to that at constant volume \(C_{v}\) and c is the speed of sound which is mainly determined by the sample gas in the resonator.

If the walls of the gas container are rigid, then the normal derivative of pressure is equal to zero at the boundary. The solution of the homogenous equation (lossless) in cylindrical coordinate using orthogonality and normalization conditions is given by

$$\begin{aligned} p_s ={\begin{array}{l} {\cos } \\ {\sin } \\ \end{array} }\left( {m\phi } \right) \left[ {J_m \left( {\frac{\pi \alpha _{mn} }{a}r} \right) } \right] \cos \left( {\left( {\frac{\pi }{L}} \right) n_z z} \right) \hbox {,} \, \omega _s =c\sqrt{\left( {\frac{\pi \alpha _{mn} }{a}} \right) ^{2}+\left( {\left( {\frac{\pi }{L}} \right) n_z } \right) ^{2}},\nonumber \\ \end{aligned}$$
(5)

where \(\omega _{s}\) is the angular resonant frequency and a and L are the radius and length of cell, respectively. m, n,  and \(n_{z}\) refer to the eigenvalues of the radial, azimuthal, and longitudinal modes, respectively. \(\alpha _{mn}\) is the nth root of the equation involving the mth-order Bessel function.

The acoustic pressure p can be expressed as an expansion over eigenmodes \(p_{s}\) with mode amplitudes \(A_{s}\), and the solution of the inhomogeneous wave equation (Eq. 4) can be written as a series expansion in the eigenfunction basis of Eq. 5.

$$\begin{aligned} p\left( {r,\omega } \right) =\sum _s {A_s } \left( \omega \right) p_s \left( r \right) \end{aligned}$$
(6)

The physically unreasonable situation of the absence of any loss mechanism in the chamber can be corrected by adding the quality factor \(Q_{s}\), so the amplitude for each mode is expressed in Eq. 7 [16]:

$$\begin{aligned} A_s \left( \omega \right) =\frac{i\omega }{\omega _s ^{2}}\frac{\left[ {\left( {\gamma -1} \right) /V_c } \right] }{\left( {\omega ^{2}/\omega _s ^{2}-1-i\omega /\omega _s Q_s } \right) }\int {p_s ^{*} \hat{{H}} \left( {r,\omega } \right) \mathrm{d}V}. \end{aligned}$$
(7)

If the intensity of the incident beam is \(\hat{{I}}(r,\omega )\), and \(\hat{{H}}(r,\omega )\) is generated by absorption of the light, Ĥ and Î are related by the absorption coefficient \(\alpha \) which is a function of the wavenumber \(\nu \).

$$\begin{aligned} \hat{{H}}\left( {r,\omega } \right) =\alpha \left( \nu \right) \hat{{I}}\left( {r,\omega } \right) \end{aligned}$$
(8)

In order to show the dependence between incident light and acoustic signal, Ĥ is replaced with Î in Eq. 8 and Eq. 7 becomes

$$\begin{aligned} A_s \left( \omega \right) =\frac{i\omega }{\omega _s ^{2}}\frac{\alpha \left( \nu \right) \left[ {\left( {\gamma -1} \right) /V_c } \right] }{\left( {\omega ^{2}/\omega _s ^{2}-1-i\omega /\omega _s Q_s } \right) }\int {p_s ^{*}\hat{{I}}\left( {r,\omega } \right) \mathrm{d}V}. \end{aligned}$$
(9)

In the FTIR step scan, an optical chopper is applied to provide the external modulation at angular frequency \(\omega _{0}\) as amplitude modulation (AM). A lock-in amplifier is tuned to accept the component and demodulate the signal at \(\omega _{0}\) when it becomes equal to the resonant angular frequency \(\omega _{001} (m=n=0, n_{z}=1)\), providing the well-known interferograms. \(\omega _{001}\) is substituted for \(\omega _{1}\) in what follows, so the amplitude at \(\omega _{1}\) can be written as

$$\begin{aligned} A\left( {\omega _1 } \right) =\sum _s {\beta _s } A_s \left( {\omega _1 } \right) , \end{aligned}$$
(10)

where \(\beta _{s}\) is the linear coefficient. However, \(A_{1}(\omega _{1})\) is the most predominant element of \(A(\omega _{1})\), so only the fundamental frequency should be considered. The pressure in the cylinder varies in the axial direction:

$$\begin{aligned} p\left( {r,\omega _1 } \right)= & {} A(\omega _1 )p_1 =2\frac{\alpha \left( \nu \right) Q_1 \left[ {\left( {\gamma -1} \right) /V_c } \right] }{\omega _1 }\nonumber \\&\quad \cos \left( {\frac{\pi }{L}z} \right) \int _V {\cos \left( {\frac{\pi }{L}z} \right) \hat{I} \left( {r,\omega _1 } \right) \mathrm{d}V}. \end{aligned}$$
(11)

Here, \(p_1 (r)=\cos \left( {\frac{\pi }{L}z} \right) \). Considering Eq. 6, the photoacoustic signal is given in Eq. 12 when the cell is resonant at the fundamental frequency when the microphone is at the position \(z_{1}\).

$$\begin{aligned} B_{PAS} \left( {\sigma _k ,z_1 } \right)&= \chi \cos \left( {\frac{\pi }{L}z_1 } \right) \int _V {\cos \left( {\frac{\pi }{L}z} \right) \bar{I} \left( 0 \right) \mathrm{d}V}\nonumber \\&\quad +2\chi \sum _{j=1}^{N-1} {\mathop {\cos \left( {\frac{\pi }{L}z_1 } \right) \cos \left( {2\pi \sigma _k jh} \right) \int _V {\cos \left( {\frac{\pi }{L}z} \right) \bar{I} \left( {jh} \right) \mathrm{d}V} }} \, \nonumber \\&j :1,2,3 \ldots N-1,\quad k :1, 2, 3\ldots K, \end{aligned}$$
(12)

and

$$\begin{aligned} \chi =\frac{2\alpha \left( \nu \right) Q_1 \left[ {\left( {\gamma -1} \right) /V_c } \right] }{\omega _1 }. \end{aligned}$$
(13)

Heat conduction and viscous losses inside of gas volume are neglected since the power loss is quite small compared to the surface loss due to viscosity and thermal conduction at the wall of the resonator [18]. Surface losses can be calculated from Eq. 14 [16]:

$$\begin{aligned} 1\big /{Q_j^{s_\kappa } }=\frac{1}{2}\left( {\gamma -1} \right) \frac{d_\kappa }{V_c }\int \limits _{s_c } {|p_j |^{2}\mathrm{d}S} , \qquad 1\big /{Q_j^{s_\eta } }=\frac{1}{2}\left( {\frac{c}{\omega _j }} \right) ^{2}\frac{d_\eta }{V_c }\int \limits _{s_c } {|\nabla _t p_j |^{2}\mathrm{d}S},\nonumber \\ \end{aligned}$$
(14)

where \(Q_j^{s_\kappa } \) and \(Q_j^{s_\eta } \) refer to the thermal and viscous losses at the surface, respectively, when the cell responds at the resonant angular frequency \(\omega _{j;}\) \(\eta \) is the viscosity and \(\kappa \) is the thermal conductivity. \(\rho \) is the gas density. \(d_{\kappa }\) and \(d_{\eta }\) refer to the thermal and viscous loss layers which are defined as follows in Eq. 15 [18]:

$$\begin{aligned} d_\kappa =\sqrt{\frac{2\kappa }{C_p \rho \omega _s }},\hbox { }d_\eta =\sqrt{\frac{2\eta }{\rho \omega _s }}. \end{aligned}$$
(15)

2.2 Description of the T-cell

The basic T-cell geometry consists of three parts: the absorption, buffer, and resonance cylinders [6], as depicted in Fig. 1a. A pressure wave propagating in the resonance cylinder will be reflected at the open end with the opposite phase, and resonate when its length is equal to an odd integer of a quarter wavelength. The corresponding resonance frequencies can be obtained from the following expressions:

$$\begin{aligned} f_{2q-1} =\frac{\left( {2n_z -1} \right) c}{4\left( {L+\Delta l} \right) } ; \quad n_z =1,2,3\ldots \end{aligned}$$
(16)

Here \(\Delta l\) is the end correction, which should be added to the length of the resonance cylinder with an open end. The end correction is an effect of the mismatch between the one-dimensional acoustic field inside the pipe and the three-dimensional field outside that is radiated at the open end [19].

2.3 FEM Analysis of T-cells

A T-cell simulation model was built with Comsol Multiphysics 4.3 software. The geometry is shown in Fig. 1a. Aluminum walls and \(\hbox {CaF}_{2}\) windows were used. D and L refer to the diameter and length of the three parts, respectively. A 20-mm-diameter collimated Gaussian beam was used to simulate the incident interference optical beam exciting the T-cell from the FTIR interferometer. Lossy boundary conditions were applied due to the thermal and viscous losses at the boundary [20]. All the results were calculated along the microphone area which is located at the top of the resonance cylinder.

Fig. 1
figure 1

(a) T-cell model and (b) FTIR-PAS schematic

Full size image

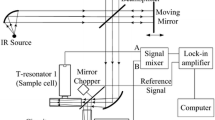
3 Experimental Arrangement

The FTIR-PAS setup based on a commercial FTIR spectrometer (McPherson Vertex 70), and the gas sampling assembly are shown in Fig 1b. The MIR source (intensity, 30 mW) inside FTIR spectrometer and a Proimo \(\hbox {EM}158^{*}\) electronic condenser microphone (sensitivity, 25 mV/Pa at 1 kHz) are adopted. The incident interference light is modulated by a chopper (SR540, Standard Research System) and propagates inside the resonator. Then, a photoacoustic wave is generated by the gas sample inside the resonator, detected by the microphone on top of the resonance cylinder. Each wavelength is modulated at the same frequency which is equal to the fundamental resonance frequency. The output of the lock-in amplifier (Model 850, Standard Research System) is detected and stored in the FTIR memory. The experimental setup includes the gas dilution assembly which consists of analyte and dilution gas cylinder (supplied by Linde Gas/AGA), pressure reducers, flow meter (FE7300, Matheson) as well as recovery apparatus. We chose carbon dioxide as the preferred gas for analysis and several concentrations were made by a home-made apparatus, setting the flow rate of each tube of our flow meter to the desired value. After the gas mixture filled up the resonator cell, it needed to be kept for 3–4 h before commencing measurements [21]. The incident source radiant power at the carbon dioxide absorption peak at around \(2349\,\hbox {cm}^{-1}\) was estimated to be 0.0126 mW according to the distribution and intensity of the MIR source inside the FTIR spectrometer.

4 Results

The amplitude and phase responses obtained by simulation and frequency scan measurements chopping the illuminated beam from the MIR source in the spectrometer and detecting the signal with the lock-in amplifier are shown in Fig. 2a, b, respectively. There is a good agreement between simulated and measured results since the experimental resonant frequency in air is approximately 342 Hz to be compared to 341 Hz from the simulation. The simulated signal fits the experimental data reasonably well, and the small deviations are probably due to neglecting the loss in the volume of the sample gas and cell design imperfections. From Eq. 9, the step-scan FTIR-PA phase \(\theta \) of \(A_{s} (\omega )\) in Eq. 9 for regular cylindrical cell is given by the expression:

$$\begin{aligned} \tan \theta =\frac{1}{Q_s }\left( {\frac{\omega _s }{\omega }-\frac{\omega }{\omega _s }} \right) \end{aligned}$$
(17)

which decreases with frequency in the range \([-\pi /2, \pi /2]\). This expression shows very similar behavior with the T-cell experimental phase frequency response. Figure 2a, b shows excellent agreement between simulated and measured amplitude and phase results overall. The cell constant of the T-cell was calculated to be 2063 \(\hbox {Pa} \cdot \hbox {cm}^{-1} \cdot \hbox {W}\).

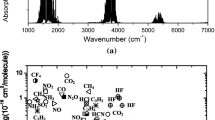
The selectivity of the experimental setup can be estimated from Fig.  2c and the results are normalized with the spectrum of the MIR source we use. The results are measured with both the resolution (\(\upsilon =\Delta ^{-1}\), where \(\upsilon \) is the resolution and \(\Delta \) is the maximum retardation of an interferometer) and the spectral resolution of \(6\,\hbox {cm}^{-1}\). The minimal resolution of the FTIR spectrometer is \(0.5\,\hbox {cm}^{-1}\). In the infrared absorption spectrum, it is possible to distinguish the rotational vibrational levels especially for the strong absorption peak at around \(2349\, \hbox {cm}^{-1}\) with the resolution of \(6\,\hbox {cm}^{-1}\). The SNR (signal-to-noise ratio) for the FTIR-PAS of carbon dioxide concentration of 5000 ppmv was found to be 1515.5 calculated with the method mentioned in [22]. Therefore, the theoretical detection limit is \(5000/1515.5=4\) ppmv for \(\hbox {SNR} = 1\). The theoretical detection limit is comparable with results in [22] based on optical cantilever detection with an FTIR spectrometer, but the system presented here is simpler. Although the theoretical detection limit cannot be compared with some laser-based detection methods, the T-cell FTIR-PAS system has inherent multi-component gas detection capability advantages due to the very broad spectral range of FTIR and the small footprint of the spectrometer with potential for portable use in the field.

The FTIR-PAS signal of the asymmetric stretch C=O vibration of carbon dioxide molecule [23] vs. concentration was found to change linearly as expected [24], and it is shown in Fig. 2d. The linear response between the step-scan FTIR-PAS signal and concentration is powerful evidence of the capability of the spectrometer for quantitative analysis of ambient gases using this method. It can be especially valuable because non-linear behavior in practice would require non-linear calibration and more complicated algorithms [25].

Fig. 2
figure 2

(a) Amplitude response of T-cells, (b) phase response of T-cells, (c) step-scan FTIR-PAS of a mixture of carbon dioxide and nitrogen at volume ratio 1:200, and (d) linearity analysis of carbon dioxide in nitrogen at the absorption peak around \(2349\,\hbox {cm}^{-1}\)

Full size image

5 Conclusions

A step-scan FTIR-PAS system has been established based on a commercial FTIR interferometer for monitoring environmental pollutants. The step-scan FTIR-PAS theory of a conventional cylindrical resonator outfitted with a T-cell for use with the small FTIR spectrometer chamber and low resonance frequency which otherwise requires a long resonant cell was introduced. This design is very appealing for in-field use of the spectrometer. Simulated results indicate excellent agreement with the experimental data both in amplitude and phase responses. The theoretical detection limit for \(\hbox {CO}_{2 }\) was found to be 4ppmv. The feasibility of T-cell step-scan FTIR-PAS as a quantitative analysis method for ambient pollutant gases was demonstrated through its linear response to various \(\hbox {CO}_{2}\) concentrations in \(\hbox {N}_{2}\).