Eccentricity Effects on Bearing Capacity of Strip and Square Footings on Two-Layered Clay

Abstract

The undrained ultimate capacity to combined (M, V) loading of strip and square foundations on a two-layered clay deposit is investigated. Extensive two and threedimensional parametric finite element analyses are carried out in terms of the ratio of the undrained shear strength of two layers, the normalized thickness of the top layer and the normalized load eccentricity. Two basic cases are separately investigated, referring to strength ratios higher or lower than unity. The assumption of effective width of the foundations, to account for eccentricity, generally adopted for homogeneous soil, is extended for two layers. The results are mainly presented in terms of modified bearing capacity factors for strip or square footings for a wide range of dimensionless problem parameters. However, for a better visual understanding of how the bending moment affects the ultimate vertical load failure loci diagrams (“yield surfaces”) in M, V space are also presented. Emphasis is given to developing insight into the particular failure mechanisms of most examined cases.

1 Introduction

The bearing capacity (BC) of foundations based on homogeneous soil layer and subjected either to vertical or combined loading, has been extensively investigated. Results are widely available in the form of semi-empirical coefficients for shape, depth, inclination and eccentricity effects (i.e. Meyerhof 1953; Brinch Hansen 1970; Poulos et al. 2001). Apparent upper and lower bounds to a plausible solution were obtained by Houlsby and Puzrin (1999) for strip footing under combined loading. Rigorous solution for centric loads has been later presented by Salgado et al. (2004). Alternatively, the effects of the combined loading can be illustrated by the locus of all the critical combinations of moment, vertical and shear loads, which form a three-dimensional bearing strength surface (i.e. Georgiadis 1985; Taiebat and Carter 2000; Pender 2017).

However, the natural deposits often consist of distinct soil layers having significantly different shear strength parameters. The effect of strength non-homogeneity (shear strength linearly increasing with depth), on the shape of failure envelopes for combined loading was examined by Gourvenec and Randolph (2003). The problem of foundations on two-layered system could be important, if the width of footing is large enough, in comparison with the thickness of upper layer. Early modifications of the 2D theoretical BC formulae to account for two layers, using circular slip surfaces, had been presented by Button (1953) with satisfactory approximation (Puzrin et al. 2010). Brown and Meyerhof (1969) proposed empirical modification factors from small-scale model tests on circular and strip footings, where punching failure through the top layer was observed. Meyerhof and Hanna (1978) made similar proposals on the basis of additional model tests for footings on clay or sand layers, under inclined loading. More rigorous theoretical results using upper bound and lower bound limit analyses were presented by Chen (1975), Michalowski and Shi (1995), Merifield et al. (1999), Michalowski (2002).

Two-dimensional (2D) finite element analyses were performed by many researchers (for example Burd and Frydman 1997; Zhu 2004), for a strip footing on two layered system. The 2D case of two-layered clay system with undrained shear strength either constant or varying continuously with depth was examined by Benmebarek et al. (2012). The case of either rectangular or square foundations was examined by 3D finite element analyses by Zhu and Michalowski (2005), Merifield and Nguyen (2006), while Salgado et al. (2013) reexamined such failure cases of foundations on layered soils. Yu et al. (2011) presented results from 3D large deformation FE analyses for square footings on two layered clays (stiff over soft). All the above-mentioned studies refer to central vertical loads on foundations resting on two-layered clayey soil. Several publications however, have presented results for combined loading on strip footings (Zhan and Luan 2011; Rao et al. 2015).

In the present paper the effect of load eccentricity is investigated systematically with 2D and 3D finite element analyses for combined moment and vertical loading (M, V) on strip and square footings. Parametric analyses are performed for a wide range of parameters, most important of which is the undrained shear strength ratio SR = s_u,2/s_u,1 of the two layers. The results of the analyses are evaluated in conjunction with the developing failure mechanism. The cases of SR < 1 or SR > 1 are separately investigated in the paper, since the corresponding mechanisms are qualitative different in the two cases. These results fill several gaps in determining the ultimate capacity under combined M, V loading.

2 Problem Definition and Simulation Details

In the simplest case of strip footing of width B on homogeneous clay under undrained conditions, the ultimate central load, V_u,o is given by:

$${\text{V}}_{{{\text{u,o}}}} = {\text{ q}}_{{\text{u}}} \,{\text{B }} = {\text{ N}}_{{\text{C}}} \,{\text{s}}_{{\text{u}}} \,{\text{B}}$$

(1a)

where s_u the undrained shear strength of the clay (φ_u = 0 conditions) and N_C = (2 + π) Prandtl’s bearing capacity factor.

For two-layered clay system, the ultimate central load will be written as:

$${\text{V}}_{{{\text{u,o}}}} = {\text{ N}}_{{{\text{C1}}}} \,{\text{s}}_{{{\text{u,1}}}} \,{\text{B}}$$

(1b)

where s_u,1 the undrained shear strength of the upper clay layer and N_C1 the equivalent bearing capacity factor, function of the normalized thickness of the upper layer (H₁/B) and the strength ratio SR = s_u,2/s_u,1.

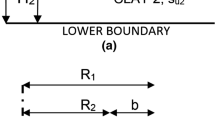
A schematic diagram of the eccentric loading of a strip footing, on homogeneous clay is shown in Fig. 1a. The combined moment and vertical (M, V) loading results in eccentricity e = M/V, which influences the ultimate vertical load, V_u,e, according to the well-known formula:

$${\text{V}}_{{{\text{u, e}}}} = {\text{ q}}_{{\text{u}}} \,{\text{B}}^{\prime } = {\text{ N}}_{{\text{C}}} \,{\text{s}}_{{\text{u}}} \,{\text{B}}^{\prime } = {\text{ N}}_{{\text{C}}} \,{\text{s}}_{{\text{u}}} \,\left( {{\text{B}} - 2{\text{e}}} \right)$$

(2a)

where N_C the bearing capacity factor (identical to this of Eq. 1a) and B′ = B − 2e is the effective width, across which the uniform soil reaction at failure is assumed to be. For two-layered clay (Fig. 1b) Eq. (2a) is conveniently modified also:

$${\text{V}}_{{{\text{u}},{\text{e}}}} = {\text{ N}}_{{{\text{C1}},{\text{e}}}} {\text{s}}_{{{\text{u}}, 1}} \left( {{\text{B}} - 2 {\text{e}}} \right)$$

(2b)

where N_C1,e the bearing capacity factor, which is a function of the dimensionless parameters, e/B, H₁/B and SR.

Fig. 1

a and b Ultimate eccentric load on strip foundation: the concept of equivalent width, B′ and the geometry of the studied problem, c Example of 3D Finite element mesh

Generalizing the simple plane-strain problem into three dimensional conditions (for example rectangular or square footings) the ultimate vertical load is written, as follows:

$${\text{V}}_{{{\text{u, o}}}} = {\text{N}}_{{{\text{C1}}}}^{*} \,{\text{s}}_{{{\text{u,1}}}} \,{\text{LB}},\quad {\text{for}}\;{\text{e }} = 0$$

(3a)

$${\text{V}}_{{{\text{u}},{\text{e}}}} = {\text{ N}}^{*}_{{{\text{C1}},{\text{e}}}} {\text{s}}_{{{\text{u}}, 1}} {\text{L }}\left( {{\text{B}} - 2 {\text{e}}} \right),\quad {\text{ for e }} \ne \, 0$$

(3b)

where L, B the dimensions of a rectangular footing and N ^*_C1 , N ^*_C1,e the bearing capacity factors incorporating additionally the shape effects. Obviously, Eqs. (3a) and (3b) are valid for moment (M) vector, which is parallel to the long side L (eccentricity along the axis of the width, B).

The analyses are carried out using the 2D and 3D versions of the FE Plaxis program, for the cases of strip and square footings, respectively. In both cases, 15-node triangular or wedge elements for the soil modelling were used with 12 stress points of each of them. The foundation (either strip or square) is modeled as a rigid plate. The interface between foundation and soil is modeled with contact elements, including five pairs of nodes, taking into account that the mesh consists of 15-node triangular or wedge elements. Typically, the interaction between the footing and the soil is intermediate between smooth and fully rough, but usually approaches the latter case. The roughness is modeled by choosing an appropriate value for the strength reduction factor in the interface (R_inter). This factor relates the interface strength to the soil strength. In all analyses, the case of rough interface was considered by selecting R_inter = 1. The dimensions of FE mesh in a vertical plan view are always large enough to ensure that the plastic zones and displacements are restricted to the model boundaries, thus avoiding spurious boundary effects. This is especially important for low strength ratios (SR < 1). The normalized thickness of the upper layer H₁/B varies parametrically from 0.10 to 2. The thickness of the second layer, H₂ is large enough to have any effect; hence, for strong over soft clay (SR < 1), the lower boundary is set to depth up to 5B, in most cases. On the contrary, for SR > 1, this depth is selected much smaller, since the failure mechanism is quite shallow. A typical finite element mesh is shown in Fig. 1c, simulating a square footing, subjected to a highly eccentric load, where the front plane was selected at the principle axis parallel to the width B, taking advantage of symmetry, and the area of the mesh refinement is visible.

The soil was modeled as linear elastic-perfectly plastic Mohr–Coulomb material, with φ_u = 0 for the undrained conditions under consideration. The water table is at the ground surface. Taking the undrained shear strength of the upper layer as s_u,1 = 100 kPa, the undrained shear strength of the lower layer was accordingly assumed s_u,2 = 13.3–500 kPa, so the strength ratio varies widely (SR = 0.13–5). The modulus of elasticity in each analysis was selected as E = 300 s_u, while the Poisson’s ratio ν = 0.495. Nevertheless, neither E nor ν have any measurable effect on the resulting ultimate loads. The unit weight of the top layer is γ₁ = 20 kN/m³, while for the lower one γ₂ = (16–22) kN/m³. The latter one (γ₂) has no effect on the results. In contrast, from the sensitivity analyses performed, it seems that the unit weight of the upper layer has generally a very low effect, which becomes quite appreciable for a weightless soil, (γ₁ = 0). It is noted that in several cases of previous investigations the soil was assumed as weightless. However, this assumption is indisputably accurate only for homogeneous clay and undrained conditions.

The analyses are in most cases performed with 0 ≤ e/B ≤ 0.475, although the usual threshold of normalized eccentricity, in practice is e/B = 1/3. It is well known that the performance and accuracy of Plaxis programs have been carefully tested in the past. Nevertheless, before carrying out the parametric analyses of the present work, the FE results were compared with relevant from conventional methods, for the special case of homogeneous clay. Indicative results for the BC factors from preliminary F.E. results were: (1) For rough strip footing, N_C = 5.164, i.e. slightly higher than the theoretical value for smooth footing (2 + π), (2) For rough square footing ${\text{N}}^{*}_{\text{C}}$ = 6.171, corresponding to shape factor s_c = 1.195. Moreover, the validation evidence of the assumption of effective width, B′ = Β − 2e for strip footings is presented in Fig. 2. From Eqs. (1a) and (2a), the load ratio is V_ue/V_uo = 1 − ($\frac{{2{\text{e}}}}{\text{B}}$), according to the conventional BC methods. This linear relationship is verified by the F.E. analyses, while the distribution of contact pressures at failure, approaches the uniform soil reaction across the effective width, B′ (Figs. 1a, 2).

Fig. 2

Validation evidence of the assumption of effective width for SR = 1: comparison of V_ue/V_uo vs e/B diagrams

3 Strip Footing Subjected to Combined M, V Loading (Plane-Strain Problem)

3.1 Strong Over Soft Clay Layer (SR < 1)

For central vertical loading (e = 0) and strength ratios SR < 1, three mechanisms of failure have been identified in our analyses:

• i. Failure mechanism similar to Prandtl’s, for relatively high values of H₁/B and SR ratios only slightly lower than the unity (Type I).

• ii. An intermediate type mechanism (II) for several combinations of the parameters H₁/B and SR.

• iii. “Punching failure”, according to Meyerhof and Hanna (1978), for relatively low values of H₁/B and/or low strength ratios (Type III).

The influence of normalized eccentricity e/B is now illustrated in the indicative Fig. 3, for H₁/B = 0.50 and a relatively low strength ratio SR = 0.20. The failure mechanisms are revealing from the contours of displacements at failure (vectors of total displacements in shading). For central vertical loading (Fig. 3a), a punching failure (Type III) is expectedly clear, while the mechanism extends up to depth 2B approximately, much higher than the theoretical depth of influence of 0.7 B for a homogeneous clay. The gradual increase of normalized eccentricity, Fig. 3b and c results into rotation of the footing, enhanced accumulation of the plastic deformations into the upper layer and shrinking of the failure mechanism. Still, the mechanism goes deeper than on homogeneous clay.

Fig. 3

Contours of displacement revealing failure mechanisms of strip footing with a e/B = 0, b e/B = 0.10, c e/B = 0.333

The results of the analyses for various strength ratios and normalized eccentricities are cumulatively shown in Fig. 4 for H₁/B = 0.25 and 0.50. The bearing capacity factor for a homogeneous soil (SR = 1) is independent of e/B, so the adoption of effective width at failure B′ = Β − 2e seems realistic and according to Fig. 2 and Eq. (2a) remains valid. In contrast, for SR < 1, the equivalent factor N_C1,e, from Eq. (2b) increases with the increasing of eccentricity; the rate of increase is higher for the lower strength ratios. Evidently, when the normalized thickness increases, the factor N_C1,e reaches the maximum value N_C1,e = 5.164 ≈ (2 + π) for high e/B values and for a wide range of SR. This stems from the fact that the failure mechanism is restricted into the crust (for example Fig. 3c). The influence of the strength ratio on the equivalent factor N_C1,e for various eccentricities is depicted in Fig. 5, for three cases H₁/B = 0.25, 0.50 and 1.00. The higher the normalized eccentricity e/B, the higher N_C1,e values for all strength ratios SR. This trend is attributed to the decreased influence of the lower, weaker clay layer 2 on the bearing capacity, as the normalized eccentricity increases. The Plaxis BC factors of the present paper are in agreement with relevant results by Kamenou (2017), who investigated a similar problem using the F.E. program Abaqus, for strip footing and three cases of SR. The influence of eccentricity on the ultimate vertical load, V_u,e could be illustrated through the ratio V_u,e/V_u,o, where V_u,o is the ultimate vertical centric load. Figure 6 presents the variation of normalized ultimate load, versus e/B, for various SR values, according to relationship (4), resulting from the Eqs. (1b) and (2b):

Fig. 4

Strip footing, influence of eccentricity on the BC, factor N_C1,e for seven strength ratios (SR < 1): a case H₁/B = 0.25, b case H₁/B = 0.50

Fig. 5

Influence of the strength ratio on the BC factor N_C1,e for various eccentricities and H₁/B values

Fig. 6

Effect of eccentricity on the normalized ultimate load V_u,e for several strength ratios and two H₁/B values

$$\frac{{{\text{V}}_{{{\text{u,e}}}} }}{{{\text{V}}_{{{\text{u,o}}}} }} = \frac{{{\text{N}}_{{{\text{C1,e}}}} }}{{{\text{N}}_{{{\text{C1}}}} }}\left( {1 - 2\frac{{\text{e}}}{{\text{B}}}} \right)$$

(4)

Note that the rate of decrease of the ultimate load V_u,e with the ratio e/B, generally decreases as the strength ratio becomes lower, and thereby, the upper stronger clay layer has a dominant effect on the bearing capacity. For example, in case of H₁/B = 0.50 and the relatively high value e/B = 1/3, Fig. 6b indicates for SR = 0.133 that V_u,e/V_u,o = 0.75, whereas for the homogeneous clay (SR = 1) this ratio is only 0.33. On the other hand, for very high eccentricities (i.e. e/B > 1/3), a rapid decrease of the normalized ultimate load is expected, since for the theoretical threshold e/B = 0.5, V_u,e = 0.

3.2 Soft Over Strong Clay Layer (SR > 1)

For centric vertical load, two types of failure mechanisms are observed, as follows:

• i. Failure mechanism which extends into the lower, stronger layer, for low thickness of the upper layer and/or SR values only slightly higher than unity (Type IV).

• ii. Failure mechanism restricted to the upper, weaker layer, for relatively high values H₁/B and/or higher values of the strength ratio (Type V).

In the latter case the mechanism develops either below the ends of width B (for very low value of H₁/B) or it also extends to the central portion of the foundation.

The combined loading M, V results in modifications of the basic types of failure IV and V, as shown in Fig. 7 for H₁/B = 0.25, SR = 1.25. For centric load, a failure mechanism IV is clearly developed (case a), while for a high normalized eccentricity (case b), the failure surface is restricted to the upper layer. The results for various strength ratios SR are presented in Fig. 8 for two values of the normalized thickness H₁/B. The following conclusions emerge:

Fig. 7

Failure mechanisms of strip foundation with centric and eccentric loading for SR > 1 (soft over stiff layer). Case H₁/B = 0.25 and SR = 1.25: a e/B = 0, b e/B = 0.333

Fig. 8

Normalized eccentricity and strength ratio effects on BC factor N_C1,e, soft over stiff layer (SR > 1)

• The equivalent bearing capacity factor N_C1,e decreases, as H₁/B increases for a given SR.

• The factor N_C1,e increases as SR increases, for a given e/B.

• The equivalent factor N_C1,e decreases with increasing e/B for a specific SR. This trend is attributed to the shrinking up of the failure mechanism, so the upper, weaker layer dominates the bearing capacity. As the strength ratio decreases, the rate of variation of N_C1,e also decreases, while the BC factor is almost constant in case of homogeneous clay (SR = 1).

The effect of SR on N_C1,e for various normalized eccentricities is illustrated in Fig. 9. As the ratio SR increases the factor N_C1,e approaches the maximum N_C1,e, corresponding to a critical ratio (SR)_cr. For SR > (SR)_cr, the BC factor remains constant (N_C1,e = max N_C1,e), since the failure mechanism is restricted to the upper layer. The critical value of (SR)_cr, where N_C1,e reaches the maximum values is higher for the lower values H₁/B and lower eccentricities e/B, as well. For the high value e/B = 1/3, it seems that the second, stronger layer has no beneficial effect on the bearing capacity, since the factor N_C1,e is almost independent of the strength ratios SR. Moreover, the ratio V_u,e/V_u,o decreases with increasing of eccentricity and the rate of the variation increases for the higher values of the strength ratio, in contrast with the trends discussed for SR < 1.

Fig. 9

Influence of the strength ratio, SR on the factor N_C,1e for various eccentricities (stiff over soft layer)

3.3 Combined M, V Bearing Capacity Envelopes for Strip Footing

It is well known, that in the general case of (M, V, H,) loading of footing in homogeneous soil, the locus of all combinations of moment, vertical and horizontal loads, which combined leads to shear failure, forms a three-dimensional bearing strength surface (BSS). These surfaces reduce to bearing capacity lines in M, V space. Such lines have been extensively developed by Butterfield and his collaborators (i.e. Butterfield and Tikof 1979; Butterfield and Gottardi 1994), as well as by many others (Georgiadis 1985; Houlsby and Puzrin 1999; Pender 2017). For two-layered clay and H = 0 the failure loci form a curve on the M, V plane, which can be defined in terms of the normalized ultimate vertical loads and moments, as:

$${\text{v }} = \frac{{{\text{V}}_{{{\text{u,e}}}} }}{{{\text{V}}_{{{\text{u,o}}}} }},\quad {\text{m }} = \frac{{{\text{M}}_{{\text{u}}} }}{{{\text{V}}_{{{\text{u,o}}}} \cdot {\text{B}}}}$$

(5)

According to Eq. (4), v = $\frac{{{\text{N}}_{{{\text{C}}1,{\text{e}}}} }}{{{\text{N}}_{{{\text{C}}1}} }}$ (1 − 2 $\frac{{\text{e}}}{{\text{B}}}$) and since M_u = V_u,e e or m = v $\frac{{\text{e}}}{{\text{B}}}$, the following relationship can be written:

$${\text{m }} = \frac{1}{2}{\text{v }}\left( { 1- {\text{v}}\frac{{{\text{N}}_{{{\text{C}}1}} }}{{{\text{N}}_{{{\text{C}}1,{\text{e}}}} }}} \right)$$

(6)

For homogeneous soil, the adoption of the equivalent width, B′ = Β − 2e was verified by the FE analyses, since N_C1,e ≈ N_C1. In this case (SR = 1) Eq. (6) is simplified to a parabolic relationship with maximum m = 0.125 for v = 0.5. For a two-layered clay and SR < 1 (stiff over soft clay), N_C1,e > N_C1, thus for any value v the corresponding m according to Eq. (6) is higher than for SR = 1. On the contrary, when SR > 1 (soft over stiff clay), the factor N_C1,e is lower than N_C1, so for a given v Eq. (6) results in lower value m in comparison with the case SR = 1. Consequently, the parabola for SR = 1 comes in-between the curves v–m corresponding to SR < 1 and SR > 1. As a result, the maximum normalized ultimate moment, for SR < 1 is max m > 0.125 (corresponding to homogeneous clay), while for SR > 1, max m < 0.125. These trends are illustrated in the interaction diagrams of Fig. 10 for SR = 0.20 and 5, i.e. five times lower or higher than SR = 1. Especially, for SR = 0.20, it is verified that max m is much higher than 0.125, since the ratio N_C1/N_C1,e is quite lower than unity. From the comparison of diagrams (Fig. 10), it is clear that the divergences of the curves SR = 1 and SR = 5 are more visible for the lower normalized thickness, H₁/B = 0.25. Evidently, in case of H₁/B = 0.50, for increasing eccentricity e/B, the upper layer has predominant effect, so the deviations of the curves v–m for SR = 1 and 5 are negligible.

Fig. 10

V–M Failure envelopes (interaction diagrams) for strip foundation on two-layered clay

4 Square Footings Subjected to Combined (M, V) Loading

4.1 Stiff Over Soft Clay Layer (SR < 1)

For centric loads and homogeneous clay (SR = 1), the conventional bearing capacity factor for square foundations is ${\text{N}}^{*}_{\text{C}}$ = s_c N_C, where N_C ≈ (2 + π), while the shape factor s_c ≈ 1.2, as adopted from well-known analytical methods and also verified by 3D FE analyses. In case of inhomogeneous two-layered clay, ${\text{N}}^{*}_{\text{C1}}$ = s_c N_C1, where N_C1 is the corresponding equivalent BC factor for strip foundation and the factor s_c now incorporates both the shape and inhomogeneity effects, through the ratios H₁/B and SR. Therefore, the shape factor is not constant if SR < 1, but according to current results increases when the strength ratio decreases, reaching values as high as s_c = 2.0 for low SR. It is also clear from the analyses that in case of square footing on two-layered clay with SR < 1, the failure mechanisms present similarities with those of strips (types I, II and III). However, for square footings, these mechanisms are shallower, i.e. they extend down to lower depths, thus the unfavourable effects of the lower weaker clay on the bearing capacity decrease. Consequently, the influence of the shape through the factor s_c becomes more significant.

In case of combined M, V loading, the increase of normalized eccentricity e/B results into moving up of the failure mechanism. Figure 11, referring to a low value SR = 0.133, shows how the failure mechanism moves up for increasing eccentricity. The failure surfaces of the three cases of Fig. 11 are indicated by the total displacements, illustrated in shadings, along the vertical plane of symmetry of the square foundation. Note that all three mechanisms of Fig. 11 for the square footing are quite different than corresponding mechanisms for the strip footing of Fig. 3.

Fig. 11

Failure mechanisms of a square footing for H₁/B = 0.25 and SR = 0.133, cases a e/B = 0, b e/B = 0.20 and c e/B = 0.40

For centric loads, a punching failure (type III) is clearly developed, while the failure surface for e/B = 0.20 and 0.40 seems to be restricted below a part of the base. The effective width, B′, decreases the ultimate vertical load, according to Eq. (3b), but on the other hand, it has favourable effect on the BC factor ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}}$, rather through the ratio H₁/B′ than H₁/B.

The effect of normalized eccentricity on the BC factor ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}}$, is presented in Fig. 12. The trends are similar to those for the strip footing. The eccentricity influences the normalized ultimate vertical load, V_u,e, according to the following Eq. (7):

$$\frac{{{\text{V}}_{{{\text{u,e}}}} }}{{{\text{V}}_{{{\text{u,o}}}} }} = \frac{{{\text{N}}_{{{\text{C1,e}}}}^{*} }}{{{\text{N}}_{{{\text{C1}}}}^{*} }}\left( {1 - 2\frac{{\text{e}}}{{\text{B}}}} \right)$$

(7)

where V_u,o the ultimate centric load and ${\text{N}}^{*}_{\text{C1}}$ the corresponding equivalent BC factor for this special case e/B = 0. Although the decrease of the ultimate load V_u,e for increasing eccentricities, is significant, in any case, due to the term 1 − (2e/B), the unfavourable effect of e/B on the bearing capacity for SR < 1 is quite lower than in the case of homogeneous clay, since ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}} > {\text{ N}}^{*}_{\text{C1}}$, as indicated in Fig. 13. For very high eccentricities e/B > 1/3, the normalized ultimate load drops to low values, approaching these for homogeneous clay.

Fig. 12

Square footing, BC factor ${\text{N}}^{\text{ * }}_{{{\text{C1}},{\text{e}}}}$ as function of the normalized eccentricity

Fig. 13

Effect of the normalized eccentricity on the normalized ultimate load

4.2 Soft Over Stiff Clay Layer (SR > 1)

In this case (strength ratio SR > 1) the square footing subjected to centric load, fails with mechanisms similar to those ascertained for strip foundations (type IV and V), which are generally extended to even lower depths.

The combined M, V loading results in modifications of these types of failure, which are characterized by a trend of shrinking. The case of strength ratio slightly higher than unity (SR = 1.25) is presented in Fig. 14, for H₁/B = 0.25. The failure mechanism for centric load, which is illustrated by the total displacements (case a), is extended into the second clay layer and the cross-section of the failure surface by a vertical plane of symmetry, is similar to Prandtl’s. On the contrary, for the high normalized eccentricity e/B = 1/3, the failure mechanism is clearly restricted to the upper layer. Results are presented in Fig. 15 for two values of normalized thickness of the upper layer (H₁/B = 0.15 and 0.25). The BC factor ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}}$ (according to Eq. 3b and L = B) for a given normalized eccentricity increases with increasing SR, but the higher values of this factor correspond to a centric load. For a given value SR the factor ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}}$ decreases when the eccentricity decreases, as it was expected, because for higher e/B values, the failure mechanism moves up, thus the strength of the upper, weaker layer has the main effect on the ultimate load V_u,e. The BC factor reaches the maximum values (max ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}}$) earlier in case of lower strength ratios than those for central loading. This observation is more noticeable for the relatively higher values H₁/B. In case of H₁/B = 0.25 and e/B = 0.333 (Fig. 15b), the bearing capacity factor ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}}$ is almost constant, irrespectively of the strength ratio, so it seems that the lower strong layer has no influence on the ultimate load.

Fig. 14

Square footing, failure mechanisms in case of H₁/B = 0.25 and SR = 1.25: a e/B = 0, b e/B = 0.333

Fig. 15

Square foundation, influence of the strength ratio on the BC factor ${\text{N}}^{\text{ * }}_{{{\text{C1}},{\text{e}}}}$ for various eccentricity cases

The effect of the normalized thickness H₁/B on max ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}}$ values is an important issue. The beneficial effect of the second layer on the bearing capacity (SR > 1) can be demonstrated through the modification coefficient $\uplambda^{*}_{\text{N}} = {\text{N}}^{*}_{\text{C1}} / {\text{N}}^{*}_{\text{C}} \left( {{\text{or N}}^{*}_{\text{C1,e}} / {\text{N}}^{*}_{\text{C,e}} } \right)$. Figure 16 presents the normalized values max $\uplambda^{*}_{\text{N}} = {\text{ max N}}^{*}_{\text{C1,e}} /{\text{N}}^{*}_{\text{C,e}}$, where ${\text{N}}^{*}_{\text{C,e}}$ is the BC factor for homogeneous soil (SR = 1), which is almost equal to the factor for centric loads (${\text{N}}^{*}_{{{\text{C}},{\text{e}}}} \approx {\text{ N}}^{*}_{\text{C}} \approx { 6}. 2$). The modification coefficient indicates how the low values of the normalized thickness of the upper layer H₁/B result into higher BC factors, max ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}}$. For centric loads and the quite low value H₁/B = 0.10, the maximum value of ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}}$ is about 40–45% higher than the corresponding one for homogeneous soil. For eccentric loadings, the values of max $\uplambda^{*}_{\text{N}}$ are quite lower, reaching the unity for H₁/B < 0.5. It could be concluded that for relatively high eccentricities, the generally favourable effect on the BC of the second stronger layer seems almost negligible, even in cases of low thickness of the upper layer. The comparison of values max $\uplambda^{*}_{\text{N}}$ or max λ_Ν for various H₁/B, in case of centrally loaded square, circle and strip footings is illustrated in Fig. 17. These maximum modification coefficients correspond to failure surfaces restricted to the upper, weaker layer. For homogeneous clay, the failure mechanism of the strip is extended deeper, thus the restriction of the failure surface for SR > 1 and a given thickness H₁/B results in higher maxλ_N values. Consequently, the beneficial effect of the second layer for strip footing is more important in comparison with the square or circle.

Fig. 16

Square footing, SR > 1: Relation between H₁/B and max $\uplambda^{*}_{\text{N}}$ for various normalized eccentricities

Fig. 17

Comparison of maximum modification coefficients for centrally loading footings

4.3 Interaction Diagrams for Square Footings

According to Eq. (7) and following the procedure for strip footings, the failure loci form the curve defined by the Eq. (8):

$${\text{m }} = {\text{v }}\left( { 1 { } - {\text{ v}}\frac{1}{2}\frac{{{\text{N}}_{{{\text{C}}1}}^{\text{ * }} }}{{{\text{N}}_{{{\text{C}}1,{\text{e}}}}^{\text{ * }} }}} \right)$$

(8)

The trends are also similar to those for strip footings, therefore it is expected that the curve for SR = 1 comes in-between the v–m relationships for SR < 1 and SR > 1, as it’s illustrated in Fig. 18. The cases of SR five times lower or higher than SR = 1 are presented, for the same values of normalized thickness, as in the corresponding Fig. 10. From the comparison of interaction diagrams for strips or square footings, it can be observed that for SR = 0.2, the values maximum m are lower for the latter case. The divergences between the curves SR = 1 and 5 are smaller in case of square footings, while for H₁/B = 0.5 the interaction diagrams are almost identical, since for a wide range of eccentricities, only the upper layer affects the bearing capacity, in this case.

Fig. 18

V–M Failure envelopes (interaction diagrams) for square foundation on two-layered clay

5 Comments on the General (M, V, H) Loading

The typical (M, V, H) case and the three-dimensional bearing strength surface (BSS), which is forming from all the critical combinations of loadings on shallow footings even for homogeneous clay, is by itself a quite complicated problem (i.e. Pender 2017). The paper in hand studies the problem on the M, V plane (H = 0), for practical reasons, in order to examine separately the effects of eccentricity, on the vertical ultimate load.

In the general case, the failure mechanism for two-layered clay moves up due to the eccentricity and the horizontal component of the loading, as well. Consequently, the unfavourable effects of the second layer in case of SR < 1 decrease and the effects on the V_u,e due to the eccentricity are less important in comparison with the homogeneous clay. The indicative Fig. 19 illustrates the effects of inclination tanθ = H/V = H_u/V_u,e of the resultant load, on the interaction diagrams (v–m) in the simple case of strip. For the homogeneous clay, the effects of horizontal force H are considerable. On the contrary, for SR = 0.2, these effects seem less important. It is noticeable that even for centric and inclined loading (e = 0), the ratio V_u,e/V_u,o is quite higher in case of SR = 0.2, due to the shrinking up of the failure mechanism into the upper layer (i.e. for tanθ = 0.30, V_u,e/V_u,o = 0.87 and 0.62 for SR = 0.2 and 1 respectively). From Fig. 19, it can be also observed that for any inclination tanθ the maximum normalized value m for SR = 0.2 is much higher than the corresponding maximum m to the homogeneous clay. Therefore, it can be estimated that despite the fact that the base shear in any case, results in decreased V_u,e values, the key conclusions of the paper are still qualitatively valid.

Fig. 19

Interaction diagrams in the general case of (V, M, H) loading on strip: a homogeneous clay, b SR = 0.20, H₁/B = 0.25

6 Conclusions

The undrained ultimate capacity to combined (M, V,) loading is examined following the convenient form of equations, which is based on the effective width Β′ = B − 2e. Due to increasing eccentricity, the failure surface moves up, thus the effects of the second layer (either unfavourable or favourable) gradually become less important. The modified BC factors N_C1,e or ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}}$ (for strip or square) are evaluated separately for the cases SR < 1, SR > 1. The strength ratio (either lower or higher than unity) also results in modification of the interaction diagrams, relating the normalized ultimate values V_u,e and M_u.

• a. The case of stronger crust (SR < 1) is of peculiar interest, since for centric loadings and low SR values, the failure mechanism could be extended deep enough into the lower, weaker clay, even for high normalized thickness (i.e. H₁/B = 1.5–2.0). Following the normalized eccentricity increase, the failure surface moves up and as a result, the BC factors N_C1,e and ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}}$ also increase. This trend could be considerable for low strength ratios and relatively high normalized thickness. From the V_u,e/V_u,o diagrams for both cases of strip or square footings, it is deduced that the unfavourable effect of the lower clay on the ultimate loads decreases as the normalized eccentricity increases. Consequently, it may be concluded that for high eccentricities the predominant factor affecting the bearing capacity is the undrained shear strength of the upper layer.

• b. In case of weaker upper layer (SR > 1), the equivalent bearing capacity factors generally increase with increasing strength ratios, reaching the limit values max N_C1,e and max ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}}$ (strip and square footings). The eccentricity results in shrinking up of the failure mechanism, thus failure seems to be developed entirely within the top layer, especially for high normalized values e/B. The modification factors maximum λ_N or maximum $\uplambda^{*}_{\text{N}}$, which indicate the effect of the lower, stronger clay, drop with increasing the normalized thickness. In any case, for H₁/B > 0.5, it seems from the practical point of view, that the second layer has not any noticeable effect on the ultimate loads. Especially, for square footings, the values maximum $\uplambda^{*}_{\text{N}}$ for eccentricities e/B > 0.15 are quite low, even in cases of very low normalized thickness, so the two-layered system could be considered as uniform clay having the undrained strength of the upper layer.

• c. The shape and maximum values of interaction diagrams of the normalized ultimate vertical loads (v) and moments (m) depend on the ratios N_C1,e/N_C1 or ${\text{N}}^{*}_{{{\text{C1}},{\text{e}}}} /{\text{N}}^{*}_{\text{C1}}$, for strips and square footings. It is concluded that the parabola for SR = 1 comes in-between the failure loci curves for SR < 1 and SR > 1. Generally, the divergences between the curves SR = 1 and SR > 1 are small or almost negligible.